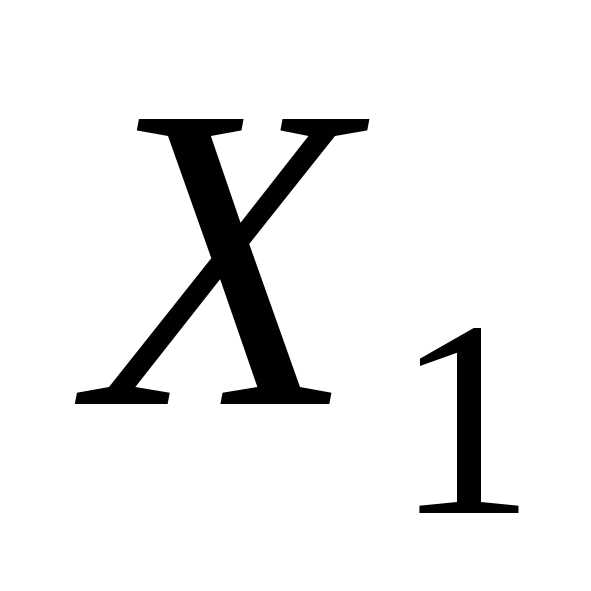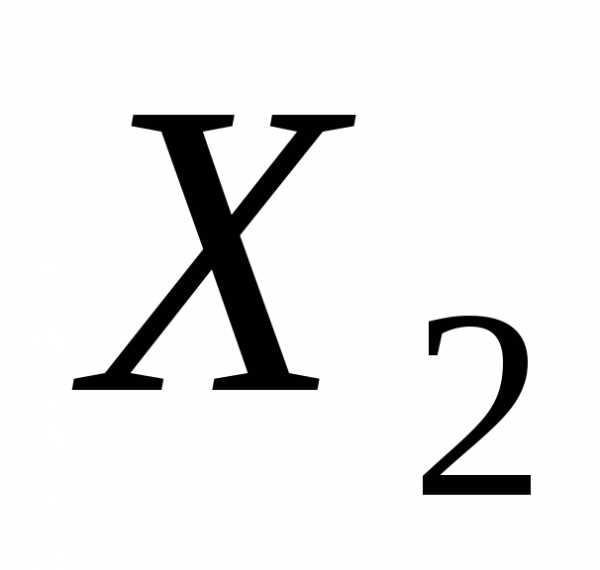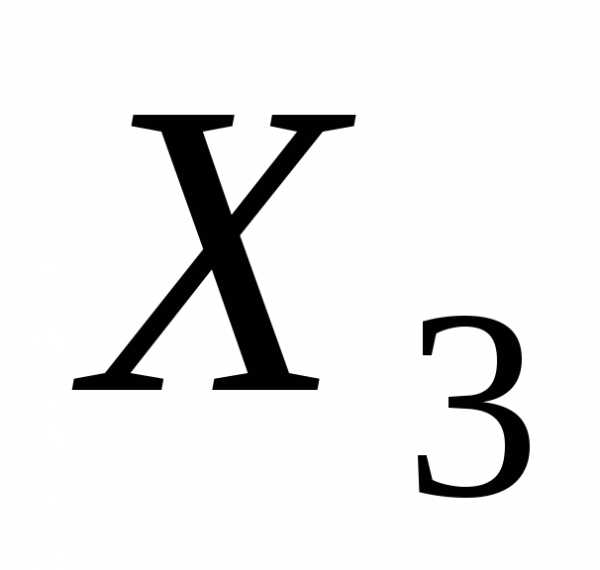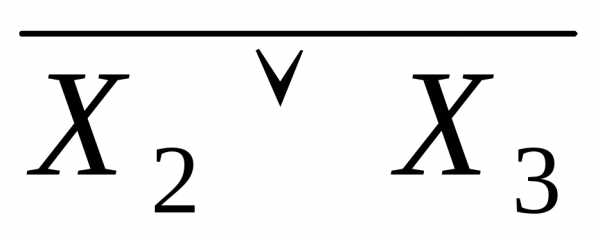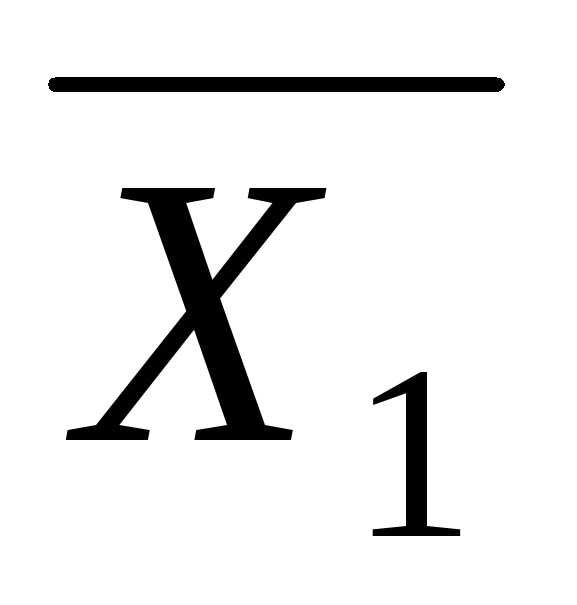Основы алгебры

Содержание

Основы школьной алгебры

На этой странице рассмотрены самые основы школьной математики от обычных чисел до логарифмов и формул сокращенного умножения. Даже человек, далекий от математики должен знать это, если вы не прошли этот материал, то за что-то более сложное даже браться не стоит.

Все лекции читает доцент Сентяков Владимир Александрович.

Арифметические операции. Числовые множества.
В этом видео-уроки вы узнаете основные виды числовых множеств и их различия. Поданы свойства арифметических операций и их особенности, не только для обычных чисел, но и для дробей. Также подано много конкретных примеров с подробно разобранным решением.
Жмите, что бы скачать видео – урок!
Модуль действительного числа
В начале разобрано определение модуля действительного числа с формулой. Также пошагово рассмотрены решения упражнений с корнем квадратным или модулем, как при этом надо использовать выше упомянутое определение.
Жмите, что бы скачать видео – урок!
Свойства степени.
В видео курсе поданы формулы, которые надо знать и использовать на практике, они, например, здорово упростят нахождение корня показательного уравнения. Ещё лектор показываете удачно подобранные примеры для решения, которых используются выше упомянутые формулы.
Жмите, что бы скачать видео – урок!
Логарифм числа.
Как продолжение предыдущей темы рассматривается логарифм со всеми основными формула и свойствами, которые применяются очень часто. Ну и как всегда, в конце лектор комментирует подробное нахождение ответа задачи по данной теме.
Жмите, что бы скачать видео – урок!
Формулы сокращенного умножения.
Они очень часто используются, например, для упрощения алгебраических выражений, нахождения корней разных уравнений и т.д. Здесь вы увидите хорошие упражнения, в которых очень удачно используются такие формулы, как квадрат суммы, квадрат разности, разность квадратов и практически тоже самое для куба, с подробным комментированием каждого шага.

Жмите, что бы скачать видео – урок!

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com

ОСНОВЫ АЛГЕБРЫ. 100 великих научных открытий

ОСНОВЫ АЛГЕБРЫ

Новый подъем античной математики в III веке нашей эры связан с творчеством великого математика Диофанта. Его основной труд — «Арифметика». К сожалению, лишь шесть книг из тринадцати книг дошли до нашего времени. Диофант сумел возродить и развить числовую алгебру вавилонян, освободив ее от геометрических построений, которыми пользовались греки. У Диофанта впервые появляется буквенная символика. Он ввел обозначения: неизвестной, квадрата, куба, четвертой, пятой и шестой степеней, а также первых шести отрицательных степеней. В «Истории математики» это отмечено особо: «Книга Диофанта свидетельствует о наличии у него буквенной символики. Значение этого шага огромно. Только на такой основе могло быть создано буквенное исчисление, развит формульный аппарат, позволяющий часть наших мыслительных операций заменить механическими преобразованиями. Однако Диофант, видимо, не нашел в этом деле последователей ни в его эпоху, ни много позднее. Лишь с конца XV века в Европе началась интенсивная разработка алгебраической символики, а завершение создания буквенного исчисления произошло только в конце XVI — начале XVII века в трудах Виета и Декарта».

«Диофант — пишет В.А. Никифоровский, — сформулировал правила алгебраических операций со степенями неизвестной, соответствующие нашим умножению и делению степеней с натуральными показателями, и правила знаков приумножении. Это дало возможность компактно записывать многочлены, производить умножение их, оперировать с уравнениями. Он указал также правила переноса отрицательных членов уравнения в другую часть его с обратными знаками, взаимного уничтожения одинаковых членов в обеих частях уравнения».

Начиная с V века центр математической культуры постепенно перемещается на восток — к индусам и арабам. Математика индусов была числовой. Она отмечена стремлением достичь строгости эллинов в доказательствах и обосновании геометрии, довольствуясь чертежами. Основные достижения индусов состоят в том, что они ввели в обращение цифры, называемые нами арабскими, и позиционную систему записи чисел, обнаружили двойственность корней квадратного уравнения, двузначность квадратного корня и ввели отрицательные числа. Первое известное нам применение десятичной позиционной системы относится к 595 году — сохранилась плита, на которой число лет 346 записано в такой системе.

Наиболее известными математиками Индии были Ариабхата (прозванный «первым», около 500 г.) и Брахмагупта (около 625 г.). Индусы рассматривали числа безотносительно к геометрии. Они распространили правила действия над рациональными числами на числа иррациональные, производя над ними непосредственные выкладки.

Еще одно достижение индусов в совершенствовании алгебраической символики состоит в том, что они ввели обозначения нескольких различных неизвестных и их степеней. Как у Диофанта, они были по сути дела сокращениями слов.

Вслед за индийскими математиками пользоваться правилом положения стали математики Ближнего и Среднего Востока. Особую роль в истории развития алгебры в первой половине IX века сыграл трактат аль-Хорезми на арабском языке под названием «Книга о восстановлении и противопоставлении» (на арабском языке — «Китаб аль-джебр валь-мукабала»). Позднее при переводе на латинский язык арабское название трактата было сохранено. С течением времени «аль-джебр» сократили до «алгебры».

В трактате решение уравнений рассматривается уже не в связи с арифметикой, а как самостоятельный раздел математики. Арабский математик показывает, что в алгебре применяются неизвестные, их квадраты и свободные члены уравнений. Аль-Хорезми назвал неизвестное «корнем». При решении различных видов уравнений аль-Хорезми предлагает переносить отрицательные члены уравнений из одной части в другую, называя это восстановлением. Вычитание равных членов из обеих частей уравнения при этом он называет противопоставление (валь мукабала).

«В своем трактате аль-Хорезми, — отмечает Александр Свечников, — рассматривает неизвестное число как величину особого рода, вводит термин корень, свободный член называет дирхем (так в то время называли и денежную единицу). Он распределяет уравнения по видам, разъясняет, как применять правила восполнения и противопоставления, формулирует правила решения уравнений различных видов.

В рукописях аль-Хорезми все математические выражения и все выкладки записаны словами, вот почему алгебру того времени и более поздних времен называли риторической, т. е. словесной. В период работы над алгебраическим трактатом аль-Хорезми уже знал о числовой алгебре Вавилона и других стран Востока. Он был знаком с геометрической алгеброй греков и достижениями индийских астрономов и математиков.

Аль-Хорезми выделил алгебраический материал в особый раздел математики и освободил его от геометрического толкования, хотя в некоторых случаях пользовался геометрическими доказательствами. Алгебраический труд аль-Хорезми стал образцом, который изучали и которому подражали многие математики более позднего времени. Последующие алгебраические сочинения и учебники по своему характеру стали приближаться к современным. Алгебраический трактат аль-Хорезми послужил началом создания науки алгебры. Он был в числе первых сочинений по математике, переведенных на латинский язык. В то время в Европе все научные труды писали и печатали на латинском языке».

При решении задачи главное — осмысление содержания задачи, способность выразить его на языке алгебры. Проще говоря, записать условие задачи посредством символов — математических знаков.

Диофант, как уже говорилось, дал понятие об алгебраическом уравнении, записанном символами, однако очень далекими от современных. Первым стал обозначать буквами не только неизвестные, но и данные величины Франсуа Виет. Тем самым ему удалось внедрить в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т. е. ввести понятие математической формулы. Этим он внес решающий вклад в создание буквенной алгебры, чем завершил развитие математики эпохи Возрождения и подготовил почву для появления результатов Ферма, Декарта, Ньютона.

Франсуа Виет (1540–1603) родился на юге Франции в небольшом городке Фантене-ле-Конт. Отец Виета был прокурором. По традиции сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери — двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.

В 1671 году Виет перешел на государственную службу, став советником парламента, а затем советником короля Франции Генриха III.

В 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать от имени короля выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.

Находясь на государственной службе, Виет оставался ученым. Он прославился тем, что сумел расшифровать код перехваченной переписки короля Испании с его представителями в Нидерландах, благодаря чему король Франции был полностью в курсе действий своих противников.

В 1584 году по настоянию Гизов Виета отстранили от должности и выслали из Парижа. Именно на этот период приходится пик его творчества. Получив неожиданный досуг, ученый поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи. У него сложилось убеждение в том, «что должна существовать общая, неизвестная еще наука, обнимающая и остроумные измышления новейших алгебраистов, и глубокие геометрические изыскания древних».

Виет изложил программу своих исследований и перечислил трактаты, объединенные общим замыслом и написанные на математическом языке новой буквенной алгебры, в изданном в 1591 году знаменитом «Введение в аналитическое искусство». Перечисление шло в том порядке, в каком эти труды должны были издаваться, чтобы составить единое целое — новое направление в науке. К сожалению, единого целого не получилось. Трактаты публиковались в совершенно случайном порядке, и многие увидели свет только после смерти Виета. Один из трактатов вообще не найден. Однако главный замысел ученого замечательно удался: началось преобразование алгебры в мощное математическое исчисление. Само название «алгебра» Виет в своих трудах заменил словами «аналитическое искусство». Он писал в письме к де Партене: «Все математики знали, что под алгеброй и алмукабалой… скрыты несравненные сокровища, но не умели их найти. Задачи, которые они считали наиболее трудными, совершенно легко решаются десятками с помощью нашего искусства…»

Основы своего подхода Виет называл видовой логистикой. Следуя примеру древних, он четко разграничивал числа, величины и отношения, собрав их в некую систему «видов». В эту систему входили, например, переменные, их корни, квадраты, кубы, квадрато-квадраты и т. д., а также множество скаляров, которым соответствовали реальные размеры — длина, площадь или объем. Для этих видов Виет дал специальную символику, обозначив их прописными буквами латинского алфавита. Для неизвестных величин применялись гласные буквы, для переменных — согласные.

Виет показал, что, оперируя с символами, можно получить результат, который применим к любым соответствующим величинам, т. е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление.

Демонстрируя силу своего метода, ученый привел в своих работах запас формул, которые могли быть использованы для решения конкретных задач. Из знаков действий он использовал «+» и «-», знак радикала и горизонтальную черту для деления. Произведение обозначал словом «in». Виет первым стал применять скобки, которые, правда, у него имели вид не скобок, а черты над многочленом. Но многие знаки, введенные до него, он не использовал. Так, квадрат, куб и т. д. обозначал словами или первыми буквами слов.

Символика Виета позволила и решать конкретные задачи, и находить общие закономерности, полностью обосновывая их. Таким образом, алгебра выделались в самостоятельную ветвь математики, не зависящую от геометрии. «Это нововведение и особенно применение буквенных коэффициентов положило начало коренному перелому в развитии алгебры: только теперь стало возможным алгебраическое исчисление как система формул, как оперативный алгоритм».

Символики Виета придерживался впоследствии Пьер Ферма. Дальнейшее значительное усовершенствование алгебраической символики принадлежит Декарту. Рене Декарт ввел для обозначения коэффициентов строчные буквы латинского алфавита. Для обозначения неизвестных он использовал последние буквы того же алфавита. Это нововведение получило широкое распространение в работах математиков и с небольшими изменениями сохранилось до наших дней.

Поделитесь на страничке

Следующая глава >

info.wikireading.ru

ОСНОВЫ АЛГЕБРЫ это что такое ОСНОВЫ АЛГЕБРЫ: определение — История.НЭС

Считается, что эллины заимствовали первые сведения по алгебре у вавилонян. Греческий философ-неоплатоник Прокл Диадох отмечал в своем сочинении: «Согласно большинству мнений, геометрия была впервые открыта в Египте, имела свое происхождение в измерении площадей». Воздействие традиций вавилонской алгебры на математику Древней Греции и алгебраическую школу стран ислама подчеркивается в «Истории математики». Создание основ математики в том виде, к которому мы привыкли при изучении этой науки в школе, выпало на долю греков и относится к VI–V векам до нашей эры. Античная наука достигла вершины в работах Евклида, Архимеда, Аполлония. Новый подъем античной математики в III веке нашей эры связан с творчеством великого математика Диофанта. Его основной труд — «Арифметика». К сожалению, лишь шесть книг из тринадцати книг дошли до нашего времени. Диофант сумел возродить и развить числовую алгебру вавилонян, освободив ее от геометрических построений, которыми пользовались греки. У Диофанта впервые появляется буквенная символика. Он ввел обозначения: неизвестной, квадрата, куба, четвертой, пятой и шестой степеней, а также первых шести отрицательных степеней. В «Истории математики» это отмечено особо: «Книга Диофанта свидетельствует о наличии у него буквенной символики. Значение этого шага огромно. Только на такой основе могло быть создано буквенное исчисление, развит формульный аппарат, позволяющий часть наших мыслительных операций заменить механическими преобразованиями. Однако Диофант, видимо, не нашел в этом деле последователей ни в его эпоху, ни много позднее. Лишь с конца XV века в Европе началась интенсивная разработка алгебраической символики, а завершение создания буквенного исчисления произошло только в конце XVI — начале XVII века в трудах Виета и Декарта». «Диофант — пишет В.А. Никифоровский, — сформулировал правила алгебраических операций со степенями неизвестной, соответствующие нашим умножению и делению степеней с натуральными показателями, и правила знаков приумножении. Это дало возможность компактно записывать многочлены, производить умножение их, оперировать с уравнениями. Он указал также правила переноса отрицательных членов уравнения в другую часть его с обратными знаками, взаимного уничтожения одинаковых членов в обеих частях уравнения». Начиная с V века центр математической культуры постепенно перемещается на восток — к индусам и арабам. Математика индусов была числовой. Она отмечена стремлением достичь строгости эллинов в доказательствах и обосновании геометрии, довольствуясь чертежами. Основные достижения индусов состоят в том, что они ввели в обращение цифры, называемые нами арабскими, и позиционную систему записи чисел, обнаружили двойственность корней квадратного уравнения, двузначность квадратного корня и ввели отрицательные числа. Первое известное нам применение десятичной позиционной системы относится к 595 году — сохранилась плита, на которой число лет 346 записано в такой системе. Наиболее известными математиками Индии были Ариабхата (прозванный «первым», около 500 г.) и Брахмагупта (около 625 г.). Индусы рассматривали числа безотносительно к геометрии. Они распространили правила действия над рациональными числами на числа иррациональные, производя над ними непосредственные выкладки. Еще одно достижение индусов в совершенствовании алгебраической символики состоит в том, что они ввели обозначения нескольких различных неизвестных и их степеней. Как у Диофанта, они были по сути дела сокращениями слов. Вслед за индийскими математиками пользоваться правилом положения стали математики Ближнего и Среднего Востока. Особую роль в истории развития алгебры в первой половине IX века сыграл трактат аль-Хорезми на арабском языке под названием «Книга о восстановлении и противопоставлении» (на арабском языке — «Китаб аль-джебр валь-мукабала»). Позднее при переводе на латинский язык арабское название трактата было сохранено. С течением времени «аль-джебр» сократили до «алгебры». В трактате решение уравнений рассматривается уже не в связи с арифметикой, а как самостоятельный раздел математики. Арабский математик показывает, что в алгебре применяются неизвестные, их квадраты и свободные члены уравнений. Аль-Хорезми назвал неизвестное «корнем». При решении различных видов уравнений аль-Хорезми предлагает переносить отрицательные члены уравнений из одной части в другую, называя это восстановлением. Вычитание равных членов из обеих частей уравнения при этом он называет противопоставление (валь мукабала). «В своем трактате аль-Хорезми, — отмечает Александр Свечников, — рассматривает неизвестное число как величину особого рода, вводит термин корень, свободный член называет дирхем (так в то время называли и денежную единицу). Он распределяет уравнения по видам, разъясняет, как применять правила восполнения и противопоставления, формулирует правила решения уравнений различных видов. В рукописях аль-Хорезми все математические выражения и все выкладки записаны словами, вот почему алгебру того времени и более поздних времен называли риторической, т. е. словесной. В период работы над алгебраическим трактатом аль-Хорезми уже знал о числовой алгебре Вавилона и других стран Востока. Он был знаком с геометрической алгеброй греков и достижениями индийских астрономов и математиков. Аль-Хорезми выделил алгебраический материал в особый раздел математики и освободил его от геометрического толкования, хотя в некоторых случаях пользовался геометрическими доказательствами. Алгебраический труд аль-Хорезми стал образцом, который изучали и которому подражали многие математики более позднего времени. Последующие

interpretive.ru

Математические основы курсов алгебры и геометрии

Как известно, обучение математике в основной школе происходит, согласно учебному плану, в рамках двух учебных предметов «Алгебра» и «Геометрия», а неоднократные попытки, делавшиеся в мировой школе, создать единый курс математики, опиравшиеся на единство математической науки, не имели успеха — следование принципам структурирования науки натолкнулось на существенные объективные противоречия между наукой и обучением основам науки, между математикой и педагогикой и дидактикой математики. Этот негативный опыт попыток интеграции, создания в основной школе единого предмета «Математика» является в определенном смысле обоснованием для сохранения классического учебного плана.

Существование разделов «Алгебра» и «Геометрия» в математической науке связано с их разной ролью в отношении объекта математики: если геометрия изучает «пространственные формы», то предмет алгебры — это «количественные отношения». При этом, разумеется, эти параметры понимаются в науке обобщенно, далеко от их «бытового», достаточно примитивного понимания в пору, когда они были определены Ф.Энгельсом как основополагающие для математики в соответствии с состоянием математической науки в то время, а современное их понимание дает вполне точное представление и о современной математике, и эту точку зрения разделял А.Н.Колмогоров. Геометрия в настоящее время рассматривается как часть раздела математики «Топология» и, как считал соратник Колмогорова П.С.Александров, эти две области математического знания являются столпами всей математической науки.

Для школьного математического образования главным являются вытекающие из общенаучных соображений представления, что задача алгебры — создание некоторого аппарата преобразований для использования в любой математической области, и именно это является ее предметом, но не объектом, тогда как задача геометрии — это изучение пространств, она имеет свой объект изучения. Разумеется, алгебра всегда обретает и объект изучения — как только встает задача создания аппарата для конкретной области науки, в первую очередь, математики. Поэтому, в частности, можно вести речь не только о теории групп, теории колец и полей, но и — в школьной математике — «алгебре дробей», «алгебре многочленов», «алгебре степеней», «алгебре логарифмов» и «алгебре тригонометрии» как совершенно различных алгебрах, основанных на абсолютно непохожих аксиомах преобразований.

Главной особенностью нынешнего традиционного курса алгебры является его исключительно конгломератный характер: в этот курс входит, по существу, все то, что совершенно не относится к геометрии, имеющей, как сказано выше, определенный и очевидный объект. В этом смысле два школьных учебных предмета могли бы называться «Математика» и «Геометрия», если бы такое именование не создавало впечатления, что геометрия не является частью математики. Первый из названных предметов мог бы, впрочем, называться «Общей математикой» — в этом аспекте геометрия была бы действительно одной из «частных» математик, как, впрочем, и «Начала анализа» и «Элементы теории вероятностей и математической статистики».

Решение этих проблем и даже простая их постановка и обсуждение, однако, не является в настоящее время для российской школы актуальным, и в соответствии с принципом разумного консерватизма классическое разделение обучения математике на соответствующие учебные предметы было сохранено — в обучении дидактические принципы имеют, на наш взгляд, безусловный приоритет перед общими принципами «науковедения».

Ну, а чтобы быстро и правильно разобраться с самыми сложными домашными заданиями можно посмотреть гдз готовые домашние задания решебники онлайн на сайте gdz4you.com.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com

Вопрос 3. Основы алгебры высказываний

Алгебра высказываний — базовый раздел математической логики. Ее изучение является непременным условием успешного освоения теоретической информатики. Математическая логика изучает высказывания или утверждения, а также способы доказательств их истинности или ложности. В математической логике составные высказывания состоят из элементарных высказываний, предикатов, логических операций и кванторов существования и всеобщности. При изучении дисциплины «Информатика» рассматривается только один раздел математической логики — алгебра высказываний.

Объектами обычной (школьной) алгебры являются числа, а основными операциями — сложение и умножение. Объектами алгебры высказываний являются элементарные (неразложимые) высказывания, а операциями — логические связки И, ИЛИ, НЕ.

Важность изучения алгебры высказываний в курсе «Информатика» не вызывает сомнения. Например, поиск информации в наиболее распространенных в экономике реляционных базах данных в основном производится формированием запроса в виде составных высказываний, элементами которых являются характеристики полей записей. Кроме того, высказывания используются при построении алгоритмов, содержащих ветвящиеся процессы.

Элементарные высказывания обычно обозначаются большими буквами латинского алфавита А, В, С, D, … В алгебре высказываний содержательный смысл высказываний не рассматривается; высказывания делятся на истинные и ложные.

Смысл операций И, ИЛИ и НЕ алгебры высказываний общепринят.

Высказывание А И В истинно тогда и только тогда, когда Одновременно истинны высказывания А и В.

Высказывание А ИЛИ В ложно тогда и только тогда, когда одновременно ложны высказывания А к В.

Высказывание НЕ А истинно тогда и только тогда, когда южно высказывание А.

Операцию И называют конъюнкцией (или операцией логического умножения) и обозначают символами &, /\ или отсутствием символа.

Операцию ИЛИ называют дизъюнкцией (или операцией логического сложения) и обозначают символами V или +

Операцию НЁ называют отрицанием (или инверсией) и обозначают чертой над высказыванием.

В дальнейшем для обозначения операций И, ИЛИ и НЕ будут использованы символы /\ и V и черта над высказыванием.

В математической логике применяются также операции импликация и эквиваленции. Для обозначения операций импликация и эквиваленция используют символы 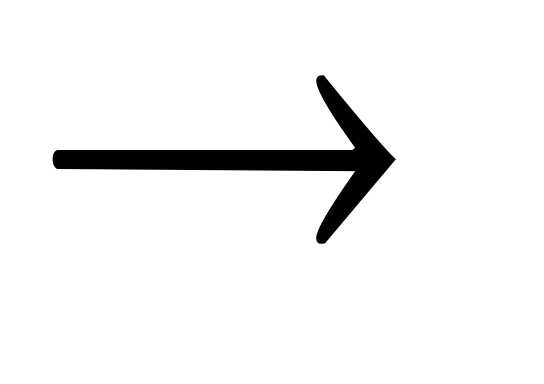и ~ соответственно.

Высказывание А 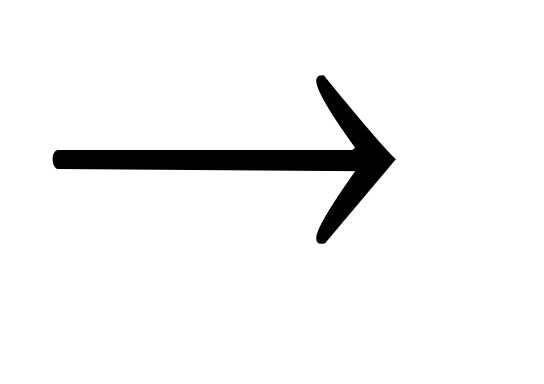B ложно тогда и только тогда, когда высказывание А истинно, а высказывание В ложно.

Высказывание А ~ В истинно тогда и только тогда, когда оба высказывайся А и В истинны или когда оба высказывания А и В ложны.

Из элементарных высказываний, применяя операции булевой алгебры, можно начать составные высказывания любой сложности.

Например: и т.д.

Истинность или ложность конкретного составного высказывания зависит от истинности или ложности входящих в него элементарных высказываний. Так возникает понятие логической функции. При рассмотрении логических функций вводят понятие логической переменной – элементарного высказывания, которое может быть истинным или ложным. Логическая переменная, соответствующая истинном (ложному) высказыванию, равна 1 (равна 0).

Логическую функщ₁₁₀ (функцию алгебры логики), как и функцию в математическом анализе, можно задать в виде формулы или в виде таблицы-

Формула алгебры высказываний определяется следующим образом.

Элементарное высказывание является формулой алгебры высказываний.

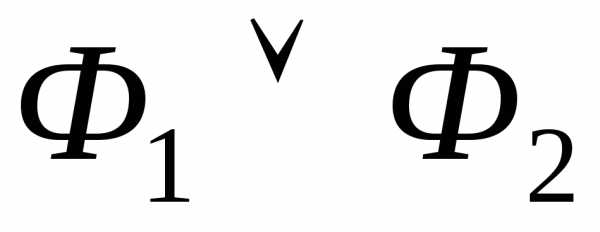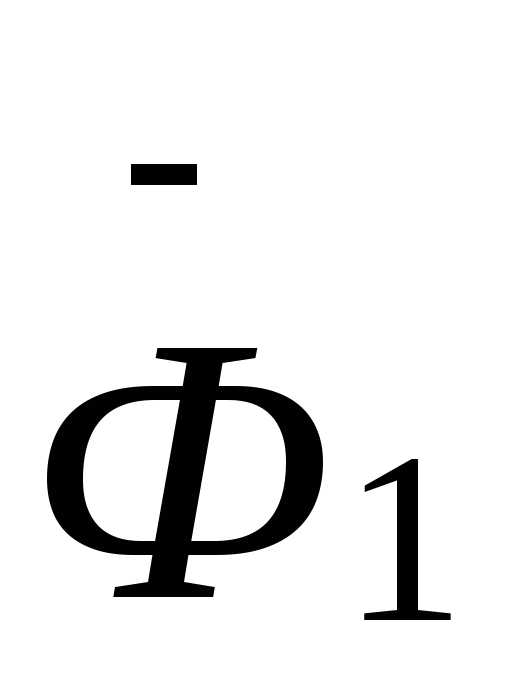Если Ф₁ и Ф₂ — формулы алгебры высказываний, то (), () иявляются формулами алгебры высказываний.

Пример формул алгебры высказываний от трех логических переменных.X₁, X₂ и X_3:

Отметим, что при написании формул алгебры высказываний действуют обычные правила приоритета операций при расстановке скобок.

Табличное задание функции алгебры логики называется ее таблицей истинности. В таблице истинности наборы значений логических переменных обычно располагают в порядке возрастания соответствующих этим наборам двоичных чисел (рис. 1).

X₁	X₂	X₃	F
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

Рис. 1. Пример таблицы истинности булевой функции F от трех логических переменных X₁, Х₂ и Х₃

Отметим, что таблица истинности булевой функции от п переменных состоит из 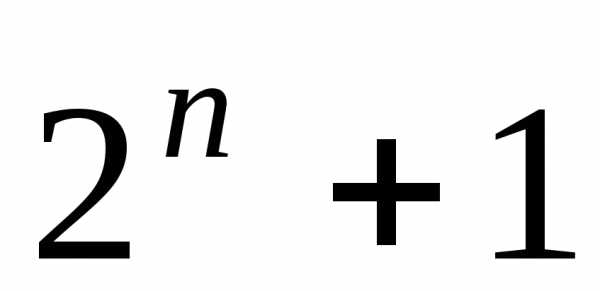строк ип + 1 столбцов. Напомним, что число двоичных наборов длины п равно 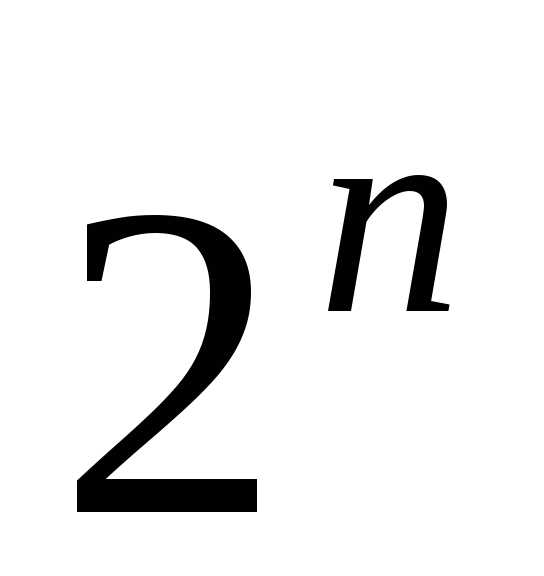. Таким образом, формирование таблицы истинностиконкретной булевой функции от n переменных сводится к заполнению нулями и единицами 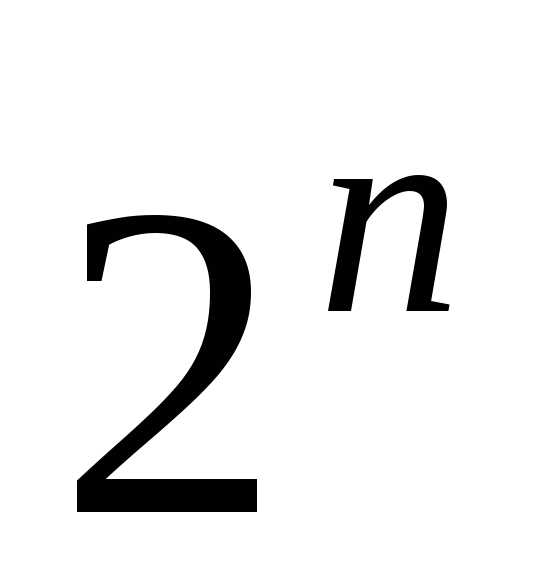компонент ее последнего столбца.

Рассмотрим построение таблицы истинности булевой функции, заданной формулой алгебры высказываний.

Существуют два подхода к решению этой задачи.

В первом подходе при вычислении значения функции на наборе течений переменных эти значения подставляют в формулу и, используя определение логических операций, находят значение формулы на этом наборе.

Например, значение формулы при (на наборе (0,1,0)) равно 1.

При использовании второго подхода формулу последовательно раскладывают па более простые подформулы и последовательно (в обратном порядке) строят таблицы истинности этих подформул.

Например, при построении таблицы истинности булевой функции, заданной формулой F(X₁, Х₂, X₃) = рассматривают подформулы Х₂ v Х₃,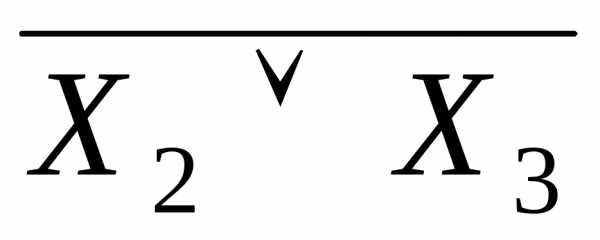,,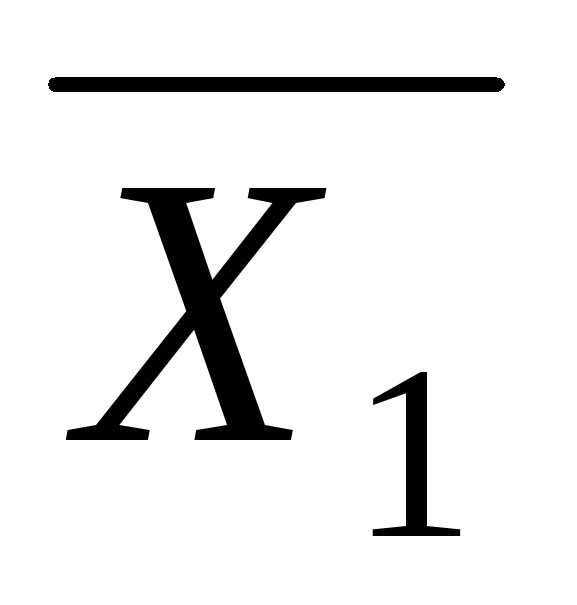 (рис. 2).

							F
0	0	0	0	1	1	1	0
0	0	1	1	0	1	1	0
0	1	0	1	0	1	1	0
0	1	1	1	0	1	1	0
1	0	0	0	1	0	1	0
1	0	1	1	0	0	0	1
1	1	0	1	0	0	0	1
1	1	1	1	0	0	0	1

Рис. 2. Таблица истинности булевой функции,

заданной формулой F(X_1,X_2,X₃)

Рассмотрим теперь обратную задачу: по таблице истинности булевой функции следует написать формулу алгебры высказываний.

Введем определение некоторых формул специального вида.

Элементарной конъюнкцией называется логическое произведение переменных или их отрицаний, в котором переменная может входить не более одного раза. Число переменных или их отрицаний в элементарной конъюнкции называют ее длиной. Отметим, что длина элементарной конъюнкции может быть равна единице.

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Число элементарных конъюнкций в ДНФ может быть равно единице.

Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой все элементарные конъюнкции имеют длину, равную числу переменных.

Примеры:

1. Формула является ДНФ.

2. Формула не является СДНФ.

3. Формулы 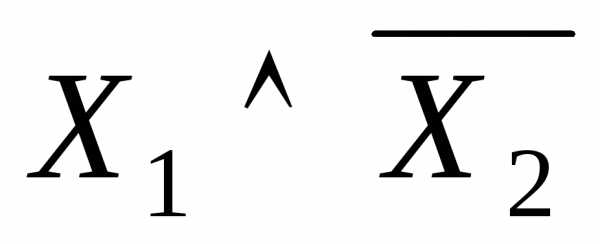иявляются СДНФ булевых функций от переменныхХ₁ и X₂

Отметим свойство элементарной конъюнкции, имеющей длину, равную числу переменных. Она обращается в 1 ровно на одном наборе значений переменных. Таким образом, каждому набору течений переменных соответствует ровно одна такая элементарная конъюнкция.

Например, набору (0,1,0) соответствует конъюнкция . На этом свойстве основан следующий алгоритм нахождения формулы алгебры высказываний — булевой функции.

Для каждого набора, на котором булева функция F нравна 1, находим элементарную конъюнкцию, равную числу переменных длины, которая обращается в 1 на этом наборе. Дизъюнкция этих конъюнкций является формулой алгебры высказываний булевой функции F.

Булева функция, равная 0 (равная 1) на всех наборах значений её переменных, называется: тождественно ложной (тождественно истинной). Тождественно ложную (тождественно истинную) булеву функцию будем обозначать через 0 (через 1).

Отметим, что описанный выше алгоритм не дает результата в случае тождественно ложных булевых функций. Но для таких функций формулой алгебры высказываний является, например, формула .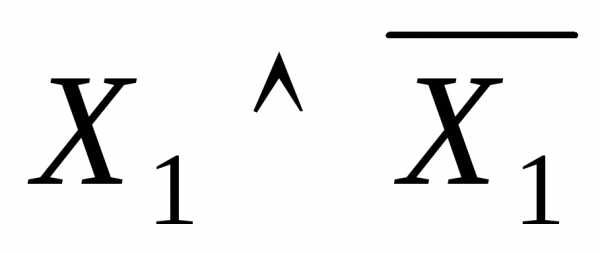

Если подформулу Ф₁ формулы алгебры высказываний Ф заменить равносильной Ф₁ формулой, то полученная формула Ф₂, будет равносильна формуле Ф. Говорят, что формула Ф₂, получена из Ф равносильны преобразованием. Такой подход используется для нахождения равносильной исходной формуле формулы, оптимальной в некотором смысле (например, имеющей наименьшее число вхождений переменных). Для реализации этого подхода разработан набор пар равносильных формул. Приведем примеры таких пар.

AВ и ВА; AА и А; А1 и 1; A 0 и А — свойства дизъюнкции;

В и ВА; АА и А; А1 и А; А0 и 0 — свойства конъюнкции;

А и А — закон отрицания отрицания;

А ВВ и А — закон поглощения;

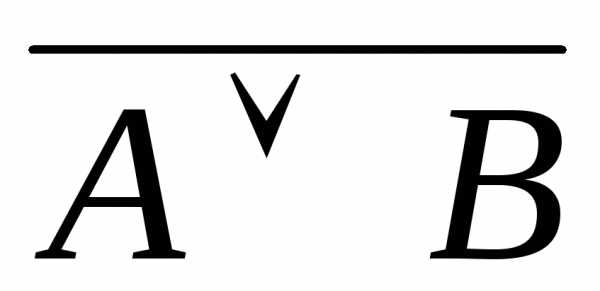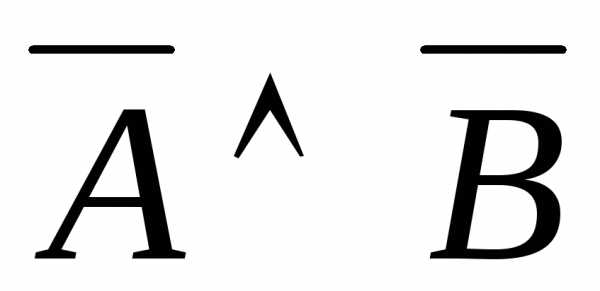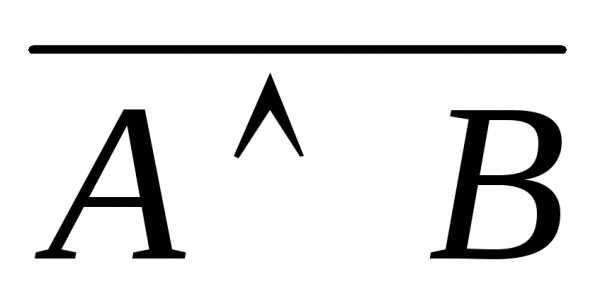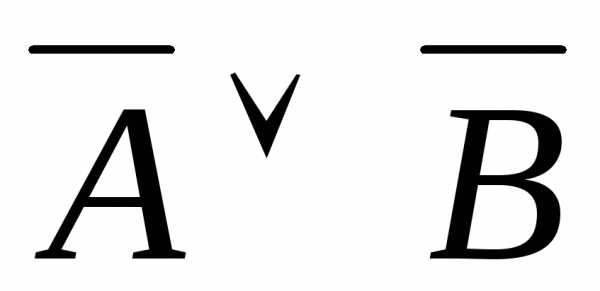= ; = — законы де Моргана.

Проверку равносильных формул Ф₁ и Ф₂ (от одних и тех же переменных) наиболее просто осуществить следующим образом. Для этих формул построить таблицы истинности Т₁ и Т₂. Формулы Ф₁ и Ф₁ равносильны тогда и только тогда, когда таблицы истинности Т. и Т₂ одинаковы. В качестве примера следует проверить равносильность формул А → В и .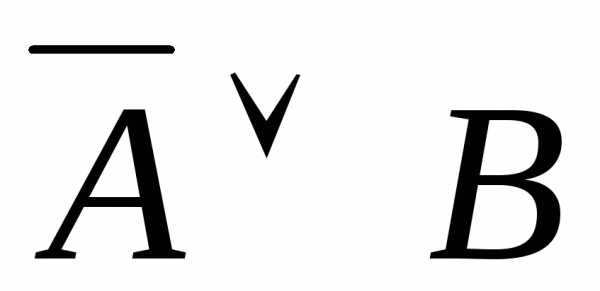

Из формулы , применяя законы де Моргана и закон отрицания отлипания, можно получить равносильную ей формулу .

Отметим, что для любой формулы алгебры высказываний существует равносильная ей формула, в которой операция отрицания применяется только к переменным.

В качестве примера использования алгебры высказываний можно продемонстрировать равносильность высказываний «Неверно, что Иванов не сдал зачет по информатике и не защитил курсовую работу» и «Иванов сдал зачет по информатике или защитил курсовую работу».

<< Возврат на ВОПРОСЫ ТЕМЫ >>

studfiles.net

Основы алгебры

Считается, что эллины заимствовали первые сведения по алгебре у вавилонян. Греческий философ-неоплатоник Прокл Диадох отмечал в своем сочинении: «Согласно большинству мнений, геометрия была впервые открыта в Египте, имела свое происхождение в измерении площадей». Воздействие традиций вавилонской алгебры на математику Древней Греции и алгебраическую школу стран ислама подчеркивается в «Истории математики».

Создание основ математики в том виде, к которому мы привыкли при изучении этой науки в школе, выпало на долю греков и относится к VI-V векам до нашей эры. Античная наука достигла вершины в работах Евклида, Архимеда, Аполлония.

У Диофанта впервые появляется буквенная символика. Он ввел обозначения: неизвестной, квадрата, куба, четвертой, пятой и шестой степеней, а также первых шести отрицательных степеней. В «Истории математики» это отмечено особо: «Книга Диофанта свидетельствует о наличии у него буквенной символики. Значение этого шага огромно. Только на такой основе могло быть создано буквенное исчисление, развит формульный аппарат, позволяющий часть наших мыслительных операций заменить механическими преобразованиями. Однако Диофант, видимо, не нашел в этом деле последователей ни в его эпоху, ни много позднее. Лишь с конца XV века в Европе началась интенсивная разработка алгебраической символики, а завершение создания буквенного исчисления произошло только в конце XVI — начале XVII века в трудах Виета и Декарта».

«Диофант-пишет В.А. Никифоровский, — сформулировал правила алгебраических операций со степенями неизвестной, соответствующие нашим умножению и делению степеней с натуральными показателями, и правила знаков приумножении. Это дало возможность компактно записывать многочлены, производить умножение их, оперировать с уравнениями. Он указал также правила переноса отрицательных членов уравнения в другую часть его с обратными знаками, взаимного уничтожения одинаковых членов в обеих частях уравнения».

Начиная с V века, центр математической культуры постепенно перемещается на восток — к индусам и арабам. Математика индусов была числовой. Она отмечена стремлением достичь строгости эллинов в доказательствах и обосновании геометрии, довольствуясь чертежами.

Основные достижения индусов состоят в том, что они ввели в обращение цифры, называемые нами арабскими, и позиционную систему записи чисел, обнаружили двойственность корней квадратного уравнения, двузначность квадратного корня и ввели отрицательные числа. Первое известное нам применение десятичной позиционной системы относится к 595 году — сохранилась плита, на которой число лет 346 записано в такой системе.

Наиболее известными математиками Индии были Ариабхата (прозванный «первым», около 500г.) и Брахмагупта (около 625г.). Индусы рассматривали числа безотносительно к геометрии. Они распространили правила действия над рациональными числами на числа иррациональные, производя над ними непосредственные выкладки.

Франсуа Виет (1540-1603) родился на юге Франции в небольшом городке Фантене-ле-Конт. Отец Виета был прокурором. По традиции сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери — двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.

Понравилась статья? Расскажи друзьям!

< Предыдущая		Следующая >

Добавить комментарий

megaznanie.ru

Кострикин А.И. Введение в алгебру. Часть I. Основы алгебры [DJVU]

Учебник для вузов. М.: Физико-математическая литература, 2000, 272 стр.Рассмотрены системы линейных уравнений, элементарная теория матриц, теория определителей, простейшие свойства групп, колец и полей, комплексные числа и корни многочленов. Помещено большое число упражнений различной степени трудности. Специальный раздел посвящен обсуждению некоторых нерешенных задач о многочленах.
Для студентов младших курсов университетов и вузов с повышенными требованиями по математике.Истоки Алгебры
Алгебра вкратце
Некоторые модельные задачи
Задача о разрешимости уравнений в радикалах
Задача о состояниях многоатомной молекулы
Задача о кодировании сообщения
Задача о нагретой пластинке
Системы линейных уравнений. Первые шаги
Терминологи
Эквивалентность линейных систем
Приведение к ступенчатому виду
Исследование системы линейных уравнений
Отдельные замечания и примеры
Определители небольших порядков
Упражнения
Множества и отображения
Множества
Отображения
Упражнения
6. Отношения эквивалентности. Факторизация отображений
Бинарные отношения
Отношение эквивалентности
Факторизация отображений
Упорядоченные множества
Упражнения
Принцип математической индукции
Упражнения
Перестановки
Стандартная запись перестановки
Цикловая структура перестановки
Знак перестановки(56
Действие Sn на функциях
Упражнения
Арифметика целых чисел
Основная теорема арифметики
НОД и НОК в Z
Алгоритм деления в Z
Упражнения
Матрицы
Векторные пространства строк и столбцов
Мотивировка
Основные определения
Линейные комбинации. Линейная оболочка
Линейная зависимость
Базис. Размерность
Упражнения
Ранг матрицы
Возвращение к уравнениям
Ранг матрицы
Критерий совместности
Упражнения
Линейные отображения. Действия с матрицами
Матрицы и отображения
Произведение матриц
Транспонирование матриц
Ранг произведения матриц
Квадратные матрицы
Классы эквивалентных матриц
Вычисление обратной матрицы
Пространство решений
Упражнения
Определители
Определители: построение и основные свойства
Геометрическая мотивировка
Комбинаторно- аналитический подход
Основные свойства определителей
Упражнения
Дальнейшие свойства определителей
Разложение определителя по элементам столбца или строки
Определители специальных матриц
Упражнения
Применения определителей
Критерий невырожденности матрицы
Формулы Крамера
Метод окаймляющих миноров
Упражнения
К построению теории определителей
Первое аксиоматическое построение
Второе аксиоматическое построение
Построение методом полной индукции
Характеризация мультипликативными свойствами
Упражнения
Группы. Кольца. Поля
Множества с алгебраическими операциями
Бинарные операции
Полугруппы и моноиды\
Обобщённая ассоциативность; степени
Обратимые элементы
Упражнения
Группы
Определение и примеры
Циклические группы
Изоморфизмы
Гомоморфизмы
Словарик. Примеры
Упражнения
Кольца и поля
Определение и общие свойства колец
Сравнения. Кольцо классов вычетов
Гомоморфизмы колец
Типы колец. Поле
Характеристика поля
Замечание о линейных системах
Упражнения
Комплексные числа и Многочлены
Поле комплексных чисел
Вспомогательная конструкция
Плоскость комплексных чисел
Геометрическое истолкование действий с комплексными числами
Возведение в степень и извлечение корня
Теорема единственности
Элементарная геометрия комплексных чисел
Упражнения
Кольцо многочленов
Многочлены от одной переменной
Многочлены от многих переменных
Алгоритм деления с остатком
Упражнения
Разложение в кольце многочленов
Элементарные свойства делимости
НОД и НОК в кольцах
Факториальность евклидовых колец
Неприводимые многочлены
Упражнения
Поле отношений
Построение поля отношений целостного кольца
Поле рациональных дробей
Простейшие дроби
Упражнения
Корни Многочленов
Общие свойства корней
Корни и линейные множители
Полиномиальные функции
Дифференцирования кольца многочленов
Кратные множители
Формулы Виета
Упражнения
Симметрические многочлены
Кольцо симметрических многочленов
Основная теорема о симметрических многочленах
Метод неопределённых коэффициентов
Дискриминант многочлена
Результант
Упражнения
Алгебраическая замкнутость поля С
Формулировка основной теоремы
Доказательство основной теоремы
Ещё одно доказательство основной теоремы
Многочлены с вещественными коэффициентами
Разложение на неприводимые множители в R[X]
Простейшие дроби над С и R
Проблема локализации корней многочлена
Вещественные многочлены с вещественными корнями
Устойчивые многочлены
Зависимость корней многочлена от коэффициентов
Вычисление корней многочлена
Рациональные корни целочисленных многочленов
Упражнения
Приложение: Нерешённые Задачи о Многочленах
Проблема якобиана
Задача о дискриминанте
Задача о двух порождающих кольца многочленов
Задачи о критических точках и критических значениях
Задача о глобальной сходимости метода Ньютона
Предметный указатель

Основы школьной алгебры

ОСНОВЫ АЛГЕБРЫ. 100 великих научных открытий

ОСНОВЫ АЛГЕБРЫ это что такое ОСНОВЫ АЛГЕБРЫ: определение — История.НЭС

ОСНОВЫ АЛГЕБРЫ

Математические основы курсов алгебры и геометрии

Вопрос 3. Основы алгебры высказываний

Основы алгебры

Добавить комментарий

Кострикин А.И. Введение в алгебру. Часть I. Основы алгебры [DJVU]

Добавить комментарий Отменить ответ