Площадь линии – Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 1

Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 1

Площадь — линия

Cтраница 1

Площадь линии может быть существенно уменьшена при разветвлении потока на участках охлаждения, что также легко осуществить на роликовом конвейере. Для той же цели используют транспортные тележки, не связанные между собой цепью и перемещающиеся по рельсовому пути. Достоинством роликового конвейера и транспортных тележек является также то, что отдельные их секции приводятся в действие не строго одновременно. В результате резко уменьшаются динамические нагрузки, пере-даваемыена строительные конструкции.  [1]

Площадь линии фотоэлектронного спектра данного соединения, ионизованного фотонами, должна быть пропорциональна концентрации этого соединения, так как эффективность ионизации зависит от потока фотонов, сечения ионизации орбитали и количества молекул образца, взаимодействующих с фотонами. Для УФЭС это предположение еще недостаточно проверено. Результаты двух выполненных к настоящему моменту работ [21] вызывают сомнения из-за наличия в них серьезных экспериментальных трудностей.  [2]

СБИС, площадь линий связи на кристалле начинает превышать площадь, занимаемую логическими элементами в схеме. В [9, 10] показано, что чем больше степень интеграции СБИС, тем больше часть площади кристалла, приходящаяся на линии связи. В указанных работах делается вывод о том, что без осуществления оптимизации межэлементных связей на кристалле процесс повышения степени интеграции практически будет приостановлен, вследствие достижения физических пределов при распределении площади кристалла.  [3]

Таким образом, площадь лоренцевой линии, обрезанной достаточно далеко от точки половинной мощности, очень близка к площади обычной лоренцевой линии.  [4]

На участке ABCDEF требуется выделить

площадь S линий MN, параллельной АВ.  [6]

При частичном загружении q множится на площадь линии влияния, находящейся под нагрузкой.  [8]

Равномерно распределенная нагрузка располагается над всей площадью линии влияния одного знака. В к А, соединяются Л и С и проводится DE AC; точка Е располагается на критическом грузе.  [9]

Площадь между линией влияния и осью абсцисс дает площадь линии влияния. Отыскание по линии влияния наибольшей величины соответствующего усилия ведется без особого затруднения.  [10]

Так как нагр зка расположена па всем пролете, то площади линий влияния надо вычислять на протяжении всего пролета.  [11]

Наиболее точный метод определения величин / и / заключается в измерении площади линии резонансного поглощения, наблюдаемой в скоростном спектре.  [12]

А если хоть для одного положительного е такой области не удастся найти, тогда площадь линии не равна нулю.  [13]

При равномерно распределенной нагрузке для определения изгибающего момента величину погонной нагрузки q множат на площадь линии влияния. При частичном загружении балки величину q множат на ту часть площади линии влияния, которая расположена под нагрузкой.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 3

Площадь — линия

Cтраница 3

При разбавлении диметилформамидом растворов хлорида железа ( Ш), содержащих полиядерные частицы Fe ( III), в мессбауэровском спектре начинают проявляться особенности, характерные для мономерной структуры. Предполагая, что факторы Дебая — Уэллера индивидуальных сольватов одинаковы, из значений площадей линий в спектрах можно рассчитать отношение концентраций различных мономерных и полиядерных комплексов железа.  [31]

Если щель уже нормальной, освещенность линии пропорциональна ширине щели, так как при уменьшении ширины щели световой по-ток уменьшается, как это следует из (III.15), а площадь линии остается постоянной. Если щель шире нормальной, освещенность линии от ширины не зависит, так как с увеличением ширины щели пропорционально увеличиваются и площадь линии и световой поток.  [33]

Диапазон изменения значений коэффициента Q достаточно широкий. Они могут быть очень малы, например, в случае расчета процесса торможения, при котором эффективная площадь входной линии значительно больше

площади выхлопной линии. Здесь приведены графики для диапазона изменения Q от 0 25 до 10, что достаточно для обычных процессов.  [34]

С помощью метода ЯМР можно легко изучать кинетику медленно протекающих реакций, применяя обычную аналитическую методику для измерения концентраций реагентов и продуктов реакции по площади линии поглощения.  [35]

В нашей работе [65] была измерена не только величина ( х) — — ( х), но и абсолютные значения ( х — 0 48 10 — 18 см. и ( х) 1 76 10 — 18 см3 для ядер олова в молекулах SnO, химически сорбированных на поверхности силикагеля при температуре 213 К. В обеих работах наблюдался рост асимметрии компонент квадрупольного расщепления с увеличением температуры, что является одной из характерных особенностей асимметрии, связанной с анизотропией фактора Дебая — Валлера, отличающей ее ( наряду с различием

площадей линий, соответствующих разным переходам) от релаксационной асимметрии по Блюму [123], которая ослабевает с ростом температуры.  [36]

Рисунок 3.55 показывает изменения интенсивности для компонентов линии НЗОо за три года. Площадь линии отнесена к излучению в континууме калибровочного источника DR21, имеющего большую интенсивность и стабильность. Кажется есть небольшое уменьшение относительной интенсивности широкополосного компонента линии ( пьедестала), но отношение сигнал / шум недостаточное. Временные изменения красного компонента отчетливо видны относительно ошибок измерений. Интенсивность меняется в пределах трех раз с нерегулярным характером. Аналогичная картина наблюдается у голубого компонента.  [37]

В квантометрах и спектроскопах, как правило, щели и осветительные устройства постоянны и не подлежат перестройке. При фотографической регистрации спектра желательно увеличение площади линий. Фотоэмульсия неоднородна, между светочувствительными зернами имеются участки, нечувствительные к свету. При узкой щели линия может попасть на пустой участок пластинки или на участок с большой концентрацией светочувствительных зерен.  [38]

Ферма жесткости мостового крана имеет, как правило, ту же схему, что и главная. Это позволяет проектанту использовать построенные ранее линии влияния для определения усилий в элементах — фермы жесткости. Они могут быть найдены путем умножения площадей линий влияния, построенных для стержней, на величину погонной нагрузки от собственного веса фермы жесткости. Учет сосредоточенных сил производится умножением ординат линий влияния на величины сосредоточенных сил, приложенных к ферме.  [39]

Невыгоднейшее положение системы грузов ( линия влияния — треугольник): 1) По крайней мере один из грузов ( называемый критическим) находится над вершиной линии влияния. Критический груз выбирается по следующему признаку: если он расположен слева от вершины, то средняя погонная нагрузка левого участка превышает правую, а при расположении его справа от вершины — наоборот. Равномерно распределенная нагрузка располагается над всей площадью линии влияния одного знака. Графический прием определения критического груза для треугольной линии влияния показан на фиг.  [40]

Невыгоднейшее положение системы грузов ( линия влияния — треугольник): 1) По крайней мере один из грузов ( называемый критическим) находится над вершиной линии влияния. Критический груз выбирается по следующему признаку: если он расположен слева от вершины, то средняя погонная нагрузка левого участка превышает правую, а при расположении его справа от вершины — наоборот. Равномерно распределенная нагрузка располагается над всей

площадью линии влияния одного знака. Графический прием определения критического груза для треугольной линии влияния показан па фиг.  [41]

Вышеприведенное рассмотрение предполагало, что линии имеют естественные ширины. Однако легко видеть, что оно остается в силе также и в том случае, когда Гизл Г, Гпогл Г, но Гизл — ГПОГл; в выражение (1.31) не входит экспериментальная ширина линии. ГПОГл, но уширение обусловлено причинами, не изменяющими площадь линии поглощения, например паразитными вибрациями установки.  [42]

Если размер плоской линии менее 1 / 8 длины волны, ее емкость с достаточной точностью описывается формулой плоского конденсатора C 0 9S / a, здесь С — емкость в пикофарадах; 5 —

площадь линии в квадратных сантиметрах; d — зазор между линией и землей в миллиметрах.  [44]

На линии Л-450 ( КВ-301) ком с отливкой выдавливается без разрушения вверх, затем толкателем по столу перемещается на пластинчатый конвейер для дальнейшего охлаждения. На конвейере вплотную друг к другу устанавливаются три кома. Шаг кома примерно в 2 раза меньше шага тележек литейного конвейера, поэтому скорость охлаждающего конвейера в 6 — 7 раз меньше скорости литейного конвейера. Такое решение позволяет значительно сократить площадь линии, существенно уменьшает парк опок, однако оно возможно только при использовании высокопрочных смесей. Мелкие и средние отливки отделяются от смеси на вибрационных выбивных решетках или в решетчатых барабанах.  [45]

Страницы:      1    2    3    4

www.ngpedia.ru

Вычисление площадей фигур, ограниченных заданными линиями

Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.

Определение.

Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).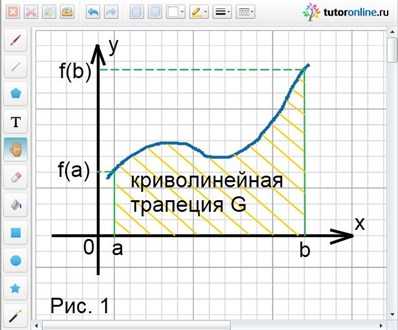

Определенный интеграл ʃ_а^b f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.

То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл  ʃ_а^b f(x)dx.

Таким образом, S(G) = ʃ_а^b f(x)dx.

В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃ_а^b f(x)dx.

Пример 1.

Вычислить площадь фигуры, ограниченной линиями у = х³; у = 1; х = 2.

Решение.

Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.

Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.

Используя формулу S = ʃ_а^b f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:

{у = х³,
{у = 1.

Таким образом, имеем х₁ = 1 – нижний предел и х = 2 – верхний предел.

Итак, S = S_DACE – S_DABE = ʃ₁² x³ dx – 1 = x⁴/4|₁² – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).

Ответ: 11/4 кв. ед.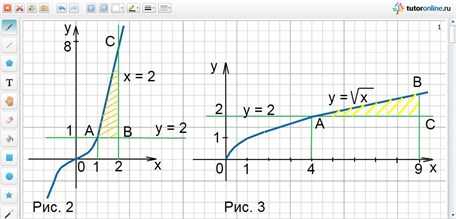

Пример 2.

Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.

Решение.

Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции

у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.

Искомая площадь равна S = ʃ_а^b(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:

{у = √х,
{у = 2.

Таким образом, имеем, что х = 4 = а – это нижний предел.

Итак, S = ∫₄⁹ (√x – 2)dx = ∫₄⁹ √x dx –∫₄⁹ 2dx = 2/3 x√х|₄⁹ – 2х|₄⁹ = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).

Ответ: S = 2 2/3 кв. ед.

Пример 3.

Вычислить площадь фигуры, ограниченной линиями у = х³ – 4х; у = 0; х ≥ 0.

Решение.

Построим график функции у = х³ – 4х при х ≥ 0. Для этого найдем производную у’:

y’ = 3x² – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.

Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции у_min = -16/(3√3) ≈ -3.

Определим точки пересечения графика с осями координат:

если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;

если у = 0, то х³ – 4х = 0 или х(х² – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х₁ = 0, х₂ = 2, х₃ = -2 (не подходит, т.к. х ≥ 0).

Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.

Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.

Так как функция у = х³ – 4х принимает на (0; 2) отрицательное значение, то

S = |ʃ₀² (x³ – 4x)dx|.

Имеем: ʃ₀² (x³ – 4х)dx =(x⁴/4 – 4х²/2)|₀²= -4, откуда S = 4 кв. ед.

Ответ: S = 4 кв. ед.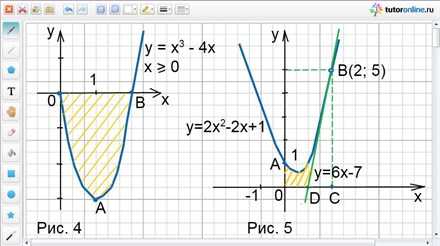

Пример 4.

Найти площадь фигуры, ограниченной параболой у = 2х² – 2х + 1, прямыми  х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х₀ = 2.

Решение.

Сначала составим уравнение касательной к параболе у = 2х² – 2х + 1 в точке с абсциссой х₀ = 2.

Так как производная y’ = 4x – 2, то при х₀ = 2 получим k = y’(2) = 6.

Найдем ординату точки касания: у₀ = 2 · 2² – 2 · 2 + 1 = 5.

Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.

Построим фигуру, ограниченную линиями:

у = 2х² – 2х + 1, у = 0, х = 0, у = 6х – 7.

Г_у =  2х² – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение  2х² – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:

x_b = -b/2a;

x_b = 2/4 = 1/2;

y_b = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).

Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.

Имеем: S_ОAВD = S_OABC – S_ADBC.

Найдем координаты точки D из условия:

6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.

Площадь треугольника DBC найдем по формуле S_ADBC = 1/2 · DC · BC. Таким образом,

S_ADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.

Далее:

S_OABC = ʃ₀²(2x² – 2х + 1)dx = (2x³/3 – 2х²/2 + х)|₀² = 10/3 (кв. ед.).

Окончательно получим: S_ОAВD = S_OABC – S_ADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).

Ответ: S = 1 1/4 кв. ед.

Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 2

Площадь — линия

Cтраница 2

При равномерно распределенной нагрузке для определения изгибающего момента величину погонной нагрузки q множат на площадь линии влияния. При частичном загружении балки вели-чину q множат на ту часть площади линии влияния, которая расположена под нагрузкой.  [16]

При равномерно распределенной нагрузке, расположенной на части фермы, погонную нагрузку q множат на площадь линии влияния, расположенную под нагрузкой. При определении усилия в раскосе от равномерно распределенной нагрузки принимают алгебраическую сумму площадей участков линии влияния, расположенных под нагрузкой.  [17]

Таким образом, площадь лоренцевой линии, обрезанной достаточно далеко от точки половинной мощности, очень близка к площади обычной лоренцевой линии.  [18]

С помощью метода ЯМР можно легко изучать кинетику медленно протекающих реакций, применяя обычную аналитическую методику для измерения концентрации реагентов и продуктов реакции по площади линии поглощения.  [19]

Если щель уже нормальной, освещенность линии пропорциональна ширине щели, так как при уменьшении ширины щели световой по-ток уменьшается, как это следует из (III.15), а площадь линии остается постоянной. Если щель шире нормальной, освещенность линии от ширины не зависит, так как с увеличением ширины щели пропорционально увеличиваются и площадь линии и световой поток.  [21]

Садижан [11] указывает, что при квадратичном эффекте Штарка электроны ( ударная теория) ведут к симметричному, а ионы ( статистическая теория) — к асимметричному уширению. Разделяя всю площадь линии по вертикали пополам, он определял величину смещения, отсюда — плотность ионов и наконец температуру. При исследовании профиля линии сравниваемые результаты измерений и расчетов должны всегда относиться к одинаковой полной площади.  [22]

Конденсаторы представляют собой короткие и широкие отрезки линии, близко расположенные друг от друга. Чем больше площадь линий и чем ближе они расположены к подложке платы, тем больше емкость конденсатора.  [23]

Для определения общего поглощения в спектре ЭПР использовались элементы аналоговых ЭВМ, схематически представленные на фиг. Прямое определение площади линии по описанному в данной работе методу иллюстрируется на фиг. На форму же кривой первой производной перемодуляция влияет гораздо сильнее. Это очень важное замечание, поскольку при регистрации слабых сигналов неизбежно используется большая глубина модуляции. ЭПР структура спектров разрешается лучше. С целью получения еще лучшего разрешения Джонсон и Чанг [80] записывали даже третью производную сигнала поглощения.  [24]

Это равносильно измерению площади линии. Оуэне и Джиардино ( 1963) указывали, что в идеальном случае интенсивность ионов следует измерять, предварительно превращая каждую точку профиля почернения линии в интенсивность с помощью характеристической кривой и затем интегрируя полученный профиль интенсивности. Для строго линейной характеристической кривой в результате интегрирования профиля почернения получается величина, пропорциональная интегралу интенсивности. На практике интегрирование профиля почернения предпочитают другим методам оценки интенсивности линий, поскольку этот способ учитывает все изменения формы линии.  [25]

Однако эти случаи следует рассматривать скорее как исключения. Большей частью приходится принимать в расчет всю площадь линии и, следовательно, интегральное поглощение А. При определении температуры по интенсивности одной линии измерения должны производиться в абсолютных единицах. Кроме того, должна быть хотя бы приблизительно известна оптическая толщина слоя; впрочем, часто бывает достаточно знать, лежит ли она в пределах оптически тонких или оптически толстых слоев. Этим, конечно, данный метод сильно усложняется, поэтому он и применяется для определения температуры сравнительно редко. Эленбаас [13], измеряя температуру плазмы ртутного разряда при высоком давлении, полагал, что работает с оптически тонким слоем. По интенсивности излучения дублета 5570 / 90 А с помощью формулы ( 20) он установил, что температура на оси равна 5900 К — При этом, конечно, необходимо было учитывать ее спад у стенок и интегрировать излучение по всем слоям.  [26]

При равномерно распределенной нагрузке для определения изгибающего момента величину погонной нагрузки q множат на площадь линии влияния. При частичном загружении балки величину q множат на ту часть площади линии влияния, которая расположена под нагрузкой.  [27]

При равномерно распределенной нагрузке для определения изгибающего момента величину погонной нагрузки q множат на площадь линии влияния. При частичном загружении балки вели-чину q множат на ту часть площади линии влияния, которая расположена под нагрузкой.  [28]

Основу такой классификации составляет атомарная единица ( пространства), содержащая представления площадей линий и точек.  [29]

Страницы:      1    2    3    4

www.ngpedia.ru

Как вычислить площадь фигуры, ограниченной графиками функций 🚩 вычислите площадь фигуры ограниченной графиком функции 🚩 Математика

Инструкция

По определению интеграла, он равен площади криволинейной трапеции, ограниченной графиком заданной функции. Когда требуется найти площадь фигуры, ограниченной линиями, речь идет о кривых, заданных на графике двумя функциями f1(x) и f2(x). Пусть на некотором интервале [a, b] заданы две функции, которые определены и непрерывны. Причем одна из функций графике расположена выше другой. Таким образом, образуется визуальная фигура, ограниченная линиями функций и прямыми x = a, x = b.

Тогда площадь фигуры можно выразить формулой, интегрирующей разность функций на интервале [a, b]. Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.

Пример1.
Найти площадь фигуры, ограниченной прямыми линиями y = -1/3·x – ½, x = 1, x = 4 и параболой y = -x² + 6·x – 5.

Решение.
Постройте графики всех линий. Вы можете увидеть, что линия параболы находится выше прямой y = -1/3·x – ½. Следовательно, под знаком интеграла в данном случае должна стоять разность между уравнением параболы и заданной прямой. Интервал интегрирования, соответственно, находится между точками x = 1 и x = 4:
S = ∫(-x² + 6·x – 5 – (-1/3·x – 1/2))dx = (-x² +19/3·x – 9/2)dx на отрезке [1, 4].

Найдите первообразную для полученного подынтегрального выражения:
F(-x² + 19/3x – 9/2) = -1/3x³ + 19/6x² – 9/2x.

Подставьте значения концов отрезка:
S = (-1/3·4³ + 19/6·4² – 9/2·4) – (-1/3·1³ + 19/6·1² – 9/2·1) = 13.

Пример2.
Вычислите площадь фигуры, ограниченной линиями y = √(x + 2), y = x и прямой x = 7.

Решение.
Эта задача является более сложной по сравнению с предыдущей, поскольку в ней нет второй прямой, параллельной оси абсцисс. Это значит, что второе граничное значение интеграла неопределенно. Следовательно, его нужно найти из графика. Постройте заданные линии.

Вы увидите, то прямая линия y = x проходит диагонально относительно координатных осей. А график функции корня – это положительная половина параболы. Очевидно, что линии на графике пересекаются, поэтому точка пересечения и будет нижним пределом интегрирования.

Найдите точку пересечения, решив уравнение:
x = √(x + 2) → x² = x + 2 [x ≥ -2] → x² – x – 2 = 0.

Определите корни квадратного уравнения с помощью дискриминанта:
D = 9 → x1 = 2; x2 = -1.

Очевидно, что значение -1 не подходит, поскольку абсцисса токи пересечения – положительная величина. Следовательно, второй предел интегрирования x = 2. Функция y = x на графике выше функции y = √(x + 2), поэтому в интеграле она будет первой.
Проинтегрируйте получившееся выражение на интервале [2, 7] и найдите площадь фигуры:
S = ∫(x — √(x + 2))dx = (x²/2 – 2/3·(x + 2)^(3/2)).

Подставьте интервальные значения:
S = (7²/2 – 2/3·9^(3/2)) – (2²/2 – 2/3·4^(3/2)) = 59/6.

www.kakprosto.ru

ЦЕНТР ТЯЖЕСТИ ОБЪЁМА, ПЛОЩАДИ, ЛИНИИ

Сила, с которой тело притягивается к Земле, называется силой тяжести. Точка приложения этой силы — центром тяжести. Поскольку силы тяжести действуют на каждую частицу тела, то её надо считать распределённой. При небольших (по сравнению с Землей) размерах тела силы тяжести с большой степенью точности можно считать параллельными. Для определения равнодействующей и точки приложения силы тяжести разобьём тело на » » достаточно малых элементов. Предельным переходом, устремляя , получим точные формулы.

Вес элементарного объема можно выразить через удельный вес формулой . При вычислении центра тяжести пластинки постоянной толщины его элементарный объём можно представить в виде . При вычислении элементарного объёма стержня можно воспользоваться соотношением , где — площадь поперечного сечения стержня.

Тогда формулы для определения центра тяжести плоской фигуры

криволинейного стержня (линии)

Динамика

Динамика — раздел механики, в котором изучается движение материальных объектов в зависимости от действующих на них сил. Простейшим материальным объектом является материальная точка. Это модель материального тела любой формы, размерами которого в рассматриваемых задачах можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты — механические системы и сплошные тела — считают состоящими из материальных точек.

Сила считается в механике основным, первичным понятием. Свойства сил, приложенных к твердому телу и точке, рассматривались в статике. В динамике силы оцениваются по их динамическому действию, т.е. по изменению ими характеристик движения материальных объектов.

Движение материальных объектов следует рассматривать относительно определенной системы отсчета. Оно совершается в пространстве с течением времени. В классической механике пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. Время в классической механике инвариантно по отношению к выбору системы координат.

В основу классической механики положены законы или аксиомы Ньютона, которые были получены им путём обобщений целого ряда опытных данных и теоретических исследований.

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

Задачи динамики материальной точки можно разделить на три раздела:

· Динамика свободной материальной точки;

· Динамика несвободной материальной точки;

· Динамика относительного движения материальной точки.

Динамика свободной материальной точки

Основные законы классической механики были сформулированы как законы движения по отношению к некоторой абсолютно неподвижной системе — «абсолютному пространству». Ньютон принимал «абсолютное время», не зависящее от движения тел и систем отсчёта.

Законы механики Галилея-Ньютона

Закон инерции

«Изолированная материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока действие других тел не изменит это состояние».

Материальная точка, на которую не действуют силы или действует уравновешенная система сил, называется изолированной (свободной) материальной точкой.

Смысл закона инерции заключается в постулировании существования так называемых инерциальных систем отсчёта, которые движутся по отношению к “абсолютному пространству” поступательно, равномерно и прямолинейно. В этих системах отсчета выполняются законы классической механики.

Закон инерции характеризует основное свойство материи постоянно находиться в состоянии равномерного прямолинейного движения (движения по инерции).

Свойство материальной точки сохранять при движении свою скорость называется инертностью. Количественная мера инертности материальной точки, пропорциональная количеству вещества, заключенного в ней, называется массой материальной точки.

Масса представляет собой основную динамическую характеристику точки, она является скалярной положительной величиной.

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Найти площадь фигуры, ограниченной линиями

Из данной статьи вы узнаете, как найти площадь фигуры, ограниченной линиями, используя вычисления с помощью интегралов. Впервые с постановкой такой задачи мы сталкиваемся в старших классах, когда только-только пройдено изучение определенных интегралов и пора приступить к геометрической интерпретации полученных знаний на практике.

Итак, что потребуется для успешного решения задачи по поиску площади фигуры с помощью интегралов:

• Умение грамотно строить чертежи;
• Умение решать определенный интеграл с помощью известной формулы Ньютона-Лейбница;
• Умение «увидеть» более выгодный вариант решения — т.е. понять, как в том или ином случае будет удобнее проводить интегрирование? Вдоль оси икс (OX) или оси игрек (OY)?
• Ну и куда без корректных вычислений? ) Сюда входит понимание как решать тот иной тип интегралов и правильные численные вычисления.

Алгоритм решения задачи по вычислению площади фигуры, ограниченной линиями:

1. Строим чертеж. Желательно это делать на листке в клетку, с большим масштабом. Подписываем карандашом над каждым графиком название этой функции. Подпись графиков делается исключительно ради удобства дальнейших вычислений. Получив график искомой фигуры, в большинстве случаев будет видно сразу, какие пределы интегрирования будут использованы. Таким образом мы решаем задачу графическим методом. Однако бывает так, что значения пределов дробные или иррациональные. Поэтому, можно сделать дополнительные расчеты, переходим в шагу два.

2. Если явно не заданы пределы интегрирования, то находим точки пересечения графиков друг с другом, и смотрим, совпадает ли наше графическое решение с аналитическим.

3. Далее, необходимо проанализировать чертеж. В зависимости от того, как располагаются графики функций, существуют разные подходы к нахождению площади фигуры. Рассмотрим разные примеры на нахождение площади фигуры при помощи интегралов.

3.1. Самый классический и простой вариант задачи, это когда нужно найти площадь криволинейной трапеции. Что такое криволинейная трапеция? Это плоская фигура, ограниченная осью икс ( у = 0 ), прямыми х = а, х = b и любой кривой, непрерывной на промежутке от a до b. При этом, данная фигура неотрицательна и располагается не ниже оси абсцисс. В этом случае, площадь криволинейной трапеции численно равна определенному интегралу, вычисляемого по формуле Ньютона-Лейбница:

Пример 1. Вычислить площадь фигуры, ограниченной линиями y = x2 — 3x + 3, x = 1, x = 3, y = 0.

Решение:

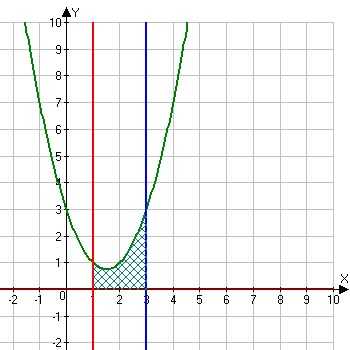Какими линиями ограничена фигура? Имеем параболу y = x2 — 3x + 3, которая располагается над осью ОХ, она неотрицательна, т.к. все точки этой параболы имеют положительные значения. Далее, заданы прямые х = 1 и х = 3, которые пролегают параллельно оси ОУ, являются ограничительными линиями фигуры слева и справа. Ну и у = 0, она же ось икс, которая ограничивает фигуру снизу. Полученная фигура заштрихована, как видно из рисунка слева. В данном случае, можно сразу приступать к решению задачи. Перед нами простой пример криволинейной трапеции, которую далее решаем с помощью формулы Ньютона-Лейбница.

3.2. В предыдущем пункте 3.1 разобран случай, когда криволинейная трапеция расположена над осью икс. Теперь рассмотрим случай, когда условия задачи такие же, за исключением того, что функция пролегает под осью икс. К стандартной формуле Ньютона-Лейбница добавляется минус. Как решать подобную задачу рассмотрим далее.

Пример 2. Вычислить площадь фигуры, ограниченной линиями y = x2 + 6x + 2, x = -4, x = -1, y = 0.

Решение:

В данном примере имеем параболу y = x2 + 6x + 2, которая берет свое начало из-под оси ОХ, прямые х = -4, х = -1, у = 0. Здесь у = 0 ограничивает искомую фигуру сверху. Прямые х = -4 и х = -1 это границы, в пределах которых будет вычисляться определенный интеграл. Принцип решения задачи на поиск площади фигуры практически полностью совпадает с примером номер 1. Единственное различие в том, что заданная функция не положительная, и все также непрерывная на промежутке [-4; -1]. Что значит не положительная? Как видно из рисунка, фигура, которая заключается в рамках заданных иксов имеет исключительно «отрицательные» координаты, что нам и требуется увидеть и помнить при решении задачи. Площадь фигуры ищем по формуле Ньютона-Лейбница, только со знаком минус в начале.

 

Статья не завершена.

matematyka.ru