Функция и плотность распределения
Для
количественной характеристики
распределения вероят-ностей удобней
пользоваться не вероятностью того
события, что случайная величина 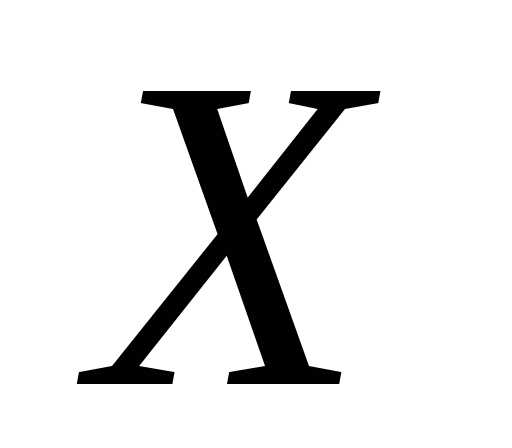 примет значение
примет значение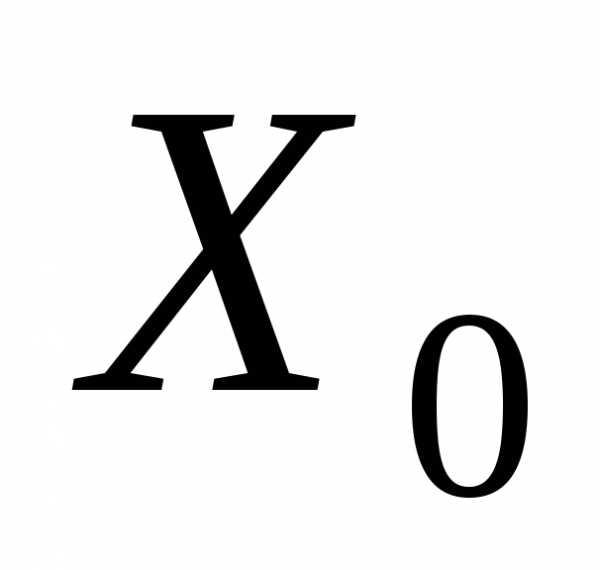 ,т.е.,
а ве-роятностью события,
т.е. того, что случайная величина
,т.е.,
а ве-роятностью события,
т.е. того, что случайная величина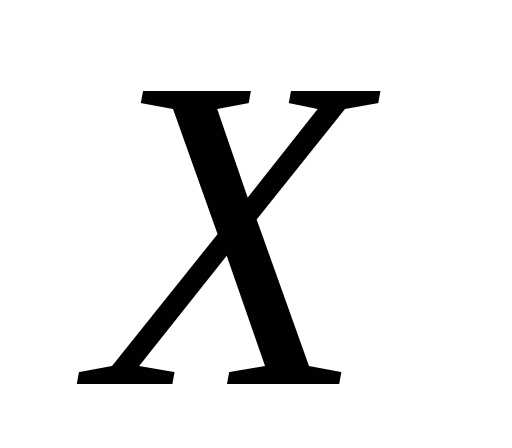 примет значение, меньшее некоторой
текущей переменной
примет значение, меньшее некоторой
текущей переменной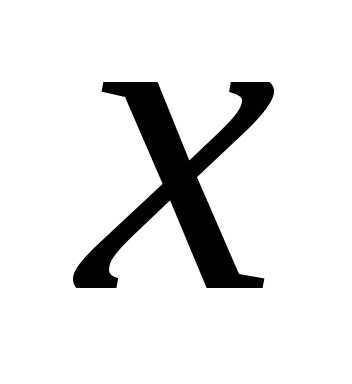 .
Вероятность этого события зависит от
значения
.
Вероятность этого события зависит от
значения ,
т.е. является функцией
от
,
т.е. является функцией
от 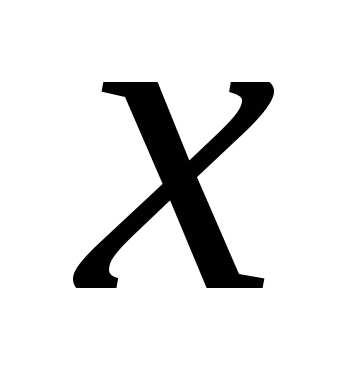
случайной
величины 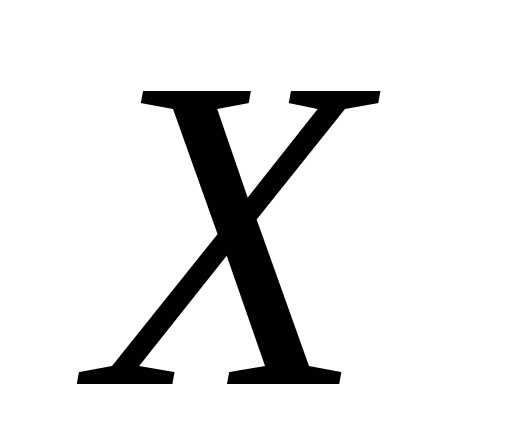 и обозначается
и обозначается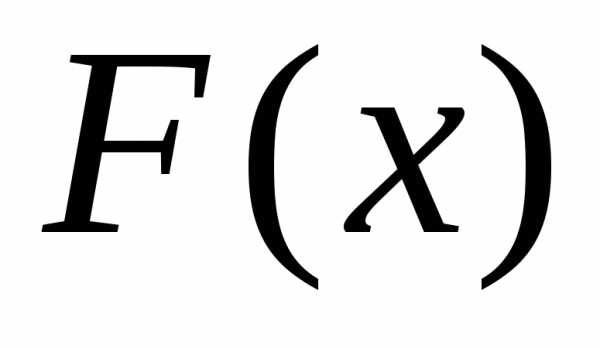 :
:
(1.6)
Функция распределения случайной величины самая универ-сальная характеристика случайной величины, она существует как для дискретных случайных величин, так и для непрерывных. Функ-ция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Функции распределения обладают некоторыми об-щими свойствами:
1.
Функция распределения 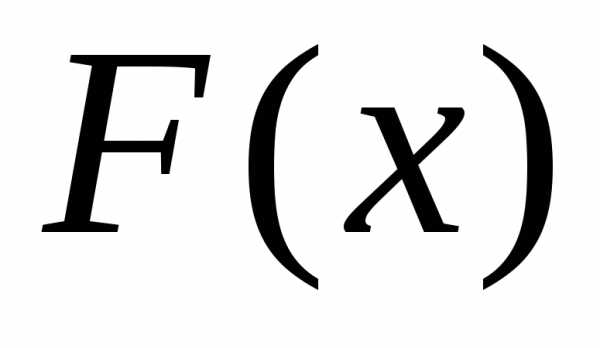 есть неубывающая функция сво-его
аргумента, т.е. при
есть неубывающая функция сво-его
аргумента, т.е. при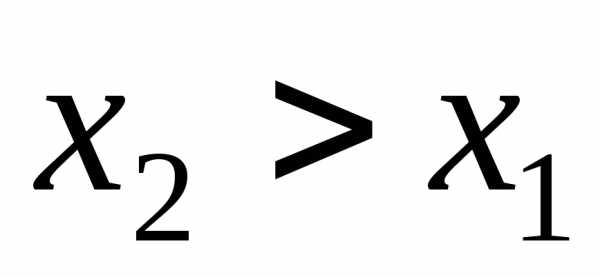
2. На минус бесконечности функция распределения равна нулю: .
3. На плюс бесконечности функция распределения равна едини-це: .
График функции распределения в общем случае может быть представлен как график неубывающей функции (рис.1), значения которой начинаются от 0 и доходят до 1, причем в отдельных точ-ках функция может иметь скачки (разрывы).
Пусть имеется
непрерывная случайная величина 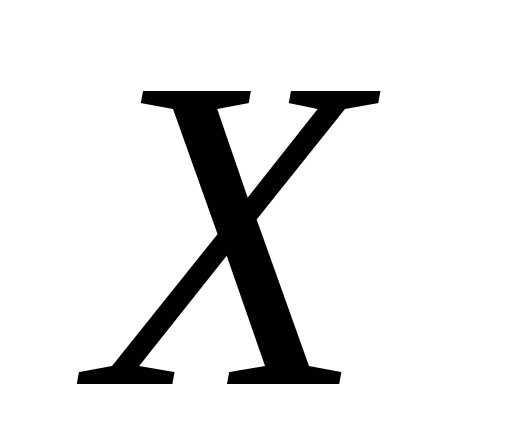 с функцией распределения
с функцией распределения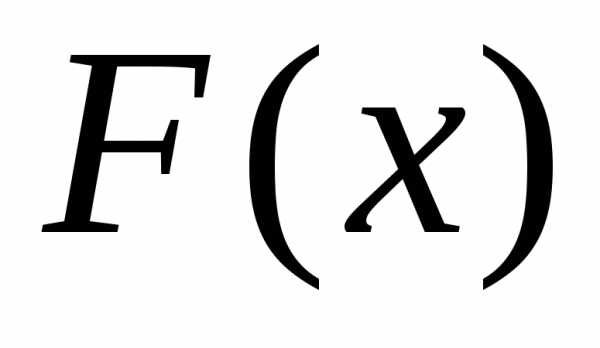 ,
которую мы предположим непрерывной и
дифференцируемой. Посколькудля непрерывной случайной величи—ны
вероятность принятия случайной величиной
любого отдельного значения равна нулю,
то вычислим вероятность попадания этой
,
которую мы предположим непрерывной и
дифференцируемой. Посколькудля непрерывной случайной величи—ны
вероятность принятия случайной величиной
любого отдельного значения равна нулю,
то вычислим вероятность попадания этой
случайной величины
на участок от 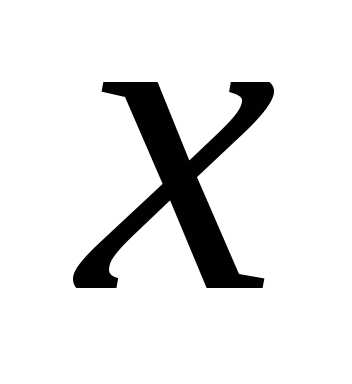
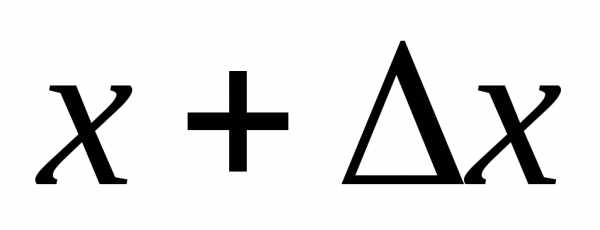 :
:(1.7)
Вероятность
попадания в указанный интервал
рассчитывается как приращение
функции распределения на этом участке.
Рассмот-рим отношение этой вероятности
к величине интервала, т.е. сред-нюю
вероятность, приходящуюся на единицу
длины на этом участ-ке, и будем приближать 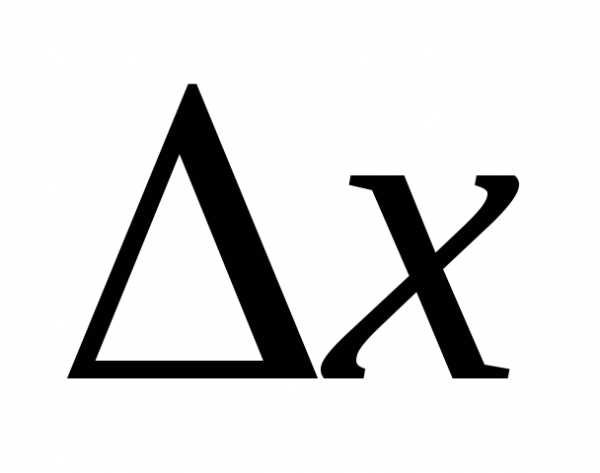 к нулю. В пределе получим производ-ную
от функции распределения:
к нулю. В пределе получим производ-ную
от функции распределения:
(1.8)
Введем обозначение для производной от функции распределе-ния:
(1.9)
Функция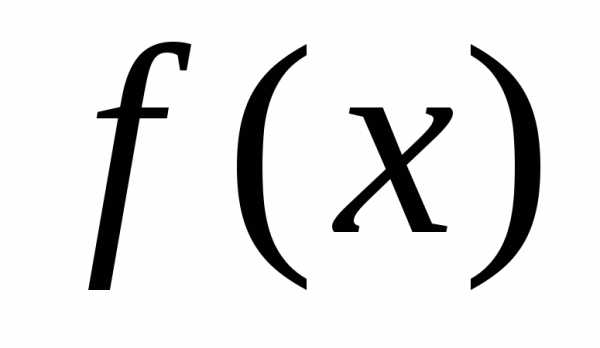 характеризует как бы плотность, с которой
рас-пределяется значение случайной
величины в данной точке (а на самом деле
отражает быстроту возрастания функции
распределе-ния). Функция
характеризует как бы плотность, с которой
рас-пределяется значение случайной
величины в данной точке (а на самом деле
отражает быстроту возрастания функции
распределе-ния). Функция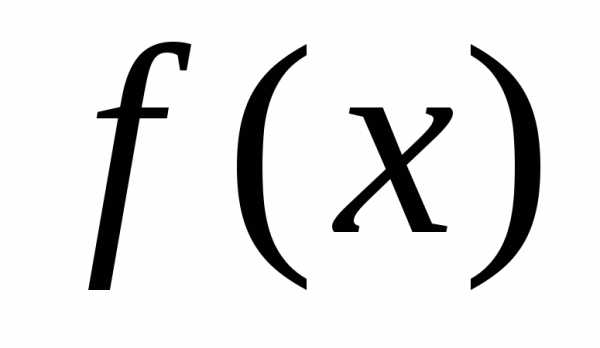
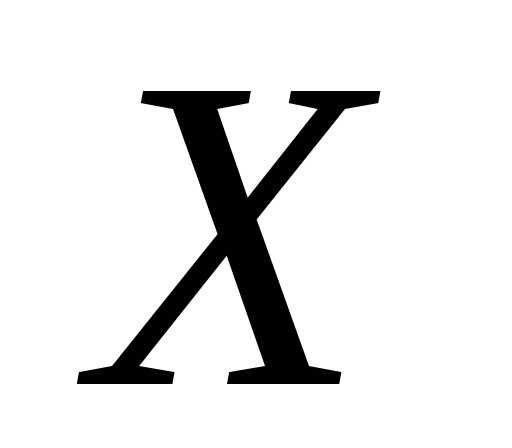 .
В отличие от функции распределения,
плотность распределения не является
универсальной–
она существует только для непрерывных
величин. Кривая, изображающая плотность
распределения случай-ной величины,
называется кривой распределения (рис.2).
.
В отличие от функции распределения,
плотность распределения не является
универсальной–
она существует только для непрерывных
величин. Кривая, изображающая плотность
распределения случай-ной величины,
называется кривой распределения (рис.2). Геометрически
вероятность попадания величины  в участок
в участок равна площади кривой распределения,опирающейся
на этот участок.Значение
же функции распределения
равна площади кривой распределения,опирающейся
на этот участок.Значение
же функции распределения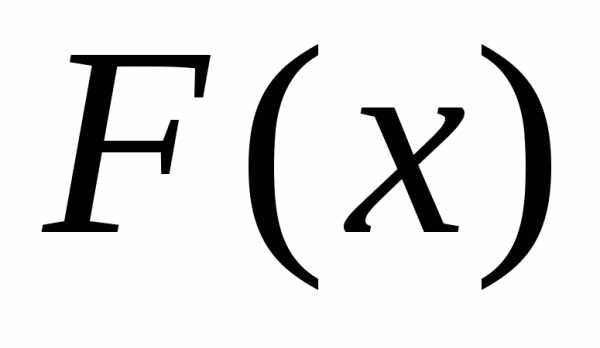
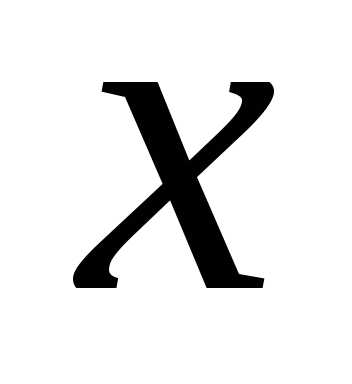 .
.Для дискретных величин аналогом графика распределения может служить гистограмма, отображающая величину прироста функции распределения (рис.3).
Плотность распределения обладает следующими свойствами:
1.
Плотность распределения есть
неотрицательная функция: 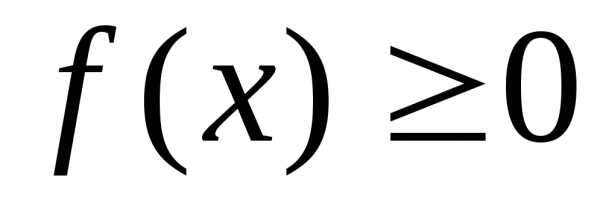 .
Это свойство вытекает непосредственно
из того, что
.
Это свойство вытекает непосредственно
из того, что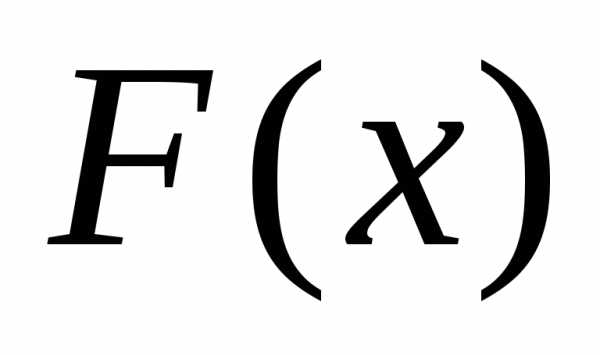 есть функция неубывающая.
есть функция неубывающая.
2.
Интеграл в бесконечных пределах от
плотности вероятности равен единице: 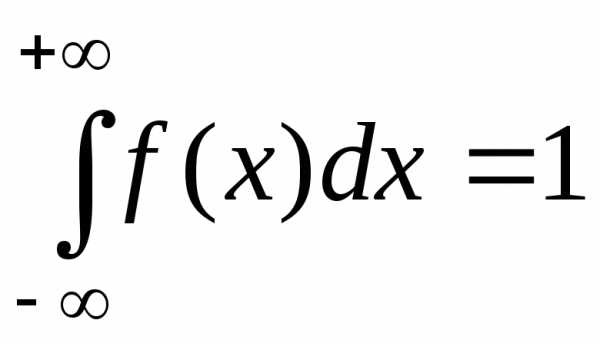
studfiles.net
Функция, плотность распределения
2.1. Функция распределения.
Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений.
Однако, такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?
Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. Х < x, обозначим через F(x).
Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.
Функцию распределения также называют интегральной функцией.
Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет вид:
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение хi.
 |
Так для примера, рассмотренного выше, функция распределения будет иметь вид:
Свойства функции распределения:
1) значения функции распределения принадлежат отрезку [0, 1].
2) F(x) – неубывающая функция.
при
3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале.
4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.
5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.
Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.
2.2. Плотность распределения.
Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.
Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.
Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением( может быть, конечного числа точек.
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше.
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.
Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
Свойства плотности распределения:
1) Плотность распределения – неотрицательная функция:
2) Несобственный интеграл от плотности распределения в пределах от — ¥ до ¥ равен единице:
Пример. Случайная величина подчинена закону распределения с плотностью:
Требуется найти коэффициент а, построить график функции плотности распределения, определить вероятность того, что случайная величина попадет в интервал от 0 до .
Построим график плотности распределения:
Для нахождения коэффициента а воспользуемся свойством .
Находим вероятность попадания случайной величины в заданный интервал.
Пример. Задана непрерывная случайная величина х своей функцией распределения f(x).
Требуется определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал .
Найдем коэффициент А.
Найдем функцию распределения:
1) На участке :
2) На участке
3) На участке
Итого:
Построим график плотности распределения:
f(x)
Построим график функции распределения:
F(x)
Найдем вероятность попадания случайной величины в интервал .
Ту же самую вероятность можно искать и другим способом:
2. Числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение, мода, медиана).
Пусть непрерывная случайная величина Х задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [a,b].
Закон распределения полностью характеризует случайную величину. Однако, когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.
Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно.
С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания:
1) Математическое ожидание постоянной величины равно самой постоянной.
2) Постоянный множитель можно выносить за знак математического ожидания.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
Это свойство также справедливо для произвольного числа случайных величин.
Пусть производится п независимых испытаний, вероятность появления события А в которых равна р.
Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
Однако, математическое ожидание не может полностью характеризовать случайный процесс. Кроме математического ожидания надо ввести величину, которая характеризует отклонение значений случайной величины от математического ожидания.
Это отклонение равно разности между случайной величиной и ее математическим ожиданием. При этом математическое ожидание отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.
Математическим ожиданиемнепрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
При этом, конечно, предполагается, что несобственный интеграл сходится.
Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Пример. Для рассмотренного выше примера закон распределения случайной величины имеет вид:
Найти математическое ожидание и дисперсию случайной величины.
Математическое ожидание случайной величины равно:
Возможные значения квадрата отклонения:
Тогда
| [X-M(X)]2 | 2,25 | 0,25 | 0,25 |
| p | 0,0625 | 0,375 | 0,5625 |
Дисперсия равна:
Однако, на практике подобный способ вычисления дисперсии неудобен, т.к. приводит при большом количестве значений случайной величины к громоздким вычислениям.
Поэтому применяется другой способ.
Вычисление дисперсии.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания.
Доказательство. С учетом того, что математическое ожидание М(Х) и квадрат математического ожидания М2(Х) – величины постоянные, можно записать:
Применим эту формулу для рассмотренного выше примера:
| X | |||
| X2 | |||
| p | 0,0625 | 0,375 | 0,5625 |
Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:
Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю:
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин:
Справедливость этого равенства вытекает из свойства 2.
Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в каждом испытании.
Рекомендуемые страницы:
lektsia.com
Плотность распределения вероятностей.
Непрерывную с. в. можно задать, используя функцию, которую называют плотностью распределения или плотностью вероятности, или дифференциальной функцией распределения.
Плотностью распределения вероятностей непрерывной с. в. Х называют функцию f(x) – первую производную от функции распределения F(x):
f(x) = F′(x)
Из этого определения следует, что функция распределения является первообразной для плотности распределения.
Для описания распределения вероятностей дискретной с. в. плотность распределения не применима.
Вероятностный смысл плотности распределения.
Таким образом, предел отношения вероятности того, что непрерывная с. в. примет значение, принадлежащее интервалу (x, x +∆x), к длине этого интервала (при ∆x → 0) равен значению плотности распределения в точке х.
Функция плотности характеризует каждое значение непрерывной случайной величины в отдельности, а не целый диапазон как это имеет место для функции распределения.
Вероятность попадания непрерывной с. в. в заданный интервал.
По формуле Ньютона – Лейбница:
P{a < X b}= F(b) – F(a),
таким образом
Нахождение функции распределения по известной функции плотности.
Полагая в предыдущей формуле а = -∞, b = х, и заменив переменную интегрирования х на t имеем:
F(х) = P{X х}=P{-∞< X х},
следовательно
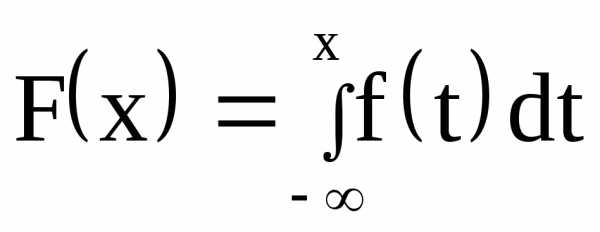
Свойства плотности распределения
Свойство 1. Плотность распределения – неотрицательная функция: f(x)0 (т.к. интегральная функция распределения – неубывающая функция, а плотность распределения ее первая производная).
Свойство 2: 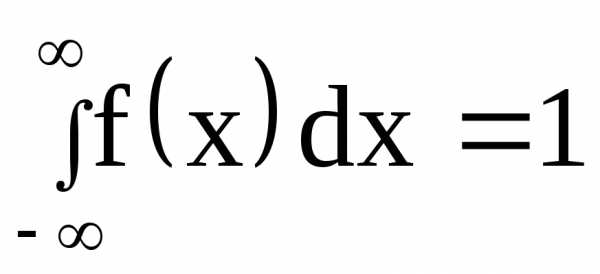
Доказательство.
Несобственный интеграл 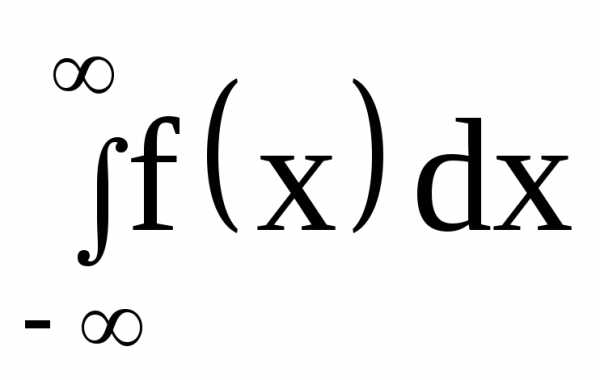 выражает вероятность события, состоящего
в том, что случайная величина примет
значение, принадлежащая интервалу (-∞,
∞). Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице.
выражает вероятность события, состоящего
в том, что случайная величина примет
значение, принадлежащая интервалу (-∞,
∞). Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице.
Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью 0х и кривой распределения, равна единице.
Вчастности, если все возможные значения
случайной величины принадлежат интервалу
(а,b),
то 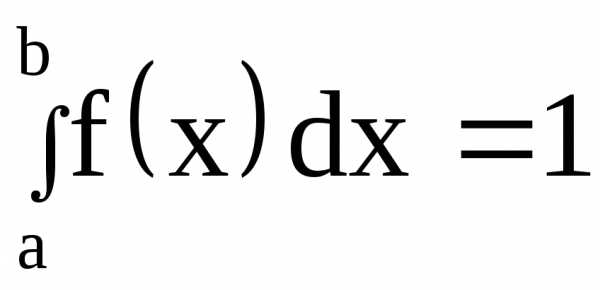 .
.
Возможный график плотности распределения (пример)
Задача .
f1(x) – плотность распределения размера выигрыша в 1-й игре
f2(x) – плотность распределения размера выигрыша во 2-ой игре
Какая игра предпочтительней ?
Числовые характеристики случайных величин. .
Данные характеристики позволяют решать многие задачи, не зная закона распределения случайных величин.
Характеристики положения случайной величины на числовой оси.
Математическое ожидание это есть среднее взвешенное значений случайной величины Х, в которое абсцисса каждой точки хi входит с «весом», равным соответствующей вероятности.
Математическое ожидание иногда называют просто средним значением с.в.
Обозначение: mxили M [X].
Для дискретной случайной величины
M
[X]
= 
Для непрерывной случайной величины
Мода – это наиболее вероятное значение случайной величины (то для которого вероятность pi, или плотность распределения f(x) достигает максимума).
Обозначение:
Различают унимодальные распределения ( имеют одну моду), полимодальные распределения ( имеют несколько мод) и анимодальные (не имеют моды)
унимодальное
Медиана – это такое значение случайной величины хm, для которого выполняется следующее равенство:
P{X < хm}= P{X > хm}
Медиана делит площадь,ограниченную f(x), пополам
Если плотность распределения случайной величины симметрична и унимодальна, то М[X], и хm совпадают
М[X], , хm – неслучайные величины
studfiles.net
19. Плотность и функция распределения непрерывной двумерной случайной величины и их свойства.
Функцией распределения n-мерной случайной величины называется функция, выражающая вероятность совместного выполненияn неравенств , т.е.
Геометрически
функция распределения двухмерной
случайной величины 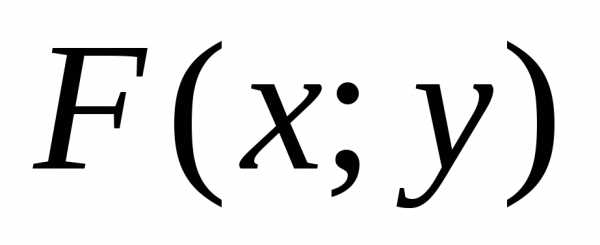 означает
вероятность попадания случайной точки
(x;y)
в заштрихованную область, расположенную
левее и ниже точки M(x;y).
означает
вероятность попадания случайной точки
(x;y)
в заштрихованную область, расположенную
левее и ниже точки M(x;y).
Квадрант
Правая и верхняя границы не включаются в квадрант – это означает, что функция распределения непрерывна слева по каждому из аргументов.
В случае дискретной двумерной случайной величины ее функция распределения определяется по формуле:
,
где суммирование
вероятностей распространяется на все i,
для которых 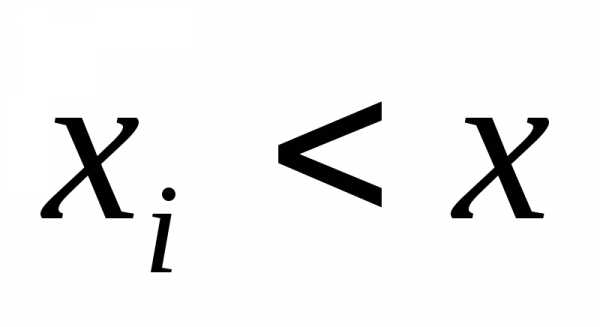 ,
и всеj,
для которых
,
и всеj,
для которых 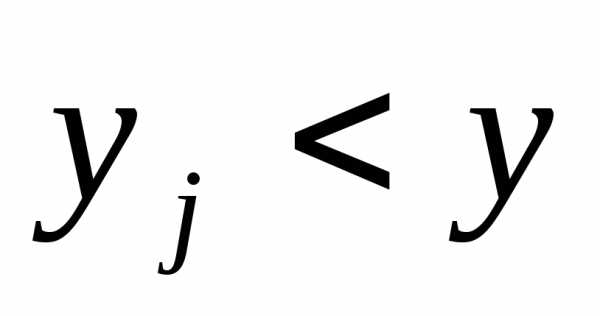
Свойства функции распределения двумерной случайной величины:
Функция распределения
 есть
неотрицательная функция, заключенная
между нулем и единицей, т.е.
есть
неотрицательная функция, заключенная
между нулем и единицей, т.е.
Функция распределения
 есть
неубывающая функция по каждому из
аргументов, т.е.
есть
неубывающая функция по каждому из
аргументов, т.е.
при 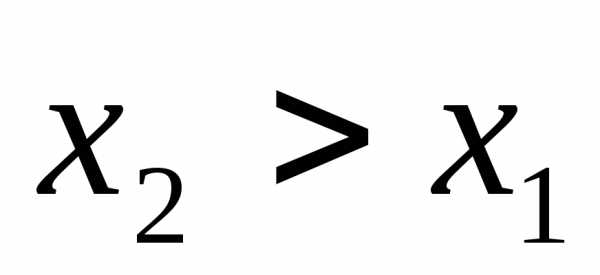
при 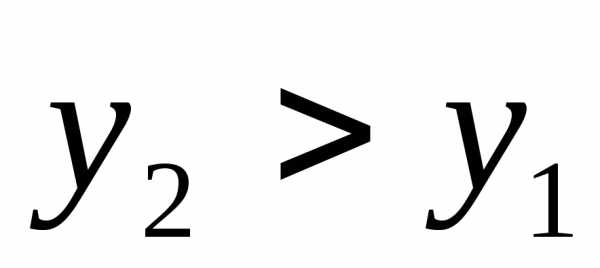
Если хотя бы один из аргументов обращается в -∞, функция распределения F(x;y) равна нулю, т.е.
Если один из аргументов обращается в
 ,
функция распределения
,
функция распределения становится
равной функции распределения случайной
величины, соответствующей другому
аргументу:
становится
равной функции распределения случайной
величины, соответствующей другому
аргументу:
где 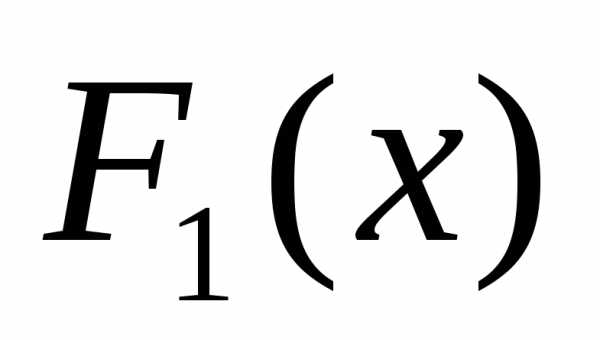 и
и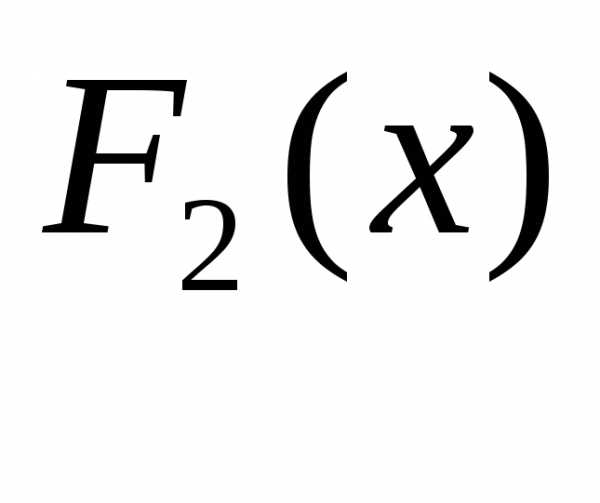 —
функции распределения случайных величинX и Y,
т.е.
—
функции распределения случайных величинX и Y,
т.е.
,
5. Если оба аргумента
равны + ,
то функция распределения равна единице:
,
то функция распределения равна единице:
Геометрически
функция распределения есть некоторая
поверхность, обладающая указанными
свойствами. Для дискретной случайной
величины (X,Y)
ее функция распределения представляет
собой некоторую ступенчатую поверхность,
ступени которой соответствуют скачкам
функции 
Зная функцию распределения можно найти вероятность попадания случайной точки (X,Y) в пределы прямоугольника ABCD, т.е. .
A(x1; y2) B(x2; y2)
y2
y1
D(x1; y1) C(x2; y1)
x1 x2
Плотность вероятности двумерной случайной величины.
Двумерная случайная
величина (X,Y)
называется непрерывной, если ее функция
распределения F(x;y)
– непрерывная функция, дифференцируемая
по каждому из аргументов, и существует
вторая смешанная производная 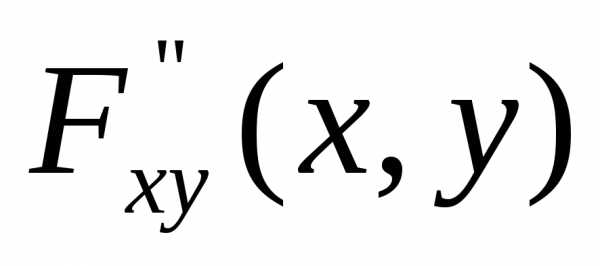 .
.
Плотностью вероятности непрерывной двумерной случайной величины (X;Y) называется вторая смешанная частная производная ее функции распределения, т.е.
Геометрически плотность вероятности двумерной случайной величины (X,Y) представляет собой поверхность распределения в пространстве Oxyz.
Плотность вероятности 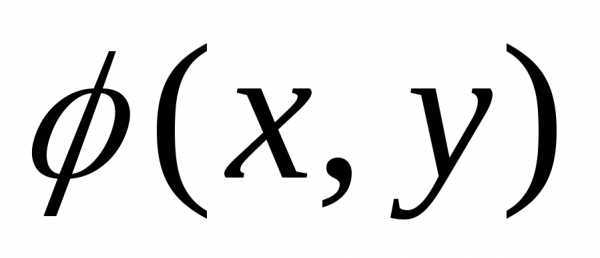 обладает свойствами аналогичными
свойствам плотности вероятности
одномерной случайной величины.
обладает свойствами аналогичными
свойствам плотности вероятности
одномерной случайной величины.
Свойства плотности вероятности:
Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е.
Вероятность попадания непрерывной двумерной случайной величины (X,Y) в область D равна
функция распределения непрерывной случайной величины может быть выражена через ее плотность вероятности
 по формуле:
по формуле:
Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице.
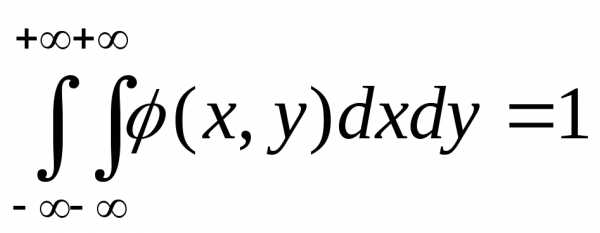
Геометрически последнее свойство означает, что полный объем тела, ограниченного поверхностью распределения и плоскостью Oxy, равен 1.
Замечание: Если
имеется кривая распределения 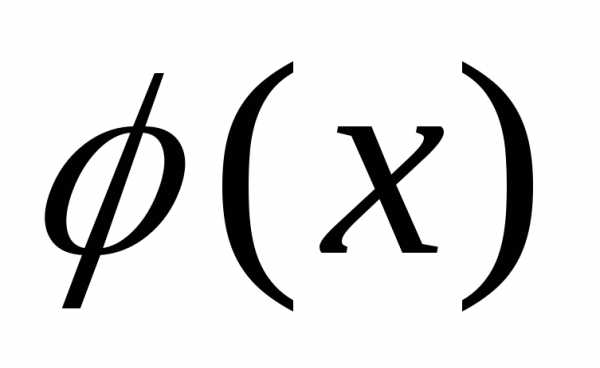 одномерной случайной величины, то
конкретное значение ее плотности
вероятности в данной точкеX
определяется ординатой кривой
одномерной случайной величины, то
конкретное значение ее плотности
вероятности в данной точкеX
определяется ординатой кривой 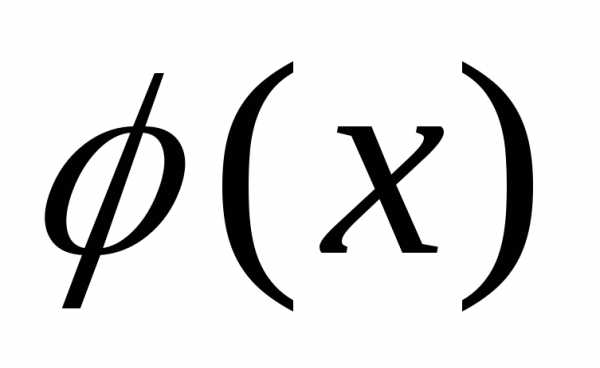
Если имеется
распределение поверхности 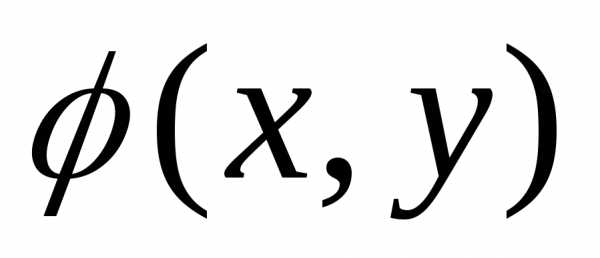 двухмерной
случайной величины, то конкретное
значение ее совместной плотности в
данной точке (x,y)
определяется геометрически аппликатой
поверхности
двухмерной
случайной величины, то конкретное
значение ее совместной плотности в
данной точке (x,y)
определяется геометрически аппликатой
поверхности 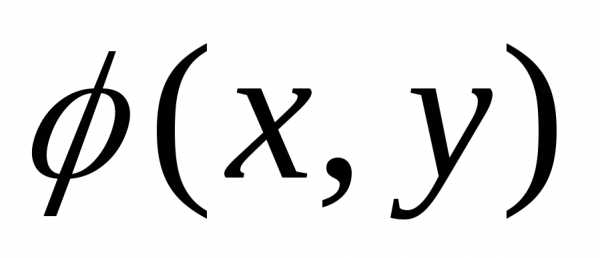 ,
а конкретное значение плотности
вероятности
,
а конкретное значение плотности
вероятности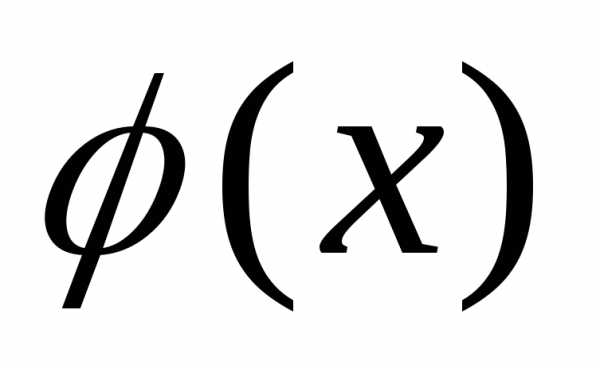 определится
геометрически площадью сечения
поверхности
определится
геометрически площадью сечения
поверхности .
Плоскость параллельна плоскостиOyz
и отсекает на оси OX
отрезок x.
.
Плоскость параллельна плоскостиOyz
и отсекает на оси OX
отрезок x.
studfiles.net
Плотность распределения / Теория вероятности [Калинин В.М., Тихомиров С.Р.] / 3dstroyproekt.ru
Плотность распределения вероятностей непрерывной случайной величины
Опр Плотностью распределения вероятностей непрерывной случайной величины $X$ называют функцию $f( x )-$ первую производную от функции распределения $F( x )$ \begin{equation} \label { eq2 } { F } ‘( x )=f( x ) \end{equation}
Следовательно, функция распределения $F( x )$ является первообразной для функции плотности распределения вероятностей $f( x )$.
Теорема Вероятность того, что непрерывная случайная величина X примет значение принадлежащее интервалу $( { a,b } )$ равна определенному интегралу от плотности. \begin{equation} \label { eq3 } P( { a\leqslant X<b } )=\int\limits_a^b { f( x )dx } \end{equation}
Геометрически этот результат можно трактовать так: вероятность того, что случайная величина $X$ примет значение принадлежащее интервалу $( { a,b } )$ равна площади криволинейной трапеции.
Нахождение функции распределения по известной плотности распределения
Зная плотность распределения вероятностей $f( x )$ можно найти функцию распределения $F( x )$ по формуле: \begin{equation} \label { eq4 } F( x )=\int\limits_ { -\infty } ^x { f( x )dx } \end{equation}
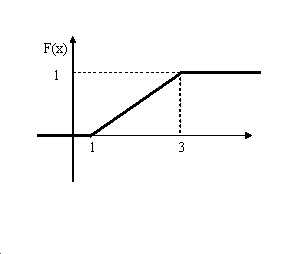
Пример. Найти функцию распределения по данной плотности и построить график. $ f( x )=\left\{ { { \begin{array} { \c } { 0,при\,x=1 } \\ { \frac { 1 } { 2 } ,при\,1<x\leqslant 3 } \\ { 0,при\,x>3 } \\ \end{array} } }\right. $
Решение. Построим график функции плотности распределения вероятностей.
$F( x )=\int\limits_ { -\infty } ^x { f( x )dx } $
Воспользуемся формулой
- при $x\leqslant 1$ из условия $f( x )=0,\Rightarrow F( x )=0 $
- при $\,1<x\leqslant 2,\, f( x )=\frac { 1 } { 2 } $, тогда
$F( x )=\int\limits_ { -\infty } ^x { f( x )dx } =\int\limits_ { -\infty } ^1 { 0dx } +\int\limits_1^x { \frac { 1 } { 2 } dx } =\frac { 1 } { 2 } x\left| { _ { _1 } ^ { ^x } }\right.=\frac { x-1 } { 2 } $
если $x>3$, тогда $ F( x )=\int\limits_ { -\infty } ^x { f( x )dx } =\int\limits_ { -\infty } ^1 { 0dx } +\int\limits_1^3 { \frac { 1 } { 2 } dx } +\int\limits_3^x { 0dx } =\frac { x } { 2 } \left| { _ { _1 } ^ { ^3 } }\right.=1. $
Итак $ F( x )=\left\{ { { \begin{array} { \c } { 0,если\,x\leqslant 1 } \\ { \frac { x-1 } { 2 } ,если\,1<x\leqslant 3 } \\ { 1,если\,x>3 } \\ \end{array} } }\right. $
Построим график функции распределения
Свойства плотности распределения
1). Плотность распределения неотрицательная функция $f( x )\geqslant 0$.
Доказательство Известно, что функция распределения $F( x )-$ неубывающая, следовательно, ее производная $ { F } ‘( x )=f( x )$ неотрицательная функция.
Геометрически это означает, что график $f( x )$ расположен выше оси OX или на оси OX.
График $f( x )$плотности распределения называется кривой распределения.
2). Несобственный интеграл от плотности распределения в пределах от $( { -\infty ,\infty } )$ равен 1. \begin{equation} \label { eq5 } \int\limits_ { -\infty } ^\infty { f( x ) } dx=1 \end{equation}
Если $X$ задана на $( { a,b } )$, то $\int\limits_a^b { f( x )dx=1 } $
Геометрически это означает, что площадь под кривой распределения равна 1.
3dstroyproekt.ru
Функция и плотность распределения
Для
количественной характеристики
распределения вероят-ностей удобней
пользоваться не вероятностью того
события, что случайная величина 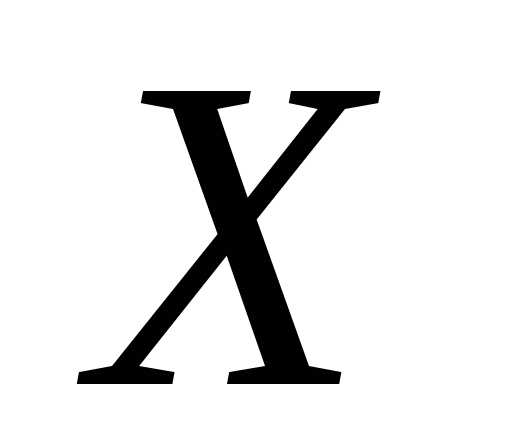 примет значение
примет значение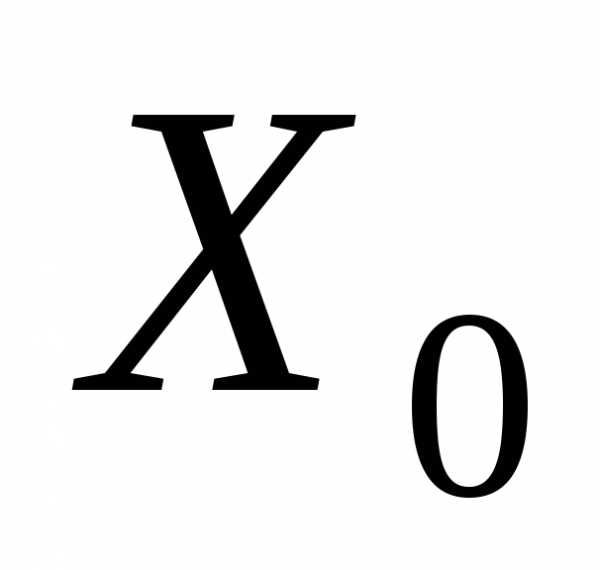 ,т.е.,
а ве-роятностью события,
т.е. того, что случайная величина
,т.е.,
а ве-роятностью события,
т.е. того, что случайная величина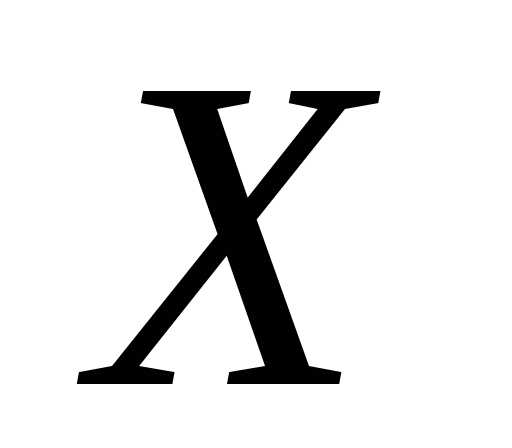 примет значение, меньшее некоторой
текущей переменной
примет значение, меньшее некоторой
текущей переменной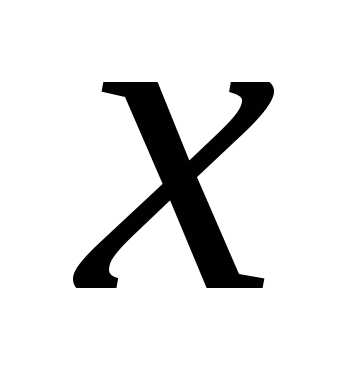 .
Вероятность этого события зависит от
значения
.
Вероятность этого события зависит от
значения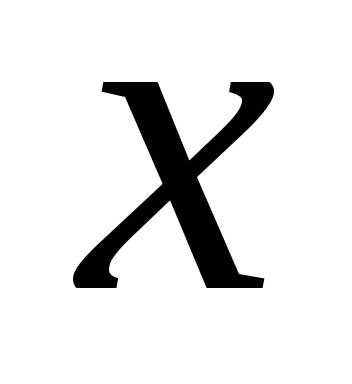 ,
т.е. является функцией
от
,
т.е. является функцией
от 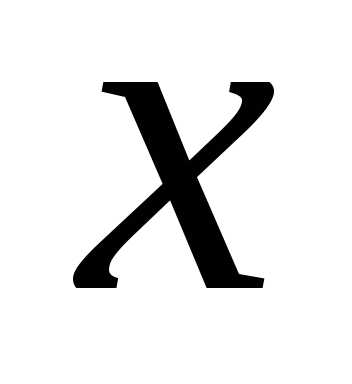 .
Эта функция называется функцией
распределения
.
Эта функция называется функцией
распределения
случайной
величины 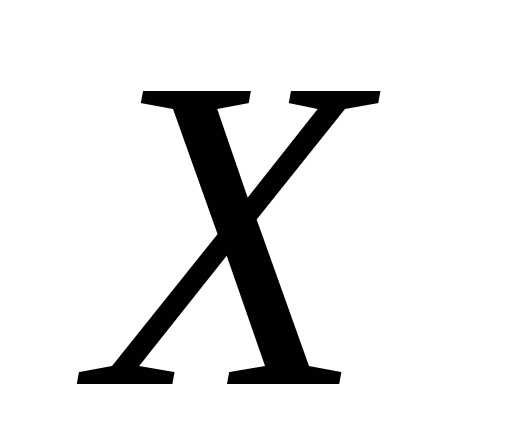 и обозначается
и обозначается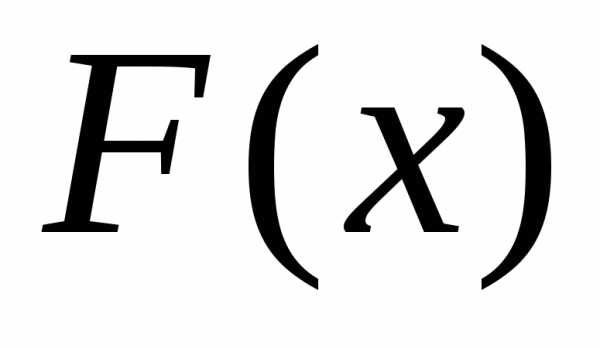 :
:
(1.6)
Функция распределения случайной величины самая универ-сальная характеристика случайной величины, она существует как для дискретных случайных величин, так и для непрерывных. Функ-ция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Функции распределения обладают некоторыми об-щими свойствами:
1.
Функция распределения 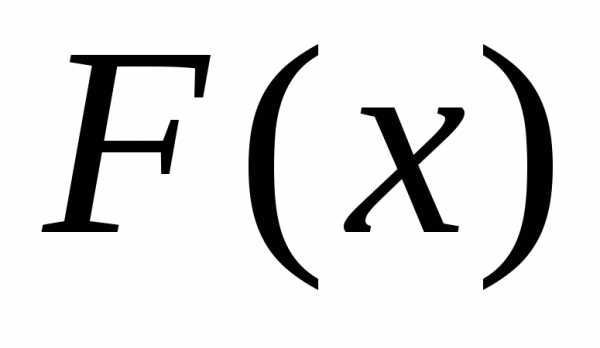 есть неубывающая функция сво-его
аргумента, т.е. при
есть неубывающая функция сво-его
аргумента, т.е. при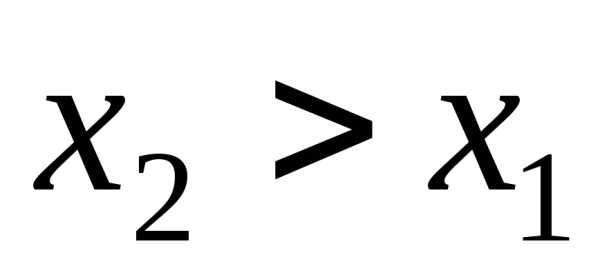 выполняется.
выполняется.
2. На минус бесконечности функция распределения равна нулю: .
3. На плюс бесконечности функция распределения равна едини-це: .
График функции распределения в общем случае может быть представлен как график неубывающей функции (рис.1), значения которой начинаются от 0 и доходят до 1, причем в отдельных точ-ках функция может иметь скачки (разрывы).
Пусть имеется
непрерывная случайная величина 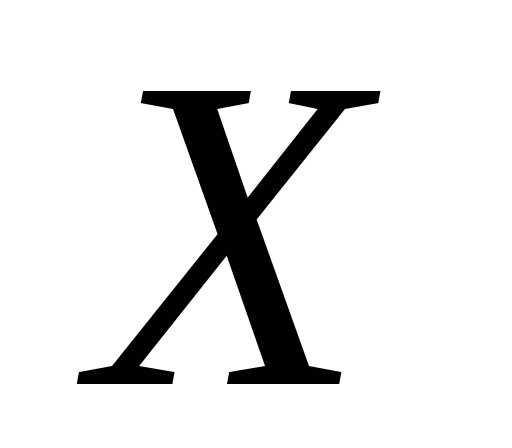 с функцией распределения
с функцией распределения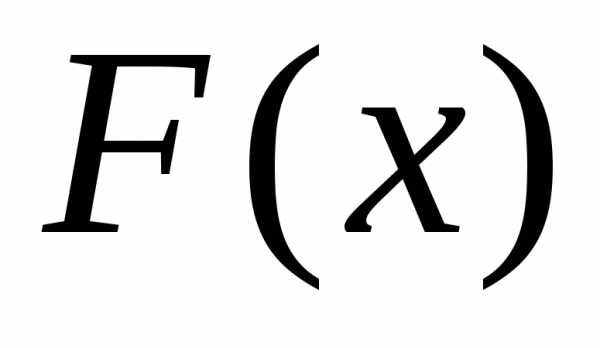 ,
которую мы предположим непрерывной и
дифференцируемой. Посколькудля непрерывной случайной величи—ны
вероятность принятия случайной величиной
любого отдельного значения равна нулю,
то вычислим вероятность попадания этой
,
которую мы предположим непрерывной и
дифференцируемой. Посколькудля непрерывной случайной величи—ны
вероятность принятия случайной величиной
любого отдельного значения равна нулю,
то вычислим вероятность попадания этой
случайной величины
на участок от 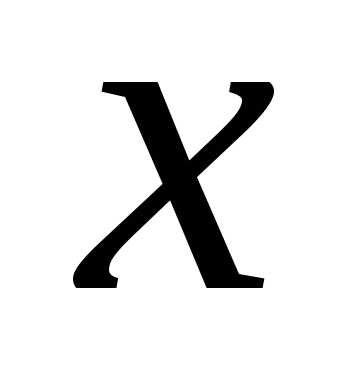 до
до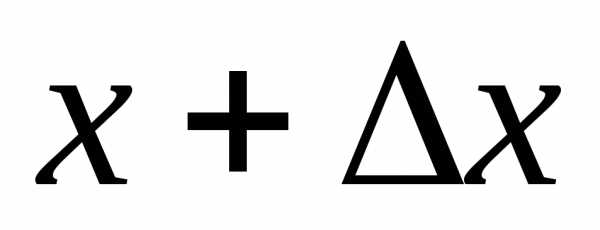 :
:
(1.7)
Вероятность
попадания в указанный интервал
рассчитывается как приращение
функции распределения на этом участке.
Рассмот-рим отношение этой вероятности
к величине интервала, т.е. сред-нюю
вероятность, приходящуюся на единицу
длины на этом участ-ке, и будем приближать 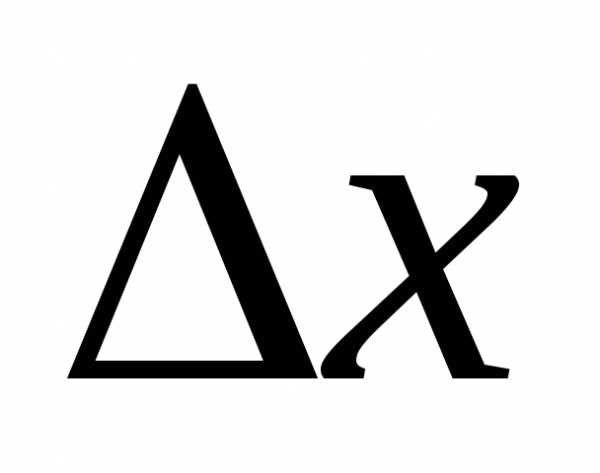 к нулю. В пределе получим производ-ную
от функции распределения:
к нулю. В пределе получим производ-ную
от функции распределения:
(1.8)
Введем обозначение для производной от функции распределе-ния:
(1.9)
Функция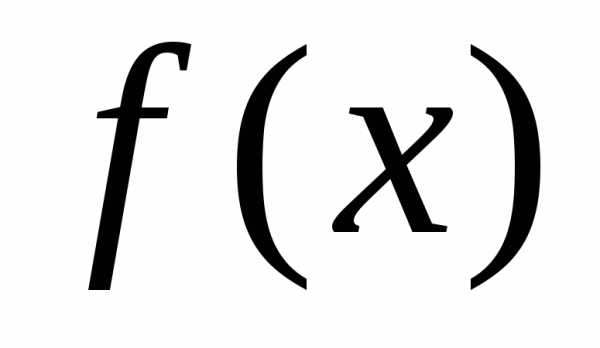 характеризует как бы плотность, с которой
рас-пределяется значение случайной
величины в данной точке (а на самом деле
отражает быстроту возрастания функции
распределе-ния). Функция
характеризует как бы плотность, с которой
рас-пределяется значение случайной
величины в данной точке (а на самом деле
отражает быстроту возрастания функции
распределе-ния). Функция называется плотностью распределения
(или плотностью вероятности) непрерывной
случайной величины
называется плотностью распределения
(или плотностью вероятности) непрерывной
случайной величины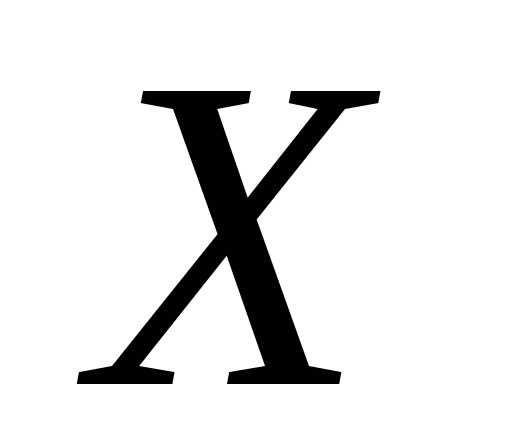 .
В отличие от функции распределения,
плотность распределения не является
универсальной–
она существует только для непрерывных
величин. Кривая, изображающая плотность
распределения случай-ной величины,
называется кривой распределения (рис.2).
.
В отличие от функции распределения,
плотность распределения не является
универсальной–
она существует только для непрерывных
величин. Кривая, изображающая плотность
распределения случай-ной величины,
называется кривой распределения (рис.2).
Геометрически
вероятность попадания величины 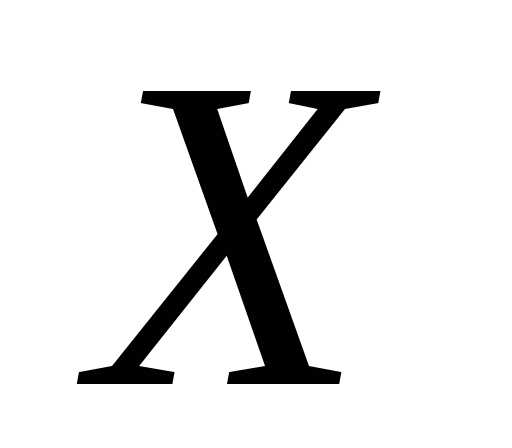 в участок
в участок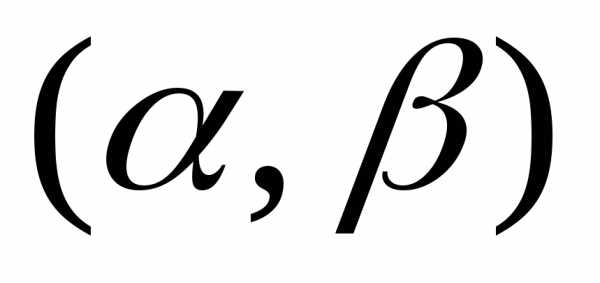 равна площади кривой распределения,опирающейся
на этот участок.Значение
же функции распределения
равна площади кривой распределения,опирающейся
на этот участок.Значение
же функции распределения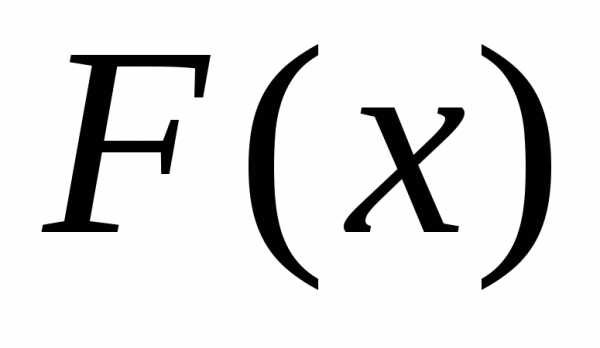 есть не что иное,как
площадь кривой распределения, лежащей
левее точки
есть не что иное,как
площадь кривой распределения, лежащей
левее точки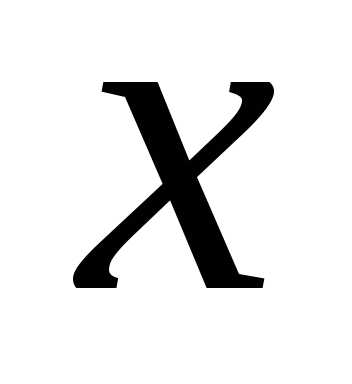 .
.
Для дискретных величин аналогом графика распределения может служить гистограмма, отображающая величину прироста функции распределения (рис.3).
Плотность распределения обладает следующими свойствами:
1.
Плотность распределения есть
неотрицательная функция: 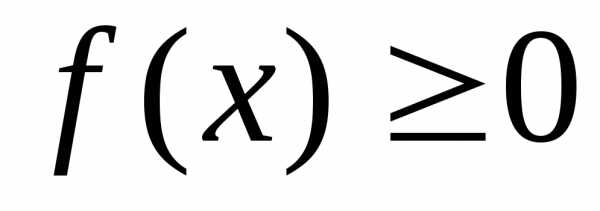 .
Это свойство вытекает непосредственно
из того, что
.
Это свойство вытекает непосредственно
из того, что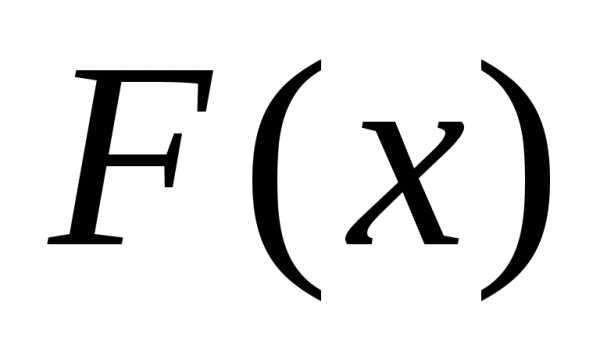 есть функция неубывающая.
есть функция неубывающая.
2.
Интеграл в бесконечных пределах от
плотности вероятности равен единице: 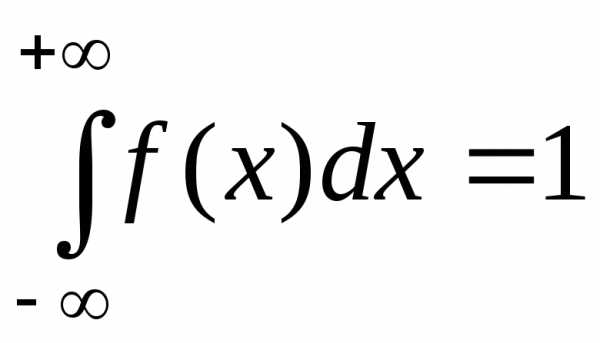 (условие
нормировки).
Условие говорит о том, что вероятность
принятия случайной величиной какого–ли-бо
значения равна единице.
(условие
нормировки).
Условие говорит о том, что вероятность
принятия случайной величиной какого–ли-бо
значения равна единице.
studfiles.net
Плотность распределения вероятностей — f(x)
Для непрерывных случайных величин наряду с законом распределения вероятностей рассматривают плотность вероятностей, которую обозначают так .
Плотностью вероятностей случайной величины называют первую производную от интегральной функции распределения вероятностей
откуда дифференциал
Поскольку прирост определяют зависимости
куплена плотности вероятностей на прирост случайной величины соответствует вероятность того, что случайная величина содержаться в промежутке где .
Геометрически на графике плотности вероятностей соответствует площадь прямоугольника с основанием и высотой
Свойства плотности вероятностей
1. Плотность вероятностей принимает положительные значения . Это свойство следует из определения первой производной от функции распределения , которая в свою очередь является неубывающей функцией.
2. Условие нормирования случайной величины
3.Вероятность попадания случайной величины в промежуток определяется зависимостью
4. Функция распределения вероятностей непрерывной случайной величины определяется через плотность распределения вероятностей интегрированием
—————————————
Рассмотрим задачи для закрепления материала на практике.
Пример 1. Закон распределения случайной величины заданы функцией
Найти плотность распределения вероятностей и построить графики обеих функций . Вычислить вероятность того, что случайная величина принадлежит промежутку
Решение. Вычисляем функцию плотности вероятностей
Графики функций изображены на рисунках
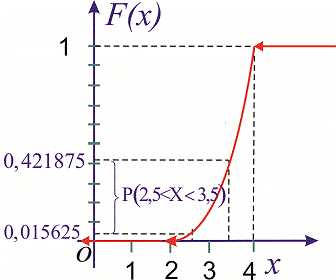
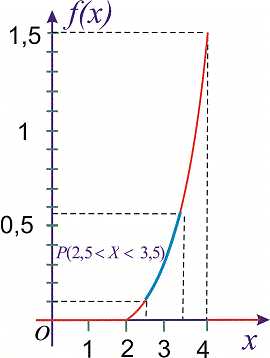
Вероятность события вычислим по формуле
Согласно приведенной выше формулы получим
На этом задача решена.
———————————————
Пример 2. По заданной функцией плотности распределения вероятностей
установить параметры и функцию распределения вероятностей . Построить графики функций.
Решение. Значение постоянной определяем из условия нормировки
При найденном значении плотность вероятностей будет иметь вид
Функция распределения вероятностей определяется интегрированием:
Записываем общий вид функции ,
Графики функций распределения вероятностей и ее плотности показаны на рисунках ниже

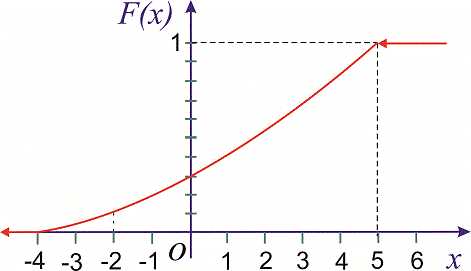
—————————————
Пример 3. Случайная величина имеет закон распределения вероятностей в виде треугольника
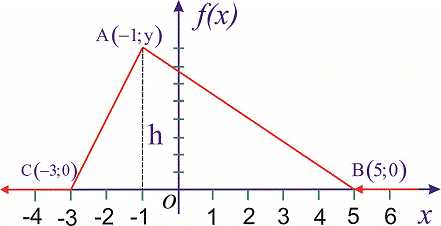
Записать выражения для плотности вероятностей и функции распределения вероятностей, построить график и вычислить .
Решение. На промежутках и плотность вероятностей меняется по линейному закону вида
для первого и второго участки соответственно. Для нахождения неизвестных констант установим ординаты вершины треугольника . Используем условие нормирования, согласно которому площадь треугольника равна единице:
При известных координатах всех вершин находим уравнение прямых
Есть другой способ нахождения уравнения прямых, предусматривающий отыскания по одной константе на уравнение. Если известна точка пересечения прямой с осью ординат , то уравнение прямой которая через эту точку проходит следующее
где – ордината пересечения с осью . Подстановкой второй точки прямой находят неизвестную константу . Для заданных точек получим
Со временем второй метод для Вас станет проще и практичнее в использовании. Плотность вероятностей примет значение
а ее функция примет вид
Функцию распределения вероятностей находим интегрированием:
а) на промежутке :
2) на промежутке
Следовательно, функция распределения вероятностей такая
Ее график приведен ниже
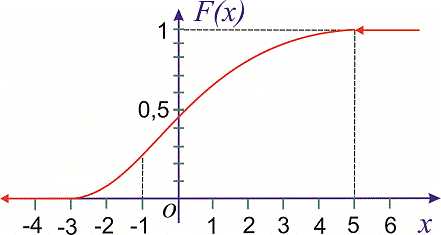
Вычисляем вероятность события согласно формуле
или
Следовательно, вероятность равна
————————-
Хорошо проанализируйте приведенные примеры — это поможет научиться быстро находить плотность распределения вероятностей и выполнять построение графика. Будьте внимательны при интегрировании и выбирайте удобную для вычислений методику.
yukhym.com

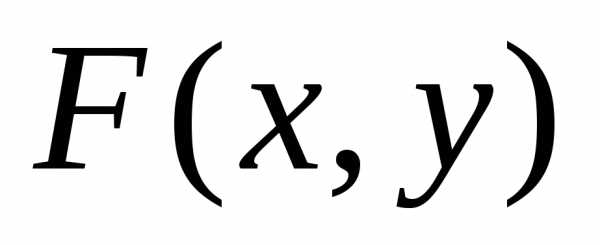 есть
неотрицательная функция, заключенная
между нулем и единицей, т.е.
есть
неотрицательная функция, заключенная
между нулем и единицей, т.е.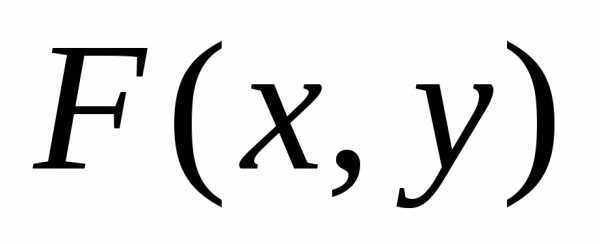 есть
неубывающая функция по каждому из
аргументов, т.е.
есть
неубывающая функция по каждому из
аргументов, т.е. ,
функция распределения
,
функция распределения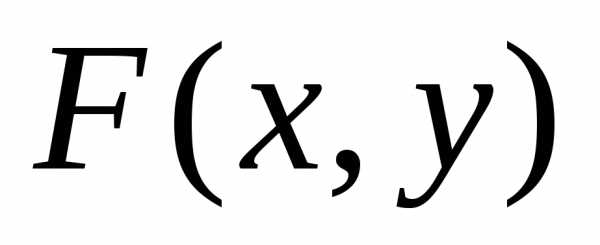 становится
равной функции распределения случайной
величины, соответствующей другому
аргументу:
становится
равной функции распределения случайной
величины, соответствующей другому
аргументу: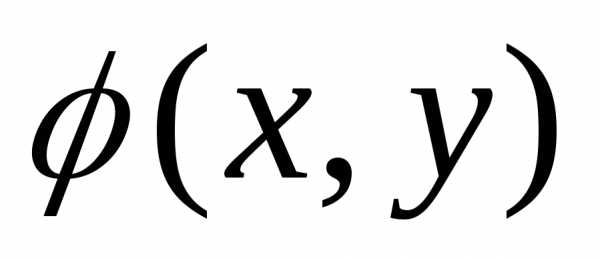 по формуле:
по формуле: