Подобие треугольников задачи – Задачи на подобие треугольников

Задачи на подобие треугольников

Рассмотрим некоторые задачи на подобие треугольников.

I. В треугольнике проведен отрезок, параллельный стороне. Концы отрезка лежат на других сторонах треугольника.

 

Рассмотрим треугольники ABC и A1BC1.

 

 

 

 

Решать задачи на подобие треугольников удобнее, используя цветовую визуализацию, поэтому выделим данные треугольники разными цветами:

1) ∠B — общий;

2)∠ BAC=∠BA1C1 (как соответственные углы при AC∥A1C1 и секущей AB).

Следовательно, треугольники ABC и A1BC1 подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

 

Задача

Прямая, параллельная стороне АС треугольника АВС, пересекает сторону АВ в точке А1, а сторону ВС — в точке В1. Найти длину отрезка А1С1, если АС=35,  АА1: А1В=2:5.

Решение:

Доказываем подобие треугольников ABC и A1BC1. 

   

   

Ответ: 25.

II. В треугольник вписан ромб.

Рассмотрим треугольники  AFK и BFC.

 

 

 

 

 

Выделим данные треугольники в цвете.

1) ∠F — общий;

2)∠ FAK=∠FBC (как соответственные углы при AD∥BC и секущей AB).

Следовательно, треугольники AFK и BFC подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

 

Задача.

В треугольник AFK вписан ромб ABCD так, что угол A у них общий, в вершина C принадлежит стороне FK. Найти сторону ромба, если AF=21 см, AK=24 см.

Решение.

Доказываем подобие треугольников AFK и BFC. Из трех соотношений выбираем те, в которых нам что-либо известно:

   

Примем сторону ромба за x:

   

Тогда BF=AF-AB=21-x см. Отсюда

   

Разделив обе части уравнения на 3, получаем:

   

   

   

   

Ответ: 11,2 см.

В следующий раз рассмотрим задачи на подобные треугольники в трапеции.

www.uznateshe.ru

Повторение темы «Подобные треугольники». Решение задач

На этом уроке мы займемся повторением темы «Подобные треугольники. Решение задач». Занятие начнем с повторения понятия «подобные треугольники», вспомним все три признака подобия этих фигур. После решим несколько задач на эту тему, используя полученные ранее знания.

Тема: Подобные треугольники

Урок: Повторение темы «Подобные треугольники». Решение задач

На этом уроке мы повторим тему «Подобные треугольники».

Для начала вспомним определение подобных треугольников.

Определение

Треугольники  и  называются

подобными треугольниками (), если у них все углы равны, а соответствующие стороны пропорциональны (см. Рис. 1).

Рис. 1

; .

При этом коэффициент  называется коэффициентом подобия.

Если обозначить: , можно получить следующие соотношения между сторонами подобных треугольников: .

Кроме того, площади подобных треугольников относятся как квадрат коэффициента подобия: .

Для того чтобы определить, являются ли треугольники подобными, не прибегая к определению, существуют признаки подобия треугольников.

Всего существует три признака подобия. Перечислим их:

1.      По равенству двух углов: если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны:.

2.      По пропорциональности двух сторон и равенству угла между ними: если две стороны одного треугольника пропорциональны соответственно двум сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны: .

3.      По пропорциональности трёх сторон: если три стороны одного треугольника пропорциональны соответственно трём сторонам другого треугольника, то такие треугольники подобны: .

С помощью подобия треугольников доказывается свойство средней линии треугольника. Напомним определение средней линии треугольника.

Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Свойство средней линии треугольника: средняя линия треугольника параллельна стороне треугольника и равна её половине (см. Рис. 2).

Рис. 2

.

С подобием связано доказательство ещё одного важного факта – свойства медиан треугольника (которое иногда ещё называют теоремой Архимеда): медианы треугольника пересекаются в одной точке, причём точкой пересечения делятся в отношении , считая от вершины треугольника (см. Рис. 3).

Рис. 3

;

Полезными свойства подобия оказываются и в прямоугольных треугольниках. Мы выяснили, что высота прямоугольного треугольника, проведённая к гипотенузе, делит треугольник на два подобных прямоугольных треугольника, которые подобны также исходному треугольнику. Из этого следует сразу несколько важных фактов, связывающих пропорциональные отрезки в прямоугольном треугольнике (см. Рис. 4).

Рис. 4

.

1.       (катет равен среднему геометрическому гипотенузы и своей проекции на неё).

2.       (катет равен среднему геометрическому гипотенузы и своей проекции на неё).

3.       (высота, проведённая к гипотенузе, равна среднему геометрическому проекций катетов на гипотенузу).

Рассмотрим задачу, в которой используются полученные в теме «Подобные треугольники» знания.

Задача

Дан прямоугольный треугольник . В нём проведена высота . . Найти высоту треугольника, катеты, а также синус угла  и тангенс угла .

Дано: ,  – высота, .

Найти:  – ?

Решение

Рис. 5

Воспользуемся соотношениями между пропорциональными отрезками в прямоугольном треугольнике:

.

.

.

Найдём синус угла , воспользовавшись определением синуса острого угла прямоугольного треугольника – отношение противолежащего катета к гипотенузе:

.

Найдём тангенс угла , воспользовавшись определением тангенса острого угла прямоугольного треугольника – отношение противолежащего катета к прилежащему: .

Ответ: .

На этом уроке мы повторили тему «Подобные треугольники». На следующем уроке мы начнём изучение новой темы: «Окружность».

 

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Фестиваль педагогических идей «Открытый урок» (Источник).
2. 6yket.ru (Источник).

 

Домашнее задание

1. № 144(б-г), 145(б-з), Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
2. В прямоугольном треугольнике : , . Найти расстояние от середины катета  до гипотенузы.
3. Докажите, что отношение соответствующих медиан подобных треугольников равно коэффициенту подобия. 
4. Высота дерева равна , а длина тени человека, рост которого , равна . Найдите длину тени дерева.
5. Высота параллелограмма, проведенная из вершины тупого угла, делит сторону в отношении . В каком отношении эта высота делит диагональ параллелограмма?

interneturok.ru

Решение задач по теме «Подобие треугольников»

Просмотр содержимого документа
«Решение задач по теме «Подобие треугольников»»

1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4, АС = 9.

2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.

3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.

4. В трапеции ABCD меньшая диагональ BD, равная 6, перпендикулярна основаниям AD=3 и DC=12. Найдите сумму тупых углов B и D.

5. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.

___________________________________________________________________

1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4, АС = 9.

2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.

3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.

4. В трапеции ABCD меньшая диагональ BD, равная 6, перпендикулярна основаниям AD=3 и DC=12. Найдите сумму тупых углов B и D.

5. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.

Задачи для изучения (с решением):

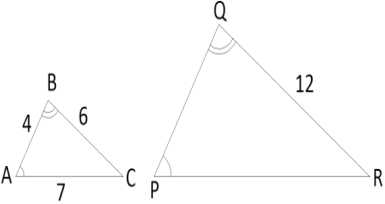
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными. Решение: Так как длины сторон обоих треугольников известны, то здесь можно применить третий признак подобия треугольников: PQ/AB=6/2=3  QR/CB=12/4=3  PR/AC=15/5=3, Т.к. все отношения равны 3, то треугольники подобны	Третий признак подобия треугольников
Пример №2: Докажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.	Первый признак подобия
Пример №3: Определите длину AB в данном треугольнике.	Первый признак подобия
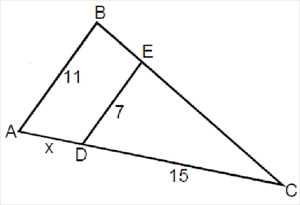
Пример №4:Определить длину AD (x) геометрической фигуры на рисунке. Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C. Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически. AB || DE, CD || AC и BC || EC ∠BAC = ∠EDC и ∠ABC = ∠DEC Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны. Следовательно: x = AC — DC = 23,57 — 15 = 8,57

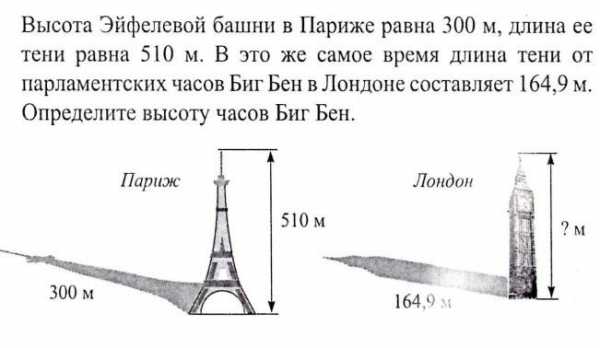
ТЕСТ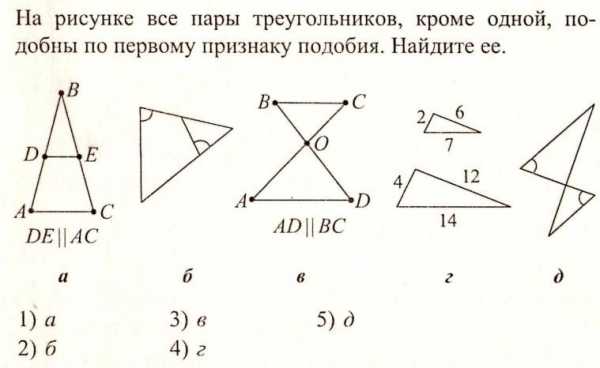

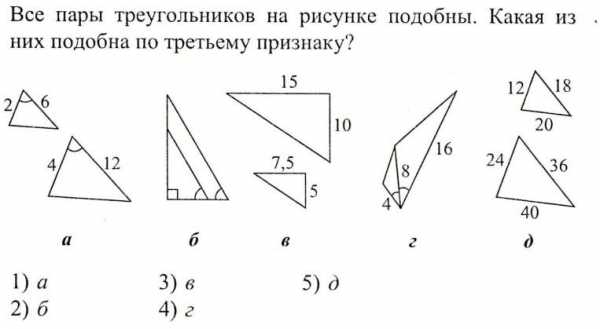
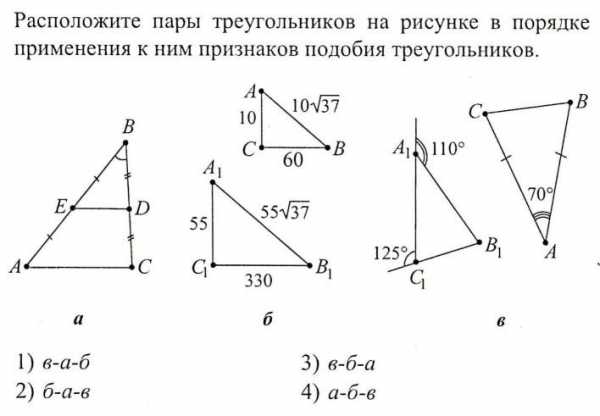
multiurok.ru

При подготовке к ЕГЭ по математике наиболее сложными являются задачи по геометрии – C4. Причем это задачи по планиметрии. Для успешного их решения надо, чтобы у абитуриента была очень хорошая база по простым задачам. Но чтобы уметь быстро и хорошо решать, надо много решать. Я уже ранее приводил список простых задач по использованию подобных треугольников.

Приведу условия подобия двух треугольников. Два треугольника подобны, если…

1.  равны их углы.

2. пропорциональны все стороны.

3. две стороны пропорциональны, а углы между ними равны.

При формулировке 3-го условия всегда возникает вопрос “А подобны ли треугольники, если пропорциональны две стороны и равен один из углов?”. Приведите пример, когда данное условие не выполняется.

Теперь привожу подборку чуть более сложных задач.

В скобках указаны ответы к задачам и иногда решения задач.

1. В прямоугольном ΔABC к гипотенузе AC проведена высота BD, BC = 2 см, AD = 3 см. Найдите DC, BD, AB. [DC = 1см, BD = 3 см, AB= 2 3 см. Для решения можно воспользоваться подобием ΔCDB и ΔBDA, а также теоремой Пифагора]

2. Треугольники ABC и MNK подобны. Их сходственные стороны относятся как 8:5. Площадь ΔABC больше площади ΔMNK на 25 см². Найдите площади треугольников. [Указание. Учесть, что если стороны относятся ка 8:5, то квадраты относятся как 64:25. Ответ: 16 см² и 41 см² ]

3. Основания трапеции равны 8 см и 12 см. Боковые стороны, равные 4,5 см и 5,2 см, продолжены до пересечения в точке M. Найдите расстояния от точки M до концов меньшего основания.
Решение. Пусть x, y – неизвестные расстояния, тогда находим из пропорций x:(x+4,5)=8:12 и y:(y+5,2)=8:12. [9 см и 10,4 см]

4. В прямоугольном треугольнике с углом 30°и меньшим катетом 6 см проведены средние линии. Найдите периметр треугольника, образованного средними линиями.
Решение. Используя тангенсы, найти второй катет. Далее учесть, что площадь неизвестного треугольника в 4 раза меньше площади исходного. [9 + 3 см]

5. На сторонах AB, BC, AC треугольника ABC отмечены точки D, E, P соответственно; AB = 9 см, AD = 3 см, AP = 6 см, DP = 4 см, BE = 8 см, DE = 12 см.
а) Найдите отношение площадей ΔDBE и ΔADP. [4]
б) Докажите, что DE и AC параллельны.

6. Диагонали выпуклого четырехугольника ABCD пересекаются в точке O так, что OC = 5 см, OB = 6 см, OA = 15 см, OD = 18 см.
а) Найдите отношение площадей ΔAOD и ΔBOC.[9]
б) Докажите, что четырехугольник ABCD – трапеция.

7. Высоты, проведенные из вершины тупого угла параллелограмма, относятся как 2 : 4. Чему равна меньшая сторона параллелограмма, если периметр равен 90 см? [15 см]

8. Две сходственные стороны подобных треугольников равны 5 см и 6 см. Разность площадей этих треугольников составляет 22 см2. Чему равна площадь меньшего треугольника? Указание. Учесть решение задачи 2. [50 см2]

9. Катеты прямоугольного ΔABC равны 5 см и 12 см. К гипотенузе в ее середине восставлен перпендикуляр OD, пересекающий продолжение меньшего катета в точке D. Чему равна длина отрезка CD?[11,9 см]

10. В прямоугольном ΔABC с прямым углом C проведен перпендикуляр CD. Чему равна гипотенуза треугольника ABC, если CD = 6 см, AD = 4,5 см? [12,5 см]

Задачи взяты из журнала 1 сентября. Хотя многие из этих задач уже имеются на различных сайтах.

Связанные статьи

mathi.ru

Комплекс задач по теме «Подобие треугольников»

Комплекс задач по теме «Подобие треугольников»

Какие задачи из элементарной математики считаются самыми трудными? Геометрические. ЕГЭ по математике предъявляет требования определенного уровня к «геометрической» культуре и подготовке выпускников, к умению логически мыслить, к знаниям методов решения задачи. В алгебре, началах математического анализа разработана целая серия алгоритмов решения типовых задач. В геометрии, как правило, алгоритмов нет. Тем не менее можно использовать некоторые общие положения и рекомендации, которые полезно соблюдать любому решающему геометрическую задачу (тем более при подготовке к ЕГЭ). К таким положениям можно отнести следующие:

1. Обучать учащихся технологии решения задачи, т.е. самостоятельному выполнению каждого из этапов процесса решения задачи.

2. Обучать решению геометрических задач через выделение ключевых задач.

3. Устанавливать связи между задачами, разрабатывать (составлять) комплекс задач.

Комплекс задач — это набор задач, который:

— имеет одинаковую основу;

— имеет последовательность, при которой каждая следующая задача обогащала бы опыт предыдущей;

— сформулирован таким образом, чтобы осуществлялся переход от одной задачи к другой.

Основой комплекса может быть:

— единая геометрическая конструкция;

— метод решения;

— единая тематика;

— теорема;

— ключевая задача;

— дополнительное построение и др.

Большую трудность у учащихся всегда вызывают задачи на применение подобия, поэтому предлагаю комплекс задач по теме «Подобие треугольников» (по материалам спецкурса для 10—11 классов).

Ключевые задачи.

1.

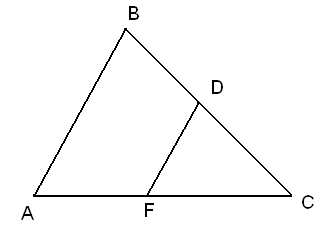∆DCF∆BCA

DF || АВ

2.

1) ∆ADC∆ACB, ()

2) ∆BDC∆BCA, ()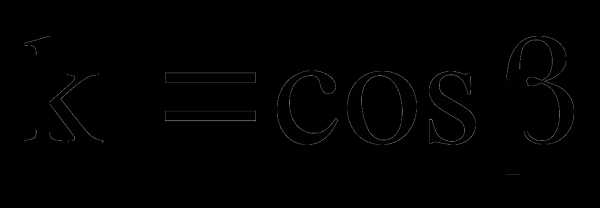

3) ∆ADC∆CDB, ()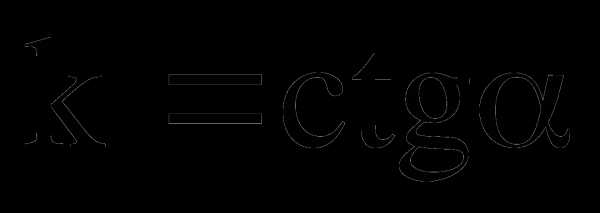

Следствия

AC²=AB∙BD

BC²=AB∙BD

CD²=AD∙BD

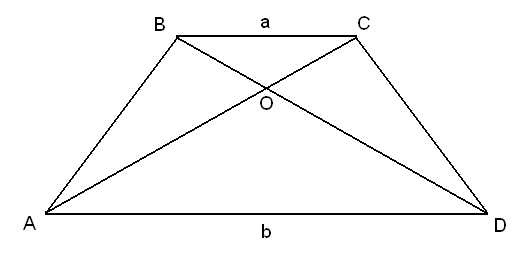
3.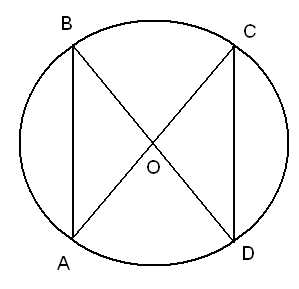

∆BAO∆COD

4.

∆BOC∆DOA

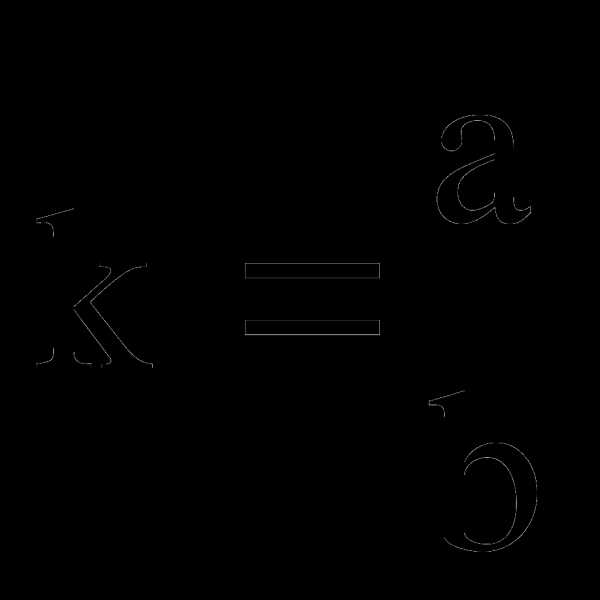
Н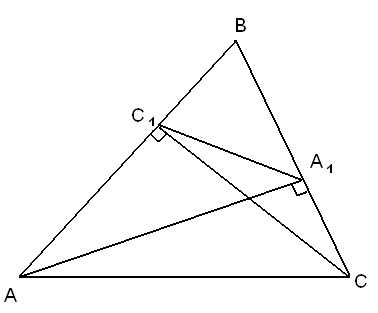аиболее подробно представлю задачу №5 и комплекс задач, основой которого является данная задача (данная задача была представлена в 2004 г. на пробном ЕГЭ).

В остроугольном треугольнике отрезок, соединяющий основания двух высот, отсекает треугольник, подобный данному.

Доказательство:

1. ∆BA₁A∆BC₁C по двум углам ()

Значит, ; ; по свойству пропорции

2. Рассмотрим: ∆A₁ВС₁ и ∆ABC

— общий, стороны, заключающие общий угол, пропорциональны.

Вывод: ∆BA₁A∆BC₁C по || признаку подобия.

Следствие:

Из подобия треугольников следует: ;

В комплекс входят задачи:

I уровень:

1. На отработку определения подобия в данной конструкции.

2. На отработку , — общий угол треугольников

3. 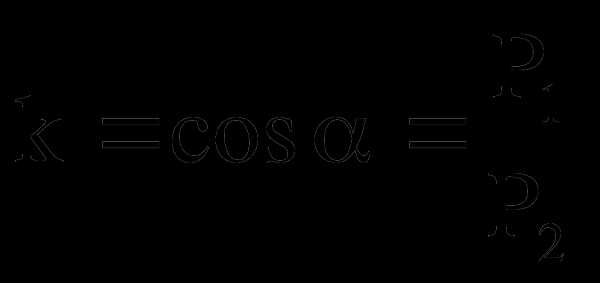, (взаимосвязь)

II уровень:

тот же тип задач, но конструкция завуалирована.

III уровень:

привлечение других фактов или теорий к заданной конструкции.

VI уровень:

контрпример (конструкция сходна, но теорема «не работает»)

I уровень:

1. В остроугольном — ∆АВС AA₁ и CC₁ высоты. АВ=15 см, ВС=12 см, АС=18 см, Л,С,=0,6 дм.

a) Найти ВА, и ВС,

b) Найти угол В.

2. В остроугольном ∆АВС AA₁ и CC₁ — высоты, .

а) Найти периметр ∆А₁В₁С₁, если периметр равен 52 см

b) Найти площадь ∆АВС, если площадь ∆А₁В₁С₁ 17 см².

II уровень:

1. В ∆MNK на стороне МК как на диаметре построена окружность, пересекающая стороны MN и NK в точках Е и F соответственно, .

Найти угол FEN.

Анализ ситуации и поиск решения.

1. Как связаны элементы фигур, данных в условии?

* сторона треугольника МК — диаметр окружности

* Е и F — общие точки сторон треугольника и окружности

* угол MKN треугольника — вписанный в окружность.

2. Какие дополнительные построения обычно выполняют для получения дополнительной информации?

* соединяем центр окружности с точками окружности или соединяем точки окружности (возможные предложения ОЕ и OF; MF, КЕ)

* какие при этом образовались фигуры, что о них известно? Как связаны элементы фигур с данными в условии?

3. Остановимся (в результате обсуждения) на ∆MFK

* — вписанный в окружность

* — вписанный в окружность, опирается на диаметр, значит, тогда в ∆MFK MF — высота.

4. Аналогично КЕ — высота ∆MFK.

Вывод: получили известную конструкцию: в остроугольном ∆MFK проведены две высоты, значит, по ключевой задаче, FE отсекает треугольник, подобный данному, т.е. ∆MFK∆FNE.

значит соответственные углы равны, т.е. Искомый угол 40°.

Ответ: 40°.

Задача 5.

Отрезок АВ — диаметр круга, а точка Р — вне его так, что АР и РВ пересекают окружность в точках С и В соответственно

1) Найти расстояние между С и В, если радиус окружности .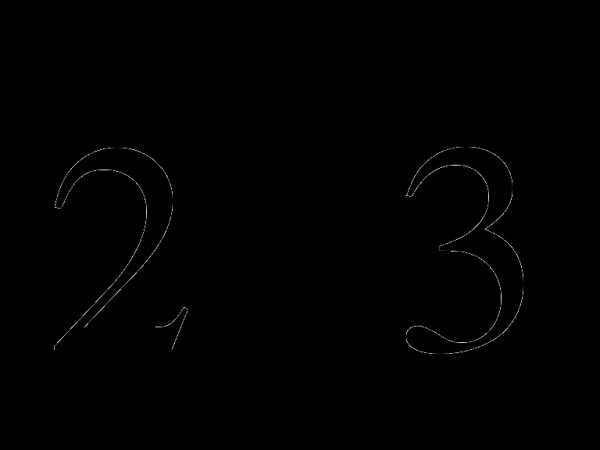

2) Найти площадь ∆ABP, если площадь ∆CDP равна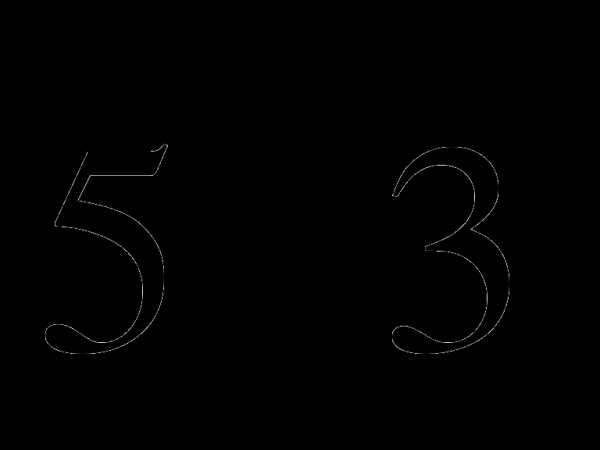

Решение:

1. Ситуация аналогична предыдущей задаче; в результате анализа приходим к выводу, что ∆ABP∆DPC. .

Пары сходственных элементов подобных треугольников неизвестны, но известен общий угол, поэтому

; ; ; .

; ; ; .

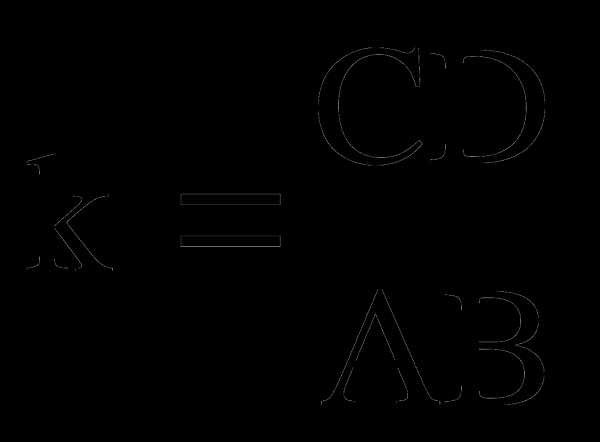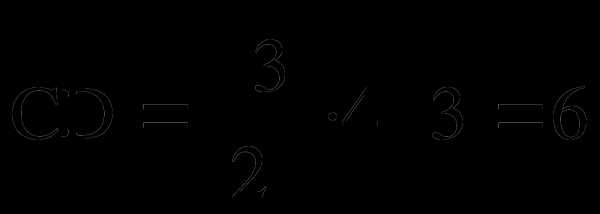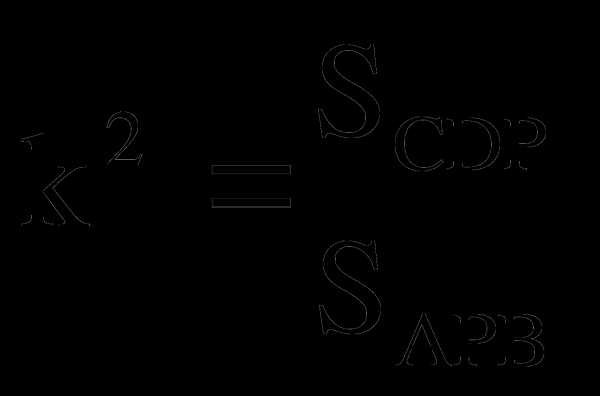Ответ:

Задача 6.

АВ — диаметр круга, а точка Р вне его выбрана так, что АР и РВ пересекают окружность в точках С и D соответственно, причем CD делит ∆ABP на части, площади которых относятся как 1:3. Найти угол между АР и ВР (или угол, под которым виден диаметр круга из точки Р).

Решение:

Ситуация аналогична.

В результате анализа приходим к выводу, что ∆APB∆DPC. Т.к. отношение площадей и четырехугольника ACDB равно , то отношение площадей подобных треугольников равно . Задача сводится к нахождению общего угла подобных треугольников, значит 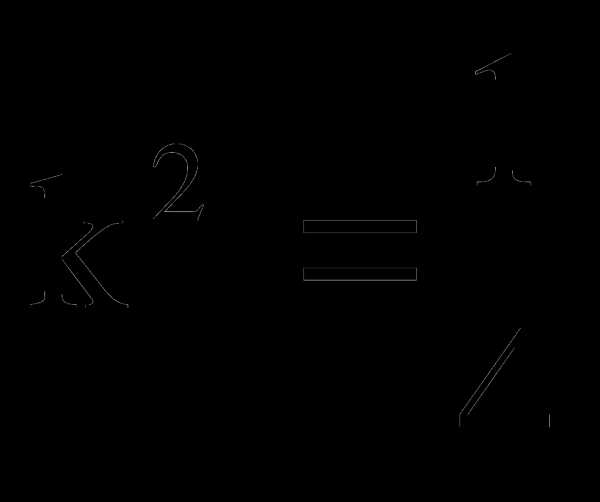; ; , где — величина общего угла — АРВ. 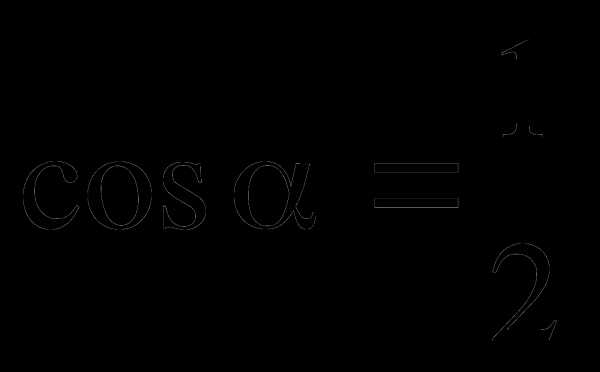, искомый угол 60°.

Ответ: 60°.

III уровень.

Задача 7.

В остроугольном треугольнике ABC CF и AD высоты. АС=1. Угол ACF равен . Найти площадь круга, описанного около ∆FBD.

Решение:

1. По ключевой задаче ∆ABD∆DBF. (из прямоугольного ∆FBC)

2. По следствию из теоремы синусов , где R — радиус окружности, описанной около ∆ABC.

; .

3. 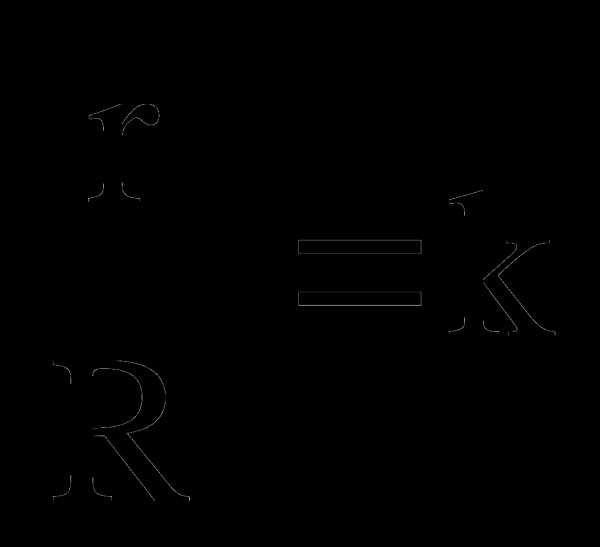, где r — радиус окружности, описанной около ∆FBD

; ; .

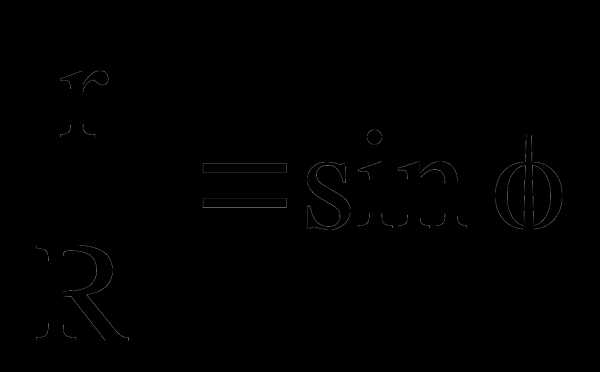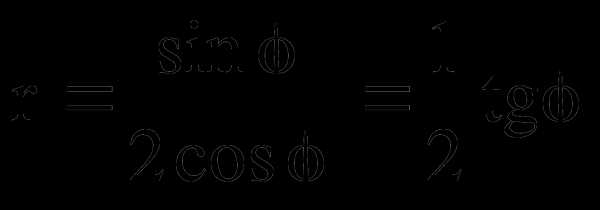4. .

Ответ:

Задача 8.

В остроугольном треугольнике ABC CF и AD высоты. Периметры треугольников ABC и FBD соответственно равны 15 см и 9 см. Радиус окружности, описанной около AFBD, равен 1,8 см. Найти АС.

Задача 9.

В равнобедренном ∆ABС с основанием АС высота AF делит высоту BD на отрезки 40 см и 5 см. Найти площадь треугольника АОВ, где О — точка пересечения высот.

Конструкция сходна с ключевой задачей — в треугольнике проведены две высоты, однако в этой задаче данный «ключ» не работает.

infourok.ru

8 класс. Геометрия. Подобные треугольники. Практические приложения подобия треугольников. — Повторение темы «Подобные треугольники». Решение задач.

Комментарии преподавателя

По­вто­ре­ние темы «По­доб­ные тре­уголь­ни­ки». Ре­ше­ние задач

На этом уроке мы по­вто­рим тему «По­доб­ные тре­уголь­ни­ки».

Для на­ча­ла вспом­ним опре­де­ле­ние по­доб­ных тре­уголь­ни­ков.

Опре­де­ле­ние

Тре­уголь­ни­ки  и  на­зы­ва­ют­ся по­доб­ны­ми тре­уголь­ни­ка­ми (), если у них все углы равны, а со­от­вет­ству­ю­щие сто­ро­ны про­пор­ци­о­наль­ны (см. Рис. 1).

Рис. 1

; .

При этом ко­эф­фи­ци­ент  на­зы­ва­ет­ся ко­эф­фи­ци­ен­том по­до­бия.

Если обо­зна­чить: , можно по­лу­чить сле­ду­ю­щие со­от­но­ше­ния между сто­ро­на­ми по­доб­ных тре­уголь­ни­ков: .

Кроме того, пло­ща­ди по­доб­ных тре­уголь­ни­ков от­но­сят­ся как квад­рат ко­эф­фи­ци­ен­та по­до­бия: .

Для того чтобы опре­де­лить, яв­ля­ют­ся ли тре­уголь­ни­ки по­доб­ны­ми, не при­бе­гая к опре­де­ле­нию, су­ще­ству­ют при­зна­ки по­до­бия тре­уголь­ни­ков.

Всего су­ще­ству­ет три при­зна­ка по­до­бия. Пе­ре­чис­лим их:

1.      По ра­вен­ству двух углов: если два угла од­но­го тре­уголь­ни­ка равны двум углам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны:.

2.      По про­пор­ци­о­наль­но­сти двух сто­рон и ра­вен­ству угла между ними: если две сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны со­от­вет­ствен­но двум сто­ро­нам дру­го­го тре­уголь­ни­ка, а углы, за­клю­чён­ные между этими сто­ро­на­ми, равны, то такие тре­уголь­ни­ки по­доб­ны: .

3.      По про­пор­ци­о­наль­но­сти трёх сто­рон: если три сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны со­от­вет­ствен­но трём сто­ро­нам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны: .

С по­мо­щью по­до­бия тре­уголь­ни­ков до­ка­зы­ва­ет­ся свой­ство сред­ней линии тре­уголь­ни­ка. На­пом­ним опре­де­ле­ние сред­ней линии тре­уголь­ни­ка.

Сред­няя линия тре­уголь­ни­ка – от­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны двух сто­рон тре­уголь­ни­ка.

Свой­ство сред­ней линии тре­уголь­ни­ка: сред­няя линия тре­уголь­ни­ка па­рал­лель­на сто­роне тре­уголь­ни­ка и равна её по­ло­вине (см. Рис. 2).

Рис. 2

.

С по­до­би­ем свя­за­но до­ка­за­тель­ство ещё од­но­го

www.kursoteka.ru

Подобные треугольники, формулы и примеры

Определение и формулы подобных треугольников

ОПРЕДЕЛЕНИЕ Треугольники называются подобными, если у них равные углы и соответствующие стороны пропорциональны.

Рис.1

Например, на рисунке 1 изображены треугольники и , у которых

   

По определению, эти треугольники подобные. Пишут: .

Число 2, которое равняется отношению соответствующих сторон, называют коэффициентом подобия.

Если и , то .

ЛЕММА

Лемма (Про подобные треугольники). Прямая параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от данного треугольника ему подобный.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com