Поверхности второго порядка
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
1. Эллипсоид.
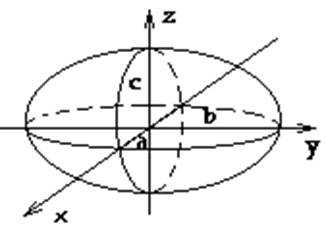 Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением :
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением :(1)
Уравнение (1) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h , где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
(2)Исследуем уравнения (2) при различных значениях h .
1) Если
> c (c>0), то и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости2) Если
, то и линия (2) вырождается в точки (0; 0; + c ) и (0; 0; — c ) (плоскости касаются эллипсоида).3) Если
, то уравнения (2) можно представить в видеоткуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями
и . При уменьшении значения и увеличиваются и достигают своих наибольших значений при , т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями и .Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz .
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферо й .
2. Однополосный гиперболоид.
Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением (3)Уравнение (3) называется каноническим уравнением однополосного гиперболоида.
Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy ( y=0) и Oyx (x=0). Получаем соответственно уравнения
ииз которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy . Линия, получающаяся в сечении, определяется уравнениями
или (4)из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями
и ,достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании
величины a* и b* возрастают бесконечно.Величины a, b, c называются полуосями однополосного гиперболоида.
3. Двуполостный гиперболоид.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
(5)
Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.
Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
ииз которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями
или (6)из которых следует, что при
>c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями и . При увеличении величины a* и b* тоже увеличиваются.При
уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости касаются данной поверхности).При
уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.Величина a, b и c называются полуосями двуполостного гиперболоида.
4. Эллиптический параболоид.
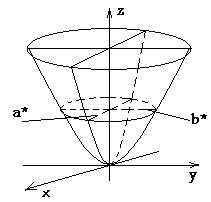
Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
 (7)
(7)где p>0 и q>0.
Уравнение (7) называется каноническим уравнением эллиптического параболоида.
Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
ииз которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.
Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
или (8)из которых следует, что при
плоскость z=h пересекает эmirznanii.com
Поверхности второго порядка.
Поверхностью второго порядка будем называть геометрическое место точек в пространстве, удовлетворяющих уравнению:
где по крайней мере один из a11 a22 a33 0. Это уравнение называется общим уравнением поверхности второго порядка.
Назовем группу слагаемых группой старших членов, а — линейной частью. a44 – свободный член.
Перейдем к новой системе координат с целью упростить общее уравнение.
Сначала осуществим параллельный перенос:
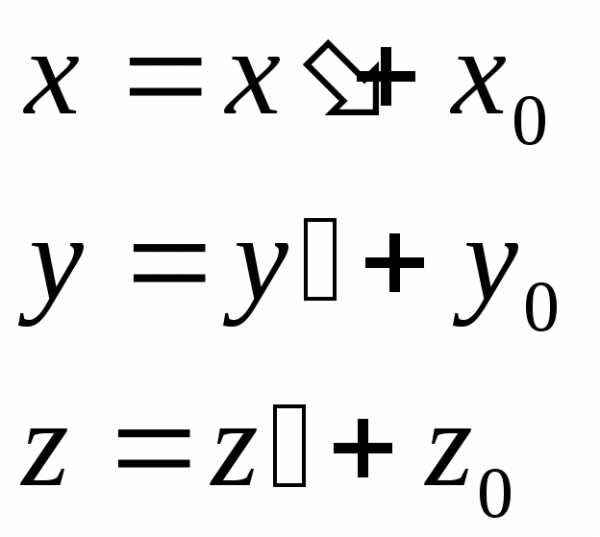
Подставив в общее уравнение, получим:
где (*)
Важный вывод: при параллельном переносе системы координат коэффициенты при старших членах не изменяются! Преобразуются коэффициенты группы линейных членов по некоторым формулам.
Рассмотрим поворот осей:
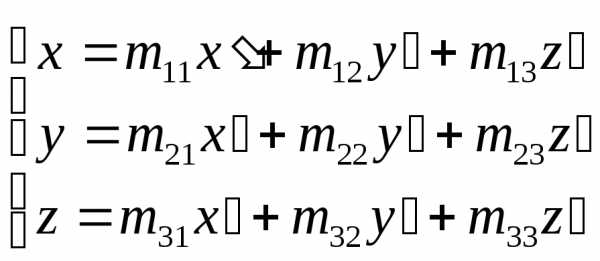
Если введем эти координаты в общее уравнение поверхности, сгруппируем члены при различных степенях x’ y’ z’ и получим:
Легко
убедиться, если расписать коэффициенты 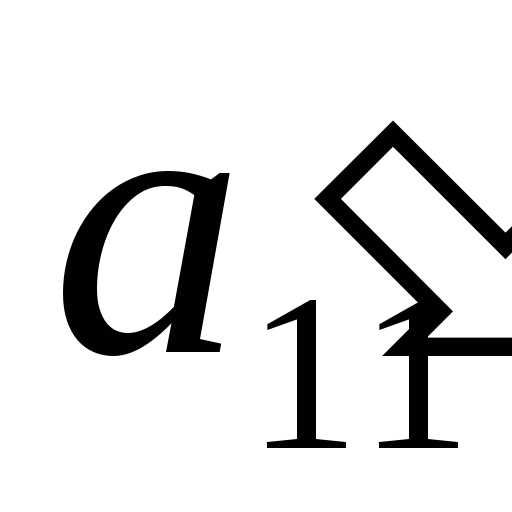
 не изменяется! При этом, если в исходном
уравнении коэффициенты были равны нулю, то и будут равны нулю! Другими словами, при
параллельном переносе можно упрощать
группу линейных членов, а при повороте
– упрощать группу старших членов
уравнения.
не изменяется! При этом, если в исходном
уравнении коэффициенты были равны нулю, то и будут равны нулю! Другими словами, при
параллельном переносе можно упрощать
группу линейных членов, а при повороте
– упрощать группу старших членов
уравнения.Оказывается, существуют инварианты относительно любого преобразования системы. Это величины:

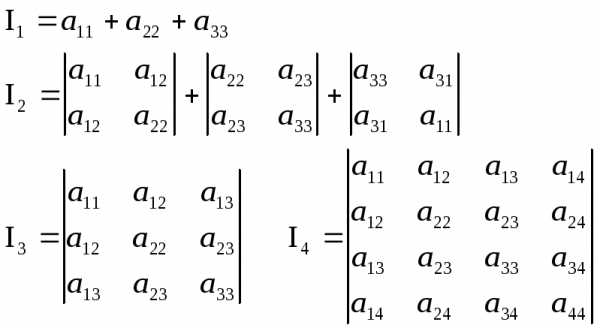
Центр поверхности второго порядка.
Поставим задачу найти такую систему координат, в которой уравнеие поверхности не содержало бы линейных слагаемых, т.е. . Пусть точка O(x 0 y0 z0) это точка начала координат искомой системы. Тогда, вспоминая формулы для параллельного переноса системы координат (*), имеем:
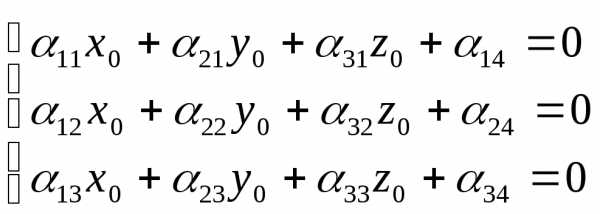 (**)
(**)
Эти уравнения называются уравнениями центра поверхности второго порядка. Если координаты центра найдены, то осуществляя параллельный перенос начала координат в центр, получим уравнение поверхности:
Ну и наконец, запишем без доказательства, что всегда существует некоторая декартова система координат, в которой последнее уравнение не содержит членов с x’y’ ; x’z’ ; z’y’. К этой системе можно прийти путем поворота осей координат координатной системы. В этой системе координат уравнение поверхности примет вид:
Процедура параллельного переноса и последующего поворота системы координат с целью получения этого уравнения называется стандартным упрощением уравнения поверхности.
Заметим, что не всякая поверхность может быть центральной, а лишь та, где I3 0.
Действительно, I3 является определителем системы уравнений (**) и для существования единственного решения этой системы по теореме Кронеккера-Капелли I3 не должен быть равен нулю. Если же I3 = 0, то у поверхности нет центральной точки. Ее уравнение может быть сведено к виду
Такая поверхность называется нецентральной.
Лекция 10. Классификация поверхностей 2го порядка
Итак, путем стандартного упрощения уравнения поверхности, уравнение может принять вид:
a11 x2 + a22 y2 + a33
z2 + a44 = 0Это уравнение есть уравнение только центральной поверхности! Тогда, поскольку I3 0, то I3 = a11* a22* a33 0 означает, что a11 0, a22 0, a33 0.
Возможны следующие случаи:
1). a11 a22 a33 одного знака. а44 0. Поверхность S называется эллипсоидом. Причем мы будем рассматривать только случай, когда знак у a11 a22 a33 и у а44 противоположный – вещественный эллипсоид. Каноничаская форма уравнения эллипсоида:
2). Два коэффициента одного знака, два противоположного:
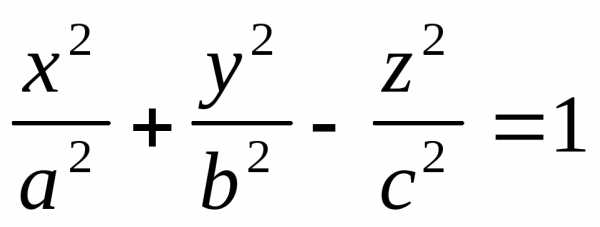 — это уравнение
однополостного гиперболоида.
— это уравнение
однополостного гиперболоида.
3). Наконец, знак у а11, а22и а44противоположензнаку у а33
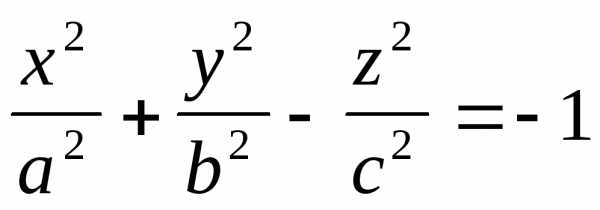 — уравнение
двухполостного гиперболоида.
— уравнение
двухполостного гиперболоида.
4). Левая часть равна нулю. Очевидно, для вещественного конуса необходимо, чтобы знак при a11 a22 или a33 был противоположен двум другим
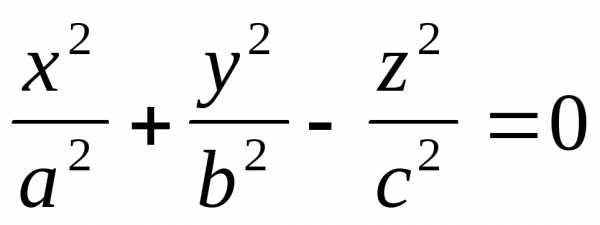 — вещественный
конус второго порядка.
— вещественный
конус второго порядка.
Оси OX OY OZ – центральные оси этих четырех поверхностей.
studfiles.net
ГЛАВА 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Поверхностью второго порядка называется множество точек пространства, удовлетворяющих какому-либо уравнению 2-ой степени.
Теорема. Для любой поверхности второго порядка в пространстве существует ортонормированная система координат, в которой эта поверхность задается каноническим уравнением.
Эта теорема у нас также остаётся пока что без доказательства, но она позволяет классифицировать все поверхности второго порядка.
Классификация поверхностей 2-го порядка
— эллипсоид;
— мнимый эллипсоид;
— точка ;
— однополостный гиперболоид;
— двуполостный гиперболоид;
— конус 2-го порядка;
— эллиптический параболоид;
— эллиптический цилиндр;
— мнимый эллиптический цилиндр;
— ось Oz;
— гиперболический параболоид;
— гиперболический цилиндр;
или — пара пересекающихся плоскостей;
— параболический цилиндр;
или — пара параллельных плоскостей;
— сдвоенная плоскость;
— пара мнимых параллельных плоскостей
§1. Эллиптический, гиперболический и параболический
Цилиндры
Пусть в пространстве заданы кривая и прямая A, пересекающая L. Поверхность, образованная при перемещении прямой А параллельно самой себе так, что, она все время пересекает кривую L, называется Цилиндрической. Прямые, которые получаются при перемещении прямой А называются Образующими этой цилиндрической поверхности, а кривая L – её Направляющей.
Теорема. Уравнение
(1)
В пространстве задает цилиндрическую поверхность, образующие которой параллельны оси , а уравнение направляющей, лежащей в плоскости , совпадает с уравнением (1).
►Обозначим L — множество точек плоскости, удовлетворяющих (1), а S – множество точек пространства, удовлетворяющих этому же уравнению. Тогда:
.
Итак, если , то поверхности S принадлежит вся прямая, проходящая через эту
Рис. 1 точку параллельно оси (рис. 1), что и доказывает, что S – цилиндрическая поверхность. ◄
Таким образом, уравнения , , задают цилиндрические поверхности, или цилиндры, с образующими, параллельными оси , а названия «гиперболический», «эллиптический», «параболический» они получили по названию своей направляющей. Гиперболический, эллиптический и параболический цилиндры изображены соответственно на рисунках 2, 3 и 4.
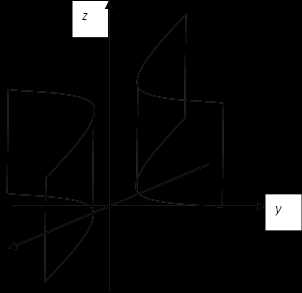
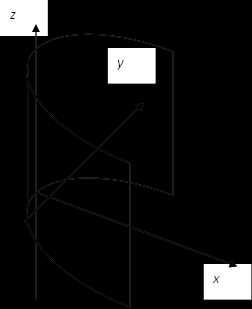 Рис. 2
Рис. 2
Рис. 3. Рис. 4.
§2. Конус второго порядка
Конусом второго порядка мы назвали поверхность, которая задаётся каноническим уравнением
. (1)
Из этого уравнения видно, что конус проходит через начало координат; симметричен относительно всех координатных осей, координатных плоскостей и относительно начала координат.
Теорема. Если точка , не совпадающая с началом координат, принадлежит конусу (1), то и вся прямая , проходящая через эту точку и начало координат, принадлежит этому конусу.
►В качестве направляющего вектора прямой возьмём вектор , тогда её уравнение будет выглядеть так:
.
Таким образом,
.
Итак, конус второго порядка состоит из прямых, проходящих через начало координат.◄
Дальнейшее исследование всех поверхностей будем проводить методом параллельных сечений, который состоит в следующем: пересекаем поверхность плоскостями, параллельными координатным плоскостям, и по виду линий, получающихся в сечениях, делаем вывод о форме поверхности.
Пусть задана поверхность уравнением . Пересечем эту поверхность плоскостью . Линия пересечения задаются системой:
,
Которая равносильна следующей:
. (2)
 Так как в системе (2) первое уравнение – уравнение цилиндрической поверхности с образующими, параллельными оси , то мы просто линию пересечения заданной поверхности плоскостью заменили линией пересечения той же плоскостью цилиндрической поверхности. Если эту Цилиндрическую поверхность пересечь плоскостями, параллельными плоскости , то в сечениях будут получаться линии, одинаковые по форме. В частности, такую же форму, как и все линии пересечения, будет иметь кривая, лежащая в плоскости , которая является их Проекцией на плоскость (рис. 1). Уравнение же последней кривой, т. е. направляющей цилиндрической поверхности, совпадает с уравнением . ТаКим образом, чтобы получить уравнение проекции на плоскость линии пересечения некоторой поверхности плоскостью следует из системы, задающей эту линию пересечения, исключить (это же справедливо и для проекции линии пересечения двух произвольных поверхностей).
Так как в системе (2) первое уравнение – уравнение цилиндрической поверхности с образующими, параллельными оси , то мы просто линию пересечения заданной поверхности плоскостью заменили линией пересечения той же плоскостью цилиндрической поверхности. Если эту Цилиндрическую поверхность пересечь плоскостями, параллельными плоскости , то в сечениях будут получаться линии, одинаковые по форме. В частности, такую же форму, как и все линии пересечения, будет иметь кривая, лежащая в плоскости , которая является их Проекцией на плоскость (рис. 1). Уравнение же последней кривой, т. е. направляющей цилиндрической поверхности, совпадает с уравнением . ТаКим образом, чтобы получить уравнение проекции на плоскость линии пересечения некоторой поверхности плоскостью следует из системы, задающей эту линию пересечения, исключить (это же справедливо и для проекции линии пересечения двух произвольных поверхностей).
Возвращаясь к исследованию формы конуса (1), пересечем его плоскостью . В сечении получаем кривую, заданную уравнением:
. (3)
При уравнение (3) задаёт точку — начало координат, т. е. плоскость Пересекает конус в одной только точке – в его вершине. Если , то, разделив (3) на правую часть, получаем уравнение
,
Которое задаёт эллипс с полуосями
. (4)
Рис. 2. Если растет, то полуоси увеличиваются, т. е. конус состоит из расширяющихся эллипсов. Внешний вид конуса изображен на рис. 2. При конус называется конусом вращения или прямым круговым конусом.
При пересечении конуса плоскостью в сечении можно получить не только эллипс, но также гиперболу и даже параболу, поэтому эти кривые называются коническими сечениями.
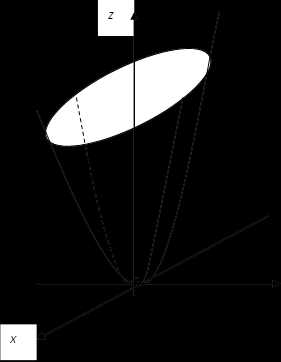
§3. Однополостный гиперболоид
Однополостным гиперболоидом называется поверхность, которая задаётся каноническим уравнением:
. (1)
Так же, как и конус второго порядка, эта поверхность симметрична относительно всех координатных плоскостей, всех координатных осей и относительно начала координат, но, в отличие от конуса, через начало координат не проходит. Пересекая её плоскостью , получаем кривую с уравнением
,
Которое после преобразований принимает вид
И задаёт эллипс с полуосями:
. (2)
Таким образом, как и конус второго порядка, однополостный гиперболоид состоит из расширяющихся эллипсов. Самый малый эллипс получаем при . Он называется горловым эллипсом.
Сравнивая (2) и (4) §2, видим, что и . Таким образом, если однополостный гиперболоид (1) и конус второго порядка
(3)
Пересечь одной и той же плоскостью , то эллипс для конуса находится внутри эллипса для гиперболоида, значит конус (3) лежит внутри гиперболоида (1). Кроме того,
. Аналогично получаем, что , т. е. при неограниченном удалении от плоскости однополостный гиперболоид (1) бесконечно близко приближается к конусу (3), который поэтому называется его асимптотическим конусом.
Пересекая однополостный гиперболоид (1) плоскостью в сечении получаем гиперболу
Рис. 1 с действительной осью — осью . При пересечении же его плоскостью , получаем гиперболу с действительной осью – осью . Однополостный гиперболоид изображен на рис. 1. При он называется однополостным гиперболоидом вращения.
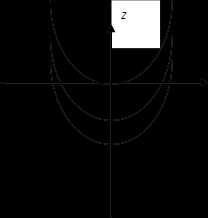
§4. Двуполостный гиперболоид
Двуполостным гиперболоидом называется поверхность, заданная каноническим уравнением
. (1)
Так же, как и конус второго порядка и однополостный гиперболоид, эта поверхность симметрична относительно всех координатных плоскостей, всех координатных осей и относительно начала координат, но опять же, в отличие от конуса, через начало координат не проходит. Пересекая двуполостный гипребролоид плоскостью получаем кривую с уравнением
. (2)
Из (2) видно, что при плоскость не пересекается с двуполостным гиперболоидом (1), каждая из плоскостей и пересекает двуполостный гиперболоид в одной точке. Эти точки и называются вершинами двуполостного гиперболоида. Если же , то линией пересечения является эллипс
С полуосями
Рис. 1 . (3)
Наряду с гиперболоидом (1) опять же рассмотрим конус
. (4)
Пересекая гиперболоид (1) и конус (4) одной и той же плоскостью и сравнивая (3) и (4) §2, делаем вывод: и , т. е. двуполостный гиперболоид (1) лежит внутри конуса (4). Так же, как и в §3, получаем:
и ,
Откуда видно, что при неограниченном удалении от плоскости двуполостный гиперболоид (1), так же как и однополостный, бесконечно близко приближается к конусу (4) (только уже изнутри), который также называется его асимптотическим конусом.
Пересекая гиперболоид (1) плоскостью , в сечении получаем гиперболу , а пересекая его плоскостью — гиперболу . Для обеих этих гипербол действительной является ось .
Двуполостный гиперболоид изображён на рис. 1.
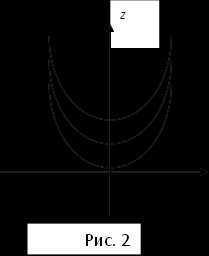
§ 5. Эллиптический параболоид
Эллиптический параболоид – это поверхность, заданная каноническим уравнением
. (1)
Эллиптический параболоид симметричен относительно координатных плоскостей и , а относительно плоскости симметрии не имеет. Если его пересечь плоскостью , то увидим, что при плоскость не пересекается с эллиптическим параболоидом, при в сечении получается единственная точка – начало координат, которая называется вершиной эллиптического параболоида (1), а при линией пересечения является эллипс с полуосями . Таким образом, и эллиптический параболоид состоит из расширяющихся эллипсов.
Пересечём теперь эту поверхность плоскостью . В сечении получаем кривую, заданную уравнением
,
Которое после преобразований принимает вид:
. (2) Из (2) видно, что плоскости, параллельные плоскости , пересекают поверхность эллиптического параболоида по параболам, имеющим
 |
Одинаковые фокальные параметры (т. е., по конгруэнтным параболам), ветви которых направлены в сторону положительного направления оси
 , причём с ростом вершина параболы смещается вверх. На рис. 1 изображены проекции этих парабол на плоскость . То же самое имеем и при пересечении плоскостями . Уравнения линий пересечения:
, причём с ростом вершина параболы смещается вверх. На рис. 1 изображены проекции этих парабол на плоскость . То же самое имеем и при пересечении плоскостями . Уравнения линий пересечения:
,
При проектировании их на плоскость получаем картинку, изображённую на рис. 2. Сам же эллиптический параболоид изображён на рис. 3. При эллиптический параболоид называется параболоидом вращения.
§ 6. Гиперболический параболоид
Гиперболическим параболоидом мы назвали поверхность, каноническое уравнение которой выглядит так:
.
Гиперболический параболоид, так же, как и эллиптический, симметричен относительно координатных плоскостей и , а относительно плоскости не имеет симметрии.
Пересечём эту поверхность плоскостью . В сечении получаем кривую, заданную уравнением:
.
Из него мы видим, что плоскости, параллельные плоскости , пересекают поверхность гиперболического параболоида по параболам, имеющим одинаковые фокальные параметры (т. е., по конгруэнтным параболам), их ветви направлены в сторону отрицательного направления оси , причём с ростом вершина параболы смещается вверх. На рис. 1 изображены проекции этих парабол на плоскость . Если же пересечь гиперболический параболоид плоскостями , то в сечениях получаем кривые
,
Т. е. опять конгруэнтные параболы, но их ветви направлены в сторону положительного направления оси , а с ростом вершина параболы смещается вниз. При проектировании их на плоскость получаем
 |
картинку, изображённую на рис. 2.
Теперь пересечём гиперболический параболоид плоскостью . В сечении получается кривая, заданная уравнением
. (1)
При это уравнение задаёт пару пересекающихся прямых
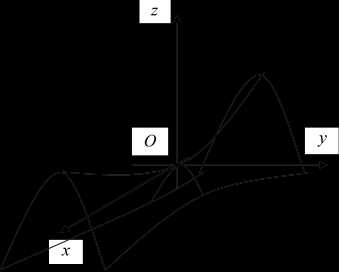 Рис. 3
Рис. 3
. (2)
Если , то плоскость пересекает гиперболический параболоид по гиперболам
,
Асимптотами которых являются прямые (2), действительной осью – ось , причём с ростом вершины этих гипербол удаляются от центра (от оси ). Если же ,
То уравнение (1) задаёт гиперболы
С теми же самыми асимптотами, но с осью в качестве действительной. Проекции линий пересечения гиперболического параболоида плоскостями на плоскость изображены на рис. 3, а сам гиперболический параболоид — на рис. 4. Эта поверхность напоминает седло, часто её так и называют.
§ 7. Эллипсоид
Эллипсоидом называется поверхность, заданная каноническим уравнением . Пересекая его координатными плоскостями, каждый раз в сечении получаем эллипсы с различными полуосями. Эллипсоид изображён на рис. 1, по внешнему виду он напоминает яйцо. При эллипсоид называется эллипсоидом вращения, а при — это просто сфера.
www.webpoliteh.ru
поверхности второго порядка
Поверхности второго порядка.
Если в пространстве R3 ввести прямоугольную систему координат Oxyz, то каждая поверхность определяется некоторым уравнением F(x,y,z)=0,
(x,y,z) – координаты любой точки поверхности. Если F(x,y,z) – многочлены не выше второй степени относительно совокупности переменных x,y,z, то уравнение F(x,y,z)=0 называется уравнением второго порядка, а поверхность изображаемая этим уравнением называется поверхностью второго порядка.
Если поверхность имеет специфическое расположение относительно системы координат ( например, симметрична относительно некоторых координатных плоскостей, или имеет вершину в начале координат и пр.), то её уравнение имеет достаточно простой вид, который называется каноническим.
Канонический вид уравнений поверхностей второго порядка. Геометрическое изображение.
1). Сфера радиуса R с центром в начале координат (рис.56)
x2+y2+z2=R2.
Уравнение (x—x0)2+(y—y0)2+(z—z0)2=R2 изображает сферу радиуса R с центром в точке M0(x0,y0,z0).
2). Эллипсоид с полуосями a,b,c и центром в начале координат (рис. 57)
+ + =1.
При a=b=c=R эллипсоид превращается в сферу радиуса R.
3). Однополостный гиперболоид с полуосями a, b, c и осью Oz (рис. 58)
+ — =1.
Сечения гиперболоида горизонтальными плоскостями z=h являются эллипсами
+ =1+
Сечения гиперболоида вертикальными плоскостями x=h или y=h являются гиперболами.
— =1- или — =1-
4). Двуполостсный гиперболоид с полуосями a,b,c и осью Oz (рис.59)
+ — = -1.
Сечение гиперболоида горизонтальными плоскостями z=h, c являются эллипсами
+ = – 1.
Сечения гиперболоида вертикальными плоскостями x=h или y=h являются гиперболами.
— = — -1 или — =- -1.
5). Параболоид эллиптический с параметрами a,b,p и вершиной в начале координат ( рис.60)
+ = 2pz.
Сечение параболоида горизонтальными плоскостями z=h (h>0 при h< 0 при
P<0) есть эллипсы
+ = 2ph.
Сечение параболоида вертикальными плоскостями x=h или y=h являются параболами.
= 2pz — или = 2pz — .
6). Параболоид гиперболический с параметрами a, b, p и вершиной начале координат (рис.61)
— = 2pz.
Сечение параболоида горизонтальными плоскостями z=h представляют собой гиперболы
— = 1
Сечение вертикальными плоскостями x=h и y=h являются параболами
=-2pz + и = 2pz+ .
7). Конус эллиптический с вершиной в начале координат и осью Oz (рис.62)
+ — =1.
Если a=b, то конус круглый или круговой. Пересечение конуса горизонтальными плоскостями являются эллипсами
+ =
(при h=0 эллипс вырождается в точку).
Сечение конуса вертикальными плоскостями x=h и y=h являются гиперболами
— = — — =- . при h0
Или парой пересекающих прямых
— =0 — =0 при h=0
К поверхностям второго порядка относятся цилиндры направляющие которых – линии второго порядка. Мы ограничимся пересечением цилиндров, направляющие – прямые , параллельные оси Oz.
8) Цилиндры:
(1) Эллиптический (рис.63)
+ =1.
Если a=b=R, то цилиндр – круговой x2+y2=R.
(2) Гиперболический (рис.64)
— =1.
(3) Параболический (рис.65)
y2=2px.
Примечание . Если в каждом из приведённых канонических уравнений заменить x=x1—x0, y=y1—y0, z=z1—z0, где (x0,y0,z0) – фиксированные числа, то новые уравнения представляют те же поверхности и они занимают в системе координат O1x1y1z1 такое же положение относительно плоскостей x1=x0, y1=y0, z1=z0 как поверхности, заданные канонически относительно координатных плоскостей x=0, y=0, z=0. Другими словами, приведённые формулы представляют параллельный сдвиг поверхности на вектор OM=(x0,y0,z0).
Метод параллельных сечений
Если задано уравнение той или иной поверхности, то возникает задача исследования её формы и расположения относительно координатных осей. Для решения этой задачи обычно применяют метод параллельных сечений: поверхность пересекается несколькими плоскостями, параллельными плоскостями координат. Форма и размер полученных сечений позволяют выяснить геометрическую форму самой поверхности.
Пересечение поверхности с плоскостью
Линию в пространстве R3 можно определить как пересечение двух плоскостей. Таким образом уравнение линии можно записать в виде системы
Для исследования этой линии удобно воспользоваться цилиндром, проектирующем её на ту или иную координатную плоскость. Если, например, проектируем линию на плоскость Oxy, то исключим z из системы и получим уравнение (x,y)=0.Оно изображает направляющую проектирующего цилиндра на плоскость Oxy. В зависимости от того, будет ли (x,y)=0 эллипсом, гиперболой, параболой, парой прямых – изучаемая линия сохранит соответствующее название.
5.5.1. Сохранить уравнение сферы с центром в точке М0(-5;3;2) и касающейся плоскости 2x-2y+z-4=0.
Для составления уравнения сферы нужен её радиус. В данном случае R – расстояние от М0 до плоскости:
R= =6.
Искомое уравнение : (x+5)2+(y-3)2+(z-2)2=36.
5.5.2. Составить уравнение сферы, касающейся двух параллельных плоскостей 6x-3y-2z-35=0 и 6x-3y-2z+63 =0, если её центр расположен на прямой = = .
1) Определим точки М1 и М2 пересечения прямой с плоскостями (заметим что прямая перпендикулярна плоскостям ). Для этого параметрическое уравнение прямой x = 11+6t, y=-4-3t, z=-3-2t подставляем в уравнения плоскостей, находим t и возвращаемся к этим уравнениям.
6(11+6t) – 3(-4-3t) – 2(-3-2t)-35=0,
t=-1, M1 (5,-1,-1).
Аналогично находим М2(-7,5,3).
2) Центр сферы М0 — середина отрезка М1М2:М0(-1,2,1).
Радиус сферы R = М0М1==7.
3) Уравнение сферы (x+1)2+(y-2)2+(z-1)2=49.
5.5.4. Составим уравнение сферы ,проходящей через четыре точки О(0;0;0), А(2;0;0), В(1;1;0), С(1;0;-1).
Уравнение сферы ищем в виде
(x—a)2+(y—b)2+(z—c)2=R2.
Где (a, b, c) – координаты центра и – координаты центра и R – радиус неизвестные. Координаты данных точек превращают уравнение сферы в верные равенства, т.е.
После возведения в квадрат, приведения подобных слагаемых получается система, из которой a=1, b=0, c=0, R2=1.
Ответ. (x-1)2+y2+z2=1.
5.5.6. Найти точки пересечения поверхности + – =1 и прямой = = .
Параметрические уравнения прямой x=4t, y=-3t, z=-2+4t подставим в уравнение однополосного гиперболоида и определим значение t: + – =1, (t-1)2=0, t1,2=1. Следовательно, x=4, y=-3, z=-2. Прямая имеет с гиперболоидом две совпадающие точки пересечения, т. е. прямая касается поверхности гиперболоида в точке М1(4;-3;2).
5.5.7. При каких значениях параметра p плоскость 2x-2y—z=p касается сферы x2+y2+z2=81?
Если плоскость касается сферы, то расстояние от её центра до плоскости равно радиусу сферы, т. е . =9.
Отсюда =27, т.е. p=27.
5.5.10. Методом параллельных сечений исследовать поверхность, определяемую уравнением + – = -1.
1) Перепишем уравнение в виде + = -1. И пересекаем поверхность плоскостями z=h параллельными координатной плоскости Oxy.
В сечениях получаются линии с уравнениями + = -1.
При 2 эти уравнения имеют изображения ( мнимые эллипсы) при h = 2 они изображают точки (0;0;2) и (0;0;-2), а при 2 получаются эллипсы
+ = 1, где c=.
С увеличением увеличиваются и полуоси эллипсов 4с и 3с, т. е. эллипсы расширяются (рис.66). Поверхность симметрична относительно плоскости Oxy.
2) Перепишем уравнение поверхности в виде – = — -1 и пересечём её вертикальными плоскостями y=l. При каждом l (- ; + ) соответствующие уравнения описывают гиперболы. В частности, при l=0 получаем гиперболу – = -1, расположенную в плоскости Oxz.
3) Сечение поверхности плоскостями x=r также гиперболы
– =-1- .
Но из пп. 1) и 2) уже можно сделать вывод о строении поверхности : она состоит из эллипсов , <<нанизанных>> на гиперболу – =-1 ( =0). Поскольку два сечения, параллельных Oxz и Oyz – гиперболы, а одно – параллельное Oxy –эллипс, то поверхность называется гиперболоидом эллиптическим; для уточнения – двуполостный, ибо состоит из двух отдельных частей ( над и под плоскостью Oxy).
5.5.12. Определить линию пересечения поверхностей
(x-4)2+(y-7)2+(z+1)2=36 и 3x+y-z-9=0.
Первая поверхность это сфера, вторая- плоскость. Они пересекаются или по окружности, или в одной точке , или вовсе не пересекаются .
Найдём расстояние d от центра сферы М0(4;7;-1) до плоскости 3x+y—z-9=0.
d= = = .
Поскольку d <R (R=6- радиус сферы ), то плоскость пересекает эту сферу по окружности.
Центр O(x1;y1;z1) этой окружности расположен на перпендикуляре М0О, опущенным из центра сферы М0 на заданную плоскость (рис.67).
Уравнение перпендикуляра М0О в параметрической форме имеет вид
x = 4+3t, y=7+t, z=-1-y.
Подставим эти равенства в уравнение плоскости и находим t.
3(4+3t) + (7+t)- (-1-t)-9 =0, t=-1.
Подставим t= -1 в параметрические уравнения перпендикуляра М0О.
Находим : x=1, y=6 , z=0, т. е. О(1;6;0) – центр окружности пересечения сферы и плоскости.
Из ОМ0А (рис.67) находим r2=R2—d2, r2=36-11=25, r=5.
Таким образом получено, что кривая
Представляя собой окружность радиуса 5 с центром в точке О(1;6:0).
5.5.13. Составить уравнения касательных плоскостей к сфере
(x-2)2+ (y+1)2 + (z-3)2=6 в точках её пересечения с прямой = = .
Точки пересечения прямой со сферой получаются подстановкой равенств
x=1+t, y= —t, z=1+2t в уравнение сферы, определением t и подстановкой обратно в уравнение прямой .
Имеем (1+t-2)2 + (-t+1)2 + (1+2t-3)2=6 , 6(t-1)2=6, t1=0, t2=2. Далее x1=1, y1=0, z1=1, x2=3, y2=-2, z2=5. Итак, М1(1;0;1), М2(3;-2;5) – точки пересечения прямой и сферы.
Составим уравнение первой касательной плоскости, проходящей через
М1(1;0;1). Её нормальный вектор , где М0(2;-1;3) центр сферы:
= (-1;+1;-2) , а уравнение плоскости: — (x-1) + y-2(z-1)=0 или x=y+2z-15=0.
Уравнение второй плоскости по аналогии: x—y+2z-15=0.
Полученные плоскости параллельны потому, что данная прямая проходит через центр сферы М0(2;-1;3) (получается при t=1).
5.5.14. Установить, что плоскость y-2=0 пересекает эллипсоид
+ + =1 по эллипсу. Найти его полуоси и вершины.
Пересечение двух поверхностей в пространстве представляет некоторую линию, принадлежащую как одной так и другой поверхности. Уравнение этой линии в нашем случае имеет вид
Подставим y=2 в первое уравнение и получаем + =.
Это уравнение эллипса, расположенного в плоскости y-2=0.
Поско4льку каноническое уравнение полученного эллипса имеет вид + =1, то полуоси равны a= и b=, а вершины эллипса расположены в точках А1(0;2;-) и А2(8;2;0) — на большом диаметре,
В1(0;2;-) и В2(0;2;) – на меньшем диаметре.
5.5.15. Исследовать линию пересечения гиперболоида + — z2=1 с плоскостью 4x-3y-12z-6=0, пользуясь её проекциями на координатные плоскости.
Линия пересечения гиперболоида с плоскостью определяется системой
Выражаем из второго уравнения
Z= и z2=
И подставляем в первое уравнение. Получаем
9y2+8xy+16x-12y-60=0.
Это уравнение проекции на плоскость Oxy линии пересечения гиперболоида с плоскостью. Вместе с тем это уравнение цилиндрической поверхности с образующей, параллельной оси Oz, направляющая которой есть исследуемая линия. Уравнение этой линии следует привести к каноническому виду известными формулами преобразования координат (поворот осей и сдвиг). В данном случае методом разложения на множители можно получить ( y+2)(9y+8x-30)=0, т.е. наша линия представляет пару прямых y+2=0 и 8x+9y-30=0, которые пересекаются в точке
Т.е. М1(6;-2).
По аналогии с этим, проектируем искомую линию на плоскость Oxz. Получаем пару прямых x-3z=0 и 5x-9z-12=0, которые пересекаются в точке М2(6;2).
Наконец, на плоскость Oyz искомая линия проектируется в прямые y+2=0 и 5y+8z-6=0, которые пересекаются в точке М3(-2;2).
Если проекции на координатные плоскости данной линии являются пересекающимися прямыми, то сама линия представляет пару пересекающихся в точке М(6;-2;2) прямых. Координаты М получаются из координат её проекции М1, М2,М3.
5.5.17. Дан гиперболический параболоид x2- =z и одна из его касательных плоскостей: 10x-2y—z-21=0. Найти уравнение каждой из тех двух прямых, по которой плоскость касается с параболоидом.
Уравнение искомых прямых задаются системой уравнений, которую последовательно преобразуем.
studfiles.net
Приложение 02 — Свойства поверхностей второго порядка
Приложение 2 66
Свойства поверхностей второго порядка
Приложение 2
СВОЙСТВА ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
В теореме 4.5.1. были перечислены конкретные типы поверхностей второго порядка, различие между которыми сохраняется при переходе из одной декартовой системы координат в другую. В данном приложении будут рассмотрены основные свойства поверхностей этих типов.
§Пр.2.1. Вырожденные поверхности второго порядка
К вырожденным поверхностям второго порядка относятся типы, указанные в первой части таблицы формулировки теоремы 4.5.1.
В
первых двух столбцах этой таблицы
перечислены типы пустых множеств, а
также объекты точечно-линейного типа,
исследование которых полностью аналогично
случаям, рассмотренным в приложении 1,
в ортонормированной, канонической
системе координат  .
.
Первые
три типа поверхностей, содержащиеся в
третьей колонке таблицы, являются
частными случаями цилиндрической
поверхности, образующая которых
параллельна прямой
,
а направляющими служат плоские кривые
— эллипс, гипербола и парабола,
соответственно расположенные в плоскости .
.
Описание
свойств невырожденных поверхностей
второго порядка будет также выполнено
в ортонормированной системе координат  .
.
В общем случае можно показать, что в сечении поверхности второго порядка плоскостью получается кривая второго порядка. Однако для описания основных свойств невырожденных поверхностей второго порядка достаточно рассмотреть сечения, параллельные координатным плоскостям.
§Пр.2.2. Эллипсоид
Определение Пр.2.2.1. | Поверхность, задаваемая в некоторой ортонормированной системе координат каноническим уравнением вида , называется эллипсоидом. |
Свойства эллипсоида:
1. Эллипсоид — ограниченная поверхность, поскольку из его канонического уравнения следует, что .
2. Эллипсоид обладает:
— центральной симметрией относительно начала координат;
— осевой симметрией относительно координатных осей;
— плоскостной симметрией относительно координатных плоскостей.
3. В сечении эллипсоида плоскостью, ортогональной любой из осей координат, получается эллипс. Например, рассматривая секущую плоскость , где, получаем следующее уравнение линии сечения являющейся эллипсом. (Рис. Пр.2.2.1.) | x | z | y |
§Пр.2.3. Эллиптический параболоид
Определение Пр.2.3.1. | Поверхность, задаваемая в некоторой ортонормированной системе координат каноническим уравнением вида , называетсяэллиптическим параболоидом. |
Свойства эллиптического параболоида:
1. Эллиптический параболоид — неограниченная поверхность, поскольку из его канонического уравнения следует, что и принимает сколь угодно большие значения.
2. Эллиптический параболоид обладает
—
осевой симметрией относительно оси  ;
;
—
плоскостной симметрией относительно
координатных плоскостей 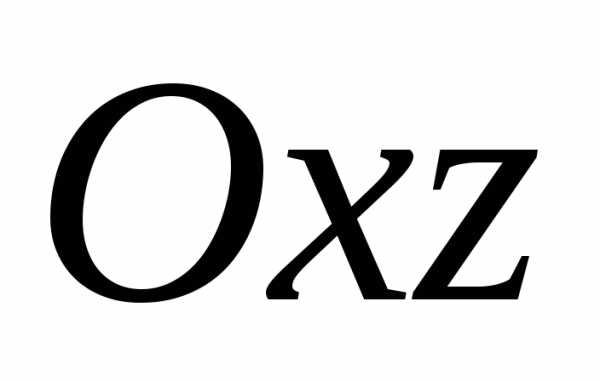 и
и 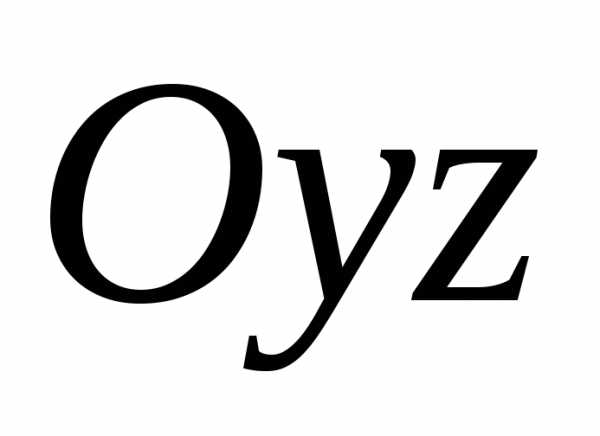 .
.
3.
В сечении эллиптического параболоида
плоскостью, ортогональной оси  ,
получаетсяэллипс,
а плоскостями, ортогональными осям
,
получаетсяэллипс,
а плоскостями, ортогональными осям 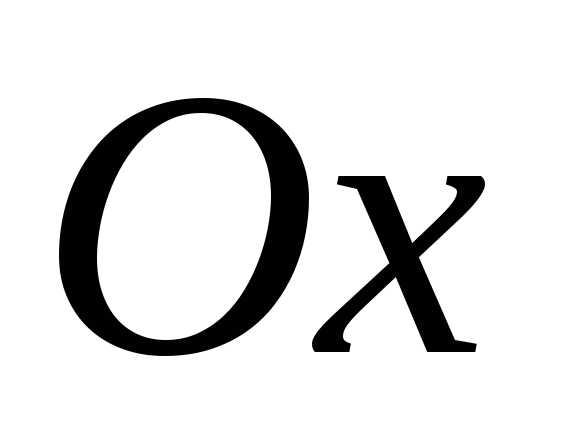 или
или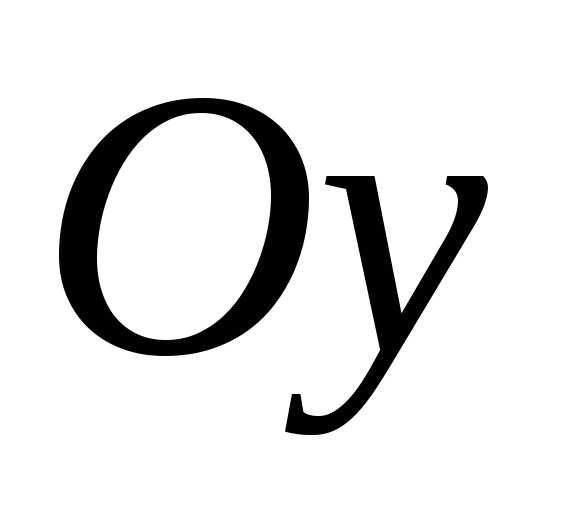 — парабола.
Например, рассматривая секущую плоскость
,
получаем следующее уравнение плоской
линии
— парабола.
Например, рассматривая секущую плоскость
,
получаем следующее уравнение плоской
линии
, являющейся
эллипсом. (Рис. Пр.2.3.1.) С другой стороны,
сечение плоскостью являющейся
параболой. Для случая сечения плоскостью | x | z Рисунок Пр.2.3.1. | y |
 .
.
§Пр.2.4. Гиперболический параболоид
Определение Пр.2.4.1. | Поверхность,
задаваемая в некоторой ортонормированной
системе координат каноническим
уравнением вида |
Свойства гиперболического параболоида:
1. Гиперболический параболоид — неограниченная поверхность, поскольку из его канонического уравнения следует, что — любое.
2. Гиперболический параболоид обладает
—
осевой симметрией относительно оси  ;
;
—
плоскостной симметрией относительно
координатных плоскостей  и
и  .
.
3.
В сечении гиперболического параболоида
плоскостью, ортогональной оси координат  ,
получается гипербола, а плоскостями
ортогональными осям
,
получается гипербола, а плоскостями
ортогональными осям или
или —
парабола. (Рис. Пр.2.4.1.)
—
парабола. (Рис. Пр.2.4.1.)
Например, рассматривая секущую плоскость z=z0>0 , получаем следующее уравнение линии сечения являющейся
гиперболой. При | x | z | y |
С
другой стороны, при сечении гиперболического
параболоида плоскостью x=x0 получаем плоскую кривую 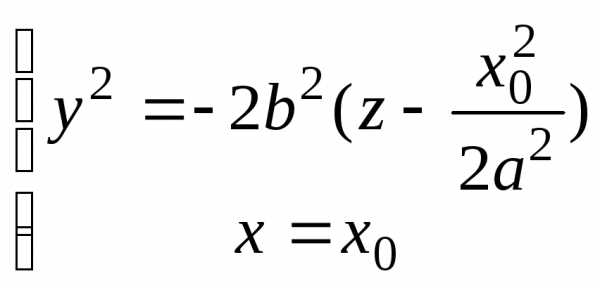 ,
являющуюся параболой. Для случая сечения
плоскостью
,
являющуюся параболой. Для случая сечения
плоскостью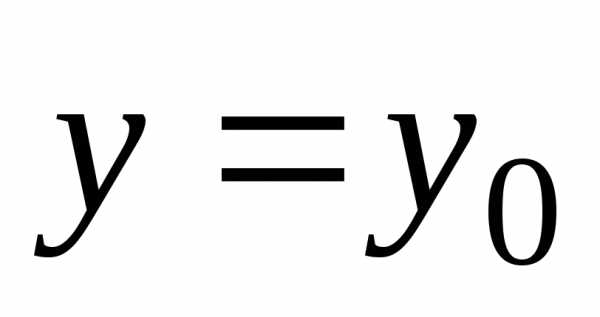 уравнение аналогично и имеет вид
уравнение аналогично и имеет вид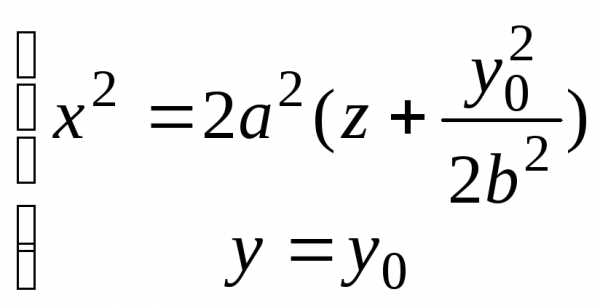 .
.
Из полученных уравнений следует, что гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.
4. Гиперболический параболоид имеет два семейства прямолинейных образующих.
Если
записать уравнение данной поверхности
в виде
, то можно прийти к заключению, что при
любых значениях параметра точки, лежащие на прямых 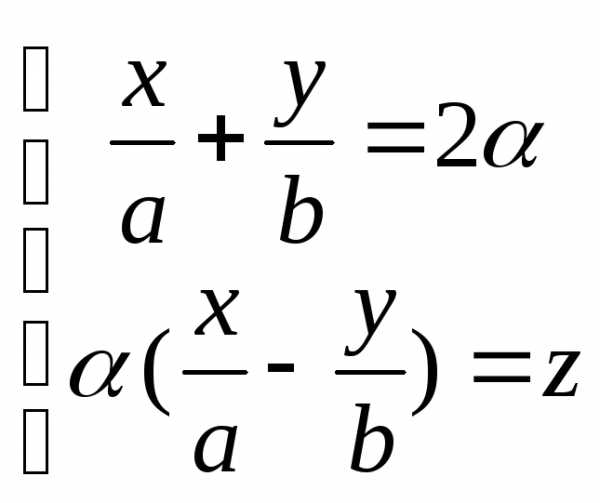 и
и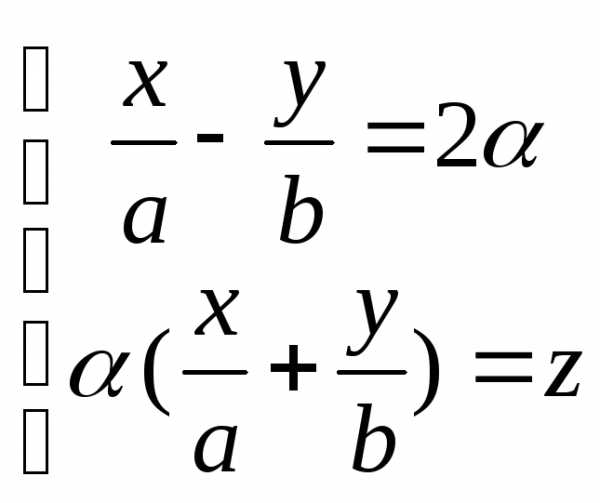 ,
также принадлежат и гиперболическому
параболоиду, поскольку почленное
перемножение уравнений плоскостей,
задающих эти прямые, дает уравнение
гиперболического параболоида.
,
также принадлежат и гиперболическому
параболоиду, поскольку почленное
перемножение уравнений плоскостей,
задающих эти прямые, дает уравнение
гиперболического параболоида.
Заметим, что для каждой точки гиперболического параболоида, существует пара прямых, проходящих через эту точку и целиком лежащих на гиперболическом параболоиде. Уравнения этих прямых могут быть получены (с точностью до некоторого общего ненулевого множителя) путем подбора конкретных значений параметра .
§Пр.2.5. Однополостный гиперболоид
Определение Пр.2.5.1. | Поверхность, задаваемая в некоторой ортонормированной системе координат каноническим уравнением вида , называетсяоднополостным гиперболоидом. |
Свойства однополостного гиперболоида:
1. Однополостный гиперболоид — неограниченная поверхность, поскольку из его канонического уравнения следует, что .
2. Однополостный гиперболоид обладает
— центральной симметрией относительно начала координат;
— осевой симметрией относительно всех координатных осей;
— плоскостной симметрией относительно всех координатных плоскостей.
3.
В сечении однополостного гиперболоида
плоскостью, ортогональной оси координат  ,
получаетсяэллипс,
а плоскостями, ортогональными осям
,
получаетсяэллипс,
а плоскостями, ортогональными осям  или
или  —гипербола.
(Рис. Пр.2.5.1.) Вывод уравнений для линий
сечения аналогичен рассмотренным ранее
случаям.
—гипербола.
(Рис. Пр.2.5.1.) Вывод уравнений для линий
сечения аналогичен рассмотренным ранее
случаям.
4. Однополостный гиперболоид имеет два семейства прямолинейных образующих. Записав уравнение данной поверхности в виде , можно прийти к заключению, что при любых и , точки, лежащие на прямых
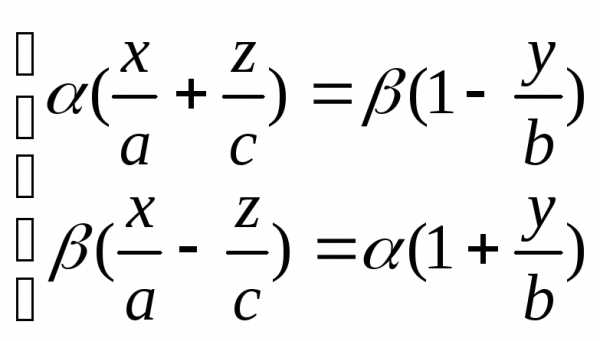 и
и 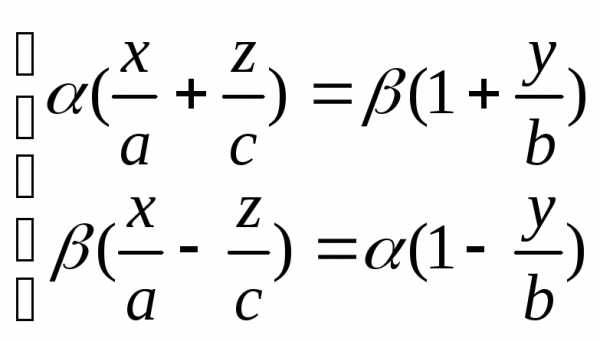 ,
,
будут принадлежать и однополостному гиперболоиду, поскольку почленное перемножение уравнений плоскостей, задающих эти прямые, дает уравнение однополостного гиперболоида. Для каждой точки однополостного гиперболоида существует пара прямых, проходящих через эту точку и целиком лежащих на однополостном гиперболоиде. Уравнения этих прямых могут быть получены путем подбора конкретных значений и . | x | z Рисунок Пр.2.5.1. | y |
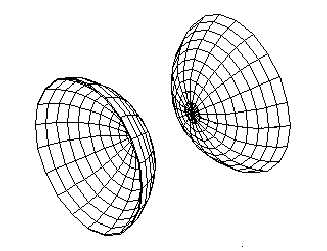
§Пр.2.6. Двуполостный гиперболоид
Определение Пр.2.6.1. | Поверхность,
задаваемая в некоторой ортонормированной
системе координат каноническим
уравнением вида |
Свойства двуполостного гиперболоида:
1. Двуполостный гиперболоид — неограниченная поверхность, поскольку из его канонического уравнения следует, что и не ограничен сверху.
z
x y
Рисунок Пр.2.6.1.
2. Двуполостный гиперболоид обладает:
— центральной симметрией относительно начала координат;
— осевой симметрией относительно всех координатных осей;
— симметрией относительно всех координатных плоскостей.
3.
В сечении двуполостного гиперболоида
плоскостью, ортогональной оси координат  , при получается эллипс,
а плоскостями, ортогональными осям
, при получается эллипс,
а плоскостями, ортогональными осям 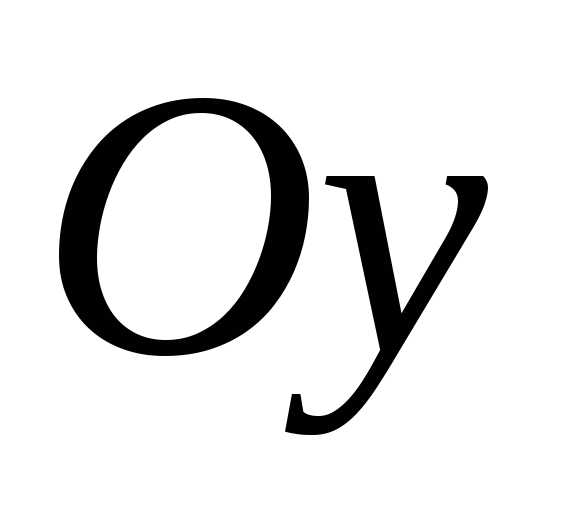 или
или — гипербола.
(Рис. Пр.2.6.1.)
— гипербола.
(Рис. Пр.2.6.1.)
§Пр.2.7. Поверхности вращения
Пусть
некоторая кривая, расположенная в
плоскости 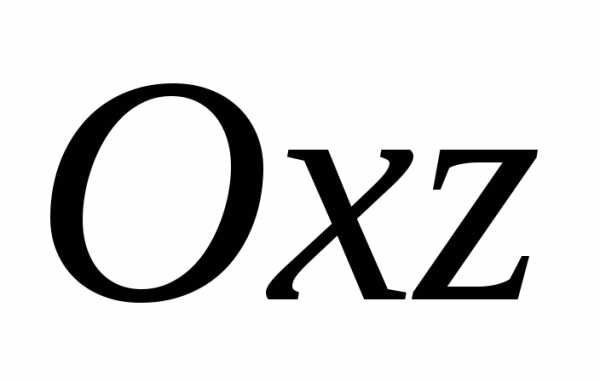 ,
имеет уравнение.
Если вращать эту кривую вокруг оси
,
имеет уравнение.
Если вращать эту кривую вокруг оси ,
то каждая ее точка будет описывать
окружность.
,
то каждая ее точка будет описывать
окружность.
Определение Пр.2.7.1. | Совокупность точек, координаты которых удовлетворяют уравнению , называетсяповерхностью вращения. |
Пример Пр.2.7.1. | К поверхностям вращения, например, относятся: 1. Эллипсоид вращения 2. Конус вращения . |
Замечание: поверхности вращения линии второго порядка не всегда задаются уравнениями второго порядка.
Например,
если вращать квадратную параболу 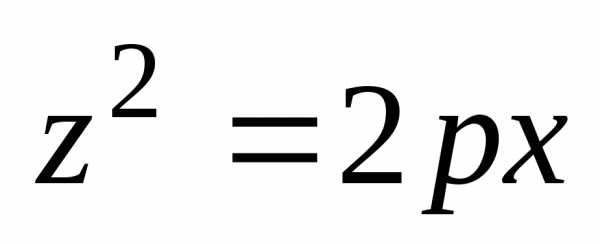 вокруг оси
вокруг оси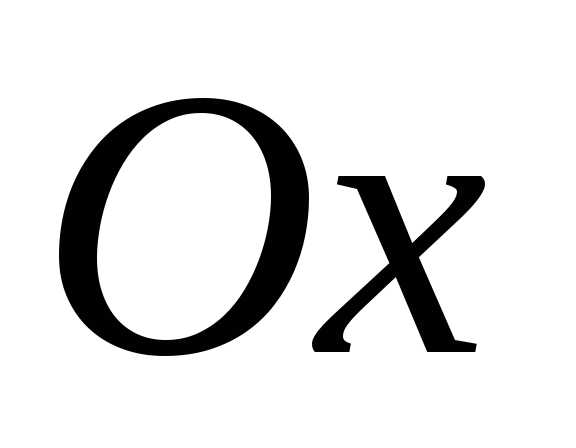 ,
получается
эллиптический параболоид вращения,
однако при вращении этой же кривой
вокруг оси
,
получается
эллиптический параболоид вращения,
однако при вращении этой же кривой
вокруг оси  получится поверхность вращения,
задаваемая уравнением видаили.
получится поверхность вращения,
задаваемая уравнением видаили.
Задача Пр.2.7.1. | Составить
уравнение поверхности вращения,
получаемой при вращении линии |
Решение.
Зафиксируем
на вращаемой линии точку с координатами
.
Линия, получаемая при вращении этой
точки вокруг оси в плоскости,
есть окружность радиуса,
с уравнением.
в плоскости,
есть окружность радиуса,
с уравнением.
С
другой стороны, 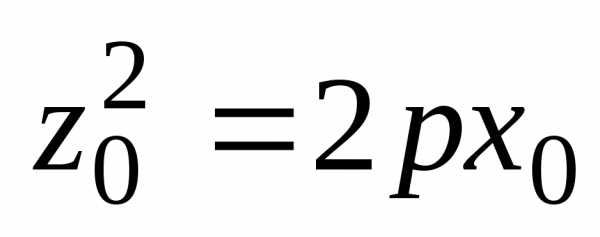 ,
поэтому.
Наконец, в силу произвольности точки,
выбранной на линии вращения, получаем,
что уравнение поверхности вращения —
эллиптического параболоида есть.
,
поэтому.
Наконец, в силу произвольности точки,
выбранной на линии вращения, получаем,
что уравнение поверхности вращения —
эллиптического параболоида есть.
studfiles.net
Поверхности второго порядка — часть 2
где p>0, q>0.
Уравнение (9) называется каноническим уравнением гиперболического параболоида.
Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение
(10)из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.
рассмотрим сечение данного параболоида плоскостью Oyz (x=0).
Получаем уравнение
из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения
из которых следует, что при любом h в сеченииполучается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).
Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения
илииз которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых
иточка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
6. Конус второго порядка.
Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
(11)Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию
распадающуюся на две пересекающиеся прямые
иАналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые
иРассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим
илииз которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями
. При увеличении абсолютной величины h полуоси a* и b* также увеличиваются.При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).
C писок использованной литературы :
1.Шипачёв В.С.:”Высшая математика”
mirznanii.com
Поверхности второго порядка
Содержание.
· Понятие поверхности второго порядка.
1. Инварианты уравнения поверхности второго порядка.
· Классификация поверхностей второго порядка.
1. Классификация центральных поверхностей.
-1°. Эллипсоид.
-2°. Однополостный гиперболоид.
-3°. Двуполостный гиперболоид.
-4°. Конус второго порядка.
2. Классификация нецентральных поверхностей.
-1°. Эллиптический цилиндр, гиперболический цилиндр, эллиптический параболоид, гиперболический параболоид.
-2°. Параболический цилиндр
•Исследование формы поверхностей второго порядка по их каноническим уравнениям.
1. Эллипсоид.
2. Гиперболоиды.
— 1°. Однополостный гиперболоид.
-2°. Двуполостный гиперболоид.
3. Параболоиды.
-1°. Эллиптический параболоид.
-2°. Гиперболический параболоид.
4 . Конус и цилиндры второго порядка.
— 1°. Конус второго порядка.
-2°. Эллиптический цилиндр.
-3°. Гиперболический цилиндр.
-4°. Параболический цилиндр.
Список использованной литературы.
§ 1. Понятие поверхности второго порядка.
Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
a11 х2 + а 22 у2 +a 33 z2 +2a 12xy +2 a 23уz + 2a 13xz + 2а 14x + 2а 24у+2а 34z +а 44 = 0 (1)
в котором по крайней мере один из коэффициентов a11 , а 22 , a 33 , a12 , a23 , a13 отличен от нуля.
Уравнение (1) мы будем называть общим уравнением поверхности второго порядка .
Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной декартовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравнение (1) и уравнение, полученное после преобразования координат, алгебраически эквивалентны.
1. Инварианты уравнения поверхности второго порядка.
Справедливо следующее утверждение.
являются инвариантами уравнения (1) поверхности второго-порядка относительно преобразований декартовой системы координат.
Доказательство этого утверждения приведено в выпуске «Линейная алгебра» настоящего курса.
§ 2. Классификация поверхностей второго порядка
1. Классификация центральных поверхностей. Пусть S — центральная поверхность второго порядка. Перенесем начало координат в центр этой поверхности, а затем произведем стандартное упрощение уравнения этой поверхности. В результате указанных операций уравнение поверхности примет вид
a11 х2 + а 22 у2 +a 33 z2 + а 44 = 0 (2)
Так как инвариант I3 для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения (2) , равно a11 • а 22 • a 33 , то коэффициенты a11 ,а 22 , a 33 удовлетворяют условию :
Возможны следующие случаи:
—1°. Коэффициенты a11 ,а 22 , a 33 одного знака, а коэффициента 44 отличен от нуля. В этом случае поверхность S называется эллипсоидом.
Если коэффициенты a11 ,а 22 , a 33 , а 44 одного знака, то левая часть (2) ни при каких значениях х, у, z не обращается в нуль, т. е. уравнению поверхности S не удовлетворяют координаты никакой точки. В этом случае поверхность S называется мнимым эллипсоидом .
Если знак коэффициентов a11 ,а 22 , a 33 противоположен знаку коэффициента а 44 , то поверхность S называется вещественным эллипсоидом . В дальнейшем термином «эллипсоид» мы будем называть лишь вещественный эллипсоид.
Обычно уравнение эллипсоида записывают в канонической форме. Очевидно, числа
положительны. Обозначим эти числа соответственно а 2 , b2 , с2 . После несложных преобразований уравнение эллипсоида (2) можно записать в следующей форме:
Уравнение (3) называется каноническим уравнением эллипсоида .
Если эллипсоид задан своим каноническим уравнением (3), то оси Ох, Оу и Оz . называются его главными осями.
—2°. Из четырех коэффициентов a11 ,а 22 , a 33 , а 44 два одного знака, а два других—противоположного. В этом случае поверхность S называется однополостным гиперболоидом .
Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности, a11 > 0,а 22 >0, a 33 <0,а 44 <0. Тогда числа
положительны. Обозначим эти числа соответственно а 2 , b2 , с2 . После несложных преобразований уравнение (2) однополостного гиперболоида можно записать в следующей форме:
Уравнение (4) называется каноническим уравнением однополостного гиперболоида .
Если однополостный гиперболоид задан своим каноническим уравнением (4), то оси Ох, Оу иOz называются его главными осями.
—3° . Знак одного из первых трех коэффициентов a11 ,а 22 , a 33 , а 44противоположен знаку остальных коэффициентов. В этом случае поверхность S называется двуполостным гиперболоидом.
Запишем уравнение двуполостного гиперболоида в канонической форме. Пусть, ради определенности, a11 < 0,а 22 <0, a 33 >0,а 44 <0. Тогда :
Обозначим эти числасоответственно через a2 , b2 , с2 . Поcли несложных преобразований уравнение (2) двуполостного гиперболоида можно записать в следующей форме:
Уравнение (5) называется каноническим уравнением двуполостного гиперболоида .
Если двуполостный гиперболоид задан своим каноническим
уравнением, то оси Ох, Оу и Оz называются его главными осями.
— 4° . Коэффициент а 44равен нулю. В этом случае поверхность S называетсяконусом второго порядка .
Если коэффициенты a11 ,а 22 , a 33 одного знака, то левая часть (2) обращается в нуль (а 44 =0) лишь для х=у=z=0, т. е. уравнению поверхности S удовлетворяют координаты только едной точки. В этом случае поверхность S называется мнимым конусом второго порядка . Если коэффициенты a11 ,а 22 , a 33 имеют разные знаки, то поверхность S является вещественным конусом второго порядка.
Обычно уравнение вещественного конуса второго порядка записывают в канонической форме. Пусть, ради определенности,
a11 > o, а 22 > 0,a 33 <0. Обозначим
соответственно через а2 , b2 , с2 . Тогда уравнение (2) можно записать в виде
Уравнение (6) называется каноническим уравнением вещественного конуса второго порядка .
2. Классификация нецентральных поверхностей второго порядка.
Пусть S — нецентральная поверхность второго порядка, т. е. поверхность, для которой инвариантI 3 равен нулю. Произведем стандартное упрощение уравнения этой поверхности. В результате уравнение поверхности примет вид
a´11 х ´ 2 + а ´22 у ´ 2 +a´ 33 z´ 2 + 2а ´ 14x´ + 2а ´ 24у ´ +2а ´ 34z´ +а ´ 44 = 0 (7)
для системы координат Ox´y´z´
Так как инвариант I 3 =0 и его значение, вычисленное дл
mirznanii.com

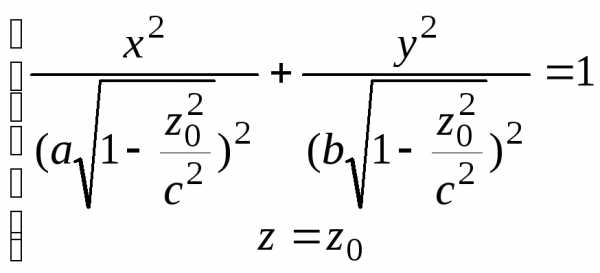 ,
, Рисунок Пр.2.2.1.
Рисунок Пр.2.2.1.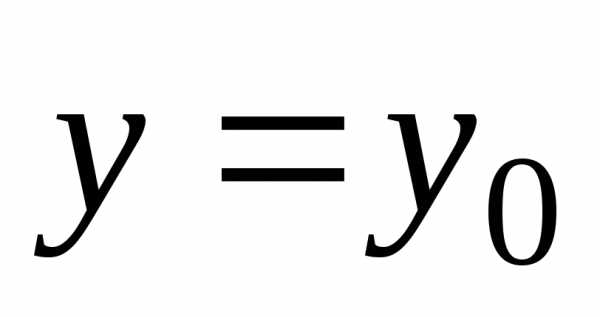 приводит к уравнению линии
приводит к уравнению линии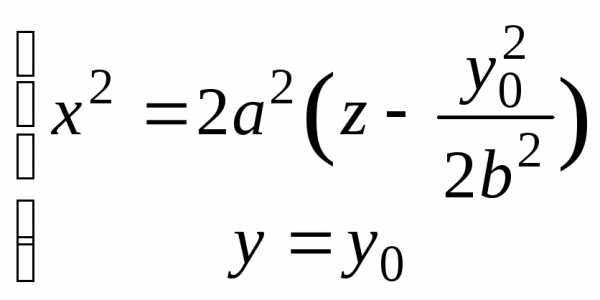 ,
,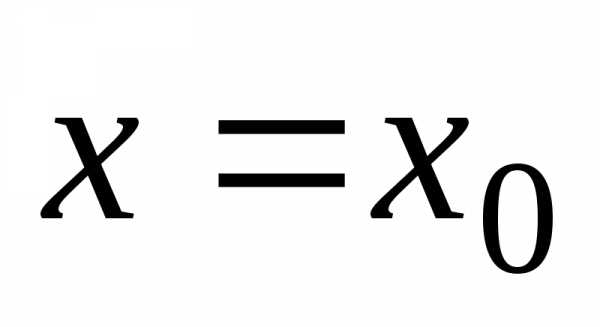 уравнение
сечения имеет аналогичный вид.
уравнение
сечения имеет аналогичный вид.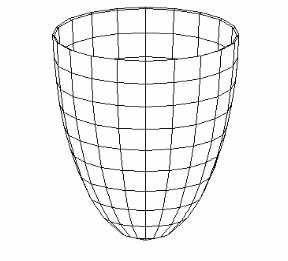
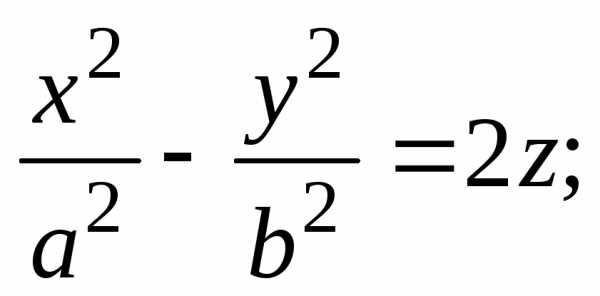 ,
называетсягиперболическим
параболоидом.
,
называетсягиперболическим
параболоидом.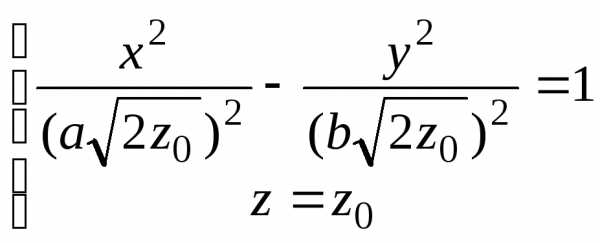 ,
, уравнение гиперболы будет иметь вид:
уравнение гиперболы будет иметь вид: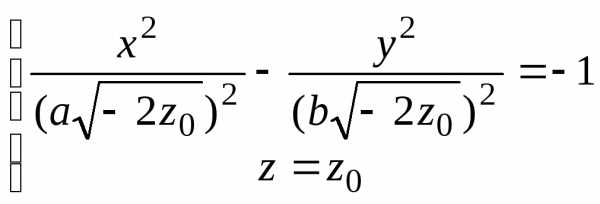 .
.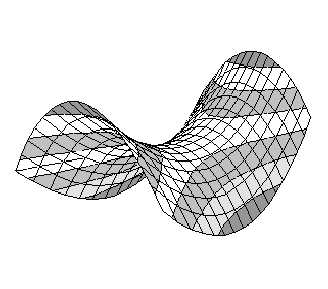 Рисунок Пр.2.4.1.
Рисунок Пр.2.4.1.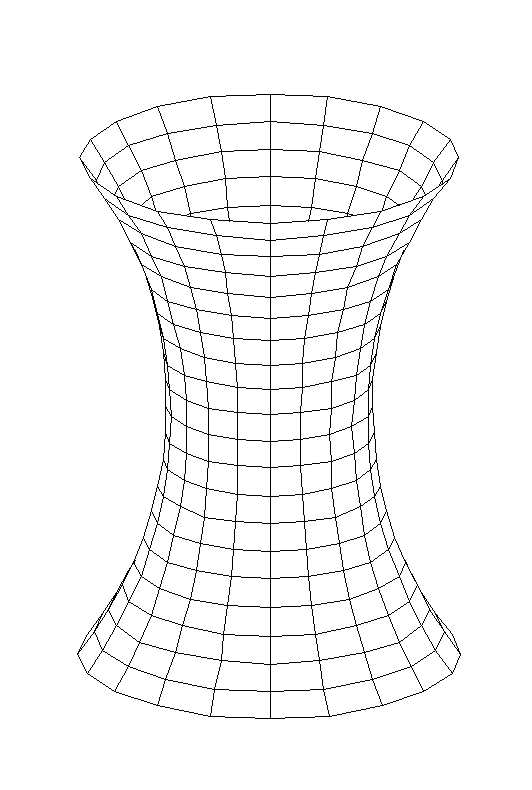
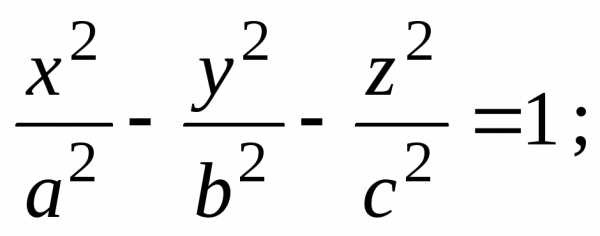 ,
называетсядвуполостным
гиперболоидом.
,
называетсядвуполостным
гиперболоидом.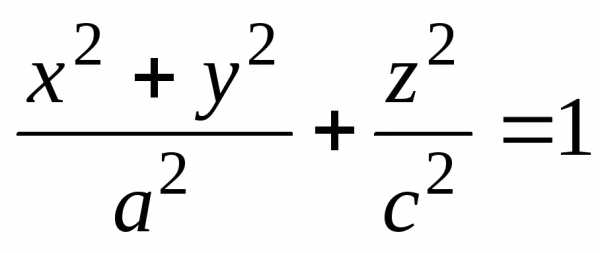 .
.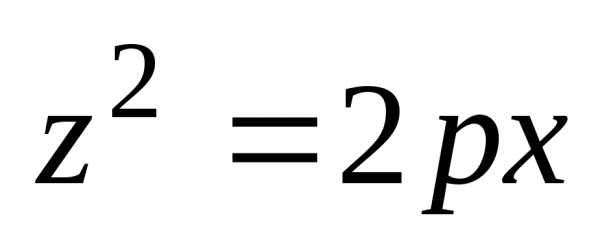 вокруг оси
вокруг оси .
.