Начальная симплекс-таблица
Базис
Переменные
Свободный член
xm+1 … xk … xn
x1
.
.
.
xi
.
.
.
xm

 …
…
.
.
.
 …
… …
…
.
.
.
 …
… …
…

.
.
.

.
.
.


 …
… …
…

Таблица 6.6
Симплекс-таблица для угловой точки x1
Базис
Переменные
Свободный член
xm+1 … xq … xn
x1
.
.
.
xk
.
.
.
xm
…
 …
…
.
.
.
 …
… …
…
.
.
 …
… …
…

.
.
.

.
.
.


 …
… …
…

6.2.4. Алгоритм решения задач симплекс – методом
Для определенности считаем, что решается задача на отыскание минимума.
Задачу линейного программирования привести к каноническому виду.
После введения добавочных переменных систему уравнений и линейную функцию записываем в виде, который называется расширенной системой:

Предполагаем, что все добавочные переменные имеют тот же знак, что и свободные члены; в противном случае используем так называемый М– метод, который будет рассмотрен ниже.
Определить базисные и свободные переменные.
Исходную расширенную систему заносим в первую симплекс – таблицу. Последняя строка таблицы, в которой приведено уравнение для линейной функции цели, называется
оценочной. В ней указываются коэффициенты функции цели .
В левом столбце таблицы записываем
основные переменные (базис), в последующих
– коэффициенты
.
В левом столбце таблицы записываем
основные переменные (базис), в последующих
– коэффициенты при свободных переменных. В предпоследнем
столбце – свободные члены расширенной
системы.
Последний столбец подготовлен для
оценочных отношений, необходимых для
определения базисной переменной
при свободных переменных. В предпоследнем
столбце – свободные члены расширенной
системы.
Последний столбец подготовлен для
оценочных отношений, необходимых для
определения базисной переменной на основании соотношения (6.29).
на основании соотношения (6.29).Определить возможность решения задачи по значениям
 согласно теоремам 6.7,…, 6.9.
согласно теоремам 6.7,…, 6.9.Выбрать разрешающий (опорный) элемент
. Если критерий оптимальности не выполнен (не выполнены условия теоремы 6.7 или 6.8), то наибольший по модулю отрицательный коэффициент
 в последней строке определяет разрешающий
(опорный) столбец
в последней строке определяет разрешающий
(опорный) столбец .
.
Составляем оценочные отношения каждой строки по следующим правилам:
10) ,
если все
,
если все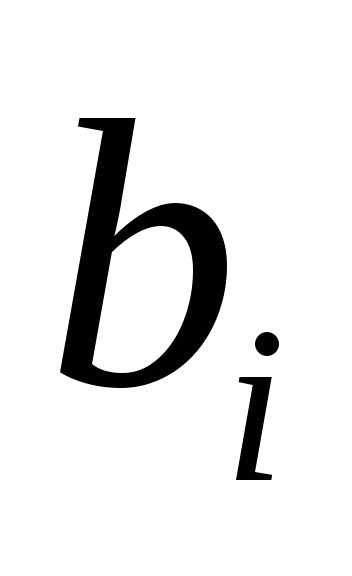 и
и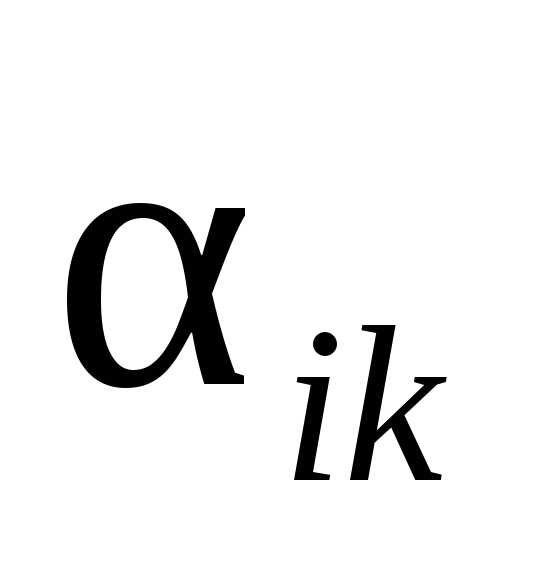 имеют разные знаки;
имеют разные знаки;
20) ,
если все
,
если все
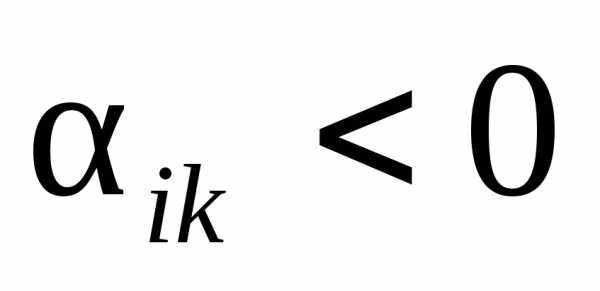 ;
;30) ,
если
,
если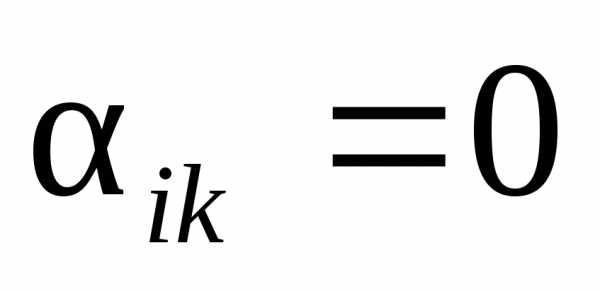 ;
;
40)
0, если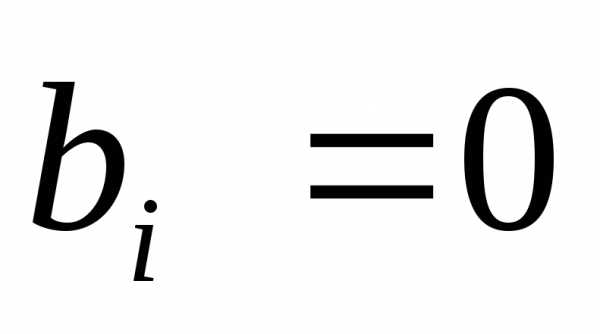 и
и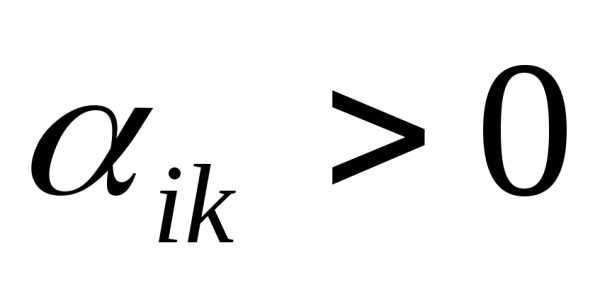 ;
;
50)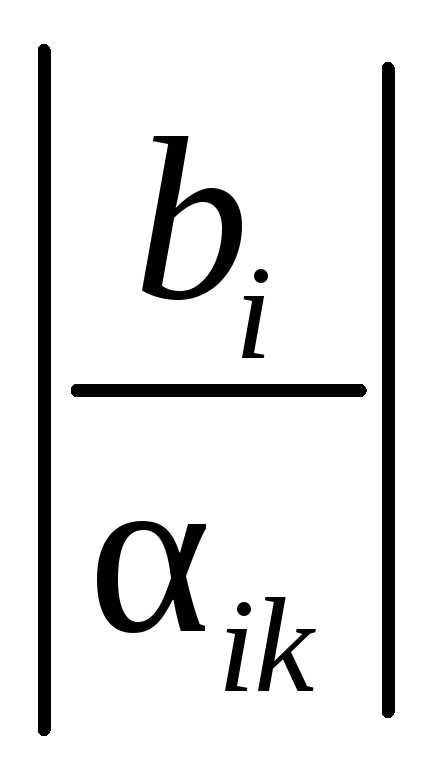 ,
если
,
если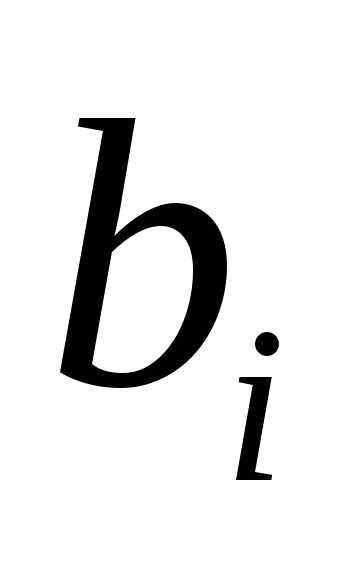 и
и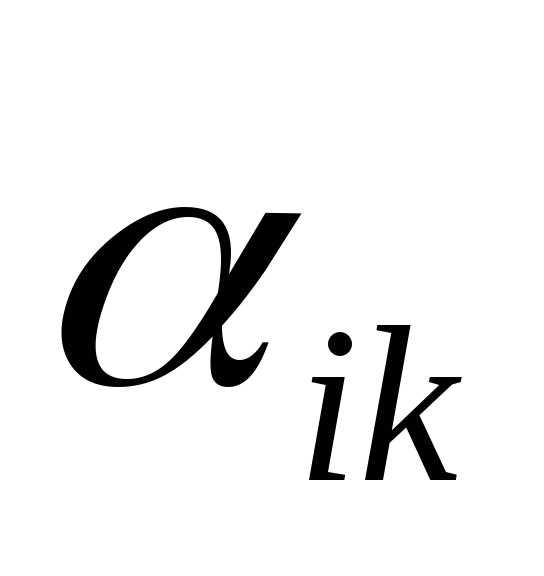 имеют одинаковые знаки.
имеют одинаковые знаки.
Определим 
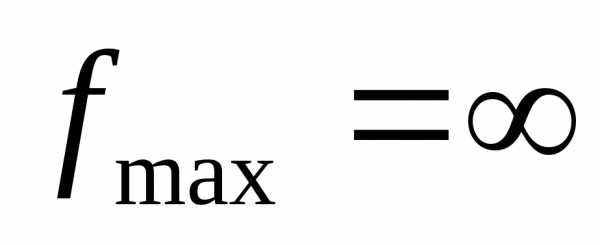 ).
Если минимум конечен, то выбираем строкуq, на которой он достигается (любую,
если их несколько), и называем ее
разрешающей (опорной) строкой. На
пересечении разрешающих строки и столбца
находится разрешающий (опорный) элемент
).
Если минимум конечен, то выбираем строкуq, на которой он достигается (любую,
если их несколько), и называем ее
разрешающей (опорной) строкой. На
пересечении разрешающих строки и столбца
находится разрешающий (опорный) элемент .
.60) Переход к следующей таблице по правилам:
а) в левом столбце
записываем новый базис: вместо основной
переменной 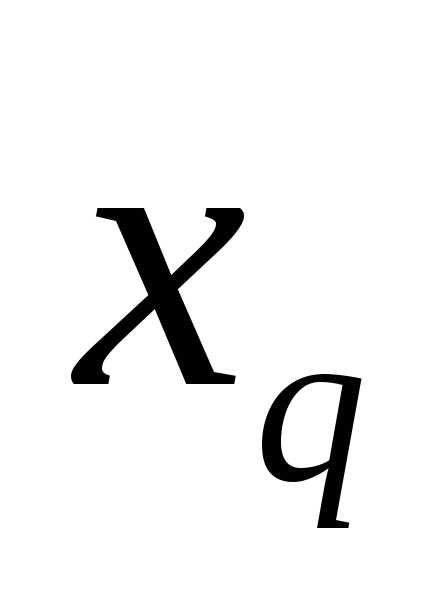 – переменную
– переменную ,
т.е. поменяем местами переменные
,
т.е. поменяем местами переменные
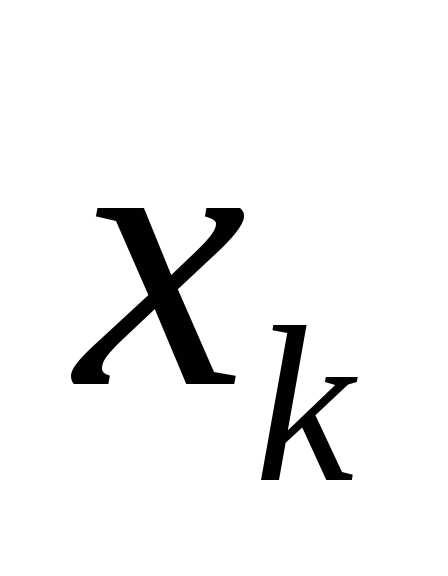 ;
; б) на место опорного
элемента 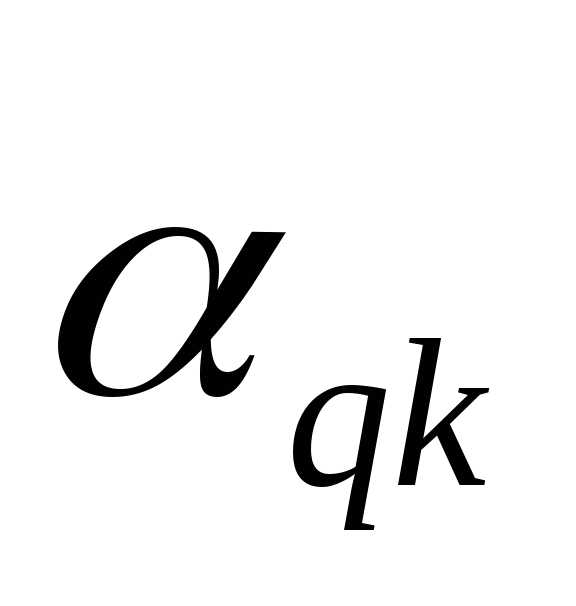 поставить 1;
поставить 1;
в) на остальных местах опорной строки в новой таблице оставить элементы исходной таблицы;
г) на остальные места в опорном столбце поставить соответствующие элементы исходной таблицы, умноженные на –1;
д) на оставшиеся
свободные места элементов 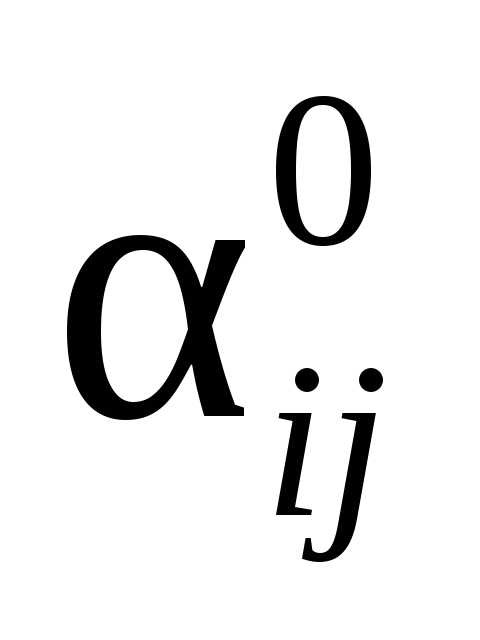 ,
,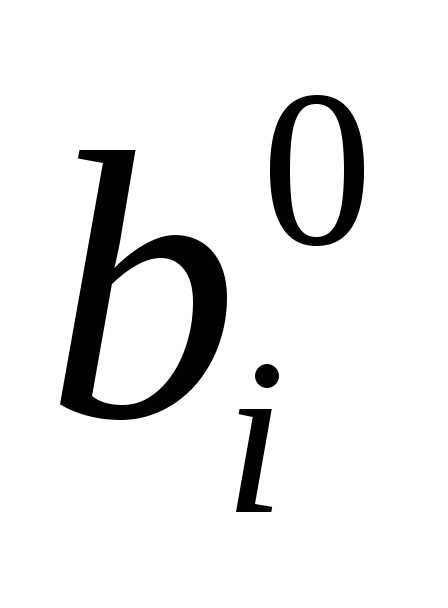 ,
, в новой таблице записать числа
в новой таблице записать числа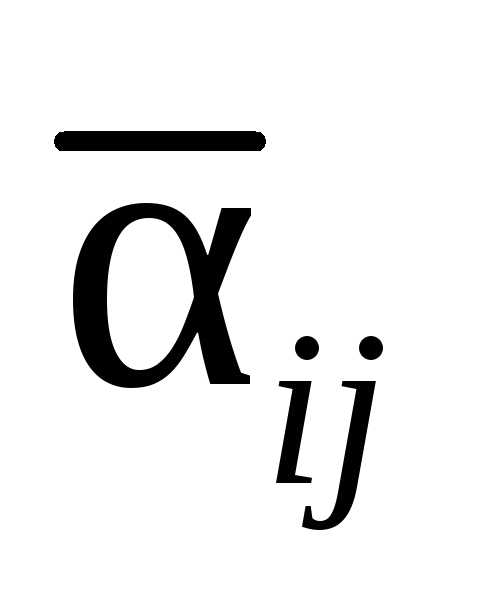 ,
, ,
, ,
которые находятся следующим образом:
,
которые находятся следующим образом:
, ,.
Для упрощения
вычислений по этим формулам их можно
сформулировать в виде «правила
прямоугольника»(рис. 6.8): элементы на
диагоналях прямоугольника с вершинами(или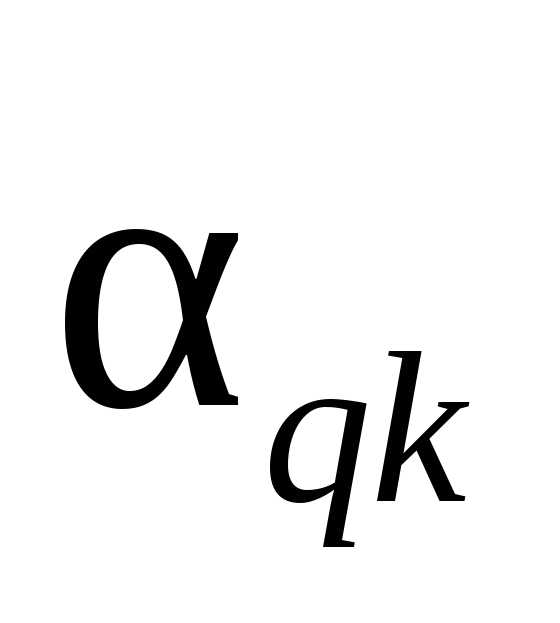 ,
, ,
,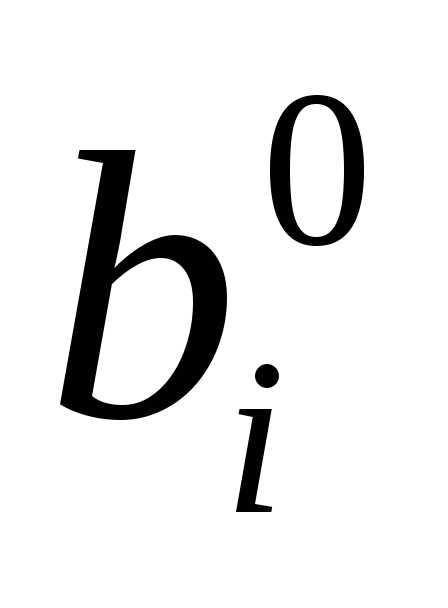 ,
,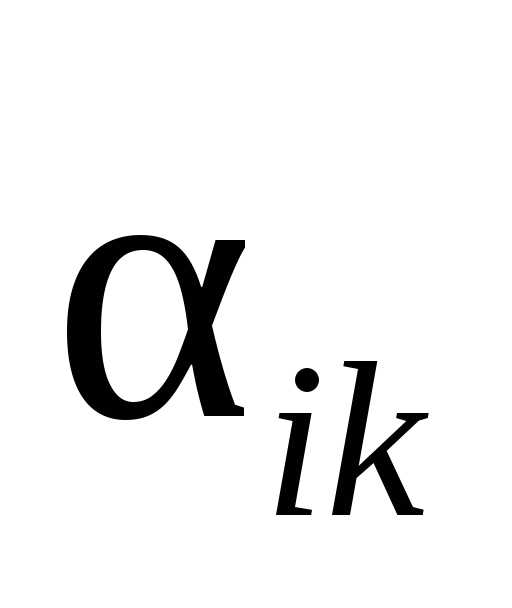 ,
или
,
или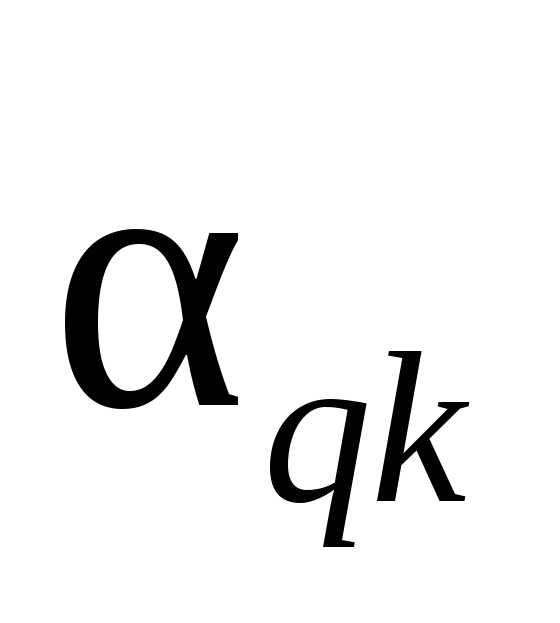 ,
,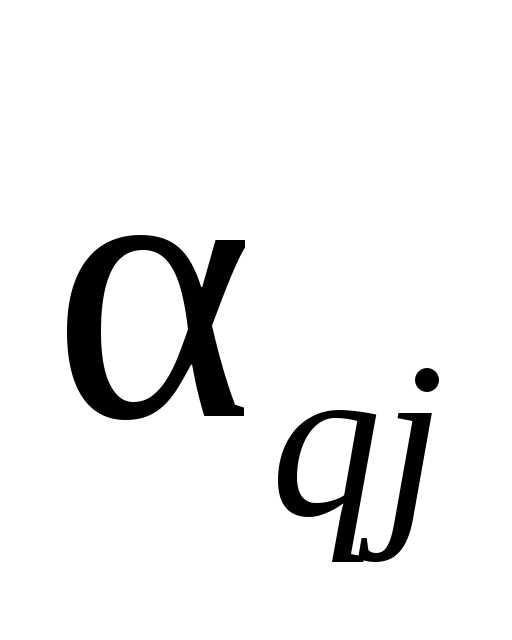 ,
,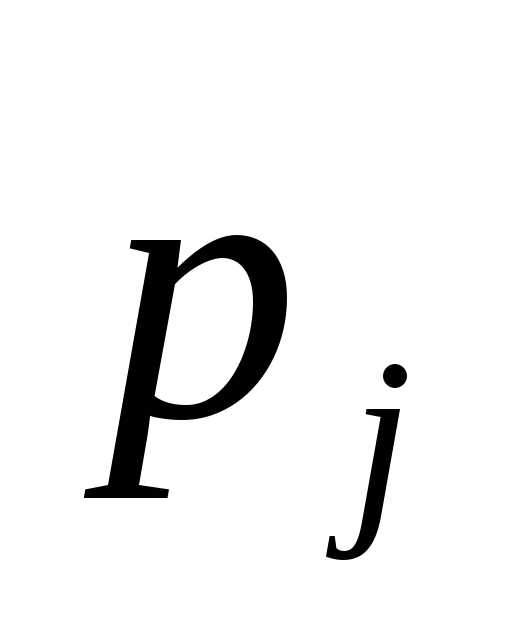 ,
,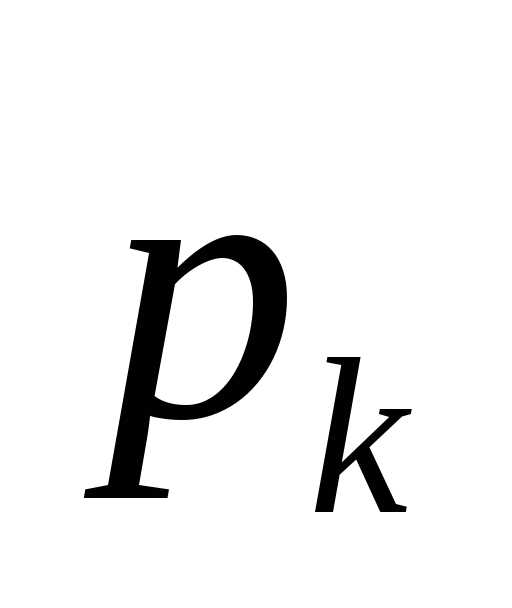 )
перемножаются (произведение, не содержащее
опорного элемента
)
перемножаются (произведение, не содержащее
опорного элемента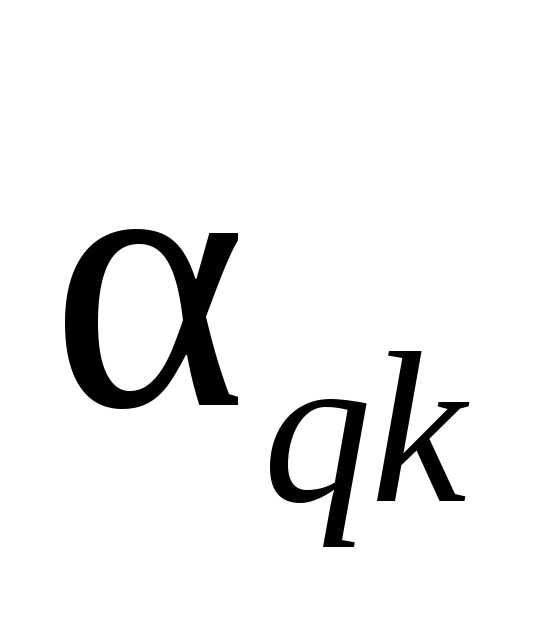 ,
берется со знаком минус) и полученные
произведения складываются;
,
берется со знаком минус) и полученные
произведения складываются;
е) все полученные
элементы новой таблицы разделить на
опорный элемент 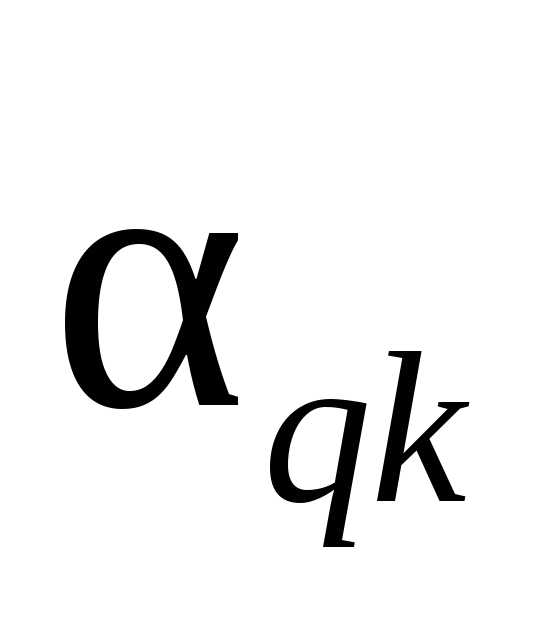 .
.
70)
По значению элемента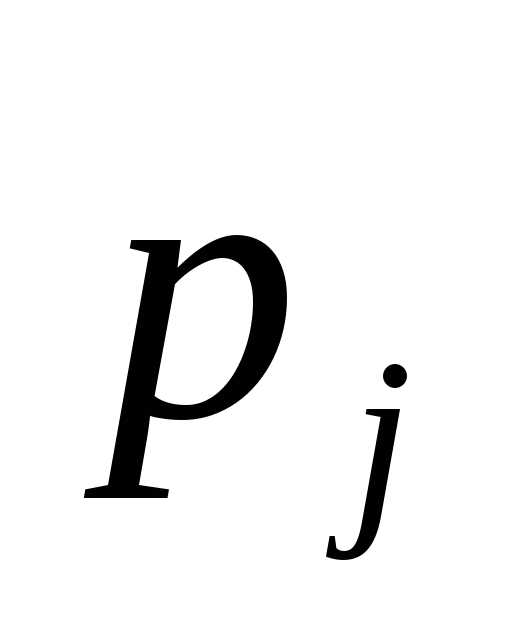 определить, найдено ли оптимальное
значение целевой функции. В случае
отрицательного ответа продолжить
решение (возврат к пункту 6).
определить, найдено ли оптимальное
значение целевой функции. В случае
отрицательного ответа продолжить
решение (возврат к пункту 6).
Рис. 6.8. Правило прямоугольника для определения чисел:
а − 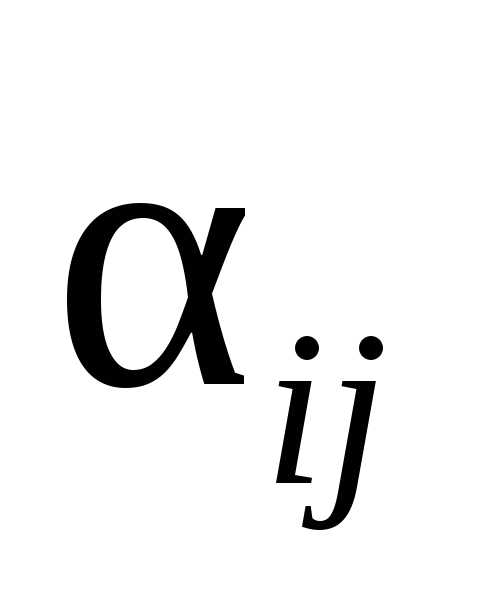 ,
б −
,
б −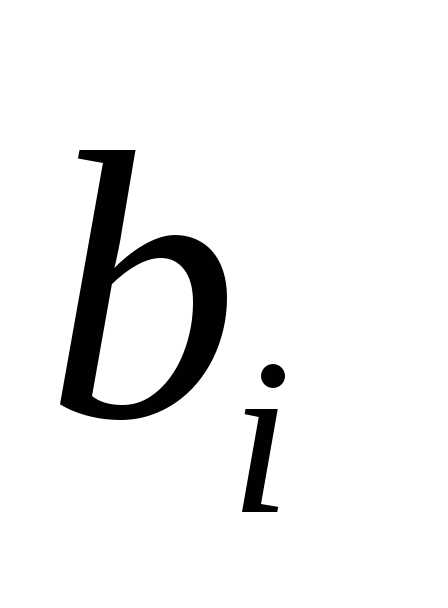 ,
в −
,
в − .
.
Рассмотрен алгоритм преобразования симплекс – таблиц для невырожденных допустимых базисных решений, т.е. выполнялась ситуация, описанная теоремой 6.9. Если исходная задача линейного программирования является вырожденной, то в ходе ее решения симплекс – методом могут появиться и вырожденные базисные решения. При этом возможны холостые шаги симплекс – метода, т.е. итерации, на которых f(x)не изменяется. Возможно так же и зацикливание, т.е. бесконечная последовательность холостых шагов. Для его предотвращения разработаны специальные алгоритмы – антициклины. Однако в подавляющем большинстве случаев холостые шаги сменяются шагами с убыванием целевой функции и процесс решения завершается в результате конечного числа итераций.
Пример 6.8.Решить задачу, приведенную в примере 6.7, симплекс методом.
Решение.
В качестве начальной симплекс – таблицы возьмем таблицу, найденную в примере 6.7 и соответствующую допустимому базисному решению :
Таблица 6.7
Начальная симплекс — таблица
Базис | Переменные | Свободный член | Оценочное отношение | |
x1 | x2 | |||
x3 x4 x5 | 1 2 0 | 2 1 1 | 7 8 3 | 7 4 |
f(x) | -3 | -3 | 0 | |
В последней строке
таблицы есть два отрицательных элемента, 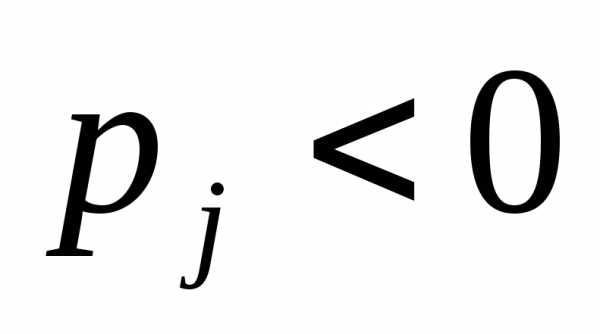 ,
и столбец, соответствующий каждому из
них можно считать опорным. Выберем,
например, первый столбец (этот столбец
отмечен стрелкой). Согласно теореме 6.9
существует допустимое базисное решение.
Опорную строку найдем по правилу (6.29).
В соответствии с пунктом 5 находим
оценочные отношения:,
т.е. это вторая строка. Опорный элемент
,
и столбец, соответствующий каждому из
них можно считать опорным. Выберем,
например, первый столбец (этот столбец
отмечен стрелкой). Согласно теореме 6.9
существует допустимое базисное решение.
Опорную строку найдем по правилу (6.29).
В соответствии с пунктом 5 находим
оценочные отношения:,
т.е. это вторая строка. Опорный элемент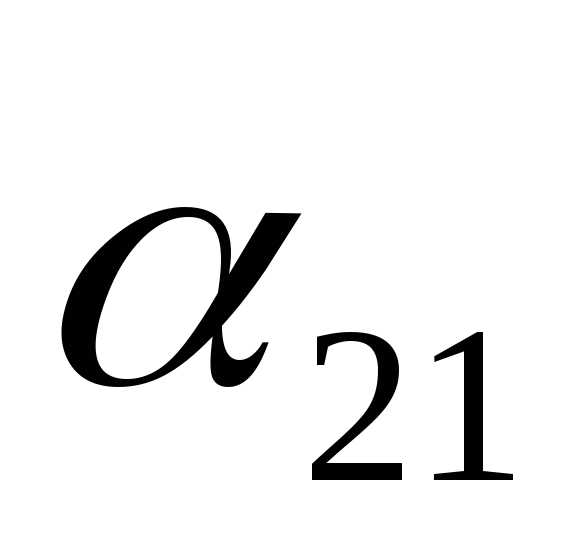 обведен рамкой.
обведен рамкой.
Будем формировать новую таблицу в соответствии с описанным алгоритмом
п.6 а,б п.6 в,г
x4 | x2 | x4 | x2 | |||||
x3 | x3 | -1 | ||||||
x1 | 1 | x1 | 1 | 1 | 8 | |||
x5 | x5 | 0 | ||||||
3 |
Свободные места последней таблицы заполним по «правилу прямоугольника». Например, число, стоящие в строке при x3и столбце приx2этой таблицы, равно 2∙2-1∙1 = 3. Дляи т.д. В результате этих вычислений, а также пункта 6е (т.е. деления на опорный элемент) получим искомую симплекс – таблицу:
п.6д п.6е
x4 | x2 | x4 | x2 | |||||
х3 | -1 | 3 | 6 | x3 | -1/2 | 3/2 | 3 | |
х1 | 1 | 1 | 8 | x1 | 1/2 | 1/2 | 4 | |
х5 | 0 | 2 | 6 | x5 | 0 | 1 | 3 | |
3 | -3 | 24 | 3/2 | -3/2 | 12 |
Отметим, что в результате перехода к новому допустимому решению значение целевой функции уменьшилось с 0 до –12 (см. нижний элемент последнего столбца таблицы).
В качестве опорного
(см. п. 6е) можно взять только второй
столбец (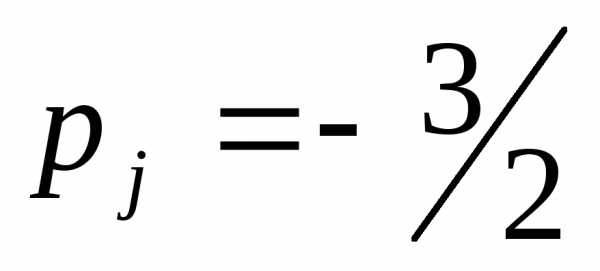 ).
С учетом (6.29) находим опорную строку:
).
С учетом (6.29) находим опорную строку:
Таблица 6.8
Симплекс-таблица для угловой точки х1
Базис | Переменные | Свободный член | Оценочное отношение | |
x4 | x2 | |||
x3 x1 x5 | -1/2 1/2 0 | 3/2 1/2 1 | 3 4 3 | 2 8 3 |
f(x) | 3/2 | -3/2 | 12 | |
,
т.е. это первая строка. Опорный элемент 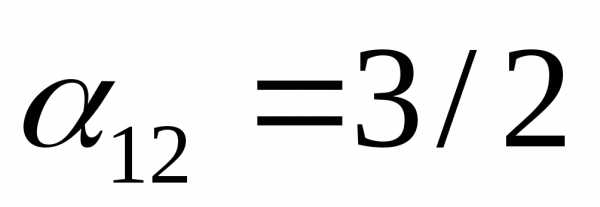 обведен рамкой.
обведен рамкой.
Преобразуем таблицу согласно алгоритму, получаем
x4 | x3 | x4 | x3 | x4 | x3 | ||||||||
x2 | -1/2 | 1 | 3 | x2 | -1/2 | 1 | 3 | x2 | -1/3 | 2/3 | 2 | ||
x1 | -1/2 | x1 | 1 | -1/2 | 9/2 | x1 | 2/3 | -1/3 | 3 | ||||
x5 | -1 | x5 | 1/2 | -1 | 3/2 | x5 | 1/3 | -2/3 | 1 | ||||
3/2 | 3/2 | 3/2 | 45/2 | 1 | 1 | 15 |
Таким образом, на данной итерации значение f(х) уменьшилось с –12 до –15.
Так как все элементы 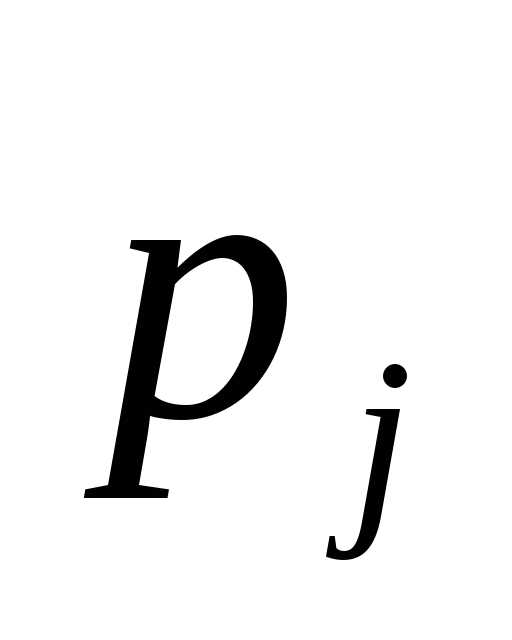 в последней строке таблицы неотрицательны,
то, согласно теореме 6.9, базисное решение
является точкой минимума в рассматриваемой
задаче, т.е.х* = (3;2;0;0;1),f*
= –15. Графическое решение задачи
представлено на рис. 6.8, откуда видно,
чтох* = (3;2),f* =f(х*) = –15
в последней строке таблицы неотрицательны,
то, согласно теореме 6.9, базисное решение
является точкой минимума в рассматриваемой
задаче, т.е.х* = (3;2;0;0;1),f*
= –15. Графическое решение задачи
представлено на рис. 6.8, откуда видно,
чтох* = (3;2),f* =f(х*) = –15
Рис. 6.8. Графическое решение задачи 6.10
studfiles.net
Презентация на тему: Правило прямоугольника на практике.
План | Базис |
|
|
|
|
|
| х3 |
|
| В | х1 | х2 | ||||
1 | х4 |
|
| 1100 | 0.1 | 0.2 |
| |
|
| |||||||
| х5 | 120 | 0.05 | 0.02 | 0.02 | |||
• НЭ= |
|
|
|
| НЭ= |
|
|
|
НЭ= 1100:0.2=5500 | НЭ= 0.1:0.2=0.5 |
| ||||||
Необходимо преобразовать все элементы симплексной таблицы по правилу прямоугольника(кроме элементов столбца Q и элементов находящихся в столбце с разрешающим элементом.)
В столбце “Базис” меняем базисные переменные на переменные уравнения.(Переменные уравнения выбираем по разрешающему элементу.)

Внимание
План | Бази | В | х1 | х2 | х3 | х4 | х5 | х6 | Q |
| с |
|
|
|
|
|
|
|
|
2 | х4 | 1100 | 0.1 | 1 | 0.4 | 1 | 0 | 0 |
|
| х5 | 120 | 0.05 | 0 | 0.02 | 0 | 1 | 0 |
|
| х6 | 8000 | 3 | 0 | 2 | 0 | 0 | 1 |
|
Индексн | F(X1) 0 | -3 | 0 | -4 | 0 | 0 | 0 | 0 | |
ая | |||||||||
строка |
|
|
|
|
|
|
|
|
|
Разрешающий элемент необходимо привести к 1 . Для этого делим 0,2/0,2=1.
Коэффициенты под разрешающим элементом записываются нулями.

7. Сформировать следующую часть симплексной таблицы, пользуясь правилом прямоугольника.
План | Ба | В | х1 | х2 | х3 | х4 | х5 | х6 | Q |
| зи |
|
|
|
|
|
|
|
|
| с |
|
|
|
|
|
|
|
|
2 | x2 | 5500 | 0.5 | 1 | 2 | 5 | 0 | 0 |
|
| x5 | 10 | 0.04 | 0 | -0.02 | -0.1 | 1 | 0 |
|
| x6 | 2500 | 2.5 | 0 | 0 | -5 | 0 | 1 |
|
Индексна | F(X227500 | -0.5 | 0 | 6 | 25 | 0 | 0 |
| |
я строка | ) |
|
|
|
|
|
|
|
|
*После построения новой симплексной таблицы необходимо проверить знаки в индексной строке. * Если в индексной строке есть отрицательные элементы, то находим разрешающий элемент и продолжаем преобразования.

Разрешающий элемент
План | Ба | В | х1 | х2 | х3 | х4 | х5 | х6 | Q |
| зи |
|
|
|
|
|
|
|
|
| с |
|
|
|
|
|
|
|
|
2 | x2 | 5500 | 0.5 | 1 | 2 | 5 | 0 | 0 | 11000 |
|
|
|
|
|
|
|
|
| |
| x5 | 10 | 0.04 | 0 | -0.02 | -0.1 | 1 | 0 | 250 |
| x6 | 2500 | 2.5 | 0 | 0 | -5 | 0 | 1 | 1000 |
Индексна | F(X227500 | -0.5 | 0 | 6 | 25 | 0 | 0 | 0 | |
я строка | |||||||||
| ) |
|
|
|
|
|
|
|
|
1. Находим наименьшее Q. 2.Находим разрешающий элемент.
Новая симплекс таблица.
План | Бази | В | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Q |
| с |
|
|
|
|
|
|
|
|
3 | x2 | 5375 | 0 | 1 | 2.25 | 6.25 | -12.5 | 0 |
|
| x1 | 250 | 1 | 0 | -0.5 | -2.5 | 25 | 0 |
|
Индексн | x6 | 1875 | 0 | 0 | 1.25 | 1.25 | -62.5 | 1 |
|
F(X3) | 2762 | 0 | 0 | 5.75 | 23.75 | 12.5 | 0 |
| |
ая |
| ||||||||
строка |
| 5 |
|
|
|
|
|
|
|
Формируем новую симплекс таблицу пользуясь правилом прямоугольника. Проверяем знаки в индексной строке, если все знаки положительны, то найдено оптимальное решение.
Оптимальным решение будет число находящиеся на пересечении индексной строки и столбца В.
Ответ= 27625.
Его можно проверить такподставляем получившиеся значения базисных элементов в функцию. Ответ должен совпадать.
studfiles.net
5.2. Симплексные таблицы и алгоритм решения задач
Рассмотрим алгоритм решения задач симплексным методом17.
1. Математическая модель задачи должна бать канонической. Если она неканоническая, то ее надо привести к каноническому виду.
2. Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплекс-таблицу. Все строки таблицы 1-го шага, за исключением строки j (индексная строка), заполняем по данным системы ограничений и целевой функции.
Симплексная таблица имеет следующий вид:
сi | Базисная переменная (БП) | с1 | с2 | | сm | сm+1 | | сn | f(X) |
x1 | x2 | | xm | xm+1 | | xn | b1 | ||
c1 | x1 | 1 | 0 | | 0 | h1, m+1 | | h1n | l1 |
c2 | x2 | 0 | 1 | | 0 | h2, m+1 | | h2n | l2 |
| | | | | | | | | |
cm | xm | 0 | 0 | | 1 | hm, m+1 | | hmn | lm |
j | 0 | 0 | | 0 | m+1 | | n | f(X1) |
Индексная строка (j) для переменных находится по формуле
и для свободного члена по формуле
.
При этом возможны следующие случаи решения задачи на максимум:
— если все оценки j 0, то найденное решение оптимальное;
— если хотя бы одна оценка j 0, но при соответствующей переменной нет ни одного положительного коэффициента, решение задачи прекращают, так как f(X) , т.е. целевая функция не ограничена в области допустимых решений;
— если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;
— если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка.
Пусть одна оценка k 0 или наибольшая по абсолютной величине k 0, тогда k-й столбец принимают за ключевой (разрешающий). За ключевую (разрешающую) строку принимают ту, которой соответствует минимальное отношение свободных членов (bi) к положительным коэффициентам k-го столбца. Элемент, находящийся на пересечении ключевых строки и столбца, называют ключевым (разрешающим) элементом.
3. Заполнение симплексной таблицы 2-го шага:
— переписывается ключевая строка, разделив ее элементы на ключевой элемент;
— заполняют базисные столбцы;
— остальные коэффициенты таблицы находят по правилу «прямоугольника». Оценки можно считать по приведенным выше формулам или по правилу «прямоугольника». Получается новое опорное решение, которое проверяется на оптимальность и т.д.
Примечание. Если целевая функция f(X) требует нахождения минимального значения, то критерием оптимальности задачи является неположительность оценок j при всех .
Правило «прямоугольника» состоит в следующем. Пусть ключевым элементом 1-го шага является элемент 1-й строки (m+1)-го столбца h1, m+1. Тогда элемент i-й строки (m+2)-го столбца 2-го шага, который обозначим , по правилу «прямоугольника» определяется по формуле
,
где h1, m+1, hi, m+1, hi, m+2 – элементы 1-го шага.
5.3. Применение симплексного метода в экономических задачах
Рассмотрим применение симплексного метода на примерах экономических задач18.
Пример. Предприятие располагает тремя производственными ресурсами (сырьем, оборудование, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов и амортизация оборудования за один месяц и общий ресурс при каждом способе производства заданы в таблице (в ден. ед.).
Производственный ресурс | Расход ресурсов за 1 месяц при работе | Общий ресурс | |
по 1 способу | по 2 способу | ||
Сырье | 1 | 2 | 4 |
Оборудование | 1 | 1 | 3 |
Электроэнергия | 2 | 1 | 8 |
При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором – 4 тыс. изделий.
Сколько месяцев должно работать предприятие по каждому из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции?
Решение. Обозначим: х1 – время работы предприятия по первому способу; х2 – время работы предприятия по второму способу. Экономико-математическая модель задачи:
при ограничениях:
Приведем задачу к каноническому виду:
при ограничениях:
Составляем симплексную таблицу 1-го шага:
сi | БП | 3 | 4 | 0 | 0 | 0 | |||||||
х1 | х2 | х3 | х4 | х5 | bi | ||||||||
0 | x3 | 1 | 2 | 1 | 0 | 0 | 4 | ||||||
0 | x4 | 1 | 1 | 0 | 1 | 0 | 3 | ||||||
0 | x5 | 2 | 1 | 0 | 0 | 1 | 8 | ||||||
j | -3 | -4 | 0 | 0 | 0 | 0 | |||||||
= (0, 0, 4, 3, 8), = 0.
В индексной строке j имеются две отрицательные оценки, значит найденное решение не является оптимальным и его можно улучшить. В качестве ключевого столбца следует принять столбец базисной переменной х2, а за ключевую строку – строку переменной х3, где min (4/2, 3/1, 8/1) = min (2, 1, 8) = 2.
Ключевым элементом является «2». Вводим в столбец БП переменную х2, выводим х3. Составляем симплексную таблицу 2-го шага:
сi | БП | 3 | 4 | 0 | 0 | 0 | |||||||
х1 | х2 | х3 | х4 | х5 | bi | ||||||||
4 | x2 | 1/2 | 1 | 1/2 | 0 | 0 | 2 | ||||||
0 | x4 | 1/2 | 0 | -1/2 | 1 | 0 | 1 | ||||||
0 | x5 | 3/2 | 0 | -1/2 | 0 | 1 | 6 | ||||||
j | -1 | 0 | 2 | 0 | 0 | 8 | |||||||
= (0, 2, 0, 1, 6), =8.
В индексной строке имеется одна отрицательная оценка. Полученное решение можно улучшить. Ключевым элементом является «1/2». Составим симплексную таблицу 3-го шага:
сi | БП | 3 | 4 | 0 | 0 | 0 | |||||||
х1 | х2 | х3 | х4 | х5 | bi | ||||||||
4 | x2 | 0 | 1 | 1 | -1 | 0 | 1 | ||||||
3 | x1 | 1 | 0 | -1 | 2 | 0 | 2 | ||||||
0 | x5 | 0 | 0 | 1 | -3 | 1 | 3 | ||||||
j | 0 | 0 | 1 | 2 | 0 | 10 | |||||||
Все оценки свободных переменных j 0, следовательно, найденное опорное решение является оптимальным:
= (2, 1, 0, 0, 3), = 10.
Ответ: максимальный выпуск продукции составит 10 тыс. ед., при этом по первому способу предприятие должно работать два месяца, по второму – один месяц.
studfiles.net
Основы симплекс — метода линейного программирования
Симплекс — метод представляет собой итеративную процедуру решения задач ЛП, в каноническом виде (любую задачу ЛП можно привести к каноническому виду:
 (1)
(1)
Всего в задаче будет n+m переменных.
Переменные, входящие с единичными коэффициентами только в одно уравнение системы и с нулевыми — в остальные, называются базисными. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Остальные n переменных называются небазисными переменными.
Будем считать, что решается задача на максимум (задачу на минимум можно свести к задаче на максимум, умножив целевую функцию на (-1))
Пример 1.
Решим задачу:

Приведем систему ограничений к каноническому виду. Получим расширенную систему:
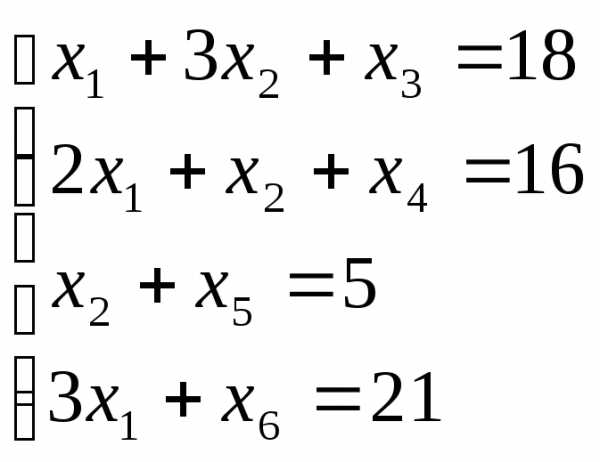
Для нахождения первоначального базисного решения разобьем переменные на основные и неосновные. Так как определитель матрицы коэффициентов при х3, х4 х5 и х6 отличен от нуля (каждая из этих переменных входит только в одно ограничение причем с коэффициентом 1, то есть матрица коэффициентов при них будет единичной), то их можно взять за базисные переменные. Остальные переменные х1 и х2 будит неосновными.
Правило: на первом шаге в качестве основных переменных следует выбирать такие из них, которые входят только в одно из уравнений системы ограничений, при этом нет таких уравнений, в которое не входит ни одна их этих переменных.
Если дополнительные переменные имеют тот же знак что и свободные члены в правой части, то они удовлетворяют этом правилу.
1). Получим на первом шаге:
Базисные переменные | Не базисные переменные |
х3, х4 х5 х6 | х1 х2 |
Выразим неосновные переменные через основные:
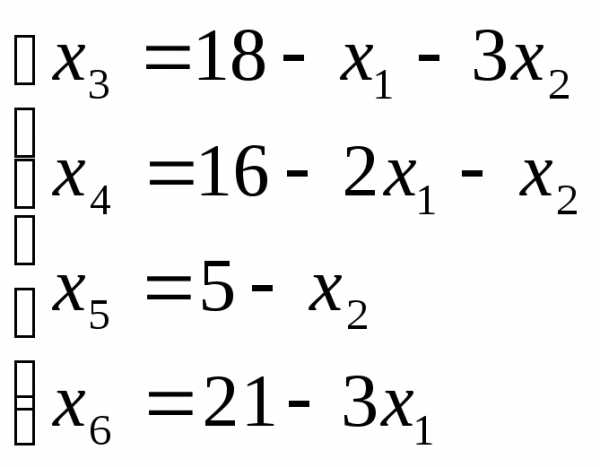 (*)
(*)
Получим базисное решение системы Х1=(0; 0; 18; 16; 5; 21). Если сравнить с графическим решением этой задачи, то Х1 соответствует точке О(0;0) многоугольника ОАВСДЕ (см. рис. 1).
Так как это решение допустимое, нельзя исключать, что оно оптимальное.
Выразим целевую функцию через неосновные переменные: ,z(X1)=0.
Функцию z можно увеличить за счет неосновной переменной (обе они входят в уравнение с коэффициентом >0). Это можно осуществить, перейдя к новому допустимому базисному решению, в котором одна из этих переменных станет основной. Если новое решение будет вырожденным, то целевая функция сохранит свое значение. Геометрически это переход к другой соседней вершине, в которой целевая функция будет по крайней мере не хуже. В рассматриваемой задаче можно переводить в базисные переменные как х1 так и х2, так как обе входят в целевую функцию со знаком «+».
Для определенности будем выбирать в такой ситуации переменную с наибольшим коэффициентом в целевой функции. В данной задаче это х2.
Система ограничений (*) накладывает ограничения на рост х2, так как необходимо сохранять допустимость решения (все переменные должны быть »0). Поэтому следующие неравенства должны быть выполнены при х1=0:
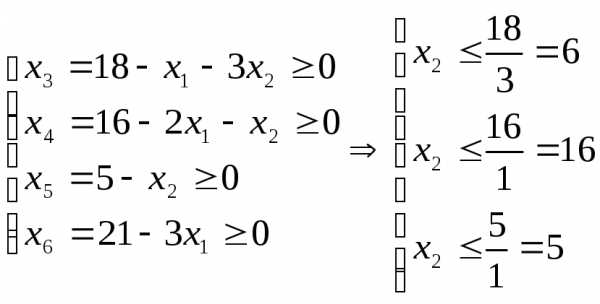
Любое уравнение системы (*) (кроме последнего) определяет оценочное отношение – границу роста переменной х2, сохраняющую неотрицательность соответствующей переменной. Эта граница определяется абсолютной величиной отношения свободного члена к коэффициенту при х2, если они имеют разные знаки. Так как в последнее ограничение х2 не входит (входит с коэффициентом 0), то рост х2 не ограничен, х2<∞. Будем так же считать, сто граница переменной х2 равно ∞, если коэффициент перед х2 и свободный член имеют одинаковые знаки. Нет ограничений на рост х2 и в том случае, если свободные член равен 0. Но если при этом коэффициент при х2 отрицательный, то рост этой переменной ограничен 0.
Так как неотрицательность должны сохранять все переменные, по новая базисная переменная х2=min(6; 16; 5; ∞)=5. Уравнение, которое соответствует минимальной оценке, называется разрешающим. В этом примере – это третье уравнение
Следовательно, переменная х5=0 и переходит в небазисные переменные.
2). Получим на втором шаге:
Базисные переменные | Не базисные переменные |
х3, х4 х2 х6 | х1 х5 |
Из третьего уравнения системы выразим :х2:
Подставляя правую часть равенства во все остальные уравнения вместо х2 получим:

Получим новое базисное решение системы Х2=(0; 5; 3; 11; 0; 21). Это соответствует точке А(0;5) многоугольника ОАВСДЕ (см. рис. 1).
Выразим целевую функцию через неосновные переменные: ,z(X2)=15.
Аналогично рассуждениям, проведенным на первом шаге, сделаем вывод, что целевую функцию можно улучшить введя в базисные переменные х1.
х1=min(∞; 13; 11/2; ∞)=3, следовательно второе уравнение разрешающее и х3 выводится из базиса.
3). Получим на третьем шаге:
Базисные переменные | Не базисные переменные |
х1, х4 х2 х6 | х3 х5 |
Из второго уравнения системы выразим :х1:
Подставляя правую часть равенства во все остальные уравнения вместо х1 получим:

Получим новое базисное решение системы Х3=(3; 5; 0; 5; 0; 12). Это соответствует точке В(3;5) многоугольника ОАВСДЕ (см. рис. 1).
Выразим целевую функцию через неосновные переменные: ,z(X3)=21.
Аналогично первым двум шагам введем в базисные переменные х5.
х5=min(∞; 5; 1;4/3)=1, следовательно, третье уравнение разрешающее и х4 выводится из базиса.
4). Получим на четвертом шаге:
Базисные переменные | Не базисные переменные |
х1, х5 х2 х6 | х3 х4 |
Из третьего уравнения системы выразим :х5:
Подставляя правую часть равенства во все остальные уравнения, вместо х5 получим:
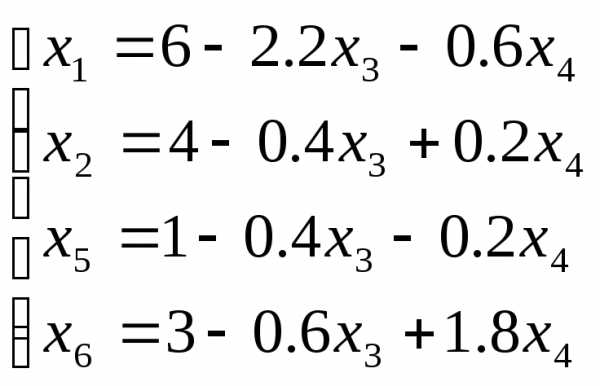
Получим новое базисное решение системы Х4=(6; 4; 0; 0; 1; 6). Это соответствует точке С(6;4) многоугольника ОАВСДЕ (см. рис. 1).
Выразим целевую функцию через неосновные переменные: ,z(X4)=24.
Целевую функцию нельзя улучшить переходя к другому базисному решению, так как все коэффициенты при небазисных переменных меньше 0, следовательно, задача решена. Максимальная прибыль при этом равна 24, а оптимальный план производства: 6 единиц первой продукции и 4 единицы второй продукции. Дополнительные переменные показывают разницу между затратами ресурсов каждого вида и их потреблением. х3=х4=0, следовательно ресурсы S1 иS2 расходуются полностью в процессе производства, а остатки S3 иS4 равны 1 и 3 соответственно.
На практике расчеты при решении задач симплекс-методом выполняются с помощью симплекс-таблиц. Рассмотрим алгоритм симплекс-метода с использованием симплекс-таблиц.
Алгоритм симплекс — метода:
После введения добавочных переменных, система уравнений записывается в виде, который называется расширенной системой (1). Предполагается, что все добавочные переменные имеют тот же знак, что и свободные члены.
Исходную расширенную систему заносим в первую симплекс таблицу. Последняя строка в которой приведено уравнение для линейной функции цели, называется оценочной. В ней указываются коэффициенты функции цели с противоположным знаком. В левом столбце таблицы записываем базисные переменные (на первом шаге за базисные переменные берутся дополнительные переменные), в первой строке – все переменные, во втором столбце – свободные члены расширенной системы b1,…,bm. Последний столбец подготовлен для оценочных отношений, необходимый при расчете. В рабочую часть таблицы, начиная с третьего столбца и второй строки, занесены коэффициенты при переменных aij расширенной системы. Далее таблица преобразуется по определенным правилам.
Проверяем выполнение критерия оптимальности (при решении задачи на максимум критерий оптимальности состоит в отсутствии отрицательных коэффициентов в оценочной строке). Если критерий оптимальности выполнен, то следовательно, максимум достигнут и оптимальное значение z равно с0 (в левом нижнем углу таблицы). Базисные переменные принимают значения bi, остальные переменные равны 0. Если критерий оптимальности не выполнен, переходим к следующему шагу.
По оценочной строке выбираем переменную вводимую в базис. Находим наибольший по модулю отрицательный коэффициент в оценочной строке. Соответствующая этому столбцу переменная хs будет вводимой в базис, а сам столбец называется разрешающим.
Находим переменную, выводимую из базиса. Для этого составляем оценочные отношения (они заносятся в столбец для оценочных отношений) по следующим правилам:
, если bi и ais имеют разные знаки;
, если bi=0 и ais<0;
, если ais=0;
0, если bi=0 и ais>0;
 ,
если bi и ais имеют одинаковые знаки.
,
если bi и ais имеют одинаковые знаки.
Определяем  .
Если конечного минимума нет, то задача
не имеет конечного оптимума (zmax=).
Если минимум конечен, то выбираем строку
q,
на которой он достигается (если их
несколько, то любую), и называем ее
разрешающей строкой. На пересечении
разрешающей строки и разрешающего
столбца находится разрешающий элемент
aqs.
.
Если конечного минимума нет, то задача
не имеет конечного оптимума (zmax=).
Если минимум конечен, то выбираем строку
q,
на которой он достигается (если их
несколько, то любую), и называем ее
разрешающей строкой. На пересечении
разрешающей строки и разрешающего
столбца находится разрешающий элемент
aqs.
Переходим к следующей таблице по правилам (преобразования Гаусса-Жордана или правило прямоугольника):
в левом столбце записываем новый базис: вместо основной переменной xq – переменную xs;
в столбцах, соответствующих базисным переменным, проставляем нули и единицы: 1- на пересечении строки и столбца, соответствующих одной и той же базисной переменной; 0 – во всех других позициях столбцов базисных переменных;
Новую строку q получаем из старой делением на разрешающий элемент aqs;
все остальные элементы аij‘ вычисляем по правилу:
 (2)
(2)
Далее переходим к шагу III.
Пример 6.
Решим задачу:
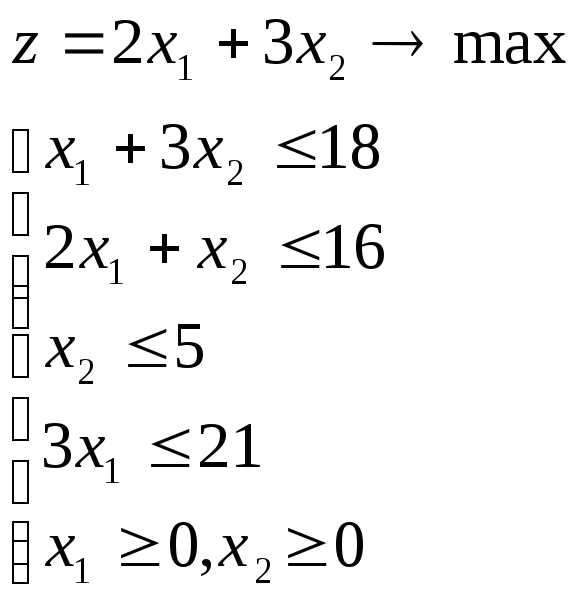
Приведем систему ограничений к каноническому виду. Получим расширенную систему:
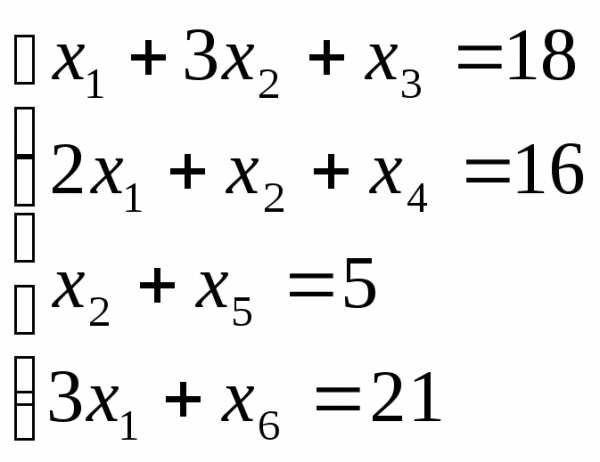
Целевую функцию представим в виде z-2x1-3x2=0.
Базисными переменными будут являться дополнительные переменные x3,x4,x5,x6.
Заполним первую симплекс-таблицу:
Базис | Свободный член | Переменные | Оценочные отношения | |||||
x1 | x2 | x3 | x4 | x5 | x6 | |||
x3 | 18 | 1 | 3 | 1 | 0 | 0 | 0 | 18/3 |
x4 | 16 | 2 | 1 | 0 | 1 | 0 | 0 | 16 |
x5 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5 |
x6 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | |
z | 0 | -2 | -3 | 0 | 0 | 0 | 0 | |
Проверяем критерий оптимальности задачи. В последней оценочной строке имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю – (-3). Следовательно s=2, переменная х2является вводимой базис, а соответствующий ей столбец – разрешающим.
Находим оценочные отношения и выбираем из них минимальное (=5). Следовательно, q=3, переменная х5является выводимой из базиса, а соответствующая ей строка – разрешающей.
Переходим к новой симплекс-таблице:
в новом базисе основные переменные x3,x4,x2,x6;
расставляем 0 и1; например, на пересечении столбца и строки, соответствующих переменной х3ставим 1, а остальные элементы столбца х3равны 0 и т.д. Третья строка получается делением на разрешающий элемент а33=1. Остальные клетки таблицы заполняем по формулам (2). Например:

Получаем вторую симплекс таблицу:
Базис | Свободный член | Переменные | Оценочные отношения | |||||
x1 | x2 | x3 | x4 | x5 | x6 | |||
x3 | 3 | 1 | 0 | 1 | 0 | -3 | 0 | 3 |
x4 | 11 | 2 | 0 | 0 | 1 | -1 | 0 | 11/2 |
x2 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | |
x6 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | 7 |
z | 15 | -2 | 0 | 0 | 0 | 3 | 0 | |
Критерий оптимальности вновь не выполнен. Теперь разрешающий первый столбец и х1– вводимая переменная. Считаем оценочные отношения и находим разрешающую строку – первая и выводимую из базиса переменную – х3. Разрешающий элемент а11.
Переходим к новой симплекс-таблице:
Базис | Свободный член | Переменные | Оценочные отношения | |||||
x1 | x2 | x3 | x4 | x5 | x6 | |||
x1 | 3 | 1 | 0 | 1 | 0 | -3 | 0 | |
x4 | 5 | 0 | 0 | -2 | 1 | 5 | 0 | 5/5 |
x2 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5/1 |
x6 | 12 | 0 | 0 | -3 | 0 | 9 | 1 | 12/9 |
z | 21 | 0 | 0 | 2 | 0 | -3 | 0 | |
И на этот раз критерий оптимальности не выполнен.
Выводимая переменная х4; вводимая х5. Переходим к новой таблице.
Базис | Свободный член | Переменные | Оценочные отношения | |||||
x1 | x2 | x3 | x4 | x5 | x6 | |||
x1 | 6 | 1 | 0 | -1/5 | 3/5 | 0 | ||
x5 | 1 | 0 | 0 | -2/5 | 1/5 | 1 | 0 | |
x2 | 4 | 0 | 1 | 2/5 | -1/5 | 0 | 0 | |
x6 | 3 | 0 | 0 | 3/5 | -9/5 | 0 | 1 | |
z | 24 | 0 | 0 | 4/5 | 3/5 | 0 | 0 | |
Критерий оптимальности выполнен, значит zmax=24. Оптимальное решение (6; 4; 0; 0; 1; 3).
studfiles.net
Табличный симплекс-метод
Для упрощения процесса решения исходные данные задачи линейного программирования при решении ее симплекс методом записываются в специальные симплекс-таблицы. Поэтому одна из модификаций симплекс метода получила название табличный симплекс метод. Задача линейного программирования в каноническом виде:
F=a0,1x1+a0,2x2+…a0,nxn +b → max
a1,1x1+a1,2x2+…a1,nxn + xn+1=b1
a2,1x1+a2,2x2+…a2,nxn +xn+2 =b2
…………………………………
am,1x1+am,2x2+…am,nxn+xn+m=bm
Исходная таблица для задачи имеет следующий вид:
| x1 | x2 | … | xn-1 | xn | b | |
| F | -a0,1 | -a0,2 | … | -a0,n-1 | -a0,n | -b |
| xn+1 | a1,1 | a1,2 | … | a1,n-1 | a1,n | b1 |
| xn+2 | a2,1 | a2,2 | … | a2,n-1 | a2,n | b2 |
| … | … | … | … | … | … | … |
| xn+m | am,1 | am,2 | … | am,n-1 | am,n | bm |
x1, x2, xn — исходные переменные, xn+1, xn+2, xn+m — дополнительные переменные. Все дополнительные переменные мы приняли как базисные, а исходные переменные как небазисные (дополнительные записаны в первый столбец симплекс-таблицы а исходные в первую строку). При каждой итерации элементы симплекс-таблицы пересчитывают по определенным правилам.
Алгоритм симплекс-метода.
Подготовительный этап
Приводим задачу ЛП к каноническому виду
F=a0,1x1+a0,2x2+…a0,nxn +b → max
a1,1x1+a1,2x2+…a1,nxn+xn+1=b1
a2,1x1+a2,2x2+…a2,nxn+xn+2=b2
…………………………………
am,1x1+am,2x2+…am,nxn+xn+m=bm
В случае если в исходной задаче необходимо найти минимум — знаки коэффициентов целевой функции F меняются на противоположные a0,n=-a0,n. Знаки коэффициентов ограничивающих условий со знаком «≥» так же меняются на противоположные. В случае если условие содержит знак «≤» — коэффициенты запишутся без изменений.
Шаг 0. Составляем симплексную таблицу, соответствующую исходной задаче
| x1 | x2 | … | xn-1 | xn | b | |
| F | -a0,1 | -a0,2 | … | -a0,n-1 | -a0,n | -b |
| xn+1 | a1,1 | a1,2 | … | a1,n-1 | a1,n | b1 |
| xn+2 | a2,1 | a2,2 | … | a2,n-1 | a2,n | b2 |
| … | … | … | … | … | … | … |
| xn+m | am,1 | am,2 | … | am,n-1 | am,n | bm |
Шаг 1. Проверка на допустимость.
Проверяем на положительность элементы столбца b (свободные члены), если среди них нет отрицательных то найдено допустимое решение (решение соответствующее одной из вершин многогранника условий) и мы переходим к шагу 2. Если в столбце свободных членов имеются отрицательные элементы то выбираем среди них максимальный по модулю — он задает ведущую строку k. В этой строке так же находим максимальный по модулю отрицательный элемент ak,l — он задает ведущий столбец — l и является ведущим элементом. Переменная, соответствующая ведущей строке исключается из базиса, переменная соответствующая ведущему столбцу включается в базис. Пересчитываем симплекс-таблицу согласно правилам.
Если же среди свободных членов есть отрицательные элементы — а в соответствующей строке — нет то условия задачи несовместны и решений у нее нет.
Если после перерасчета в столбце свободных членов остались отрицаетельные элементы, то переходим к первому шагу, если таких нет, то ко второму.
Шаг 2. Проверка на оптимальность.
На предыдущем этапе найдено допустимое решение. Проверим его на оптимальность Если среди элементов симплексной таблицы, находщихся в строке F (не беря в расчет элемент b0 — текущее значение целевой функции) нет отрицательных, то найдено оптимальное решение.
Если в строке F есть отрицательные элементы то решение требует улучшения. Выбираем среди отрицательных элементов строки F максимальный по модулю (исключая значение функции b)
a0,l=min{a0,i }
l — столбец в котором он находится будет ведущим. Для того, что бы найти ведущую строку, находим отношение соответсвующего свободного члена и элемента из ведущего столбца, при условии, что они неотрицательны.
bk/ak,l =min {bi/ai,l } при ai,l>0, bi>0
k — cтрока, для которой это отношение минимально — ведущая. Элемент ak,l — ведущий (разрешающий). Переменная, соответствующая ведущей строке (xk) исключается из базиса, переменная соответствующая ведущему столбцу (xl) включается в базис.
Пересчитываем симплекс-таблицу по формулам. Если в новой таблице после перерасчета в строке F остались отрицательные элементы переходим к шагу 2
Если невозможно найти ведущую строку, так как нет положительных элементов в ведущем столбце, то функция в области допустимых решений задачи не ограничена — алгоритм завершает работу.
Если в строке F и в столбце свободных членов все элементы положительные, то найдено оптимальное решение.
Правила преобразований симплексной таблицы.
При составлении новой симплекс-таблицы в ней происходят следующие изменения:
- Вместо базисной переменной xk записываем xl; вместо небазисной переменной xl записываем xk.
- ведущий элемент заменяется на обратную величину ak,l‘= 1/ak,l
- все элементы ведущего столбца (кроме ak,l) умножаются на -1/ak,l
- все элементы ведущей строки (кроме ak,l) умножаются на 1/ak,l
- оставшиеся элементы симплекс-таблицы преобразуются по формуле ai,j‘= ai,j— ai,lx ak,j/ ak,l
Схему преобразования элементов симплекс-таблицы (кроме ведущей строки и ведущего столбца) называют схемой ”прямоугольника”.
Преобразуемый элемент ai,j и соответствующие ему три сомножителя как раз и являются вершинами ”прямоугольника”.
Пример
uchimatchast.ru
Симплекс-метод. Табличный способ решения.
Поиск ЛекцийОсновным методом решения задач линейного программирования является симплексный метод. На практике преобразования системы уравнений, проводятся в специальных таблицах, называемых симплексными. Это более удобно для решения задач на ЭВМ. Правила вычислений с помощью этих таблиц рассмотрим на следующем примере.
Пример 3.1. Найти наибольшее значение линейной функции
(3.1)
при следующих ограничениях на переменные:
(3.2)
Решение. Сначала систему ограничений (3.2) необходимо привести к каноническому виду . Для этого вводят дополнительные
переменные, которые прибавляют к левой части каждого из неравенств (3.2). После этого преобразованная система (3.2) будет иметь
вид:
(3.2’)
Примем за базисные переменные дополнительные переменные . Тогда свободными переменными будут , т. е. все остальные переменные. Целевая функция z должна быть выражена через свободные переменные. В нашем примере функция z уже выражена через , поэтому она не требует дополнительных преобразований.
Итак, предварительные преобразования задачи состоят в том, чтобы систему ограничений преобразовать с помощью введения дополнительных переменных в систему уравнений, принять за базисные переменные дополнительные переменные, выразить целевую функцию z через свободные переменные.
После этого заполняется первая симплексная таблица.
Таблица 3.1
Первая симплексная таблица
В первую таблицу заносят исходные данные задачи, содержащиеся в системе (3.2′) и уравнении (3.1). В табл. 3.1 приняты следующие обозначения: БП — базисные переменные. В этот столбец заносятся переменные , которые мы приняли за базисные. СЧ — свободные члены. В столбец СЧ заносят правые части уравнения (3.2′). Далее идет перечень всех переменных . В столбец , записывают коэффициенты, стоящие перед в уравнениях системы (3.2′). В третьем уравнении (3.2′). | отсутствует, т. е. коэффициент перед , равен нулю. Аналогично, в столбцы переменных заносят коэффициенты при этих переменных из системы (3.2′). Осталось объяснить, как заполняется последняя строка С. Эта строка отводится для коэффициентовцелевой функции z (см. 3.1). В столбец СЧ записывают свободный член (т.е. постоянное слагаемое) функции z. В данном случае он равен нулю. В столбцы заносят соответствующие коэффициенты с противоположными знаками. Коэффициент при равен 7, поэтому в табл.3.1 записывается -7. Таблица 3.1 заполнена.
В таблице 3.1 содержится решение задачи (3.1) — (3.2):
х3= 19, х4= 13, х5= 15, х6=18, х1 = 0, х2 = 0. (3.3)
Решение (3.3) называется опорным решением. Посмотрим, нельзя ли улучшить решение (3.3), т. е. нельзя ли, изменяя значения переменных , увеличить значение функции z (пока z = 0). Рассмотрим последнюю строку табл. 3.1, Она содержит отрицательные числа в столбцах . Это признак неоптимальности решения (3.3). Его можно улучшить. Для перехода к следующему улучшенному решению в табл. 3.1 выбирают разрешающий столбец и разрешающую сроку.
За разрешающий столбец принимается тот, который в последний строке С имеет наибольшее по абсолютной величине отрицательное число. (Среди других отрицательных чисел строки С). В табл. 3.1 это столбец . Он отмечается стрелкой. После этого определяется разрешающая строка. Для ее определения составляют отношения свободных членов табл. 3.1 к соответствующим положительным элементам разрешающего столбца ( ): 19:2 = 9,5; 13 : 2 = 6,5; 18:3 = 6.
За разрешающую строку принимается та, которая имеет наименьшее такое отношение. В табл. 3.1 эта строка х6. Она также отмечена стрелкой. Эти отношения записывают в последний столбец табл. 3.1. Элемент, стоящий на пересечении разрешающей строки и разрешающего столбца называется разрешающим элементом. В табл. 3.1 он равен трем.
Теперь мы подготовились к тому, чтобы заполнить вторую симплексную таблицу, содержащую улучшенное решение. Во-первых, в табл. 3.2 изменяется состав базисных переменных. Из столбца БП надо вывести переменную , а на ее место поставить . На это указывают стрелки в табл. 3.1.
Вторая симплексная таблица (промежуточный этап заполнения)
Таблица 3.2а
В первую очередь табл. 3.2 заполняется строка , которая в табл. 3.1 была разрешающей. Поэтому она называется начальной строкой. Для ее заполнения все элементы разрешающей строки х6табл. 3.1
делят на разрешающий элемент 3 и результаты записывают в соответствующие столбцы строки x1 табл. 3.2:
18:3 = 6; 3 : 3 = 1; 0 : 3 = 0;…, 1 : 3 = 1/3.
После этого заполняется тот столбец табл. 3.2, который был разрешающим в табл. 3.1. В данном случае это столбец . Во всех строках этого столбца (кроме строки где уже стоит единица), пишут нули (см. табл. 3.2а).
Остальные элементы табл. 3.2 вычисляются по правилу прямоугольника.
Вторая симплексная таблица
Таблица 3.2
Вычислим, например, элемент табл. 3.2, стоящий в столбце СЧ строки .
В табл. 3.1 рассмотрим элемент, стоящий на такой же позиции – он равен 19.
Мысленно построим прямоугольник, в одной вершине которого стоит число 19, в другой — разрешающий элемент (число 3), а две другие вершины отмечены в табл. 3.1 кружками. Искомый элемент табл. 3.2 равен произведению элементов, стоящих на главной диагонали прямоугольника минус произведение элементов на второй диагонали ; разность надо разделить на разрешающий элемент:
.
Элемент столбца СЧ строки х4 табл. 3.2 вычисляется по формуле
.
Элемент столбца СЧ строки х5:
.
Наконец, элемент строки С столбца СЧ равен:
Аналогично, с помощью построения прямоугольника в табл. 3.1 в одной из вершин которого всегда находится разрешающий элемент, находят остальные коэффициенты табл. 3.2.
Например, x32— элемент строки х3 столбца х2 вычисляется по формуле (см. табл.3.1):
Так заполняется вся таблица 3.2. Решение, содержащееся в этой таблице неоптимально, т. к. в строке С есть отрицательное число — 5. Следовательно это решение можно улучшить. Перейдем к построению таблицы 3.3. Все выкладки, проведенные нами для перехода к таблице 3.2 повторяются, начиная с нахождения разрешающего столбца и разрешающей строки. Разрешающим столбцом в таблице 3.2 является столбец х2. Составим отношения СЧ к элементам столбца х2:7:3=7/3;1:1=1;15 : 3 = 5. Наименьшее отношение дает строка х4 — она и является разрешающей. Разрешающий элемент: 1.
Третья симплексная таблица
Таблица 3.3
Базисными переменными в таблице 3.3 являются х3, х2, х5, x1. Вначале заполняется строка х2 (начальная), которая получается из строки x4 табл. 3.2 делением на разрешающий элемент. Т.к. разрешающий элемент равен 1, строка x4 просто переписывается в табл. 3.3.
Затем в столбце х2 (бывшем разрешающем) пишем нули. Остальные элементы табл. 3.3 находим по правилу прямоугольника с помощью табл. 3.2. Решение, содержащееся в табл. 3.3 — неоптимально, т. к. в последней строке в столбце х6 есть отрицательное число — 1. Еще раз применяя алгоритм симплекс-метода, получаем оптимальное решение.
Четвертая симплексная таблица
Таблица 3.4
Запишем оптимальное решение, содержащееся в табл. 3.4. Базисные
переменные равны свободным членам, т. е. , а свободные переменные (те, которых нет в столбце БП) равны нулю: . Элемент столбца СЧ строки С дает максимальное значение функции z : zmax = 50.
Замечание. Если задача решается на минимум целевой функции: то разрешающий столбец выбирается по наибольшему положительному числу последней строки. Признаком неоптимальности является наличие положительных чисел в последней строке. Остальные правила алгоритма не меняются.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru


 …
…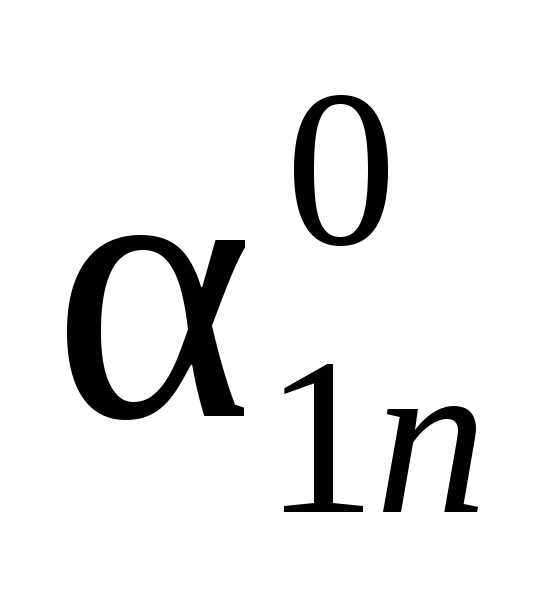
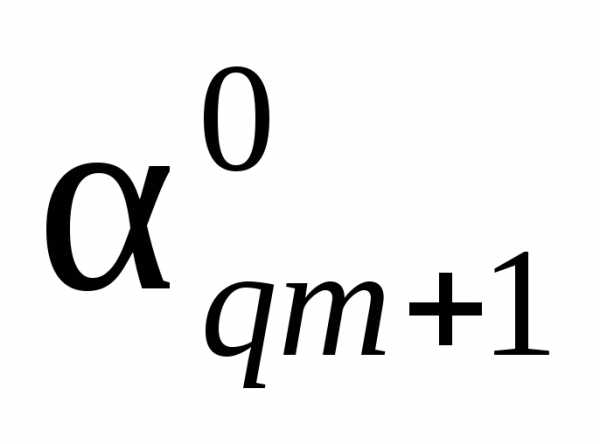 …
…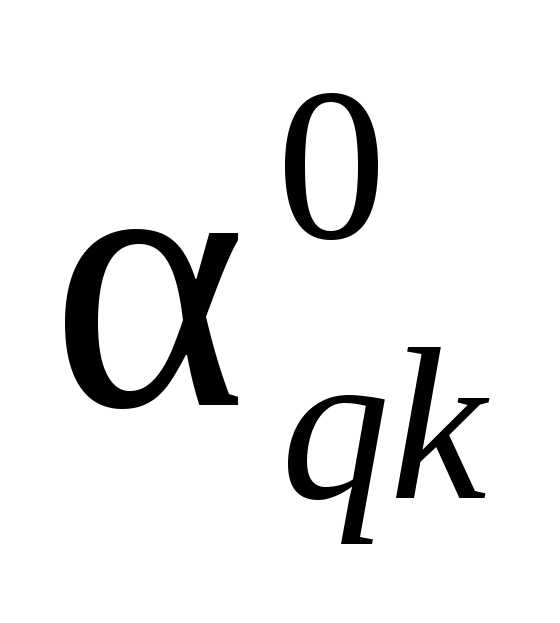 …
…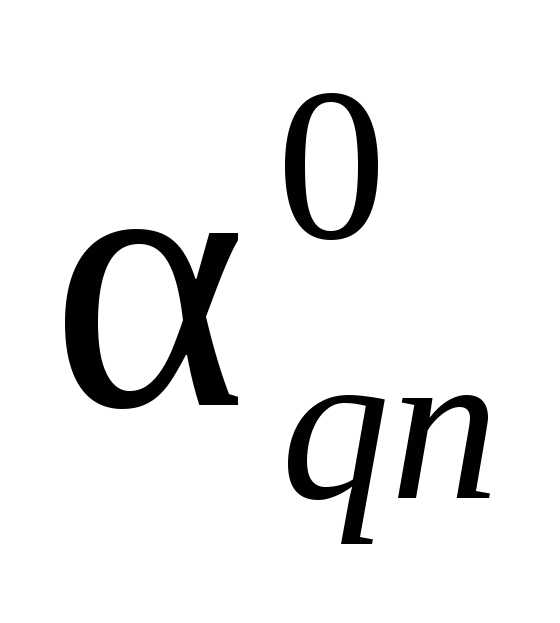
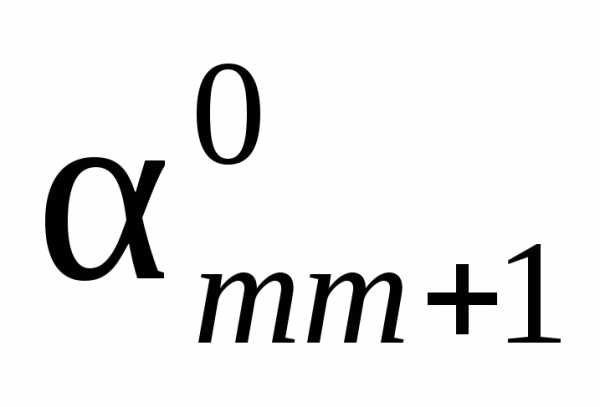 …
…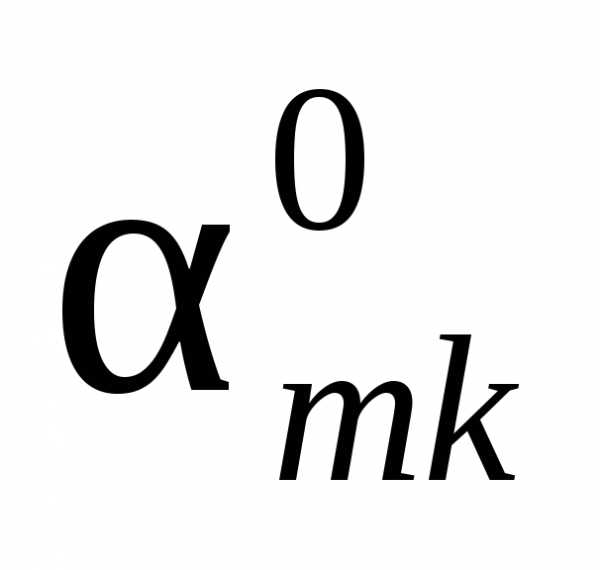 …
…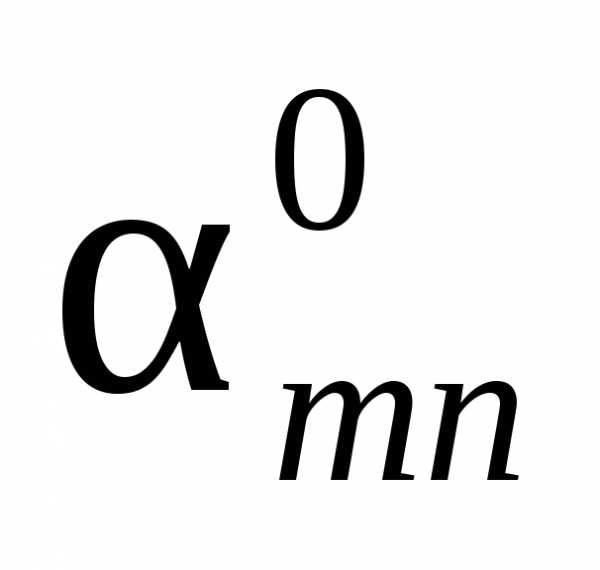

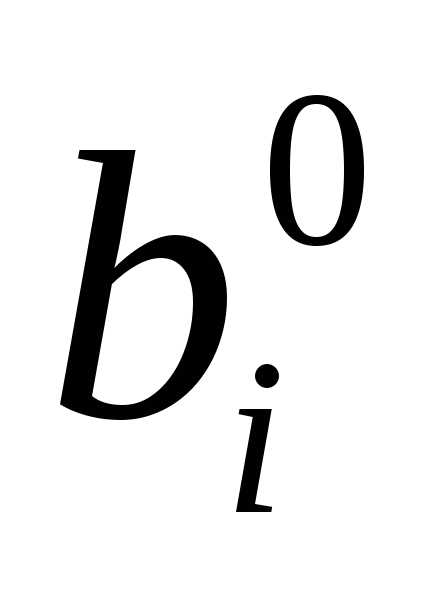
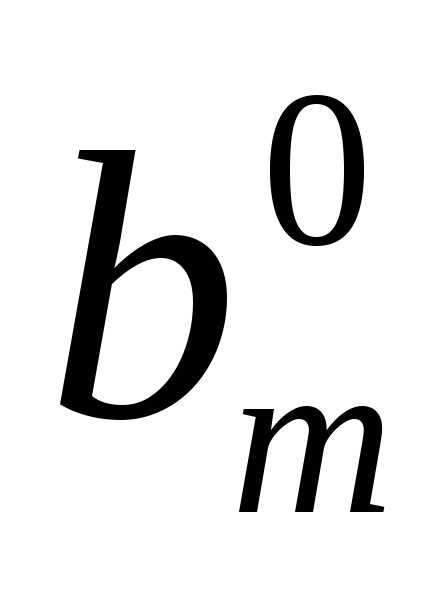
 …
… …
…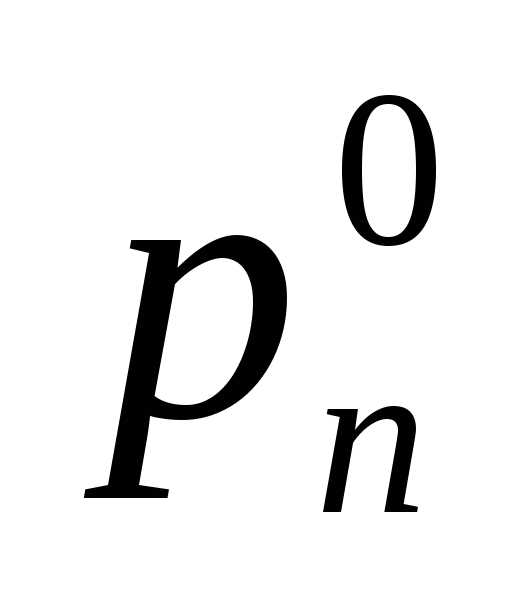
 …
…
 …
… …
…
 …
… …
…
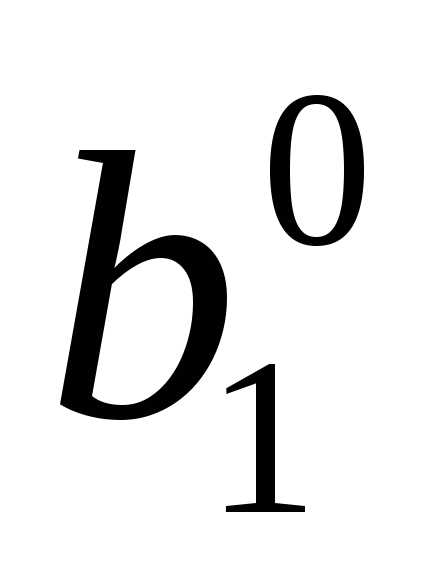
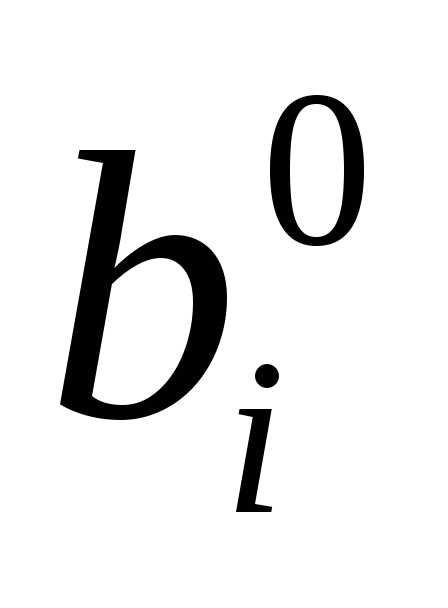

 …
… …
…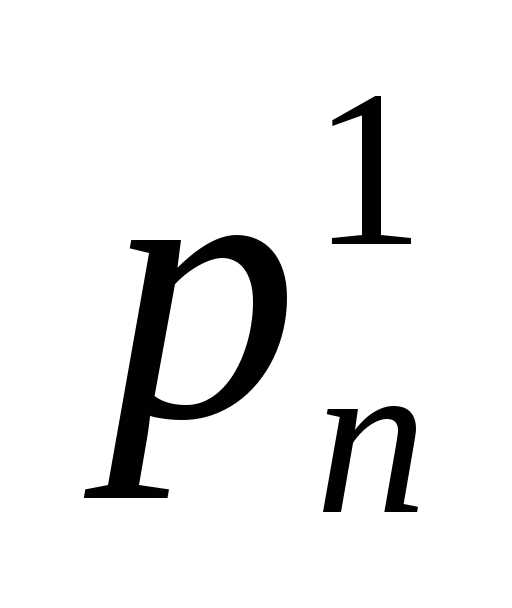
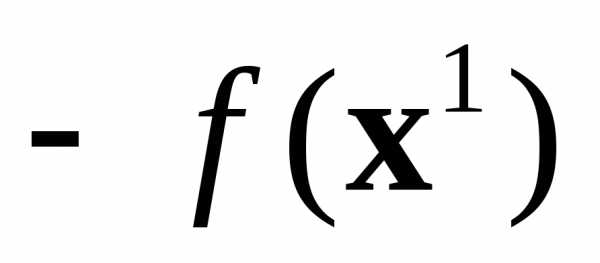
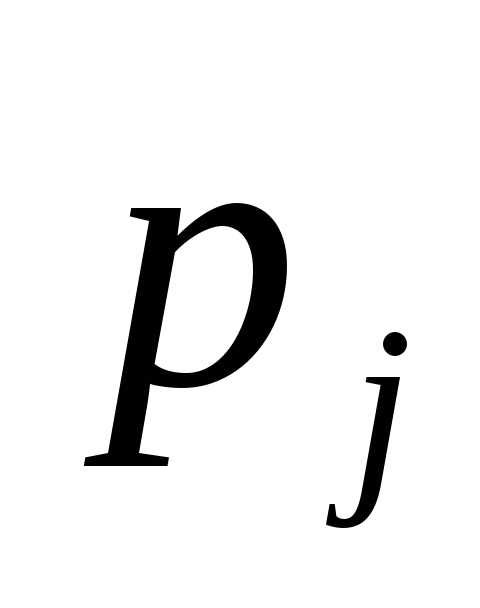 .
В левом столбце таблицы записываем
основные переменные (базис), в последующих
– коэффициенты
.
В левом столбце таблицы записываем
основные переменные (базис), в последующих
– коэффициенты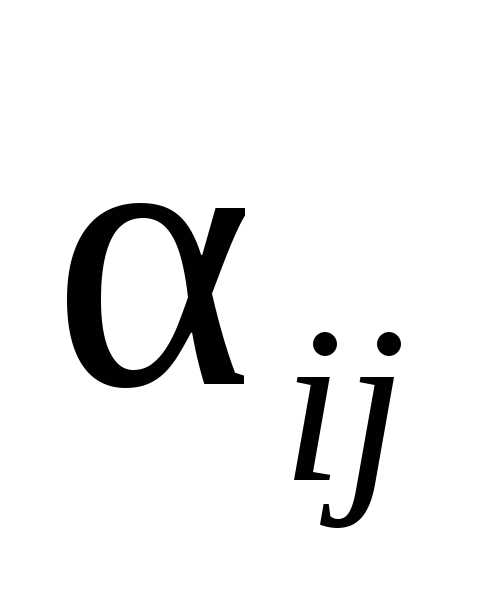 при свободных переменных. В предпоследнем
столбце – свободные члены расширенной
системы.
Последний столбец подготовлен для
оценочных отношений, необходимых для
определения базисной переменной
при свободных переменных. В предпоследнем
столбце – свободные члены расширенной
системы.
Последний столбец подготовлен для
оценочных отношений, необходимых для
определения базисной переменной на основании соотношения (6.29).
на основании соотношения (6.29).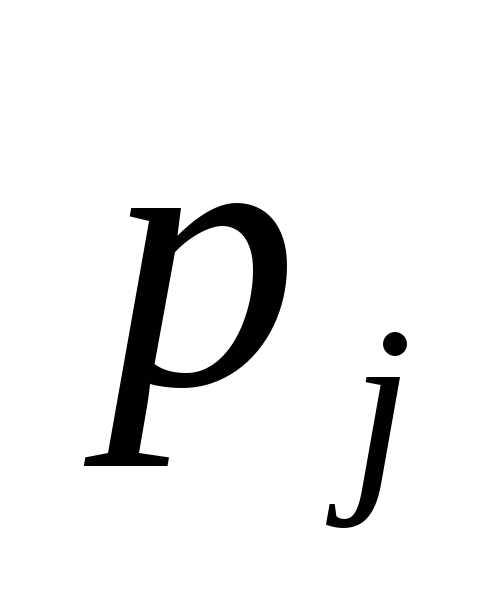 согласно теоремам 6.7,…, 6.9.
согласно теоремам 6.7,…, 6.9.
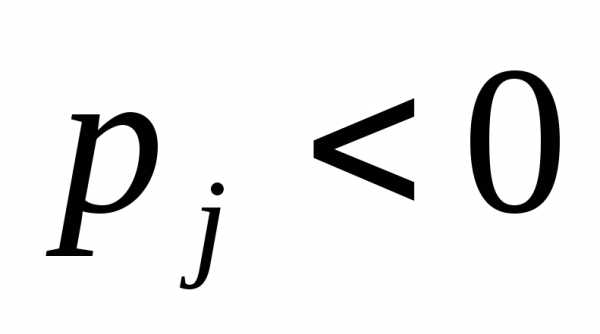 в последней строке определяет разрешающий
(опорный) столбец
в последней строке определяет разрешающий
(опорный) столбец .
.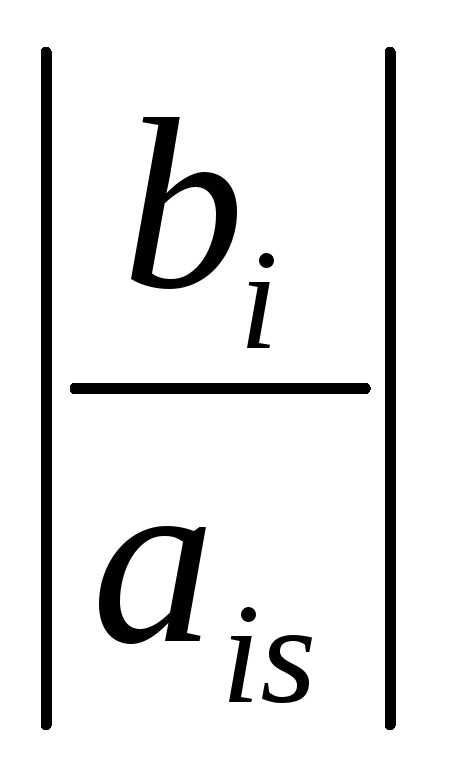 ,
если bi и ais имеют одинаковые знаки.
,
если bi и ais имеют одинаковые знаки.