Синус, косинус, тангенс, котангенс угла
Понятие синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника
Будем измерять величины углов в радианах. Поворот координатной плоскости вокруг начала координат на угол $\alpha $ радиан будем обозначать символом $R^{\alpha }$.
Через $P_{\alpha }$ будем обозначать точку единичной окружности $x^2+y^2=1$ которая получается из точки $P_0$ с координатами $(1,0)$ путем поворота плоскости вокруг начала координат на угол $\alpha $.
Рассмотрим в Декартовой системе координат окружность с радиусом $R >0$ и центром $(0,0)$ (рис. 1).
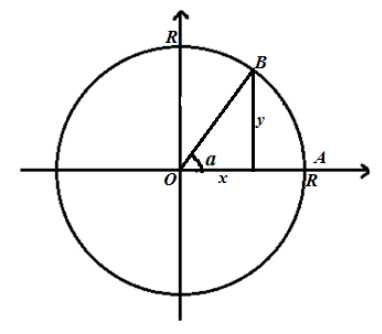
Рисунок 1. Окружность радиуса $R >0$.
$\left[OB\right]$ получается из $\left[OA\right]=R$ путем поворота на угол $\alpha $ радиан. Пусть $x$ и $y$ абсцисса и ордината точки $B$, соответственно, тогда
Так как в определениях синуса и косинуса их значения не зависят от радиуса окружности, то можно принять $R=1$. Поэтому, другим способом, тригонометрические значения определяются следующим образом:
Определение 1
Синусом острого угла называется ордината единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан.
Определение 2
Косинусом острого угла называется абсцисса единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан.
Определение 3
Тангенсом угла называется отношение значения синуса этого угла к значению косинуса этого угла.
Определение 4
Котангенсом угла называется отношение значения косинуса этого угла к значению синуса этого угла.
Основное тригонометрическое тождество
Определение 5
Проверим следующее тождество:
\[{sin}^2A+{cos}^2A=1\]Для этого будем рассматривать прямоугольный треугольник $ABC$ c прямым углом $C$ (рис. 2).
Рисунок 2.
Из него получим
\[{\left(\frac{BC}{AB}\right)}^2+{\left(\frac{AC}{AB}\right)}^2=\frac{{BC}^2+{AC}^2}{{AB}^2}\]Из теоремы Пифагора мы знаем, что ${BC}^2+{AC}^2={AB}^2$, следовательно
\[{sin}^2A+{cos}^2A=\frac{{BC}^2+{AC}^2}{{AB}^2}=\frac{{AB}^2}{{AB}^2}=1\]Это тождество называется основным тригонометрическим тождеством.
Основные значения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника
Вычислим значения для углов в ${30}^{{}^\circ },\ {45}^{{}^\circ }$ и ${60}^{{}^\circ }$. Для этого вспомним следующую теорему.
Пусть для начала у нас $\angle A={30}^{{}^\circ }$. Так как треугольник прямоугольный, то $\angle B={60}^{{}^\circ }$.
По теореме 1, имеем $AB=2BC$.
Используя основное тригонометрическое тождество (5), получим:
Теперь нетрудно найти тангенсы и котангенсы этих углов.
Пусть теперь $\angle A={45}^{{}^\circ }$. Тогда $\angle B={45}^{{}^\circ }$, то есть прямоугольный треугольник — равнобедренный. По теореме Пифагора ${BC}^2+{AC}^2={AB}^2$, следовательно, ${AB}^2={2BC}^2=2{AC}^2$, то есть
Тогда
Сведем все полученные данные в таблицу (таблица 1).
Рисунок 3.
Пример задачи
Пример 1
Найти все тригонометрические значения угла $A$, если$AB=25,\ BC=20,\ AC=15.$
Решение.
Все решение задачи будем производить с помощью прямоугольного треугольника (рис. 2).
\[sinA=\frac{BC}{AB}=\frac{20}{25}=0,8\] \[cosA=\frac{AC}{AB}=\frac{15}{25}=0,6\] \[tgA=\frac{BC}{AC}=\frac{20}{15}=1\frac{1}{3}\] \[ctgA=\frac{AC}{BC}=\frac{15}{20}=0,75\]spravochnick.ru
кто знает что такое синус косинус и тангенс?? пожалуйсто обьясните на примере,а не теоремами!!!!
Щас.. . это легко Оси координат себе представляешь? Ну вот.. . Начерти окружность с центров в ноле и радиусом 1. Берешь и чертишь любой луч (отрезок) , который выходит их точки 0 и пересекает окружность. Окружность пересекает пускай в точке А. у тебя получился угол. Из точки А опускаешь перпендикуляры на ось ОХ и ОУ. Это ты получила координаты точки А. так вот координата х — это косинус, координата у — это синус. Отсюда кстати понятно почему sin А в квадрате + cosА в квадрате =1. так как это катеты прямоугольного треугольника и сумма их квадратов равна гипотенузе, которая является радиусом и равняется единице для любого угла. Че непонятно пиши в комментах — расскажу В итоге sin — отношение противолежащего катета к гипотенузе cos — отношение прилежащего катета к гипотенузе tg — отношение sin к cos или противолежащего катета к прилежащему
Синус — это отношение противолежащего катета к гипотенузе, косинус — это отношение прилежащего катета к гипотенузе, тангенс — это отношение противолежащего катета к прилежащемуВ теореме куда понятнее…. отношение углов. Прилежащего к противолежащему, и. т. д Это же элементарно. Имеется в виду отношение угловых величин.
Синус — проекция точки единичной окружности на ординату числовой оси, а косинус — на абсциссу. Тангенс это отношение синуса к косинусу. <img src=»//content.foto.my.mail.ru/mail/qxz_550/_answers/i-2.jpg» >
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ, функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec). Их можно определить как отношения длины r и проекций а и b на оси координат радиуса-вектора, образующего с положительным направлением оси Ох угол (или отсекающего дугу) a. Именно: sin a=b/r, cos a=a/r, tg a=b/a, сtg a=a/b, sec a=r/а, cosec a=r/b. Играют важнейшую роль в математике.Вас в классе заперли и не пообещали не выпускать пока не сдадите экзамен?
SIN и COS-это тригонометрические гармонические функции, при этом синус-функция несимметричная, а косинус-симметричная. Катринки есть в любом учебнике. Ну а тангенс-есть отношение синуса к косинусу. Незнание элементарных функций опасно для жизни.
Синус — отношение противолежащего катета к гипотенузе. Косинус — отношение прилежащего катета к гипотенузе. Отношение синуса к косинусу есть тангенс.touch.otvet.mail.ru
| 3ГОНОМЕТРИЯ В НАЧАЛО | |
|
РЕШЕНИЕ КОСОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ |
|
|
2. Теорема косинусов 3. Формулы для вычисления площади треугольника 4.Теорема тангенсов 5.Решение треугольника по двум его углам и стороне 6.Решение треугольника по двум сторонам и углу между ними. 7.Решение треугольника по двум сторонам и углу, противолежащему одной из них. 8.Решение треугольника по трём сторонам |
|
|
При решении прямоугольных треугольников мы использовали только определения основных тригонометрических функций. Для решения же косоугольных треугольников нам потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим. В дальнейшем мы будем пользоваться следующими обозначениями: a, b и с — стороны треугольника; А, В и С — противолежащие им углы; S — площадь; 2р — периметр; R — радиус описанного круга; r — радиус вписанного круга; hа, lа и mа — высота, биссектриса и медиана, соответствующие стороне а.
|
|
|
1. Теорема синусов |
|
|
Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов: |
|
|
Доказательство. Опишем круг около данного треугольника ABC . Пусть R — радиус этого круга. Возьмём одну из вершин треугольника, например А; через одну из других вершин, например через В, проведём диаметр ВА’ описанного круга. Вспомогательный треугольник А’ВС прямоугольный, так как вписанный угол А’СВ опирается на диаметр. Из вспомогательного треугольника найдём: а = 2Rsin A’. Если угол А острый, то А = А’, так как вписанные углы A и A’ опираются на одну и ту же дугу. Итак, или A = А’, или A’ = — A, в обоих случаях sin A’ = sin A, а потому а = 2R sin A. (1) Если угол A прямой, то а = 2R, sin A = 1 и равенство (1) также справедливо.Аналогичные равенства найдём и для прочих углов В и С. Итак, а = 2R sin A; b = 2R sin В; с = 2R sin С, откуда = 2R |
|
|
Следствие. Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника. |
|
| Упражнения. | |
|
2. Теорема косинусов |
|
|
Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними: |
|
|
а2 =b2 + с2 — 2bc cos А b2 =c2 + a2 — 2ca cos B c2 =a2 + b2 — 2ab cos C
|
|
|
Доказательство. Докажем первое равенство. |
|
|
Случай 1. Угол A острый. Пусть ВН — высота, опущенная из вершины В ; из геометрии известно (см. А.Киселев Геометрия . Планиметрия. Книга3, глава3,теорема 208), что
|
|
|
Случай 2. Угол A тупой. Из треугольника АВН найдём: Подставив в формулу (2), получим доказываемое равенство. |
|
|
Случай 3. Угол А прямой. В этом случае (по теореме Пифагора): а2 = b2 + с2 = b2 + с2 — 2bc cos А (так как cos А = 0). Итак, во всех случаях а2 =b2 + с2 — 2bc cos А
|
|
| Упражнения | |
|
3. Формулы для вычисления площади треугольника |
|
|
1. Из геометрии известна формула Г е р о н а: S = \/р (р — а)(р — b) (р — с) (где р = (а+ b+c)/2 -полупериметр ), позволяющая вычислять площадь треугольника по его сторонам. |
|
|
2. Теорема. Площадь треугольника равна половине произведения двух сторон на синус угла между ними: S = 1/2 bc sin A. |
|
|
Доказательство. Из геометрии известно, что площадь треугольника равна половине произведения стороны треугольника на высоту, опущенную на эту сторону из противоположной вершины. S = 1/2 b · hb (1) |
|
|
Если угол А острый, то из треугольника АВН найдём ВН = hb = с sin A. Если угол A тупой, то ВН = hb = с sin (-A) = с sin A. Если угол A прямой, то sin A = 1 и Следовательно, во всех случаях hb = с sin A. Подставив в равенство (1), получим доказываемую формулу. |
|
|
Точно так же получим формулы: S = 1/2 ab sin C = 1/2 ac sin B |
|
|
3. На основании теоремы синусов: |
|
|
Подставив эти выражения в формулу (1), получим следующую формулу: |
|
| Упражнения | |
|
4.Теорема тангенсов |
|
|
Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов: |
|
|
(и две аналогичные формулы для прочих пар сторон а, с и b, с). |
|
|
Доказательство. В силу теоремы синусов имеем: |
|
|
Разделив почленно эти равенства, получим доказываемую формулу.
|
|
|
5.Решение треугольника по двум его углам и стороне |
|
|
Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.Даны В, С и а; требуется найти b, с и А. |
|
|
Решение. Условие возможности построения треугольника по этим данным: А + В < 180°— будем считать выполненным. |
|
|
Для вычисления сторон b и с достаточно применить теорему синусов: , откуда |
|
|
Площадь вычисляется по формуле:
|
|
|
6.Решение треугольника по двум сторонам и углу между ними |
|
|
Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла. |
|
|
Пусть, например, даны а, b и С, требуется вычислить А, В и с. |
|
|
Решение. Формула косинусов даёт выражение стороны с непосредственно через известные элементы: с = \/ а2 + b2 — 2ab cos С |
|
|
Для вычисления А можно также воспользоваться формулой косинусов: |
|
|
а2 =b2 + с2 — 2bc cos А |
|
|
Так как 0 < А < 180°, то ; (ясно, что достаточно найти лишь один из углов, третий же угол легко определить исходя из суммы углов треугольника)
|
|
|
7.Решение треугольника по двум сторонам и углу, противолежащему одной из них. |
|
|
Задача. Даны две стороны треугольника и угол А, лежащей против одной из них; вычислить третью сторону и два остальных угла. |
|
|
Пусть даны a, b и А; требуется вычислить B, С и с |
|
|
Решение. |
|
|
С л у ч а й 1. а > b, т. е, заданный угол А лежит против большей стороны. Построение показано на чертеже. Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А. |
|
|
Острый угол В, противолежащий меньшей стороне, находится по теореме синусов: |
|
|
откуда |
|
|
и затем С = 180° — (A + В). Сторона с находится по теореме синусов: |
|
|
С л у ч а й 2. а < b, т. e. угол A лежит против меньшей стороны; поэтому он не может быть тупым или прямым. |
a) |
|
Значения угла В вычисляются по теореме синусов: откуда и B2 = 180° — B1 Значения угла С и стороны с вычисляются так же, как в предыдущем случае. |
|
|
Из чертежа b) видно, что при CD = b sin А > а окружность не пересечёт другой стороны угла А; задача не имеет решений. В этом случае и угол В вычислить нельзя. При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.
|
b) |
|
Случай 3. а = b. В этом случае треугольник ABC равнобедренный. Такой треугольник можно решить, разбразбив его высотой CD на два прямоугольных треугольника: В = А; С = 180° — 2А; с = 2AD = 2а cos A.
|
|
|
8.Решение треугольника по трём сторонам |
|
|
Задача. Даны три стороны треугольника; вычислить его углы. Пусть даны длины трёх сторон треугольника. Обозначим через а меньшую сторону, через b — среднюю, а через с — большую: а < b < с. По трём данным сторонам можно построить единственный треугольник, если большая сторона меньше суммы двух других сторон: с < а + b. Если же с > а + b, то треугольник с данными сторонами не существует. Будем считать, что с < а + b. Решение1. Углы треугольника можно вычислить по теореме косинусов: а2 =b2 + с2 — 2bc cos А и (тал как 0°< А <180°). Аналогично найдём: и, наконец, С =180°- (А + В).
|
|
|
Решение 2. Вычислим сначала площадь треугольника (формула Герона):S = \/р (р — а)(р — b) (р — с) , где р = (а+ b+c)/2 Имеем далее: S = 1/2 bc sin A. откуда |
|
|
Угол А острый, так как он лежит против меньшей стороны; следовательно, |
|
|
и, наконец, С = 180° — (А + В) |
|
| Упражнения | |
| 3ГОНОМЕТРИЯ В НАЧАЛО | |
oldskola1.narod.ru
Синус, косинус и тангенс острого угла прямоугольного треугольника
- Войти
- Регистрация
- Схемы
- Биология
- География
- История
- Математика и алгебра
- Медицина
- Обществознание
- Педагогика
- Политология
- Право
- Психология
- Русский язык
- Социология
- Физика
- Философия
- Химия
- Экономика
- Прочее
- Книги
- Биология
- География
- История
- Математика и алгебра
- Медицина
- Обществознание
- Педагогика
- Политология
- Право
- Психология
- Русский язык
- Социология
- Физика
- Философия
- Химия
- Экономика
- Прочее
xn--e1aogju.xn--p1ai
