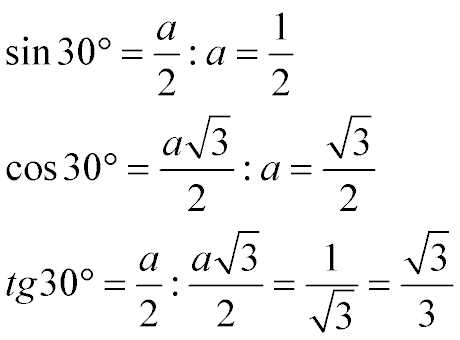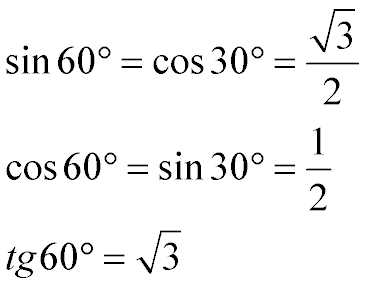Разузнай! — Тангенс — чему равен тангенс 30, 60, 45, 90, 120, 0,135 и 150 градусов
К основным тригонометрическим функциям относятся: синус, косинус, тангенс, котангенс, секанс и косеканс. Исходя из этого, тангенс угла в тригонометрии определяют как тригонометрическую функцию, которая выражает отношение синуса этого угла к косинусу этого же угла. Если необходимо определить тангенс острого угла в прямоугольном треугольнике, то его можно вычислить геометрически, так как тангенс в этом случае будет равен отношению противолежащего катета к прилежащему катету прямоугольного треугольника. Сам термин «тангенс» является заимствованным из латинского языка, его дословный перевод означает «касающийся». Обозначается тангенс латинскими буквами. Тангенс угла х будет обозначен как «tg x», хотя западные математики традиционно обозначают тангенс сокращением от английского слова: тангенс угла х там обозначается как «tan x».
Чему равен тангенс 30 градусов
Исходя из того, что тангенс угла равен отношению синуса угла к косинусу этого же угла, тангенс угла в 30 градусов можно получить, разделив значение синуса угла в 30 градусов на значение косинуса этого же угла. Тангенс будет равен 0.5774.
Чему равен тангенс 60 градусов
Схожим образом вычисляется тангенс угла в 60 градусов: деление синуса угла в 60 градусов на значение косинуса этого же угла дает число 1.7321, которое и является тангенсом 60 градусов.
Чему равен тангенс 45 градусов
Так как значение синуса угла в 45 градусов равно значению косинуса того же угла, значение тангенса угла в 45 градусов, получаемое делением синуса на косинус даёт единицу (тангенс равен 1).
Чему равен тангенс 90 градусов
Тангенс угла в 90 градусов вычислить невозможно, так как косинус угла в 90 градусов равен нулю, а одним из основных правил деления является правило, согласно которому «на ноль делить нельзя», в то время как тангенс в этом случае нужно получить именно делением синуса на косинус, то есть на ноль. Значение тангенса 90 градусов не определяется.
Чему равен тангенс 120 градусов
Схожим образом, вычисляя тангенс угла в 120 градусов, можно получить число -1.7321 (отрицательное), которое и будет тангенсом угла в 120 градусов.Чему равен тангенс 0 градусов
В силу того, что синус угла в 0 градусов равен нулю, а косинус этого же угла равен 1, тангенс получаем путем деления нуля на единицу, что дает 0. Тангенс 0 градусов, таким образом, равен 0.
Чему равен тангенс 135 градусов
Тангенс 135 градусов равен -1 (минус единице) посредством схожего исчисления.
Чему равен тангенс 150 градусов
Тангенс угла в 150 градусов равен -0.5774 (отрицательное), то есть значение тангенса 30 градусов с противоположным знаком.
Производная тангенса
Производная тангенса угла х (обозначение: tg x со штрихом) равна единице, деленной на косинус угла х в квадрате.
- < Икосаэдр
- Как сделать костюм пирата и пиратки >
razuznai.ru
| Развернуть структуру обучения | Свернуть структуру обучения |
| Примечание. См. также таблицу значений тригонометрических функций для всех углов. Как были вычислены эти значения?Также вы можете сразу перейти к:
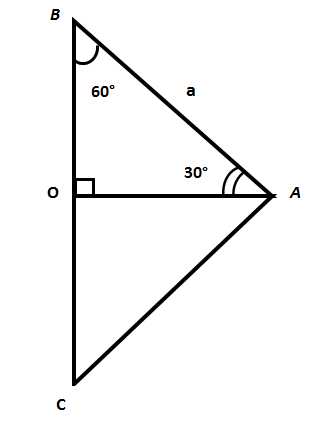
Табличные значения sin 30, cos 30 и tg 30 градусов:
То есть: Учитывая таблицу формул приведения тригонометрических функций, Так как sin( 90°- 30°) = sin60°, а sin60°=cos30°, то: Табличные значения sin 60, cos 60 и tg 60 градусов:Как именно были вычислены эти функции, описано выше. Здесь же приведены сами значения:
Примечание. Данная статья показывает, как вычисляется значение sin 60, cos 60 и подобных значений. Если Вы хотите посмотреть сводную справочную информацию — перейдите на таблицу значений тригонометрических функций Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45) | Описание курса | Синус, косинус, тангенс угла 105 градусов (sin 105 cos 105 tg 105)
|
profmeter.com.ua
Таблица тангенсов | Cubens
Таблица тангенсов— это записанные в таблицу посчитанные значения тангенсов углов от 0° до 360°. Используя таблицу тангенсов, вы можете делать вычисления, даже если под руками не будет инженерного калькулятора. Чтобы узнать значение тангенса от нужного вам угла достаточно найти его в таблице.
Используя таблицу тангенсов, вы можете провести расчеты даже если под рукой не окажется инженерного калькулятора.
Чтобы найти значение тангенсанужного угла, достаточно воспользоваться данной таблицей.
Таблица тангенсов в радианах
Таблица тангенсов— наравне с таблицей косинусов и таблицей синусов изучается в самом начале тригонометрии. Без понимания таблицы тангенсов будет очень сложно изучать тригонометрию и применять тригонометрические формулы.
Тригонометрические функции имеют большое практическое значение в геометрии. Является по сути лишь показателями отношения различных сторон прямоугольного треугольника друг к другу, они способны помощь в решении большинства задач, результат которых сводится к решений прямоугольных треугольников.
Одной из основных тригонометрических функций тангенс. Поэтому в данной таблице тангенсоввы сможете найти любое значение тангенса.
Таблица тангенсов углов от 0° до 180°
Таблица тангенсов углов от 0° до 180°
| tg(0°) = 0 tg(1°) = 0.01746 tg(2°) = 0.03492 tg(3°) = 0.05241 tg(4°) = 0.06993 tg(5°) = 0.08749 tg(6°) = 0.1051 tg(7°) = 0.12278 tg(8°) = 0.14054 tg(9°) = 0.15838 tg(10°) = 0.17633 tg(11°) = 0.19438 tg(12°) = 0.21256 tg(13°) = 0.23087 tg(14°) = 0.24933 tg(15°) = 0.26795 tg(16°) = 0.28675 tg(17°) = 0.30573 tg(18°) = 0.32492 tg(19°) = 0.34433 tg(20°) = 0.36397 tg(21°) = 0.38386 tg(22°) = 0.40403 tg(23°) = 0.42447 tg(24°) = 0.44523 tg(25°) = 0.46631 tg(26°) = 0.48773 tg(27°) = 0.50953 tg(28°) = 0.53171 tg(29°) = 0.55431 tg(30°) = 0.57735 tg(31°) = 0.60086 tg(32°) = 0.62487 tg(33°) = 0.64941 tg(34°) = 0.67451 tg(35°) = 0.70021 tg(36°) = 0.72654 tg(37°) = 0.75355 tg(38°) = 0.78129 tg(39°) = 0.80978 tg(40°) = 0.8391 tg(41°) = 0.86929 tg(42°) = 0.9004 tg(43°) = 0.93252 tg(44°) = 0.96569 tg(45°) = 1 tg(46°) = 1.03553 tg(47°) = 1.07237 tg(48°) = 1.11061 tg(49°) = 1.15037 tg(50°) = 1.19175 tg(51°) = 1.2349 tg(52°) = 1.27994 tg(53°) = 1.32704 tg(54°) = 1.37638 tg(55°) = 1.42815 tg(56°) = 1.48256 tg(57°) = 1.53986 tg(58°) = 1.60033 tg(59°) = 1.66428 tg(60°) = 1.73205 |
tg(61°) = 1.80405 tg(62°) = 1.88073 tg(63°) = 1.96261 tg(64°) = 2.0503 tg(65°) = 2.14451 tg(66°) = 2.24604 tg(67°) = 2.35585 tg(68°) = 2.47509 tg(69°) = 2.60509 tg(70°) = 2.74748 tg(71°) = 2.90421 tg(72°) = 3.07768 tg(73°) = 3.27085 tg(74°) = 3.48741 tg(75°) = 3.73205 tg(76°) = 4.01078 tg(77°) = 4.33148 tg(78°) = 4.70463 tg(79°) = 5.14455 tg(80°) = 5.67128 tg(81°) = 6.31375 tg(82°) = 7.11537 tg(83°) = 8.14435 tg(84°) = 9.51436 tg(85°) = 11.43005 tg(86°) = 14.30067 tg(87°) = 19.08114 tg(88°) = 28.63625 tg(89°) = 57.28996 tg(90°) = ∞ tg(91°) = -57.28996 tg(92°) = -28.63625 tg(93°) = -19.08114 tg(94°) = -14.30067 tg(95°) = -11.43005 tg(96°) = -9.51436 tg(97°) = -8.14435 tg(98°) = -7.11537 tg(99°) = -6.31375 tg(100°) = -5.67128 tg(101°) = -5.14455 tg(102°) = -4.70463 tg(103°) = -4.33148 tg(104°) = -4.01078 tg(105°) = -3.73205 tg(106°) = -3.48741 tg(107°) = -3.27085 tg(108°) = -3.07768 tg(109°) = -2.90421 tg(110°) = -2.74748 tg(111°) = -2.60509 tg(112°) = -2.47509 tg(113°) = -2.35585 tg(114°) = -2.24604 tg(115°) = -2.14451 tg(116°) = -2.0503 tg(117°) = -1.96261 tg(118°) = -1.88073 tg(119°) = -1.80405 tg(120°) = -1.73205 |
tg(121°) = -1.66428 tg(122°) = -1.60033 tg(123°) = -1.53986 tg(124°) = -1.48256 tg(125°) = -1.42815 tg(126°) = -1.37638 tg(127°) = -1.32704 tg(128°) = -1.27994 tg(129°) = -1.2349 tg(130°) = -1.19175 tg(131°) = -1.15037 tg(132°) = -1.11061 tg(133°) = -1.07237 tg(134°) = -1.03553 tg(135°) = -1 tg(136°) = -0.96569 tg(137°) = -0.93252 tg(138°) = -0.9004 tg(139°) = -0.86929 tg(140°) = -0.8391 tg(141°) = -0.80978 tg(142°) = -0.78129 tg(143°) = -0.75355 tg(144°) = -0.72654 tg(145°) = -0.70021 tg(146°) = -0.67451 tg(147°) = -0.64941 tg(148°) = -0.62487 tg(149°) = -0.60086 tg(150°) = -0.57735 tg(151°) = -0.55431 tg(152°) = -0.53171 tg(153°) = -0.50953 tg(154°) = -0.48773 tg(155°) = -0.46631 tg(156°) = -0.44523 tg(157°) = -0.42447 tg(158°) = -0.40403 tg(159°) = -0.38386 tg(160°) = -0.36397 tg(161°) = -0.34433 tg(162°) = -0.32492 tg(163°) = -0.30573 tg(164°) = -0.28675 tg(165°) = -0.26795 tg(166°) = -0.24933 tg(167°) = -0.23087 tg(168°) = -0.21256 tg(169°) = -0.19438 tg(170°) = -0.17633 tg(171°) = -0.15838 tg(172°) = -0.14054 tg(173°) = -0.12278 tg(174°) = -0.1051 tg(175°) = -0.08749 tg(176°) = -0.06993 tg(177°) = -0.05241 tg(178°) = -0.03492 tg(179°) = -0.01746 tg(180°) = 0 |
Тангенс 0 (тангенс нуля)
равна (равна нулю)
Тангенс 1 (тангенс единицы)
равна
Тангенс 3 (тангенс трех)
равна
Тангенс 90 (тангенс 90 градусов)
(равен бесконечности)
Тангенс 30 (тангенс 30 градусов)
равна
Тангенс 45 (тангенс 45 градусов)
равна
Тангенс 60 (тангенс 60 градусов)
равна
Таблица тангенсов углов от 181° до 360°
| tg(181°) = 0.01746 tg(182°) = 0.03492 tg(183°) = 0.05241 tg(184°) = 0.06993 tg(185°) = 0.08749 tg(186°) = 0.1051 tg(187°) = 0.12278 tg(188°) = 0.14054 tg(189°) = 0.15838 tg(190°) = 0.17633 tg(191°) = 0.19438 tg(192°) = 0.21256 tg(193°) = 0.23087 tg(194°) = 0.24933 tg(195°) = 0.26795 tg(196°) = 0.28675 tg(197°) = 0.30573 tg(198°) = 0.32492 tg(199°) = 0.34433 tg(200°) = 0.36397 tg(201°) = 0.38386 tg(202°) = 0.40403 tg(203°) = 0.42447 tg(204°) = 0.44523 tg(205°) = 0.46631 tg(206°) = 0.48773 tg(207°) = 0.50953 tg(208°) = 0.53171 tg(209°) = 0.55431 tg(210°) = 0.57735 tg(211°) = 0.60086 tg(212°) = 0.62487 tg(213°) = 0.64941 tg(214°) = 0.67451 tg(215°) = 0.70021 tg(216°) = 0.72654 tg(217°) = 0.75355 tg(218°) = 0.78129 tg(219°) = 0.80978 tg(220°) = 0.8391 tg(221°) = 0.86929 tg(222°) = 0.9004 tg(223°) = 0.93252 tg(224°) = 0.96569 tg(225°) = 1 tg(226°) = 1.03553 tg(227°) = 1.07237 tg(228°) = 1.11061 tg(229°) = 1.15037 tg(230°) = 1.19175 tg(231°) = 1.2349 tg(232°) = 1.27994 tg(233°) = 1.32704 tg(234°) = 1.37638 tg(235°) = 1.42815 tg(236°) = 1.48256 tg(237°) = 1.53986 tg(238°) = 1.60033 tg(239°) = 1.66428 tg(240°) = 1.73205 |
tg(241°) = 1.80405 tg(242°) = 1.88073 tg(243°) = 1.96261 tg(244°) = 2.0503 tg(245°) = 2.14451 tg(246°) = 2.24604 tg(247°) = 2.35585 tg(248°) = 2.47509 tg(249°) = 2.60509 tg(250°) = 2.74748 tg(251°) = 2.90421 tg(252°) = 3.07768 tg(253°) = 3.27085 tg(254°) = 3.48741 tg(255°) = 3.73205 tg(256°) = 4.01078 tg(257°) = 4.33148 tg(258°) = 4.70463 tg(259°) = 5.14455 tg(260°) = 5.67128 tg(261°) = 6.31375 tg(262°) = 7.11537 tg(263°) = 8.14435 tg(264°) = 9.51436 tg(265°) = 11.43005 tg(266°) = 14.30067 tg(267°) = 19.08114 tg(268°) = 28.63625 tg(269°) = 57.28996 tg(270°) = ∞ tg(271°) = -57.28996 tg(272°) = -28.63625 tg(273°) = -19.08114 tg(274°) = -14.30067 tg(275°) = -11.43005 tg(276°) = -9.51436 tg(277°) = -8.14435 tg(278°) = -7.11537 tg(279°) = -6.31375 tg(280°) = -5.67128 tg(281°) = -5.14455 tg(282°) = -4.70463 tg(283°) = -4.33148 tg(284°) = -4.01078 tg(285°) = -3.73205 tg(286°) = -3.48741 tg(287°) = -3.27085 tg(288°) = -3.07768 tg(289°) = -2.90421 tg(290°) = -2.74748 tg(291°) = -2.60509 tg(292°) = -2.47509 tg(293°) = -2.35585 tg(294°) = -2.24604 tg(295°) = -2.14451 tg(296°) = -2.0503 tg(297°) = -1.96261 tg(298°) = -1.88073 tg(299°) = -1.80405 tg(300°) = -1.73205 |
tg(301°) = -1.66428 tg(302°) = -1.60033 tg(303°) = -1.53986 tg(304°) = -1.48256 tg(305°) = -1.42815 tg(306°) = -1.37638 tg(307°) = -1.32704 tg(308°) = -1.27994 tg(309°) = -1.2349 tg(310°) = -1.19175 tg(311°) = -1.15037 tg(312°) = -1.11061 tg(313°) = -1.07237 tg(314°) = -1.03553 tg(315°) = -1 tg(316°) = -0.96569 tg(317°) = -0.93252 tg(318°) = -0.9004 tg(319°) = -0.86929 tg(320°) = -0.8391 tg(321°) = -0.80978 tg(322°) = -0.78129 tg(323°) = -0.75355 tg(324°) = -0.72654 tg(325°) = -0.70021 tg(326°) = -0.67451 tg(327°) = -0.64941 tg(328°) = -0.62487 tg(329°) = -0.60086 tg(330°) = -0.57735 tg(331°) = -0.55431 tg(332°) = -0.53171 tg(333°) = -0.50953 tg(334°) = -0.48773 tg(335°) = -0.46631 tg(336°) = -0.44523 tg(337°) = -0.42447 tg(338°) = -0.40403 tg(339°) = -0.38386 tg(340°) = -0.36397 tg(341°) = -0.34433 tg(342°) = -0.32492 tg(343°) = -0.30573 tg(344°) = -0.28675 tg(345°) = -0.26795 tg(346°) = -0.24933 tg(347°) = -0.23087 tg(348°) = -0.21256 tg(349°) = -0.19438 tg(350°) = -0.17633 tg(351°) = -0.15838 tg(352°) = -0.14054 tg(353°) = -0.12278 tg(354°) = -0.1051 tg(355°) = -0.08749 tg(356°) = -0.06993 tg(357°) = -0.05241 tg(358°) = -0.03492 tg(359°) = -0.01746 tg(360°) = 0 |
Кроме таблицы тангенсов, на нашем сайте вы можете просмотреть таблицу косинусов, таблицу котангенсів, таблицу синусов.
cubens.com