Видеоурок комплексные числа 10 класс – План-конспект урока по алгебре (10 класс) по теме: Урок – лекция по алгебре в 10 классе: «Комплексные числа и операции над ними» | скачать бесплатно

Комплексные числа — Математика — 10 класс

Комплексные числа и квадратные уравнения.

10 класс ( профильный уровень).

«Мысль выражать все числа знаками

настолько проста, что именно из-за

этой простоты сложно осознать,

сколь она удивительна»

Пьер Симон Лаплас

Цели урока:

1.Обучающая:

• формирование у школьников различных приёмов мыслительной деятельности;

• включение новой информации в структуру прежних знаний;

• расширить сведения учащихся о числах;

2. Воспитательная:

• привитие интереса к предмету;

• формирование уверенности в своих знаниях.

• воспитание чувства ответственности.

3. Развивающая:

Задачи урока:

• Обобщить и систематизировать знания, умения и навыки учащихся по теме урока.

• Развивать умения применять теоретические знания при решении заданий; умение анализировать, сравнивать, обобщать, устанавливать причинно-следственные связи; классифицировать.

• Формировать навыки самостоятельной деятельности

Учебно-методическая карта фрагмента урока

№	Этап урока	Содержание этапа	Методы и методические приемы	Формируемые компетенции
1	Организационный момент	Приветствие
2	Мотивация и целеполагание. Активизация деятельности.	Мотивация Определение целей урока (слайды 2-4)
3	Актуализация	Историческая справка Решение кроссворда (для сильных) Тест (для слабых) (слайд 5-6) Индивидуальная работа (на карточках)	Наглядно-иллюстративный Частично-поисковый Работа в парах Индивидуальная работа ( проверка через документ камеру)	Умение осознавать основное содержания темы Умение использовать полученные знания Умение синтезировать данные
4	Сообщение новых знаний	Решение квадратных уравнений на множестве комплексных чисел. (слайд 7-8)	Наглядно-иллюстративный Исследовательский Частично-поисковый Практический
5	Этап обобщения и систематизации	Индивидуальная работа. (слайд 9-10) Индивидуальная работа (на карточках)		Умение проявлять гибкость, оказавшись в нестандартных ситуациях Умение организовывать взаимосвязь своих знаний и упорядочивать их Умение принимать решения и брать на себя ответственность за их последствия Взаимоконтроль
6	Домашнее задание	Задания различного уровня сложности		Поиск, анализ и отбор необходимой информации, ее преобразование, сохранение и передача
7	Рефлексия	Ответы на вопросы (слайд 11-12)
8	Итог урока	Качественная характеристика работы учащихся

На прошлых уроках мы познакомились с понятием комплексного числа, алгебраической формой записи комплексного числа, научились выполнять различные действиями над комплексными числами, научились находить модуль и аргумент комплексного числа.

Актуализация

Работа в парах — решение кроссворда (историческая справка), для слабых тестирование. (проверка)

Индивидуальная работа. Заполняют лист само оценивания.

Вариант 1

1. Даны два комплексных числа Z₁= (10 + 2i ) и Z₂=(1 – 6i ). Найдите их сумму, разность, произведение и частное.

Вариант 2.

Даны два комплексных числа z₁= (12 + 2i ) и z₂=(3 – 4i ). Найдите их сумму, разность, произведение и частное.

Ответы:

Вариант 1

1. Z₁+ Z₂=11 – 4i

2. Z₁— Z₂=9 +8i

3. Z₁ Z₂=22 -58i

4.

Вариант 2

1. Z₁+ Z₂=15 – 2i

2. Z₁— Z₂=9 +6i

3. Z₁ Z₂=44 -42i

4. (Проверка по тетрадям учащихся через документ камеру)

Решите квадратные уравнения:

х² – 5х + 6=0 х² +6х+9=0 9х²-12х + 5 = 0

Решение квадратных уравнений в поле комплексных чисел

ax² + bx + c = 0

1 cлучай: D0, 2 корня, х_1,2 =

2 случай D=0, 1 коре нь, х_1,2 =

3 cлучай: D_1,2 =

Сколько корней может иметь записанное на доске квадратное уравнение?

9х²-12х + 5 = 0

У доски решает ученик:

9х²-12х+5=0

D= 144-180= -36, считаем, что

-Теперь вы можете блеснуть эрудицией, услышав, что при D

— Вот и сделали мы шаг в глубину математического айсберга. Комплексные числа широко применяются в электротехнике, в аэродинамике. Отец русской авиации, Н.Г. Жуковский использовал их при разработке теории крыла самолета. Возможно, они пригодились для получения промежуточного результата.

x ²– 4x + 13 = 0.
  9 x ²+ 12x + 29 = 0.

Взаимопроверка

Ответы:

1) 𝑥=(4+6𝑖)/2=2+3i 𝑥=(4−6𝑖)/2=2-3i

2) 𝑥=(−12−30𝑖)/18=(−2)/3 − 5/3 𝑖 , 𝑥=(−12+30𝑖)/18=(−2)/3+ 5/3 𝑖

Самопроверка.

1. Решите уравнение x² – 4x + 5 = 0.

Решение. D = – 4 уравнение имеет мнимые корни:   2+i, 2-i

2. Решите уравнение x² – x + 10 = 0.

Решение. D = – 39 , уравнение имеет мнимые корни:  

3. Решите уравнение x² – 4x + 13 = 0.

Решение. D = – 36 уравнение имеет мнимые корни:   2+3i, 2-3i

4. Решите уравнение x² – 2x + 15 = 0.

Решение. D = – 56 , уравнение имеет мнимые корни:  

А как бы вы решили следующее квадратное уравнение?

1. х² + (5 – 2i) x + 5(1– i) = 0;???????

Вот над этой проблемой будем работать на следующем уроке, а желающие могут попробовать самостоятельно попробовать свои силы.

Домашнее задание п.35 №7-8(а, б),10.

Спасибо за урок!

Вариант 1

1. Даны два комплексных числа Z₁= (10 + 2i ) и Z₂=(1 – 6i ). Найдите их сумму, разность, произведение и частное.

2. Проверьте правильность следующих утверждений:

а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.

Для проверки возьмите числа: Z₁=2i, Z₂=-3i

б) Произведение двух чисто мнимых чисел равно действительному числу.

Для проверки возьмите числа: Z₁=-5i, Z₂=3i

в) Квадрат чисто мнимого числа равен действительному отрицательному числу.

Для проверки возьмите числа: Z₁=10i

г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.

Для проверки возьмите числа: Z

1=7i, Z₂=3

которых равны 2.

Вариант 2.

Даны два комплексных числа z₁= (12 + 2i ) и z₂=(3 – 4i ). Найдите их сумму, разность, произведение и частное.

2. Проверьте правильность следующих утверждений:

а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.

Для проверки возьмите числа: Z₁=2i, Z₂=-3i

б) Произведение двух чисто мнимых чисел равно действительному числу.

Для проверки возьмите числа: Z₁=-5i, Z₂=3i

в) Квадрат чисто мнимого числа равен действительному отрицательному числу.

Для проверки возьмите числа: Z₁=10i

г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.

Для проверки возьмите числа: Z₁=7i, Z₂=3

1. Решите уравнение x² – 4x + 5 = 0.    2+i, 2-i

2. Решите уравнение x

2 – x + 10 = 0.  

3. Решите уравнение x² – 4x + 13 = 0. 2+3i, 2-3i

4. Решите уравнение x² – 2x + 15 = 0.

1. Решите уравнение x² – 4x + 5 = 0.    2+i, 2-i

2. Решите уравнение x² – x + 10 = 0.  

3. Решите уравнение x² – 4x + 13 = 0. 2+3i, 2-3i

4. Решите уравнение x² – 2x + 15 = 0.

		1
						2								3
																												5
4
								6																																8
																								7
										9
																								10
																								11
ВОПРОСЫ:
По горизонтали:
3.			Кто впервые упомянул о мнимых числах, назвав их «софически отрицательными»?
4.			Одна из форм задания комплексного числа.
6.			Чье имя носит формула = ?
7.			arg z.
9.			Длина вектора соответствующего комплексного числа.
10.			bi — …… часть числа.
11.			Геометрическая интерпретация комплексного числа.
По вертикали:
1.			Кто ввел название «мнимые числа»?
2.			Французский математик, предложивший изображать комплексные числа на координатной плоскости.
3.			Число вида ?
5.			Числа
8.			Сколько форм записи комплексных чисел Вы знаете?

Карточка само оценивания. 

Ф. И. _______________________________________________

 Система оценивания:

«+» — справился с заданием без затруднений,

«±» — справился с заданием, но возникали сложности,

«-» — не справился с заданием.

№ задания	Задание	Оценка	Оценка учителя
1	Работа в парах
2	Работа по карточкам
3	Решение квадратных уравнений (взаимопроверка)
4	Решение квадратных уравнений (самопроверка)
5	Итого: ваша оценка за урок

Если у вас: 5- 4,5 «+» — ставим оценку «5»;

4- 3,5 «+» — «4»;

3- 2,5 «+» — «3».

multiurok.ru

Презентация по теме: «Комплексные числа» 10 класс.

1.История развития числа.

Докладчик: А вы знаете, что нас с вами в древние времена скорей всего считали колдунами? В древние времена человек, который умел считать, казался колдуном. Не все грамотные люди владели подобным «колдовством». Считать умели, в основном, писцы, а еще, конечно, купцы.

Появляются купцы.
Купцы. Сложение, самое простое арифметическое действие, освоить при определенном воображении можно. Надо было только представить одинаковые палочки, камешки, ракушки.

А дальше – просто. Знай себе, прибавляй к палочке палочку и считай общее количество.

Докладчик: Приблизительно так и нас обучали счету в первом классе. В пятом классе УЗНАЛИ название этих чисел. Как они называются и обозначаются? (Натуральные «N» — natural, Слайд №1) Какие операции допустимы на множестве натуральных чисел? (сложение, умножение)
А вот с вычитанием уже начинались проблемы. Не всегда получалось вычесть из одного числа другое. Иногда отнимаешь, отнимаешь, глядь – ничего уже не осталось. Нечего больше отнимать! Так что вычитание считалось действием мудреным и не всегда его произвести удавалось.
Но тут пришли на помощь купцы.

Купцы: «Можно было бы начать вычитать белые палочки, а потом, когда ничего не останется, начать выкладывать черные палочки, как бы про запас.»

«Две черные палочки – это, предположим, две овцы, которые ты должен отдать, но пока еще не отдал. Это долг!»

Докладчик: В общем, человечеству же на толкование отрицательных чисел, а вместе с этим на определение понятия целых чисел Z-«zero» понадобилось тысячу с лишним лет. Зато стали допустимы операции…( сложение, вычитание и умножение).

Вообще, проблемы, подобные вышеописанным с отрицательными числами, возникали со всеми «обратными» арифметическими действиями. Два целых числа можно было перемножить, и в результате получалось целое число. А вот результат от деления двух целых чисел целым числом оказывался не всегда. Это тоже приводило к недоумениям.

Купцы: сцена деления шоколада. Вот смотри, мы сладость какую заработали. Давай делить!!!

А как? она одна, а нас двое , а еще и гости… Придумал-дроби ее на части…

Докладчик: То есть, для того, чтобы результат деления существовал всегда, пришлось ввести, освоить и понять, так сказать, «физический смысл» дробных чисел. Так вошли в дело рациональные числа — Q-«quotient» — «отношение».

В системе рациональных чисел стали допустимы многие операции. Но, что не всегда получалось? (извлечение корней из неотрицательных чисел была допустима частично. Например «корень из 81» и «корень из 2».)

Эта необходимость привела к введению множества действительных чисел (R – real), для которого и извлечение корней из неотрицательных чисел было допустимой алгебраической операцией. И все же оставался один недостаток – это…? (извлечение корня из отрицательных чисел.)

2. Новый материал.

В 18-м веке математики придумали специальные числа для того, чтобы получалось еще одно «обратное» действие, извлечение квадратного корня из отрицательных чисел. Это – так называемые «комплексные» числа (C-complex). Представить их сложно, но привыкнуть к ним – возможно. Считается, что на множестве комплексных чисел допустимы все алгебраические операции. И польза от применения комплексных чисел большая. Существование этих «странных» чисел значительно облегчило расчет сложных электротехнических цепей переменного тока, а также позволило рассчитать профиль авиационного крыла. Познакомимся с ними поближе.

Перечислим минимальные условия, которым должны удовлетворять комплексные числа:

• С1: Существует комплексное число, квадрат которого равен -1

• С2 Множество комплексных чисел содержит все действительные числа.

• С3 Операции сложения, вычитания, умножения и деления удовлетворяют законам арифметических действий(сочетательному, переместительному, распределительному)

Число, квадрат которого равен -1, называется мнимой единицей и обозначается i – imaginary – мнимый, воображаемый.. Это обозначение предложил Леонард Эйлер в 18 веке. Таким образом:

i² =-1, i-мнимая единица

Определение 1:

Числа вида bi, где i – мнимая единица, называются чисто мнимыми.

Например 2i, -3i, 0,5i

Определение 2:

Комплексным числом называют сумму действительного числа и чисто мнимого числа.

Комплексное число записывают как z = a + bi.

Число a называется действительной частью числа z,

число bi– мнимой частью числа z.

Их обозначают соответственно: a = Re z, b = Im z.

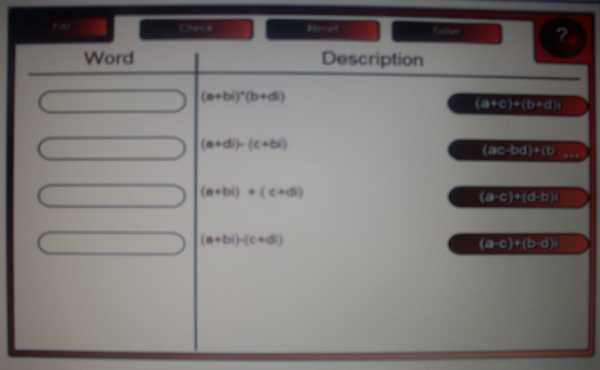
Арифметические действия:

Сравнение

a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части)

Сложение

(a + bi) + (c + di) = (a + c) + (b + d)i

Вычитание

(a + bi) − (c + di) = (a − c) + (b − d)i

Умножение

(a + bi) × (c + di) = ac + bci + adi + bdi² = (ac − bd) + (bc + ad)i

Деление

3. Практика.

Учебник Мордкович А.Г. Профильный уровень. 11 класс. Рассмотрим простейшие примеры работы на множестве комплексных чисел.

Рассмотреть пример № 1,2 – два способа. (стр.245).

Работа с учебником. №32.7, 32,10, 32,12

4.Тест (Приложение)

Д/З №32.5, 32,8, 32,11 а,б

www.metod-kopilka.ru

Мастер-класс 10 класса профильной группы «Комплексные числа»

мастер –класс Профильной группы 10 класса

Тема : Комплексные числа

Цель занятия: повышение математической культуры учащихся; углубление представлений о понятии числа; дальнейшее развитие представлений о единстве математики как науки.

1.Вступительное слово учителя

Здравствуйте уважаемые ребята, коллеги!

Сегодня у нас необычное занятие, оно посвящается дорогие выпускники ВАМ.

Учащиеся профильной группы 10 класса постараются рассказать вам материал, который пригодится вам в дальнейшем обучении в ВУЗах.

Числа не управляют миром, но показывают, как управляется мир И. Гёте слайд 1

Давайте, вспомним известные нам множества чисел. Слайд 2

2. Проблемный вопрос

Решите уравнения: x² +1 =0 x² +9 = 0 слайд 3

Данные уравнения решений не имеют в множестве действительных чисел. В математике существует ещё одно множество чисел, которое называется Комплексные числа, они позволяют решить предыдущие уравнения. Словарь Ожигова слайд 4

3. Информационный блок

Комплексные числа, как, впрочем, и отрицательные, возникли из внутренней потребности самой математики, конкретнее – из практики и теории решения алгебраических уравнений. С комплексными числами впервые математики встретились при решении квадратных уравнений. Вплоть до 16 века математики всего мира, не находя приемлемого толкования для комплексных корней, возникавших при решении квадратных уравнений, объявляли их ложными и не принимали во внимание. И только в начале 19 века, когда уже была выяснена роль комплексных чисел в различных областях математики, была разработана очень простая и естественная их геометрическая интерпретация. Ознакомление и изучение комплексных чисел позволит вам ребята углубить познания во многих разделах математики, вооружит вас дополнительным инструментом для решения различных задач.

4. Практическая часть

Слово я предоставляю учащимся 10а класса.

1 учащийся .Полякова Даша.

Слайд5,6 Историческая справка

2учащийся Щеглова Катя

Слайд 7,8,9 Определение№1,2,3

3учащийся Пляскин Семён Модуль комплексного числа

Слайд 10,11

4учащийся Ярославцев Демид

Слайд 12.Действия с комплексными числами в алгебраической форме.

Слайд 13,14 Сложение к. Ч

5 учащийся Панов Вадим

Слайд 15 Вычитание к. Ч

6учащийся Воложанин Женя

Слайд 16. Умножение К.Ч

7 учащийся Полякова Даша

Слайд 17 Деление К.Ч

5.Итог занятия

Учитель: Завершая разговор о комплексных числах сегодня, хотим подчеркнуть ,что мы показали вам действия с комплексными числами в алгебраической форме, а есть еще тригонометрическая форма записи комплексного числа . и Действия над комплексными числами в тригонометрической форме записи. Мы думаем ,вы можете рассмотреть этот материал самостоятельно.

А теперь посмотрите, как выглядит решение квадратного уравнения в множестве комплексных чисел

6. Рефлексия

Попробуй решить Сам.

«Комплексное число –

это тонкое и поразительное средство божественного духа,

почти амфибия между бытием и небытием».

Г. Лейбниц

infourok.ru

Конспект урока по алгебре и началам математического анализа «Комплексные числа»( 10 класс)

Название методической разработки конспект урока по алгебре и началам математического анализа

Автор методической разработки Чепкасова Наталья Юрьевна,

учитель математики, высшая квалификационная категория

Класс 10

Количество компьютеров на уроке 11

Интерактивная доска

Мультимедийные продукты:

-Мультимедийная презентация;

-Тест «Контрольный». Программное обеспечение MyTest (автоматизированная проверка выполнения теста).

Глава 6. Название темы: «Комплексные числа».

Урок № 66. Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость.

Цели урока:

Систематизировать  теоретический материал по теме.

Обобщить  знания учащихся по теме  и  рассмотреть вопросы по теме «Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость».

Повторить   векторный и алгебраический подходы к определению комплексных чисел,   действия с комплексными числами.

Развивать: способности анализировать, планировать, контролировать свою деятельность (взаимо- и самоконтроль).

Формировать  коммуникативные навыки,  оперировать математической терминологией.

Продолжить освоение интерактивной доски.

План проведения урока

1.

Мотивация

Целеполагание

I. Организационный момент

Учащиеся записывают тему урока «Действия с комплексными числами».

Учитель: Продумаем план проведения урока. Что вы предлагаете повторить по теме?

Какие вопросы вас интересуют?

Что, по вашему мнению, требует углубления? Какие виды контроля считаете наиболее рациональными на этом уроке?

Постановка цели урока.

После обсуждения учащиеся знакомятся с предполагаемым планом.

План работы на уроке:

1 этап — повторение вопросов теории.

2 этап – рассмотрение различных способов действий с комплексными числами;

3 этап — вычислительная  работа, 

4 этап – итоговый контроль.

Учитель:  Вы согласны, что эти этапы необходимы?

2.

Актуализация опорных знаний и умений

Работа с теоретическим материалом

Слайд 1:

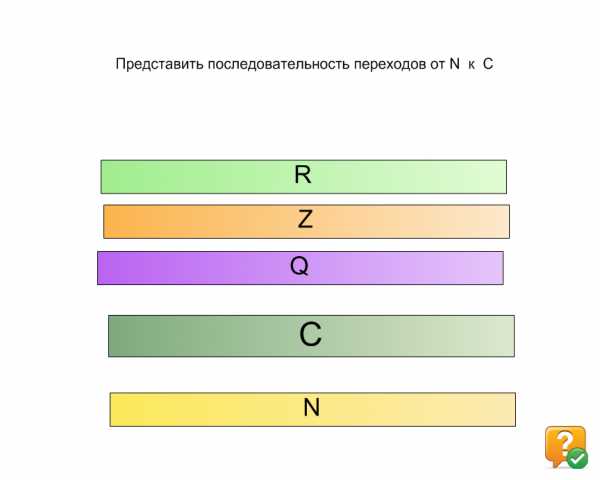
« Представить последовательность переходов числовых систем от N к C».

Слайд 2:  

« Повторение вопросов теории. Основные определения».

1) Сформулируйте определение комплексного числа.
2) Как изображается комплексное число на плоскости?
3) Как вычислить модуль комплексного числа?
4) Какое число называется сопряженным
5) Какое единственное число является одновременно действительным и чисто мнимым?
6) Мнимой единицей называют…

Слайд 3: «Основные формулы. Повторение формул сложения, вычитания, произведения комплексных чисел».

3.

Проблема

Векторный и алгебраический подходы к определению комплексных чисел,   действиям с комплексными числами

Слайд 4: «Векторный и алгебраический подходы к действиям с комплексными числами».

Вычисление суммы, разности компл. чисел разными способами.

Даны комплексные числа z₁=-2+2i z₂=1-3i

Изобразите их на координатной плоскости.

Используя векторный и алгебраический подходы к действиям с комплексными числами найдите:

1)Z₃= z₁ + z₂ ;

2) z₄ , сопряженное числу z₁ ;

3) z₅, противоположное числу z_{2 ;}

4) разность _{z1 и z2 ;}

5) число, сопряженное числу z₁ + z₂ .

4.

Обобщение и систематизация знаний и способов выполнения работы

Вычислительный практикум

Даны комплексные числа z₁=1-i z₂=4+i

Нахождение частного данных комплексных чисел 3 различными способами.

(3 ученика работают у доски)

Проверка умений выполнения действий с комплексными числами:

№ 32.26(б)

№ 32.34(а,б)

№ 32.33

Выполняется  проверка с помощью  режима интерактивной доски (документ камера), вызывается ученик со своим решением.

Найдите z⁶, если

В режиме интерактивной доски рассматриваются решения учащихся.

Контроль полученных знаний

Самостоятельная работа учащихся на компьютере

-Тест «Контрольный» (файл MyTest).

1) (3+2i)+3(-1+3i)

2) i-2-(6-5i)

3) (1+i)(1-i)

4) i³+i¹⁰¹

5) 3/i

6) (1 +i)⁴

Домашнее задание

№89, 92, 94 , №98- по выбору учащихся

Итог урока

Учитель: Удалось ли реализовать цели  данного урока? Что узнали нового? Что не совсем получилось?

На основании геометрической  интерпретации применение комплексных чисел эффективно в тех областях, где приходится оперировать с величинами, которые можно представить в виде точки на плоскости или плоского вектора.   Поэтому теория функции комплексного переменного нашла широкое употребление для решения вопросов теоретической физики, гидродинамики, электротехники, кораблестроения, картографии.

Те из вас, кто продолжит свое образование в технических вузах, смогут глубже ознакомиться с теорией функции комплексного переменного и её приложениями в различных областях науки и техники.

.

infourok.ru

No related posts.