Вычисление криволинейных интегралов: теория и примеры
Криволинейные интегралы — обобщение понятия определённого интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:
где f(x, y) — функция двух переменных, а L — кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB.
Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?
Пусть на плоскости расположен отрезок AB некоторой кривой L, а функция двух
переменных
- Разделить кривую AB на части точками (рисунки ниже).
- В каждой части свободно выбрать точку M.
- Найти значение функции в выбранных точках.
- Значения функции умножить на
- длины частей в случае криволинейного интеграла первого рода;
- проекции частей на ось координат в случае криволинейного интеграла второго рода.
- Найти сумму всех произведений.
- Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.
Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f( x, y) по кривой AB.
Случай криволинейного интеграла
первого рода
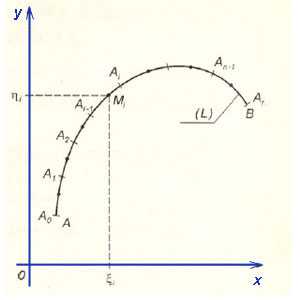
Случай криволинейного интеграла
второго рода
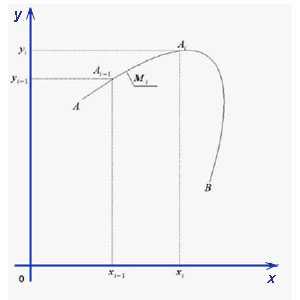
Введём следующие ообозначения.
Mi(ζi; ηi) — выбранная на каждом участке точка с координатами.
fi(ζi; ηi) — значение функции f(x, y) в выбранной точке.
Δsi — длина части отрезка кривой (в случае криволинейного интеграла первого рода).
Δxi — проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).
Криволинейные интегралы первого рода
Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:
.
Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл. Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:
.
В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B) считать началом отрезка, а какую концом, то есть
.
Криволинейные интегралы второго рода
Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:
.
В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:.
При составлении интегральной суммы криволинейного интеграла второго рода значения функции fi(ζi; ηi) можно умножать также на проекции частей отрезка кривой на ось Oy. Тогда получим интеграл
.
На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P(x, y) и f = Q(x, y) и интегралы
,
а сумма этих интегралов
называется общим криволинейным интегралом второго рода.
Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.
Кривая дана в декартовых прямоугольных координатах
Пусть на плоскости задана кривая y = y(x) и отрезку кривой AB соответствует изменение переменной x от a до b. Тогда в точках кривой подынтегральная функция f(x, y) = f(x, y(x)) («игрек» должен быть выражен через «икс»), а дифференциал дуги и криволинейный интеграл можно вычислить по формуле
.
Если интеграл проще интегрировать по y, то из уравнения кривой нужно выразить x = x(y) («икс» через «игрек»), где и интеграл вычисляем по формуле
.
Пример 1. Вычислить криволинейный интеграл
,
где AB — отрезок прямой между точками A(1; −1) и B(2; 1).
Решение. Составим уравнение прямой AB, используя формулу (уравнение прямой, проходящей через две данные точки A(x1; y1) и B(x2; y2)):
.
Из уравнения прямой выразим y через x:
.
Тогда и теперь можем вычислять интеграл, так как у нас остались одни «иксы»:

Кривая дана в параметрической форме
Пусть в пространстве задана кривая
Тогда в точках кривой функцию нужно выразить через параметр t () а дифференциал дуги , поэтому криволинейный интеграл можно вычислить по формуле
Аналогично, если на плоскости задана кривая
,
то криволинейный интеграл вычисляется по формуле
.
Пример 2. Вычислить криволинейный интеграл
,
где L — часть линии окружности
,
находящаяся в первом октанте.
Решение. Данная кривая — четверть линии окружности, расположенная в плоскости z = 3. Она соответствует значениям параметра . Так как
,
то дифференциал дуги
Подынтегральную функцию выразим через параметр t:
.
Теперь, когда у нас всё выражено через параметр t, можем свести вычисление данного криволинейного интеграла к определённому интегралу:
Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.Кривая дана в декартовых прямоугольных координатах
Пусть дана кривая на плоскости уравнением функции «игрек», выраженной через «икс»: y = y(x) и дуге кривой AB соответствует изменение x от a до b. Тогда в подынтегральную функцию подставим выражение «игрека» через «икс» и определим дифференциал этого выражения «игрека» по «иксу»: . Теперь, когда всё выражено через «икс», криволинейный интеграл второго рода вычисляется как определённый интеграл:
Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции «икс», выраженной через «игрек»: x = x(y), . В этом случае формула для вычисления интеграла следующая:
, если
а) L — отрезок прямой OA, где О(0; 0), A(1; −1);
б) L — дуга параболы y = x² от О(0; 0) до A(1; −1).
Решение.
а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке — синяя). Напишем уравнение прямой и выразим «игрек» через «икс»:
.
Получаем dy = dx. Решаем данный криволинейный интеграл:
б) если L — дуга параболы y = x², получим dy = 2xdx. Вычисляем интеграл:
В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.
Теорема. Если функции P(x,y), Q(x,y) и их частные производные , — непрерывные в области D функции и в точках этой области частные производные равны, то криволинейный интеграл не зависит от пути интегрирования по линии L, находящейся в области D.
Кривая дана в параметрической форме
Пусть в пространстве дана кривая
.
Тогда
,
а в подынтегральные функции подставим
—
выражения этих функций через параметр t. Получаем формулу для вычисления криволинейного интеграла:
Пример 4. Вычислить криволинейный интеграл
,
отвечающая условию y ≥ 0.
Решение. Данная кривая — часть эллипса, находящаяся в плоскости z = 2. Она соответствует значению параметра .
Так как
,
можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Если дан криволинейный интеграл и L — замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина.
Пример 6. Вычислить криволинейный интеграл
,
где L — дуга параболы между точками О(0; 0) и B(2; 2).
Решение. Так как , то .
Теперь можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:
Пример 7. Вычислить криволинейный интеграл
,
где L — дуга астроиды
в первом квадранте.
Решение. В первом квадранте . Определим дифференциал дуги:
Представляем криволинейный интеграл в виде определённого интеграла и вычисляем его:

Пример 8. Вычислить криволинейный интеграл
,
где L — первая арка циклоиды
Решение. Циклоида образует первую арку при изменении параметра t от 0 до 2π. Определим дифференциал дуги:
Таким образом,
.
Подставим в криволинейный интеграл dl и y, выраженные через параметр t и получаем:

Пример 9. Вычислить криволинейный интеграл
,
где L — отрезок прямой от точки A(1; 1) до точки B(3; 5).
Решение. Составим уравнение прямой AB:
.
Из полученного уравнения прямой выразим «игрек»:
Поэтому и теперь можем вычислить данный криволинейный интеграл:
Пример 10. Вычислить криволинейный интеграл
,
где L — первая арка циклоиды
Решение. Из уравнений кривой следует
.
Так как циклоида образует первую арку при изменении параметра t от 0 до 2π, то получаем соответствующие пределы интегрирования. Решаем данный криволинейный интеграл:

Кратные и криволинейные интегралы
Поделиться с друзьями
function-x.ru
Криволинейный интеграл первого рода | Вычисление криволинейный интеграл 1 рода
Определение: Пусть в каждой точки гладкой кривой L = AB в плоскости Oxy задана непрерывная функция двух переменных f(x,y). Произвольно разобьем кривую L на n частей точками A = М0, М1, М2, … Мn = B. Затем на каждой из полученных частей выберем любую точку и составим сумму
где — дуга дуги . Полученная сумма называется интегральной суммой первого рода для функции f(x,y), заданой на кривой L.
Обозначим через d наибольшую из длин дуг (таким образом, d = ). Если при d ? 0 существует предел интегральных сумм Sn (не зависящих от способа разбиения кривой L на части и выбора точек ), то этот предел называется криволинейным интегралом первого порядка от функции f(x,y) по кривой L и обозначается
Можно доказать, что если функция f(x,y)непрерывна, то криволинейный интеграл существует.
Свойства криволинейного интеграла 1 рода
Криволинейный интеграл первого рода обладает свойствами, аналогичными соответствующим свойства определеннного интеграла:
- аддитивность,
- линейность,
- оценка модуля,
- теорема о среднем.
Однако есть отличие:
т.е. криволинейный интеграл первого рода не зависит от направления интегрирования.
Вычисление криволинейных интегралов первого рода
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла. А именно:
- Если кривая L задана непрерывно дифференцируемой функцией y=y(x), x [a,b], то
при этом выражение называется дифференциалом длины дуги.
- Если крива L задана параметрически, т.е. в виде x=x(t), y=y(t), где x(t), y(t) — непрерывно дифференцируемые функции на некотором отрезке , то
Это равенство распространяется на случай пространственной кривой L, заданной параметрически: x=x(t), y=y(t), z=z(t), . В этом случае, если f(x,y,z) — непрерывная функция вдоль кривой L, то
- Если плоская кривая L задана полярным уравнением r=r( ), , то
Криволинейные интегралы 1 рода — примеры
Пример 1
Вычислить криволинейный интеграл первого рода
где L дуга параболы y2=2x, заключенная между точками (2,2) и (8,4).
Решение: Найдем дифференциал дуги dl для кривой . Имеем:
Следовательно данный интеграл равен:
Пример 2
Вычислить криволинейный интеграл первого рода , где L — окружность x2+y2=ax (a>0).
Решение: Введем полярные координаты: , . Тогда поскольку x2+y2=r2, уравнение окружности имеет вид: , то есть , а дифференциал дуги
.
При этом . Следовательно,
shkolnaiapora.ru
МА. Криволинейные интегралы первого рода и поверхностные интегралы первого рода
Теоретический минимумКриволинейные и поверхностные интегралы часто встречаются в физике. Они бывают двух видов, первый из которых рассматривается здесь. Этот
тип интегралов строится согласно общей схеме, по которой вводятся определённые, двойные и тройные интегралы. Коротко напомним эту схему.
Имеется некоторый объект, по которому проводится интегрирование (одномерный, двумерный или трёхмерный). Этот объект разбивается на малые части,
в каждой из частей выбирается точка. В каждой из этих точек вычисляется значение подынтегральной функции и умножается на меру той части, которой
принадлежит данная точка (длину отрезка, площадь или объём частичной области). Затем все такие произведения суммируются, и выполняется предельный
переход к разбиению объекта на бесконечно малые части. Получающийся предел и называется интегралом.
1. Определение криволинейного интеграла первого рода
Рассмотрим функцию , определённую на кривой . Кривая предполагается спрямляемой. Напомним, что это означает, грубо говоря,
что в кривую можно вписать ломаную со сколь угодно малыми звеньями, причём в пределе бесконечно большого числа звеньев длина ломаной должна оставаться
конечной. Кривая разбивается на частичные дуги длиной и на каждой из дуг выбирается точка . Составляется произведение ,
проводится суммирование по всем частичным дугам . Затем осуществляется предельный переход с устремлением длины наибольшей
из частичных дуг к нулю. Предел является криволинейным интегралом первого рода
.
Важной особенностью этого интеграла, прямо следующей из его определения, является независимость от направления интегрирования, т.е.
.
2. Определение поверхностного интеграла первого рода
Рассмотрим функцию , определённую на гладкой или кусочно-гладкой поверхности . Поверхность разбивается на частичные области
с площадями , в каждой такой области выбирается точка . Составляется произведение , проводится суммирование
по всем частичным областям . Затем осуществляется предельный переход с устремлением диаметра наибольшей из всех частичных
областей к нулю. Предел является поверхностным интегралом первого рода
.
3. Вычисление криволинейного интеграла первого рода
Методика вычисления криволинейного интеграла первого рода просматривается уже из формальной его записи, а фактически следует непосредственно из
определения. Интеграл сводится к определённому, только нужно записать дифференциал дуги кривой, вдоль которой проводится интегрирование.
Начнём с простого случая интегрирования вдоль плоской кривой, заданной явным уравнением . В этом случае дифференциал дуги
.
Затем в подынтегральной функции выполняется замена переменной , и интеграл принимает вид
,
где отрезок отвечает изменению переменной вдоль той части кривой, по которой проводится интегрирование.
Очень часто кривая задаётся параметрически, т.е. уравнениями вида . Тогда дифференциал дуги
.
Формула эта очень просто обосновывается. По сути, это теорема Пифагора. Дифференциал дуги — фактически длина бесконечно малой части кривой.
Если кривая гладкая, то её бесконечно малую часть можно считать прямолинейной. Для прямой имеет место соотношение
.
Чтобы оно выполнялось для малой дуги кривой, следует от конечных приращений перейти к дифференциалам:
.
Если кривая задана параметрически, то дифференциалы просто вычисляются:
и т.д.
Соответственно, после замены переменных в подынтегральной функции криволинейный интеграл вычисляется следующим образом:
,
где части кривой, по которой проводится интегрирование соответствует отрезок изменения параметра .
Несколько сложнее обстоит дело в случае, когда кривая задаётся в криволинейных координатах. Этот вопрос обычно обсуждается в рамках дифференциальной
геометрии. Приведём формулу для вычисления интеграла вдоль кривой, заданной в полярных координатах уравнением :
.
Приведём обоснование и для дифференциала дуги в полярных координатах. Подробное обсуждение построения координатной сетки полярной системы координат
см. здесь. Выделим малую дугу кривой, расположенную по отношению к координатным линиям так, как показано на рис. 1. В силу малости всех фигурирующих
дуг снова можно применить теорему Пифагора и записать:
.
Отсюда и следует искомое выражение для дифференциала дуги.
С чисто теоретической точки зрения достаточно просто понять, что криволинейный интеграл первого рода должен сводиться к своему частному случаю —
определённому интегралу. Действительно, выполняя замену, которая диктуется параметризацией кривой, вдоль которой вычисляется интеграл, мы устанавливаем
взаимно-однозначное отображение между частью данной кривой и отрезком изменения параметра . А это и есть сведение к интегралу
вдоль прямой, совпадающей с координатной осью — определённому интегралу.
4. Вычисление поверхностного интеграла первого рода
После предыдущего пункта должно быть ясно, что одна из основных частей вычисления поверхностного интеграла первого рода — запись элемента поверхности ,
по которой выполняется интегрирование. Опять-таки начнём с простого случая поверхности, заданной явным уравнением . Тогда
.
Выполняется замена в подынтегральной функции, и поверхностный интеграл сводится к двойному:
,
где — область плоскости , в которую проектируется часть поверхности, по которой проводится интегрирование.
Однако часто задать поверхность явным уравнением невозможно, и тогда она задаётся параметрически, т.е. уравнениями вида
.
Элемент поверхности в этом случае записывается уже сложнее:
.
Соответствующим образом записывается и поверхностный интеграл:
,
где — область изменения параметров, соответствующая части поверхности , по которой проводится интегрирование.
5. Физический смысл криволинейного и поверхностного интегралов первого рода
Обсуждаемые интегралы обладают очень простым и наглядным физическим смыслом. Пусть имеется некоторая кривая, линейная плотность которой не является
константой, а представляет собой функцию точки . Найдём массу этой кривой. Разобьём кривую на множество малых элементов,
в пределах которых её плотность можно приближённо считать константой. Если длина маленького кусочка кривой равна , то его масса
, где — любая точка выбранного кусочка кривой (любая, так как плотность в пределах
этого кусочка приближённо предполагается постоянной). Соответственно, масса всей кривой получится суммированием масс отдельных её частей:
.
Чтобы равенство стало точным, следует перейти к пределу разбиения кривой на бесконечно малые части, но это и есть криволинейный интеграл первого рода.
Аналогично разрешается вопрос о полном заряде кривой, если известна линейная плотность заряда .
Эти рассуждения легко переносятся на случай неравномерно заряженной поверхности с поверхностной плотностью заряда . Тогда
заряд поверхности есть поверхностный интеграл первого рода
.
Замечание. Громоздкая формула для элемента поверхности, заданной параметрически, неудобна для запоминания. Другое выражение получается в дифференциальной геометрии,
оно использует т.н. первую квадратичную форму поверхности.
Примеры вычисления криволинейных интегралов первого рода
Пример 1. Интеграл вдоль прямой.
Вычислить интеграл
вдоль отрезка прямой, проходящей через точки и .
Сначала запишем уравнение прямой, вдоль которой проводится интегрирование: . Найдём выражение для :
.
Вычисляем интеграл:
Пример 2. Интеграл вдоль кривой на плоскости.
Вычислить интеграл
по дуге параболы от точки до точки .
Заданные точки и позволяют выразить переменную из уравнения параболы: .
Вычисляем интеграл:
.
Однако можно было проводить вычисления и иначе, пользуясь тем, что кривая задана уравнением, разрешённым относительно переменной .
Если принять переменную за параметр, то это приведёт к небольшому изменению выражения для дифференциала дуги:
.
Соответственно, интеграл несколько изменится:
.
Этот интеграл легко вычисляется подведением переменной под дифференциал. Получится такой же интеграл, как и в первом способе вычисления.
Пример 3. Интеграл вдоль кривой на плоскости (использование параметризации).
Вычислить интеграл
вдоль верхней половины окружности .
Можно, конечно, выразить из уравнения окружности одну из переменных, а затем провести остальные вычисления стандартно. Но можно использовать и
параметрическое задание кривой. Как известно, окружность можно задать уравнениями . Верхней полуокружности
отвечает изменение параметра в пределах . Вычислим дифференциал дуги:
.
Таким образом,
Пример 4. Интеграл вдоль кривой на плоскости, заданной в полярных координатах.
Вычислить интеграл
вдоль правого лепестка лемнискаты .
На чертеже выше изображена лемниската. Вдоль её правого лепестка нужно проводить интегрирование. Найдём дифференциал дуги для кривой :
.
Следующий шаг — определение пределов интегрирования по полярному углу. Ясно, что должно выполняться неравенство , а потому
.
Вычисляем интеграл:
Пример 5. Интеграл вдоль кривой в пространстве.
Вычислить интеграл
вдоль витка винтовой линии , соответствующего пределам изменения параметра .
Вычисляем дифференциал дуги:
.
Подставляем в интеграл:
.
Примеры вычисления поверхностных интегралов первого рода
Пример 6. Интеграл по поверхности, заданной явно.
Вычислить интеграл
по поверхности тела .
Поверхность интегрирования состоит из двух частей: части плоскости , которую обозначим и поверхности , заданной
уравнением . Эта поверхность представляет собой верхнюю половину конуса второго порядка. Проекция той её части,
по которой проводится интегрирование, на плоскость представляет собой круг, ограниченный окружностью .
Запишем элемент поверхности:
.
Таким образом, поверхностный интеграл сводится к следующему двойному:
где — круг . Такой интеграл проще всего вычислять в полярных координатах:
.
Теперь интегрируем по плоскости . Это совсем простое интегрирование, так как поверхностный интеграл сразу превращается
в двойной без каких-либо дополнительных вычислений. Он будет отличаться только множителем от только что вычисленного.
Окончательный ответ получается суммированием двух вычисленных интегралов:
.
Пример 7. Интеграл по сфере.
Вычислить интеграл
по верхней полусфере .
Можно выразить явно, например, аппликату из уравнения сферы и проводить вычисления дальше, но при интегрировании по сфере удобно использовать
сферические координаты. Тем более элемент поверхности сферы в этом случае хорошо известен:
.
Осталось только выполнить замену в подынтегральной функции:
.
Пример 7. Интеграл по параметрически заданной поверхности.
Вычислить интеграл
по части поверхности геликоида , отвечающей границам изменения параметров .
Поверхность интегрирования задана параметрически, поэтому для написания элемента поверхности нужно предварительно вычислить три якобиана:
.
Таким образом, элемент поверхности
.
Следовательно, поверхностный интеграл сводится к следующему двойному:
.
Детали вычисления определённого интеграла здесь опущены: они не имеют отношения к теме. Тем более, сам интеграл достаточно простой.
corum.mephist.ru
6. Криволинейный интеграл первого рода
Пусть
на плоскости дана непрерывная простая
спрямляемая кривая  ,
вдоль которой расположены массы, причём
известна их линейная плотность
,
вдоль которой расположены массы, причём
известна их линейная плотность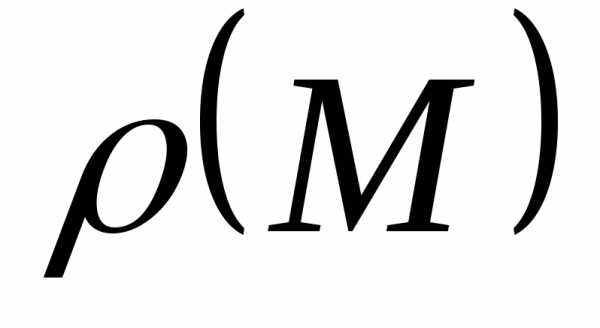 во всех точках
во всех точках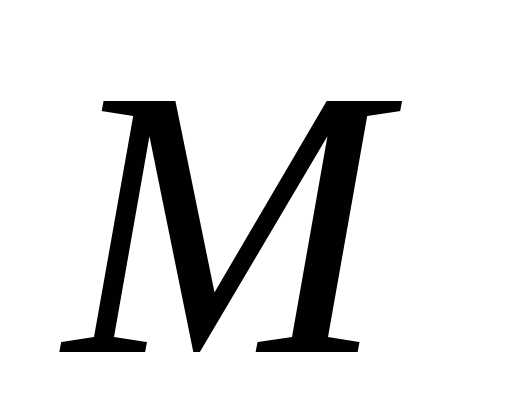 кривой. Требуется определить массу
кривой. Требуется определить массу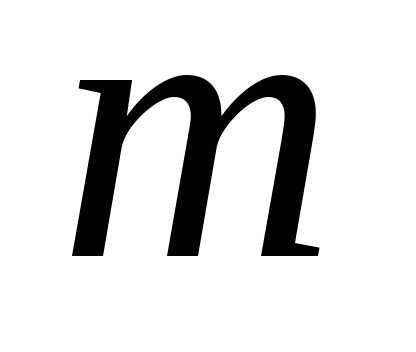 всей кривой.
всей кривой.
С
этой целью разобьём кривую на отрезки
точками
,
причем
начальная точка кривой,
начальная точка кривой, 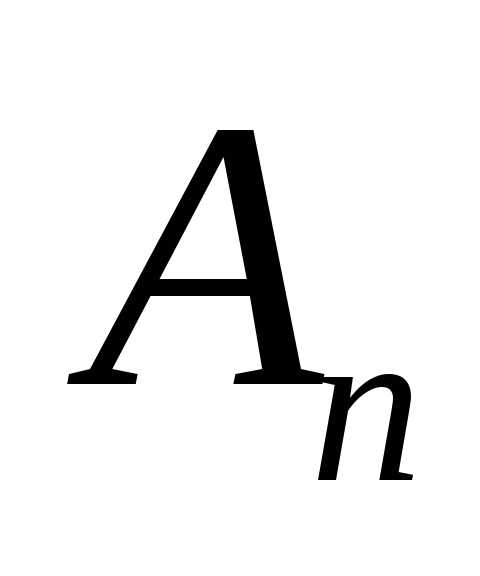
конечная точка;
длина
конечная точка;
длина 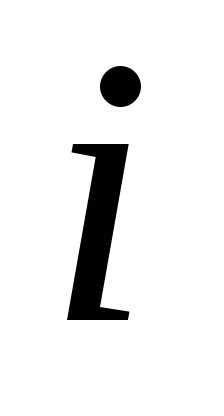 -го
отрезка кривой. Фиксируем произвольно
точку
-го
отрезка кривой. Фиксируем произвольно
точку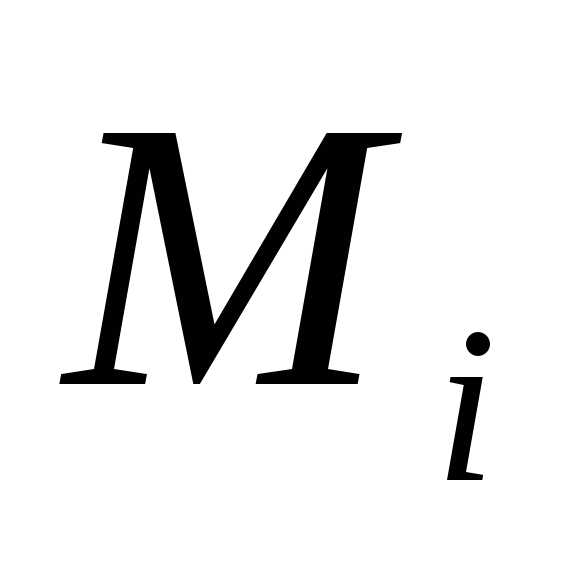 на отрезке
на отрезке и будем считать, что плотность
и будем считать, что плотность сохраняет свое значение во всех точках
отрезка.
сохраняет свое значение во всех точках
отрезка.
Тогда
масса отрезка  ,
,
а масса всей кривой
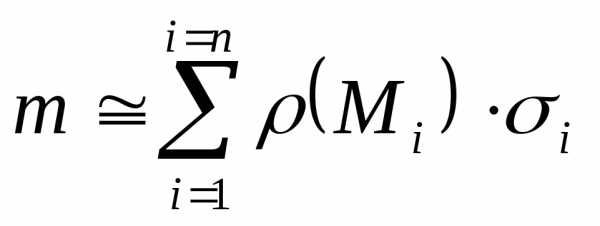
Погрешность
последнего выражения будет стремиться
к нулю, если длины всех отрезков  стремятся к нулю. Обозначив через
стремятся к нулю. Обозначив через наибольшую из длин
наибольшую из длин ,
точное значение массы кривой получим
в результате предельного перехода:
,
точное значение массы кривой получим
в результате предельного перехода:
.
Отвлекаясь
от задачи о массе кривой, можно рассмотреть
функцию точки
,
заданную на кривой ,
и повторив рассуждения, аналогичные
проведенным выше, получить интегральную
сумму:
,
и повторив рассуждения, аналогичные
проведенным выше, получить интегральную
сумму:
. (6.1)
Определение. Конечный
предел
,
если он существует для любого разбиения
кривой на отрезки
на отрезки и не зависит от выбора точек,
называется криволинейным интегралом
первого рода от функции
и не зависит от выбора точек,
называется криволинейным интегралом
первого рода от функции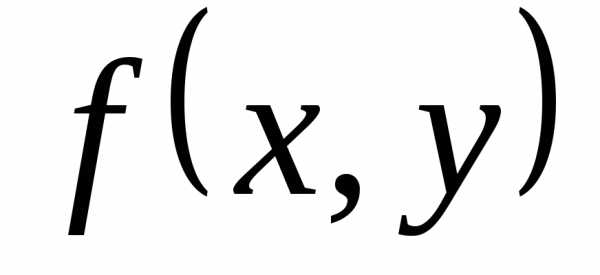 по кривой
по кривой и обозначается символом
и обозначается символом
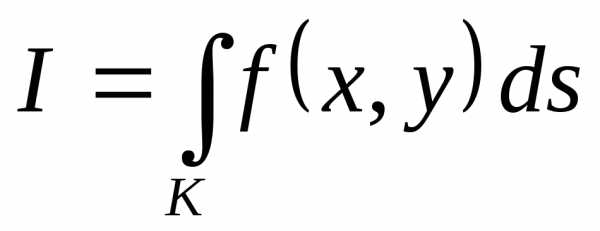 . (6.2)
. (6.2)
(Здесь  есть длина дуги кривой, а
есть длина дуги кривой, а
«дифференциал дуги».)
«дифференциал дуги».)
Криволинейный
интеграл первого рода по пространственной
кривой  определяется аналогично:
определяется аналогично:
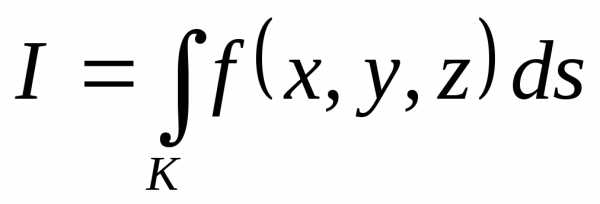 . (6.3)
. (6.3)
Свойства криволинейного интеграла первого рода
Криволинейный интеграл первого рода не зависит от выбора направления на пути интегрирования:
;
2. ;
3. .
Если путь интегрирования
 разбит на части,
то
разбит на части,
то
.
Рис. 6.1
Дифференциал
дуги  приближенно
можно выразить в соответствии с теоремой
Пифагора (рис. 6.1):
приближенно
можно выразить в соответствии с теоремой
Пифагора (рис. 6.1):
для
случая кривой  ,
принадлежащей плоскости, или
,
принадлежащей плоскости, или
для трёхмерного случая. При эти выражения становятся точными.
Пусть
кривая  задана в параметрической форме:
задана в параметрической форме:

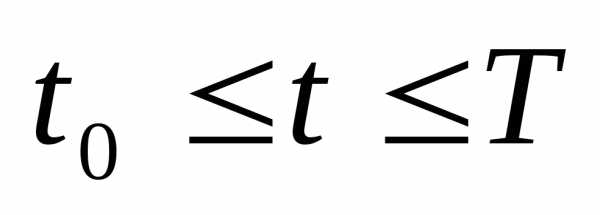 ,
,
причём,
функции  и
и непрерывны вместе со своими производными
непрерывны вместе со своими производными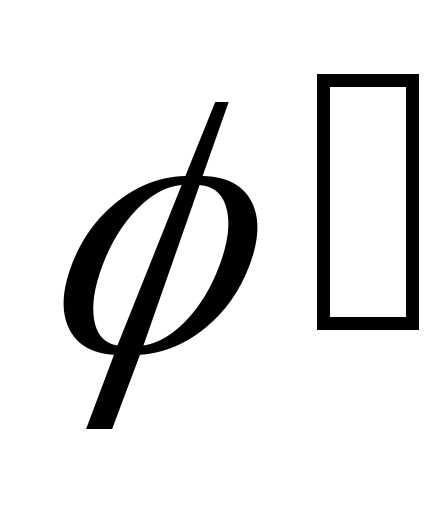 и,
то есть кривая
и,
то есть кривая
гладкая или кусочно-гладкая. Если кратных
точек на кривой нет, она спрямляемая.
Криволинейный интеграл (6.2) существует,
если подынтегральная функция
гладкая или кусочно-гладкая. Если кратных
точек на кривой нет, она спрямляемая.
Криволинейный интеграл (6.2) существует,
если подынтегральная функция 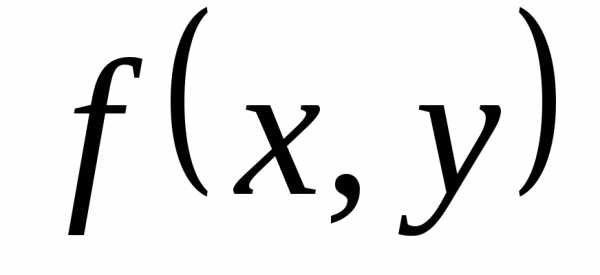
непрерывная.
непрерывная.
Дифференциал дуги в этом случае имеет следующий вид:
.
Подставив в интеграл (6.2), получим:
. (6.4)
В
случае кривой  ,
заданной явным уравнением в декартовых
координатах
,
заданной явным уравнением в декартовых
координатах
,
формула (6.2) принимает вид:
. (6.5)
Пусть
кривая  задана в полярных координатах:
задана в полярных координатах:
,
тогда:
,
.
Следовательно, дифференциал дуги
,
а интеграл (6.2) принимает вид
.
Пример 6.1. Вычислить интеграл:
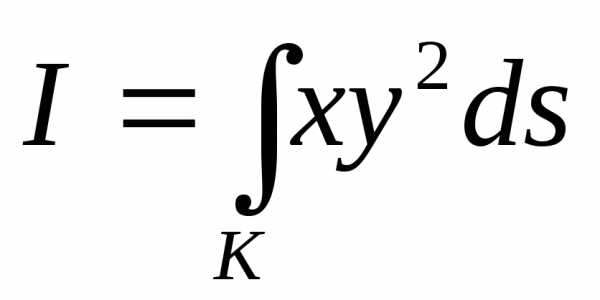 ,
,
если 
отрезок прямой между точками
отрезок прямой между точками 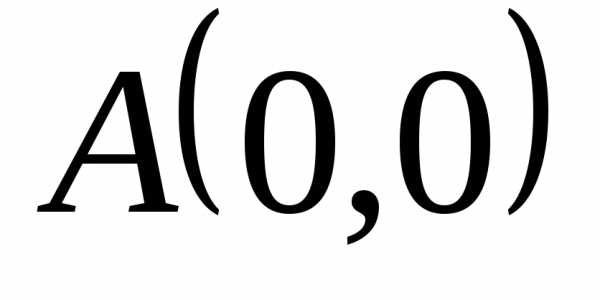 и
и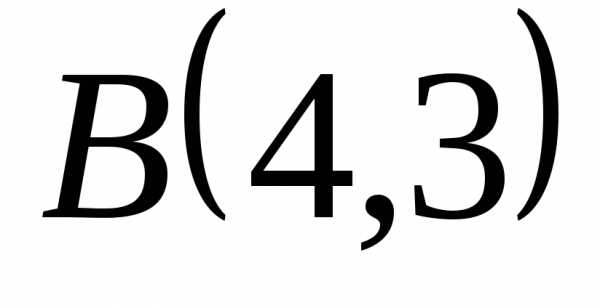 .
.
Решение.
Направляющий вектор прямой 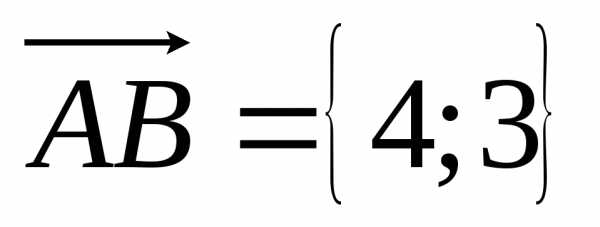 .
.
Уравнение прямой
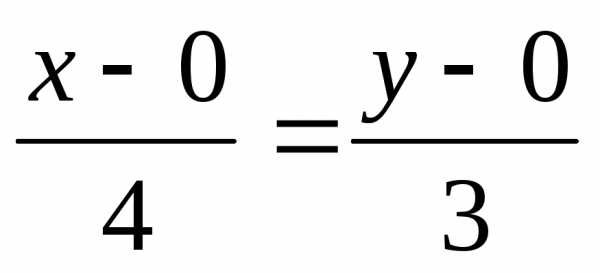 или
или 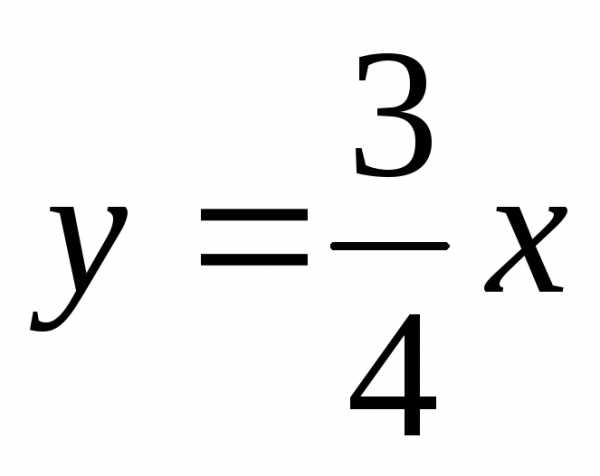 .
.
Дифференциал дуги
.
.
Пример 6.2. Вычислить интеграл
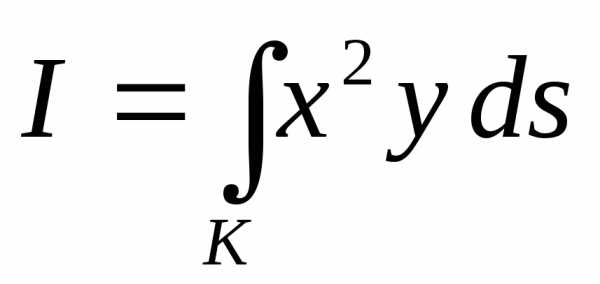 ,
,
если  есть дуга окружности
есть дуга окружности
,
принадлежащая первой четверти (рис. 6.2).
Решение.
.
Рис. 6.2
Подставим найденные выражения в интеграл и вычислим его:
.
Пример 6.3. Вычислить длину первой арки циклоиды:
.
(Циклоида представляет собой траекторию точки катящегося колеса, изображенную на рис. 6.3.)
Решение. Длину кривой можно найти, вычислив криволинейный интеграл
.

Рис. 6.3
Подставив в интеграл производные
получим:
.
Пример 6.4. Вычислить длину винтовой линии, заданной уравнениями
.
Решение.
.
.
Пример 6.5. Вычислить длину спирали Архимеда (рис.6.4).
от 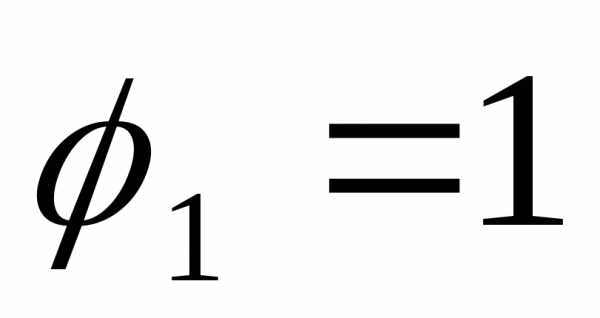 до
до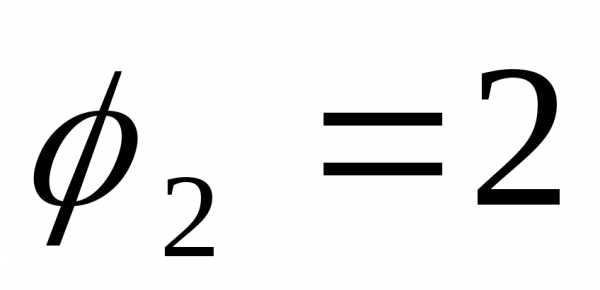 .
.
(Угол  здесь выражен в радианах).
здесь выражен в радианах).
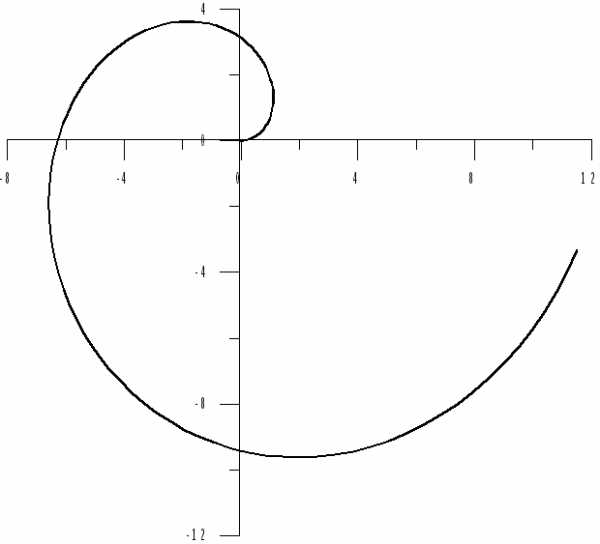
Рис. 6.4
Решение.

.
Первый интеграл в последней строке совпадает с исходным интегралом. Перенесём его влево и разделим на 2 полученный результат:
.
Решить самостоятельно: [1] № 3770, 3772, 3774, 3775, 3777.
studfiles.net
Вычисление криволинейного интеграла
Криволинейные интегралы являются обобщением определенного интеграла в случае, когда область интегрирования это некоторая кривая.
Криволинейный интеграл первого рода
Пускай на прямой AB задано функцию $f\left(x,y\right).$ Разбив эту кривую на n частей и выбрав на каждой из частей произвольную точку $M_k\left({\xi }_k,{\eta }_k\right),$ найдем значение $f\left({\xi }_k,{\eta }_k\right),$ и составим интегральную сумму
$I_n=\sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle l_k,}$где $\vartriangle l_k-$длина k-ой части кривой.
Найдем
Определение
Если при $\lambda \to 0\ \left(\lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}\ }\right)$ эта граница существует и не зависит от способа разбития кривой AB на части и выбора точки $M_k$, то его называют криволинейным интегралом первого рода от функции $f\left(x,y\right)$ по кривой AB и обозначают
\[\int\limits_{AB}{f\left(x,y\right)dl.}\]Значит,
\[\int\limits_{AB}{f\left(x,y\right)dl=}{\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle l_k}\ }\]В этом случае функцию $f\left(x,y\right)$ называют интегрированной вдоль кривой AB, а кривую AB — контуром интегрирования, A — начальная, а B — конечной точками интегрирования.
Свойства интеграла первого рода:
- $\int\nolimits_{AB}{f\left(x,y\right)dl=\int\nolimits_{BA}{f\left(x,y\right)dl.}}$
- Если $f\left(x,y\right)\ge 0$ на отрезке AB, то криволинейный интеграл $\int\limits_{AB}{f\left(x,y\right)dl}$ не отрицательный на отрезке AB.
- $\int\nolimits_{AB}{C\ f\left(x,y\right)dl=C\ \int\nolimits_{AB}{f\left(x,y\right)dl.}}$
- $\int\nolimits_{AB}{\left(f\left(x,y\right)\mp g\left(x,y\right)\right)dl=\int\nolimits_{AB}{f\left(x,y\right)dl\mp \int\nolimits_{AB}{g\left(x,y\right)dl.}}}$
- Если кривую AB разбить точкой C на части, то \[\int\limits_{AB}{f\left(x,y\right)dl=\int\limits_{AС}{f\left(x,y\right)dl+\int\limits_{СB}{f\left(x,y\right)dl.\ }}}\]
Криволинейный интеграл второго рода
Пускай на плоской кривой AB задано непрерывную функцию $f\left(x,y\right).$ Разобьем кривую AB точками $A=A0, A1, A2, \dots , An=B$ на $n$ частей. На каждом промежутке $Ak-1Ak$ выберем произвольную точку $M_k\left({\xi }_k,{\eta }_k\right)$ и составим сумму $\sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k},$ где $\vartriangle x_k-$проекция вектора $\overline{A_{k-1}A_k}$ на ось Ox. Эту сумму называют интегральной. Найдем ее границу:
\[{\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k,\ \ \ \ \lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}.\ }}\ }\]Определение
Если при $\lambda \to 0\ \left(\lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}\ }\right)$ граница интегрированной суммы существует и не зависит от способа разбития кривой AB на части и от выбора точки Mk , то его называют криволинейным интегралом от функции $f\left(x,y\right)$ по абсциссе $x$ вдоль кривой AB и обозначают $\int\nolimits_{AB}{f\left(x,y\right)dx.}$
Таким образом
\[\int\limits_{AB}{f\left(x,y\right)dx={\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k}\ }.}\]Свойства криволинейного интеграла второго рода:
- $\int\nolimits_{AB}{f\left(x,y\right)dx=-\int\nolimits_{BA}{f\left(x,y\right)dx.}}$
- $\int\nolimits_{AB}{\left(f\left(x,y\right)\mp g\left(x,y\right)\right)dx=\int\nolimits_{AB}{f\left(x,y\right)dx\mp \int\nolimits_{AB}{g\left(x,y\right)dx.}}}$
- $\int\nolimits_{AB}{C\ f\left(x,y\right)dx=C\ \int\nolimits_{AB}{f\left(x,y\right)dx.}}$
- $\int\nolimits_{AB}{f\left(x,y\right)dx=\int\nolimits_{AС}{f\left(x,y\right)dx+\int\nolimits_{СB}{f\left(x,y\right)dx.\ }}}$
- $\int\nolimits_{AB}{f\left(x,y\right)dx=0,}$ когда $AB\parallel OY; \ \ \int\nolimits_{AB}{f\left(x,y\right)dy=0,}$ когда $AB\parallel OX$
Условия независимости криволинейного интеграла от пути интегрирования.
Теорема 1
Для того, что б в связной области D, криволинейный интеграл $\int\limits_{AB}{P\left(x,y\right)dx+Q\left(x,y\right)dy}$ независим от пути AB. Необходимо и достаточно, что бы интеграл по замкнутому контуру в этой области равнялся нулю:
\[\int\limits_{AB}{P\left(x,y\right)dx+Q\left(x,y\right)dy}=0.\]Пример
Вычислить интеграл
$I=\ \int\limits_{AB}{2xy\ dx+x^2dy}$ от т. А(0,0) до точки В(1,1).
- Найдем по прямой$\ y=x$, $dy=dx$ \[I=\ \int\limits^1_0{2xx\ dx+x^2dx=}\int\limits^1_0{3x^2dx=}{\left.\frac{3x^3}{3}\right|}^1_0=1.\]
- Найдем по ветке параболы $y=x^2$, $dy=2x\ dx$ \[I=\ \int\limits^1_0{2x^3\ dx+{2x}^3dx=}\int\limits^1_0{4x^3dx=}{\left.\frac{4x^4}{4}\right|}^1_0=1.\]
- Найдем по контуру ОСВ: \[I=\int\limits_{OCB}{P\ dx+Qdy=\int\limits_{OCB}{2xy\ dx+x^2dy=\int\limits_{OC}{\left(2xy\ dx+x^2dy\right)}+}}+\int\limits_{CB}{\left(2xy\ dx+x^2dy\right)}\]
- Найдем для ОС — $y=0$, $dy=0$ и подставим в формулу: \[\int\limits_{OC}{2xy\ dx+x^2dy=0}\]
- Найдем для СВ — $x=1,\ \ dx=0$ и подставим в формулу: \[\int\limits_{CB}{2xy\ dx+x^2dy=1\int\limits^1_0{dy}=1}.\]
Пример хорошо показывает независимость криволинейного интеграла от пути интегрирования. В данном примере мы выбрали три разных пути, и при вычислении интеграла во всех случаях получили один и тот же ответ.
Для работы с криволинейными интегралами не менее важной есть следующая теорема.
Теорема 2
Если в односвязной области D функции $P\left(x,y\right)$ и $Q\left(x,y\right)$ и их производные $\frac{\partial P}{\partial y}$ и $\frac{\partial Q}{\partial x}$ непрерывные, то для того что бы интеграл по замкнутому контуру в этой области был равен нулю необходимо и достаточно что бы выполнялось равенство:
$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$во всех точках этой области.
Связь между криволинейным интегралом первого и второго рода
С помощью определения интегралов первого и второго рода и определения интеграла, очень просто показать связь между криволинейным интегралом первого и криволинейным интегралом второго рода.
От криволинейного интеграла второго рода очень просто перейти до криволинейного интеграла первого рода. Переход между ними выражается формулой:
\[\int\limits_{AB}{P\left(x,y\right)dx+Q\left(x,y\right)dy}=\int\limits_{AB}{Pdl{cos \alpha \ }+Qdl{cos \beta \ }}\]spravochnick.ru
Вычисление криволинейного интеграла первого рода.
Параметризуем дугу L: AB x = x(t), y = y(t), z =z(t). Пустьt0 соответствует точкеA, аt1 соответствует точкеB. Тогда криволинейный интеграл первого рода сводится к определенному интегралу (- известная из 1 семестра формула для вычисления дифференциала длины дуги):
Пример.Вычислить массу одного витка однородной (плотность равнаk)винтовой линии:.
.
Криволинейный интеграл 2 рода. Задача о работе силы.
Организуем разбиение области- дуги ABна элементы – элементарные дуги
 так,
чтобы эти элементы не имели общих
внутренних точек и
так,
чтобы эти элементы не имели общих
внутренних точек и (условие
А)
(условие
А)Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции

Построим интегральную сумму
 ,
где
,
где  вектор, направленный по хорде, стягивающей
-дугу
вектор, направленный по хорде, стягивающей
-дугу  .
.Переходя к пределу при условии (условие В), получим криволинейный интеграл второго рода как предел интегральных сумм (и работу силы):
. Часто обозначают
Теорема существования.
Пусть вектор — функция непрерывна на кусочно-гладкой дугеL12. Тогда криволинейный интеграл второго рода существует как предел интегральных сумм.
.
Замечание.Предел этот не зависит от
способа выбора разбиения, лишь бы выполнялось условие А
выбора «отмеченных точек» на элементах разбиения,
способа измельчения разбиения, лишь бы выполнялось условие В
Свойства криволинейного интеграла 2 рода.
1. Линейностьа) свойство суперпозиции
б) свойство однородности .
Доказательство. Запишем интегральные суммы для интегралов в левых частях равенств. Так как в интегральной сумме число слагаемых конечно, используя свойство скалярного произведения, перейдем к интегральным суммам для правых частей равенств. Затем перейдем к пределу, по теореме о предельном переходе в равенстве получим желаемый результат.
2. Аддитивность. Если, то 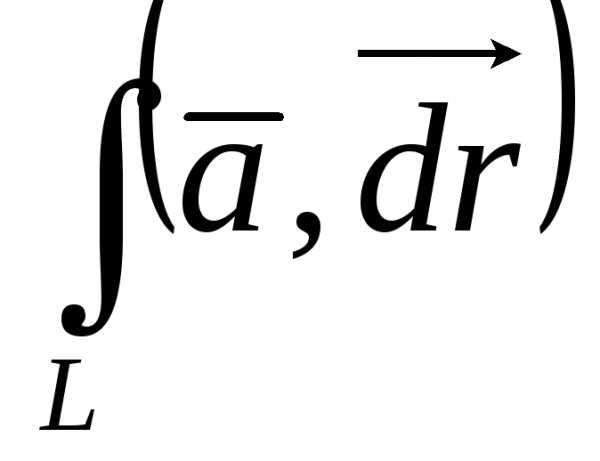 =
=
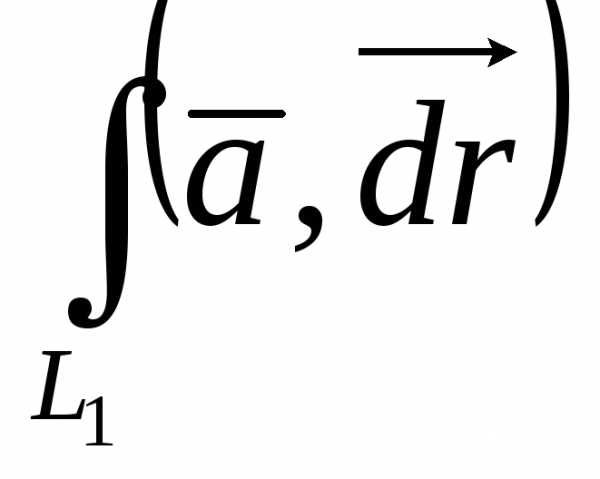 +
+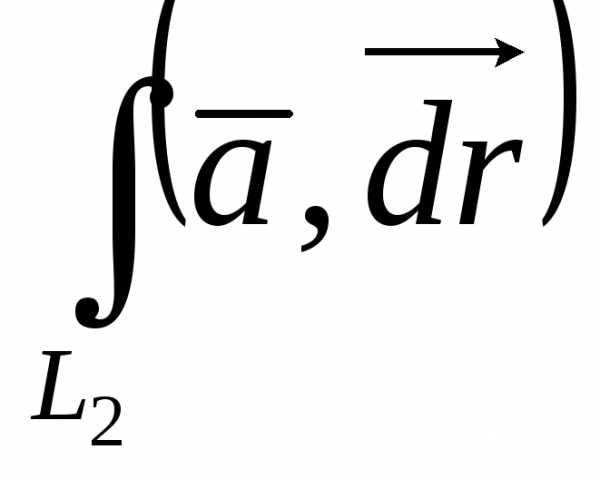 .
.
Доказательство. Выберем разбиение области Lтак, чтобы ни один из элементов разбиения ( первоначально и при измельчении разбиения) не содержал одновременно как элементыL1, так и элементыL2. Это можно сделать по теореме существования (замечание к теореме). Далее проводится доказательство через интегральные суммы, как в п.1.
3. Ориентируемость.
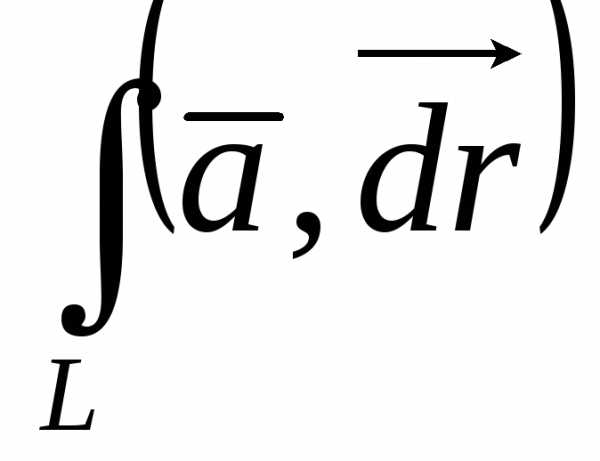 =
—
=
—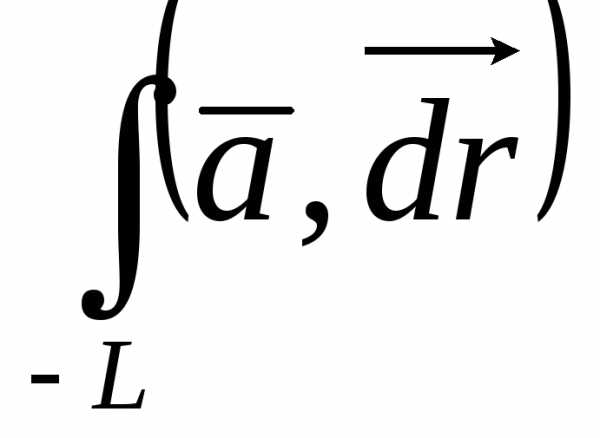
Доказательство.
Интеграл по дуге –L, т..е.
в отрицательном направлении обхода
дуги есть предел интегральных сумм, в
слагаемых которых вместо  стоит
(
стоит
( ).
Вынося «минус» из скалярного произведения
и из суммы конечного числа слагаемых,
переходя к пределу, получим требуемый
результат.
).
Вынося «минус» из скалярного произведения
и из суммы конечного числа слагаемых,
переходя к пределу, получим требуемый
результат.
Заметим, что свойство ориентируемости в криволинейном интеграле первого рода отсутствует. Зато в криволинейном интеграле второго рода отсутствуют свойства интегрирования неравенств, теорема об оценке и теорема о среднем, которые есть в криволинейном интеграле первого рода.
studfiles.net
21.1. Криволинейные интегралы первого рода
Рассмотрим пространственную кусочно-гладкую кривую, ограниченную точкамиИ(рис. 21.1), и определенную на ней непрерывную функцию Где- точка кривой. ДугуРазобьем точками
НаЭлементарных дуг
Длины которых обозначим соответственно черезА
Наибольшую из этих длин-через.На каждой из элементарных дугВыберем произвольно
Одну точкуИ составим сумму
(21.1)
Называемую интегральной суммой для функции По длине дуги кривой Криволинейным интегралом первого родаили криволинейным интегралом по дуге кривойОт функцииНазывается предел интеграль — Рис — 21.1
Ной суммы (21.1) при
На кривойЦеликом лежащей на плоскостиФункцияОт координаты не зависит, поэтому по определению имеем
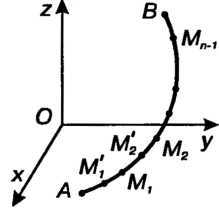
Если подынтегральную функциюРассматривать как линейную
Плотность кривойТо криволинейный интеграл первого рода представляет собой массу этой кривой.
Основные свойства криволинейного интеграла первого рода следующие.
1. Криволинейный интеграл первого рода не зависит от направления пути интегрирования:
4. Если йуть интегрированияРазбит на части, то
Вычисление 1фиволинейного интеграла первого рода сводится к вычислению определенного интеграла.
Если пространственная криваяЗадана параметрическими уравнениями
, то
(21.2)
Если криваяЛежит в плоскости, то
(21.3)
В частности, для плоской кривой, заданной уравнениемИмеем
(21.4)
Если плоская кривая задана уравнениемВ полярных
Координатах, то
(21.5)
Если кривая задана уравнением, то криволинейный интеграл
Вычисляется по формуле
(21.6)
Пример 21.1. Вычислить криволинейный интеграл, где
— дуга кривойМежду точками, для которых
Поскольку,И на дуге кривойФункция
, то по формуле (21.4) находим
Пример 21.2. ВычислитьГде- дуга кривой
Между точками, для которых
Применяем формулу (2J.6). В данном случае
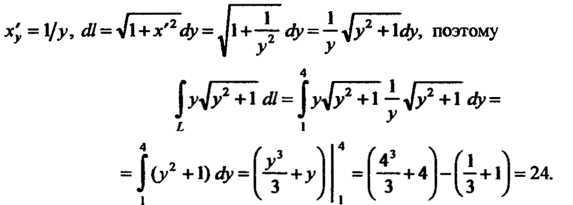
Пр имер 21.3. Вычислить криволинейный интегралГде-
Контур треугольника(рис. 21.2) с вершинами
В соответствии со свойством 4) криволинейного интегра первого рода имеем
На отрезкеПоэтому
На отрезкеНа отрезке
Принимая во внимание свойство 1) криволинейного интеграла, используя формулы (21.4) и (21.6), получаем
Пример 21.4. ВычислитьГде- лепесток лемнискаты
Расположенный в первом координатном углу.
ЛинияЗадана уравнением в полярных координатах, поэтому здесь целесообразно воспользоватьсяформулой (21.S).
Так какТо
Заметив еще, чтоТ. е.По формуле (21.5) получим
Пример 21.5. ВычислитьГде- отрезок прямой
Между точками
Составим сначала уравнения прямой, проходящей через точкиИ
Или
Таким образом, получаем параметрические уравнения прямой:
ТочкаПробегает отрезок, когдаИзменяется отДо 1, т. е.
Так какТо
По формуле (21.2) находим
Пример 21.6. ВычислитьГде-дуга винтовой линии
Отраниченной точками, для которых Применяем формулу (21.2). Поскольку
И
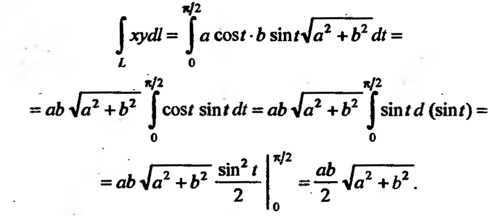
| < Предыдущая | Следующая > |
|---|
matica.org.ua

 разбит на части,
то
разбит на части,
то так,
чтобы эти элементы не имели общих
внутренних точек и
так,
чтобы эти элементы не имели общих
внутренних точек и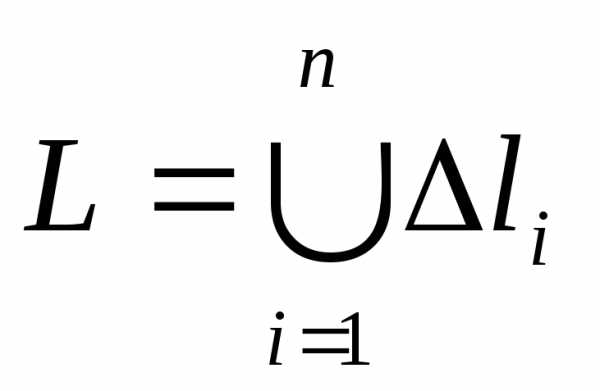 (условие
А)
(условие
А)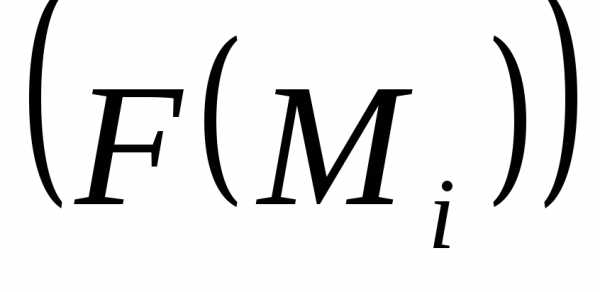
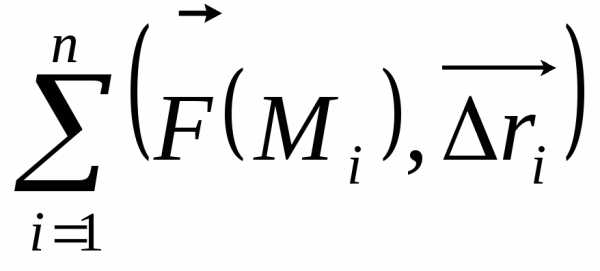 ,
где
,
где 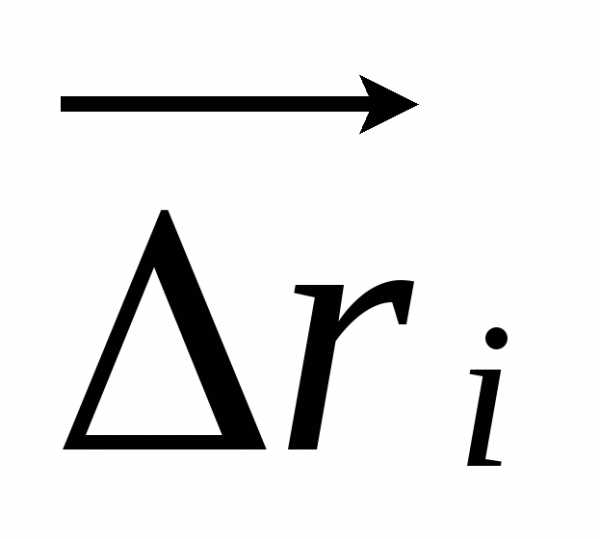 вектор, направленный по хорде, стягивающей
-дугу
вектор, направленный по хорде, стягивающей
-дугу  .
.