Урок решения задач по теме «Закон Ома для участка цепи, последовательное и параллельное соединения»
Разделы: Физика
Цель урока: Закрепить изученный материал путем решения задач.
Задачи:
Образовательные:
- Научить учащихся решать задачи на последовательное и параллельное соединение проводников;
- Углубить и расширить знания о данных видах соединения проводников;
- Научить определять силу тока, напряжение, сопротивление при последовательном и параллельном соедини проводников;
- Научить решать задачи на смешанное соединение проводников;
- Научить учащихся разбираться в схемах электрических цепей.
Воспитательные:
- Развить личные качества учащихся: аккуратность, внимание, усидчивость;
- Воспитывать культуру общения при работе в группах.
Развивающие:
- Продолжить развитие навыков решения задач на данную тему;
- Продолжить развитие умений анализировать условия задач и ответов, умений делать выводы, обобщения;
- Продолжить развитие памяти, творческих способностей.
План урока
| № | Этап | Время | Метод |
| Организационный момент | 2 мин | Словесный | |
| I | Актуализация знаний | 5 мин | Письменная работа в парах |
| II | Вводная часть | 2 мин | Слово учителя, опрос учащихся |
| III | Решение задач | 45-50 мин | Работа учителя, учащихся у доски |
| IV | Работа учащихся в группах | 20 мин | Групповой работы, устный, письменный |
| V | Итог урока | 1-2 мин |
Оформление класса: Проектор с экраном, доска с мелом. Раздаточный материал.
Слайд 1 включен в начале урока. Урок начинается с физического диктанта.
I. Актуализация знаний.
На слайде физический диктант. (Слайд 2). Учащимся выдается таблица для заполнения.
1. Заполнить двенадцать ячеек таблицы на карточке:
| Ученый | Физическая величина | Формула | Единица измерения |
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| Выполнил ______________ Проверил __________ Оценка__________ | |||
2. После заполнения таблиц учащиеся меняют карточками с соседом по парте, проверяют вместе с учителем и выставляют оценку:
| Кол-во ошибок | 1 | 2-3 | 4-6 | 7 и более |
| Оценка | 5 | 4 | 3 | 2 |
II. Вводное слово.
Запишите тему урока. (Слайд 4).
Для этого вспомним формулы и законы, которые нам пригодятся при решении задач.
III. Решение задач.
(3 ученика выходят к доске и записывают: первый закон Ома и выражает и него напряжение и сопротивление; второй – формулы справедливые для последовательного соединения; третий – формулы справедливые для последовательного соединения).
Задача 1. Для начала решим устную задачу на запоминание закона Ома. (Слайд 5)
a) U = 20B,R=10Om,I-?
б) I=10A,R = 5Om, R-?
в) I = 5A,U=15B,R-?
Ответ: а) I = 2А; б) U= 50 Ом; в) R = 3 Ом.
Задача 2. (Решает учитель с использованием презентации) Слайд 6.
Рассчитать силу тока, проходящую по медному проводу длиной 100м, площадью поперечного сечения 0,5мм2, если к концам провода приложено напряжение 6,8B.
Дано:
I=100м
S=0,5мм2
U=6,8В
I-?
Решение:
Ответ: Сила тока равна 2А.
Вопросы: Что известно из условия
задачи? Какую величину необходимо определить? По
какому закону будем определять силу тока? Какие
величины нам неизвестны для нахождения силы тока
и как их найти? ( – берется из таблицы). Теперь найдем
R и полученное значение подставим в формулу
для нахождения силы тока.
Задача 3. (Решает у доски сильный ученик) Условия задачи Слайд 7.
В электрическую цепь включены последовательно резистор сопротивлением 5 Ом и две электрические лампы сопротивлением 500 Ом. Определите общее сопротивление проводника.
Дано:
RAB=5 Ом
RBC=500 Ом
RCD=500 Ом
RAD-?
Решение:
Ответ: Общее сопротивление проводника равно 1005 Ом.
Вопросы: Какие элементы цепи нам даны? Как найти общее сопротивление?
Задача 4. (Класс делится на 2 группы, каждая из которой решает задачу своим способом (одни находя силу тока используя закон Ома, вторые используя формулу параллельного соединения). Затем по одному представителю пишут решения на доске) Условия задачи Слайд 8.
Два резистора сопротивлением r 1 = 5 Ом и r2= 30 Ом включены, как показано на рисунке, к зажимам источника тока напряжением 6В. Найдите силу тока на всех участках цепи.
Дано:
r1=5 Ом
r2=30 Ом
U=6B
I0-?
Решение:
Ответ: Сила тока на всех участках цепи равна 1,4 А.
Второй способ решения данной задачи:
Дано:
r1=5 Ом
r2=30 Ом
U=6B
I0-?
Решение:
Ответ: Сила тока на всех участках цепи равна 1,4А.
Вопросы: Какой тип соединения рассматривается в задаче? Что известно из условия? Какие величины необходимо найти? По какой формуле будем находить общий ток в цепи? Какая величина нам неизвестна при нахождении силы тока и как ее найти?
Задача 5. (Решает ученик, можно вызвать два ученика по очереди). Определите полное сопротивление цепи и токи в каждом проводнике, если проводники соединены так, как показано на рисунке, а r1=1 Ом, r2=2 Ом, r3= 3 Ом, UAC = 11В. Условие задачи Слайд 9.
Дано:
r1=1 Ом
r2=2 Ом
r3=3 Ом
UAB=11B
RAC-?
I1-?
I2-?
I3-?
Решение:
Ответ:
Вопросы: Какие типы соединения изображены на рисунке? Что нужно определить? Как найти полное сопротивление и величины в него входящие? Как найти силу тока в цепи? Как определить I1 и 12? Как определить UBC?
Задача 6. Условия задачи Слайд 10. (Вопросы 1,2,5 решаются устно. 3,4 – два ученика).
- Какому значению силы тока и напряжения соответствует точка А?
- Какому значению силы тока и напряжения соответствует точка В?
- Найдите сопротивление в точке А и в точке В.
- Найдите по графику силу тока в проводнике при напряжении 8 В и вычислите сопротивление в этом случае.
- Какой вывод можно проделать по результатам задачи?
Ответ:
- Сила тока = 0,4 А, напряжение – 4В.
- Сила тока = 0,6 А, напряжение – 6В.
- Сопротивление в т.А – 10 Ом, в т.В – 10 Ом.
- Сила тока = 0,8А, сопротивление – 10 Ом.
- При изменении силы тока и напряжения на одинаковую величину, сопротивление остается постоянным.
IV. Самостоятельная работа в группах.
Учащиеся делятся на 4 группы и каждой группе дается карточка с заданием.
Учитель объясняет критерии выставления оценок:
Во время работы в группах ведется наблюдение за более и менее активными участниками группы. Соответственно это будет влиять на более или менее высокую оценку при проверке записей в тетради, также будет учитываться уровень сложности решенных задач. Тетради с записями сдаются в конце урока. Время для решения задач ограниченное.
Задание 1. Слайд 11. (8 мин.)
Вопросы к карточкам:
- Перечислите все элементы цепи.
- Какие виды соединения используются?
- Рассчитайте напряжение на лампе.
- Рассчитайте напряжение на реостате.
- Рассчитайте силу тока на всем участке цепи.
Задание 2. Слайд 12. (4 мин.)
Определить общее сопротивление в цепи.
R1 = 2 Ом, R2 = 102 Ом, R 3 = 15 Ом, R4 = 4 Ом.
Задание 3. Слайд 13. (3 мин.)
Определите силу тока I при заданных U и R.
| Группа | R, Ом | U, В | I, А |
| I | 2 | 55 | ? |
| II | 14,2 | 87,4 | ? |
| III | 21 | 100 | ? |
| IV | 0,16 | 0,28 | ? |
Задание 4. Слайд 14. (5 мин)
Моток проволоки имеет сопротивление R и длину l .
Вычислить площадь поперечного сечения S.
| Группа | Материал | Параметры | ||
| Сопротивление | Длина проводника | Удельное сопротивление | ||
| R, Ом | l, мм2 | p, Ом·мм2/м | ||
| I | Медь | 0,83 | 33,9 | 1,7·10-2 |
| II | Алюминий | 16,1 | 83,1 | 2,8·10-2 |
| III | Серебро | 0,39 | 0,234 | 1,6·10-2 |
| IV | Сталь | 23,2 | 3,06 | 12·10-2 |
После выполнения заданий группами, тетради сдаются учителю.
V. Итог урока.
На сегодня все. Мы с вами научились решать задачи на последовательное и параллельное соединение проводников, закрепили знания о законе Ома для участка цепи.
Домашнее задание. Повторить все формулы и физические величины.
2.04.2010
urok.1sept.ru
Решение задач на расчет электрического сопротивления с помощью моделей
Разделы: Физика
Цели: обучающая: систематизировать знания и умения учащихся решать задачи ан расчет эквивалентных сопротивлений с помощью моделей, каркасов и т.д.
Развивающая: развитие навыков логического мышления абстрактного мышления, умений заменять схемы эквивалентности, упрощать расчет схем.
Воспитательная: воспитание чувства ответственности, самостоятельности , необходимости навыков приобретенных на уроке в будущем
Оборудование: проволочный каркас куба, тетраэдера, сетки бесконечной цепочки сопротивлений.
ХОД УРОКА
Актуализация:
1. Учитель: “Вспомним последовательное соединение сопротивлений”.
Учащиеся на доске зарисовывают схему.
и записывают
Rэк=n*R
Uоб=U1+U2
Yоб=Y1=Y2
Учитель: вспомним параллельное соединение сопротивлений.
Учащийся на доске зарисовывает элементарную схему:
Uоб=U1+U2
Yоб=Y1=Y2
; длядля n равных
Учитель: А теперь будем решать задачи на расчет эквивалентного сопротивления участок цепи представлен в виде геометрической фигуры, либо металлической сетки.
Задача № 1
Проволочный каркас в виде куба, рёбра которого представляют равные сопротивления R. Рассчитать эквивалентное сопротивление между точками А и В. Чтобы рассчитать эквивалентное сопротивление данного каркаса необходимо заменить эквивалентной схемой. Точки 1, 2, 3 имеют одинаковый потенциал, их можно соединить в один узел. А точки (вершины) куба 4, 5, 6 можно соединить в другой узел по той же причине. Учащиеся имеют на каждой парте такую модель. После выполнения описанных действий зарисовывают эквивалентную схему.
На участке АС эквивалентное сопротивление ; на СD ; на DB ; и окончательно для последовательного соединения сопротивлений имеем:
Задача № 2
Рассчитать RЭКВ. этого же куба, если куб включён в цепь в точках 2 и 4.
По тому же принципу потенциалы точек А и 6 равны, В и 3 равны. Учащиеся совмещают эти точки на своей модели и получают эквивалентную схему:
Расчёт эквивалентного сопротивления такой цепи прост
Задача № 3
Эта же модель куба, с включением в цепь между точками 2 и В. Учащиеся соединяют точки с равными потенциалами 1 и 3; 6 и 4. Тогда схема будет выглядеть так:
Точки 1,3 и 6,4 имеют равные потенциалы, и ток по сопротивлениям между этими точками не потечёт и схема упрощается до вида; эквивалентное сопротивление которой рассчитывается так:
Задача № 4
Равносторонняя треугольная пирамида, ребро которой имеет сопротивление R. Рассчитать эквивалентное сопротивление при включении в цепь.
Точки 3 и 4 имеют равный потенциал, поэтому по ребру 3,4 ток не потечёт. Учащиеся убирают его.
Тогда схема будет выглядеть так:
либо
Эквивалентное сопротивление рассчитывается так:
Задача № 5
Металлическая сетка с сопротивлением звена равном R. Рассчитать эквивалентное сопротивление между точками 1 и 2.
В точке 0 можно звенья отделить, тогда схема будет иметь вид:
- сопротивление одной половины симметричной по 1-2 точкам. Параллельно ей такая же ветвь, поэтому
Задача № 6
Рассчитать эквивалентное сопротивление проволочной звезды с сопротивлением каждого звена R, включённой в цепь между точками 1 и 2.
Звезда состоит из 5-и равносторонних треугольников, сопротивление каждого.
Между точками 1 и 2 один треугольник параллелен четырём, последовательно соединенным между собой
Имея опыт расчёта эквивалентного сопротивления проволочных каркасов можно приступить к расчету сопротивлений цепи, содержащий бесконечное число сопротивлений. Например:
Если отделить звено
от общей схемы, то схема не изменится, тогда можно представить ввиде
или ,
решаем данное уравнение относительно Rэкв.
Итог урока: мы научились абстрактно представлять схемы участков цепи, заменять их эквивалентными схемами, которые позволяют легко рассчитать эквивалентное сопротивление.
На дом:
Рассчитать эквивалентное сопротивление проволочного каркаса из двух окружностей с радиусами r1 и r2, r2=2r1 между точками А и В. Сопротивление единицы длинны проволоки?
Указание: Эту модель представить в виде:
21.03.2008
Поделиться страницей:urok.1sept.ru
Расчёт сопротивления электрических цепей с использованием законов последовательного и параллельного соединений
Разделы: Физика
Цели: Образовательная: систематизировать и закрепить знания учащихся о различных соединениях проводников, сформировать умения применять законы последовательного и параллельного соединений для расчёта электрических цепей, объединить знания, полученные на уроках физики и математики.
Тип урока: урок проверки и закрепления новых знаний по физике и математике.
Метод проведения урока: практический
Оборудование:
- Громов С.В. Учебник “Физики-9”;
- план урока;
- методика расчета участка электрической цепи постоянного тока;
- карточки-задания.
Приложение 1
Ход урока
Сегодня на уроке мы должны применить полученные ранее знания о законах последовательного и параллельного соединений для расчёта участка электрической цепи, а также определить степень усвоения изученного материала с помощью карточек – заданий.
Прежде чем приступить к рассмотрению электрических цепей, вспомним то, что мы уже знаем и ответим на вопросы:
1) Какие виды соединений бывают и как они
изображаются на электрических схемах?
2) Назовите законы последовательного соединения?
3) Назовите законы параллельного соединения?
4) Какая отличительная особенность параллельного
соединения?
Рассмотрим расчёт участка электрической цепи на примере следующих задач:
1. Рассчитайте общее электрическое сопротивление участка цепи?
1) Наиболее удалённые от источника элементы – это резисторы R2 и R3.
2) Объединяем эти два резистора в первый участок и рассчитываем их общее сопротивление. Резисторы R2 и R3 подключены параллельно, т.к образуют в соединении два узла, следовательно:
Ом
3) Изображаем получившуюся в результате свёртывания резисторы R2 и R3 электрическую схему:
4) Полученные в результате объединения схему с двумя резисторами группируем во второй участок и рассчитываем их общее сопротивление. Так как резисторы R1 и Rоб.1 соединены последовательно, значит:
Rоб = R1 + Rоб.1 = 4 Ом + 2 Ом = 6 Ом
Ответ: общее сопротивление резисторов на участке электрической цепи 6 Ом.
2. Рассчитайте общее электрическое сопротивление участка цепи?
1) Резисторы R1 и R2 соединены между собой последовательно:
Rоб.1 = R1 + R2 = 1 Ом + 2 Ом = 3 Ом
Изобразим полученный электрический участок цепи:
2) Резисторы R3 и R4 соединены между собой последовательно:
Rоб.2 = R3 + R4 = 3 Ом + 4 Ом = 7 Ом
Изобразим полученный электрический участок цепи:
3) Полученные в результате объединения схему с двумя резисторами группируем в третий участок и рассчитываем их общее сопротивление. Так как резисторы Rоб.1 и Rоб.2 соединены параллельно, значит:
Ом
Ответ: общее сопротивление резисторов на участке электрической цепи 2,1 Ом.
3. Выполните задания самостоятельно по карточкам (дифференцированные), воспользовавшись памяткой расчета участка электрической цепи постоянного тока:
а) Рассчитайте общее электрическое сопротивление участка цепи?
б) Рассчитайте общее электрическое сопротивление участка цепи?
в) Рассчитайте общее электрическое сопротивление участка цепи?
Сегодня на уроке мы рассмотрели различные схемы участков электрических цепей, научились рассчитывать цепи, применяя законы последовательного и параллельного соединений, а также закрепили полученные знания с помощью карточек – заданий.
17.06.2013
Поделиться страницей:urok.1sept.ru
Задачи на цепи переменного тока
В электротехнике большое количество задач посвящено цепям переменного тока. Рассмотрим примеры решения некоторых из них.
Задача 1
В сеть переменного тока включены последовательно катушка индуктивностью 3 мГн и активным сопротивлением 20 Ом и конденсатор емкостью 30 мкФ. Напряжение Uc на конденсаторе 50 В. Определите напряжение на зажимах цепи, ток в цепи, напряжение на катушке, активную и реактивную мощность.

Решение задачи начнём с определения тока в цепи, но для этого нужно сначала определить реактивное сопротивление конденсатора.
Как известно, реактивное сопротивление конденсатора зависит от частоты переменного тока (при её увеличении уменьшается, а при её уменьшении увеличивается), следовательно
Ток в цепи находим из соображения, что элементы в цепи соединены последовательно, а значит, ток на конденсаторе и катушке будет одним и тем же.
Следующим шагом мы определяем индуктивное сопротивление и напряжение катушки
Зная активное сопротивление обмотки катушки, можем определить падение напряжения на нем
Теперь, когда мы знаем напряжение на каждом из элементов, мы можем определить напряжение на зажимах цепи, которое будет равно
Активную мощность в данном случае можно определить как мощность, выделяемую на обмотке катушки
Для определения реактивной мощности необходимо для начала определить угол сдвига ϕ
Так как реактивная мощность имеет отрицательное значение, то цепь имеет емкостной характер.
Задача 2
В цепи как показано на схеме, подключены катушка, конденсатор и резисторы. Индуктивность катушки – 15 мГн, емкость конденсатора 20 мкФ, R1=10 Ом, R2=30 Ом. Напряжение источника 100 В, частота 100 Гц. Определить токи в цепи, активную, реактивную и полную мощность в цепи.
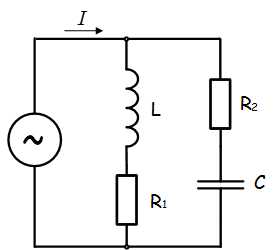
Данную задачу удобнее решать с помощью проводимостей, так как катушка и конденсатор соединены параллельно.
Тогда активная проводимость первой ветви равна
Реактивная проводимость первой ветви равна
Полная проводимость первой ветви
Аналогичный расчет произведем для второй ветви содержащей конденсатор
Полная проводимость цепи
Токи в цепи определим зная напряжение и проводимости
Коэффициент мощности определим по формуле
Активная мощность
Реактивная мощность
Полная мощность
Читайте также — расчет простых цепей постоянного тока
electroandi.ru
Примеры решения
1.1. Расчет простейших электрических цепей с помощью законов Ома и Джоуля-Ленца.
1.* Дано:
Рассчитать все токи в цепи и определить мощность, рассеиваемую на каждом резисторе.
Решение:
Эквивалентное сопротивление цепи с учетом того, что R1 и R4 соединены последовательно, а R2 и R3 параллельно, равно
;
Токи I1 и I4 находятся по закону Ома
.
Напряжение на резисторах R2 и R3 будет равно
;
Токи I2 и I3 находим также по закону Ома
;
.
Мощность, рассеиваемая в резисторах:
Мощность источника:
Суммарная мощность приемников после суммирования P1, P2 и т.д. оказывается, также равна 24,8 Вт. В этом случае говорят, что сходится баланс мощности в цепи. Последнее означает отсутствие ошибок при расчете токов.
2.* Три одинаковых резистора соединены по смешанной схеме (два в параллель и один последовательно) и потребляют от источника мощность P=100 Вт.
Определить мощность, которую будут потреблять эти резисторы от источника при параллельном и последовательном включении.
Решение:
Считая сопротивление одного резистора, равным R, общее сопротивление цепи при смешанном включении будет равно
При последовательном соединении резисторов сопротивление цепи будет равно
Так при этом ,считая напряжение источника неизменным, общее сопротивление уменьшается в 2 раза.
Мощность пропорциональна квадрату тока и первой степени сопротивления. (P=I2r)
Это означает, что при уменьшении тока в 2 раза и возрастании сопротивления цепи в 2 раза мощность в 2 раза уменьшится и составит 50 Вт.
При параллельном соединении трех резисторов сопротивление цепи составит
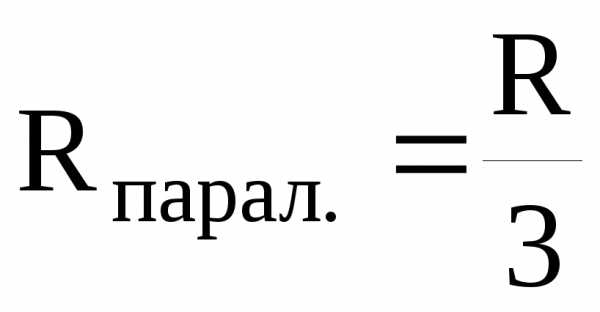
То есть, будет в 3 раза меньше, чем при смешанном соединении. Соответственно ток возрастет в 3 раза, и мощность тоже увеличится в 3 раза и составит 300 Вт.
3.* Дано:R1=5 Ом; R2=R3=10 Ом; R4=5 Ом; R5=10 Ом; U=20 В. Рассчитать все токи в цепи (рис. 2) методом пропорционального пересчета.
Решение:
Задаемся током в R2: I2’=1 А.
В этом случае напряжение на R2 и R3 (они включены параллельно) будет равно
Ток
в R3: 
Ток 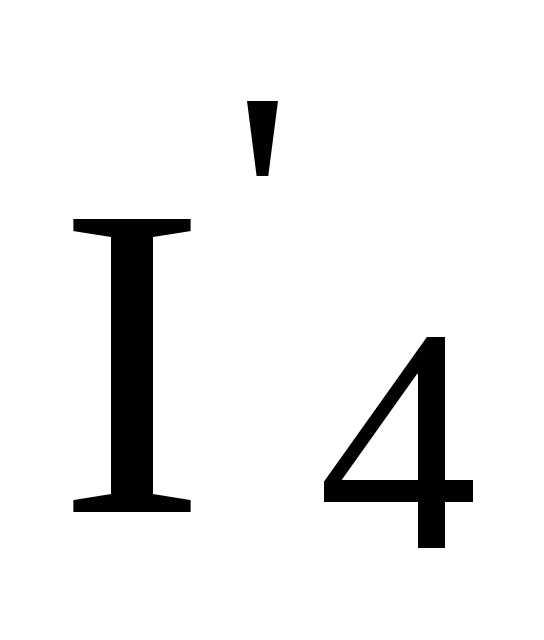 может быть найден по 1-му закону Кирхгофа
может быть найден по 1-му закону Кирхгофа
Напряжение на R5:
Ток 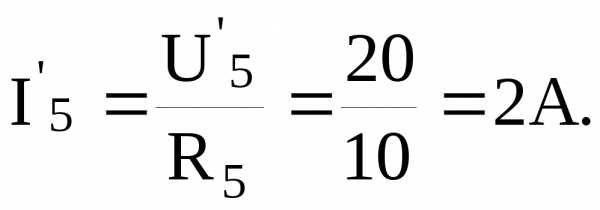
По 1-му закону Кирхгофа:
Напряжение на зажимах цепи:
Сравниваем полученное значение напряжения с заданным и определяем коэффициент пересчета

Теперь определяем действительные значения токов в цепи
и т.д.
1.2. Преобразование схем электрических цепей
4.* Три одинаковых источника с E=6B и внутренним сопротивлением r=3Ом включены в параллель и работают на общую нагрузку, сопротивление которой равно R. При каком сопротивлении нагрузки в нем выделяется максимально возможная мощность?
Решение:
В заданной схеме (рис. 3) целесообразно произвести перенос источника за узел. Для этого подключают к узлу источники с ЭДС, равной E, но направленной против ЭДС заданных источников.
Преобразование ясно из рис. 4,а и 4,б.
a)б)
Максимально возможная мощность выделится в нагрузке, если ее сопротивление равно внутреннему сопротивлению источника (режим согласованной нагрузки).
Внутреннее
сопротивление источника оказывается
равным  .
Откуда
.
Откуда
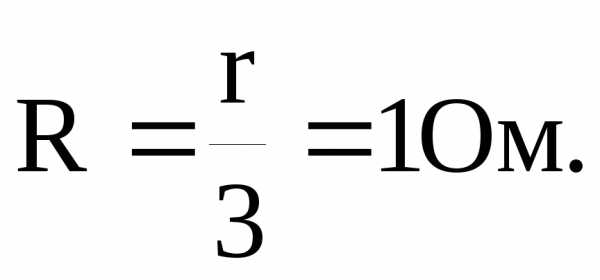
Мощность в нагрузке составит
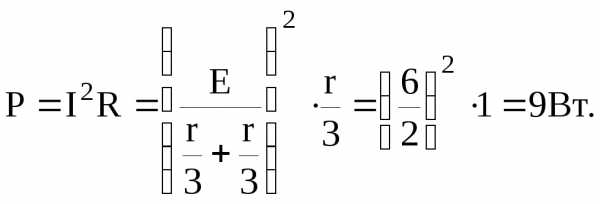
5.* Дано: E1=6B; E2=4B; R1=2Ом; R2=R3=6Ом; R4=4Ом; R5=1Ом.
Рассчитать токи источников в цепи (рис. 5)
Решение:
Схему целесообразно представить в виде рис.6, используя преобразование треугольника сопротивлений в эквивалентную звезду.
При этом
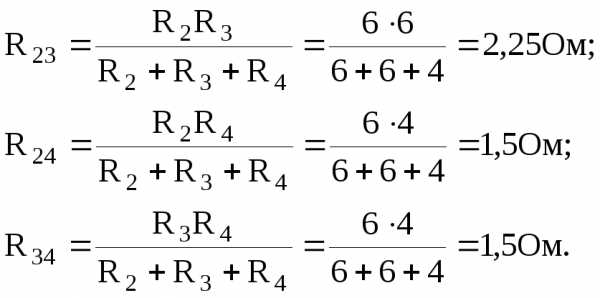
R5
Схему рис. 6 можно представить, как это показано на рис. 7, и рассчитывать ее методом наложения
Закорачиваем второй источник и находим ток первого
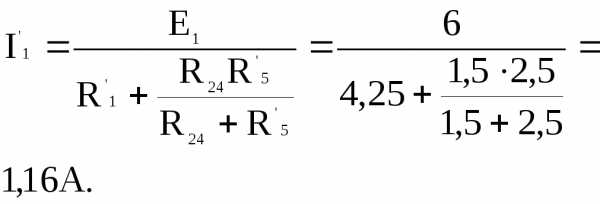
Ток
в сопротивлении  при этом будет равен
при этом будет равен
Далее закорачиваем первый источник и находим ток второго
Ток
в сопротивлении  при действии в цепи только второго
источника находим по формуле:
при действии в цепи только второго
источника находим по формуле:
В соответствии с направлениями токов, показанными на рис. 7 находим действительные значения токов источников.
6.* Дано:E2=2B;E4=4B;R1=2Ом; R2=1Ом; R3=1,5Ом; R4=1Ом; R5=1,6Ом; R6=1,2Ом.
Рассчитать все токи в цепи (рис. 8), составить баланс мощности.
Решение:
Схема цепи имеет три контура и четыре узла и расчет ее с помощью законов Кирхгофа потребует решения шести уравнений.
Однако если преобразовать участки цепи, изображенные на рис. 9 и представляющие собой активные двухполюсники, то трудоемкость расчета существенно снижается.
ЭДС 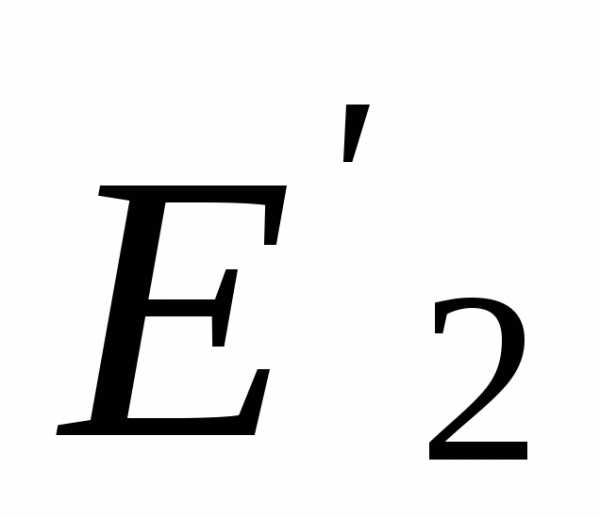 и
и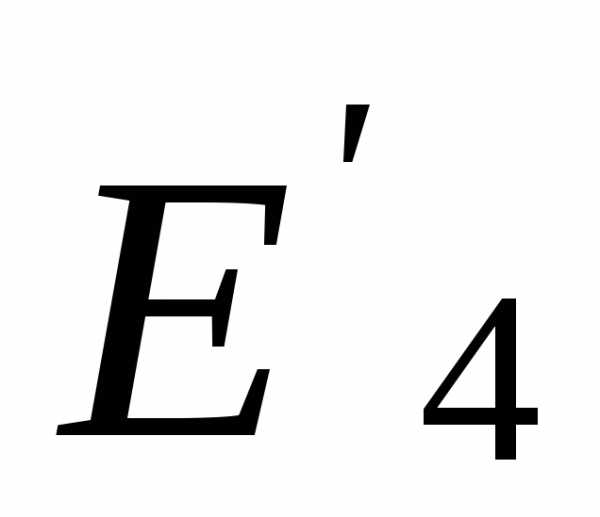 ,
сопротивления
,
сопротивления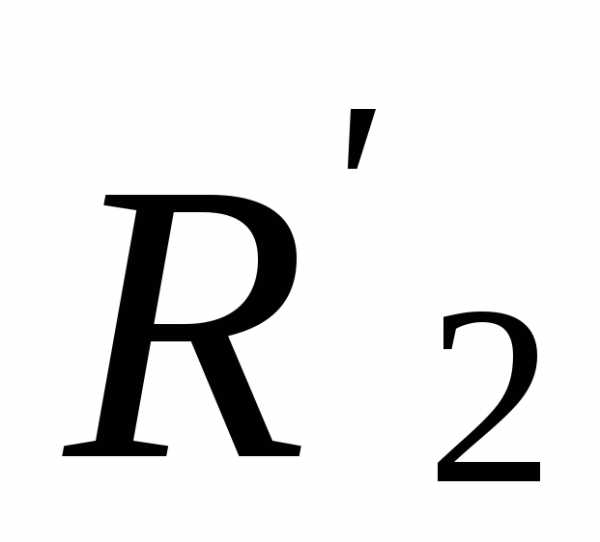 и
и можно определить следующим образом:
можно определить следующим образом:
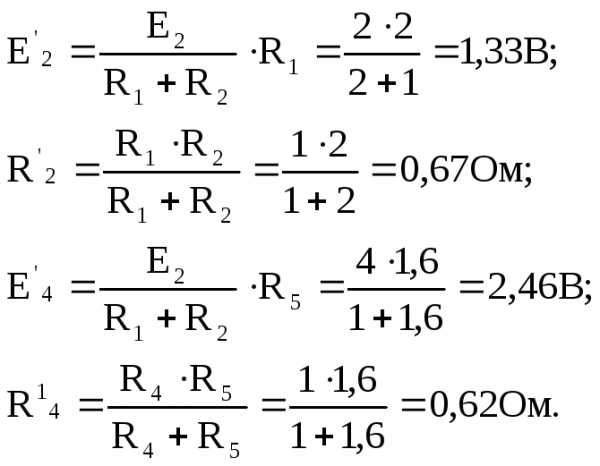
В результате такого преобразования схема цепи существенно упрощается (рис. 10)
В полученной схеме токиI3 и I6 одинаковы и равны
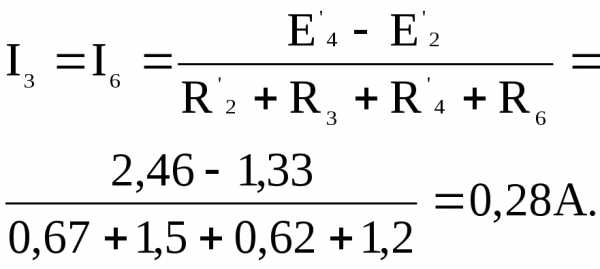
Напряжение между 3-м и 2-м узлами исходной схемы равно
Ток I5 отсюда
Ток I4 может быть определен по закону Ома
Напряжение между 1-м и 4-м узлами будет равно
Токи I1 и I2 соответственно равны
Составим баланс мощности в цепи.
Мощность, вырабатываемая источниками:
Мощность, потребляемая приемниками:
Таким образом, баланс мощностей в цепи сошелся.
1.3. Анализ сложных электрических цепей постоянного тока. Топология электрических цепей.
7.* Для схемы цепи (рис. 11) вычертить граф, выделить дерево графа, записать матрицы соединений (узловая матрица) и контуров и, используя эти матрицы, получить систему уравнений, записанную по законам Кирхгофа.
a)б)
Граф данной электрической цепи изображен на рис. 11,б. При этом дерево графа выделено жирными линиями.
Так как деревом графа называют совокупность ветвей, соединяющих все узлы схемы, но не образующей замкнутых контуров, то, очевидно, дерево, приведенное на рис. 11,б, не является единственно возможным.
Студентам предлагается самостоятельно изобразить варианты других деревьев для данного графа.
Матрица соединений (узлов) будет иметь вид:
 ,
где номера строк – узлы, а номера столбцов
– ветви.
,
где номера строк – узлы, а номера столбцов
– ветви.
Эта матрица записывается для k-1 узлов и, очевидно, поэтому тоже не является единственно возможной. Запишите матрицу А, если исключен, например, 1-й узел либо 2-й.
Задав направление обхода контуров по часовой стрелке (рис. 11,б), записываем матрицу контуров
 ,
где номера строк – контуры, а номера
столбцов – ветви.
,
где номера строк – контуры, а номера
столбцов – ветви.
Для записи уравнений по закону Кирхгофа требуется еще диагональная матрица сопротивлений цепи:
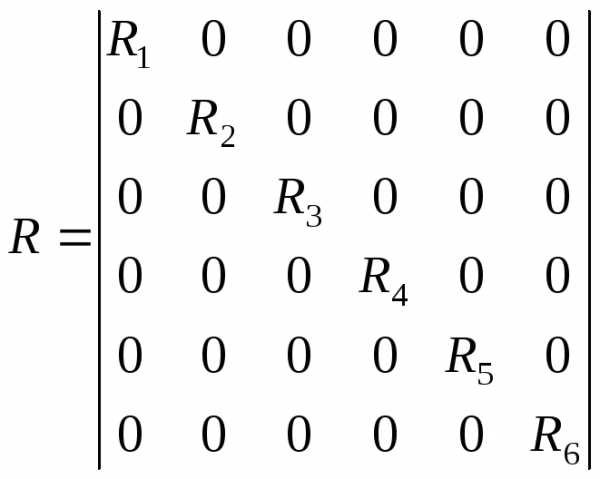
Умножая матрицу соединений на вектор-матрицу токов ветви, имеем
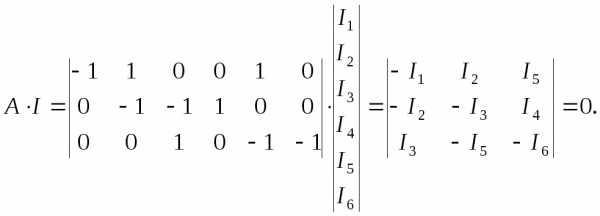
Или
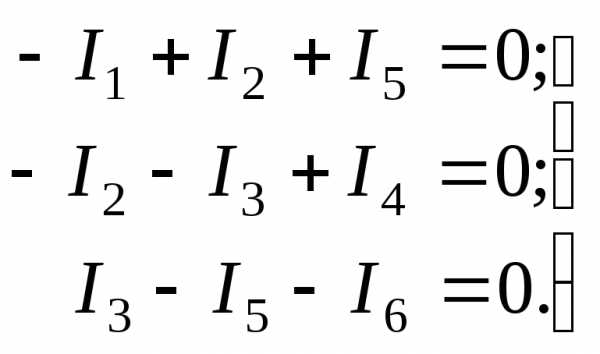
Это уравнения, записанные по 1-му закону Кирхгофа.
Далее матрицу контуров умножаем на вектор-матрицу напряжений ветвей
Или получаем уравнения:
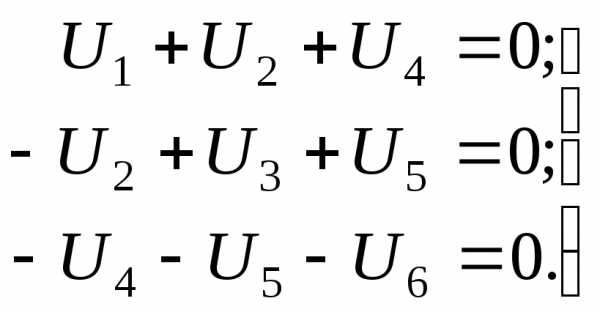
С учетом того, что
Имеем
Это уравнения, записанные по 2-му закону Кирхгофа.
8.* Для схемы, изображенной на рис. 11,а, записать системы уравнений для расчета цепи методом контурных токов и узловых потенциалов, используя матрицы контуров и соединений.
Решение:
При расчете цепи методом узловых потенциалов используется диагональная матрица проводимости ветвей:
,
где 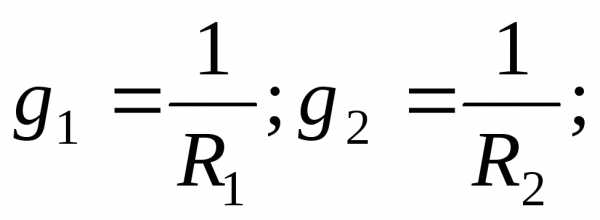 и
т.д.
и
т.д.
Умножаем матрицу соединений на матрицу проводимостей
Умножаем полученный результат на транспонированную матрицу соединений
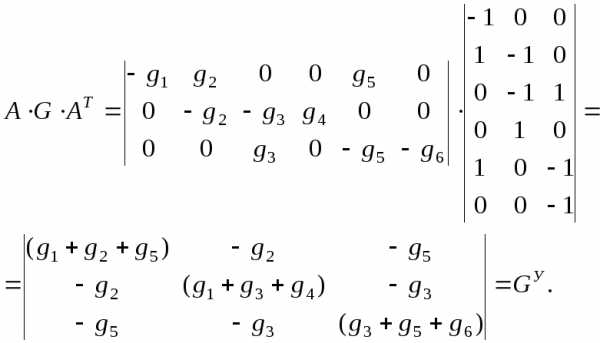
В результате получили матрицу узловых проводимостей.
Далее матрицу GУ умножаем на вектор-матрицу потенциалов узлов, а вектор-матрицу токов источников тока ветвей умножаем на матрицу соединений
, (*)
где 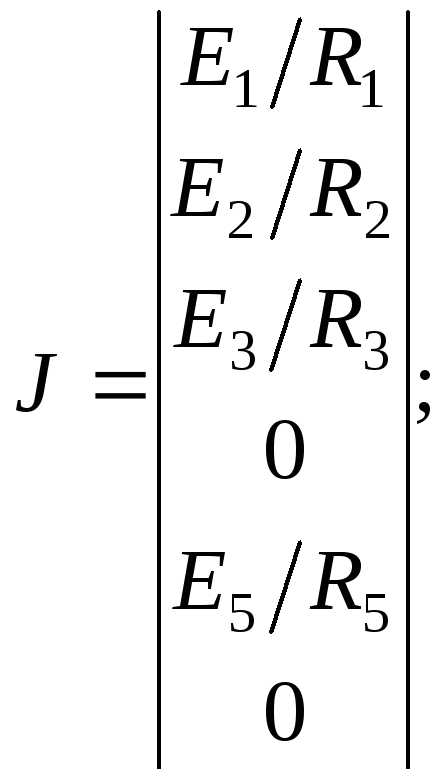 и
и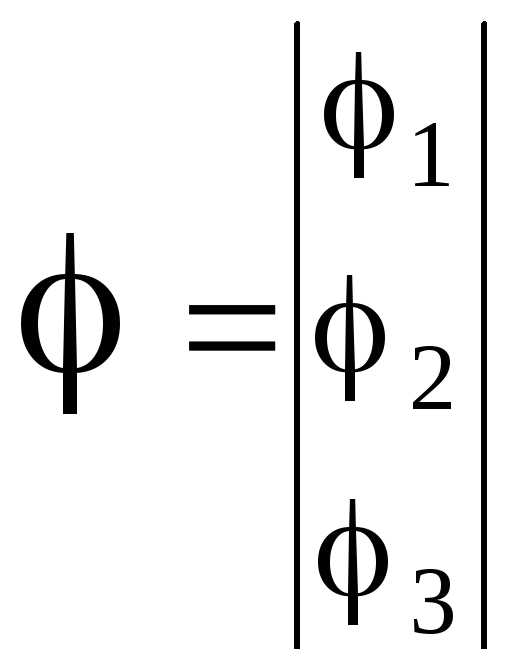 .
.
После указанных выше действий получаем
.
Переносим  в правую часть системы уравнений и
окончательно записываем:
в правую часть системы уравнений и
окончательно записываем:
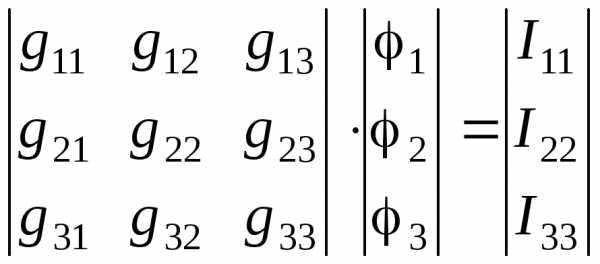 ,
,
где
Для получения системы уравнений в методе контурных токов необходимо матрицу контуров умножить на диагональную матрицу сопротивления ветвей
Полученный результат умножаем на транспонированную матрицу контуров

Получили матрицу контурных сопротивлений.
Далее матрицу контуров умножаем на вектор-матрицу ЭДС источников ветвей
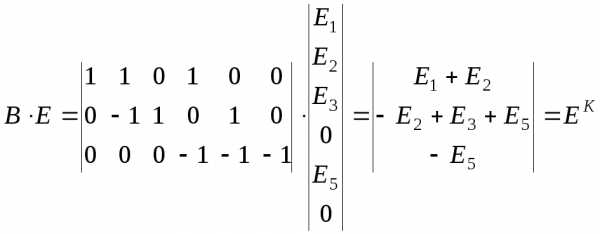 .
.
В результате получили вектор-матрицу контурных ЭДС.
Окончательно имеем
Или
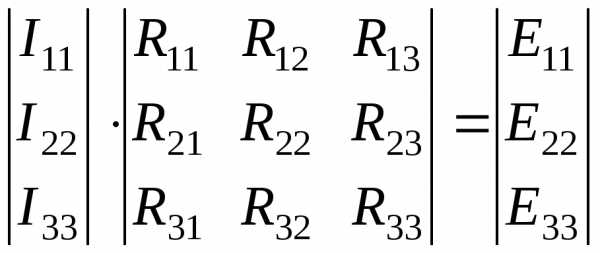 ,
,
где I11, I22, I33 – контурные токи
— контурные сопротивления и сопротивления между контурами
— контурные ЭДС.
1.4. Метод эквивалентного генератора.
9.* Определить показания приборов в схеме представленной на рис.12,а, если: R1=10Ом; R2=50Ом; R3=40Ом; R4=20Ом; R5=20Ом.
а)
б)
Решение: Определяем напряжение холостого хода на зажимах а-б при разомкнутой ветви R5.При этом токиI1 и I2 не будут зависеть друг от друга и могут быть найдены по закону Ома
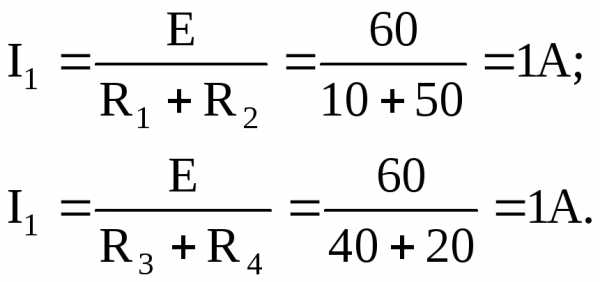
Напряжение холостого хода будет равно:
Далее находим внутреннее сопротивление активного двухполюсника относительно зажимов а-б при закороченном источнике E. (см. рис. 12,б)
Ток в сопротивленииR5 (тот, что регистрирует амперметр)
Показания вольтметра:
studfiles.net
Расчет сопротивления
36 Физика
Ðèñ. 10 á
Ответ: 6 Ом.
Заметим, что преобразуя цепь к более простой эквивалентной, можно на схемах изгибать, удлинять или укорачивать провода, перемещать узлы вдоль проводов, поскольку провода, соединяющие элементы схемы, считаются идеальными, т. е. имеющими нулевое сопротивление.
Рассмотрим теперь, как может видоизмениться цепь, состоящая из тр¸х последовательно соедин¸нных проводников, если к ним добавить другие проводники. Сначала добавим два проводника с нулевым сопротивлением, соединив ими точку А с точ- кой С, а В – с D (рис. 11).
Задача 3. Найдите сопротивление между точками А и D цепи (рис. 11), если каждый проводник имеет сопротивление 3 Ом.
Ðèñ. 11
Решение. Так как точки А и С соединены проводом с нулевым сопротивлением, то их потенциалы равны, а значит, эти точки имеют одинаковый потенциал, и их можно собрать в один общий узел. Аналогично поступим с точками В и D. Таким образом, полу- чилось, что каждый проводник оказался подключенным к одним и тем же точкам, т. е. все три проводника соединены параллельно. Теперь уже легко найти общее сопротивление цепи, учи- тывая, что все проводники имеют одинаковое сопротивление:
1 | 1 |
| 1 |
| 1 | 3 | R | R1 | 1 | Îì. | ||
R |
| R1 | R1 | R1 |
| R1 | 3 | |||||
|
|
|
|
|
|
| ||||||
Ответ: 1 Ом.
Заменим теперь один из идеальных проводников реальным – с ненулевым сопротивлением.
Задача 4. Определите сопротивление между точками А и D цепи (рис. 12), если каждый проводник имеет сопротивление 6 Ом.
Ðèñ. 12
Заметим, что точки В и D попрежнему соединены проводником с нулевым сопротивлением. Следовательно, они имеют одинаковый потенциал. Соединив их в один узел, получим эквивалентную схему (рис. 13 а). Если же затем «распрямить» е¸, то участки с параллельно и последовательно соедин¸н- ными проводниками станут хорошо видны (рис. 13 б).
Ðèñ. 13 à
Ðèñ. 13 á
После этого останется лишь произвести расч¸т сопротивления для эквивалентной схемы в три этапа:
studfiles.net
Урок решения задач. Расчёт электрических цепей.
Урок №47
Дата .
тема: Решение задач. Расчет электрических цепей.
Цель: определяет алгоритм последовательности расчета электрических схем для решения задач по типу «черный ящик»
Задачи:
Образовательная: закрепить навык решения расчетных задач на параллельное и последовательное соединение;
Развивающая: развитие внимания и памяти, уметь анализировать, делать выводы; логически рассуждать;
Воспитательная: умение работать в команде, проводить самооценку и взаимооценку.
Тип урока: формирование практических навыков.
Формы обучения: групповая работа, индивидуальная работа.
Критерии успеха:
Знает законы последовательного и параллельного соединения проводников.
Умеет решать расчетные задачи на применение законов последовательного и параллельного соединений.
Анализирует смешанные соединения, умеет их «разбивать» на более простые.
Создает схему по итогам расчетов.
Критерии оценивания: учет достижений проводится по листу самооценивания.
4 «+» — 5
3 «+» — 4
2 «+» — 3
1-0 «+» — 2
План урока:
Этап урока
Деятельность учителя
Деятельность учащихся
Организационный момент
2 мин
Приветствие учителя
Проверка готовности к уроку
Повторение правил работы в группе, критериев оценивания устных ответов
Называют правила и критерии.
Проверка выполнения домашней работы
2 мин
Проверка решения домашней задачи (индивидуально по тетрадям).
m=kIt, k=m/It, k=15*10-4/4*20*60=31*10-4 кг/А*с
Проверяют по ответу, ставят отметку о выполнении по листу ответа.
Постановка цели урока
2 мин
— Что можно сказать об этих схемах соединения?
— Как выдумаете, чем мы будем заниматься на уроке?
— Какую учебную задачу поставим перед собой на уроке?
Это разные виды соединения: последовательное, параллельное, смешанное.
Мы будем решать задачи на расчет электрических цепей.
Актуализация знаний
7 мин
Прежде чем мы приступим к решению наших задач, необходимо восстановить в памяти знания, приобретенные на предыдущих уроках. Предлагаю это сделать в форме «Деловой корзины». Мы должны постараться достаточно полно ответить на задание-вопрос.
Электрический ток.
Направленное движение заряженных частиц называют электрическим током.
Сила тока
Силой тока называется физическая величина, показывающая, какой заряд проходит через поперечное сечение проводника за единицу времени. , где I – сила тока (А), q – заряд, t – время (с).
Электрическое напряжение.
Физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда, называется электрическим напряжением. , U – электрическое напряжение (В), A – работа электрического тока по перемещению заряда, q – заряд (Кл).
Электрическое сопротивление проводника.
Физическая величина, характеризующая противодействие, оказываемое электрическому току, называется электрическим сопротивлением. Обозначается буквой R. Единица измерения сопротивления проводника – Ом.
Закон Ома.
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению. , где I – сила тока на участке цепи (А), U – напряжение на этом участке (В), R – сопротивление участка цепи (Ом).
Законы параллельного соединения проводников
При параллельном соединении проводников напряжение на всех участках цепи одно и тоже, общая сила тока равна сумме сил токов на отдельных проводниках. Общее сопротивление уменьшается.
Законы последовательного соединения проводников
При последовательном соединении проводников сила тока везде одинакова, напряжение в цепи равно сумме напряжений на отдельных участках, общее сопротивление складывается из сопротивлений отдельных проводников.
Решение задач
5 мин
10 мин
(5 мин + 5 мин)
10 мин
(7+3)
НПС
1 Резисторы сопротивлением 2 Ом и 3 Ом соединены параллельно. Определите общее сопротивление цепи. (1,2 Ом)
2. Резисторы сопротивлением 2 Ом и 3 Ом соединены последовательно. Определите общее сопротивление цепи. (5 Ом)
3. Два резистора сопротивлением 10 Ом и 5 Ом соединены параллельно. Определите общее сопротивление цепи. (1,3 Ом)
4. Два резистора сопротивлением 27 Ом и 5 Ом соединены последовательно. Определите общее сопротивление цепи. (32 Ом)
ППС
1. Два проводника сопротивлением 5 Ом и 10 Ом присоединены параллельно к источнику тока напряжением 20В. Определите силу тока в каждом проводнике и общую силу тока в цепи. (4,2,6)
2. Два резистора включены последовательно. Напряжение на резисторе, сопротивление которого 5 Ом, равно 10В. Напряжение на втором резисторе равно 20 В. Чему равно сопротивление второго резистора? (10)
3. Резисторы, сопротивление которых 30 Ом и 60 Ом, соединены последовательно и подключены к батарейке. Напряжение на первом резисторе 3В. Какое напряжение на втором резисторе? (6В)
4. Резисторы, сопротивления которых 2 Ом и 3 Ом, соединены последовательно и подключены к источнику постоянного напряжения 15 В. Найдите силу тока в цепи. (3)
ВПС
1. На рисунке дана схема электрической цепи. Напряжение на участке АВ 120В. Определите сопротивление всей цепи, силу тока в каждом резисторе.

2. Определите сопротивление участка цепи, изображенного на рисунке, между точками С и D, если при этом R1 =2 Ом, R2 =5 Ом, R3 =20 Ом, R4 =5 Ом, R5 =10 Ом
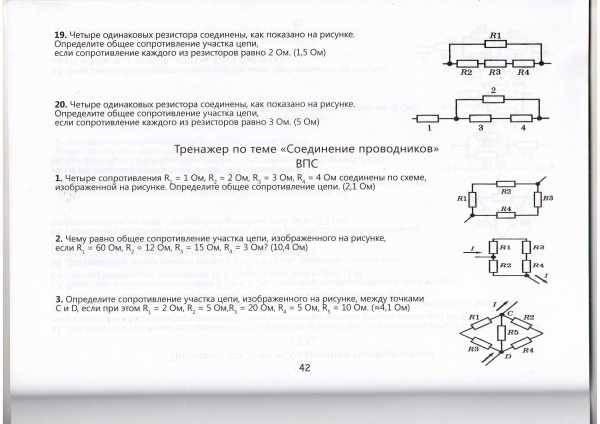

Из 4 одинаковых резисторов по 10 Ом требуется составить цепь сопротивлением 6 Ом. Произведя необходимые расчеты, начертите эту схему.
выбор лидера, спикера, таймкипера
Лидер осуществляет проверку правильности решения задач.
Решение задачи
Проверка ответа — слайд
Заполнение листа самооценивания.
Анализ цепи, моделирование способа решения.
Выступление спикера
Защита модели.
Лидер отмечает степень участия в общей работе команды.
Рефлексия
5 мин
Рефлексивный экран:
Сегодня я узнал….
Было трудно….
Я понял, что…..
Мне захотелось….
Меня удивило…..
Я выполнял задания…..
Теперь я могу…..
Было не интересно…
Продолжить фразу
Домашнее задание
5 мин
Опрос нескольких учащихся, какую оценку они получили? Почему? Как можно улучшить результат?
На следующем уроке мы выполним контрольную работу по пройденным темам, в связи с этим, какое домашнее задание мы определим для себя?
Определяют точки западения знаний по оценкам за урок.
infourok.ru
