Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачать шпаргалку со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Запишитесь и участвуйте в розыгрыше 8 уроков
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины. Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения. |
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
при прямом измерении результат можно увидеть непосредственно на шкале инструмента;
при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).

Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики. |
Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.

Траектория движения — мысленная линия, вдоль которой перемещается тело.
Путь — длина траектории тела от начальной до конечной точки.
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние. |
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.
Формула скорости равномерного криволинейного движения:
где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с2.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес. |
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Fтяж = mg
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему. |
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры.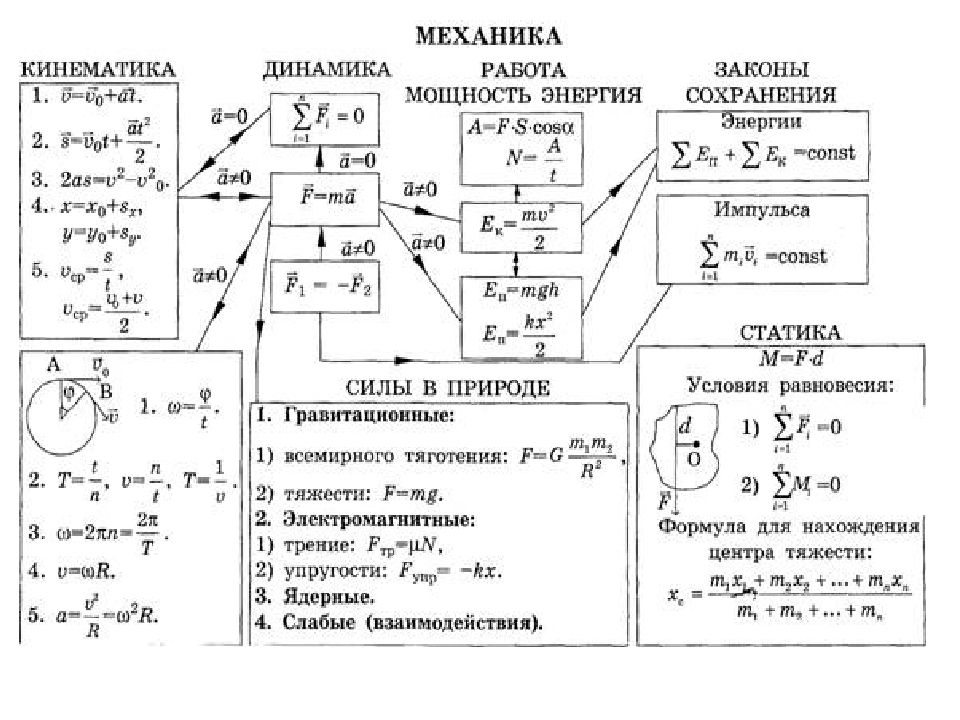 Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз. Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы. |
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.
Уравнение равновесия рычага:
F1 × l1 = F2 × l2
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.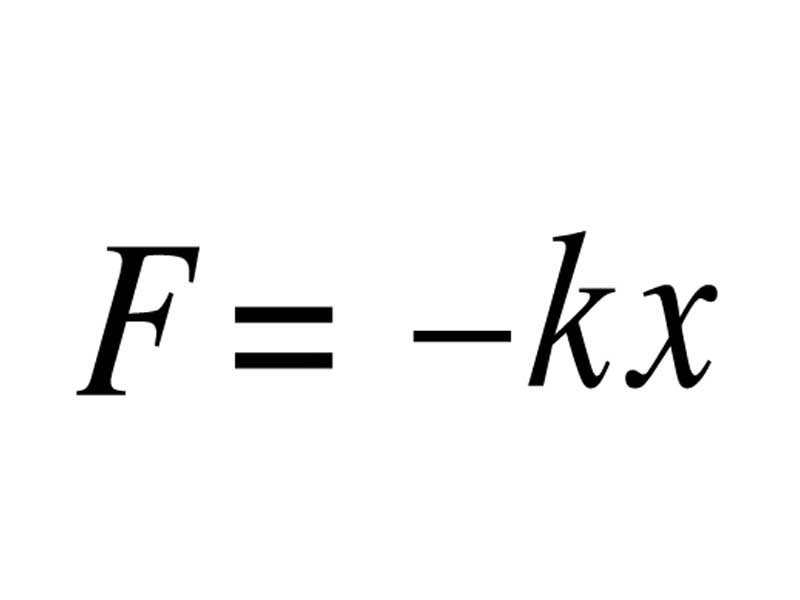
Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l. |
Формула момента силы:
M = F × l, где F — модуль силы, l — длина плеча.
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.
Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении. |
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
М1 + М2 + Мn + … = 0
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности. Сила давления направлена перпендикулярно поверхности. |
Формула давления:
p = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
1 Па = 1 Н/м2
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно:
F = p × S
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.
g = 9,8 м/с2
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления. |
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
p = F / S, где F — модуль силы, S — площадь поверхности.
Сообщающиеся сосуды
Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. |
Если ρ1 = ρ2, то h1 = h2 и ρ1gh1 = ρ2gh2, где:
p — плотность жидкости,
h — высота столба жидкости,
g = 9,8 м/с2.
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.). |
Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Следовательно,
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ. |
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с2.
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
если плотность тела выше плотности среды, оно уйдет на дно;
если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение. |
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения. |
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
Кинетическая энергия | Пропорциональна массе тела и квадрату его скорости. | Ek = mv2/2 |
Потенциальная энергия | Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания. | Ep= mgh |
Полная механическая энергия | Складывается из кинетической и потенциальной энергии. | E = Ek+Ep |
Сохранение и превращение энергии | Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу. | Ek+ Ep= const |
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии. |
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
Удачи на экзаменах!
Самые важные формулы по физике. Формулы по физике для егэ
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Как правило, именно математику, а не физику принято считать королевой точных наук. Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Секреты подготовки
Возможно, это связано с кажущейся сложностью предмета или популярностью профессий гуманитарного и управленческого профиля, но в 2016 году только 24 % всех абитуриентов приняли решение сдавать физику, в 2017 — лишь 16 %. Такие статистические данные невольно заставляют задуматься, не слишком ли завышены требования или просто уровень интеллекта в стране падает. Почему-то не верится, что так мало школьников 11 класса желают стать:
- инженерами;
- ювелирами;
- авиаконструкторами;
- геологами;
- пиротехниками;
- экологами,
- технологами на производстве и т.д.
Знание формул и законов физики в равной степени необходимо для разработчиков интеллектуальных систем, вычислительной техники, оборудования и вооружения. При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Те ученики, которые исправно посещали все уроки физики вплоть до последнего звонка, знают, что в период с 5 по 11 класс изучается около 450 формул. Выделить из этих четырех с половиной сотен хотя бы 50 крайне сложно, поскольку все они важны. Подобного мнения, очевидно, также придерживаются разработчики Кодификатора. Тем не менее, если вы одарены необыкновенно и не ограничены во времени, вам хватит 19 формул, ведь при желании из них можно вывести все остальные. За основу мы решили взять главные разделы:
- механику;
- физику молекулярную;
- электромагнетизм и электричество;
- оптику;
- физику атомную.
Очевидно, что подготовка к ЕГЭ должна быть ежедневной, но если по каким-то причинам вы приступили к изучению всего материала лишь сейчас, настоящее чудо может совершить экспресс-курс, предлагаемый нашим центром. Надеемся, эти 19 формул также будут вам полезны:
Вы, наверное, заметили, что некоторые формулы по физике для сдачи ЕГЭ остались без пояснений? Мы предоставляем вам самим их изучить и открыть для себя законы, по которым абсолютно всё вершится в этом мире.
Единый Государственный Экзамен охватывает информацию по всему курсу физики с 7 по 11 класс. Однако если некоторые формулы по физике для ЕГЭ неплохо запоминаются сами по себе, над другими приходится поработать. Мы рассмотрим некоторые формулы, которые полезны для решения различных задач.
Кинематика
Начнем традиционно с кинематики. Частая ошибка здесь – неверное вычисление средней скорости неравномерного прямолинейного движения. В данном случае задачи пытаются решать с помощью среднего арифметического. Однако все не так просто. Среднее арифметическое – только частный случай. А для нахождения средней скорости движения существует полезная формула:
где S – весь путь, пройденный телом за определенное время t.
Молекулярно-Кинетическая Теория (МКТ)
МКТ может поставить множество коварных «ловушек» для невнимательного школьника. Чтобы избежать этого, нужно свободно владеть формулами по физике для ЕГЭ в этой области.
Начнем с закона Менделеева-Клапейрона, использующегося для идеальных газов. Он звучит так:
Он звучит так:
где p –давление газа,
V – занимаемый им объем,
n – количество газа,
R – универсальная газовая постоянная,
T – температура.
Обратите внимание на примеры задач с применением этого закона.
Все представляют себе, что такое влажность. Значения относительной влажности ежедневно сообщаются в СМИ. На экзамене же пригодится формула: здесь ф – относительная влажность воздуха,
ρ – плотность водяного пара, находящегося в воздухе,
ρ0 – плотность насыщенного пара при конкретной температуре.
Эта последняя величина – табличное значение, поэтому оно должно быть в условии задачи.
Термодинамика
Термодинамика – отрасль, достаточно близкая к МКТ, поэтому многие понятия пересекаются. Термодинамика базируется на двух своих началах. Практически каждая задача этой области требует знание и применение первого начала термодинамики, выраженного формулой
Это формулируется следующим образом:
Количество теплоты Q, которое было получено системой, расходуется на совершение работы A над внешними телами и изменение ΔU внутренней энергии данной системы.
Сила Архимеда
Напоследок поговорим о поведении погруженных в жидкость тел. Очевидно, что на каждое из них действует сила тяжести, направленная вертикально вниз. Но в жидкости все тела весят меньше. Это обусловливается частичным компенсированием силы тяжести противоположно направленной силой Архимеда. Ее значение равно Таким образом, эта сила, старающаяся вытолкнуть тело из жидкости, зависит от плотности той самой жидкости и объема погруженной в нее части тела. Сила Архимеда действует и в газах, но вследствие ничтожности плотности газов ею обыкновенно пренебрегают.
ЕГЭ проверяет знания школьника в различных областях физики. Формулы для ЕГЭ по физике способствуют успешному решению задач (можно воспользоваться ) и общему пониманию основных физических процессов.
Шпаргалка с формулами по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
А потом вордовский файл , который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей — Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля — Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика — формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 — t / T
- Энергия связи атомных ядер
E CB =(Zm p +Nm n -Mя)∙c 2
СТО
- t=t 1 /√1-υ 2 /c 2
- ℓ=ℓ 0 ∙√1-υ 2 /c 2
- υ 2 =(υ 1 +υ)/1+ υ 1 ∙υ/c 2
- Е = mс 2
Формула силы в физике
Содержание:
- Определение и формула силы
- Второй закон Ньютона
- Единицы измерения силы
- Примеры решения задач
Определение и формула силы
Определение
Силой называют векторную величину, которая характеризует взаимодействия тел. {n} \bar{F}_{i}=\frac{d \bar{p}}{d t}(1)$$
{n} \bar{F}_{i}=\frac{d \bar{p}}{d t}(1)$$
где $\bar{p}=m \bar{v}$ — импульс тела, m–масса рассматриваемого тела, $\bar{v}$ — скорость. Надо отметить, что уравнение (1) строго применимо только относительно материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.
Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней (второй закон Ньютона) можно представить в виде:
$$\bar{F}=m \frac{d \bar{v}}{d t}=m \bar{a}(2)$$
где $\bar{a}$ – ускорение, которое материальная точка приобретает в результате воздействия на нее силы. Выражение (2) показывает то, что если $\bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.
Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:
$$F=\frac{\Delta p}{\Delta t}=\frac{m\left(v_{2}-v_{1}\right)}{t_{2}-t_{1}}$$
Единицы измерения силы
Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с2
В СГС: [F]=дин
1Н=105 дин
Примеры решения задач
Пример
Задание. {2}}(1.4)$$
{2}}(1.4)$$
то, учитывая выражения (1.2) и (1.3), получаем:
$a = 6 \alpha t (1.5)$
Так как ay=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение и силы совпадают, а мы получили:
$$\bar{a}=6 \alpha t \cdot \bar{i}(1.6)$$
где $\bar{i}$ – единичный вектор, направленный по оси X.
Исходя из второго закона Ньютона, имеем:
$$F=m \cdot 6 \alpha t, \bar{F}=m 6 \alpha t \cdot \bar{i}$$
Ответ. Так как $F=m \cdot 6 \alpha t$, то с течением времени сила увеличивается по модулю.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два параллелепипеда лежат на горизонтальной поверхности. {\prime}}=\left(m_{1}+m_{2}\right) \bar{a}(2.3)$$
{\prime}}=\left(m_{1}+m_{2}\right) \bar{a}(2.3)$$
В проекции на ось X уравнение (2.3) примет вид:
$$F_{0}=\left(m_{1}+m_{2}\right) a(2.4)$$
Из уравнения (2.4) выразим ускорение:
$$a=\frac{F_{0}}{m_{1}+m_{2}}$$
Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:
$$F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$$
Ответ. $F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$
Читать дальше: Формула сопротивления.
10 формул по физике
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.
Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.
Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.
В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.
Соотношения закона ОмаЗакон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:
| Искомая величина | Формула |
| Напряжение, В | U=I*R |
| Ток, А | I=U/R |
| Сопротивление, Ом | R=U/I |
| Мощность, Вт | P=U*I |
В этой таблице используются следующие общепринятые обозначения физических величин:
U — напряжение (В),
I — ток (А),
Р — мощность (Вт),
R — сопротивление (Ом),
Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:
I = U / R
Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.
Что же в этой формуле есть что? Рассмотрим переменные подробнее.
> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
> I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.
> R: искомое сопротивление токоограничивающего резистора, в омах.
В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:
R = U/I = 8,5 В / 0,050 А= 170 Ом
Расчёты сопротивленияРассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.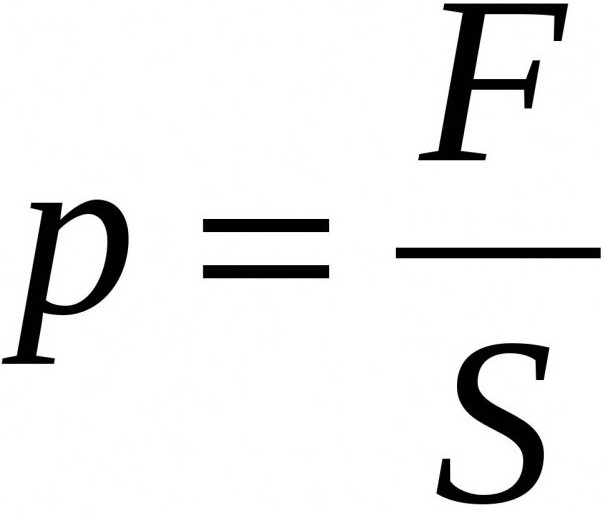
Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.
> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.
> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.
Расчет сопротивления последовательных резисторовФормула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:
Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)
В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.
Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.
Расчет сопротивления параллельных резисторовВсе немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:
R общ = R1 * R2 / (R1 + R2)
где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим
776,47 = 2640000 / 3400
Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:
Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.
Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.
Расчет емкости параллельных конденсаторовЕсли нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:
Собщ = CI + С2 + СЗ + …
В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.
Расчет емкости последовательных конденсаторовДля вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:
Собщ = С1 * С2 /( С1+С2)
где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи
Расчет емкости трех и более последовательно соединенных конденсаторовВ схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:
И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.
— суммарная величина.
Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.
Расчёт энергетических уравненийНаиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:
ватт-часы = Р х Т
В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.
Для расчета энергии в этих единицах ватт-часы делят на 3600.
В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).
Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.
Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.
T = RC
В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.
Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.
Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:
| Значение емкости конденсатора, мкФ | Емкость конденсатора для расчета |
| 10 | 0,000 01 |
| 1 | 0,000 001 |
| 0,1 | 0,000 000 1 |
| 0,01 | 0,000 000 01 |
Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:
Частота = 300000 / длина волны
Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.
Расчет длины волны сигналаТу же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:
Длина волны = 300000 / Частота
Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.
Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:
6000 миллиметров = 300000 / 50 МГц
Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!
Основные формулы по физике — ОПТИКА
Оптика — это раздел физики, изучающий природу светового излучения, его распространение и взаимодействие с веществом. Световые волны — это электромагнитные волны. Длина волны световых волн заключена в интервале [0,4·10-6 м ÷ 0,76·10-6 м]. Волны такого диапазона воспринимаются человеческим глазом.
Свет распространяется вдоль линий, называемых лучами. В приближении лучевой (или геометрической) оптики пренебрегают конечностью длин волн света, полагая, что λ→0. Геометрическая оптика во многих случаях позволяет достаточно хорошо рассчитать оптическую систему. Простейшей оптической системой является линза.
В приближении лучевой (или геометрической) оптики пренебрегают конечностью длин волн света, полагая, что λ→0. Геометрическая оптика во многих случаях позволяет достаточно хорошо рассчитать оптическую систему. Простейшей оптической системой является линза.
При изучении интерференции света следует помнить, что интерференция наблюдается только от когерентных источников и что интерференция связана с перераспределением энергии в пространстве. Здесь важно уметь правильно записывать условие максимума и минимума интенсивности света и обратить внимание на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона.
При изучении явления дифракции света необходимо уяснить принцип Гюйгенса-Френеля, метод зон Френеля, понимать, как описать дифракционную картину на одной щели и на дифракционной решетке.
При изучении явления поляризации света нужно понимать, что в основе этого явления лежит поперечность световых волн. Следует обратить внимание на способы получения поляризованного света и на законы Брюстера и Малюса.
Смотрите также основные формулы по физике — колебания и волны
Таблица основных формул по оптике
|
Физические законы, формулы, переменные |
Формулы оптики |
|
Абсолютный показатель преломления где с — скорость света в вакууме, с=3·108 м/с, v — скорость распространения света в среде. |
|
|
Относительный показатель преломления где n2 и n1 — абсолютные показатели преломления второй и первой среды. |
|
|
Закон преломления где i — угол падения, r — угол преломления. |
|
|
Формула тонкой линзы где F — фокусное расстояние линзы, d — расстояние от предмета до линзы, f — расстояние от линзы до изображения. |
|
|
Оптическая сила линзы где R1 и R2 — радиусы кривизны сферических поверхностей линзы. Для выпуклой поверхности R>0. Для вогнутой поверхности R<0. |
|
|
Оптическая длина пути: где n — показатель преломления среды; r — геометрическая длина пути световой волны. |
|
|
Оптическая разность хода: L1 и L2 — оптические пути двух световых волн. |
|
|
Условие интерференционного максимума: минимума: где λ0 — длина световой волны в вакууме; m — порядок интерференционного максимума или минимума. |
|
|
Оптическая разность хода в тонких пленках в отраженном свете: в проходящем свете: где d — толщина пленки; i — угол падения света; n — показатель преломления. |
|
|
Ширина интерференционных полос в опыте Юнга: где d — расстояние между когерентными источниками света; L — расстояние от источника до экрана. |
|
|
Условие главных максимумов дифракционной решетки: где d — постоянная дифракционной решетки; φ — угол дифракции. |
|
|
Разрешающая способность дифракционной решетки: где Δλ — минимальная разность длин волн двух спектральных линий, разрешаемых решеткой; m — порядок спектра; N — общее число щелей решетки. |
|
|
Закон Малюса: где I0 — интенсивность плоско-поляризованного света, падающего на анализатор; I — интенсивность света, прошедшего через анализатор; α — угол между плоскостью поляризации падающего света и главной плоскостью анализатора. |
|
|
Связь интенсивности естественного света Iест с интенсивностью света, прошедшего поляризатор (и падающего на анализатор): где k — относительная потеря интенсивности света в поляризаторе. |
|
|
Дисперсия вещества |
|
|
Средняя дисперсия |
|
|
Групповая скорость света |
|
|
Фазовая скорость света |
Самые сложные формулы по физике.
 Формулы по физике для егэ
Формулы по физике для егэШпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
Как правило, именно математику, а не физику принято считать королевой точных наук. Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Секреты подготовки
Возможно, это связано с кажущейся сложностью предмета или популярностью профессий гуманитарного и управленческого профиля, но в 2016 году только 24 % всех абитуриентов приняли решение сдавать физику, в 2017 — лишь 16 %. Такие статистические данные невольно заставляют задуматься, не слишком ли завышены требования или просто уровень интеллекта в стране падает. Почему-то не верится, что так мало школьников 11 класса желают стать:
- инженерами;
- ювелирами;
- авиаконструкторами;
- геологами;
- пиротехниками;
- экологами,
- технологами на производстве и т.д.
Знание формул и законов физики в равной степени необходимо для разработчиков интеллектуальных систем, вычислительной техники, оборудования и вооружения. При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Те ученики, которые исправно посещали все уроки физики вплоть до последнего звонка, знают, что в период с 5 по 11 класс изучается около 450 формул. Выделить из этих четырех с половиной сотен хотя бы 50 крайне сложно, поскольку все они важны. Подобного мнения, очевидно, также придерживаются разработчики Кодификатора. Тем не менее, если вы одарены необыкновенно и не ограничены во времени, вам хватит 19 формул, ведь при желании из них можно вывести все остальные. За основу мы решили взять главные разделы:
- механику;
- физику молекулярную;
- электромагнетизм и электричество;
- оптику;
- физику атомную.
Очевидно, что подготовка к ЕГЭ должна быть ежедневной, но если по каким-то причинам вы приступили к изучению всего материала лишь сейчас, настоящее чудо может совершить экспресс-курс, предлагаемый нашим центром. Надеемся, эти 19 формул также будут вам полезны:
Надеемся, эти 19 формул также будут вам полезны:
Вы, наверное, заметили, что некоторые формулы по физике для сдачи ЕГЭ остались без пояснений? Мы предоставляем вам самим их изучить и открыть для себя законы, по которым абсолютно всё вершится в этом мире.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.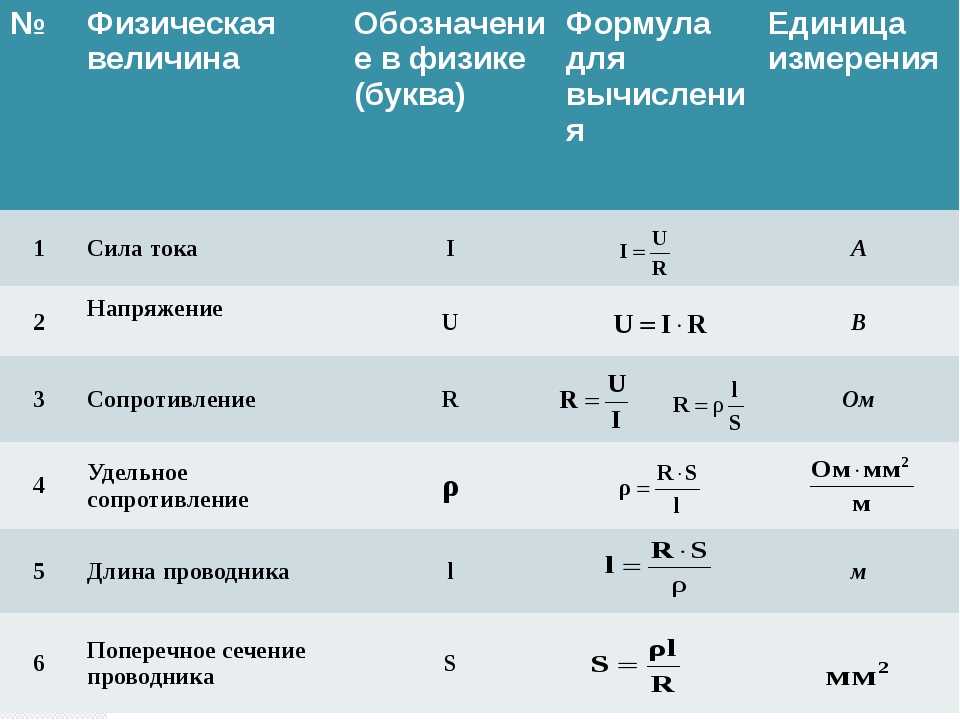
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Поэтому без формул здесь не обойтись:
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Основные формулы оптической физики
Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:
Основные формулы элементов теории относительности
И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Основные формулы световых квантов
Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач. Итак, рассмотрим их:
На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет : распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.
Более 50 основных формул по физике с пояснением
обновлено: 22 ноября, 2019
автором: Научные Статьи. Ру
Ру
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т. е. статику и гидростатику
е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг.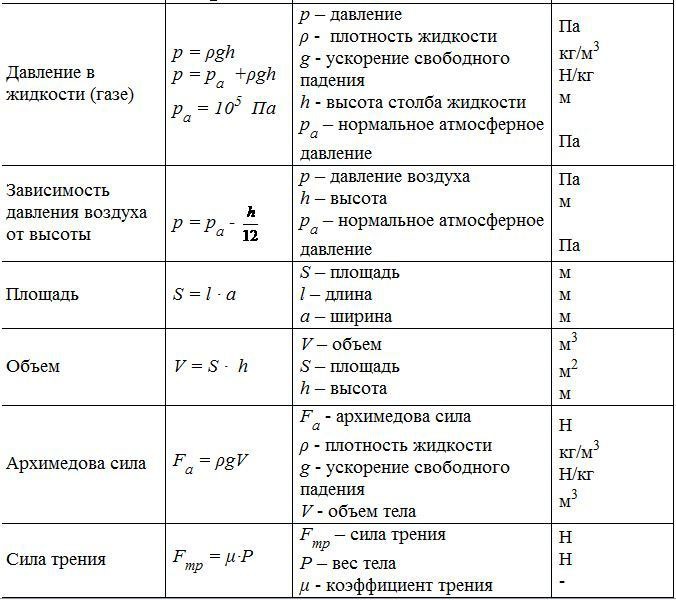 Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Расчет силы — физика для старших классов
Все ресурсы по физике для старших классов
6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по физике для старших классов » Силы » Равнодействующая сила » Расчет силы
Джерри толкает коробку с силой. Каково результирующее ускорение?
Возможные ответы:
Правильный ответ:
Пояснение:
Второй закон Ньютона утверждает, что .
В этой задаче и .
Подставьте их в уравнение, чтобы найти ускорение.
Сообщить об ошибке
Мяч катится вперед с чистым ускорением . Какова чистая сила, действующая на мяч?
Возможные ответы:
Правильный ответ:
Пояснение:
Второй закон Ньютона утверждает, что .
Подставьте полученные значения и найдите силу.
Сообщить об ошибке
Луиза с силой катит мяч. Она отмечает, что он имеет постоянное линейное ускорение . Какова масса мяча?
Возможные ответы:
Правильный ответ:
Пояснение:
Второй закон Ньютона утверждает, что .
Подставьте данные значения, чтобы найти массу.
Сообщить об ошибке
Дерек с силой толкает ящик по неровной поверхности. Он замечает, что он ускоряется только со скоростью . Чему должна быть равна сила трения?
(Предположим, что на объект действуют только две силы: трение и Дерек).
Возможные ответы:
Правильный ответ:
Пояснение:
Второй закон Ньютона утверждает, что .
Если Дерек толкает с силой, то мы должны вычислить ускорение ящика.
Дерек замечает, что ускорение ящика составляет , а не ожидаемое . На него действует внешняя сила, замедляющая ускорение.
Уравнение для чистой силы, действующей на объект: . Мы также знаем из второго закона Ньютона, что где результирующая сила и ускорение являются фактически наблюдаемыми значениями.
Подставьте полученную информацию, чтобы найти силу трения.
Вычтите из обеих сторон, чтобы найти силу трения.
Трение будет отрицательным, потому что оно действует в направлении, противоположном силе Дерека.
Сообщить об ошибке
Молоток давит на гвоздь. С какой силой гвоздь действует на молоток?
Возможные ответы:
Правильный ответ:
Пояснение:
Третий закон Ньютона гласит, что когда один объект воздействует на другой объект с силой, второй объект оказывает на первый объект силу, равную по величине, но противоположную по направлению. Это означает, что сила молотка на гвозде и сила гвоздя на молотке будут равны по величине, но противоположны по направлению.
Так как молоток воздействует на гвоздь, гвоздь должен воздействовать на молоток.
Сообщить об ошибке
Майкл толкает ящик с силой влево. Энни с силой толкает ту же коробку вправо. Какова результирующая сила, действующая на коробку?
Возможные ответы:
Правильный ответ:
Объяснение:
Для чистой силы мы складываем все силы: .
Поскольку сила представляет собой вектор, направление действия имеет значение. Мы сделаем движение влево отрицательным, а движение вправо положительным. Майкл толкает с влево, делая свою силу равной . Энни толкала вправо, так что ее сила останется.
Мы можем найти результирующую силу, сложив отдельные силы вместе.
Сообщить об ошибке
Франклин поднимает вес вертикально. Если он поднимает его таким образом, что скорость груза постоянна, какую силу он применяет?
Возможные ответы:
Правильный ответ:
Объяснение:
Если объект имеет постоянную скорость, это означает, что чистое ускорение должно быть равно нулю.
В сочетании со вторым законом Ньютона мы видим, что результирующая сила также равна нулю. Если нет чистого ускорения, то нет и чистой силы.
Поскольку Франклин поднимает груз вертикально, значит, на груз будут действовать две силы: его подъемная сила и сила тяжести. Суммарная сила будет равна сумме сил, действующих на груз.
Поскольку мы только что доказали, что результирующая сила будет равна нулю, мы можем сказать .
Мы знаем массу груза и ускорение, поэтому можем найти подъемную силу.
Сообщить об ошибке
Коробка находится в состоянии покоя и достигает скорости , пройдя расстояние . Какая сила действовала на коробку?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула силы: .
Нам известна масса, но нам нужно вычислить ускорение, чтобы использовать его в формуле.
Мы знаем начальную скорость (нулевая, потому что коробка выходит из состояния покоя), конечную скорость и пройденное расстояние. Используя эти значения, мы можем найти ускорение по формуле .
Подставьте заданные значения и найдите ускорение.
Разделите обе части на .
Теперь мы знаем и ускорение, и массу, что позволяет нам найти силу.
Сообщить об ошибке
Самолет имеет массу . Какова минимальная подъемная сила, необходимая для отрыва самолета от земли?
Возможные ответы:
Правильный ответ:
Пояснение:
В этой задаче на самолет действуют две силы: вес самолета (сила тяжести) и подъемная сила. Поскольку мы ищем минимальную силу, чтобы поднять самолет, мы можем положить две силы равными друг другу: .
Поскольку мы ищем минимальную силу, чтобы поднять самолет, мы можем положить две силы равными друг другу: .
Мы можем рассчитать гравитационную силу, используя массу.
Возвращаясь к исходному уравнению, видим, что подъемная сила должна быть .
Сообщить об ошибке
Какое усилие требуется для ускорения ящика?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула силы: . Подставьте полученные значения и решите:
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по физике для старших классов
6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept
Обзор силы гравитации Рона Куртуса
SfC Home > Physics > Gravity >
Рон Куртус
Гравитация — это сила , которая притягивает объекты к Земле. Это аппроксимация гравитационной силы , которая притягивает объекты массы друг к другу на больших расстояниях.
Это аппроксимация гравитационной силы , которая притягивает объекты массы друг к другу на больших расстояниях.
( Примечание : Гравитация на Луне — это сила, которая притягивает объекты к поверхности Луны.)
Уравнение силы тяжести: F = мг , где g — ускорение свободного падения. Единицы могут быть обозначены в метрической (СИ) или английской системе. Уравнение также указывает вес объекта ( Вт = мг ).
Главной особенностью этой силы является то, что все объекты падают с одинаковой скоростью, независимо от их массы. Гравитация на Луне и на других планетах имеет разные значения ускорения свободного падения. Однако эффекты силы аналогичны.
У вас могут возникнуть следующие вопросы:
- Что такое уравнение гравитации?
- Какая самая выдающаяся характеристика гравитации?
- Что такое гравитация в другом месте?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения
Полезный инструмент: Преобразование единиц измерения
Уравнение гравитации
Согласно закону всемирного тяготения Ньютона , гравитация — это сила, которая притягивает объекты друг к другу. Для объектов, относительно близких к Земле, эта сила называется гравитацией, и ее уравнение:
F = мг
где
- F — сила, притягивающая объекты к Земле
- м это масса объекта
- g ускорение свободного падения; это число является константой для всех масс материи
- мг является произведением м умножить на г
Примечание : Для проверки того, что сила гравитации равна силе тяжести для объектов, близких к Земле, см. Факторы постоянной гравитации.
Ускорение свободного падения
Ускорение под действием силы тяжести на Земле обозначается как g . Его значение:
Его значение:
г = 9,807 метра на секунду в квадрате (м/с 2 ) в метрической системе или системе СИ
г = 32,2 фута на секунду в квадрате (фут/с 2 ) в английской системе мер
Примечание : Поскольку в большинстве учебников используется г = 9,8 м/с 2 и 32 фут/с 2 , в этих уроках мы также будем использовать округленную версию.
В уравнении F = мг вы должны использовать ту же систему измерения массы, м , что и для г .
Примечание: Некоторые учебники небрежно определяют g как ускорение силы тяжести . Это неверно и вводит в заблуждение, поскольку гравитация не ускоряет. Выражение должно быть ускорение из-за силы тяжести , что является правильным описанием г .
Следует соблюдать осторожность при определении научных терминов.
Вес и масса
Вес объекта данной массы равен силе тяжести на этом объекте:
вес = мг
где
- w — вес в ньютонах (Н) или фунт-сила (фунт)
- m — масса в килограммах или фунт-масса (lb-mass)
Примечание : Часто возникает путаница в отношении обозначения веса и массы.
Хотя килограмм считается единицей массы, он часто используется для обозначения веса. Вы должны знать, что вес 1 кг массы равен w = 9,8 ньютона.
Кроме того, фунт считается силой, но его часто называют массой. Масса 1 фунта силы равна 1/32 фунта массы.
Опять же, вы должны быть точны в изложении научных терминов.
Взвешивание объекта
Вы можете определить вес объекта на калиброванных весах — обычно с пружиной, противодействующей силе веса.
Массу объекта можно измерить с помощью весов, сравнивая с объектом данной массы.
Объекты падают с одинаковой скоростью
Наиболее выдающейся характеристикой гравитации является тот факт, что все объекты падают с одинаковой скоростью, если предположить, что сопротивление воздуха незначительно. Это потому, что ускорение свободного падения г , является константой для всех объектов, независимо от их массы.
Это кажется нелогичным, поскольку вы ожидаете, что тяжелый объект упадет быстрее, чем объект с меньшим весом. Но это факт. Попробуйте сбросить два предмета одновременно с одинаковой высоты, убедившись, что они достаточно тяжелые, чтобы на них не влияло сопротивление воздуха. Вы увидите, как они ударятся о землю одновременно.
( Дополнительную информацию см. в Принципе эквивалентности гравитации. )
Гравитация в другом месте
Когда вы говорите о гравитации, вы имеете в виду гравитацию около Земли. Однако то же самое гравитационное уравнение верно для объектов вблизи Луны или других планет, за исключением того, что значение g другое. В таких случаях вы обычно говорите, где находится гравитация, например, «гравитация на Луне» или «гравитация на Марсе».
В таких случаях вы обычно говорите, где находится гравитация, например, «гравитация на Луне» или «гравитация на Марсе».
Гравитация на Луне
Сила гравитации на Луне составляет примерно 1/6 силы тяжести на Земле для данной массы. Таким образом:
F м = мг м
где
- F m сила или вес на Луне
- m это масса объекта
- г м ускорение свободного падения на Луне
Значение для г м равно 1,6 м/с 2 или 5,3 фут/с 2 .
Вес и масса на Луне
Значение для г м составляет примерно 1/6 от значения для г на Земле. Таким образом, объект на Луне будет весить примерно 1/6 своего веса на Земле.
Используя пружинные весы, если вы весите 60 кг (132 фунта) на Земле, вы будете весить всего 10 кг (22 фунта) на Луне. Однако, используя весы как на Земле, так и на Луне, ваша масса будет одинаковой.
Однако, используя весы как на Земле, так и на Луне, ваша масса будет одинаковой.
Падающие предметы
Если вы сбросите на Луну два предмета разного веса, они упадут на землю с одинаковой скоростью. Вам не придется беспокоиться об эффекте сопротивления воздуха, поскольку на Луне нет воздуха.
Так как г м = г /6, объекты будут падать медленнее.
( См. Уравнения гравитации для падающих предметов, а затем примените г м , чтобы получить другие значения. )
Сводка
Гравитация — это сила, которая притягивает объекты к Земле. Это частный случай гравитации. Уравнение для силы гравитации: F = мг, что приводит к тому, что все объекты падают с одинаковой скоростью, независимо от их массы. Гравитация на Луне и гравитация на других планетах имеют разные значения ускорения свободного падения, но действие силы похоже.
Будьте настолько велики, насколько это возможно,
Ресурсы и ссылки
Рон Куртус. ДЕРЕВАНИЯ
ДЕРЕВАНИЯ
Веб -сайты
9000 Gravity Resources.SICT of Gravity — Университет 9000 9000 9000 4.0350 — 177 40350 — Университет 9000 9000 9000 4.0350 — 177 40350 — 17 40350 — 17 40350 — 177. — Википедия
Как работает гравитация? — Как это работает
Стандартная гравитация — Среднее значение по сравнению с изменением из-за положения на Земле — Википедия
Международная формула силы тяжести — Изменение силы тяжести в зависимости от расстояния от экватора — Отдел геофизики. University of Oklahoma
Я чувствую себя «легче», когда поднимаюсь в гору, но так ли это? — Часто задаваемые вопросы о Национальной физической лаборатории
Книги
(Примечание: Школа чемпионов может получать комиссионные за покупку книг)
Книги с самым высоким рейтингом по простой гравитационной науке
Вопросы и комментарии
У вас есть вопросы, комментарии или мнения по этому вопросу? Если это так, отправьте электронное письмо с вашим отзывом. Я постараюсь вернуться к вам как можно скорее.
Я постараюсь вернуться к вам как можно скорее.
Поделиться этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_overview.htm
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа чемпионов
Темы гравитации
Обзор силы гравитации
Формула работы: физическое уравнение с примерами
В физике мы говорим, что сила совершает работу , если приложение силы смещает объект в направлении действия силы. Другими словами, работа эквивалентна приложению силы на расстоянии. Объем работы, которую совершает сила, прямо пропорционален тому, насколько далеко эта сила перемещает объект. Общая формула для работы и для определения количества работы, выполненной над объектом:
Объем работы, которую совершает сила, прямо пропорционален тому, насколько далеко эта сила перемещает объект. Общая формула для работы и для определения количества работы, выполненной над объектом:
- Вт = F × D × cos(Θ)
, где W — количество работы, F — вектор силы, D — величина смещения, а Θ — угол между вектором силы и вектором смещения. Единицей работы в системе СИ является джоулей ( Дж ), а его размеры равны кг•м 2 /с 2 . Другой способ понять это состоит в том, что один джоуль эквивалентен количеству энергии, передаваемой, когда сила в один ньютон перемещает объект на расстояние в один метр.
Формула работы
Всякий раз, когда сила перемещает объект, мы говорим, что работа была выполнена. Когда мяч катится с холма под действием силы тяжести, когда вы поднимаете свой рюкзак с земли, когда внутренний двигатель вашего автомобиля прикладывает силу, заставляющую ваши колеса двигаться; все эти события связаны с силой, перемещающей объект на расстояние, и поэтому требуют некоторой работы. В тех случаях, когда к объекту приложена сила, но он не перемещается, работа не совершается. Таким образом, сила человека, толкающего стену небоскреба, не совершает никакой работы, поскольку небоскреб не движется. Рассмотрим несколько простых примеров, иллюстрирующих понятие работы.
В тех случаях, когда к объекту приложена сила, но он не перемещается, работа не совершается. Таким образом, сила человека, толкающего стену небоскреба, не совершает никакой работы, поскольку небоскреб не движется. Рассмотрим несколько простых примеров, иллюстрирующих понятие работы.
Примеры задач
(1)
К ящику массой 15 кг в горизонтальном направлении приложена сила в 100 ньютонов, которая перемещает его на 5 метров по горизонтали. Сколько работы было сделано?
В этом случае мы знаем, что сила равна 100 Н, а расстояние – 5 метров. Мы также знаем, что, поскольку сила приложена в том же направлении, что и смещение, Θ равно 0. Таким образом, мы подставляем эти значения в наше уравнение
и получим:
- Вт = 100(5)cos(0)= 500 Дж
Таким образом, сила в 100 Н совершила 500 джоулей работы 5 метров 8,90 90 90
(2)
На столе лежит двухкилограммовая книга. К книге приложена сила 64 Н под углом 120° к горизонтали, которая перемещает книгу на 3 м в горизонтальном направлении. Сколько работы было сделано?
Сколько работы было сделано?
В данном случае мы знаем силу 64 Н и расстояние 3 м. Мы также знаем, что между углом направления приложенной силы и направлением движения существует угол 120°. Таким образом, подставив эти значения в наше удобное уравнение, мы получим:
- Вт = 64(3)cos(120)= 156,32 Дж
Итак, сила 64 Н под углом 120° выполнила 156,32 джоулей 3 метра 0 90 работы по перемещению книги 9001
(3)
Линда поднимает чемодан с усилием 300 Н на 3 лестничных пролета на общую высоту 16 метров. Затем она толкает чемодан с силой 100 Н оставшиеся 8 метров до своего гостиничного номера. Сколько работы было сделано за всю ее поездку?
Этот вопрос требует 2 отдельных шагов. Ее поездка состоит из двух основных частей, поэтому мы можем рассчитать работу, проделанную для каждой части в отдельности, а затем объединить два значения, чтобы получить общий объем выполненной работы. В первой части своего пути она прикладывает силу 300 Н, чтобы переместить чемодан на 16 метров по вертикали, поэтому количество выполненной работы равно:
- Вт 1 = 300(16)cos(0)= 4800 Дж
Таким образом, в первой части пути было потрачено 4800 Дж. Что касается второй части, мы знаем, что сила в 100 Н переместила чемодан по горизонтали на 8 метров, поэтому общая работа, выполненная на втором участке пути, равна:
Что касается второй части, мы знаем, что сила в 100 Н переместила чемодан по горизонтали на 8 метров, поэтому общая работа, выполненная на втором участке пути, равна:
- Вт 2 =100(8)cos(0) = 800 Дж
Объединение двух значений каждой части пути дает:
- Вт Всего = W 1 + W 2 = 4800 + 800 = 5600 Joules
, так что на протяжении всей работы Lindda’s Trip, 5600 Joules . Три основных уравнения, представляющие отношения между энергией, работой и силой. Работа и энергия в физике тесно связаны. В соответствии с принципом работы-энергии увеличение кинетической энергии твердого тела вызывается равной работой, совершаемой над этим телом силой, приложенной к этому телу. В более математических терминах отношение можно выразить следующим образом: , где KE означает кинетическую энергию. , где v обозначает скорость объекта. Единицей кинетической энергии является та же единица работы, что и джоуль. Давайте рассмотрим некоторые задачи, чтобы изучить эти математические отношения. Осел и Дидди Конг сидят в 90-килограммовой вагонетке, которая изначально движется горизонтально со скоростью 5 м/с. Носорог Рэмби толкает вагонетку сзади и ускоряет ее, так что теперь она движется со скоростью 11 м/с. Сколько работы Рэмби проделал с вагонеткой? Чтобы решить эту задачу, нам сначала нужно вычислить начальную кинетическую энергию вагонетки и ее конечную кинетическую энергию. Зная эти значения, мы можем определить общий объем работы. Мы знаем как скорость, так и массу вагонетки, поэтому мы можем определить общую кинетическую энергию в начале и в конце. Конечная кинетическая энергия вагонетки 5 =(1/2)( Следовательно, общая работа, выполненная на вагонетке, равна 5545−1125= 4420 Дж . «Наука — это знание последствий и зависимость одного факта от другого». – Томас Гоббс Автомобиль массой 1300 кг движется со скоростью 18 м/с. Если над автомобилем совершить работу 60000 джоулей, какова будет его конечная скорость? Вопрос потребует немного алгебры. Во-первых, мы должны определить начальную кинетическую энергию автомобиля. Начальная кинетическая энергия автомобиля равна: Так как мы знаем общую работу системы (60000 J) мы можем вычислить конечную кинетическую энергию автомобиля: Теперь, поскольку мы знаем конечную кинетическую энергию и массу автомобиля, мы можем определить его конечную скорость следующим образом 5 KE Окончательный = (1/2) кг*V 2 444444444444444444444444444444444444444444444444444444444444444444444444444444н. Конечная скорость автомобиля будет 20,4 м/с . Таким образом, мы говорим, что работа совершается всякий раз, когда сила перемещает объект на расстояние. Величина работы равна величине силы, умноженной на пройденный путь. Работа и кинетическая энергия тесно взаимосвязаны и могут использоваться для определения друг друга. К концу этого раздела вы сможете: Другой интересной силой в повседневной жизни является сила сопротивления объекта, когда он движется в жидкости (газе или жидкости). Вы чувствуете силу сопротивления, когда проводите рукой по воде. Вы также можете почувствовать это, если пошевелите рукой во время сильного ветра. , где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρ — плотность жидкости. Спортсмены, а также конструкторы автомобилей стремятся уменьшить силу сопротивления, чтобы сократить время своих гонок. (См. рис. 1). «Аэродинамическая» форма автомобиля может уменьшить силу сопротивления и, таким образом, увеличить расход топлива автомобиля. Рис. 1. От гоночных автомобилей до бобслеистов аэродинамическая форма имеет решающее значение для достижения максимальной скорости. Бобслей создан для скорости. Они имеют форму пули с коническими плавниками. (кредит: армия США, Wikimedia Commons) Значение коэффициента аэродинамического сопротивления, C , определяется опытным путем, обычно с использованием аэродинамической трубы. (См. рис. 2). Рис. 2. Исследователи НАСА тестируют модель самолета в аэродинамической трубе. (кредит: НАСА/Эймс) Коэффициент лобового сопротивления может зависеть от скорости, но мы будем считать, что здесь он является константой. В таблице 1 перечислены некоторые типичные коэффициенты сопротивления для различных объектов. Обратите внимание, что коэффициент сопротивления является безразмерной величиной. На скоростях шоссе более 50% мощности автомобиля используется для преодоления сопротивления воздуха. Наиболее экономичная крейсерская скорость составляет около 70–80 км / ч (около 45–50 миль / ч). Рисунок 3. В мире спорта ведутся серьезные исследования по минимизации сопротивления. Ямочки на мячах для гольфа переделываются, как и одежда, которую носят спортсмены. Велогонщики, а также некоторые пловцы и бегуны носят полные боди. Австралийка Кэти Фриман носила полный костюм на Олимпийских играх 2000 года в Сиднее и выиграла золотую медаль в беге на 400 метров. Многие пловцы на Олимпийских играх 2008 года в Пекине носили комбинезоны (спидометры); это могло бы иметь значение для побития многих мировых рекордов (см. рис. 3). Большинство элитных пловцов (и велосипедистов) бреют волосы на теле. Такие инновации могут сократить миллисекунды в гонке, иногда определяя разницу между золотой и серебряной медалью. Одним из следствий этого является то, что для поддержания целостности спорта необходимо постоянно разрабатывать тщательные и точные правила. Некоторые интересные ситуации, связанные со вторым законом Ньютона, возникают при рассмотрении воздействия сил сопротивления на движущийся объект. Например, рассмотрим парашютиста, падающего в воздухе под действием силы тяжести. На него действуют две силы: сила тяжести и сила сопротивления (без учета выталкивающей силы). Нисходящая сила тяжести остается постоянной независимо от скорости, с которой движется человек. Однако по мере увеличения скорости человека величина силы сопротивления увеличивается до тех пор, пока величина силы сопротивления не сравняется с силой гравитации, что приводит к нулевой чистой силе. Нулевая результирующая сила означает, что ускорение отсутствует, как указано во втором законе Ньютона. В этот момент скорость человека остается постоянной, и мы говорим, что человек достиг своего 9{2}\right)}}\\ & =& \text{98 м/с}\\ & =& \text{350 км/ч}\text{.}\end{массив}\\[/latex] Это означает, что парашютист массой 75 кг достигает максимальной конечной скорости около 350 км/ч, путешествуя в положении согнувшись (головой вперед), сводя к минимуму площадь и сопротивление. В этом интересном занятии исследуется влияние веса на конечную скорость. Соберите вместе несколько вложенных фильтров для кофе. Оставив их в исходной форме, измерьте время, за которое один, два, три, четыре и пять вложенных фильтров упадут на пол с одинаковой высоты (примерно 2 м). (Обратите внимание, что из-за того, что фильтры вложены друг в друга, сопротивление постоянно, а изменяется только масса.) Они довольно быстро достигают конечной скорости, поэтому найдите эту скорость как функцию массы. Постройте конечную скорость против против массы. Также постройте v 2 в зависимости от массы. Какая из этих зависимостей более линейна? Какой вывод вы можете сделать из этих графиков? Найдите конечную скорость парашютиста массой 85 кг, падающего с распростертыми крыльями. Таким образом, конечная скорость v t может быть записана как [латекс]v_{\text{t}}\sqrt{\frac{2mg}{\rho{CA}}}\\[/latex]. Все величины известны, кроме площади проекции человека. Это взрослый (82 кг) падающий распростертый орел. Мы можем оценить фронтальную площадь как A = (2 м)(0,35 м) = 0,70 м 2 . Используя наше уравнение для v , мы находим, что [латекс]\begin{array}{lll}{v}_{\text{t}}& =& \sqrt{\frac{2\left( \текст{85}\текст{кг}\справа)\слева(9{2}\right)}}\\ & =& \text{44 м/с.}\end{array}\\[/latex] Этот результат согласуется со значением для v т упомянутый ранее. 75-килограммовый парашютист, идущий вперед ногами, имел v = 98 м/с. Он весил меньше, но имел меньшую лобовую площадь и, следовательно, меньшее сопротивление воздуха. Размер объекта, падающего в воздухе, представляет собой еще одно интересное применение сопротивления воздуха. Следующая интересная цитата о размерах животных и конечной скорости взята из эссе 1928 года британского биолога Дж.Б.С. Холдейна под названием «О том, чтобы быть подходящего размера». Для мышей и любых мелких животных [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий толчок и уходит, при условии, что земля достаточно мягкая. Крыса убита, человек разбит, а лошадь забрызгана. Ибо сопротивление воздуха движению пропорционально поверхности движущегося объекта. Разделите длину, ширину и высоту животного на десять; его вес уменьшен в тысячную, а поверхность только в сотые. Таким образом, сопротивление падению маленького животного относительно в десять раз превышает движущую силу. Приведенная выше квадратичная зависимость сопротивления воздуха от скорости не выполняется, если объект очень мал, движется очень медленно или находится в более плотной среде, чем воздух. Тогда мы находим, что сила сопротивления прямо пропорциональна скорости. Это соотношение задается законом Стокса , который гласит, что F s = 6 πrηv , где r — радиус объекта, η — вязкость жидкости, а — вязкость жидкости. — скорость объекта. F s = 6 πrηv , где r — радиус объекта, η — вязкость объекта v. Рис. 4. Гуси летят V-образным строем во время длительных миграционных перемещений. Эта форма снижает сопротивление и потребление энергии для отдельных птиц, а также позволяет им лучше общаться. (кредит: Julo, Wikimedia Commons) Хорошими примерами этого закона являются микроорганизмы, пыльца и частицы пыли. Если мы сравним животных, живущих на суше, с животными, живущими в воде, то увидим, как сопротивление повлияло на эволюцию. Рыбы, дельфины и даже массивные киты имеют обтекаемую форму, чтобы уменьшить силы сопротивления. Птицы имеют обтекаемую форму, а мигрирующие виды, которые летают на большие расстояния, часто имеют особые черты, такие как длинная шея. Стаи птиц летят в форме наконечника копья, формируя обтекаемый рисунок (см. Говорят, что Галилей сбросил с Пизанской башни два объекта разной массы. Он измерил, сколько времени потребовалось каждому, чтобы достичь земли. Поскольку секундомеры были недоступны, как, по-вашему, он измерял время их падения? Если бы объекты были одного размера, но разной массы, что, по вашему мнению, он должен был бы наблюдать? Был бы этот результат другим, если бы это было сделано на Луне? Реалистичная лаборатория масс и пружин. Подвесьте грузы к пружинам и отрегулируйте жесткость пружины и демпфирование. Вы даже можете замедлить время. Перевозите лабораторию на разные планеты. Диаграмма показывает кинетическую, потенциальную и тепловую энергию для каждой пружины. 9{2}\\[/latex], где C – коэффициент сопротивления (типичные значения приведены в таблице 1), A – площадь объекта, обращенного к жидкости, а [латекс]\rho\\[ /латекс] — плотность жидкости. Отношение работы/энергии
 Другими словами, изменение кинетической энергии тела равно работе, совершенной над этим телом. В общем, формула для кинетической энергии объекта:
Другими словами, изменение кинетической энергии тела равно работе, совершенной над этим телом. В общем, формула для кинетической энергии объекта: (4)
 Начальная кинетическая энергия вагонетки:
Начальная кинетическая энергия вагонетки: (5)
 2
2 Сил сопротивления | Физика
Цели обучения
 2\\[/latex], где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρ — плотность жидкости. (Напомним, что плотность — это масса на единицу объема.) Это уравнение также можно записать в более обобщенном виде: . Мы установили показатель степени n для этих уравнений равным 2, потому что, когда объект движется с высокой скоростью в воздухе, величина силы сопротивления пропорциональна квадрату скорости. Как мы увидим через несколько страниц гидродинамики, для малых частиц, движущихся в жидкости с малыми скоростями, показатель степени 92\\[/latex],
2\\[/latex], где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρ — плотность жидкости. (Напомним, что плотность — это масса на единицу объема.) Это уравнение также можно записать в более обобщенном виде: . Мы установили показатель степени n для этих уравнений равным 2, потому что, когда объект движется с высокой скоростью в воздухе, величина силы сопротивления пропорциональна квадрату скорости. Как мы увидим через несколько страниц гидродинамики, для малых частиц, движущихся в жидкости с малыми скоростями, показатель степени 92\\[/latex],
 По этой причине в течение 19Во время нефтяного кризиса 70-х годов в США максимальная скорость на шоссе была установлена на уровне около 90 км / ч (55 миль / ч).
По этой причине в течение 19Во время нефтяного кризиса 70-х годов в США максимальная скорость на шоссе была установлена на уровне около 90 км / ч (55 миль / ч). Таблица 1. Значения коэффициента лобового сопротивления Типичные значения коэффициента лобового сопротивления C . ОБЪЕКТ С Аэродинамический профиль 0,05 Тойота Камри 0,28 Форд Фокус 0,32 Хонда Сивик 0,36 Феррари Тестаросса 0,37 Пикап Dodge Ram 0,43 Сфера 0,45 Внедорожник Hummer h3 0,64 Парашютист (ноги вперед) 0,70 Велосипед 0,90 Парашютист (горизонтальный) 1,0 Круглая плоская пластина 1,12  Боди, такие как этот LZR Racer Suit, установили множество мировых рекордов после их выпуска в 2008 году. Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % меньшее сопротивление. (Фото: НАСА/Кэти Барнсторфф)
Боди, такие как этот LZR Racer Suit, установили множество мировых рекордов после их выпуска в 2008 году. Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % меньшее сопротивление. (Фото: НАСА/Кэти Барнсторфф)
 В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. Эта конечная скорость становится намного меньше после раскрытия парашюта.
В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. Эта конечная скорость становится намного меньше после раскрытия парашюта. Возьми домой эксперимент
Пример 1. A Конечная скорость
 2\\[/latex].
2\\[/latex]. Решение
Обсуждение
 Если вы упадете с 5-метровой ветки дерева, вы, скорее всего, поранитесь — возможно, сломаете кость. Однако маленькая белка делает это все время, не причиняя себе вреда. Вы не достигаете конечной скорости на таком коротком расстоянии, но белка достигает.
Если вы упадете с 5-метровой ветки дерева, вы, скорее всего, поранитесь — возможно, сломаете кость. Однако маленькая белка делает это все время, не причиняя себе вреда. Вы не достигаете конечной скорости на таком коротком расстоянии, но белка достигает.
Закон Стокса
 Поскольку каждый из этих объектов очень мал, мы обнаруживаем, что многие из этих объектов движутся без посторонней помощи только с постоянной (конечной) скоростью. Конечная скорость для бактерий (размером около 1 мкм) может составлять около 2 мкм/с. Чтобы двигаться с большей скоростью, многие бактерии плавают с помощью жгутиков (органелл в форме маленьких хвостов), которые приводятся в действие небольшими двигателями, встроенными в клетку. Отложения в озере могут двигаться с большей конечной скоростью (около 5 мкм/с), поэтому может потребоваться несколько дней, чтобы достичь дна озера после отложения на поверхности.
Поскольку каждый из этих объектов очень мал, мы обнаруживаем, что многие из этих объектов движутся без посторонней помощи только с постоянной (конечной) скоростью. Конечная скорость для бактерий (размером около 1 мкм) может составлять около 2 мкм/с. Чтобы двигаться с большей скоростью, многие бактерии плавают с помощью жгутиков (органелл в форме маленьких хвостов), которые приводятся в действие небольшими двигателями, встроенными в клетку. Отложения в озере могут двигаться с большей конечной скоростью (около 5 мкм/с), поэтому может потребоваться несколько дней, чтобы достичь дна озера после отложения на поверхности. рис. 4). У людей одним из важных примеров упорядочения является форма сперматозоидов, которые должны эффективно использовать энергию.
рис. 4). У людей одним из важных примеров упорядочения является форма сперматозоидов, которые должны эффективно использовать энергию. Эксперимент Галилея
PhET Исследования: массы и пружины

Концептуальные вопросы
Задачи и упражнения
 Найти конечную скорость (в метрах в секунду и километрах в час) парашютиста массой 80,0 кг, падающего в положении «согнувшись» (головой вперед) с площадью поверхности 0,140 м 2 .
Найти конечную скорость (в метрах в секунду и километрах в час) парашютиста массой 80,0 кг, падающего в положении «согнувшись» (головой вперед) с площадью поверхности 0,140 м 2 . (a) Каковы величины сил сопротивления при скорости 70 км/ч и 100 км/ч для Toyota Camry? (площадь лобового сопротивления составляет 0,70 м 2 ) (b) Какова величина силы сопротивления при скорости 70 км/ч и 100 км/ч для автомобиля Hummer h3? (Площадь сопротивления составляет 2,44 м 2 ) Предположим, что все значения точны до трех значащих цифр.
(a) Каковы величины сил сопротивления при скорости 70 км/ч и 100 км/ч для Toyota Camry? (площадь лобового сопротивления составляет 0,70 м 2 ) (b) Какова величина силы сопротивления при скорости 70 км/ч и 100 км/ч для автомобиля Hummer h3? (Площадь сопротивления составляет 2,44 м 2 ) Предположим, что все значения точны до трех значащих цифр. Примем плотность бактерии равной 1,10 × 10 3 кг/м 3 .
Примем плотность бактерии равной 1,10 × 10 3 кг/м 3 .
Закон Стокса: [латекс]{F}_{s}=6\pi{r}\eta{v}\\[/latex] , где r — радиус объекта, η — вязкость жидкости, а v является скоростью объекта
Избранные решения задач и упражнений
1. 115 м/с; 414 км/ч
115 м/с; 414 км/ч
9. 0,76 кг/м·с
Формула кинетического трения
Главная > Формулы > Формулы физики > Формула кинетического трения
Формула кинетического трения
Кинетическое трение — это сила, действующая между движущимися поверхностями. Объект, который перемещается по поверхности, будет испытывать силу в направлении, противоположном его движению. Величина силы зависит от коэффициента кинетического трения между двумя видами материала. Каждая комбинация отличается. Коэффициенту кинетического трения присваивается греческая буква «мю» ( μ ), с индексом « k ». Сила кинетического трения в μ k раз превышает нормальную силу, действующую на объект, и выражается в ньютонах (Н).
force of kinetic friction = (coefficient of kinetic friction)(normal force)
F k = μ k η
F k = force of kinetic friction
μ k = коэффициент кинетического трения
η = нормальная сила (греческая буква «эта»)
Формула кинетического трения Вопросы:
1) Рабочий на складе толкает по полу большую картонную коробку. Коэффициент кинетического трения равен μ k = 0,520. Ящик имеет массу 75,0 кг , и рабочий прикладывает силу 400,0 Н вперед. Какова величина силы трения и какова результирующая сила, перемещающая ящик?
Коэффициент кинетического трения равен μ k = 0,520. Ящик имеет массу 75,0 кг , и рабочий прикладывает силу 400,0 Н вперед. Какова величина силы трения и какова результирующая сила, перемещающая ящик?
Ответ: На плоской поверхности нормальная сила, действующая на объект, равна η = мг . Using this, the formula can be used to find the force of friction:
F k = μ k η
F k = μ k mg
F k = (0.520)(75.0 kg)(9.80 m/s 2 )
F k = 382.2 kg∙m/s 2
F k = 382.2 Н
Сила кинетического трения, действующая в направлении, противоположном движению ящика, равна 382,2 Н. Суммарная сила, действующая на ящик, представляет собой сумму сил. Две силы, которые следует учитывать, — это сила кинетического трения, действующая в направлении, противоположном движению ящика, и сила, действующая со стороны рабочего, которая направлена вперед на 400 Н. Если мы определим «вперед» как положительное направление, результирующая сила составит:
Если мы определим «вперед» как положительное направление, результирующая сила составит:
F net =F worker -F k
F net =400.0 N -382.2 N
F net = 17.8 N
Чистая сила, действующая на ящик, составляет 17,8 Н вперед.
2) Женщина едет на лыжах прямо с заснеженной горки. Коэффициент кинетического трения между лыжами и снегом равен μ k = 0,0800. Холм находится под углом 60,0° к горизонтали. Масса лыжника 55,00 кг . Какова величина силы кинетического трения и какова результирующая сила вдоль направления движения лыжника?
Ответ: На плоской поверхности нормальная сила, действующая на объект, равна η = мг . На поверхности, расположенной под углом к горизонтальной оси, общая сила тяжести, F = мг, должна быть разбита на составляющие. Нормальная сила — это составляющая, перпендикулярная наклонной поверхности, а оставшаяся сила параллельна наклонной поверхности. Нормальная сила равна η = mg cosθ , а оставшаяся составляющая силы равна F = mg sinθ . Используя эту формулу, можно найти величину силы кинетического трения:
Нормальная сила равна η = mg cosθ , а оставшаяся составляющая силы равна F = mg sinθ . Используя эту формулу, можно найти величину силы кинетического трения:
F k = μ k η
F k = μ 4 k мг co F K = (0,0800) (55,00 кг ) (9,80 м/с 2 ) COS (60 °)
F K
F K
F K 99659960496049.39604960496049660 296049604604966046049660 29604604604966049603960596046039365609365659656596560 29665
).0357 кг∙м/с 2
F k = 21,6 Н
Сила кинетического трения противодействует движению лыжника. Сила, которая перемещает лыжника вниз по склону, является оставшейся составляющей силы тяжести, F θ = mg sin θ. Эта сила:
F = Mg SINθ
F = (55,0 кг ) (9,80 м/с 2 ) SIN (60 °)
,9000 4000595997777775775777575757575757575757575757575757575757575757575757575757. 975757575977575977575975759757.975779757797577757. 2 ) 2 )0357 кг∙м/с 2
975757575977575977575975759757.975779757797577757. 2 ) 2 )0357 кг∙м/с 2 F = 466,8 Н
Чистая сила, действующая на лыжника, представляет собой сумму сил. Две силы, которые следует учитывать, — это сила, направленная вниз по склону, и сила кинетического трения, направленная вверх по склону. Если мы определим положительное направление как направление вниз по склону, то есть направление движения лыжника, результирующая сила будет:0564 = 466,8 N -21,6 N
F NET = 445,2 N = 445,2 N = 445,2 n = 445,2 n = 445,2 n = 445,2 n . N .
| Ссылки по теме: Тест по потенциальной и кинетической энергии Тест по химической кинетике и скоростям Примеры определения кинетической энергии Формула кинетической энергии Примеры инерции Примеры трения качения Формула статического трения Формула тормозного пути |
Формула кинетического трения
Работа
РаботаРабота, совершаемая постоянной силой
Предположим, вы поднимаете предмет массой 20 кг с земли на высоту. 1,5 м. Предположим, что вы прилагаете постоянную силу в восходящем направлении.
направление и что вы перемещаете объект вверх с постоянной скоростью.
результирующая сила, действующая на объект, равна нулю. Сила, которую вы прилагаете, равна
по величине и противоположно по направлению силе тяжести. Пока вы поднимаетесь
объект, над которым вы работаете.
1,5 м. Предположим, что вы прилагаете постоянную силу в восходящем направлении.
направление и что вы перемещаете объект вверх с постоянной скоростью.
результирующая сила, действующая на объект, равна нулю. Сила, которую вы прилагаете, равна
по величине и противоположно по направлению силе тяжести. Пока вы поднимаетесь
объект, над которым вы работаете.
Работа Вт, совершаемая над объектом постоянной силой, определяется как W = Ф · д . Он равен величине силы, умноженной на расстояние до объекта.
движется в направлении действия силы.
В приведенном выше примере F = мг = (20 кг) (9,8 м/с 2 ) = 196 Н, W = (196
Н)(1,5 м) = 294 Нм.
Работа — это скаляр, число с единицами измерения. Единица работы СИ Нм = Джоуль (Дж).
Работа » скалярное произведение » или « скалярное произведение »
силы и вектора смещения. Скалярное произведение двух векторов A и B — скалярная величина (число с единицами), равная
произведение величин двух векторов и косинуса наименьшего
угол между ними.
А · В = ABcosθ.
В терминах декартовых компонент векторов А и Б скалярное произведение записывается как
А · В = А х В х + А у В у + А z Б z .
Работа, совершаемая силой, может быть положительной или отрицательной. Если составляющая силы в
направление перемещения положительное, то работа положительна, а если
составляющая силы в направлении перемещения отрицательна, то
произведение отрицательное.
В одном измерении скалярное произведение положительно, если два вектора
параллельны друг другу, и отрицательно, если два вектора антипараллельны
друг к другу, т. е. если они направлены в противоположные стороны.
Пример:
Предположим, вы забыли установить парковочный тормоз, и ваша машина начала катиться.
вниз по холму. Вы тщетно пытаетесь остановить его, дергая изо всех сил. бампер, но машина продолжает двигаться вперед. Вы прилагаете силу к
автомобиль против направления движения. Расстояние, пройденное в
направление силы отрицательное, вы совершаете с автомобилем отрицательную работу. Но
автомобиль тянет вас по ходу движения с силой, равной
величины (третий закон Ньютона). Машина производит на вас положительное впечатление.
бампер, но машина продолжает двигаться вперед. Вы прилагаете силу к
автомобиль против направления движения. Расстояние, пройденное в
направление силы отрицательное, вы совершаете с автомобилем отрицательную работу. Но
автомобиль тянет вас по ходу движения с силой, равной
величины (третий закон Ньютона). Машина производит на вас положительное впечатление.
Схема свободного тела объекта, поднимаемого с постоянная скорость на расстоянии d показано справа.
Суммарная сила, действующая на объект, равна нулю, F a + F г = 0,
Вектор смещения направлен вверх.
Работа, совершенная приложенной силой F a , W = F a ·d = F a д = мгд , положительный.
Работа силы тяжести F g ,
W = F g ·d = -F g d = -mgd , отрицательно.
Суммарная работа всех сил, действующих на объект, W net = F net · d равна нулю.
Проблема:
Для А = 3 i + дж — к , Б = — я + 2 я + 5 к , и C = 2 j — 3 k , найти С ·( А — В ).
Решение:
- Рассуждение:
Оцените скалярное произведение двух векторов. - Детали расчета:
A = 3 i + j — k . B = — i + 2 j + 5 k . А — В = 4 я — j — 6 k . С = 2 j — 3 k . С ·( А — В ) = -2 + 18 = 16.
Проблема:
Объясните, почему работа силы трения скольжения отрицательна. когда объект испытывает смещение на шероховатой поверхности?
Решение:
- Рассуждение:
Сила трения скольжения всегда направлена в сторону, противоположную скорости v = d r /dt. Поэтому он указывает в направлении, противоположном направлению
водоизмещение d r . dW = F f · d r = -F f др.
Поэтому он указывает в направлении, противоположном направлению
водоизмещение d r . dW = F f · d r = -F f др.
Проблема:
При движении частицы по окружности на нее действует сила, направленная центр вращения. Почему эта сила не действует на частицу?
Решение:
- Рассуждение:
Так как в любой точке окружности центростремительная сила перпендикулярна скорости v и, следовательно, к смещению d r скалярное произведение dW = F· d r это ноль.
Проблема:
Во время стрижки газона мальчик толкает газонокосилку на расстояние 350 м. траву с силой 90 Н, направленной по горизонтали. Какую работу выполнил мальчик?
Решение:
- Рассуждение:
Работа, совершаемая над телом постоянной силой, определяется как W = F · d = Fdcosθ.
Здесь F и d указывают в одном направлении, θ = 0, cosθ = 1, - Детали расчета:
Вт = F · d = 90 Н * 350 м = 31500 Дж.
Проблема:
Покупатель в супермаркете толкает тележку с силой 35 Н. направлена под углом 25 o вниз от горизонтали. Найдите работу, выполненную покупателем, когда он проходит по проходу длиной 50 м. длина.
Решение:
- Рассуждение:
Работа, совершаемая над телом постоянной силой, определяется как W = F · d = F x ∆x + F y ∆y + F z ∆z.
Тележка движется в направлении x, ∆y = ∆z = 0,
X-компонента сила F x = Fcosθ = (35 Н)cos(25 o ).
Работает только х-компонента силы, так как нет смещение тележки в направлении Y. - Детали расчета:
Работа, совершаемая покупателем, равна W = F x ∆x = (35 Н)cos(25 o )(50 м) = 1586 Дж.
Рампы
Предположим, вы хотите поднять свой мотоцикл на
свой пикап. Вероятно, вы будете использовать рампу. Вы выберете
длинная доска. Один конец доски будет опираться на кузов грузовика, а
другой конец будет лежать на земле. Вы закатите свой мотоцикл
эта рампа.
Вы выберете
длинная доска. Один конец доски будет опираться на кузов грузовика, а
другой конец будет лежать на земле. Вы закатите свой мотоцикл
эта рампа.
Вы прикладываете силу F a равную по величине и противоположное по направлению компоненту гравитационной силы параллельно рампе. Величина F a равна mgsinθ. Ты переместите мотоцикл на расстояние h/sinθ в направлении действия силы. Работа, которую вы совершаете, равна W = F·d = mgh, где mg — вес вашего мотоцикл и h высота кровати. Если бы вы подняли мотоцикл прямо, вы бы приложили силу, равную его весу. через расстояние ч. Когда вы катите его по рампе, вы должны нажать на это через гораздо большее расстояние. Чтобы выполнить ту же работу, вы, следовательно, нужна гораздо меньшая сила. Рампа обеспечивает механическое преимущество .
Работа = большая сила × малое расстояние = малая сила × большое расстояние .
Работа переменной силы в одном измерении
Если вы не знакомы с интегралами, пожалуйста, перейдите по этой ссылке, прежде чем продолжить.
Краткий обзор определенных интегралов
Работа, совершаемая переменной силой
F только с x-компонентой определяется как
W = ∫ xi xf F(x)dx = lim ∆x—>0 Σ xi xf Ф(х)∆х.
(Символ Σ обозначает сумму.
Σ xi xf F∆x представляет собой сумму произведений F∆x из
от начальной до конечной позиции с шагом ∆x.)
Мы можем построить составляющую силы F
воздействуя на объект в положении x по сравнению с положением x.
Работа силы равна площади под кривой.
График для постоянной силы, действующей от x i до x f показано справа.
Работа силы
W = F(x f — x i ).
Работа, совершаемая переменной силой в трех измерениях
В трех измерениях работа, совершаемая переменной силой, равна W = ∫ r i r f F ·dr = lim ∆ r —>0 Σ r i r f F ·∆ r .
Здесь d r — бесконечно малый отрезок пути от начального
в конечное положение. По компонентам F и d r the integral can be written as
∫ path F ·d r = ∫ path F x dx + ∫ path F y dy + ∫ путь F з дз.
Подъем объекта вблизи поверхности Земли
Чтобы поднять предмет массой m так, чтобы его высота увеличилась на
расстояние h, вы должны приложить среднюю силу mg на расстоянии h.
Работа, которую необходимо выполнить, чтобы поднять предмет, равна W = mgh.
Проблема:
Ящик на 100 Н стоит на земле и крепится к одному концу веревки.
Человек на балконе тянет веревку с постоянной силой 100 Н,
подъем ящика на расстояние 3 м.
а) Какой объем работы выполняет человек?
б) Какую работу совершает сила тяжести?
Решение:
- Рассуждение:
Человек подтягивается, и ящик движется вверх в направлении действия силы.
Работа, совершаемая человеком, положительна, W = Fd = mgd = (100 Н)d.
Сила тяжести 100 Н направлена вниз, в то время как ящик движется вверх. Гравитация совершает отрицательную работу. - Детали расчета:
(a) Работа, выполненная человеком, равна W = (100 Н) * (3 м) = 300 Дж.
(б) Гравитация совершает 300 Дж отрицательной работы.
Проблема:
(a) Рассчитайте работу, выполненную на кабине лифта массой 1500 кг
его трос, чтобы поднять его на 40 м с постоянной скоростью, при условии, что сила трения усредняется
100 Н.
б) Какую работу совершает над кабиной лифта
гравитационная сила в этом процессе?
Решение:
- Рассуждение:
Кабина лифта весит 1500*9,8 Н = 14700 Н. Чтобы заставить кабину двигаться со постоянной скорости, результирующая сила, действующая на него, должна быть равна нулю. Сила кабеля воздействующая на автомобиль должна иметь величину 14800 Н, чтобы компенсировать вес и сила трения 100 Н направлена в противоположном направлении.


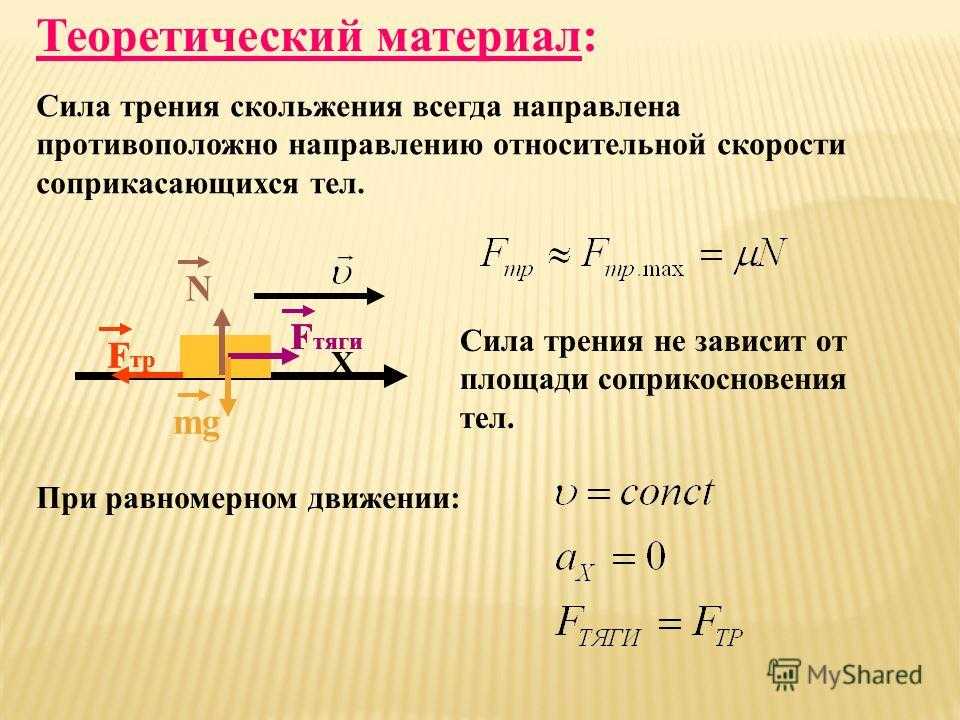
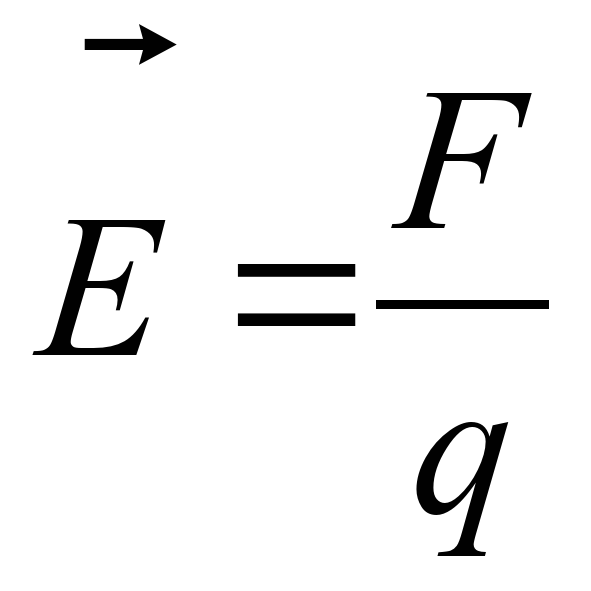 Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.
Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.

 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC


 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT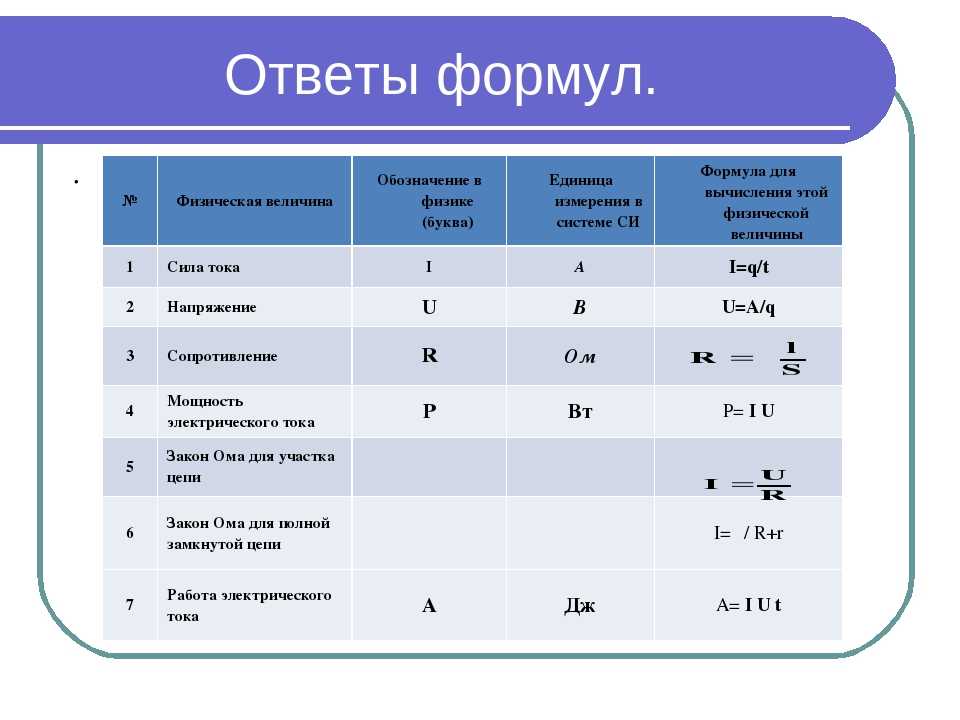 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2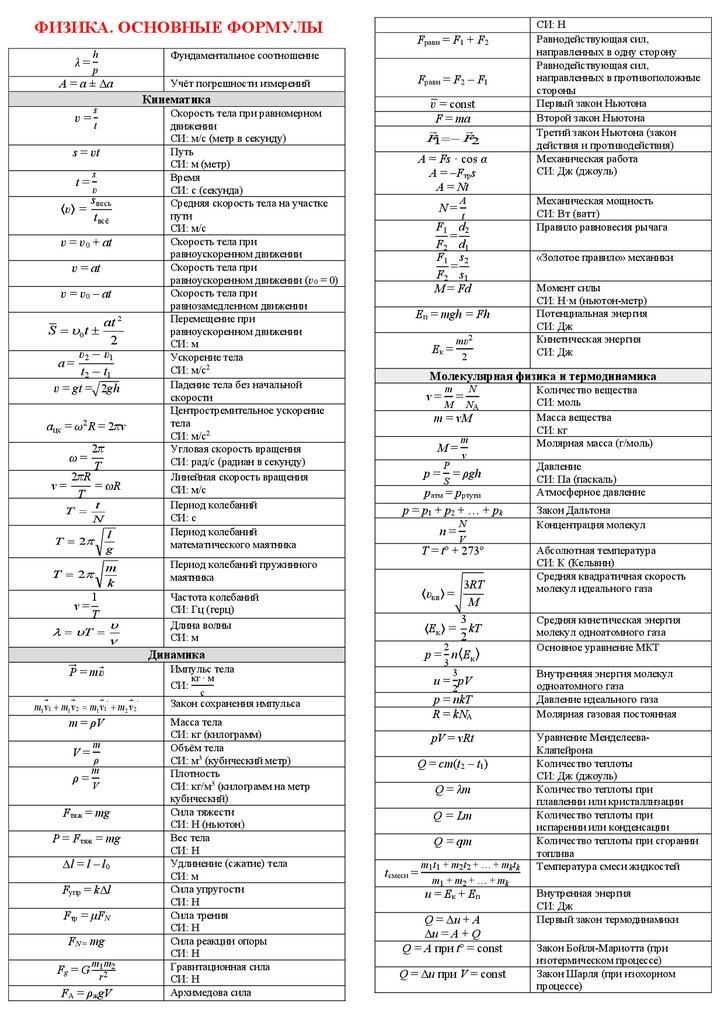 контура T=2π ∙√LC
контура T=2π ∙√LC
 Организационный этап.
Организационный этап. 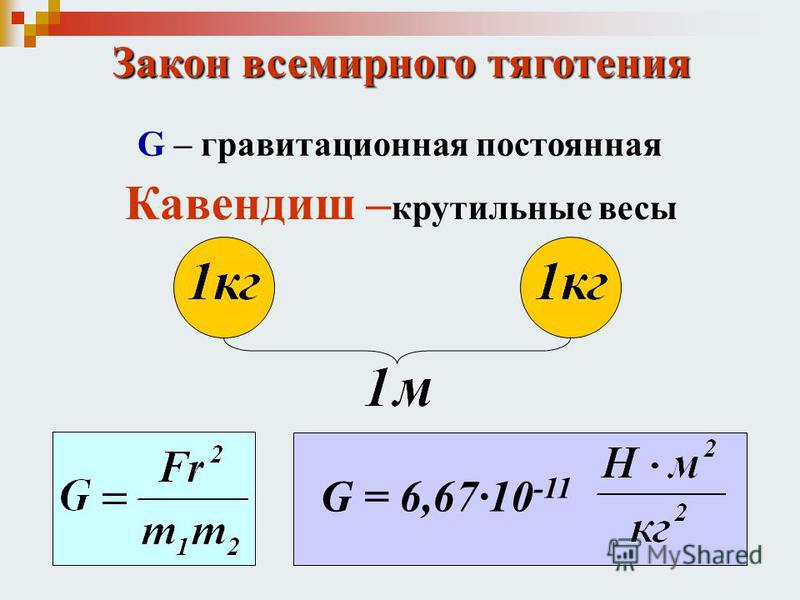




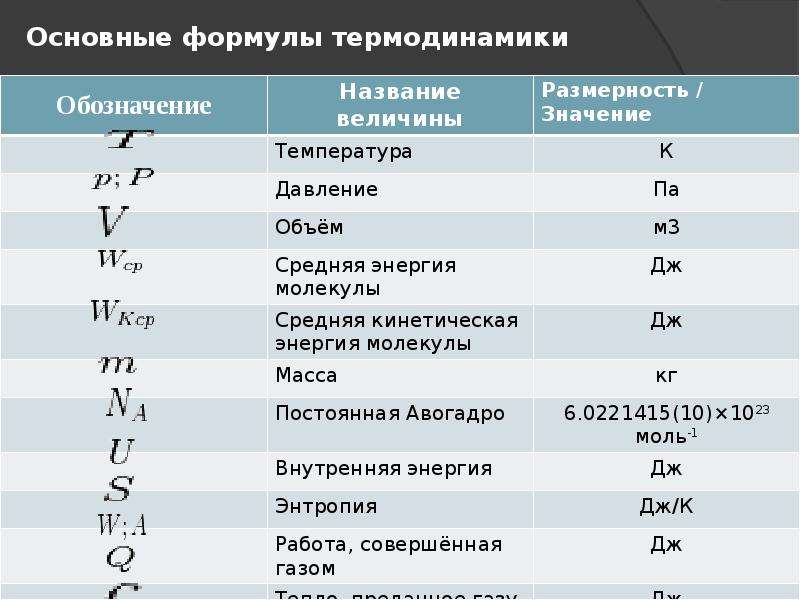
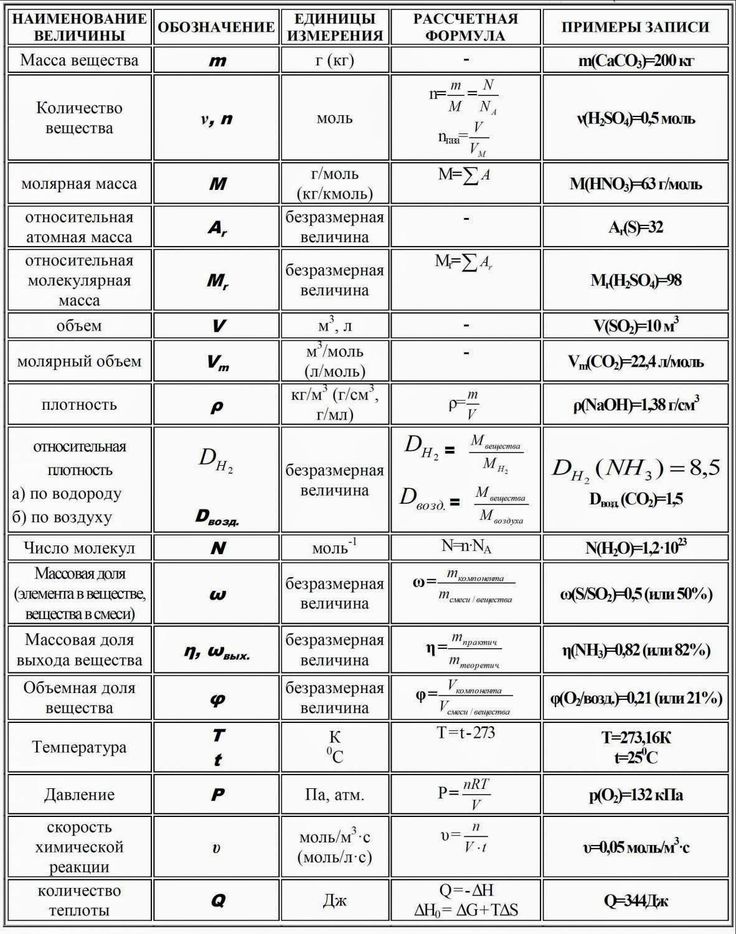


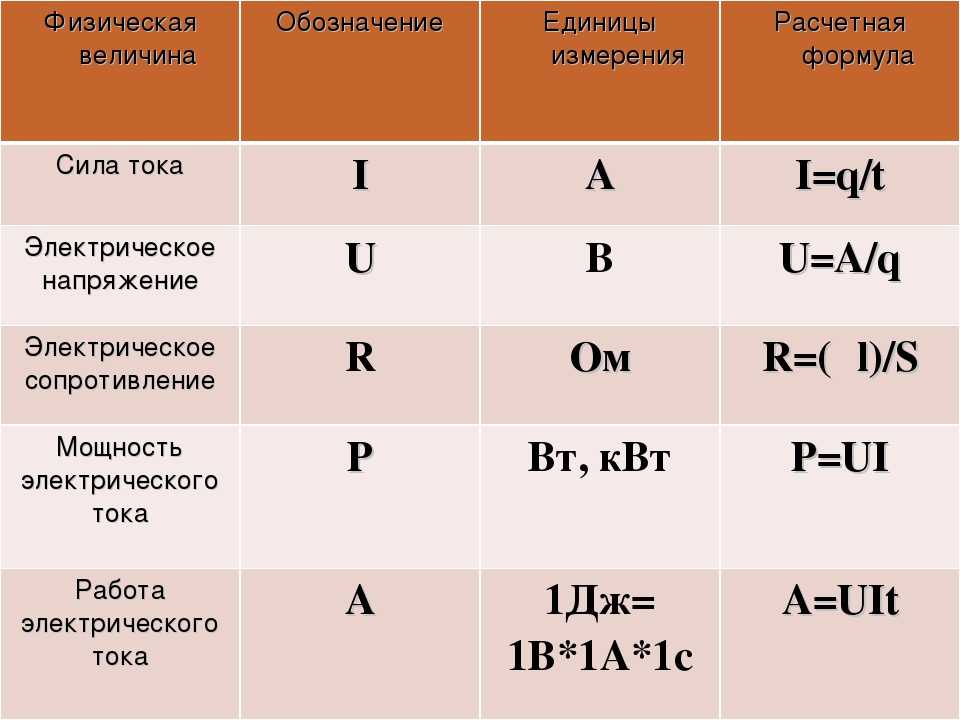

 д.
д.
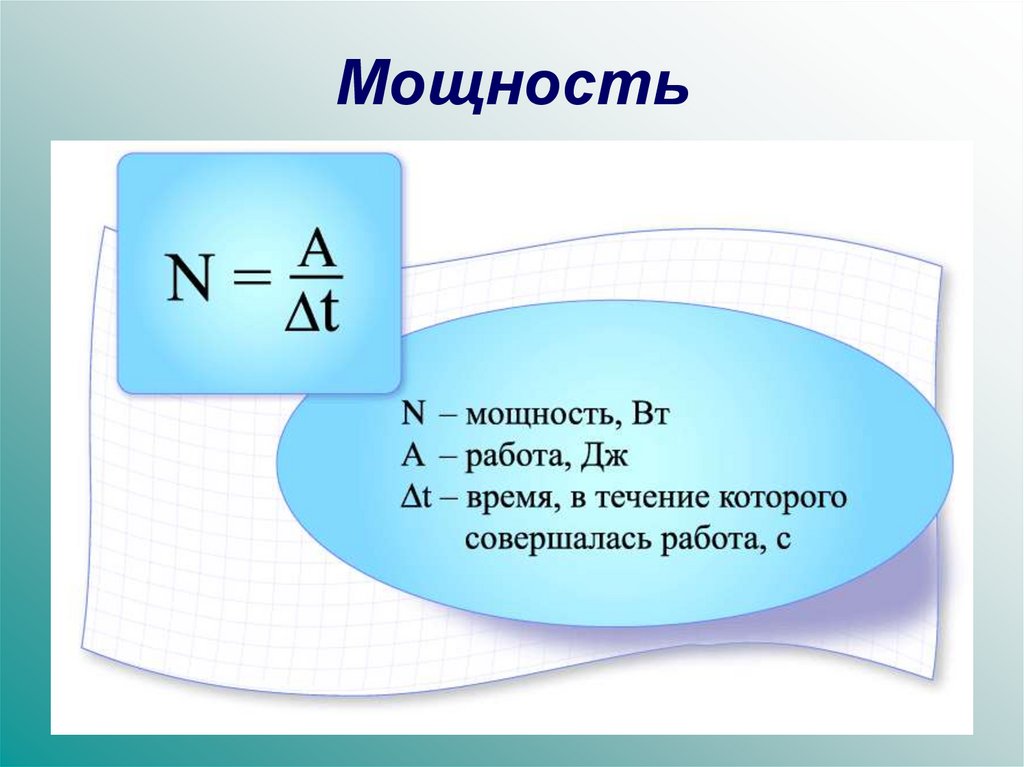

 КПД установки составляет 50% . чему равна масса груза если известно что электродвигатель работает под напряжением 360 В и потребляет силу тока 20 А
КПД установки составляет 50% . чему равна масса груза если известно что электродвигатель работает под напряжением 360 В и потребляет силу тока 20 А Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона: Если тело однородное ( ), то масса может быть рассчитана как:
Если тело однородное ( ), то масса может быть рассчитана как: 2. ESLI TELO STOIT NA PODSTAVKE — VES TELA P = mg — SILA, S KOTOROI TELO DAVIT NA PODSTAVKU. A TI NE SMEESHSJA NAD LJUDJAMI, GIRL OR GUY? SMOTRI MNE. NAROD SIR, NO MUDR!
2. ESLI TELO STOIT NA PODSTAVKE — VES TELA P = mg — SILA, S KOTOROI TELO DAVIT NA PODSTAVKU. A TI NE SMEESHSJA NAD LJUDJAMI, GIRL OR GUY? SMOTRI MNE. NAROD SIR, NO MUDR! 2/2
2/2
 Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
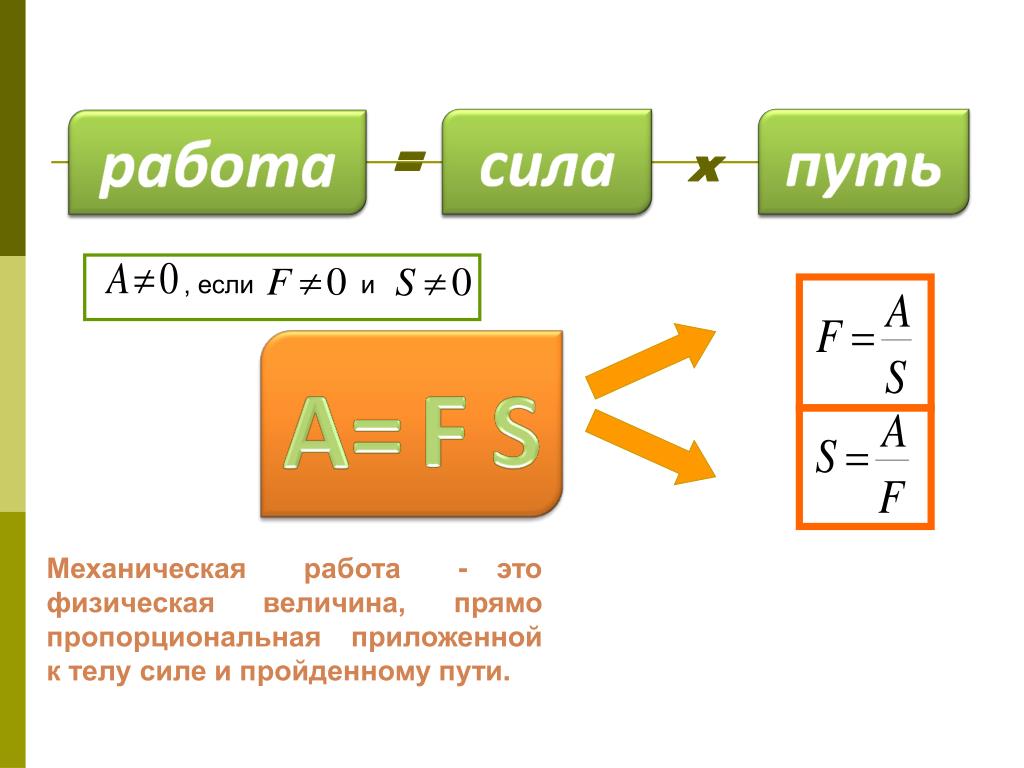
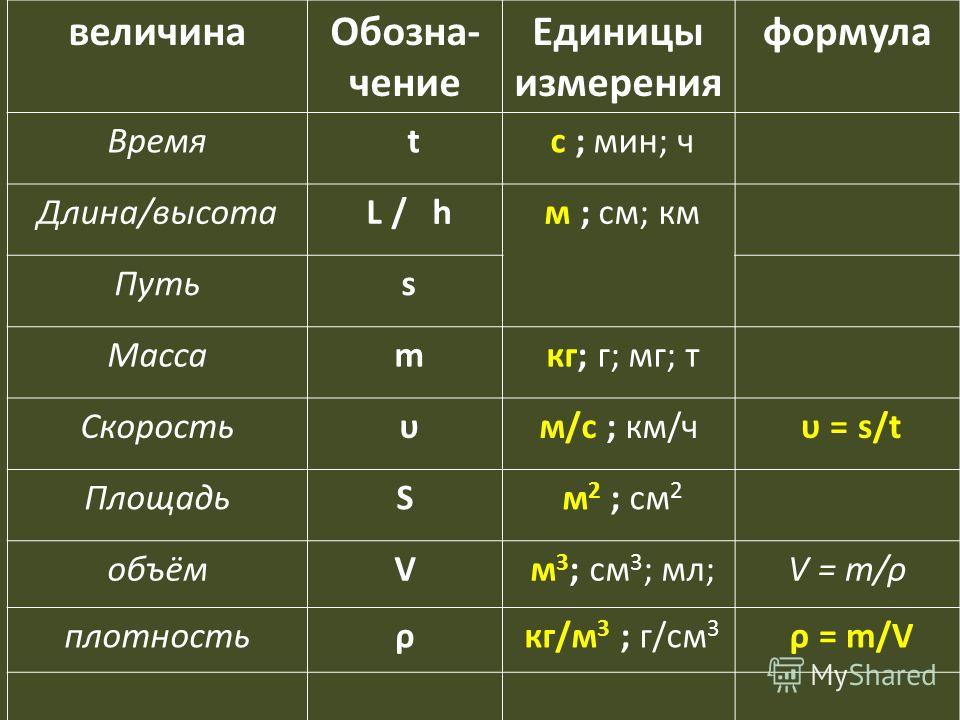 Радиоактивность
Радиоактивность ру. Обязательно посмотрите!
ру. Обязательно посмотрите! То есть бочка на 200 литров имеет объем 2 м³.
То есть бочка на 200 литров имеет объем 2 м³. Молярная масса йодида натрия – это сумма молярных масс каждого элемента: M (NaI)=M (Na)+M (I). Значение молярной массы каждого элемента можно вычислить по таблице, а можно с помощью онлайн-калькулятора на сайте : M (NaI)=M (Na)+M (I)=23+127=150 (г/моль).
Молярная масса йодида натрия – это сумма молярных масс каждого элемента: M (NaI)=M (Na)+M (I). Значение молярной массы каждого элемента можно вычислить по таблице, а можно с помощью онлайн-калькулятора на сайте : M (NaI)=M (Na)+M (I)=23+127=150 (г/моль). Масса вещества растворенного X не изменяется m (X)=m’(X). Масса раствора увеличивается на массу добавленной воды m’ (р)=m (р)+m (H 2 O).
Масса вещества растворенного X не изменяется m (X)=m’(X). Масса раствора увеличивается на массу добавленной воды m’ (р)=m (р)+m (H 2 O).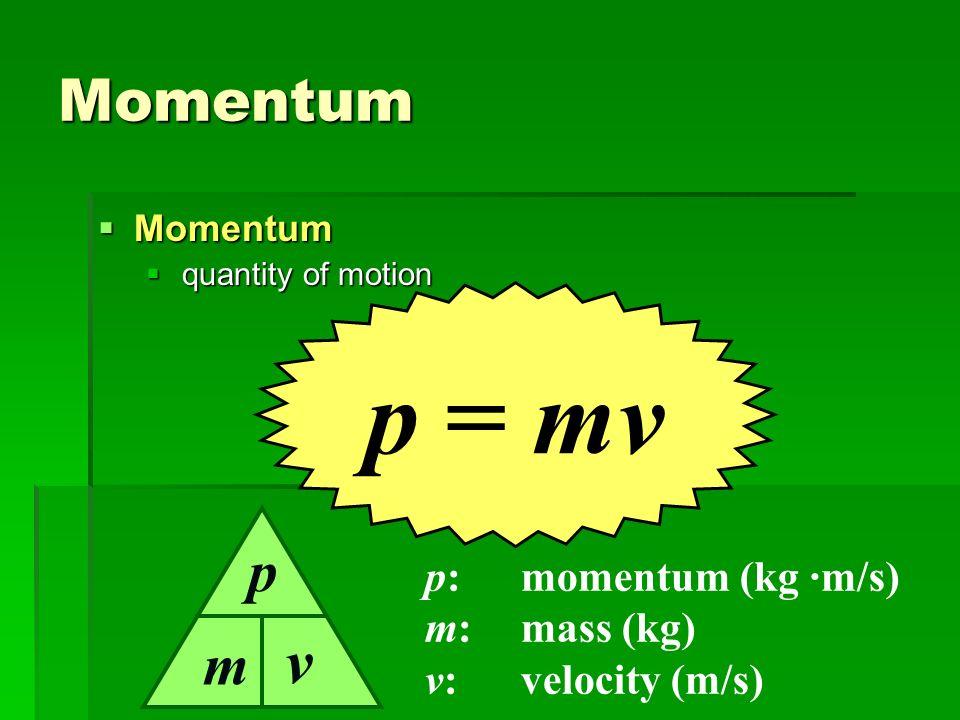 Теоретическая масса получаемого продукта всегда больше практической, в связи с погрешностью реакции, и составляет 100%. Если в задаче не дается масса продукта, полученного в практической реакции, значит, она принимается за абсолютную и равна 100%.
Теоретическая масса получаемого продукта всегда больше практической, в связи с погрешностью реакции, и составляет 100%. Если в задаче не дается масса продукта, полученного в практической реакции, значит, она принимается за абсолютную и равна 100%. Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения СИ.
Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения СИ. 5 тонн
5 тонн метров березовых дров.
метров березовых дров.  Для расчета массы тела в физике требуется знать две его величины: плотность материала тела и его объем.
Для расчета массы тела в физике требуется знать две его величины: плотность материала тела и его объем. Вам понадобитсяТаблица плотностей,…
Вам понадобитсяТаблица плотностей,…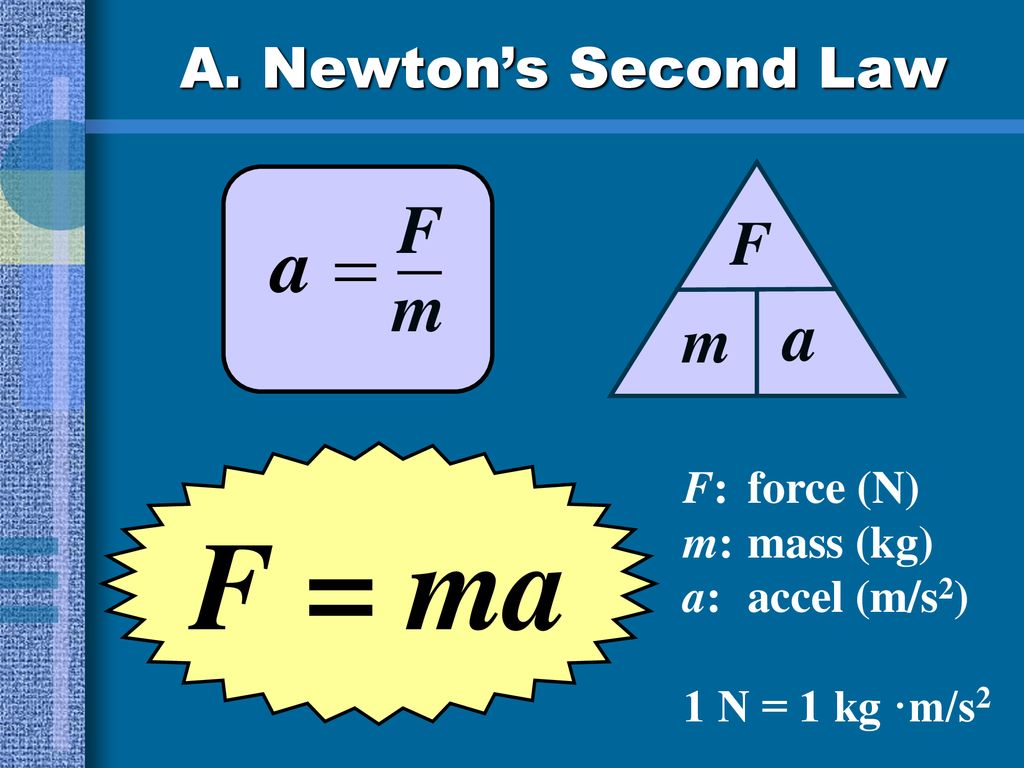 В современной физической науке есть разграничение понятия «масса»: гравитационная масса (как степень воздействия тела на земную гравитацию) и инертная масса (какое…
В современной физической науке есть разграничение понятия «масса»: гравитационная масса (как степень воздействия тела на земную гравитацию) и инертная масса (какое…

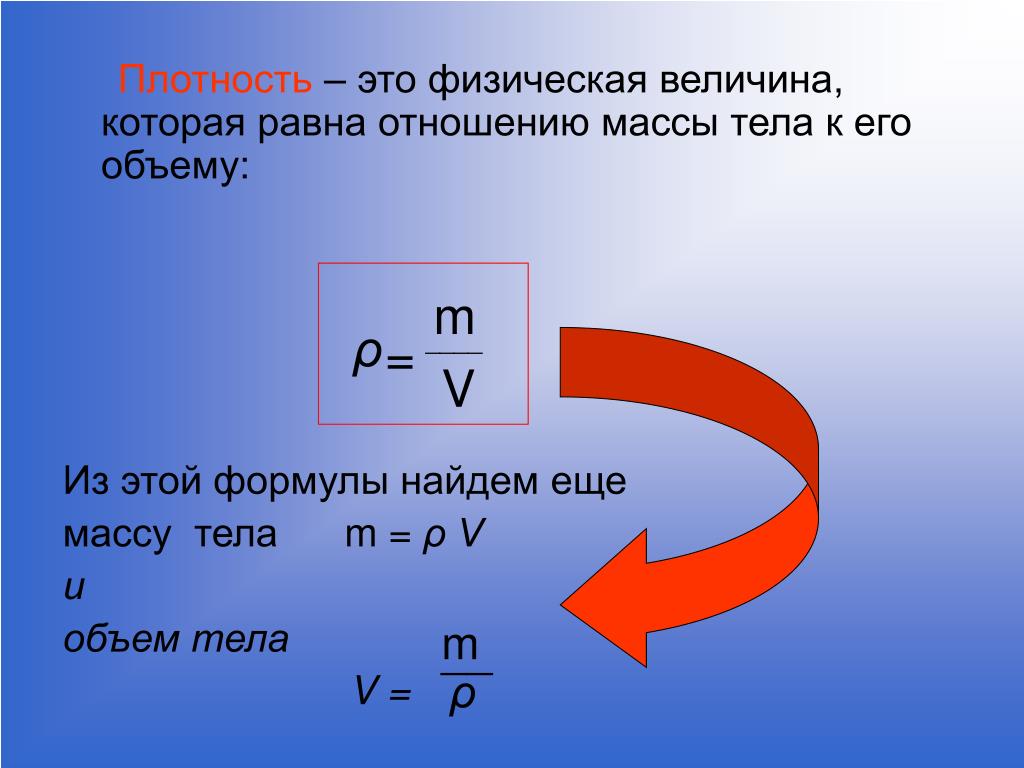
 Для того чтобы решить задачу, как найти массу тела, вам требуется знать его объем и плотность.
Для того чтобы решить задачу, как найти массу тела, вам требуется знать его объем и плотность.

 Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.
Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.  Две массы, м 1 и м 2 , разделенные расстоянием, r , притягивают друг друга в пропорции гравитационная постоянная Г :
Две массы, м 1 и м 2 , разделенные расстоянием, r , притягивают друг друга в пропорции гравитационная постоянная Г :  Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом.
Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом.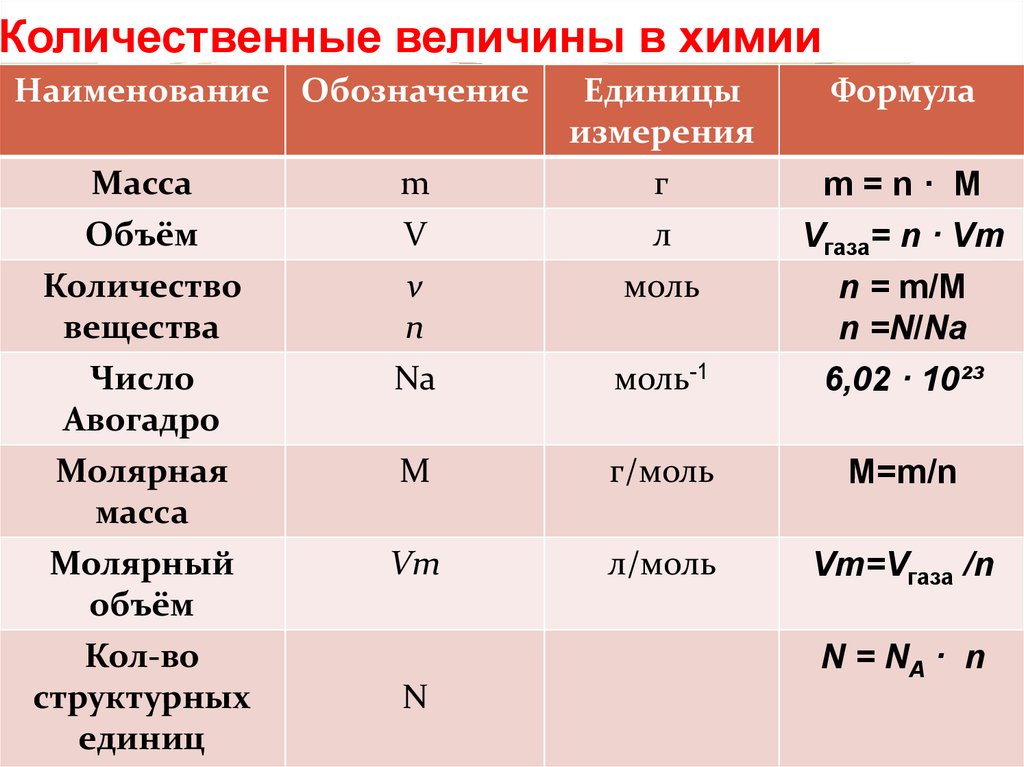

 Вблизи поверхности Земли
Вблизи поверхности Земли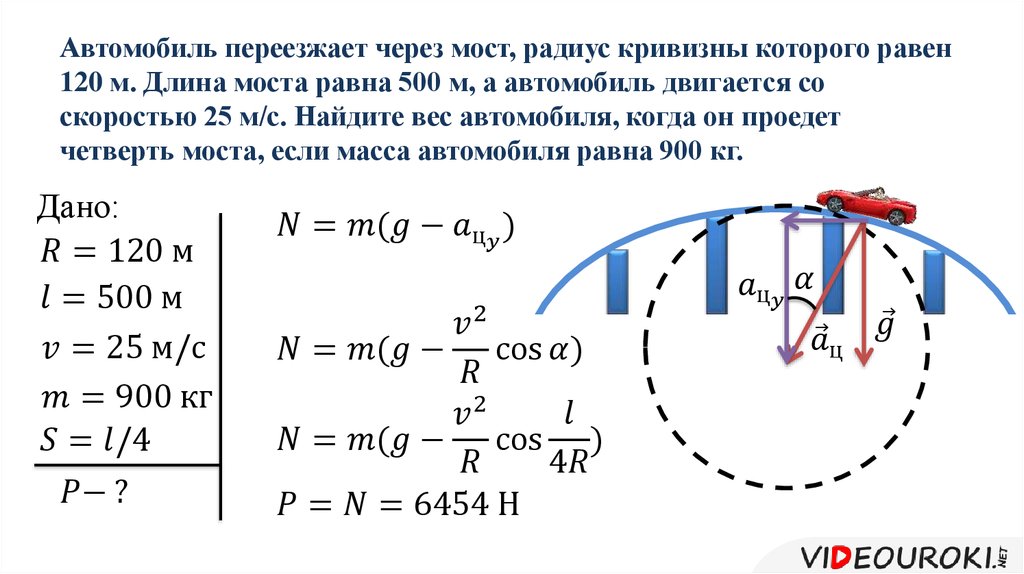 5.7).
5.7). У всех планет это отношение одинаково, так как они вращаются вокруг одной и той же звезды.
У всех планет это отношение одинаково, так как они вращаются вокруг одной и той же звезды. somit.ru/fisika7_1.html — анимация, демонстрирующая причину смены дня и ночи на Земле и движение Луны.
somit.ru/fisika7_1.html — анимация, демонстрирующая причину смены дня и ночи на Земле и движение Луны. Работа опубликована в Physical Review Letters.
Работа опубликована в Physical Review Letters. Мы уже рассказывали ранее про противоречие в экспериментах по измерению частоты перехода 1S-3S атома водорода. Такое расхождение наталкивает на мысль о том, что загадка радиуса протона, вероятно, имеет технический, а не фундаментальный характер.
Мы уже рассказывали ранее про противоречие в экспериментах по измерению частоты перехода 1S-3S атома водорода. Такое расхождение наталкивает на мысль о том, что загадка радиуса протона, вероятно, имеет технический, а не фундаментальный характер. В результате новой обработки данных обеих групп физики смогли существенно сблизить их значения.
В результате новой обработки данных обеих групп физики смогли существенно сблизить их значения. Важно, что при этом такая интерполяция способна уловить как локальные, так и глобальные особенности поведения функции, что оказалось достаточно для вычисления производной от формфактора в точке с нулевым импульсом.
Важно, что при этом такая интерполяция способна уловить как локальные, так и глобальные особенности поведения функции, что оказалось достаточно для вычисления производной от формфактора в точке с нулевым импульсом. 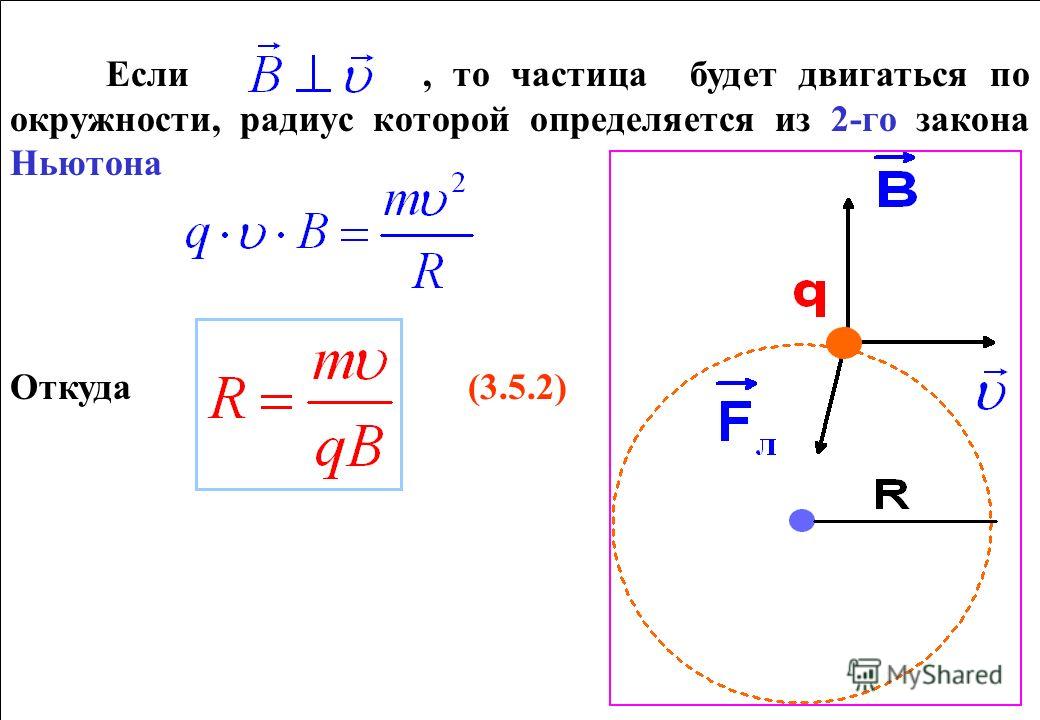
 Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
 Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Проведем радиусы к обеим точкам и обозначим угол между ними через ?. Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Тогда можно сказать, что длина хорды s равна длине дуги АВ при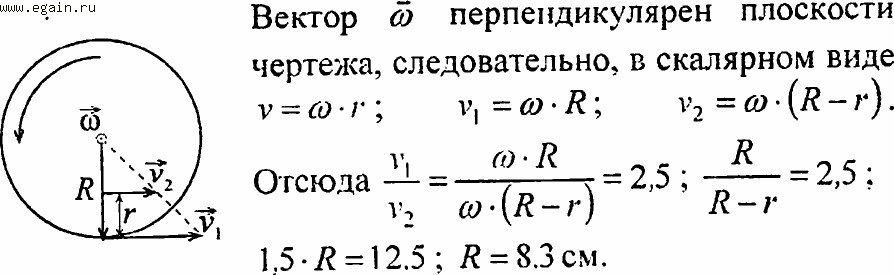 Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?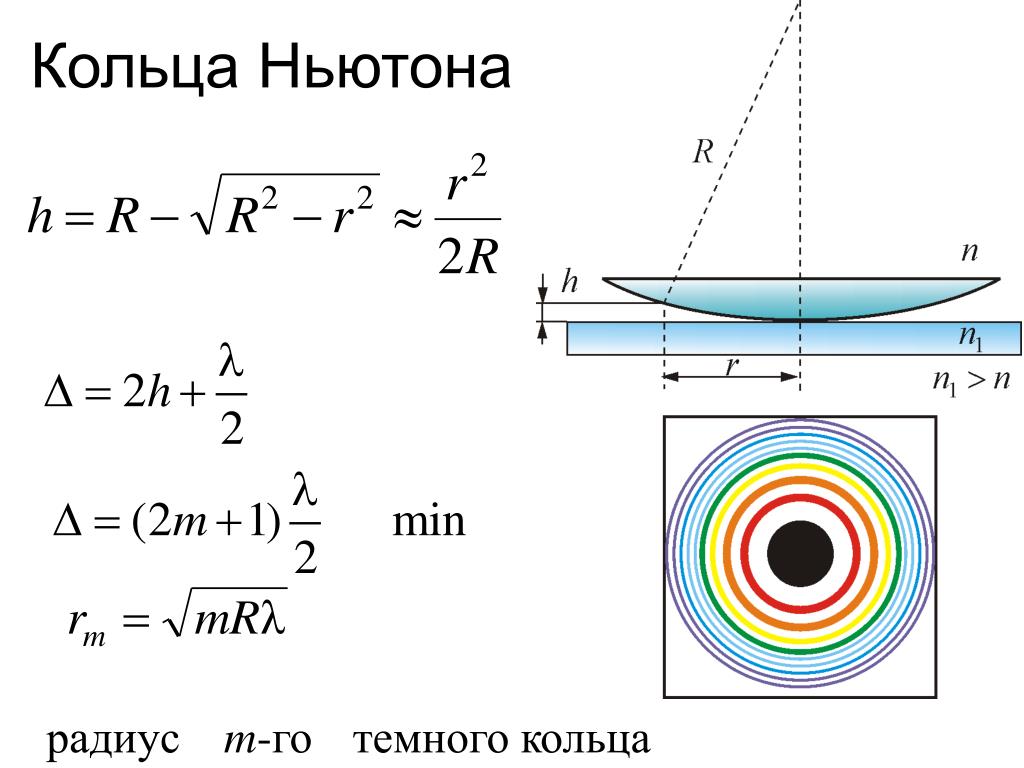
 8.
Системы отсчета
8.
Системы отсчета лет
лет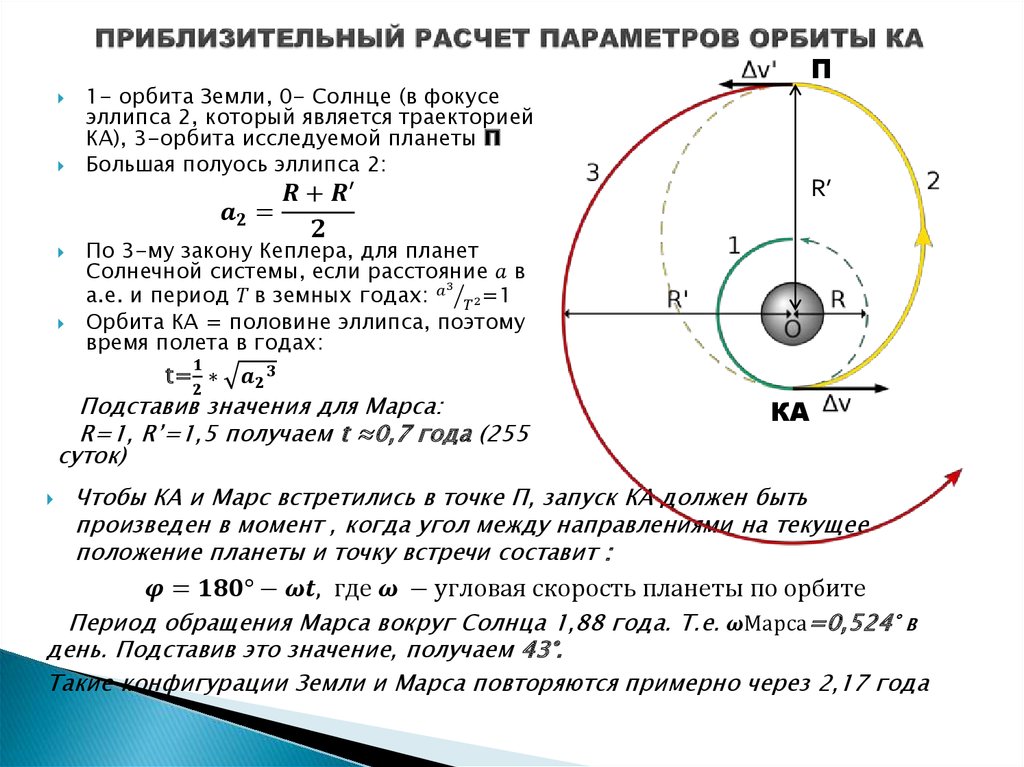 5·1017 см
5·1017 см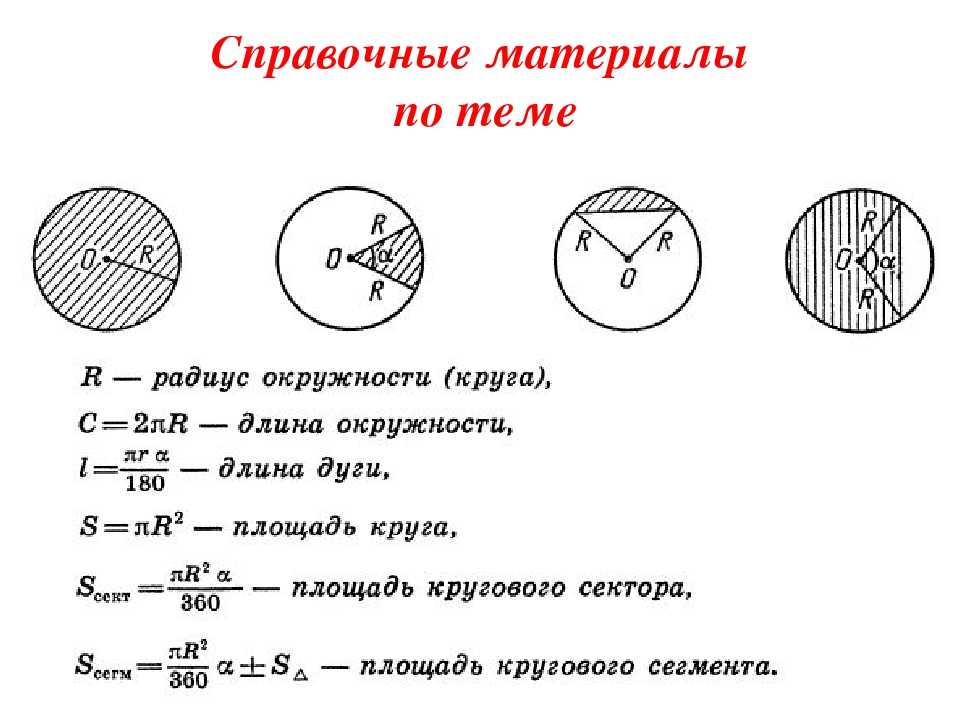 м воздуха (20°C, 1 атм.)
м воздуха (20°C, 1 атм.)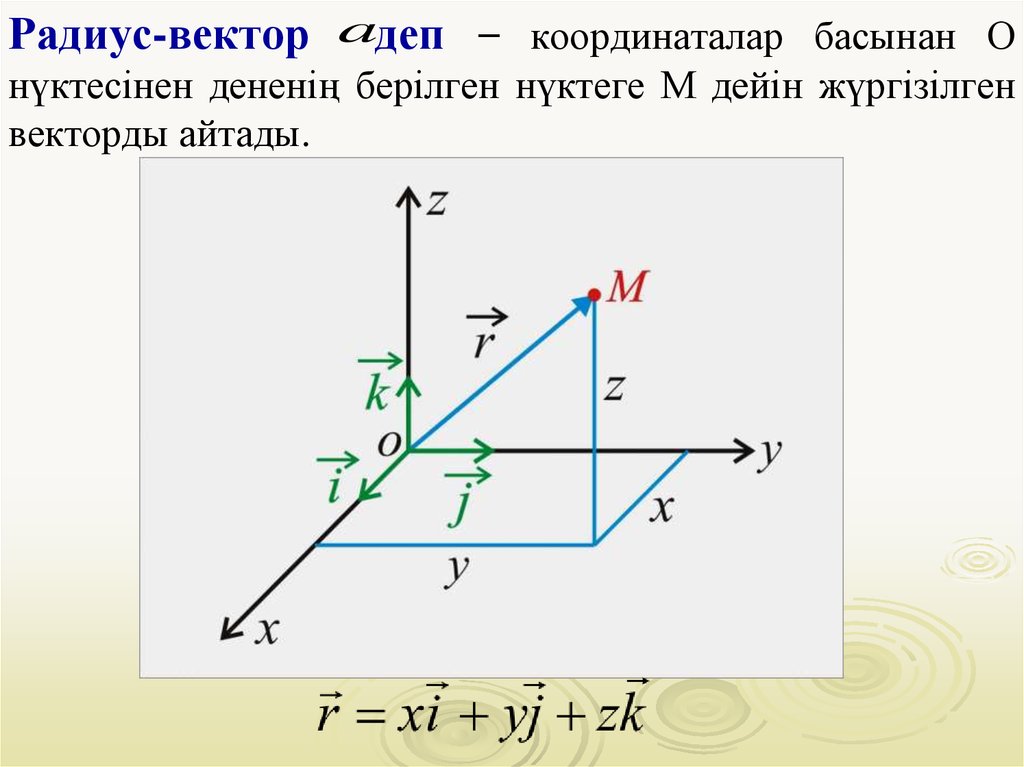 В своем первом эксперименте Резерфорд
использовал рассеяние α-частиц на
атомах для того, чтобы изучить атомную структуру. Выяснив, что вероятность
рассеяния α-частиц на атоме, как
функция угла рассеяния θ, подчиняется
формуле Резерфорда для рассеяния ее на точечном кулоновском центре
В своем первом эксперименте Резерфорд
использовал рассеяние α-частиц на
атомах для того, чтобы изучить атомную структуру. Выяснив, что вероятность
рассеяния α-частиц на атоме, как
функция угла рассеяния θ, подчиняется
формуле Резерфорда для рассеяния ее на точечном кулоновском центре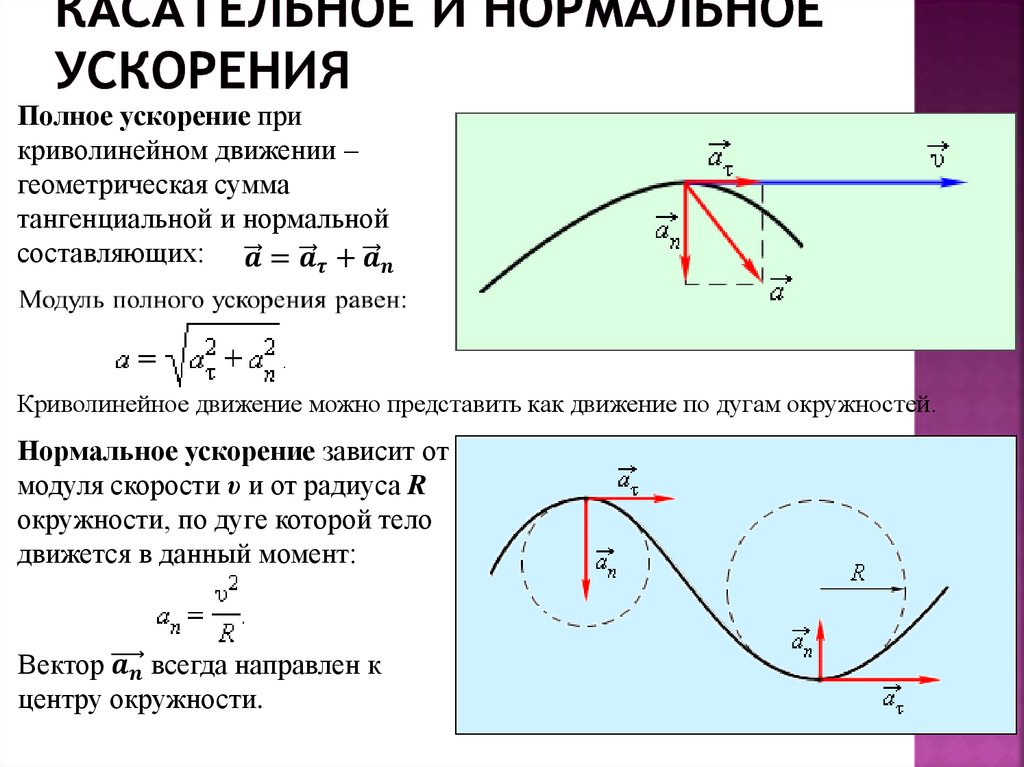
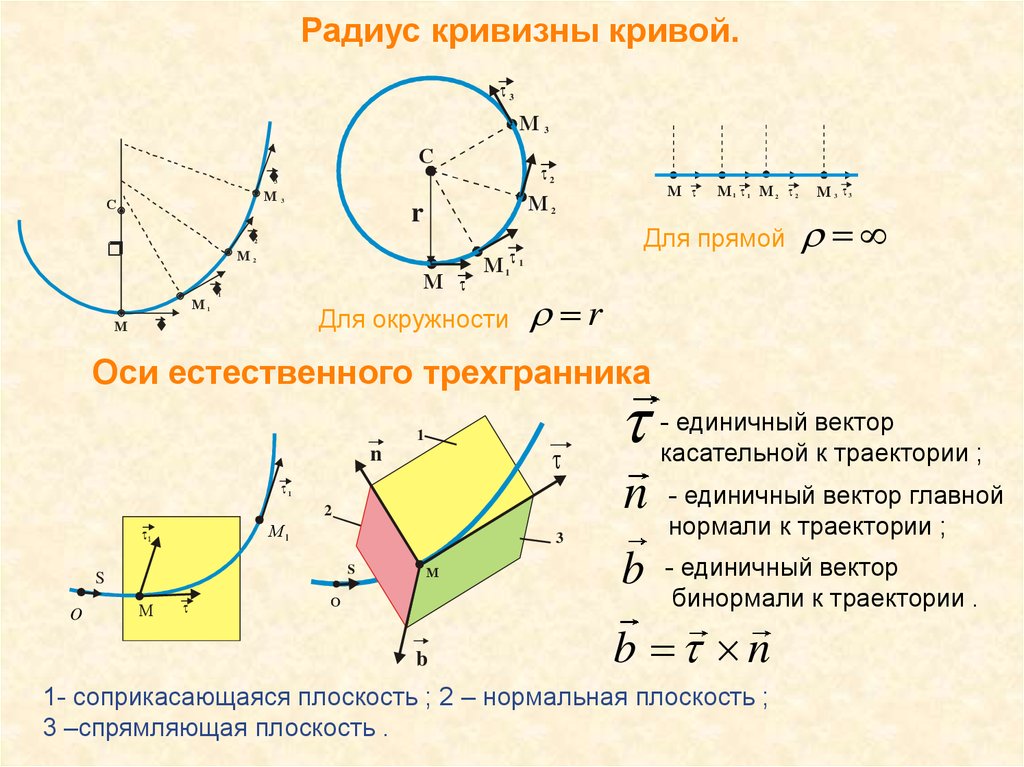 2)
2) 3·10-13·A1/3 см
= 1.3·A1/3 Фм.
3·10-13·A1/3 см
= 1.3·A1/3 Фм.
 Атомные ядра одного сорта распадаются за разное
время. Однако среднее время жизни τ ядер, вычисленное по наблюдению большого числа распадов, оказывается не
зависящим от способа получения этих ядер и от внешних условий. Среднее время
жизни τ
ядра характеризует скорость их распада. Постоянная распада λ:
Атомные ядра одного сорта распадаются за разное
время. Однако среднее время жизни τ ядер, вычисленное по наблюдению большого числа распадов, оказывается не
зависящим от способа получения этих ядер и от внешних условий. Среднее время
жизни τ
ядра характеризует скорость их распада. Постоянная распада λ: 6)
6) Период полураспада – это время, за которое число радиоактивных ядер уменьшается
вдвое:
N0/2 = N0,
откуда
Период полураспада – это время, за которое число радиоактивных ядер уменьшается
вдвое:
N0/2 = N0,
откуда 7·1010 Бк.
7·1010 Бк. 6. Преобразования Лоренца
6. Преобразования Лоренца 1.3. Штрихованная система S’
движется относительно системы S
со скоростью вдоль оси z.
1.3. Штрихованная система S’
движется относительно системы S
со скоростью вдоль оси z.
 14)
14)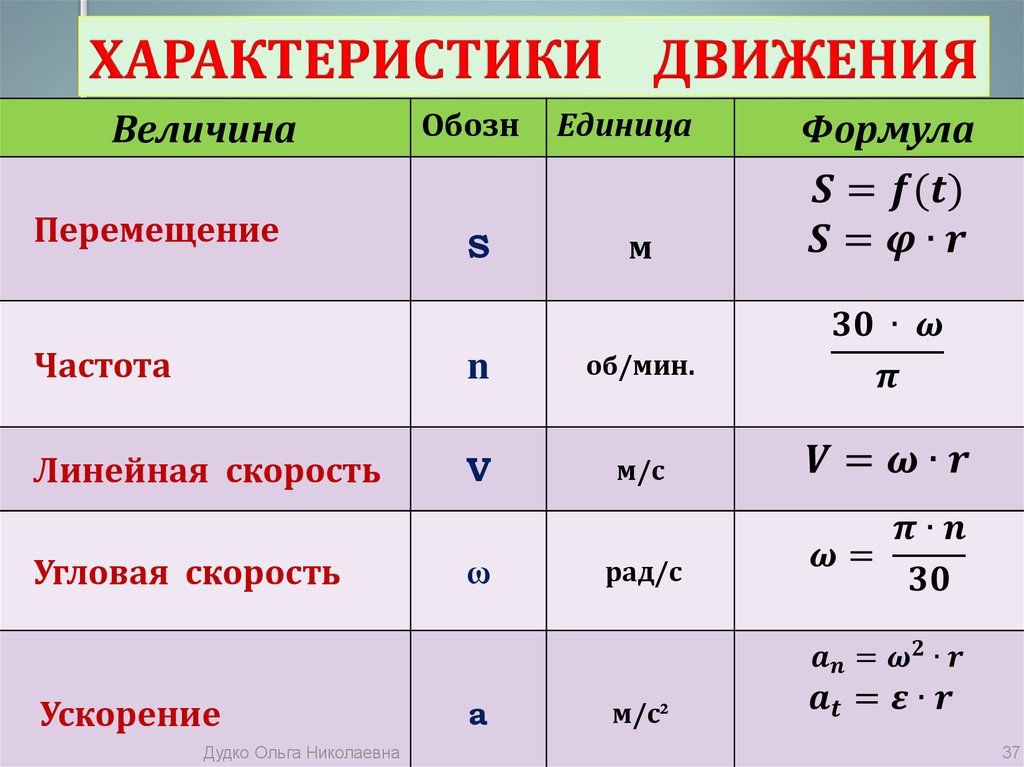 17)
17)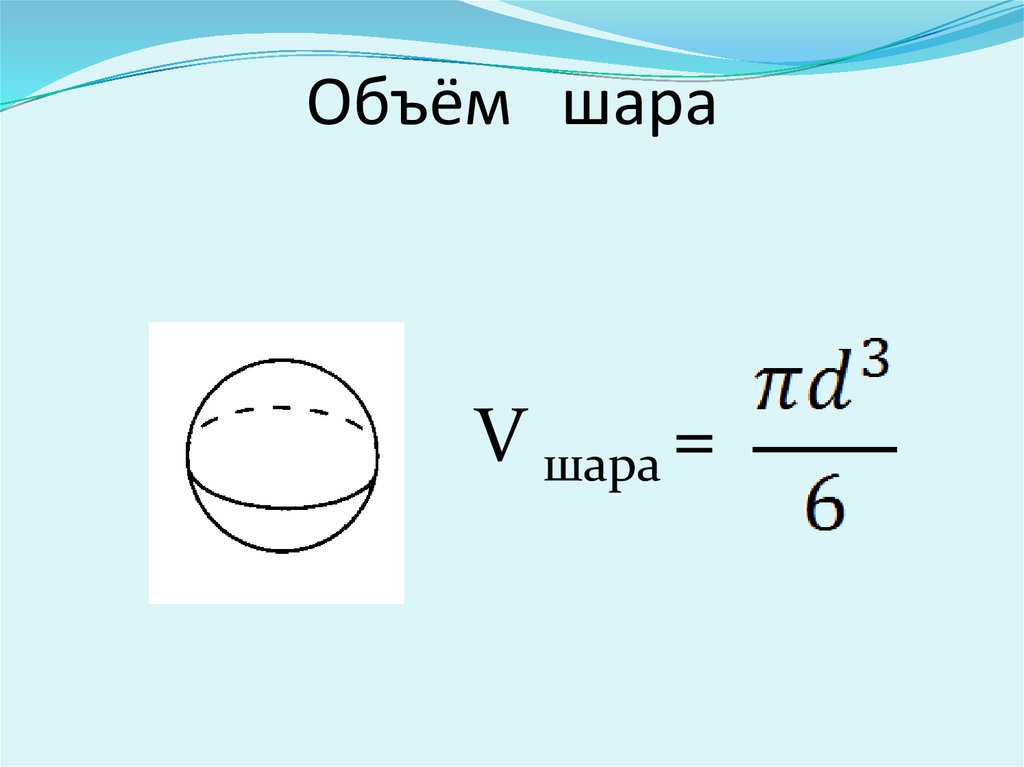
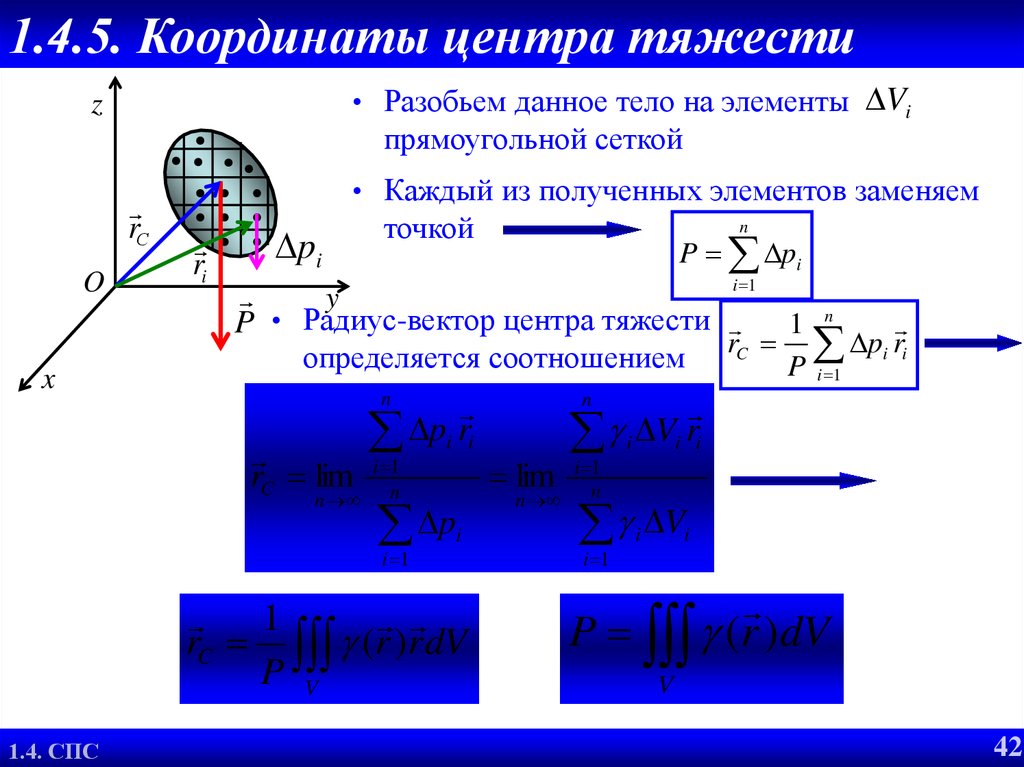
 24)
24)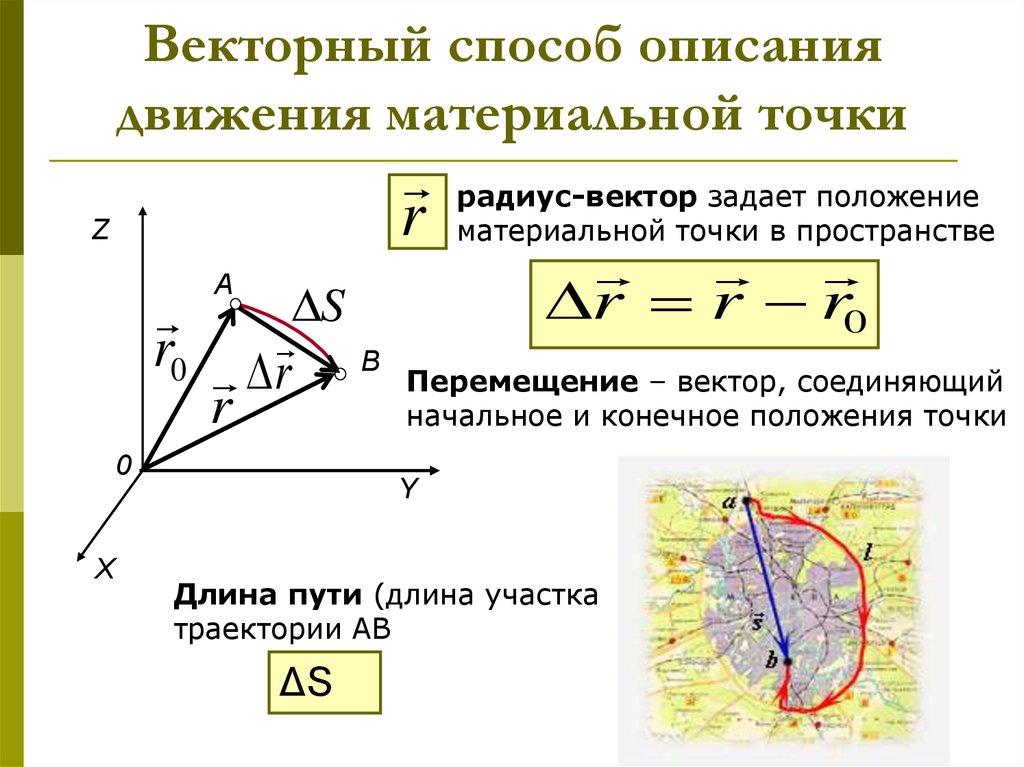
 27)
27)
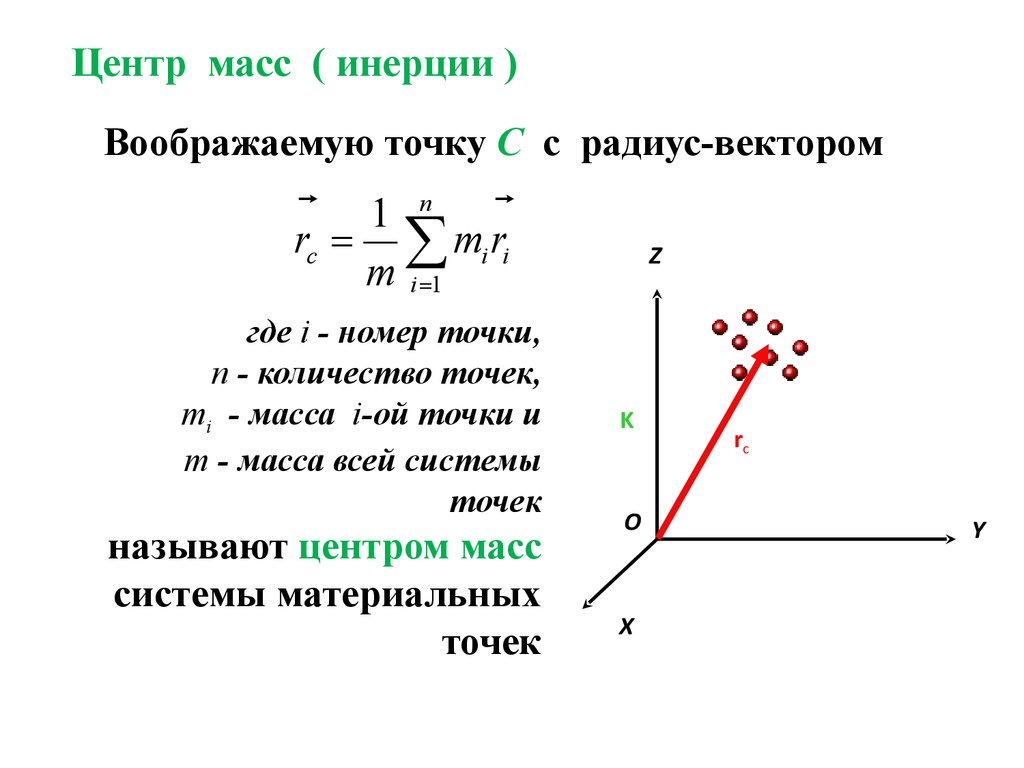 30)
30) В данной
системе диэлектрическая и магнитная проницаемости являются безразмерными
величинами, причём для вакуума они приняты равными единице. В качестве единицы
измерения энергии используется внесистемная единица 1 эВ (электрон-Вольт) –
энергия, приобретаемая электроном при прохождении потенциала в 1 Вольт.
В данной
системе диэлектрическая и магнитная проницаемости являются безразмерными
величинами, причём для вакуума они приняты равными единице. В качестве единицы
измерения энергии используется внесистемная единица 1 эВ (электрон-Вольт) –
энергия, приобретаемая электроном при прохождении потенциала в 1 Вольт.
 32)
32) Законы сохранения энергии и импульса:
Законы сохранения энергии и импульса: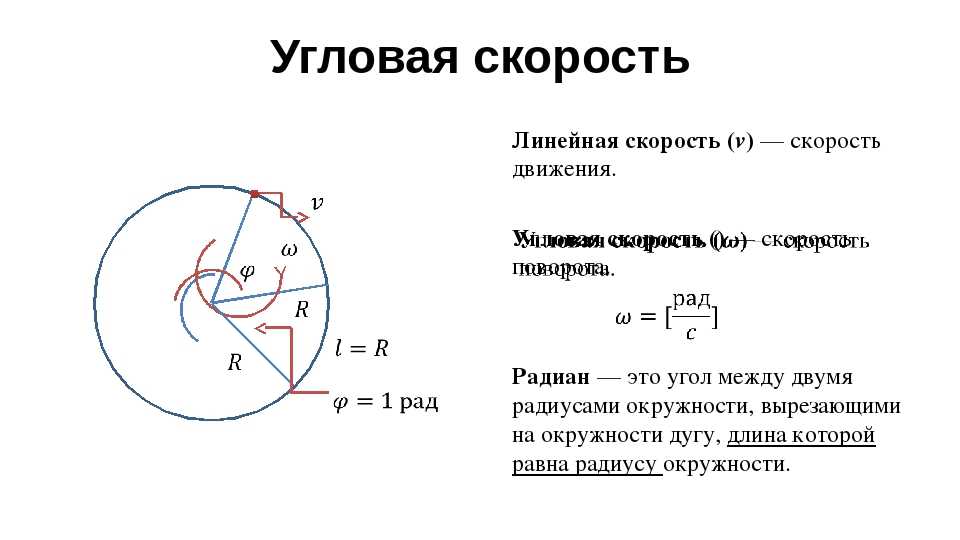 36)
36)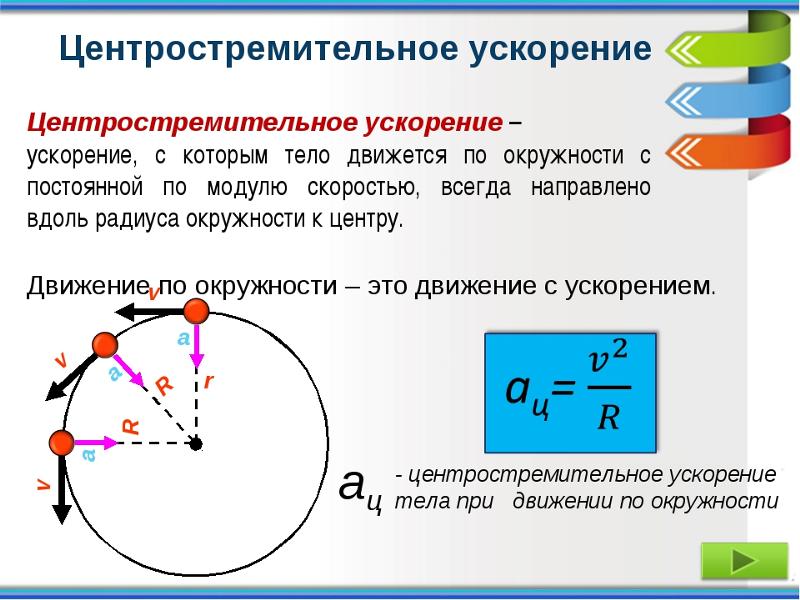 Как изменится величина дифференциального сечения рассеяния, если
в качестве рассеивающего ядра выбрать 27Al?
Как изменится величина дифференциального сечения рассеяния, если
в качестве рассеивающего ядра выбрать 27Al?
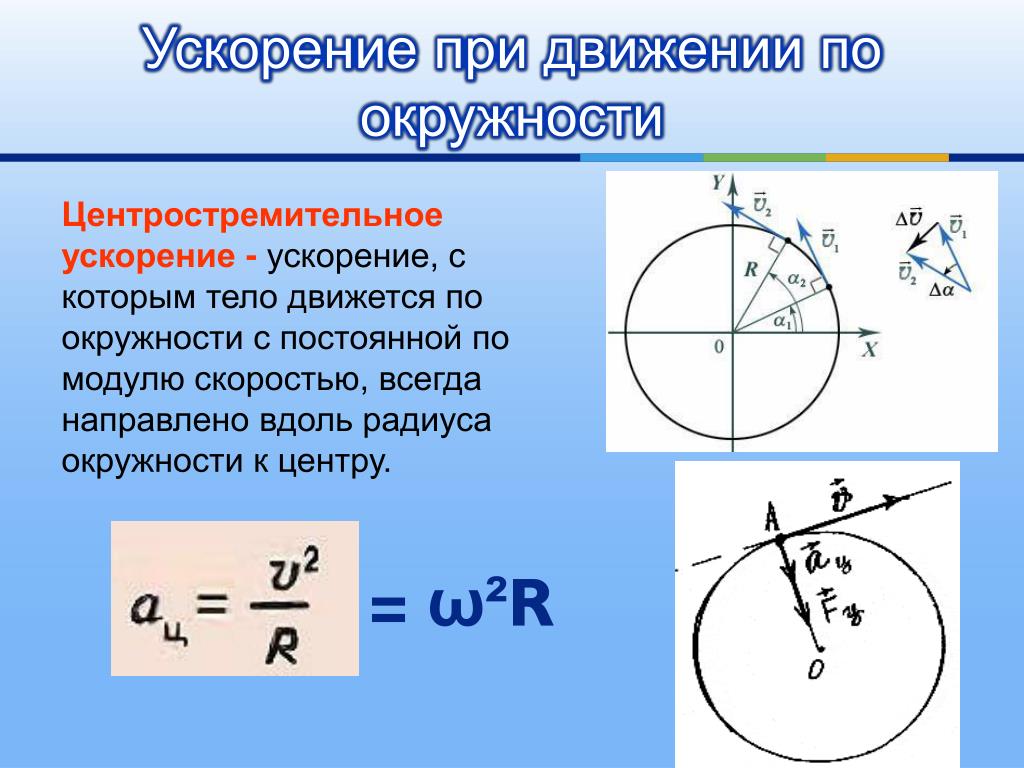
 30)
30)
 38)
38)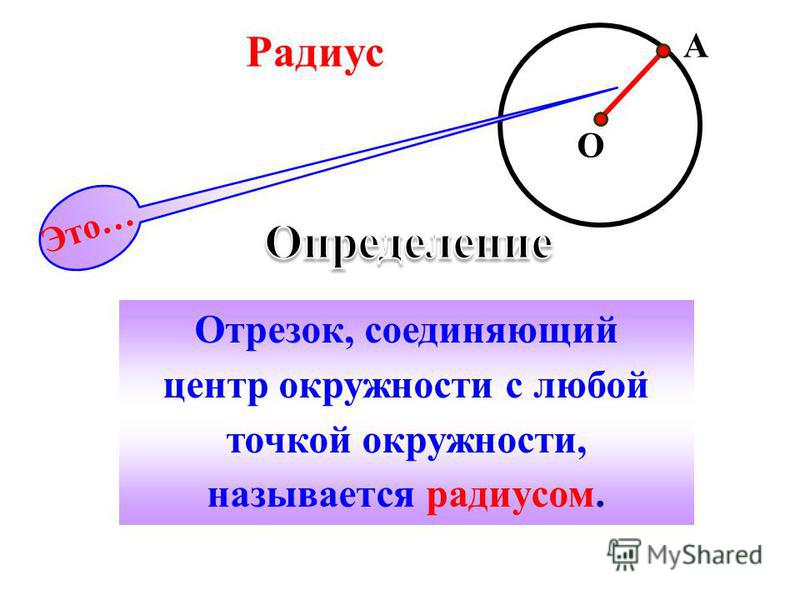
 ,
2) ∆N(90º) ≈ 0.8 част.,
3) ∆N(120º) ≈ 0.4 част.
,
2) ∆N(90º) ≈ 0.8 част.,
3) ∆N(120º) ≈ 0.4 част. 66 МэВ, τμ = 2.197·10-6 сек.
66 МэВ, τμ = 2.197·10-6 сек. 20 c
до 0.21 c,
20 c
до 0.21 c,  24. Энергия, выделяющаяся при делении одного ядра 235U,
составляет ~200 МэВ. Какое количество массы ядра урана превращается в энергию?
24. Энергия, выделяющаяся при делении одного ядра 235U,
составляет ~200 МэВ. Какое количество массы ядра урана превращается в энергию?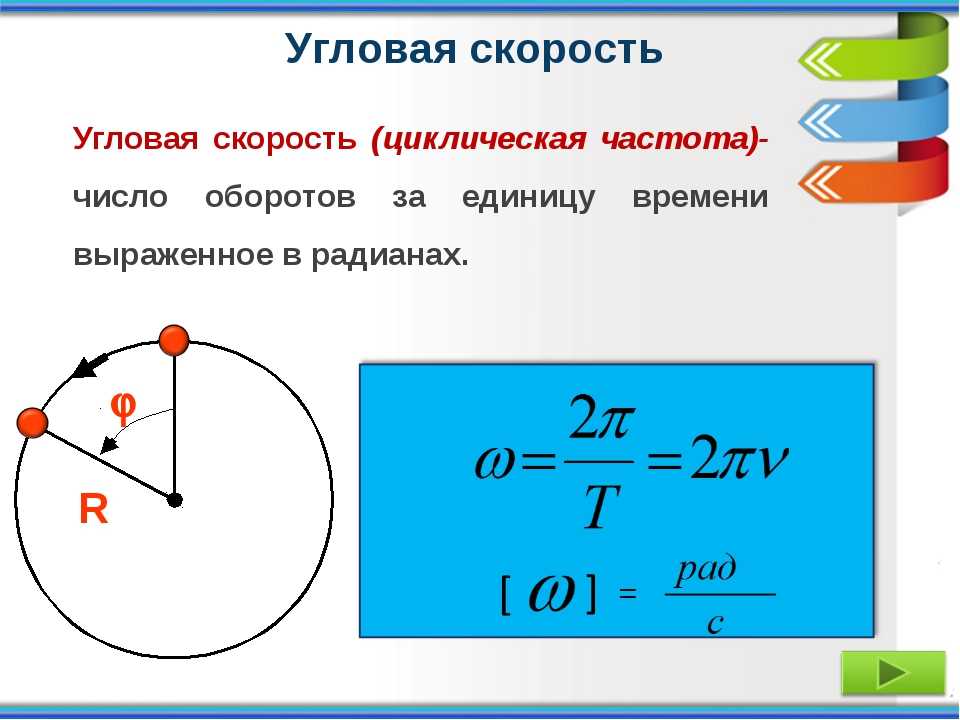 Определите скорость, с которой галактика
удаляется от Земли.
Определите скорость, с которой галактика
удаляется от Земли.

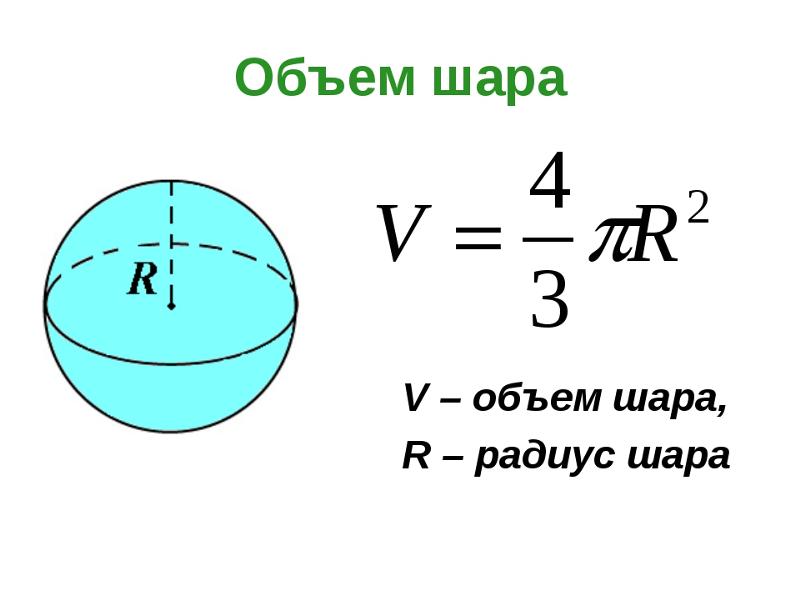 ..
.. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю): ..
.. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется: Все наши люди проверены
Все наши люди проверены  Важным методом познания является теоретическое описание всех явлений природы, на основе которых создаются физические теории. Первую физическую теорию, которую сегодня называют «классической механикой», создал И.Ньютон. Сегодня появилось компьютерное моделирование — еще один важный и перспективный метод исследования. В целом физические явления природы делятся на механические, электромагнитные, тепловые, световые, квантовые. Изучают эти физические явления отдельные разделы физики: механика, электромагнетизм, термодинамика, оптика, атомная физика, молекулярная и другие. Одновременно с этим все разделы взаимосвязаны и образуют единую физическую науку, способную описать и объяснить причины разнообразных природных явлений — от Вселенной до процессов внутри атомов. Законы физики работают практически повсеместно и ежесекундно, независимо от нас и наших желаний. Даже самые элементарные действия напрямую связаны с разными законами физики. Чтобы произвести какие-то расчеты и осуществить действие, проще всего воспользоваться онлайн калькулятором.
Важным методом познания является теоретическое описание всех явлений природы, на основе которых создаются физические теории. Первую физическую теорию, которую сегодня называют «классической механикой», создал И.Ньютон. Сегодня появилось компьютерное моделирование — еще один важный и перспективный метод исследования. В целом физические явления природы делятся на механические, электромагнитные, тепловые, световые, квантовые. Изучают эти физические явления отдельные разделы физики: механика, электромагнетизм, термодинамика, оптика, атомная физика, молекулярная и другие. Одновременно с этим все разделы взаимосвязаны и образуют единую физическую науку, способную описать и объяснить причины разнообразных природных явлений — от Вселенной до процессов внутри атомов. Законы физики работают практически повсеместно и ежесекундно, независимо от нас и наших желаний. Даже самые элементарные действия напрямую связаны с разными законами физики. Чтобы произвести какие-то расчеты и осуществить действие, проще всего воспользоваться онлайн калькулятором. С его помощью можно в считанные секунды рассчитать скорость, расстояние, время, силу, массу тела, плотность веществ, кинетическую энергию тела и т.д. Для этого вам понадобиться лишь выбрать калькулятор, ввести исходные данные. Программа сама произведет нужные действия и выдаст правильный ответ.
С его помощью можно в считанные секунды рассчитать скорость, расстояние, время, силу, массу тела, плотность веществ, кинетическую энергию тела и т.д. Для этого вам понадобиться лишь выбрать калькулятор, ввести исходные данные. Программа сама произведет нужные действия и выдаст правильный ответ. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор для физики,калькулятор для физики онлайн,калькулятор онлайн для физики,калькулятор онлайн по физике,калькулятор онлайн физика,калькулятор по физике,калькулятор по физике онлайн,калькулятор физика,калькулятор физика онлайн,калькулятор физики,калькулятор физики онлайн,калькулятор физический,калькулятор физический онлайн,онлайн калькулятор для физики,онлайн калькулятор по физике,онлайн калькулятор по физике для решения задач,онлайн калькулятор физика,онлайн калькулятор физики,физика калькулятор,физика калькулятор онлайн,физический калькулятор,физический калькулятор онлайн,физический калькулятор онлайн с формулами.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор для физики,калькулятор для физики онлайн,калькулятор онлайн для физики,калькулятор онлайн по физике,калькулятор онлайн физика,калькулятор по физике,калькулятор по физике онлайн,калькулятор физика,калькулятор физика онлайн,калькулятор физики,калькулятор физики онлайн,калькулятор физический,калькулятор физический онлайн,онлайн калькулятор для физики,онлайн калькулятор по физике,онлайн калькулятор по физике для решения задач,онлайн калькулятор физика,онлайн калькулятор физики,физика калькулятор,физика калькулятор онлайн,физический калькулятор,физический калькулятор онлайн,физический калькулятор онлайн с формулами. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор для физики. Просто введите задачу в окошко и нажмите
«решить» здесь (например, калькулятор онлайн для физики).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор для физики. Просто введите задачу в окошко и нажмите
«решить» здесь (например, калькулятор онлайн для физики). Для электриков, студентов и тех, кому необходимо часто решать задачи на расчёты закона Ома, созданы специальные калькуляторы онлайн, которые предназначены именно для этих целей.
Для электриков, студентов и тех, кому необходимо часто решать задачи на расчёты закона Ома, созданы специальные калькуляторы онлайн, которые предназначены именно для этих целей. -9
-9
 Но задания во всяком случае необходимо решать. Какими бы сложными они не были. На помощь может прийти приложение, которое автоматически решает примеры по фотографии в режиме онлайн. Рассмотрим подробнее эти инструменты и как с ними работать.
Но задания во всяком случае необходимо решать. Какими бы сложными они не были. На помощь может прийти приложение, которое автоматически решает примеры по фотографии в режиме онлайн. Рассмотрим подробнее эти инструменты и как с ними работать.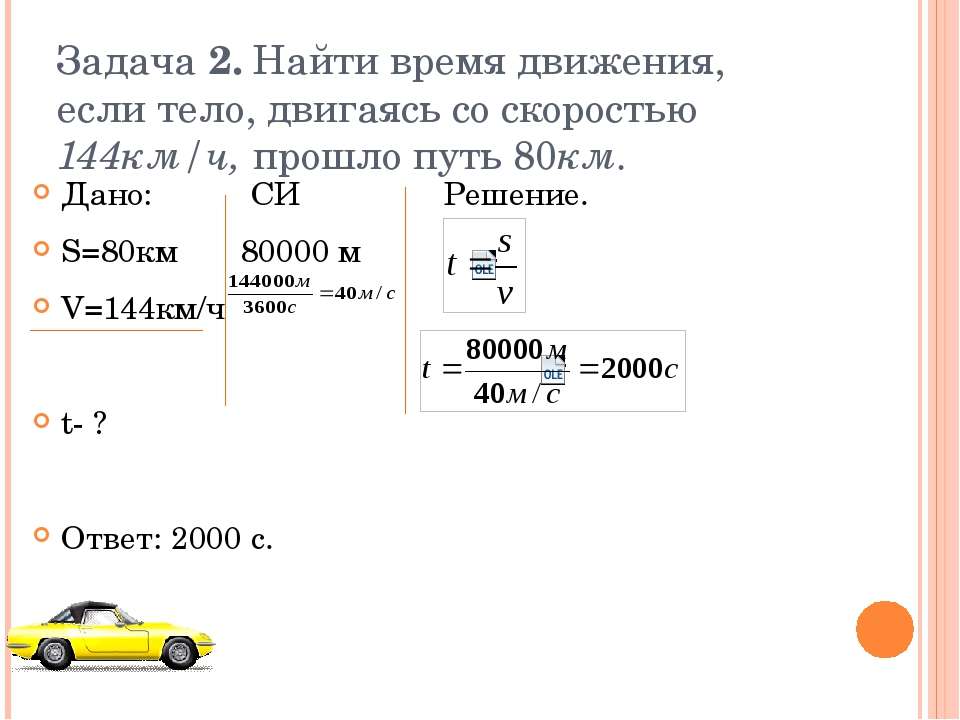



 А для решения более трудных примеров можно применять «Калькулятор дробей». С его помощью можно решать проценты со скобками, десятичные дроби. Каждый пример приводится пошагово. Поэтому он поможет понять, как такие задачи могут быть выполнены.
А для решения более трудных примеров можно применять «Калькулятор дробей». С его помощью можно решать проценты со скобками, десятичные дроби. Каждый пример приводится пошагово. Поэтому он поможет понять, как такие задачи могут быть выполнены. В нём сосредоточено большое количество функций, которые будут полезны в разных сферах деятельности. В дополнение в нём можно найти научный калькулятор, который может быть использован инженерами и студентами. Калькулятор уравнений может решать уравнения и неравенства разной сложности. В результатах отображает графики.
В нём сосредоточено большое количество функций, которые будут полезны в разных сферах деятельности. В дополнение в нём можно найти научный калькулятор, который может быть использован инженерами и студентами. Калькулятор уравнений может решать уравнения и неравенства разной сложности. В результатах отображает графики. Принцип его работы остаётся прежним: запустите камеру и наведите её на пример. Посередине экрана в нижней его части нажмите на большую круглую кнопку.
Принцип его работы остаётся прежним: запустите камеру и наведите её на пример. Посередине экрана в нижней его части нажмите на большую круглую кнопку. Преподаватель высшей категории с более чем 30-летним стажем объяснила, почему усложнение заданий на ЕГЭ — это нормально, зачем переходить в профильные классы и как подготовиться к решению нестандартных задач.
Преподаватель высшей категории с более чем 30-летним стажем объяснила, почему усложнение заданий на ЕГЭ — это нормально, зачем переходить в профильные классы и как подготовиться к решению нестандартных задач.

 Не было работы «глаза в глаза», для учеников тяжело, когда нет прямой поддержки учителя.
Не было работы «глаза в глаза», для учеников тяжело, когда нет прямой поддержки учителя.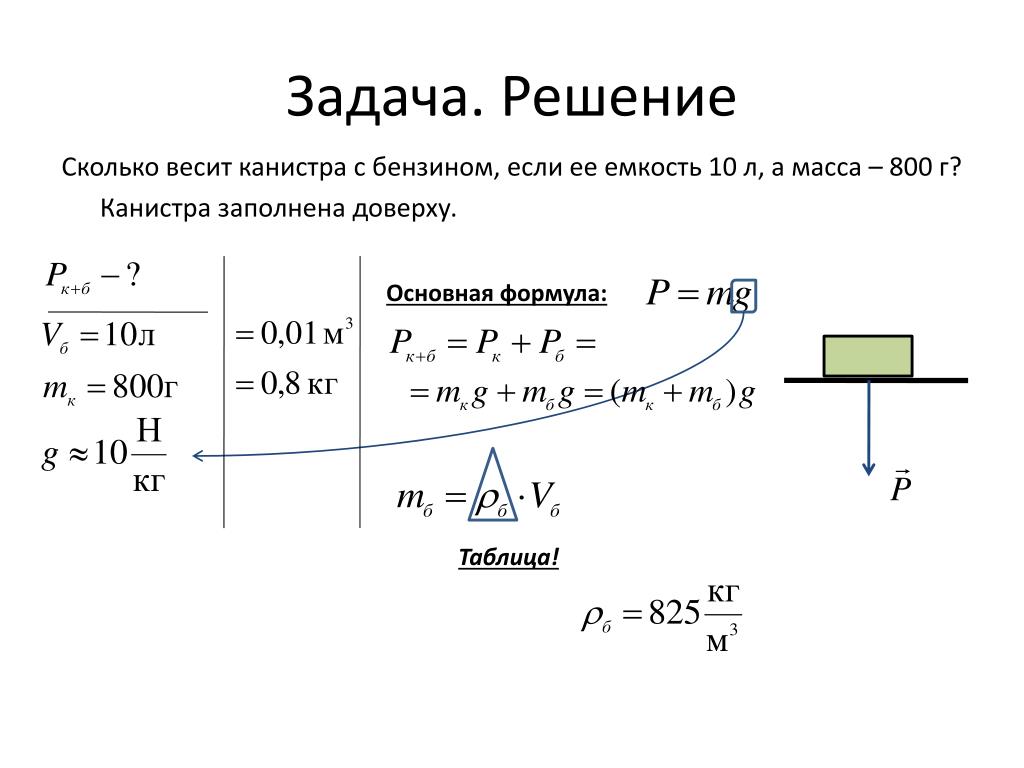 Я знаю, что на многих экзаменах ребята уходят чуть раньше, на химии все сидят до последнего. Сложная задача из второй части требует минимум полчаса на обдумывание, а ещё надо переписать без ошибок, там очень много расчётов.
Я знаю, что на многих экзаменах ребята уходят чуть раньше, на химии все сидят до последнего. Сложная задача из второй части требует минимум полчаса на обдумывание, а ещё надо переписать без ошибок, там очень много расчётов. Это рабочая специальность, и она нужна не для того, что пойти работать лаборантом, так как учащиеся нацелены на поступление в вузы. Но на первых курсах профильных вузов ребятам очень комфортно учиться, потому что они знают больше других.
Это рабочая специальность, и она нужна не для того, что пойти работать лаборантом, так как учащиеся нацелены на поступление в вузы. Но на первых курсах профильных вузов ребятам очень комфортно учиться, потому что они знают больше других. Средний балл у нас составил 80 баллов, по России средний балл — 53,8.
Средний балл у нас составил 80 баллов, по России средний балл — 53,8. Ведь в 10 и 11 классе на химию в общеобразовательной школе выделяется всего по одному часу. Это несерьёзно, никто не предполагает, что можно подготовиться к ЕГЭ, имея один час в неделю.
Ведь в 10 и 11 классе на химию в общеобразовательной школе выделяется всего по одному часу. Это несерьёзно, никто не предполагает, что можно подготовиться к ЕГЭ, имея один час в неделю.

 0. Тест создан для учеников 9 класса с целью подготовки к ОГЭ по математике по модулю «Геометрия». 7. 8. Онлайн-курси Геометрія 9 клас в інтерактивній школі GIOS 👨🎓 покращити знання 🧠 навчити вирішувати задачі та рівняння ✅ будь готовий до іспиту або контрольної ☝ вчи математику цікаво.
0. Тест создан для учеников 9 класса с целью подготовки к ОГЭ по математике по модулю «Геометрия». 7. 8. Онлайн-курси Геометрія 9 клас в інтерактивній школі GIOS 👨🎓 покращити знання 🧠 навчити вирішувати задачі та рівняння ✅ будь готовий до іспиту або контрольної ☝ вчи математику цікаво.