Подвижный и неподвижный блок, с примерами задач
Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.
Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).
Неподвижный блок
Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.
Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:
Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:
так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.
Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:
при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:
Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:
Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.
Комбинация неподвижных блоков
Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины. На рис.2 изображена схема двойного блока.
Условие равновесия для рычага на рис.2 станет формула:
Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
Подвижный блок
Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:
Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:
Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:
Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.
Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.
Золотое правило механики
Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.
В виде формулы «золотое правило№ можно записать так:
где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы .
Золотое правило является самой простой формулировкой закона сохранения энергии.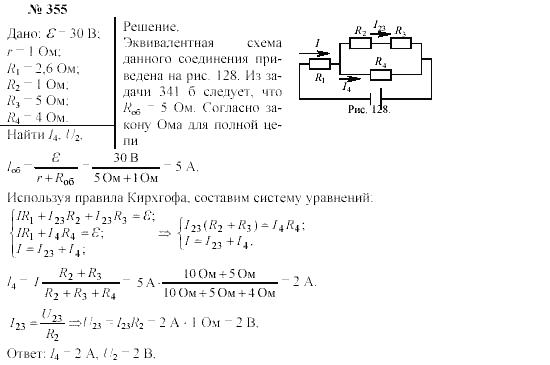 Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:
Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:
Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:
Если силы и уравновешены, то блок покоится или движется равномерно.
Примеры решения задач
Простая физика — EASY-PHYSIC
Продолжаем подготовку к олимпиадам. Сегодня закрепляем тему «статика». Поговорим про блоки, посчитаем силы, установим равновесие.
Задача 1.
Черный ящик, привязанный через систему блоков и нитей к стенке, покоится на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть его с места, непосредственно к нему необходимо приложить горизонтальную силу чуть больше Н. Какую минимальную силу надо прикладывать к черному ящику, чтобы он оставался неподвижным, если к веревке приложена сила Н? Ответ дать в Ньютонах, округлив до целых. Считать, что м/c.
Считать, что м/c.
Рисунок 1
Расставим силы:
Рисунок 2
Теперь видно, что на блок действуют три силы , поэтому общая сила равна 45 Н. 16 из них «съест» сила трения, поэтому, чтобы удержать такой ящик, не хватает Н.
Ответ: 29 Н.
Задача 2.
Все блоки в системе, представленной на рисунке − невесомые. Масса левого тела кг. При какой массе правого тела система останется в равновесии? Ответ дать в килограммах, округлив до целых. Считать, что м/c.
Рисунок 3
Расставим силы:
Рисунок 4
Теперь запишем условия равновесия:
Откуда
И
Ответ: 2 кг.
Задача 3.
Спасатели с помощью веревок, перекинутых через систему блоков, перемещают равномерно и прямолинейно массивную плиту так, как показано на рисунке. С какой результирующей силой верёвки действуют на плиту? Спасатели тянут свой конец веревки с силой Н. Массами веревок и блоков пренебречь. Ответ дать в Н, округлив до целых. Считать, что м/c.
Ответ дать в Н, округлив до целых. Считать, что м/c.
Замечание: требуется найти только силу, с которой нити действуют непосредственно на плиту. Силу, действующую на плиту со стороны верхнего крепления в ответ включать не надо.
Рисунок 5
Расставим силы:
Рисунок 6
Теперь видно, что «за нитки» плиту тянут Н, а полная сила (с учетом верхнего крепления — Н.
Ответ: 600 Н.
Задача 4.
Какую горизонтальную силу надо прикладывать к шкафу, чтобы удержать его на месте? Массы грузов равны кг, кг. Ответ дать в Ньютонах, округлив до целых. Считать, что м/c.
Рисунок 7
На шкаф действуют две силы тяжести: первого груза (20 Н) и второго (50 Н). Итого 70 Н.
Ответ: 70 Н.
Задача 5.
Два ящика покоятся на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть с места левый ящик, к нему необходимо приложить горизонтальную силу чуть больше 26 Н. Чтобы сдвинуть правый − чуть больше 14 Н.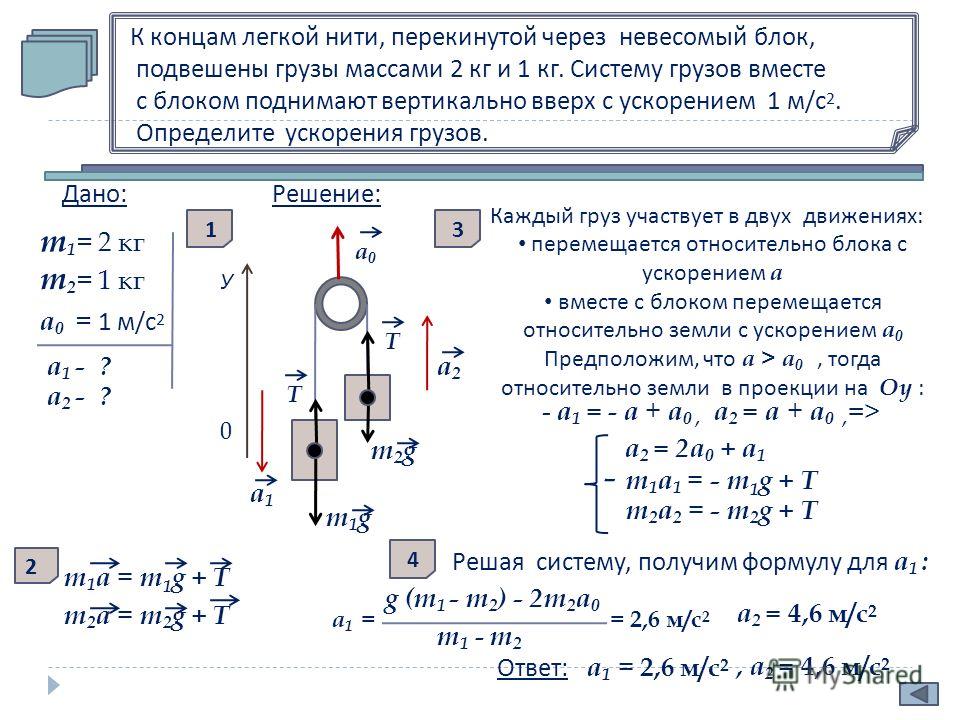 Ящики соединили нитью, переброшенной через блоки, прикреплённые к ящикам так, как показано на рисунке. Какую минимальную силу надо приложить к концу нити, чтобы расстояние между ящиками начало уменьшаться? Ответ дать в Ньютонах, округлив до целых.
Ящики соединили нитью, переброшенной через блоки, прикреплённые к ящикам так, как показано на рисунке. Какую минимальную силу надо приложить к концу нити, чтобы расстояние между ящиками начало уменьшаться? Ответ дать в Ньютонах, округлив до целых.
Рисунок 8
Расстояние будет уменьшаться при сдвиге любого из ящиков, поэтому нужно выяснить, какой легче сдвинуть. Для этого расставляем силы:
Рисунок 9
Теперь видно, что на левый ящик действует сила , а на правый — . Если
То Н, а если
То Н. Поэтому ответ – 7 Н. Этого будет достаточно, чтобы сдвинуть правый ящик и тем самым сократить расстояние.
Задача о силе нескольких объектов: два блока, связанных вместе (машина Этвуда) — Физика
- Дом
- Особенности
- Практическое руководство
- Проблемы
Брусок массой 15 кг лежит на наклонной плоскости. Плоскость составляет с горизонталью угол , а угол между бруском и плоскостью равен 0,13. Блок массой 15 кг привязан ко второму блоку (масса = 38 кг), который висит над концом наклонной плоскости после того, как веревка пройдет над . Что такое каждый из двух блоков, и что такое ?
Блок массой 15 кг привязан ко второму блоку (масса = 38 кг), который висит над концом наклонной плоскости после того, как веревка пройдет над . Что такое каждый из двух блоков, и что такое ?
- Идентифицировать
- Нарисуй картинку
- Выберите отношение
- Решить
- Понять
В этой задаче вас просят связать движение (ускорение двух блоков) с силой (натяжение веревки, трение). Сила и движение одного объекта всегда связаны вторым законом Ньютона, так что это сила или проблема 2-го закона.
Кроме того, обратите внимание, что вы должны рассматривать блоки как отдельные системы. Вас просят найти натяжение веревки между ними, и вы не можете ответить на этот вопрос, не изучив взаимодействие между ними — другими словами, эффект, который каждый из них оказывает на другой. Поэтому вам нужно будет нарисовать картинку и составить уравнения для каждого блока в отдельности.

Шаг 1
Ваш FBD для Блока 1 еще не завершен, потому что mg имеет как x-, так и y-компоненты. Перейдите к шагу 2, когда будете готовы продолжить.
———————————————— ————————————————————
Шаг 2
В окончательной FBD, нарисованной здесь, все силы на блоке 1 разделены на компоненты. Вклад каждой силы в направлении x (вдоль наклона) показан явно, как и вклад каждой силы в направлении y. FBD теперь является визуальным представлением ∑F=ma в каждом направлении.
Ключевым уравнением для любой задачи, связывающей силы и движение, является второй закон Ньютона. Независимо от того, какое количество вас просят найти, начните со Второго закона. Если потребуется дополнительная информация, она станет очевидной по мере продвижения.
Для задач с несколькими объектами вам всегда потребуется дополнительная информация, обобщенная в виде третьего закона Ньютона (взаимодействие между двумя объектами ощущается обоими объектами в равной степени и в противоположном направлении).
 В этом примере это понимание уже использовалось — взаимодействие между двумя блоками происходит за счет натяжения веревки, и натяжение обозначалось одним и тем же символом для каждого. Если вы не заметили, что натяжение по всей веревке такое же, как вы нарисовали FBD, это нормально. Когда вы начнете решать уравнения, вы обнаружите, что у вас слишком много неизвестных, и вы можете использовать это понимание, чтобы уменьшить их в этот момент.
В этом примере это понимание уже использовалось — взаимодействие между двумя блоками происходит за счет натяжения веревки, и натяжение обозначалось одним и тем же символом для каждого. Если вы не заметили, что натяжение по всей веревке такое же, как вы нарисовали FBD, это нормально. Когда вы начнете решать уравнения, вы обнаружите, что у вас слишком много неизвестных, и вы можете использовать это понимание, чтобы уменьшить их в этот момент.Шаг 1
Одним из ключей к успешному алгебраическому решению задачи с несколькими объектами является отслеживание переменных. Я использовал разные символы для масс двух блоков, потому что они не совпадают, но я использовал один и тот же символ для ускорения, потому что они движутся вместе. Я также использовал один и тот же символ для обозначения натяжения на каждом блоке.
На данный момент у вас есть два нерешенных уравнения и два неизвестных ( а и Т .
 ). Прокрутите вниз, чтобы продолжить это решение.
). Прокрутите вниз, чтобы продолжить это решение.———————————————— ————————————————————-
Шаг 2Т – 79 Н = (15 кг)
Один из подходов, который всегда работает, состоит в том, чтобы решить одно уравнение для одной из переменных и подставить его в другую.
T = 370 Н – (38 кг)а из первого уравнения
370 Н – (38 кг)а — 79 Н = (15 кг)а подставляя во второе
290 Н = (38 кг + 15 кг)а
5,5 м/с 2 =аТеперь, когда вы нашли одну из неизвестных переменных, подставьте ее в любое из исходных уравнений, чтобы найти другую переменную. Подставлю во второе уравнение.
T – 79 Н = (15 кг)(5,5 м/с 2 )
T = 79 Н + 83 Н = 160 НВ этой задаче требуется только натяжение веревки и ускорение блоков.
 Дальнейшее математическое решение не требуется.
Дальнейшее математическое решение не требуется.В этой задаче нас просили найти ускорение двух блоков, связанных между собой веревкой, а также найти натяжение веревки между ними. В задаче не указано точно, в каком направлении движутся блоки, или даже если они двигаются. Основываясь на относительных массах блоков, мы сделали предположение, что висящий блок ускоряется вниз, а скользящий вверх по склону.
При таком предположении наше решение:
1.) Подвешенный блок ускоряется вниз с a=5,5 м/с 2 , а блок на наклонной поверхности ускоряется вверх по наклонной поверхности, также с a=5,5 м/с. с 2 . Это лишь немногим больше половины ускорения, которое мог бы иметь висящий блок только из-за гравитации, что имеет смысл. Можно было бы ожидать, что он будет иметь более низкое ускорение из-за натяжения веревки вверх из-за натяжения другого блока.
2.) Натяжение веревки равно 160 Н.
 Это значение примерно равно силе гравитации, действующей на массу 16 кг, опять-таки число, которое имеет смысл. Брусок массой 38 кг движется вниз с ускорением, поэтому натяжение веревки не полностью удерживает его от силы тяжести. Следовательно, вы знаете, что натяжение в канате должно быть менее (38 кг)g или менее 370 Н.
Это значение примерно равно силе гравитации, действующей на массу 16 кг, опять-таки число, которое имеет смысл. Брусок массой 38 кг движется вниз с ускорением, поэтому натяжение веревки не полностью удерживает его от силы тяжести. Следовательно, вы знаете, что натяжение в канате должно быть менее (38 кг)g или менее 370 Н.Следовательно, мы правильно выбрали направление ускорения и трения.
- Дом
- Особенности
- Практическое руководство
- Проблемы
- Висконсинский университет Грин Бэй
- 2420 Николет Доктор
- Грин Бэй, Висконсин, 54311
Проблемы
Проблемы
Далее: Об этом документе… Up: Работа и энергия Предыдущий: Мощность
а) Автомобиль массой 2000 кг движется со скоростью 50 миль в час. Найди
кинетическая энергия в джоулях. б) Тот же автомобиль поднимают вертикально вверх, а затем
выпал из состояния покоя. Найдите высоту, с которой он упадет, если ударится о
землю со скоростью 50 миль в час (сопротивлением воздуха пренебречь).
Найдите высоту, с которой он упадет, если ударится о
землю со скоростью 50 миль в час (сопротивлением воздуха пренебречь).
Решение:
- а)
-
КЭ знак равно мв 2 знак равно (2 x 10 3 кг ) 2 знак равно 4,99 x 10 5 J (10) - б)
-
ПЭ и знак равно КЭ f мгч знак равно мв 2 ч знак равно знак равно 2 = 25,5 м (11)
Объект массой 1 кг, движущийся со скоростью 5,0 м/с, входит в область
лед, где коэффициент кинетического трения равен 0,10.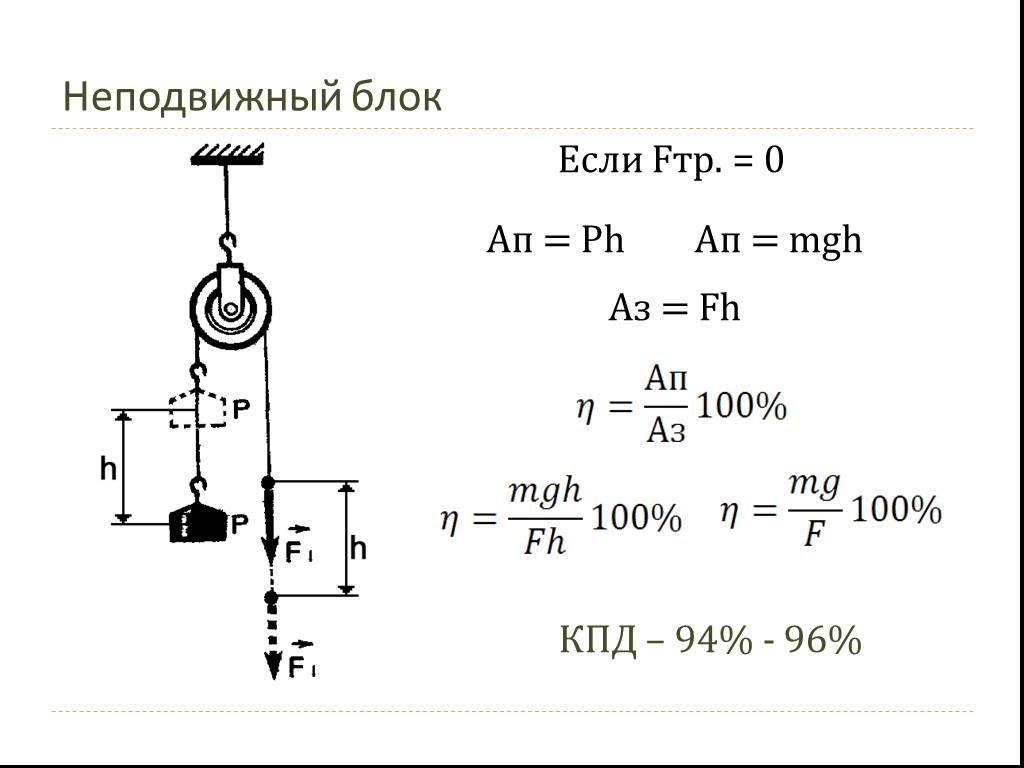 Используйте рабочую энергию
Теорема, позволяющая найти расстояние, которое проходит тело до того, как остановится.
Используйте рабочую энергию
Теорема, позволяющая найти расстояние, которое проходит тело до того, как остановится.
Решение:
Теорема об энергии работы дает Вт = КЭ . У нас есть W = — f k d = — Nd = — mgd и KE = mv f 2 — mv i 2 = — mv 2 i 4 9. Объединение,
| — мгд | знак равно | — мв и 2 | |
| д | знак равно | v i 2 | |
| знак равно | = 13 м . | (12) |
Ребенок весом 30 кг входит в финальную часть спуска с водной горки при 2,0 м/с. Последняя секция имеет длину 5,0 м и перепад высот 3,0 м. Сила трения, противодействующая движению ребенка, равна 50 Н. Найти а) потерю потенциальная энергия, б) работа, совершаемая трением на конечном участке, и в) скорость ребенка в конце секции (используя энергетические соображения).
Решение:
- а)
-
ПЭ знак равно мг ( ч f — ч i ) знак равно 30(9,8)(0 — 3) = — 882 Дж (13) - б)
-
W = — f k x = — 50(5) = — 250 J (14) - в)
-
Ш НЗ знак равно КЭ + ПЭ — 250 знак равно (30)( v f 2 ) — (30)(2.  0) 2 — 882
0) 2 — 882v f 2 знак равно v f знак равно 6,8 м / с (15)
Деревянный брусок весом 2,0 кг лежит на ровной доске и удерживается пружиной жесткости пружины k=100 Н/м, которая была сжата на 0,1 м. Блок отпустили и толкнули горизонтально через доску. Коэффициент трения между блоком и доской = 0,20. Найдите а) скорость бруска когда он покидает пружину и б) расстояние, которое проходит блок после того, как он покидает пружину весна.
Решение:
- а)
- Теорема об энергии работы дает:
Ш НЗ знак равно КЭ + ПЭ — ф к х знак равно ( мв ф 2 — 0) + (0 — кх 2 ) — мгх знак равно mv f 2 — kx 2 v f 2 знак равно знак равно v f знак равно 0,33 м / с . 
(16) - б)
- Теорема о работе энергии дает,
— мгд знак равно 0 — mv i 2 д знак равно v i 2 = = 0,028 м . (17)
Человек толкает коробку массой 100 кг по ровному полу с постоянной скорость 2,0 м/с в течение 10 с. Если коэффициент трения между коробкой и пол = 0,20, найдите среднюю мощность, выдаваемую человеком.
Решение:
Правило равновесия рычага Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил. F1, F2 — силы, действующие на рычаг l1, l2 — плечи этих сил |
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.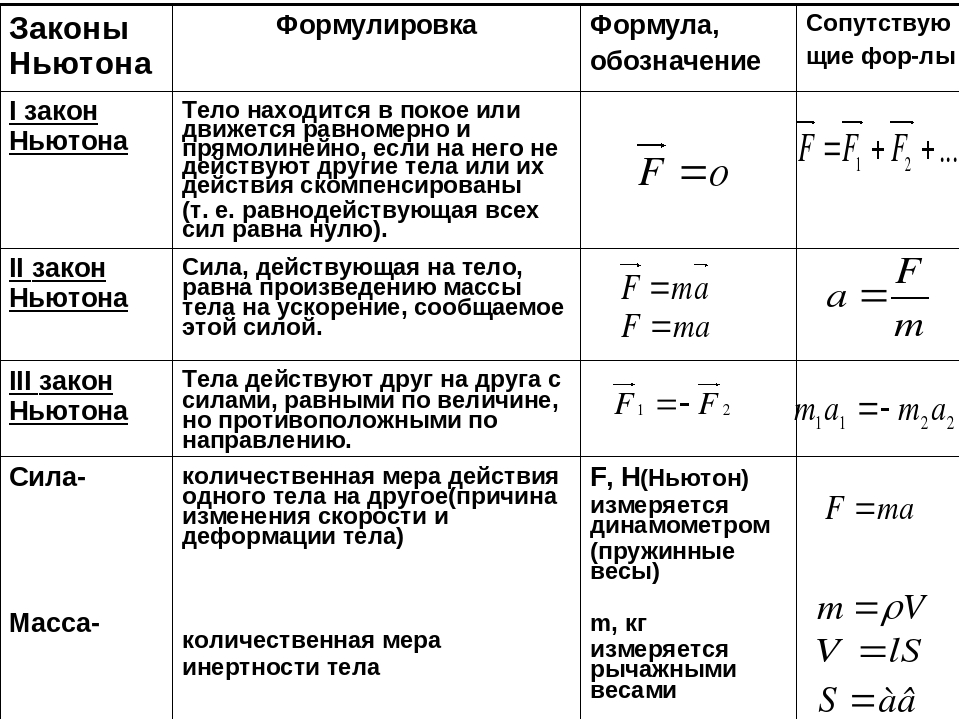
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы M = Fl M — момент силы [Н*м] |
Для примера представьте, что вы забыли, как открывать двери. Стоите перед дверью и раздумываете, как легче это сделать.
Для начала приложим силу к краю двери — туда, где самый длинный рычаг.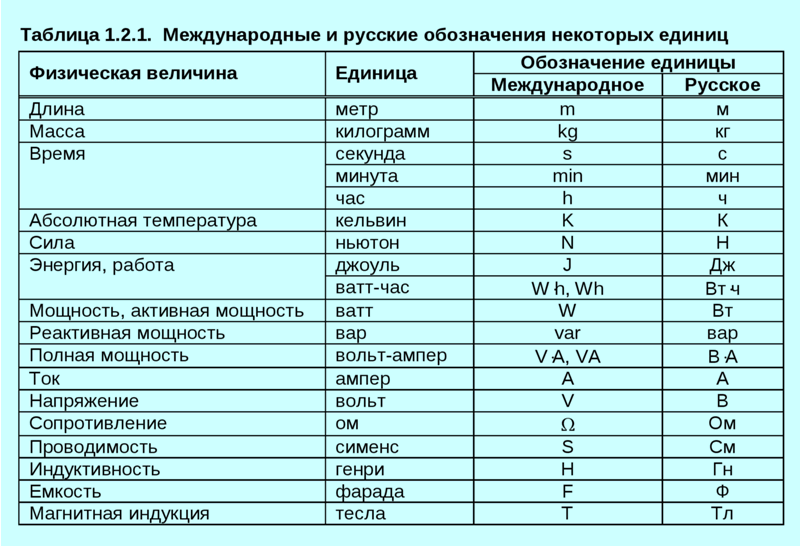 Открылась!
Открылась!
А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придется приложить силу большего значения.
Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.
Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
МА=F×AB=F×3м
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
MB=F×cos30×AB=F×cos30×3м
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
MB=F×3м
Правило моментов
Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м] M’1 + M’2 +…+ M’n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м] |
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом: — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага:
где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага
Отсюда
Ответ: Масса груза равна 0,3 кг
Задача 4 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
youtube.com/embed/OctfStSExzo» title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»» ssmarticle=»»/>
Второй закон Ньютона просто и понятно: определение и формула
Основные понятия: сила, ускорение, масса– В чем сила брат?
– В Ньютонах брат.
С этой шутки можно начать, а точнее продолжить нашу статью о законах Ньютона, на которых, словно на трех слонах стоят основы классической механики. О первом законе Ньютона мы уже писали, и сегодня очередь за вторым законом имени великого английского физика. В чем его суть, как звучит второй закон Ньютона и какая его формула, об этом читайте далее.
Основные понятия: сила, ускорение, масса
Именно с открытием второго закона Ньютона его имя стало ассоциироваться с физическим понятием силы. Впрочем, сила стала не только ассоциироваться, но и измеряться в ньютонах. Да и сам второй закон тесно связан с понятием силы, а также скорости, и ускорения, а еще массы. Но обо всем по порядку.
Впрочем, сила стала не только ассоциироваться, но и измеряться в ньютонах. Да и сам второй закон тесно связан с понятием силы, а также скорости, и ускорения, а еще массы. Но обо всем по порядку.
Что такое сила в физике? Сила это некая физическая величина, обязательно имеющая свое направление (вектор), которая является мерой действия на тело. Обозначается сила литерой F. Измерить величину силы можно при помощи специального прибора – динамометра. Обычно он состоит из пружины, связанной со стрелочным указателем. Если пружину растянуть, то произойдет отклонение стрелки, которая покажет количественную характеристику силы F.
Вот так выглядит динамометр, измеритель силы. Впрочем, существуют разные разновидности этого прибора. Обычно на тело при движении действует сразу несколько сил (к тому же имеющих разную направленность или вектор): сила гравитации, сила трения и т. д.
В прошлой статье о первом законе у нас в качестве примера фигурировала некая тележка.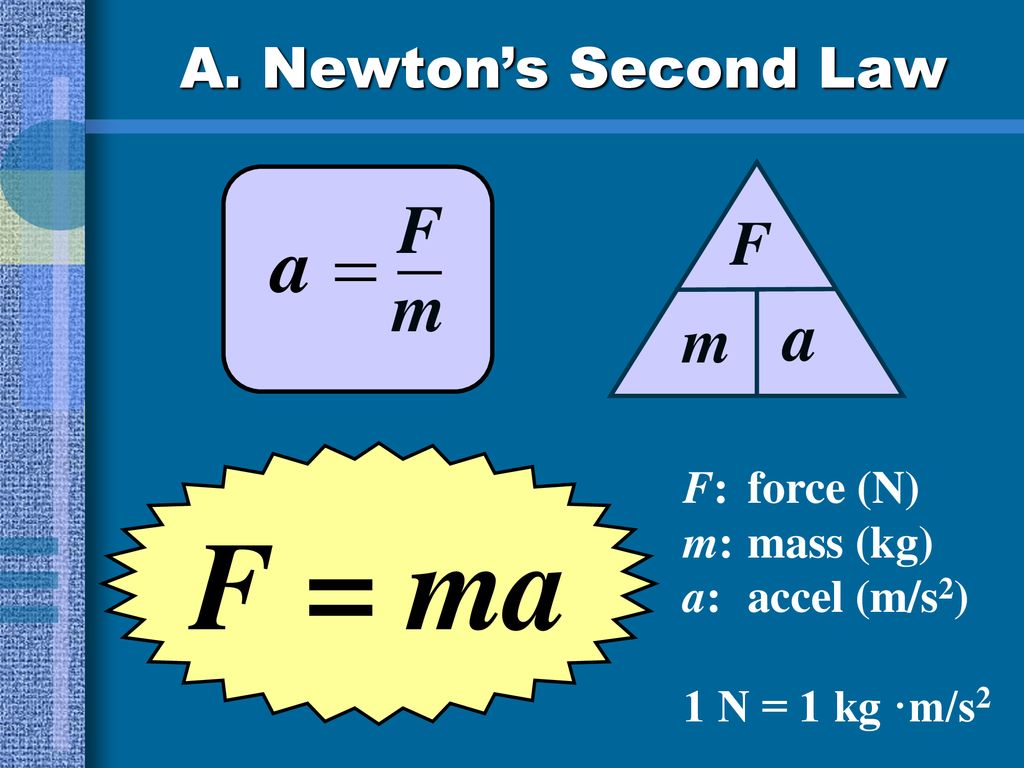 Если приложить силу к этой тележке она станет катиться, и если представить, что на тележку не действуют никакие другие силы, то она будет катиться бесконечно. Бесконечно тележки катиться могут только в придуманной Ньютоном инерциальной системе отсчета (ИСО), существующей лишь теоретически. На практике же мы прекрасно понимаем, что тележка покатится лишь какое-то время и вскоре остановится. А значит, ее скорость изменится, от некоего значения до нуля.
Если приложить силу к этой тележке она станет катиться, и если представить, что на тележку не действуют никакие другие силы, то она будет катиться бесконечно. Бесконечно тележки катиться могут только в придуманной Ньютоном инерциальной системе отсчета (ИСО), существующей лишь теоретически. На практике же мы прекрасно понимаем, что тележка покатится лишь какое-то время и вскоре остановится. А значит, ее скорость изменится, от некоего значения до нуля.
То как меняется скорость в течение времени, называется ускорением (его принято обозначать литерой a). На практике в реальной жизни все тела движутся с ускорением, причем если скорость нарастает, или убывает равномерно, то такое движение называется равноускоренным. Примером такого движение может быть падение любого тела вниз, оно будет падать с одинаковым ускорением, формируемым земной гравитацией g.
И напоследок на характеристику движения любого тела влияет его масса, которую принято обозначать литерой m. В физике масса часто является мерой инертности тела, то есть чем больше масса того или иного тела, тем труднее его сдвинуть с места, но уже сдвинув, его опять таки труднее остановить.
Определение
Если первый закон Ньютона в свое время пытался объяснить то, как работает небесная механика, каким образом планеты непрерывно движутся вокруг Солнца (и не падают на него), то второй закон в этом плане более приземлен, он объясняет движение тел тут, на Земле. По сути это основной закон динамики, базовой закон физической природы.
Существует несколько классических определений второго закона Ньютона: первое из них гласит: сила, оказывающая воздействие на тело, равна произведению массы тела на сообщаемое данной силой ускорение.
Второе определение идет не от силы, а от ускорения, оно гласит: ускорение тела прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Формула
Первое приведенное нами определение можно записать классической формулой:
F = ma
Где F – сила, действующая на тело, m – его масса, а – ускорение.
Для второго определения уравнение будет следующим:
a = F/m
Иными словами, чем больше сила, действующая на тело, тем больше его ускорения, и наоборот, чем больше масса тела, тем его ускорение будет меньшим. По сути, мы пересказали суть второго закона Ньютона своими словами.
По сути, мы пересказали суть второго закона Ньютона своими словами.
Равнодействующая сила
Как мы писали выше, на практике в реальной жизни на каждое физическое тело действует не одна, а несколько сил, причем с разными направлениями. Какое же отражения во втором законе Ньютона находит действия разных сил, обозначим их F1, F2, F3. Так вот если на тело действует несколько сил, то в формуле второго закона фигурирует равнодействующая сила F, которая высчитывается по формуле:
F = F1 + F2 + F3.
Если же равнодействующая сила будет равна нулю, то тело будет пребывать в состоянии покоя, либо равномерного прямолинейного движения.
Рекомендованная литература и полезные ссылки
- Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977.
- Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974.
- Crowell, Benjamin (2011), Light and Matter (2011, Light and Matter), especially at Section 4.
 2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.
2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law. - Feynman, R. P. (англ.)русск.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics (неопр.). — 2nd. — Pearson/Addison-Wesley, 2005. — Т. Vol. 1. — ISBN 0-8053-9049-9.
Видео
И в завершении образовательное видео по теме нашей статьи.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.
Страница про автора
Масса | Определение, единицы и факты
вес и расстояние от Земли
Посмотреть все СМИ
- Ключевые люди:
- Субрахманьян Чандрасекар
- Похожие темы:
- сохранение массы плотность Предел массы Эддингтона релятивистская масса уменьшенная масса
Просмотреть весь связанный контент →
масса , в физике количественная мера инерции, фундаментальное свойство всей материи. По сути, это сопротивление, которое материя оказывает изменению своей скорости или положения при приложении силы. Чем больше масса тела, тем меньше изменение, производимое приложенной силой. Единицей массы в Международной системе единиц (СИ) является килограмм, который определяется через постоянную Планка, которая равна 6,62607015 × 10 −34 джоулей в секунду. Один джоуль равен одному килограмму, умноженному на квадратный метр на секунду в квадрате. Поскольку секунда и метр уже определены в терминах других физических констант, килограмм определяется точными измерениями постоянной Планка. (до 2019 г.килограмм определялся платино-иридиевым цилиндром, называемым международным прототипом килограмма, хранящимся в Международном бюро мер и весов в Севре, Франция.) В английской системе измерения единицей массы является порция, масса которой уровень моря 32,17 фунта.
По сути, это сопротивление, которое материя оказывает изменению своей скорости или положения при приложении силы. Чем больше масса тела, тем меньше изменение, производимое приложенной силой. Единицей массы в Международной системе единиц (СИ) является килограмм, который определяется через постоянную Планка, которая равна 6,62607015 × 10 −34 джоулей в секунду. Один джоуль равен одному килограмму, умноженному на квадратный метр на секунду в квадрате. Поскольку секунда и метр уже определены в терминах других физических констант, килограмм определяется точными измерениями постоянной Планка. (до 2019 г.килограмм определялся платино-иридиевым цилиндром, называемым международным прототипом килограмма, хранящимся в Международном бюро мер и весов в Севре, Франция.) В английской системе измерения единицей массы является порция, масса которой уровень моря 32,17 фунта.
Вес, хотя и связан с массой, тем не менее отличается от последней. Вес, по сути, представляет собой силу, действующую на вещество гравитационным притяжением Земли, и поэтому он немного варьируется от места к месту. Напротив, масса остается постоянной независимо от ее положения при обычных обстоятельствах. Спутник, запущенный в космос, например, весит тем меньше, чем дальше он удаляется от Земли. Однако его масса остается прежней.
Напротив, масса остается постоянной независимо от ее положения при обычных обстоятельствах. Спутник, запущенный в космос, например, весит тем меньше, чем дальше он удаляется от Земли. Однако его масса остается прежней.
Еще из Британники
Галактика Млечный Путь: Масса
В соответствии с принципом сохранения массы масса объекта или набора объектов никогда не меняется, как бы ни перестраивались составные части. Если тело разделить на части, то вместе с частями делится и масса, так что сумма масс отдельных частей равна первоначальной массе. Или, если частицы соединены вместе, масса композита равна сумме масс составляющих частиц. Однако этот принцип не всегда верен.
С появлением специальной теории относительности Эйнштейна в 1905 году понятие массы подверглось радикальному пересмотру. Масса потеряла свою абсолютность. Было замечено, что масса объекта эквивалентна энергии, взаимопревращается с энергией и значительно увеличивается при чрезвычайно высоких скоростях, близких к скорости света (около 3 × 10 8 метров в секунду, или 186 000 миль в секунду). Под полной энергией объекта понималась его масса покоя, а также увеличение его массы, вызванное высокой скоростью. Было обнаружено, что масса покоя атомного ядра значительно меньше суммы масс покоя составляющих его нейтронов и протонов. Масса больше не считалась постоянной или неизменной. Как в химических, так и в ядерных реакциях происходит некоторая конверсия между массой и энергией, так что продукты обычно имеют меньшую или большую массу, чем реагенты. Разница в массе для обычных химических реакций настолько незначительна, что закон сохранения массы можно использовать в качестве практического принципа для предсказания массы продуктов. Однако закон сохранения массы недействителен для поведения масс, активно участвующих в ядерных реакторах, ускорителях частиц и в термоядерных реакциях на Солнце и в звездах. Новый принцип сохранения — сохранение массы-энергии. См. также энергия, сохранение; энергия; Соотношение массы и энергии Эйнштейна.
Под полной энергией объекта понималась его масса покоя, а также увеличение его массы, вызванное высокой скоростью. Было обнаружено, что масса покоя атомного ядра значительно меньше суммы масс покоя составляющих его нейтронов и протонов. Масса больше не считалась постоянной или неизменной. Как в химических, так и в ядерных реакциях происходит некоторая конверсия между массой и энергией, так что продукты обычно имеют меньшую или большую массу, чем реагенты. Разница в массе для обычных химических реакций настолько незначительна, что закон сохранения массы можно использовать в качестве практического принципа для предсказания массы продуктов. Однако закон сохранения массы недействителен для поведения масс, активно участвующих в ядерных реакторах, ускорителях частиц и в термоядерных реакциях на Солнце и в звездах. Новый принцип сохранения — сохранение массы-энергии. См. также энергия, сохранение; энергия; Соотношение массы и энергии Эйнштейна.
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Эриком Грегерсеном.
| Ознакомьтесь с семью определяющими константами СИ. Определения основных единиц СИ Моль, символ моль, является единицей СИ количества вещества. Один моль содержит ровно 6,022 140 76 x 10 23 элементарных частиц. Подписаться на:
Сообщения (Atom) Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев В кодификаторе ЕГЭ нет тем, непосредственно относящихся к содержанию данного листка. Введём основные величины молекулярной физики и соотношения между ними. — масса вещества, — объём вещества, — плотность вещества (масса единицы объёма). Отсюда — число частиц вещества (атомов или молекул). — концентрация вещества (число частиц в единице объёма), . Отсюда Что получится, если умножить на ? Произведение массы частицы на число частиц в единице объёма даст массу единицы объёма, т. е. плотность. Формально: Итак, Массы и размеры частиц невообразимо малы по нашим обычным меркам. Например, масса атома водорода порядка г, размер атома порядка см. Из-за столь малых значений масс и размеров число частиц в макроскопическом теле огромно. Оперировать столь грандиозными числами, как число частиц, неудобно. Один моль — это количество вещества, в котором содержится столько же атомов или молекул, сколько атомов содержится в граммах углерода. А в граммах углерода содержится примерно атомов. Стало быть, в одном моле вещества содержится частиц. Это число называется постоянной Авогадро: моль. Количество вещества обозначается . Это число молей данного вещества. Что получится, если умножить на ? Число молей, умноженное на число частиц в моле, даст общее число частиц: Масса одного моля вещества называется молярной массой этого вещества и обозначается ( = кг/моль). Ясно, что Как найти молярную массу химического элемента? Оказывается, для этого достаточно заглянуть в таблицу Менделеева! Нужно просто взять атомную массу (число нуклонов) данного элемента — это будет его молярная масса, выраженная в г/моль. Почему так получается? Очень просто. Молярная масса углерода равна г/моль по определению. В то же время ядро атома углерода содержит нуклонов. Выходит, что каждый нуклон вносит в молярную массу г/моль. Поэтому молярная масса химического элемента с атомной массой оказывается равной г/моль. Молярная масса вещества, молекула которого состоит из нескольких атомов, получается простым суммированием молярных масс. Так, молярная масса углекислого газа равна г/моль кг/моль. Будьте внимательны с молярными массами некоторых газов! Так, молярная масса газообразного водорода равна г/моль, поскольку его молекула состоит из двух атомов . То же касается часто встречающихся в задачах азота и кислорода Вместе с тем, наиболее частый персонаж задач — гелий — является одноатомным газом и имеет молярную массу г/моль, предписанную таблицей Менделеева. Ещё раз предостережение: при расчётах не забывайте переводить молярную массу в кг/моль! Если ваш ответ отличается от правильного на три порядка, то вы наверняка сделали именно эту, очень распространённую ошибку 🙂 Что получится, если умножить на ? Масса частицы, умноженная на число частиц в моле, даст массу моля, т. Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Основные формулы молекулярной физики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела. Публикация обновлена:
08.01.2023 В физике существует большое количество физических величин, которые мы учитываем при выполнении расчетов. Чтобы сделать его более удобным для пользователей, простым в использовании и запоминании, мы часто используем обозначения и символы для представления этих физических величин. Эти обозначения и символы, используемые для обозначения физических величин при решении связанных с ними задач или для других целей, являются символами. В этой статье вы найдете самые популярные физические символы, а также те, которые мы обычно используем в физике, с их именами, типом величин и соответствующими единицами измерения в табличном формате. Чтобы сдать любой конкурсный экзамен, студенты должны пройти программу и понять схему экзамена. Q1. Как найти формулу физики работы? Анс. Вы можете найти рабочие формулы физики и другие формулы физики в нашей статье, а также на нашем сайте. Q2. Что такое формула объема в физике? Анс. Формула Объема: Длина*Ширина*Высота. Для получения дополнительной информации посетите наш веб-сайт. Здесь вы можете найти все физические формулы и заметки по физике. Математические сомнения Нормальная сила определяется как сила, с которой любая поверхность действует на другой объект. Когда объект находится в состоянии покоя, результирующая сила, действующая на него, равна нулю. Формула Значение нормальной силы зависит от того, где находится объект по отношению к другому объекту. Когда объект собирается упасть, положение, в котором объект падает на землю, определяет значение нормальной силы. Нормальная сила обозначается символом F N . Его единицей измерения являются ньютоны (Н), а размерная формула определяется как [M 1 L 1 T -2 ]. Если тело опирается на плоскую силу, нормальная сила равна значению гравитационного веса, т. е. мг. F Н = мг где, F Н — нормальная сила, м — масса покоящегося объекта, g — ускорение свободного падения. Если тело соскальзывает с наклонной поверхности под некоторым углом, значение нормальной силы равно гравитационному весу, добавленному дополнительной силой F sin θ. В этом случае нормальная сила больше веса тела. Ф Н = mg + F sin θ Где, F Н — нормальная сила, m — масса скользящего объекта, g — ускорение свободного падения, θ — угол наклона . Если сила действует на тело в направлении вверх, то значение нормальной силы равно гравитационному весу, уменьшенному на силу F sin θ. В этом случае чистая нормальная сила меньше веса объекта. Ф Н = мг – F sin θ где, F Н – нормальная сила, м – масса скользящего объекта, g – ускорение свободного падения, θ – угол наклона. Если тело положить на наклонную плоскость, нормальная сила F Н равна произведению силы тяжести на косинус угла наклона. F N = мг cos θ где, F N — нормальная сила, m — масса скользящего объекта, g — ускорение свободного падения, θ — угол наклона. Задача 1. На столе лежит предмет массой 2 кг. Вычислите нормальную силу, действующую на него. Решение: Имеем, m = 2 g = 9,8 Используя формулу получаем, F N = mg = 2 (9,8) = 19,6 Н Задача 2. Тело покоится на столе с силой 39,2 Н. Вычислите нормальную силу, действующую на него. Solution: We have, F = 39.2 g = 9.8 Using the formula we get, F N = mg => m = F/g => m = 39,2/9,8 => m = 4 кг Задача 3. Решение: Мы имеем, F = 200 M = 10 G = 9,8 θ = 30 ° Использование Formula We, F N 9082 = Mgula. + F sin θ = 10 (9,8) + 200 sin 30° = 98 + 200 (1/2) = 98 + 100 = 198 Н Задача 4. Тело массой 20 кг скатывается вниз с силой 400 Н с наклонной поверхности под углом 30°. Вычислите нормальную силу, действующую на него. Решение: Мы имеем, F = 400 M = 20 G = 9,8 θ = 30 ° с использованием формулы We Get, F N = 20 (9,8) + 400 sin 30° = 196 + 400 (1/2) = 196 + 200 = 396 Н Задача 5. Содержание: Определение Плотностью вещества (плотностью вещества тела) называют скалярную физическую величину, которая равна отношению массы
(dm) малого элемента тела к его единичному объему (dV). Чаще всего плотность вещества обозначают греческой буквой
$\rho$. И так: $$\rho=\frac{d m}{d V}$$ Применяя выражение (1) для определения плотности, говорят о плотности тела в точке. Плотность тела зависит от материала тела и его термодинамического состояния. В том случае, если тело можно считать однородным (плотность вещества во всем теле одинакова (
$\rho = const$), то $\rho$ определяют следующей формулой: $$\rho=\frac{m}{V}$$ где m – масса тела, V – объем тела. Если тело является неоднородным, то иногда пользуются понятием средней плотности
$\langle\rho\rangle$, которая рассчитывается как: $$\langle\rho\rangle=\frac{m}{V}(3)$$ где m – масса тела, V – объем тела. В технике для неоднородных (например, сыпучих) тел используют понятие объемной плотности.
Объемную плотность рассчитывают так же как $\langle\rho\rangle=\frac{m}{V}(3)$ (3). Объем определяют,
включая промежутки в сыпучих и рыхлых материалах (таких как: песок, гравий, зерно и т.д.). При рассмотрении газов, находящихся в нормальных условиях для вычисления плотности применяют формулу: $$\rho=\frac{\mu}{V_{\mu}}(4)$$ где $\mu$ – молярная масса газа,
$V_{\mu}$ – молярный объем газа, который при нормальных условиях составляет 22,4 л/моль. В соответствии с определением, можно записать, что
единицами измерения плотности в системе СИ служит: [$\rho$]=кг/м3 в СГС: [$\rho$]=г/(см)3 При этом: 1 кг/м3 = (10)-3 г/(см)3 . Решение. Если считать, что молекулы в воде плотно упакованы, то ее плотность можно найти как: $$\rho=\frac{m_{0}}{\Delta V}$$ где m0 – масса молекулы воды. Найдем m0, используя известное соотношение: $$\frac{m}{\mu}=\frac{N}{N_{A}}$$ где N=1 — количество молекул (в нашем случае одна молекула), m — масса рассматриваемого количества молекул
(в нашем случае m=m0), NА=6,02• 1023 моль-1 – постоянная Авогадро,
$\mu$=18•10-3 кг/моль (так как относительная молекулярная масса воды равна Mr=18). Следовательно, применяя выражение (2)
для нахождения массы одной молекулы имеем: $$m_{0}=\frac{\mu}{N_{A}}(3)$$ Подставим m0 в выражение (1), получаем: $$\rho=\frac{\mu}{\Delta V N_{A}}(4)$$ Проведем расчет искомой величины: $\rho=\frac{18 \cdot 10^{-3}}{3 \cdot 10^{-29} \cdot 6,02 \cdot 10^{23}}=10^{3} \mathrm{kr} / \mathrm{m}^{3}$ кг/м3 Ответ. Ответ. $\rho=4047,6$ кг/м3 Читать дальше: Формула потенциальной энергии. Маменишкина Нина Васильевна, учитель физики МБОУ Кутуликская СОШ п. Кутулик, Иркутской области Предмет: физика Класс: 7 У.М.К: Авторская программа: Гутник Е.М., Перышкин А.В. «Физика 7-9» М.:Дрофа. 2010г. УМК: Перышкин А.В. «Физика 7 – 9» М.: Дрофа 2014 г А.В. Перышкин «Сборник задач по физике» М.: Экзамен 2014г. Тип урока: Урок комплексного применения знаний и умений Тема урока : Лабораторная работа №4 «Измерение объёма тела» Цель урока : развитие навыка использования физических измерительных приборов, определение цены деления и измерения физических величин при измерении объема тела; развитие навыков совместной деятельности; воспитание интереса к изучаемому материалу, Задачи урока. предметные метапредметные Личностные Закрепление понятия «объём тела», знакомство со способами измерения объемов тел, определение объёма нескольких тел, оформление результатов в виде таблиц, перевод в СИ. Развитие навыка организации учебной деятельности, самоконтроля, овладение навыками постановки цели, оценка результатов, развитие навыка работы в группе Развитие познавательного интереса к способам определения объема, самостоятельности в приобретении знаний и практических умений, оценивать результаты своих действий, умение самостоятельно принимать решение, проявление инициативы, ценностное отношение друг к другу. Универсальные учебные действия. личностные регулятивные познавательные коммуникативные Принятие социальной роли обучающегося, понимание смысла своей деятельности, готовность к самообразованию Умение оценивать свои достижения, Планировать свою деятельность при выполнении задания, определяя последовательность действий, умение работать по плану, умение решать проблемы Умение познавать цель и результат, умение применять знания в новой ситуации, контролировать и оценивать процесс и результаты своей деятельности Планирование учебного сотрудничества с учителем и сверстниками, управление поведением партнера, оценка его действий. Планируемые результаты урока. предметные метапредметные Измерять объем тела, понимать принцип измерения объема с помощью измерительного цилиндра, обрабатывать результаты измерения объема тела (перевод в СИ), представлять результаты измерений с с помощью таблиц. Овладеть познавательными УДД при выполнении учебных заданий, навыками самостоятельного приобретения новых знаний, планирования своей деятельности при измерении объема тела, уметь предвидеть возможные результаты Основные понятия урока: Объем тела, измерительный цилиндр (мензурка), единицы объема, Ресурсы: Измерительный цилиндр– 15 шт., наборы тел, учебник, тетрадь. Компьютер, проектор. Интерактивная лабораторная работа; «Измерение объема тела» http://files.school-collection. (Единая коллекция цифровых образовательных ресурсов). Формы работы: фронтальная, парная, индивидуальная. Технология проведения урока. Этапы урока Задачи этапа Деятельность учителя Деятельность ученика 1.Организационный этап (2 мин.) Настроить учащихся на работу Проверяет готовность класса к уроку, настраивает класс на продуктивную деятельность Готовятся к уроку, организуют свое рабочее место. 2.Актуализация знаний (4 мин) Повторить основные понятия, создать направленность на предстоящую работу. Задает вопросы: -На прошлом уроке мы познакомились с новой физической величиной – плотность тела. 1. Дайте определение плотности тела 2.По какой формуле можно вычислить плотность тела? 3.Какие физические величины нужно знать, чтобы вычислить плотность тела? 4. Как можно определить массу тела? 5. А возможно ли определение объема тела ? 6. Предложите способы измерения объема тела. (правильной формы) Например прямоугольный деревянный или металлический брусок). 7.Единицы объема? Отвечают на вопросы учителя. (фронтальная работа) 1.Дают определение плотности. Плотность – это физическая величина, которая равна отношению массы тела к его объему. 2. 3.Массу и объем. 4.Взвешиванием. 5.Да, можно измерить. 6. Измерить ширину, длину, высоту. И вычислить по формуле: V=abc. 7. м3. см3 3.Постановка целей и задач урока (3 мин) Определение цели и задач уроке. Создает ситуацию для постановки цели урока. 1.А если тело неправильной формы? 1. Найти способ измерения объема тела неправильной формы. 4.Этап введения нового (7 мин) Изучение правил измерения тела с помощью измерительного цилиндра. Дает задание учащимся, объясняет, консультирует Задает вопросы учащимся, отвечает на вопросы учащихся возникающие в ходе выполнения работы. Вопросы: 1.как называется прибор для определения объема жидкости? 2.Как с его помощью можно определить объем тела неправильной формы? (Поясните принцип его действия). 3.В каких единицах вы получите результат? 4. Учащиеся выполняют виртуальную лабораторную работу (фронтальная работа) (задают вопросы учителю, отвечают на вопросы учителя) 1.Измерительный цилиндр (мензурка) 2.Объем вытесненной телом воды равен объему тела. 3.1 мл = 1см3 http://files.school-collection.edu.ru/dlrstore/69639dc0-9572-4e9c-b769-b60aba0b4e92/18.swf 5.Этап закрепления новых знаний и действий (17 мин.) Закрепление и применение знаний при выполнении лабораторной работы №4 «Измерение объема тела». Индивидуальные консультации Выполняют лабораторную работу по описанию в учебнике, делают необходимые записи в тетради., предусмотренные содержанием лабораторной работы( работа в парах) делают вывод о результатах работы 6.этап рефлексии (4 мин) Проводят самоанализ своей деятельности на уроке Дает задание учащимся оценить свою деятельность на уроке: что было интересно, что было трудно, чему научился, что не успел (почему?) Записывают в тетради свои результаты, впечатления от урока. (Оформляют как вторую часть вывода в лабораторной работе) (индивидуальная работа) 7.Этап домашнего задания (2 мин) Объяснение домашнего задания 1.Измерить объем твердого тела правильной формы с помощью линейки и с помощь мерной кружки (сравнить результат). Если нет мерной кружки – провести измерения нескольких тел правильной формы. По желанию: 1.Найти и прочитать легенду об Архимеде. Записывают домашнее задание, задают уточняющие вопросы. Задать вопрос спросил Изменено
3 года, 5 месяцев назад Просмотрено
341 раз $\begingroup$
92}$ , мы сделали это без интегралов, но теперь, если я хочу сделать это как интеграл, $ I = \int_S \vec J . При вычислении интеграла вектор $ \vec J$ параллелен оси, а вектор нормали к искривленной поверхности радиален, поэтому вклад от $S_1$ исчезает, у нас остаются 2 круглых конца, $ I = \int_{S_2} \vec J . \vec da + \int_{S_3} \vec J . \vec da$ Но в этом случае $\vec J$ параллелен одному из $\vec da$ и антипараллелен другому, поэтому оба интеграла сокращаются, и мы получаем $I = 0$ , так как же нам использовать определение $ I = \int_S \vec J . \vec да$ ? $\endgroup$ 1 $\begingroup$ Но в этом случае $\vec J$ параллелен одному из $\vec da$ и антипараллелен другому, так что оба интеграла сокращаются, и получается $I = 0$ , так как же нам использовать определение $ I = \int_S \vec J . Вы только что рассчитали чистый ток для замкнутой поверхности. Как следует из текущего закона Кирхгофа, это значение равно нулю (для установившихся условий). Если вам нужен ток в цилиндре, не используйте закрытую поверхность. Просто используйте поверхность, которая разделяет цилиндр. $\endgroup$ Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Требуется, но никогда не отображается Электронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie Инструменты для творчества скоро появятся, чтобы вдохновить! Присоединяйтесь к списку рассылки, чтобы узнать, когда мы запустимся. Химия. Общая химия. Что это за гористая синяя поверхность? Это один атом кобальта. Для создания изображения использовался сканирующий туннельный микроскоп. Никакой другой микроскоп не может зафиксировать объекты размером с атомы, которые являются основными строительными элементами материи. В этой статье мы узнаем о материи, измерении материи и ее различных свойствах. Источник Все, что имеет массу и занимает пространство, называется материей. Это означает, что материя охватывает все, от мельчайшего одноклеточного организма до величайшей горы. Источник Источник Источник 1. Имеют ли значение и масса, и объем? Материя является основой всего сущего. Объем и масса — два основных качества материи. 2. Материя и масса одно и то же? Материя определяется как все, что занимает пространство (имеет объем) и имеет массу, согласно общему определению. Масса, с другой стороны, является мерой количества материи в данном предмете, частице или области. Существуют различные формы или состояния материи, а также масса. 3. Имеет ли газ вес? Все газы состоят из молекул, которые состоят из атомов. Поскольку у атомов есть масса, у газов тоже есть масса. Поскольку вес — это сила, возникающая из комбинации массы и гравитационного поля, газ имеет вес. Участники закрепят свои знания по физике 8 класса, изучат методы решения олимпиадных задач На основании портфолио (скан-копии дипломов, сертификатов, грамот различных уровней за последние 3 года, подтверждающие участие претендента в олимпиадах, конкурсах по выбранному направлению деятельности (Физика). Данная программа знакомит обучающихся с различными физическими явлениями. В процессе обучения будут рассматриваться как задачи базового уровня для закрепления пройденного материала, так и задачи повышенной сложности для олимпиадной подготовки обучающихся. В рамках данной программы запланирована подготовка участников к экспериментальным турам олимпиад. Основные разделы программы: Аспирант ННГУ им. Отзыв на программу по лингвистике: Спасибо большое за такую возможность! Присутствовала с дочерью на каждом занятии (все-таки 1-й класс, надо немного технически помогать). Очень грамотно составленная программа, приятные преподаватели. Все ясно и понятно. Очень надеемся на продолжение Отзыв на программу по лингвистике. Моя дочь Женя, учится в 4-м классе гимназии с углубленным изучением английского языка. Данные занятия построены таким образом, что способствуют повторению уже пройденного материала, его закреплению, расширению словарного запаса, а также расширению кругозора, благодаря подробному изучению культуры и традиций стран Великобритании. Особую благодарность хочется выразить педагогу нашей группы — Полине Андреевне, большое Вам спасибо за интересные и нескучные занятия! Отзыв на программу по лингвистике. Отзыв на олимпиаду «Интеллект». Вот и подошел к концу наш курс «Внимание». Хочу поблагодарить организаторов и преподавателей за чудесную возможность в развитии моей дочери! Мне важно чтобы ребенок занимался и взаимодействовал с людьми, вдохновленными и горящими тем делом, которым занимаются. Считаю это один из главных факторов в развитии детей. Спасибо за вклад в наших детей Отзыв на олимпиаду «Интеллект». Спасибо вам огромное за классный курс! Ребёнок в восторге, результат наивысший! Было здорово! Здесь представлено 20 задач по динамике для подготовки к олимпиадам по физике из методического пособия В. 1. Для нагревания некоторого количества воды от 0 °C до кипения (при нормальном атмосферном давлении) понадобилось 15 минут. После этого 1 час 20 минут потребовалось для обращения всей воды в пар при тех же условиях. Определите удельную теплоту парообразования воды. Считать мощность тепловых потерь постоянной. [ L = 2,24 МДж/кг ] CBSE Class 8 Notes подготовлены преданными преподавателями Physics Wallah. Целью этих заметок для 8-го класса является создание прочной основы по математике и естественным наукам для всех учащихся 8-го класса. Нижеуказанные ссылки состоят из заметок для 8-го класса, специально разработанных для таких предметов, как математика, физика, химия и биология для 8-го класса. Как, когда и где От торговли до территории Управление деревней Племя Дикус и видение золотого века Когда люди восстают Колониализм и история имперской столицы Ресурсы, типы и разработка Земля, почва, вода, естественная растительность и ресурсы дикой природы Минеральные и энергетические ресурсы Сельское хозяйство, класс 8 Промышленность Отдел кадров Конституция Индии Понимание секуляризма Зачем нам парламент Понимание законов Судебная Понимание нашей системы уголовного правосудия Понимание маргинализации Противостояние маргинализации Вода и жители Ченнаи Право и социальная справедливость Академическая группа Physics Wallah подготовила хорошо продуманные структурные заметки для предметов 8 класса, таких как математика, физика, химия и биология для 8 класса. Мы подготовили отдельные научные главы, потому что подход к чтению физики отличается от химии и биологии и наоборот. Каждый предмет состоит из теории, которая объясняет тему и подтемы, читайте теорию, указанную в подтеме после Учебники NCERT теория и обязательно подготовьте хорошую заметку за 8 класс. Запишите все важные формулы и пункты для дальнейшего использования. Эти заметки для 8 класса помогут вам в окончательной редакции. Мы добавили ментальную карту в конце каждой главы, которая поможет вам быстрее просмотреть главу в конце. Начните решать вопросы, данные в упражнении каждой главы, постарайтесь решить субъективные вопросы. Воспользуйтесь помощью решений, которые даны в каждом вопросе. Мы загрузили вопросы на основе MCQ в каждое упражнение, чтобы получить более глубокое понимание концепции, и у вас будет больше концептуальной ясности. Разные предметы требовали разных стратегий для эффективного обучения. В этой части мы обсудим, как использовать заметки 8 класса. Мы разделили науку 8 класса на три части: физику, химию и биологию. Для получения выводов по физике и построения концепций, начиная с 8 класса, поймите основную концепцию, объясненную в примечаниях к 8 классу Физикой Уолла, подготовьте свои заметки, а для химии прочитайте теорию по всем темам, убедитесь, что вы изучили все реакции, используемые в главе, и поняли названия элементы и активность кислорода в металлах. Для заметок по биологии подготовьте заметки по теории, запишите все важные моменты, решите MCQ упражнения. Решите упражнение всех трех частей науки. Академическая группа Physics Wallah подготовила углубленную теорию для чтения математических заметок в 8-м классе и постаралась получить хорошие концепции по математике в 8-м классе с помощью решенного примера, приведенного в этом разделе. Академическая группа Physics Wallah подготовила учебный материал для 8 класса для учеников, которые учатся в базовых группах и готовятся к вступительным экзаменам вместе со своей школой. Подготовка заметок по физике Wallah class 8 укрепит ваши представления о математике и естественных науках. Вы можете получить Онлайн-викторина для 8-го класса от Physics Wallah с дополнительными примечаниями и формулой по математике для окончательной проверки. Q1. Сколько предметов в 8 классе? Ответ. Согласно последнему учебному плану CBSE (2021–22), в 8-м классе всего 6 предметов. Здесь есть -1). Математика 2). наука 3). Социальные науки 4.) Английский 5). Хинди 6).Искусственный интеллект. Q2. Как мне подготовиться к экзамену в 8 классе? Ответ. Класс 8 — это как бы база для всего будущего образования, которое вы получите как студент. Q3. Почему для вас важны конспекты восьмого класса Physics Wallah? Ответ. Заметки по физике Wallah Class 8 помогут вам лучше понять предметы. И было замечено, что CBSE чаще задает вопросы NCERT, если у них нет одинаковых вопросов, которые они задают. Так что, если вы понимаете это, вы можете легко ответить. Q4. Как учащийся может использовать заметки 8-го класса, чтобы получить хорошие оценки на экзамене 8-го класса? Ответ. Заметки для 8-го класса, подготовленные Physics Wallah, состоят из подробной теории и подробного объяснения всех концепций, которые помогут вам создать прочную основу. Для школьного экзамена загрузите или посетите NCERT Solutions for Class 8 на Physics Wallah, ведущем образовательном портале Индии. Вы можете загрузить PDF-файлы NCERT Solution, посетив веб-сайт. Вы можете использовать его в качестве справочного материала для вашего удобства. Эти решения являются лучшим учебным пособием для всех учащихся 8-х классов. В5. Почему вы должны выбрать Physics Wallah для заметок класса 8? Ответ. Physics Wallah известен своими надежными учебными инструментами и ресурсами, а также стремлением помогать учащимся учиться быстрее и лучше. Здесь вы найдете учебные материалы для 8 класса. Мы предоставляем решения NCERT для таких предметов, как математика, английский язык, естественные и социальные науки, а также хинди и искусственный интеллект. Эти решения помогут вам улучшить свои знания и овладеть каждой темой. Вы сможете очень легко развеять все свои сомнения, используя вопросы и ответы, которые улучшат вашу подготовку к экзамену. Перейти к содержимому Уважаемые ученики, родители и руководители. Для участия в Глобальном раунде, который пройдет в Нью-Йорке с 10 по 13 июля 2023 г. 40-49 Сертификат почетного упоминания + приглашение на глобальный раунд *** Печатные копии медалей будут распространяться в рамках Глобального раунда. Программа Олимпиады следующая: Категория I – 3 и 4 классы Простые числа Категория II – 5 и 6 классы Категория I Темы Категория III — 7 и 8 классы Темы категории II Категория IV — классы 9 и 10 Темы категории III Категория V — классы 11 и 12 Темы категории IV Пожалуйста, найдите ниже прошлых экзаменационных документов Mathematics_category I.PDF Mathematics_category II.PDF Mathematics_category III.PDF MATHEMATICS_CATEGORY-IV.PDF MATHEMATICS_CATERORY WITLER WITLORY Золотые, серебряные и бронзовые медали будут присуждаться на основе следующих процентов: Калькулятор, представленный в данной статье, может решать широкий спектр задач на теплообмен (или задач на теплоемкость) — а именно, все те задачи, где отсутствует фазовый переход (то есть плавление/кристаллизация или испарение/конденсация). Для решения задач калькулятор использует уравнение теплового баланса, поэтому сначала небольшая теория: Теплопередача или теплообмен — физический процесс передачи тепловой энергии от более горячего тела к менее горячему, либо непосредственно (при контакте), или через разделяющую (тела или среды) перегородку из какого-либо материала. Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Когда физические тела одной системы находятся при разной температуре, то происходит передача тепловой энергии, или теплопередача от одного тела к другому до наступления термодинамического равновесия (состояния системы, при котором остаются неизменными во времени макроскопические величины этой системы — температура, давление, объём, энтропия, в условиях изолированности от окружающей среды). Самопроизвольная передача тепла всегда происходит от более горячего тела к менее горячему, что является следствием второго закона термодинамики. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её и теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: Количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами. Это и есть уравнение теплового баланса. Уравнение теплового баланса также можно записать и в другом виде: Интерпретация такой записи: Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю. Если раскрыть количество теплоты (про формулу для расчета количества теплоты уже было написано здесь: Формула количества теплоты), то мы получим следующее выражение: , Именно это уравнение использует калькулятор, представленный ниже. 51020501001000 Вещество Масса, кг Укажите массу вещества, или поставьте ? (знак вопроса), если ее требуется найти Удельная теплоемкость, Дж/кг*С Укажите теплоемкость вещества, или поставьте ? (знак вопроса), если ее требуется найти Начальная температура, С Укажите начальную температуру вещества, или поставьте ? (знак вопроса), если ее требуется найти Конечная температура, С Укажите конечную температуру вещества, или поставьте ? (знак вопроса), если ее требуется найти Данные Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: Lorem ipsum;Lorem ipsum;Lorem ipsum;Lorem ipsum;Lorem ipsum Загрузить данные из csv файла Количество теплоты извне, Дж Укажите подведенное извне (со знаком минус) или отведенное вовне (со знаком плюс) количество теплоты, укажите ноль если система теплоизолированная, или поставьте ? (знак вопроса), если это значение надо рассчитать Точность вычисления Знаков после запятой: 1 Искомая величина Значение Рассмотрим как нужно применять калькулятор для решения задач на теплообмен. В латунный калориметр массой 200г с водой 400г при температуре 17С опустили тело из серебра массой 600г при 85С. Вода нагрелась до 22С. Определить удельную темлоёмкость серебра. Как использовать калькулятор: Обратите внимание на использование знака вопроса в ячейке для удельной теплоемкости серебра Три килограмма воды, находившейся при температуре двадцать градусов Цельсия, вскипятили в алюминиевом чайнике массой один килограмм. Удельная теплоёмкость воды равна четыре тысячи двести Дж/(кг×°C), удельная теплоёмкость алюминия равна девятьсот двадцать Дж/(кг×°C). Определить количество теплоты, затраченное при этом процессе. Как использовать калькулятор: В медном калориметре массой 100 г находится 1 кг воды при температуре 20° С. В воду опускают свинцовую деталь массой 2 кг, имеющую температуру 90° С. До какой температуры нагреется вода? (Потерями теплоты в калориметре пренебречь.) Как использовать калькулятор: Обратите внимание на использование знака вопроса во всех трех ячейках для конечной температуры Как видим, иногда в задачах не указывают удельную теплоемкость веществ, предполагая, что ученик сможет узнать ее из справочника. Для удобства пользования калькулятором ниже приведена таблица удельной теплоемкости некоторых веществ. Источники: Цифровизация ИТ в госсекторе | Поделиться С помощью нейросети удалось радикально снизить количество уравнений,
которые требуется решать в рамках изучения одной из известнейших проблем в
квантовой физике. Это открывает колоссальные возможности для науки и создания
новых материалов. С помощью искусственного
интеллекта (ИИ) физики смогли радикально оптимизировать известную квантовую
проблему, которая до недавнего времени подразумевала решение 100 тыс. различных
уравнений. Теперь достаточно решить четыре уравнения, и это без каких-либо жертв
в плане точности результатов. Работа, опубликованная в Physical Review Letters 23 сентября 2022 г.,
может привести к революционным изменениям в том, как ученые исследуют системы,
содержащие множество взаимодействующих электронов. Если это решение удастся масштабировать
на другие аналогичные проблемы, с его помощью будет возможно создание новых
сверхпроводящих материалов или новых средств экологически чистого производства
энергии. «Мы начинаем с огромного
корпуса взаимосвязанных дифференциальных уравнений и затем с помощью машинного
обучения превращаем его в нечто настолько малое, что можно посчитать на
пальцах», — заявил глава исследовательской группы Доменико Ди Санте (Domenico Di Sante), сотрудник Центра вычислительной квантовой
физики при Институте Флатирона (США) и Университета Болоньи (Италия). Проблема, известная как
модель Хаббарда, связана с поведением электронов, движущихся внутри решеткообразной
структуры. Если два электрона занимают одну точку в решетке, они взаимодействуют. Модель Хаббарда низвели до четырех уравнений с помощью нейросети Простота модели Хаббарда,
однако, глубоко обманчива, пишет издание Phys.org. Даже когда обсчитывается скромное количество
электронов, и используются самые передовые вычислительные подходы, объем
собственно вычислений остается огромным. Дело в квантовом сцеплении: после того,
как два электрона взаимодействуют, они оказываются сцепленными, и как бы далеко
они ни оказывались друг от друга впоследствии, их нельзя рассматривать как
самостоятельные единицы. В результате физикам приходится учитывать сразу все
электроны разом, а не каждый по отдельности. Физики в таких случаях
применяют ренормализационные группы — математический аппарат, который
используется для выявления изменений в системе при модификации ее свойств,
например температуры, или последствий изменения масштабов. Однако даже
ренормализационная группа, отслеживающая все возможные сцепления между
электронами без ущерба для точности, будет содержать десятки тысяч, сотни тысяч
или даже миллионы отдельных уравнений, требующих решения. Ди Санте и его коллеги
задумались о возможности применить нейросеть для того, чтобы сделать массивную ренормализационную
группу более управляемой. И это им удалось. Никита Виноградов, Банк «ФК Открытие»: «Со сложностями достойно справились те, кто давно занимался вопросом корпоративного технологического суверенитета» Безопасность Нейросеть вначале
проиндексировала все связи в полноразмерной группе ренормализации, затем
перенастраивала силу этих соединений до тех пор, пока не выявила узко
ограниченный набор уравнений, выдающих точно такой же результат, что и исходная
ренормализационная группа. «Речь идет о способности машины
выявлять скрытые паттерны, — заявил Ди Санте. — Когда мы увидели результаты, мы
сказали: «Ого, это куда больше, чем то, на что мы рассчитывали; нам
действительно удалось получить релевантные физические результаты». Обучение нейросети
потребовало больших вычислительных ресурсов: программа проработала несколько
недель непрерывно. Однако теперь эта нейросеть может быть использована для
производства вычислений в связи с другими крупными физико-математическими
проблемами, без необходимости начинать ее обучение с нуля. Ди Санте и его соратники
также изучают, что именно их нейросеть «поняла» насчет системы, к которой была
применена, в надежде выявить закономерности, прежде неочевидные для физиков. Как получить ₽30 млн на вывод решения в области искусственного интеллекта на новые рынки Поддержка ИТ-отрасли Остается вопрос, насколько
новый подход работает с более сложными квантовыми системами, например с
материалами, в которых электроны взаимодействуют на больших дистанциях. «Результат можно назвать
потрясающим, и если выводы, сделанные в этой работе не будут опровергнуты, то,
возможно, речь идет о глобальной революции в физике, — считает Дмитрий Гвоздев, генеральный директор
компании “Информационные технологии будущего”. — Революции, которая оказалась
достижима только благодаря машинному обучению и характерной для нейросетей
способности выявлять скрытые закономерности, которые и позволяют низводить
гиперсложные системы до считанного количества параметров. Пока возможности нейросетей
находятся на начальном этапе развития, но есть основания полагать, что в
будущем с их помощью удастся решать какие-то другие проблемы и задачи физики,
которые на сегодняшний день остаются нерешенными, например уравнений
Шредингера, множественные проблемы сверхтекучести и т. Роман Георгиев Опубликовано:
19 сентября 2010 г. Автор
Мориэль Шоттлендер Категории:
Химия, Физика Любой, кто имеет какое-либо отношение к физике или математике — от относительно низкого уровня, такого как домашняя работа, до вычислений более высокого уровня — знает, что время от времени возникает разочарование, когда приходится решать физическое уравнение, включающее константы. Wolfram Alpha обычно является лучшим решением, но оно может быть немного утомительным и сложным, и чтобы использовать его правильно, я считаю, что вам нужно искать значения констант или то, как Wolfram Alpha ожидает их записи. Это означает, что иногда относительно простое уравнение может превратиться в надоедливое исследование документации Wolfram Alpha. В Интернете есть несколько хороших онлайн-калькуляторов (одним из них является Google.com), но немногие из них помогут вам ориентироваться в (многих) физических константах, которые могут использоваться в различных вычислениях. Теперь, однако, к списку добавлено еще одно, которое поможет вам решать уравнения такого типа легко и без лишней суеты, угадывая константы, которые вы имеете в виду, и решая уравнения аккуратно и быстро: Фермион Марка Дановича. Fermion отображает список констант в нижней части страницы, чтобы вы могли видеть их значения и то, как калькулятор ожидает их прочитать. Гениально просто. Действительно полезно. Забавно, мне очень нравится Wolfram Alpha за его мощь, и я довольно часто использую Mathematica и Matlab по той же (но расширенной) причине, но иногда они являются полным излишеством. Простое вычисление может превратиться в довольно много потраченного времени на копание в руководствах или объявление всех констант самостоятельно для начала. Для такого рода вычислений правила Фермиона. Посмотрите, оно того стоит. РЕДАКТИРОВАТЬ: Марк уведомил меня, что калькулятор также позволяет конвертировать единиц внутри вычислений, что также весьма полезно. Например, чтобы использовать скорость света «c» в расчетах с использованием футов в секунду, а не определенных метров в секунду, просто введите «c{ft}», и система преобразует ее автоматически. На YouTube есть полезное видео, объясняющее всю систему. Хорошо, в этом случае мы не можем просто определить силовую функцию \(F\left( x \right)\), которая будет работать для нас. Итак, нам нужно подойти к этому с другой точки зрения. Давайте сначала установим \(x = 0\) в качестве нижнего конца резервуара/конуса и \(x = 15\) в качестве верхней части резервуара/конуса. С этим определением 9*\) любая точка из \(i\) -го -го подинтервала, где \(i = 1,2, \ldots n\). Теперь для каждого подинтервала мы аппроксимируем воду в резервуаре, соответствующую этому интервалу, в виде цилиндра радиуса \({r_i}\) и высоты \(\Delta x\). Вот краткий набросок танка. Обратите внимание, что эскиз на самом деле не в масштабе, и мы смотрим на резервуар прямо спереди, поэтому мы можем видеть все различные количества, с которыми нам нужно работать. Толкование Плотность — физическая величина равная отношению массы тела к его объему, показывает массу единичного объема вещества. Более формально: плотность есть предел отношения массы вещества m к занимаемому им объёму V. Таким образом, плотность . Плотность измеряется в кг/м³ в системе СИ и в г/см³ в системе СГС. Для сыпучих и пористых тел различают Плотность находится по формуле: Плотность газов находится по формуле: , где М — молярная масса газа, Vm — молярный объём (при нормальных условиях равен 22,4 л/моль) Как правило, при уменьшении температуры плотность увеличивается, но есть вещества, чья плотность ведет себя иначе, например, вода, бронза и чугун. При фазовых переходах, изменении агрегатного состояния плотность вещества меняется скачкообразно. Самую большую плотность во Вселенной имеют черные дыры (ρ ~ 1014 кг/м³) и нейтронные звезды (ρ ~ 1011 кг/м³). Самую низкую плотность имеет межгалактическая среда (ρ ~ 10-33 кг/м³) В астрономии большое значение имеет средняя плотность небесных тел, по ней можно приблизительно определить состав этого тела. Wikimedia Foundation.
2010. Игры ⚽ Нужна курсовая? Задачи по физике — это просто! Вспомним формулы, которые связывают плотность, массу и объем:
Не забываем, что решать задачи надо всегда в системе СИ! Поэтому потренируемся в достаточно сложном переводе единиц измерения: 1 куб. см — это одна миллионная доля метра кубического, поэтому 1 куб. дм — это тысячная доля метра кубического, поэтому Существует единица объема — 1 литр. И не забудем о массе: Килограмм- это единица массы, буквенное обозначение массы
— m Метр кубический — это единица объема,
буквенное обозначение объема — V Элементарные задачи из курса школьной физики Задача 1 Определить плотность серной кислоты, если бидон емкостью 35 литров вмещает 63 кг кислоты. Задача 2 Определить объем оловянного бруска массой 146 г.
Задача 3 Какую массу имеет стеклянная пластина объемом 15 куб. дм ? Задача 4 Металлическая деталь массой 949 г имеет объем 130 куб. дм. Какой это металл? Чтобы ответить на вопрос задачи, необходимо рассчитать плотность металла, а затем по справочной таблице плотностей (она есть в учебнике) определить, для какого металла характерна вычисленная плотность. Задача 5 Чугунный шар имеет массу 70 кг, а объем 10 куб. дм. Определить, спошной этот шар или полый (с пустотами). Сплошной шар, т.е. целиком из чугуна, должен иметь плотность, равную плотности чугуна (посмотреть в таблице). Если у шара внутри есть пустоты, то такой шар называется полым. В этом случае средняя плотность шара должна быть меньше табличной плотности чугуна. Ведь пустоты заполнены воздухом, а он очень легкий. Рассчитаем по формуле плотность шара и сравним с расчетной! Задача 6 Масса чугунной плиты — 64 кг. Определить массу мраморной плиты таких же размеров. Если читать условия задачи внимательно, то ясно, что объем чугунной плиты равен объему мраморной плиты: Vч = Vм
Задача 7 Бутыль с керосином имеет массу 4 кг. Масса бутыли без керосина составляет 400 г. Обратите внимание: Емкость цистерны молоковоза составляет 10 куб. Задача 9 Задача 10 Сосновые доски нагружены на платформу и имеют массу 12 тонн. Размер одной доски составляет 500 х 20 х 10 (куб. см). Сколько досок на платформе? Следующая страница «Сила тяжести, вес тела, сила упругости. 7 класс» Назад в раздел «Решение задач по физике для 7 класса» Объем является основной физической величиной . Объем является производной величиной и выражает трехмерную протяженность объекта . Объем часто количественно измеряется с использованием производной единицы СИ, кубических метра . Например, объем внутри сферы (то есть объем шара) получается из V = 4/3πr 3 , где r — радиус сферы. Другой пример: объем куба равен произведению стороны на сторону. Поскольку каждая сторона квадрата одинакова, длина одной стороны может быть равна в кубе . Если одна сторона квадрата равна 3 метрам, объем будет равен 3 метрам на 3 метра на 3 метра или 27 кубическим метрам. Формулы для расчета различных объемов Формулы объема для некоторых обычных трехмерных объектов: Удельный объем является интенсивной переменной , тогда как объем является экстенсивной переменной. Стандартная единица измерения удельного объема в системе СИ — кубический метр на килограмм (м 3 /кг). Стандартной единицей измерения в английской системе является кубический фут на фунт-массу (ft 3 /lbm). Плотность (ρ) вещества обратна его удельный объем (ν). ρ = m/V = 1/ρ Плотность определяется как масса на единицу объема . Это также интенсивное свойство , которое математически определяется как масса, деленная на объем: ρ = m/V и нейтронов ) составляют большую часть массы обычных атомов, плотность обычной материи, как правило, ограничивается тем, насколько плотно мы можем упаковать эти нуклоны, и зависит от внутренней атомной структуры вещества. самый плотный материал , найденный на Земле, — это металлический осмий . Тем не менее, его плотность бледнеет по сравнению с плотностью экзотических астрономических объектов, таких как белые карликовые звезды и нейтронные звезды . СПИСОК ГЛАВНОГО МАТЕРИАЛА: Следует отметить, что плутоний является промышленным изотопом и создается из урана в ядерных реакторах. Но ученые обнаружили следовые количества встречающегося в природе плутония. Если мы включим изготовленные элементы, то самым плотным на данный момент будет Хассиум . За плотностью Hassium следует Meitnerium (элемент 109, названный в честь физика Лизы Мейтнер), плотность которого оценивается как 37,4 x 10 3 кг/м 3 . Изменения удельного объема Как правило, плотность и, следовательно, удельный объем может быть изменен , изменив либо давление , либо температуру . Влияние температуры на плотность жидкостей и твердых тел также очень важно. Большинство веществ расширяются при нагревании и сжимаются при охлаждении . Однако величина расширения или сжатия варьируется в зависимости от материала. Это явление известно как тепловое расширение . Изменение объема материала, подвергающегося изменению температуры, определяется следующим соотношением: где ∆T — изменение температуры, V — первоначальный объем, ∆V — изменение объема и α V — коэффициент объемного расширения . Следует отметить и исключения из этого правила. Например, вода отличается от большинства жидкостей тем, что она становится менее плотной при замерзании . Его максимальная плотность составляет 3,98 °C (1000 кг/м 3 ), тогда как плотность льда составляет 917 кг/м 3 . Отличается примерно на 9% и поэтому плавает на льду на жидкой воде Атом состоит из небольшого, но массивного ядра , окруженного облаком быстро движущихся электронов . Ядро состоит из протонов и нейтронов . Типичные радиусы ядер имеют порядок 10 −14 м. Радиусы ядер можно рассчитать по следующей формуле, предполагая сферическую форму: r = r 0 . A 1/3 где r 0 = 1,2 x 10 -15 м = 1,2 фм Если мы используем это приближение, мы, следовательно, ожидаем, что объем ядра будет порядка 4/3πr 3 или 7,23 × 10 −45 м 3 для ядер водорода или 1721×10 −45 m 3 для 238 ядер U. Объем атома примерно на 15 порядков больше чем объем ядра. Для атома урана Ван-дер-Ваальсов радиус составляет около 186 пм = 1,86 × 10 −10 м . Радиус Ван-дер-Ваальса, r w , атома — это радиус воображаемой твердой сферы, представляющий расстояние наибольшего сближения с другим атомом. Атом урана имеет объем около 26,9 × 10 −30 м 3 , имеющие сферическую форму. Но это «огромное» пространство занято в основном электронами, потому что ядро занимает лишь около 1721×10 −45 м 3 пространства. Может показаться, что пространство и материя пусты , но это не . Из-за квантовой природы электронов электроны не являются точечными частицами, а размазаны по всему атому. Классическое описание нельзя использовать для описания вещей на атомном уровне. В атомном масштабе физики обнаружили, что квантовая механика очень хорошо описывает вещи в этом масштабе. Расположение частиц в квантовой механике не находится в точном положении, и они описываются функция плотности вероятности . Поэтому пространство в атоме (между электронами и атомным ядром) не пусто. Тем не менее, он заполнен функцией плотности вероятности электронов (обычно известной как « электронное облако »). В типовых современных водо-водяных реакторах (PWR), система охлаждения реактора (RCS), показанная на рисунке, состоит из: Все компоненты СТР расположены внутри здания защитной оболочки. Внутри корпуса реактора, контуров и парогенераторов при нормальной работе находится сжатая жидкая вода. Давление поддерживается примерно на уровне 16 МПа . При таком давлении вода кипит примерно при 350°C (662°F). Температура воды на входе составляет около 290°C (554°F). Объемы типичных PWR указаны в следующей таблице. Это иллюстративный пример, и следующие данные не соответствуют какой-либо конструкции реактора. Необходимо отметить объем охлаждающей жидкости значительно изменяется с температурой охлаждающей жидкости. Общая масса теплоносителя всегда остается неизменной. Изменение объема воды не является изменением запаса воды. Объем теплоносителя реактора изменяется с температурой из-за изменений плотности . Большинство веществ расширяются с при нагревании и сжимаются при охлаждении . Однако величина расширения или сжатия варьируется в зависимости от материала. Это явление известно как тепловое расширение . Изменение объема материала, подвергающегося изменению температуры, определяется следующим соотношением: где ∆T — изменение температуры, V — первоначальный объем, ∆V — изменение объема и α V — коэффициент объемного расширения . Коэффициент объемного теплового расширения для воды непостоянен в диапазоне температур и увеличивается с температурой ( особенно при 300° С ). Поэтому изменение плотности не является линейным в зависимости от температуры (как показано на рисунке). См. также: Паровые столы. При нормальных условиях общий объем теплоносителя в системе теплоснабжения реактора почти постоянен. С другой стороны, в условиях переходной нагрузки, объем может значительно измениться . Эти изменения естественным образом отражаются в изменении уровня воды в компенсаторе давления. При постепенном снижении средней температуры теплоносителя реактора общий объем воды также уменьшается, что снижает уровень компенсатора давления. При постепенном наборе нагрузки увеличение средней температуры теплоносителя реактора вызывает расширение общего объема воды, повышая уровень компенсатора давления. Контрольный объем – это фиксированная область в пространстве, выбранная для термодинамического исследования баланса массы и энергии для проточных систем. Граница контрольного объема может быть действительной или воображаемой оболочкой . Поверхность управления является границей контрольного объема. Например, анализ контрольного объема можно использовать для определения скорости изменения количества движения жидкости. В этом анализе будет рассматриваться струйная трубка ( контрольный объем ), как и для уравнения Бернулли. В этом контрольном объеме любое изменение импульса жидкости в контрольном объеме происходит из-за действия внешних сил на жидкость в этом объеме. См. также: Формула импульса. Как видно из рисунка, метод контрольного объема можно использовать для анализа закона сохранения количества движения в жидкости. Контрольный объем может быть выбран как любой произвольный объем, через который протекает жидкость. Этот объем может быть статичным, подвижным и даже деформироваться во время течения. Чтобы решить любую задачу, мы должны решить основные законы сохранения в этом томе. Очень важно знать все относительные скорости потока к поверхности управления. Поэтому очень важно точно определить границы контрольного объема при анализе. Неподвижная плита (например, лопасть водяной мельницы) отклоняет поток воды со скоростью 1 м/с и углом 90° . Решение h Каталожные номера: Реакторная физика и теплогидравлика: Термодинамические свойства Вы должны войти в систему, чтобы опубликовать ответ. Автор: [Аноним] Можете ли вы дать мне формулу для нахождения объема в физике 10 Ответы найдены.
93 = атомный вес/плотность x n 1 . Формула, где можно найти объем V = M/D , где можно найти объем V = M/D . 2 HI 1 Привет! Объем газа V=nRT/P Где Приведенная выше формула получена путем ретроспективного теоретического объединения законов Бойля (pv = константа и Шарля (V/T = константа). 1 Hi, V = M/d V = Volume Есть некоторые вещи, которые нельзя купить за деньги, такие как манеры, мораль и интеллект. 1 Volume=m/d 2 9 Пусть плотность объекта и. Тогда d = m/v 1 hi dear M= mass of body D=density of the body спасибо аамир хан Никогда не лги тому, кто доверяет тебе. Зачетная неделя, сессия, все эти студенческие тяготы пришлись как раз период ужесточения карантина. Ситуация с мировой пандемией постоянно усугубляется, но это не мешает высшим учебным заведениям осуществлять образовательную деятельность посредством дистанционных технологий. Студенты старших курсов в большей степени адаптированы к учебному процессу, но времени на подготовку не хватает, как и прежде. Труднее всего приходится первокурсникам, которые переживают процесс адаптации к большим нагрузкам и новому формату обучения. В настоящее время огромное внимание уделено самостоятельной подготовке и изучению материала. Поэтому могут возникать трудности, с которыми помогут справиться различные ресурсы помощи студентам, где вы можете заказать решение задач по физике онлайн, написание курсовой или дипломной работы. Если раньше, такие сайты в большей степени предлагали готовые решения, своего рода шпаргалки на экзамен или контрольную, то во время эпидемии коронавируса возникает необходимость более детального изучения материала. Студенты и школьники старших классов уже не могут заручиться поддержкой родителей в решении той или иной задачи по физике, высшей математике, химии, здесь нужна помощь профессионалов. Это своего рода педагогическая поддержка, которая приобрела популярность на Западе. Секреты эффективного решения задач Подготовку к контрольной или зачету не стоит откладывать в долгий ящик. Даже несмотря на дистанционный формат обучения, ответственность на студентах лежит по-прежнему высокая. Неуспеваемость, несвоевременная сдача контрольных, неправильное решение задач – все эти факторы могут способствовать отчислению, поэтому не стоит недооценивать серьезность ситуации. Заказывая решение задач по физике онлайн, обратите внимание на рейтинг сайта, отзывы реальных пользователей и гарантии, которые он предоставляет своим пользователям. Не стоит скачивать решения задач с интернета, особенно если они находятся в широком доступе, надеясь найти похожую задачу и решить свою, по примеру. Мало того, что там могут быть опечатки и ошибки, так и найти аналогичное задание не так и просто. Куда лучше обратиться к профессиональным исполнителям, а освободившееся время потратить на подготовку к зачету, экзамену или контрольной. Задачи по физике, химии, логике будут выполнены максимально быстро и эффективно, главное вовремя сделать правильный выбор! 17 декабря 2022, 22:22 16 декабря 2022, 22:19 16 декабря 2022, 21:58 16 декабря 2022, 21:50 16 декабря 2022, 21:48 16 декабря 2022, 17:40 16 декабря 2022, 16:04 16 декабря 2022, 15:45 16 декабря 2022, 15:20 16 декабря 2022, 14:08 Вариант ЕГЭ по физике состоит из двух частей и включает в себя 32 задания. В части 1 содержится 24 задания с кратким ответом, в которых ответ записывается в виде числа, двух чисел или слова, а также задания на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр. Часть 2 содержит 8 заданий. Из них два задания с кратким ответом (25 и 26) и шесть заданий (27–32), для которых необходимо привести развернутый и обоснованный ответ. В первой части – не только формулы и графики. Есть и необычные задания. В задании 22 вы увидите фотографии или рисунки измерительных приборов. Чтобы сделать это задание, нужно уметь записывать показания приборов при измерении физических величин с учётом абсолютной погрешности измерений. Задание 23 проверяет умение выбирать оборудование для проведения опыта по заданной гипотезе. Завершает первую часть задание по астрономии на выбор нескольких утверждений из пяти предложенных. Вторая часть работы посвящена решению задач: семи расчётных и одной качественной задачи. Они распределяются по разделам следующим образом: 2 задачи по механике, 2 задачи по молекулярной физике и термодинамике, 3 задачи по электродинамике, 1 задача по квантовой физике. Задания 25 и 26 – это расчётные задачи с кратким ответом. Задание 25 по молекулярной физике или электродинамике, а задача 26 – по квантовой физике. Далее идут задания с развёрнутым ответом. Задание 27 – качественная задача, в которой решение представляет собой объяснение какого-либо факта или явления, основанное на физических законах и закономерностях. Качественная задача может быть по любому из разделов курса физики. Следующие задачи строго распределены по определенным разделам физики. Задание 28 – по механике или по молекулярной физике, задание 29 – по механике, задание 30 – по МКТ и термодинамике, задание 31 – по электродинамике, задание 32 – преимущественно по оптике. Для расчётных задач высокого уровня сложности (29–32) требуется анализ всех этапов решения. На нашем сайте размещены статьи по каждой задаче ЕГЭ. В них приведены не только типовые задания ЕГЭ по физике, но и показан подробный ход рассуждений, приводящих к решению задач. Каждое задание сопровождается ссылкой на необходимую теорию. Рассказано о секретах решения каждой задачи ЕГЭ по физике. Задание 1 Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности. Задание 2 Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения Задание 3 Закон сохранения импульса, кинетическая и потенциальные энергии, работа и мощность силы, закон сохранения механической энергии Задание 4 Механическое равновесие, механические колебания и волны. Условие равновесия твёрдого тела, закон Паскаля, сила Архимеда, Задание 5 Механика. Задание 6 Механика. Изменение физических величин в процессах. Задание 7 Механика. Установление соответствия между графиками и физическими величинами, между физическими величинами и формулами. Задание 8 Основы термодинамики. Тепловое равновесие. Уравнение Клапейрона-Менделеева. Изопроцессы. Задание 9 Термодинамика. Работа в термодинамике, первый закон термодинамики, КПД тепловой машины Задание 10 Термодинамика, тепловое равновесие. Относительная влажность воздуха, количество теплоты Задание 11 Термодинамика и молекулярно-кинетическая теория. Объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков. Задание 12 Термодинамика и молекулярно-кинетическая теория. Изменение физических величин в процессах; установление соответствия между графиками и физическими величинами, между физическими величинами и формулами. Задание 13 Электрическое поле, магнитное поле. Принцип суперпозиции электрических полей, магнитное поле проводника с током, сила Ампера, сила Лоренца, правило Ленца Задание 14 Электричество. Закон сохранения электрического заряда, закон Кулона, конденсатор, сила тока, закон Ома для участка цепи, последовательное и параллельное соединение проводников, работа и мощность тока, закон Джоуля – Ленца Задание 15 Электричество, магнетизм и оптика. Поток вектора магнитной индукции, закон электромагнитной индукции Фарадея, индуктивность, энергия магнитного поля катушки с током, колебательный контур, законы отражения и преломления света, ход лучей в линзе Задание 16 Электродинамика. Объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков Задание 17 Электродинамика и оптика. Изменение физических величин в процессах Задание 18 Электродинамика, оптика, специальная теория относительности. Установление соответствия между графиками и физическими величинами, между физическими величинами и формулами Задание 19 Ядерная физика. Задание 20 Линейчатые спектры, фотоны, закон радиоактивного распада. Задание 21 Квантовая физика. Изменение физических величин в процессах. Установление соответствия между графиками и физическими величинами, между физическими величинами и формулами Задание 22 Механика — квантовая физика, методы научного познания Задание 23 Механика — квантовая физика, методы научного познания Задание 24 Элементы астрофизики. Солнечная система, звёзды, галактики Задание 25 Молекулярная физика, термодинамика, электродинамика. Расчётная задача Задание 26 Электродинамика, квантовая физика. Расчётная задача Задание 27 Механика — квантовая физика. Качественная задача Задание 28 Механика — квантовая физика. Расчётная задача Задание 29 Механика. Расчетная задача Задание 30 Молекулярная физика. Расчетная задача Задание 31 Электродинамика. Расчетная задача Задание 32 Электродинамика. Это страница ресурсов для учащихся, интересующихся олимпиадами по физике . Пожалуйста, добавьте качественные ресурсы. Академия Хана: AP Physics 1/2 Неверное имя пользователя Войти в АоПС Имя пользователя: Пароль: Оставаться в системе О компании
Решения
Список результатов 904 участвовали команды из 59 страны До 5 старшеклассников соревнуются из дома в трехчасовом соревновании по решению физических задач
проблемы. Вам доступно 7 задач. Как только вы решите одну, вы получите другую проблему
немедленно. За каждую решенную задачу команде начисляются баллы. Лучшие команды получают призы и вечную славу в нашем конкурсе, который был проведен
ежегодно уже более десяти лет. Кружки Вольфрам Футболки Лицензия на Холщовые сумки Лицензия на Хвойное дерево может быть (с механической точки зрения) аппроксимировано однородным
прямой круговой конус высотой h = 40 м и радиусом в основании r = 1,0 м. Найдите максимальное
угол, на который его ось может быть смещена от вертикальной оси до того, как он начнет падать из-за
масса. Водопад высотой h = 30 м имеет расход Q = 1,2 м 3 ·с -1 . Найдите полную силу, с которой вода
ударяется о землю под водопадом. Предположим, что вода быстро стекает с
точка падения и глубина воды под водопадом незначительна. Найти сопротивление между двумя соседними вершинами четырехмерного куба из проволоки.
Каждое ребро куба имеет сопротивление R = 1000 Ом. Витек хотел бы набрать воды из своего колодца, но не хочет продолжать тянуть
ведро вверх. Поэтому он постепенно перемешивал воду все быстрее и быстрее, пока под углом
со скоростью ω = 11 рад·с -1 , вода сама начала вытекать из колодца. Витек знает
глубина колодца (от верхнего края до земли на забое) h = 47 м. Колодец имеет
круглое поперечное сечение радиусом r 0 = 1,6 м. Какой была высота столба воды
(от дна колодца до поверхности воды) до того, как Витек начал крутить воду
вокруг? Начало конкурса Участники получают 7 задач. Спешите! Появляется еще одна серия задач, связанных с разными областями физики.
В течение следующих получаса участники могут получать бонусные очки за решение серии. Конец бонусных баллов в Спешите! серия Задачи от Спешите! по-прежнему доступны, но без бонусных баллов. Окончание соревнований Конкурс окончен. Публикуем авторские решения и улаживаем возможные конфликты. Крайний срок подачи жалоб Мы закрываем возможность жаловаться и готовимся опубликовать официальных победителей в ближайшие дни.
31.01.2022
781
0
Звёздное небо
Астрономия является одной из древнейших наук. Предметом изучения астрономии является огромное количество объектов, от метеорных песчинок, которые сгорают в атмосфере Земли до необъятных просторов Вселенной. В зависимости от изучаемой области астрономии, её разделяют на отдельные части. Одним из разделов в курсе общей астрономии является Сферическая астрономия или как её ещё называют Астрометрия. Она изучает положение и вращение Земли, движение небесных объектов, путём измерения углов на небе, для чего необходимы длительные наблюдения небесных тел. Главными целями Сферической астрономии является:
— Установление систем небесных координат;
— Получение параметров, характеризующих наиболее полно закономерности вращения Земли.
Схема взаимного расположения основных созвездий и ярких звезд. Демонстрационный Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Вариант 9 Вариант 10 Вариант 11 Вариант 12 Вариант 13 Вариант 14 Вариант 15 Вариант 16 Вариант 17 Вариант 18 Вариант 19 Вариант 20 Создать тест С физикой дела обстоят по-особенному. Да и сложность заданий из года в год остается примерно на одном уровне, поэтому не ленитесь, готовьтесь и получайте от всего этого процесса удовольствие! Часть 1 содержит 23 задания с кратким ответом. Часть 2 содержит 8 заданий, объединенных общим видом деятельности – решение задач. Из них 3 задания с кратким ответом (24–26) и 5 заданий (27–31), для которых необходимо привести развернутый ответ. На выполнение всей экзаменационной работы отводится 3 часа 55 минут (235 минут). Задания 1–4, 8–10, 13–15, 19, 20, 22 и 23 части 1 и задания 24–26 части 2 оцениваются 1 баллом. Задания 5–7, 11, 12, 16–18 и 21 части 1 оцениваются 2 баллами, если верно указаны оба элемента ответа; 1 баллом, если допущена ошибка в указании одного из элементов ответа, и 0 баллов, если допущено две ошибки. Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу. Ознакомьтесь с подробной видеоинструкцией по использованию модуля. Создать класс Вопросы и ответы по физике — Сомнения, задачи, решения домашних заданий по физике Все уровни13 PlusA LevelGCSEIBKS3Scottish HighersUniversity Часть А) В жидкостях происходит конвекция. В этом процессе более энергичные частицы перемещаются из более теплых областей в более холодные и уносят с собой свою энергию. Конвекционный ток возникает потому, что … В БАК протоны разгоняются почти до скорости света. Они удерживаются в круговом ускорителе сверхпроводящими дипольными магнитами 1232. Насколько силен магический … Бесконечная квадратная яма — это область с постоянной потенциальной энергией (внутри ямы), окруженная областью бесконечной потенциальной энергии (снаружи ямы). Горизонтальное положение x (измеренное от оптической оси) точки на экране на расстоянии D от двойной щели с разделением щелей a связано с … Температура – это макроскопический эффект средней кинетической энергии субатомных частиц, составляющих материал. Поэтому используются кельвины, потому что это единственная истинная шкала, которая … Когда большинство студентов начинают свои курсы физики, первая форма энергии, о которой они узнают, — это кинетическая энергия, которая связана со скоростью, которую имеет объект. И наоборот, потенциал … Просто приравняйте центростремительную силу и силу тяжести, действующую на МКС и найдите v. P. S. Погуглите радиус и массу Земли, расстояние до МКС… Электродвижущая сила или ЭДС ячейки в цепи, для начала, вовсе не сила: она имеет единицу измерения вольт. Этот вопрос относится к поведению газов при сжатии. В IB мы моделируем такие ситуации, используя уравнение идеального газа, которое утверждает, что: pV = nRT, где: p — … В физике есть два типа чисел: скаляры и векторы. Скаляры — это просто обычные числа, к которым мы привыкли. Векторы также имеют связанное с ними направление. … Типовой трансформатор состоит из железного сердечника с намотанными вокруг него двумя катушками — первичной и вторичной. Любой провод с током создает вокруг себя магнитное поле, но … Это распространенный вопрос IB — довольно сложный, когда вы сталкиваетесь с ним впервые! Модель электрона в ящике использует идею о том, что энергия электрона и энергия стоячей волны в ящике аналогичны. Чтобы ответить на этот вопрос, важно помнить, что атом имеет энергию в двух формах: кинетическую (энергия, которая позволяет атому двигаться) и потенциальную (энергия … Когда я впервые столкнулся с этой проблемой, я был немного сбит с толку из-за приведенной выше аналогии с автомобилем. Так что думать об этом можно так: ваше тело и машина… Если вас попросят указать единицы измерения какой-либо сложной величины в более простых единицах, попробуйте придумать известное вам физическое уравнение, связывающее эту сложную величину (например, энергию, … Ответ: 25. Объяснение: В двоичной системе каждая цифра может быть одним из двух значений: 0 и 1. Это две возможности («би» на латыни означает «дважды»). всегда рисуйте диаграмму свободного тела. Это позволит уточнить силы, действующие на объект Определить, какой закон Ньютона действует: 1-й или 2-й, и использовать … При вычислении эквивалентности единиц наиболее простым подходом является использование формул (часто в буклете данных), которые помогут получить правильный ответ. Начнем с Джоулей; … Разделить векторы вертикальной и горизонтальной скорости, рассчитать вертикальное ускорение (под действием силы тяжести), рассчитать время до удара объекта о землю, использовать время для расчета горизонтального расстояния. Используйте уравнения «большой тройки». Resuelva diferentes Tipos de Problemas de física en poco tiempo utilizando la lista de calculadoras de
Физическая доступность. Функциональность этого сайта будет ограничена, так как в Вашем браузере отключена поддержка JavaScript! Random converter Калькулятор закона состояния идеального газа определяет одну из четырех величин, входящих в уравнение состояния (давление, объем, температура или количество), если известны три другие величины. Пример: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 800 молей метана при 30 °С. Еще несколько примеров решения задач о состоянии идеального газа под приводится калькулятором. Выберите неизвестную величину для решения уравнения состояния идеального газа: PVTn Абсолютное давление Pпаскаль (Па)мегапаскаль (МПа)килопаскаль (кПа)гектопаскаль (гПа)ньютон на кв. метр (Н/м²)бар (бар)килограмм-сила на кв. метр (кгс/м²)торр (торр)psi (psi)миллиметр ртутного столба (0°C) (мм рт.ст.)мм вод. столба (4°C) (мм вод. ст., мм H₂O)техническая атмосфера (ат)физическая атмосфера (атм) Объем Vкубический метр (м³)кубический дециметр (дм³)кубический сантиметр (см³)литр (л)миллилитр (мл)галлон американскийкварта СШАунция жидкая СШАунция жидкая британскаякубический фут (фут³)кубический дюйм (дюйм³) Температура Tградус Цельсия (°C)градус Фаренгейта (°F)градус Ранкина (°Ra)кельвин (К) Количество в молях n моль ИЛИ Молярная масса Mграмм на моль (г/моль)килограмм на моль (кг/моль) Масса mмиллиграмм (мг)грамм (г)килограмм (кг)унцияфунт Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Для расчета выберите неизвестную величину и введите три известные величины из четырех имеющихся в уравнении состояния газа (давление, объем, температура, количество). Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона) Определения и формулы Идеальный газ Закон идеального газа Закон Бойля — Мариотта (T=const, n=const) Закон Авогадро (T=const, P=const) Закон Гей-Люссака (P=const, n=const) Закон Шарля (или второй закон Гей-Люссака) (V=const, n=const) Задача 1: Плотность воздуха при нормальных условиях (температура 0 °С и атмосферное абсолютное давление 100 кПа) составляет 1,28 кг/м³. Решение: Поскольку плотность воздуха задана, это означает, что в калькулятор можно ввести массу одного кубического метра воздуха, равную 1,28 кг. Введите в калькулятор данные: Задача 2: Молярная масса газа кислорода (O₂) M = 32 г/моль. Определить абсолютную температуру 128 г. кислорода, находящегося в 10-литровом сосуде под давлением P = 3 МПа. Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи: Задача 3: В сосуде высокого давления находится газ под давлением P = 0.5 МПа при температуре T = 15 °С. Объем газа V = 5 л. Рассчитать объем этой массы газа при нормальных условиях (P = 100 кПа, T = 0 °С). Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи: Задача 4: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 12,8 кг метана (молярная масса 16 г/моль) при 30 °С. Идеальный газ — теоретическая модель, в которой газ представляется в виде множества свободно движущихся частиц бесконечно малого размера, которые взаимодействуют друг с другом абсолютно упруго, то есть при столкновении двух частиц их кинетическая энергия не изменяется и не превращается ни в какую другую форму энергию, например, в потенциальную энергию или в тепло. Считается, что суммарный размер частиц настолько мал, что занимаемый ими объем в сосуде пренебрежимо мал. Эта теоретическая модель полезна, так как она упрощает многие расчеты, а также в связи с тем, что идеальный газ подчиняется законам классической механики. В обычных условиях, например, при стандартных условиях (при температуре 273,15 К и давлении в 1 стандартную атмосферу) большинство реальных газов ведут себя как идеальный газ. В общем случае, газ ведет себя как идеальный при низком давлении и высокой температуре, когда расстояния между молекулами газа относительно велики. В этих условиях потенциальная энергия вследствие действия межмолекулярных сил намного меньше кинетической энергии частиц. Размер молекул также незначителен по сравнению с расстоянием между ними. Идеальная модель не работает при низких температурах и высоких давлениях, а также для тяжелых газов. При понижении температуры и повышении давления реальный газ может стать жидкостью или даже перейти в твердое состояние, то есть может произойти фазовый переход. В то же время, модель идеального газа не допускает жидкого или твердого состояния. Идеальный газ, как и любой другой газ, можно охарактеризовать четырьмя переменными и одной константой, а именно: Эти четыре переменные и одна константа объединены в приведенном ниже уравнении, которое называется уравнением состояния идеального газа: Это уравнение также известно под названием закона идеального газа и уравнения Менделеева — Клапейрона или уравнения Клапейрона, так как уравнение было впервые выведено в 1834 г. французским инженером Эмилем Клапейроном (1799–1864). О вкладе Д. И. Менделеева — чуть ниже. В этом уравнении: Приведенное выше уравнение показывает, что при нулевой абсолютной температуре получается нулевой объем. Однако это не означает, что объем реального газа действительно исчезает. При очень низких температурах все газы становятся жидкостями и уравнение идеального газа к ним неприменимо. Универсальная газовая постоянная соответствует работе, выполненной при расширении одного моля идеального газа при нагревании на 1 К при постоянном давлении. Размерность постоянной — работа на количество вещества на температуру. Входящая в уравнение состояния идеального газа универсальная газовая постоянная была предложена и введена в уравнение Дмитрием Менделеевым в 1877 г. Поэтому уравнение состояния идеального газа в литературе на русском языке и ее переводах на другие языки, называется уравнением Менделеева — Клапейрона. Количество газа в молях часто бывает удобно заменить массой газа. Количество газа в молях n, его масса m в граммах и молярная масса M в граммах на моль связаны формулой: Заменяя в уравнении состояния идеального газа n на m/M, имеем: Для определения молярной массы элемента, его относительная атомная масса умножается на коэффициент молярной массы в кг/моль Например, молярная масса кислорода как элемента в единицах системы СИ Если ввести в уравнение состояния идеального газа плотность ρ = m/V, мы получим: Теперь введем понятие удельной газовой постоянной, которая представляет собой отношение универсальной газовой постоянной R к молярной массе M: Например, удельная газовая постоянная сухого воздуха приблизительно равна 287 Дж·кг⁻¹·К⁻¹. Закон идеального газа объединяет четыре более простых эмпирических газовых закона, открытых в XVII–XIX вв. несколькими учеными, которые аккуратно измеряли свойства газа. Простые газовые законы можно также вывести из уравнения состояния идеального газа (PV=nRT). Поскольку в этом уравнении R является постоянной величиной, можно записать Поскольку PV/NT — постоянная величина, можно записать это иначе: Здесь индексы 1 и 2 показывают начальное и конечное состояние газа в системе. Мы будем использовать это уравнение ниже при описании четырех газовых законов. Отметим, что исторически именно эмпирические законы поведения газа, описанные ниже, привели к открытию обобщенного закона состояния идеального газа. Эти законы были открыты несколькими учеными, которые проводили эксперименты, изменяя только две переменные состояния газа и оставляя две другие переменные постоянными. Роберт Бойль Изменим предыдущее уравнение с учетом, что количество газа в молях n и его температура Т остаются неизменными: или Эдм Мариотт Это закон Бойля — Мариотта, описывающий зависимость объема V фиксированного количества газа в молях n от давления P при постоянной температуре T. Давление фиксированной массы газа при неизменной температуре обратно пропорционально его объему. Закон был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе это закон называют законом Бойля — Мариотта с учетом вклада в открытие закона французского физика и священника Эдма Мариотта. Амедео Авогадро Если температура и давление остаются неизменными, можно записать Это закон Авогадро, указывающий, что при неизменных температуре и давлении равные объемы любых газов содержат одинаковое количество молекул. Жак Шарль При постоянном давлении объем фиксированного количества газа в молях пропорционален абсолютной температуре системы с газом. В англоязычной литературе этот закон называется законом объемов и законом Шарля. Закон описывает как расширяется любой газ при увеличении его абсолютной температуры. Закон был сформулирован в неопубликованной работе французским ученым Жаком Шарлем в 80-х гг. XVIII в. Его соотечественник Жозеф Луи Гей-Люссак опубликовал этот закон в 1803 г. и указал, что приоритет открытия принадлежит Жаку Шарлю. Жозеф Луи Гей-Люссак Закон Шарля (называемый также вторым законом Гей-Люссака) гласит, что давление фиксированного количества газа в молях при его неизменном объеме прямо пропорционально абсолютной температуре газа: Закон был сформулирован Гей-Люссаком в 1802 г. В литературе на других языках этот закон также называют законом Амонтона по имени французского ученого Гийома Амонтона, который на сто лет раньше обнаружил количественную зависимость объема газа от его температуры. Иногда закон называют вторым законом Гей-Люссака и законом Шарля, так как сам Гей-Люссак считал, что закон открыт Шарлем. Закон зависимости давления от температуры был также независимо открыт английским физиком Джоном Дальтоном в 1801 г. При нагревании воздуха в оболочке воздушного шара его плотность уменьшается и становится меньше плотности окружающего воздуха; в результате шар приобретает положительную плавучесть Автор статьи: Анатолий Золотков Калькулятор зависимости температуры, давления и плотности воздуха от высоты в стандартной атмосфере Калькулятор закона Гей-Люссака Калькулятор второго закона Гей-Люссака (закона Шарля) Калькулятор закона Бойля — Мариотта Калькулятор закона Авогадро Калькуляторы Термодинамика — теплота Каждый год приходится наблюдать одни и те же ошибки, которые совершают школьники и их родители при
подготовке к ЕГЭ по физике. Ошибка первая. Спохватиться за месяц-другой до ЕГЭ. Считать, что этого количества
времени хватит на подготовку. На самом деле начинать готовиться надо осенью в 11 классе, не позже. Очень велик объем материала, очень
многим вещам предстоит научиться. Перед нами пятилетний курс физики! Курс, требующий глубокого понимания теории и
развитых навыков решения задач. Наиболее проницательные родители приводят ко мне детей-десятиклассников. И правильно делают! 10 класс — оптимальный срок начала подготовки. Есть возможность периодически возвращаться к пройденным темам и уделять время сложным
задачам, готовясь к вузовским олимпиадам. Ошибка вторая. Полагаться на хорошие школьные оценки и ничего не предпринимать.
Зачем прикладывать дополнительные усилия, если и так всё идет хорошо? На самом деле школьные четверки-пятёрки — лишь иллюзия знаний. Ученик ответил на школьном
уроке параграф, получил пятёрку и назавтра все забыл. Такой отличник не научен самому главному: решать физические задачи. Как следствие, на объективном и беспристрастном
ЕГЭ по физике, который почти целиком состоит из задач, результат нашего отличника окажется удручающим. Ошибка третья. Ограничиться вузовскими подготовительными курсами. Думать, что вузовские
курсы гарантируют высокий результат. Печальный опыт учеников, приходящих ко мне с таких курсов за помощью, показывает, что там работают с группой,
а не с каждым школьником в отдельности. Идёт обычное начитывание материала. Если ученик что-то не понял, пробел
так и останется. Лектор идет дальше, а пробелы постепенно накапливаются. Наконец, через полгода посещения этих курсов выясняется, что знаний у ребёнка как не было, так и нет.
При этом драгоценное время упущено, и поправить ситуацию нелегко. Ошибка четвёртая. При подготовке к ЕГЭ ограничиться пособиями для подготовки к ЕГЭ.
Полагать, что достаточно «натаскаться» на задачи, характерные для ЕГЭ. Никаких задач, «характерных для ЕГЭ», нет. Есть физика, которую надо изучать. Пособия для подготовки к ЕГЭ составлены по материалам ЕГЭ прошлых лет. Они дают весьма ограниченное представление
о физике. Следующий ЕГЭ будет содержать совершенно иные задачи, и вся эта «подготовка» пойдет насмарку. Вам нужна фундаментальная подготовка по физике — под руководством опытного преподавателя, с использованием
разнообразных пособий. Имеются прекрасные задачники, развивающие физическую интуицию и технику решения задач.
Лишь имея за плечами такую подготовку, можно спокойно идти на ЕГЭ по физике. Ошибка пятая. Подготовимся самостоятельно. Вызубрим формулы по учебнику или по шпаргалкам. Самостоятельная подготовка к ЕГЭ по физике — это почти гарантированный провал. Так показывает опыт.
Бесполезно учить параграфы из учебника и зубрить формулы. Физику надо понимать, надо вникать в её идеи.
Без этого не научишься решать задачи. А донести до школьника всё многообразие физических идей может только
репетитор самой высокой квалификации. Часто думают, что решение задачи сводится к подстановке числовых данных в подходящую формулу. Да, такие задачи есть
в школьных учебниках, но на ЕГЭ ничего подобного не будет! Даже самые простые задачи ЕГЭ требуют навыков. Умение решать задачи по физике — это искусство, которому
надо учиться у опытного мастера. Спору нет, формулы знать надо. Но при правильной подготовке они запоминаются сами собой, в процессе
решения большого количества задач. Ошибка шестая. Пробелы в подготовке по математике. Абсолютно всем, кому надо сдавать ЕГЭ по физике, надо хорошо сдать и ЕГЭ по математике. Тем более
вопиющей оказывается беспомощность многих ребят в элементарных математических ситуациях. Школьник не может сложить
векторы, решить простой треугольник, выразить из формулы нужную величину и многое другое. Этими нехитрыми вещами часто пренебрегают при подготовке к ЕГЭ по математике, они там как бы на периферии.
Но в физике они выходят на первый план. Отсутствие этих математических умений и навыков закрывает путь к решению
физических задач. Ошибка седьмая. Телефон вместо калькулятора. Решение многих задач ЕГЭ по физике заканчивается получением численного ответа. Для вычислений нужен калькулятор. Не офисный калькулятор с четырьмя действиями. Ни в коем случае не калькулятор в мобильном телефоне.
Нужен непрограммируемый калькулятор с синусами и логарифмами. И купить его нужно в самом начале подготовки,
чтобы школьник успел привыкнуть к нему и довести вычисления до автоматизма. Между тем, некоторые ученики упорно игнорируют это пожелание и продолжают вычислять на калькуляторе своего
телефона. В итоге нормальный калькулятор покупается накануне ЕГЭ, и на экзамене начинаются проблемы —
на какие кнопки нажимать. Результат — глупейшая потеря множества баллов. Решение
Проблемы с физикой на калькуляторе TI 83 Дэвид Доти Этот веб-сайт
сайт предназначен для того, чтобы помочь учащимся ознакомиться с использованием TI 83 и
Калькуляторы TI 83+ для использования на уроках физики. Как
для ввода научного обозначения с вашим TI (ярлык) Дополнение
и вычитание Умножение Деление Порядок операций TI Обоснование How to
ввод экспоненциальной записи с вашим TI
(ярлык) Использование клавиши [EE]. Для многих калькуляторов, включая TI –83 и
TI 83 Plus кнопка [EE] используется для ввода экспоненциального представления. Кнопку [EE] можно найти желтым цветом выше.
запятая []. Для входа
научное обозначение, следует использовать следующие нажатия клавиш: сначала введите число, затем 2 -й ключ, за которым следует запятая, [2 nd ] [] [EE], затем
по показателю. В качестве примера, чтобы
введите 3 x 10 8 тип [3] [EE] [8]. На дисплее появится 3E8.
Калькулятор может быть настроен на отображение ответов в экспоненциальном представлении или в обычном
отображать. Чтобы настроить дисплей,
просто нажмите кнопку режима и с помощью клавиш со стрелками выберите нужный
дисплей и нажмите ввод. Покинуть
меню, нажмите [2 nd ] [MODE] для выхода. Подписаться
эти примеры ввода основных операций сложения, вычитания, умножения и
разделение. (вверху) Дополнение: Добавить: 8. Тип: 8.1
[ЭЭ] 6 [+] 4.2 [ЭЭ] 5 Отображаемый ответ: 8.52E6 Числовой ответ: 8,52 x 10 6 = 8,520,000 (вверху) Вычитание Тип: 6.2
[EE] -3 [–] 2,8 [EE] -4 Числовой ответ: 5.92E-3 Числовой ответ: 5 x 10 -3 = 0,00592 (сверху) Умножение Умножение: (3
x 10 6 ) (2 x 10 3 ) Тип: 3
[EE] 6 [X] 2 [EE] 3 Отображаемый ответ: 6E9 Числовой ответ: 6 x 10 9 = 6 000 000 000 (вверху) Дивизион Разделение: Тип: 6
[EE] 8 [] 2 [EE] 10 Отображаемый ответ: 3E-2 Числовой ответ: 3 x 10 -2 = 0,03 (вверху) Проблемы с физикой образцов 1) Какова величина гравитационной силы
между электроном и протоном, разделенными расстоянием 1,0 x 10 -10 метров? ответ 2) Положительный заряд 6,0 x 10 -6 Кл равен 0,030
м от второго положительного заряда
3,0 х 10 -6 С. 3) В вакууме длина волны зеленого света составляет 5 x 10 -7 метр. Какова его частота? ответ 4) Чему равна энергия фотона с частотой
3,00 x 10 13 циклов в секунду? Ответ (вверху) Ответы на примеры задач по физике 1) Вычислить
гравитационная сила через Универсальный закон всемирного тяготения Ньютона Тип: Калькулятор
Дисплей: Отображаемый ответ: 1.0E-47 Числовой ответ: 1,0 x 10 -47 Вернуться к проблемам 2) Рассчитайте
Сила Колумба по закону Колумба: Тип
в: 8,99
[EE] 9 [X] 6. Калькулятор
Дисплей: 8.99E9
* 6.00E-6 * 3.00E-6 / .030 2 Отображаемый ответ: 179,8 Числовой
Ответ: 179,8 Вернуться к проблемам (вверху) 3) Гц Тип
в: 3
[EE] 8 [X] 5 [EE] -7 Калькулятор
дисплей: 3E8/5E-7 Отображаемый ответ: 6E14 Числовой
ответ: 6,0 x 10 14 Назад
к Проблемы 4) J Тип
в: 6.63EE-34
X 3EE13 Калькулятор
отображение: 6.63E34 * 3E13 Отображаемый ответ: 1.99E-20 Числовой
ответ: 1,99 x 10 -20 Назад к задачам (top) Inputting используя круглые скобки Для тех из вас, кто не хочет использовать кнопку EE
на калькуляторе да скобки можно использовать для ввода уравнений. В вакууме длина волны зеленого света составляет 5 х 10 -7 метр. Какова его частота? Решение: Однако, если учащийся по ошибке вводит: 9] -7 TI дает ответ 6. Это приказы о операциях, которые TI следует за этим примером: TOP Обоснование: Хотя
одной из целей новых стандартов штата Нью-Йорк является расширение концептуального
понимания физики, учащиеся все еще должны быть в состоянии математически
решать задачи по физике. TOP David Doty Дэвид Доти в настоящее время преподает Nys Regents Physics,
Наука об окружающей среде и различные научные лаборатории в городе Саламанка.
Центральные школы. У него есть степень бакалавра
искусств в области математики из Государственного университета Нью-Йорка в Буффало и является
работает над получением степени магистра физического образования в штате Буффало.
Колледж. Если вы хотите связаться со мной, напишите мне по адресу [email protected] Физический калькулятор Это приложение охватывает: Калькулятор давления Решатель задач по физике Это приложение специально разработано для решения ваших задач по физике на уровне средней школы, на уровне мыса, на уровне csec и любых общих расчетов, которые вам нужны. Версия 1.5 Исправления ошибок, обновление библиотеки и повышение производительности. 1 Рейтинг Разработчик Sunnykumar Mavani указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика. Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям: Следующие данные могут быть собраны и связаны с вашей личностью: Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

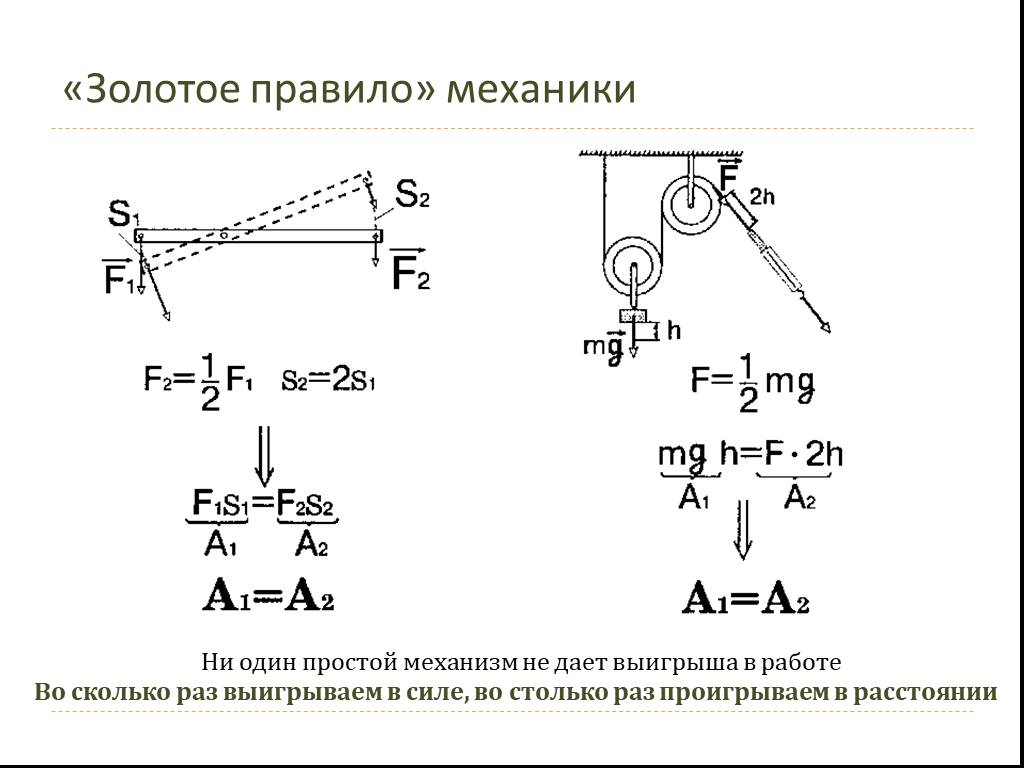
 В этом примере это понимание уже использовалось — взаимодействие между двумя блоками происходит за счет натяжения веревки, и натяжение обозначалось одним и тем же символом для каждого. Если вы не заметили, что натяжение по всей веревке такое же, как вы нарисовали FBD, это нормально. Когда вы начнете решать уравнения, вы обнаружите, что у вас слишком много неизвестных, и вы можете использовать это понимание, чтобы уменьшить их в этот момент.
В этом примере это понимание уже использовалось — взаимодействие между двумя блоками происходит за счет натяжения веревки, и натяжение обозначалось одним и тем же символом для каждого. Если вы не заметили, что натяжение по всей веревке такое же, как вы нарисовали FBD, это нормально. Когда вы начнете решать уравнения, вы обнаружите, что у вас слишком много неизвестных, и вы можете использовать это понимание, чтобы уменьшить их в этот момент. ). Прокрутите вниз, чтобы продолжить это решение.
). Прокрутите вниз, чтобы продолжить это решение. Дальнейшее математическое решение не требуется.
Дальнейшее математическое решение не требуется. Это значение примерно равно силе гравитации, действующей на массу 16 кг, опять-таки число, которое имеет смысл. Брусок массой 38 кг движется вниз с ускорением, поэтому натяжение веревки не полностью удерживает его от силы тяжести. Следовательно, вы знаете, что натяжение в канате должно быть менее (38 кг)g или менее 370 Н.
Это значение примерно равно силе гравитации, действующей на массу 16 кг, опять-таки число, которое имеет смысл. Брусок массой 38 кг движется вниз с ускорением, поэтому натяжение веревки не полностью удерживает его от силы тяжести. Следовательно, вы знаете, что натяжение в канате должно быть менее (38 кг)g или менее 370 Н.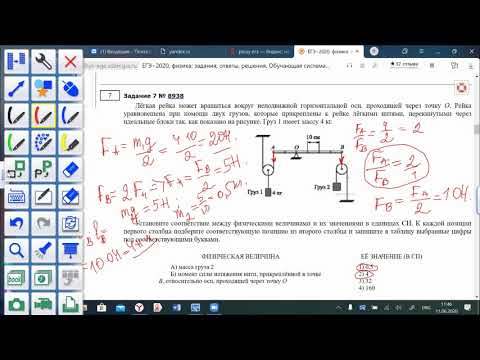 0) 2 — 882
0) 2 — 882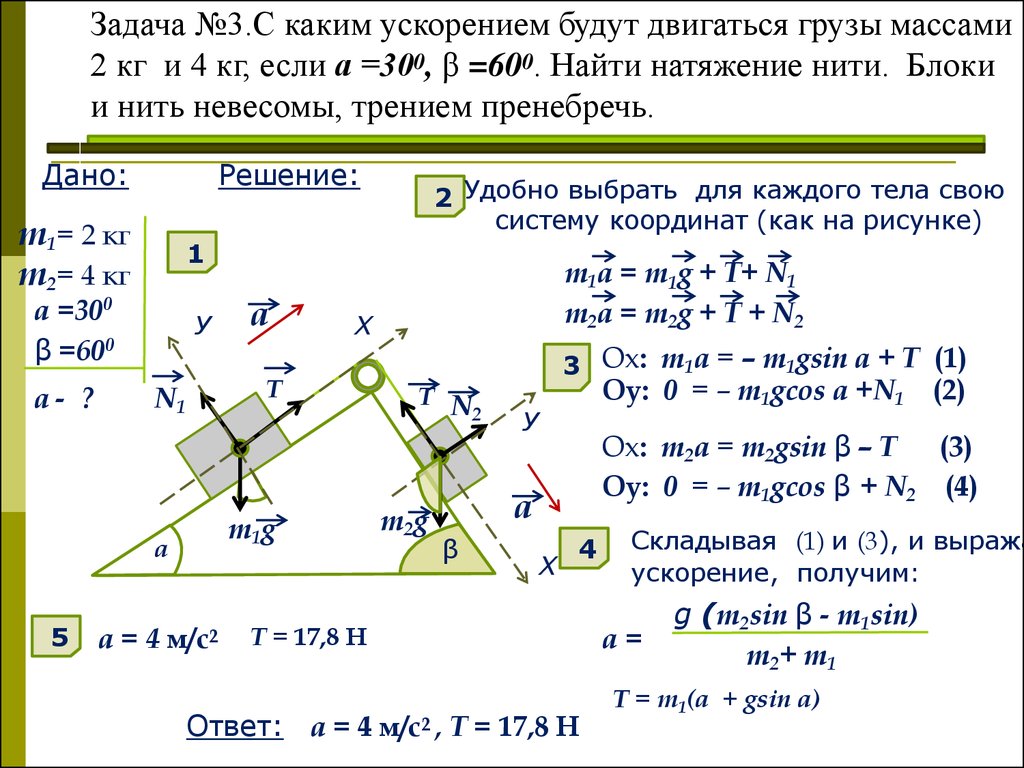

 Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить. 2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.
2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law. Следующие семь определений базовых единиц СИ основаны на Брошюре SI BIPM (9-е издание).
Следующие семь определений базовых единиц СИ основаны на Брошюре SI BIPM (9-е издание).

 Это число представляет собой фиксированное числовое значение постоянной Авогадро, N A , выраженное в единицах моль -1 , и называется числом Авогадро.
Количество вещества, символ n , системы является мерой количества определенных элементарных объектов. Элементарным объектом может быть атом, молекула, ион, электрон, любая другая частица или определенная группа частиц.
Это число представляет собой фиксированное числовое значение постоянной Авогадро, N A , выраженное в единицах моль -1 , и называется числом Авогадро.
Количество вещества, символ n , системы является мерой количества определенных элементарных объектов. Элементарным объектом может быть атом, молекула, ион, электрон, любая другая частица или определенная группа частиц.
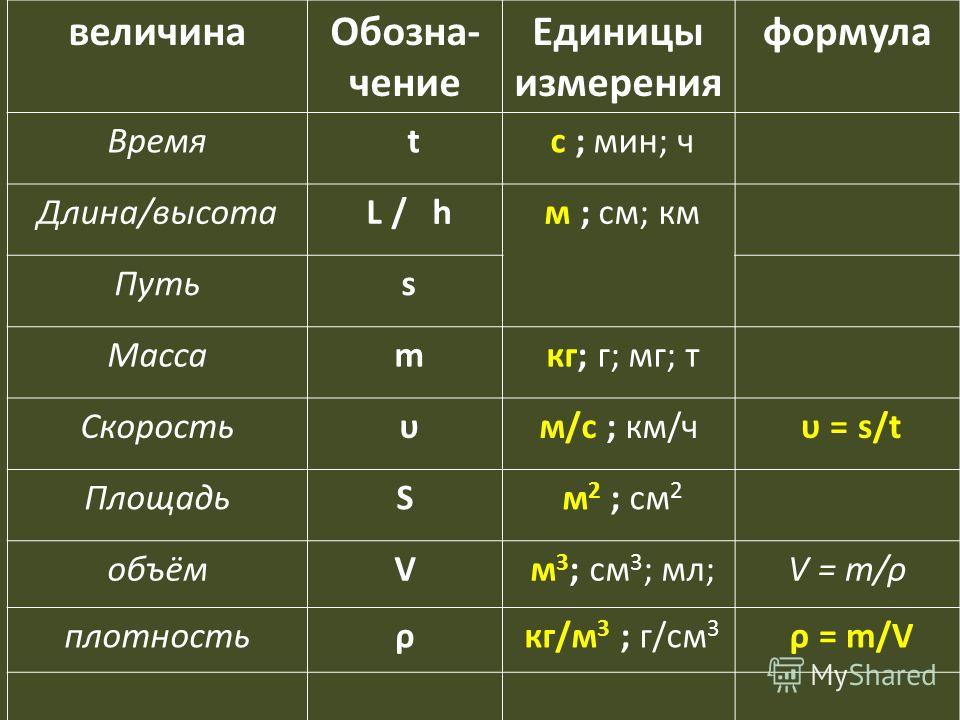 поля бесконечной плоскости
поля бесконечной плоскости Однако без этого вводного материала дальнейшее изучение молекулярной физики невозможно.
Однако без этого вводного материала дальнейшее изучение молекулярной физики невозможно. Поэтому для измерения количества вещества используют специальную единицу — моль.
Поэтому для измерения количества вещества используют специальную единицу — моль. Например, для алюминия , поэтому молярная масса алюминия равна г/моль или кг/моль.
Например, для алюминия , поэтому молярная масса алюминия равна г/моль или кг/моль. е. молярную массу:
е. молярную массу:
 Е.= ½ мв²
Е.= ½ мв² Заметки помогают учащимся во время экзамена, когда им нужен обзор темы и не нужно просматривать учебники. Студенты должны сделать советы для экзаменов и для этого они должны делать заметки. Пока вы просматриваете физические символы, вам также нужно сосредоточиться на примечаниях. Чтобы помочь вам укрепить свои знания, мы предоставили Заметки по физике , чтобы вы могли просмотреть его.
Заметки помогают учащимся во время экзамена, когда им нужен обзор темы и не нужно просматривать учебники. Студенты должны сделать советы для экзаменов и для этого они должны делать заметки. Пока вы просматриваете физические символы, вам также нужно сосредоточиться на примечаниях. Чтобы помочь вам укрепить свои знания, мы предоставили Заметки по физике , чтобы вы могли просмотреть его.
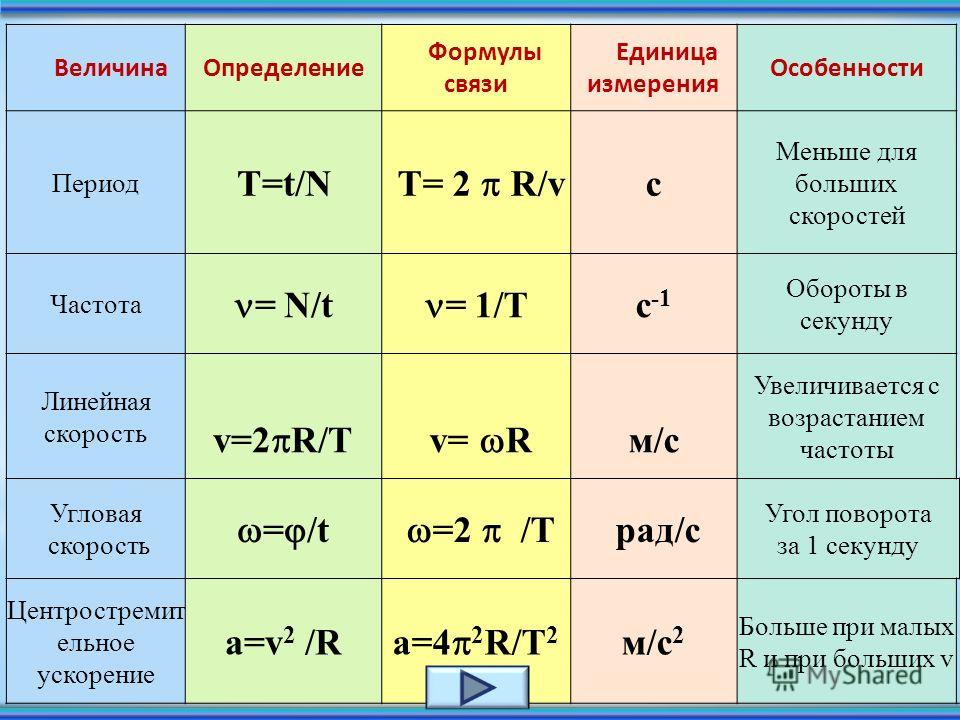
 Нормальная сила не может быть приложена к двум поверхностям, которые не соединены друг с другом. Его можно интерпретировать как составляющую силы, направленную вертикально к любой контактной поверхности. Он определяет, какую силу тело прилагает к земле. Нормальная сила равна весу объекта только в том случае, если скорость изменения скорости объекта отрицательна, что означает, что он замедляется.
Нормальная сила не может быть приложена к двум поверхностям, которые не соединены друг с другом. Его можно интерпретировать как составляющую силы, направленную вертикально к любой контактной поверхности. Он определяет, какую силу тело прилагает к земле. Нормальная сила равна весу объекта только в том случае, если скорость изменения скорости объекта отрицательна, что означает, что он замедляется.

 Тело массой 10 кг скатывается с силой 200 Н с наклонной поверхности под углом 30°. Вычислите нормальную силу, действующую на него.
Тело массой 10 кг скатывается с силой 200 Н с наклонной поверхности под углом 30°. Вычислите нормальную силу, действующую на него. 
 {-29}$ м3? Считайте, что молекулы в воде плотно упакованы.
{-29}$ м3? Считайте, что молекулы в воде плотно упакованы. {23}}=4047,6$ кг/м3
{23}}=4047,6$ кг/м3

 edu.ru/dlrstore/69639dc0-9572-4e9c-b769-b60aba0b4e92/18.swf
edu.ru/dlrstore/69639dc0-9572-4e9c-b769-b60aba0b4e92/18.swf
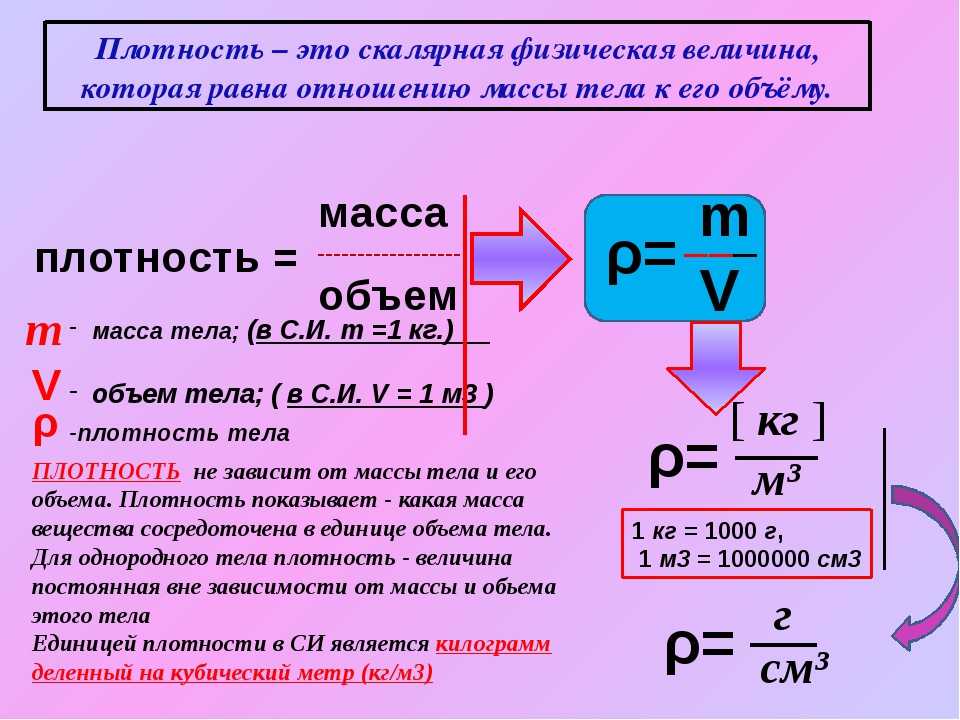
 ( чтобы найти объем тела нужно от объема жидкости и тела вычесть первоначальный объем жидкости).
( чтобы найти объем тела нужно от объема жидкости и тела вычесть первоначальный объем жидкости).
 \vec da$, где поверхность $S$ — это цилиндр, состоящий из трех частей: криволинейной поверхности и обоих круглых концов, поэтому $S = S_1 + S_2 + S_3$ соответственно.
\vec da$, где поверхность $S$ — это цилиндр, состоящий из трех частей: криволинейной поверхности и обоих круглых концов, поэтому $S = S_1 + S_2 + S_3$ соответственно.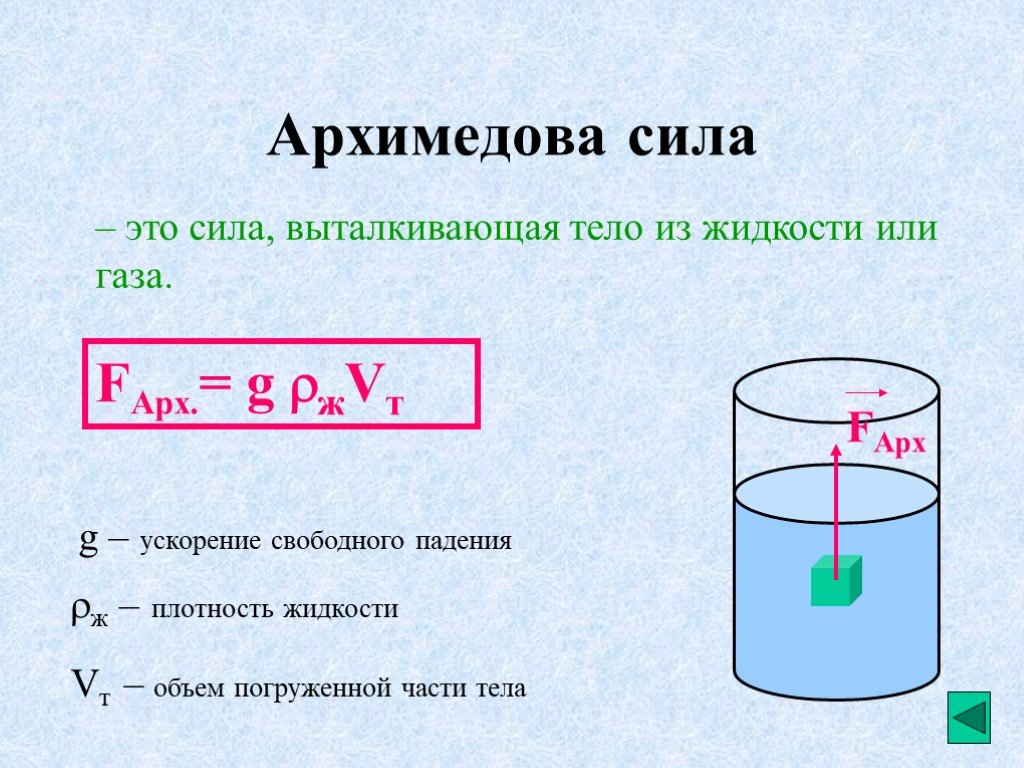 \vec да$ ?
\vec да$ ?
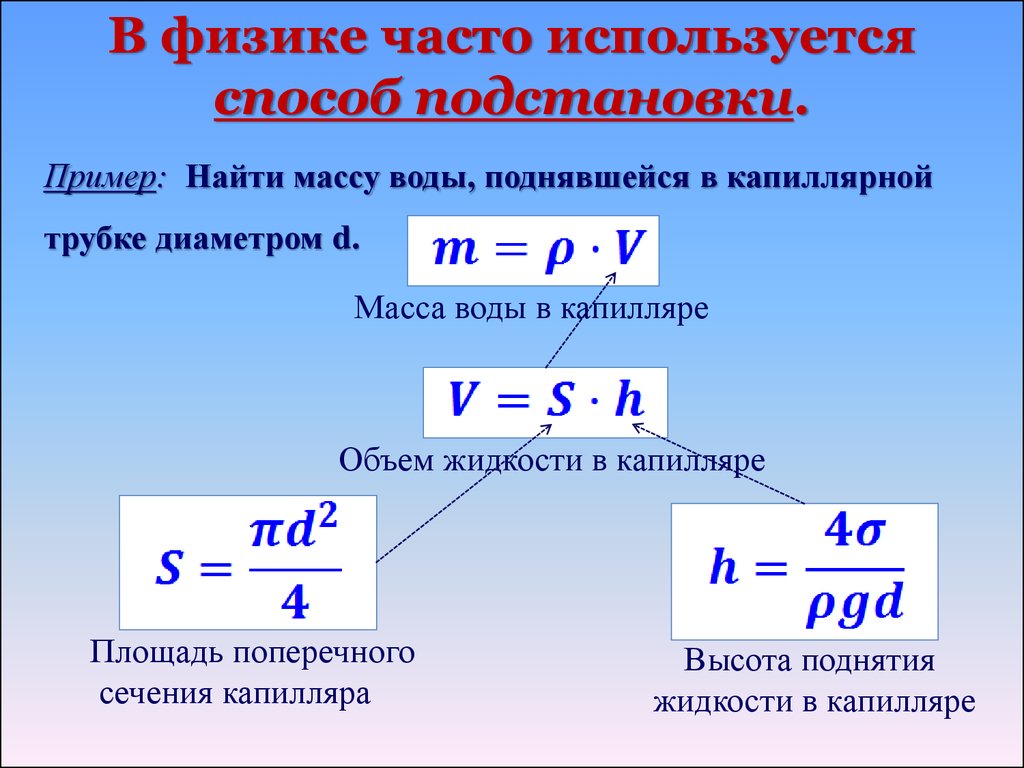 Газы, такие как воздух, которым мы дышим, также являются составными частями материи. Различные характеристики материи измеряются массой и объемом.
Газы, такие как воздух, которым мы дышим, также являются составными частями материи. Различные характеристики материи измеряются массой и объемом. Несмотря на уменьшение гравитационного притяжения, их масса останется постоянной.
Несмотря на уменьшение гравитационного притяжения, их масса останется постоянной.

 Лобачевского, радиофизический факультет, кафедра общей физики
Лобачевского, радиофизический факультет, кафедра общей физики Моему сыну очень нравится обучаться по этой программе. Для него, на данный момент, приоритетом является изучение немецкого языка. И данная программа является хорошим подспорьем. Кроме того, где,кроме школы, можно дополнительно, а главное бесплатно, улучшить свои знания? Поэтому, большая благодарность за эту программу.
Моему сыну очень нравится обучаться по этой программе. Для него, на данный момент, приоритетом является изучение немецкого языка. И данная программа является хорошим подспорьем. Кроме того, где,кроме школы, можно дополнительно, а главное бесплатно, улучшить свои знания? Поэтому, большая благодарность за эту программу. Грабцевича. Задачи имеют ответы, но предлагаются без готовых решений.
Грабцевича. Задачи имеют ответы, но предлагаются без готовых решений. [ α = 0,89 ]
[ α = 0,89 ] Определите конечную температуру пули и гири, если начальная температура гири t2 = 20 °C. Теплообменом с окружающей средой пренебречь. [ t ≈ 112 °C ]
Определите конечную температуру пули и гири, если начальная температура гири t2 = 20 °C. Теплообменом с окружающей средой пренебречь. [ t ≈ 112 °C ] Нагреватель опущен в сосуд с водой. Спустя τо = 9 мин, когда вода нагрелась от температуры t1 = 20 °С до температуры t2 = 50 °С, спираль в параллельном соединении перегорела. На сколько больше времени из-за этого придется ждать, пока вода закипит? Потери теплоты не учитывать, напряжение на клеммах постоянно. [ Δτ = 5 мин ]
Нагреватель опущен в сосуд с водой. Спустя τо = 9 мин, когда вода нагрелась от температуры t1 = 20 °С до температуры t2 = 50 °С, спираль в параллельном соединении перегорела. На сколько больше времени из-за этого придется ждать, пока вода закипит? Потери теплоты не учитывать, напряжение на клеммах постоянно. [ Δτ = 5 мин ] Определите массу смеси, если считать, что количество теплоты, получаемое системой в единицу времени, постоянно. Удельная теплота плавления льда λ = 330 кДж/кг, а удельная теплоемкость воды c = 4,2 кДж/(кг×К). Теплоемкостью сосуда пренебречь. [ M = 3 кг ]
Определите массу смеси, если считать, что количество теплоты, получаемое системой в единицу времени, постоянно. Удельная теплота плавления льда λ = 330 кДж/кг, а удельная теплоемкость воды c = 4,2 кДж/(кг×К). Теплоемкостью сосуда пренебречь. [ M = 3 кг ] Потери теплоты не учитывать. [ t = 26 °C ]
Потери теплоты не учитывать. [ t = 26 °C ] Ускорение свободного падения g = 9,8 м/с2. [ H ≈ 34 км ]
Ускорение свободного падения g = 9,8 м/с2. [ H ≈ 34 км ] Находящийся в комнате точный водяной термометр опускают в воду. На сколько процентов его показание будет отличаться от первоначальной температуры воды, если теплоемкость термометра меньше теплоемкости сосуда с водой в n раз, а температура в комнате по сравнению с температурой сосуда с водой – в m раз?
Находящийся в комнате точный водяной термометр опускают в воду. На сколько процентов его показание будет отличаться от первоначальной температуры воды, если теплоемкость термометра меньше теплоемкости сосуда с водой в n раз, а температура в комнате по сравнению с температурой сосуда с водой – в m раз? Затем залили этот лёд водой такой же массой M. Вода полностью покрыла лёд и достигла уровня H = 20 см. Определите, какова была температура воды, если после установления теплового равновесия уровень воды в сосуде опустился на h = 0,4 см. Плотность воды и льда равны 1000 и 920 Дж/(кг×°C) соответственно. Удельная теплота плавления льда λ = 330 кДж/кг.
Затем залили этот лёд водой такой же массой M. Вода полностью покрыла лёд и достигла уровня H = 20 см. Определите, какова была температура воды, если после установления теплового равновесия уровень воды в сосуде опустился на h = 0,4 см. Плотность воды и льда равны 1000 и 920 Дж/(кг×°C) соответственно. Удельная теплота плавления льда λ = 330 кДж/кг. Заметки 8 класса очень полезны для учащихся, которые готовятся к вступительным экзаменам, таким как NTSE, олимпиады, основа для JEE и NEET.
Заметки 8 класса очень полезны для учащихся, которые готовятся к вступительным экзаменам, таким как NTSE, олимпиады, основа для JEE и NEET. Чтобы дать вам дополнительные знания по естественным наукам 8 класса, мы разделили 8 класс на три части: физику, химия и биология.
Чтобы дать вам дополнительные знания по естественным наукам 8 класса, мы разделили 8 класс на три части: физику, химия и биология. Запишите важные моменты, прежде чем решать упражнение по конспектам 8 класса. Убедитесь, что вы выполнили упражнение NCERT, воспользуйтесь помощью Physics Wallah 9.0003 Решения NCERT.
Запишите важные моменты, прежде чем решать упражнение по конспектам 8 класса. Убедитесь, что вы выполнили упражнение NCERT, воспользуйтесь помощью Physics Wallah 9.0003 Решения NCERT. 
 Для хорошего будущего нужно иметь хороший фундамент. Для этого вам нужно иметь дисциплину и составить лучший план, вот несколько из них, которым вы можете следовать —
Для хорошего будущего нужно иметь хороший фундамент. Для этого вам нужно иметь дисциплину и составить лучший план, вот несколько из них, которым вы можете следовать — Добавленные вопросы MCQ в разделе «Упражнения» помогут вам проверить свои концепции. Этих записей достаточно для конкурсного вступительного экзамена.
Добавленные вопросы MCQ в разделе «Упражнения» помогут вам проверить свои концепции. Этих записей достаточно для конкурсного вступительного экзамена.
 , учащиеся должны набрать 40% и выше в Отборочном онлайн-раунде.
, учащиеся должны набрать 40% и выше в Отборочном онлайн-раунде.  Правильные многоугольники
Правильные многоугольники 

 Кроме того, калькулятор умеет учитывать количество теплоты, отданное или полученное извне системы. Чтобы использовать калькулятор, необходимо правильно заполнить таблицу, описывающую теплообмен в термодинамической системе. Как это сделать, описано под калькулятором на примерах типовых задач.
Кроме того, калькулятор умеет учитывать количество теплоты, отданное или полученное извне системы. Чтобы использовать калькулятор, необходимо правильно заполнить таблицу, описывающую теплообмен в термодинамической системе. Как это сделать, описано под калькулятором на примерах типовых задач.
 3 (в принципе, немного не совпадает с приводимой везде удельной теплоемкостью серебра, но все равно достаточно близко к ней).
3 (в принципе, немного не совпадает с приводимой везде удельной теплоемкостью серебра, но все равно достаточно близко к ней). Минус в данном случае означает, что из внешней среды потребовалось отдать указанное количество теплоты.
Минус в данном случае означает, что из внешней среды потребовалось отдать указанное количество теплоты.
 уравнений до четырех
уравнений до четырех
 Модель Хаббарда — «идеальный» вариант нескольких важных классов материалов; с
ее помощью ученые полчают представление о том, как поведение электронов
обеспечивает искомые состояния вещества, такие как сверхпроводимость, при
которой электроны движутся, не встречая сопротивления. Модель также
используется для отработки новых методов работы с более комплексными квантовыми
системами.
Модель Хаббарда — «идеальный» вариант нескольких важных классов материалов; с
ее помощью ученые полчают представление о том, как поведение электронов
обеспечивает искомые состояния вещества, такие как сверхпроводимость, при
которой электроны движутся, не встречая сопротивления. Модель также
используется для отработки новых методов работы с более комплексными квантовыми
системами.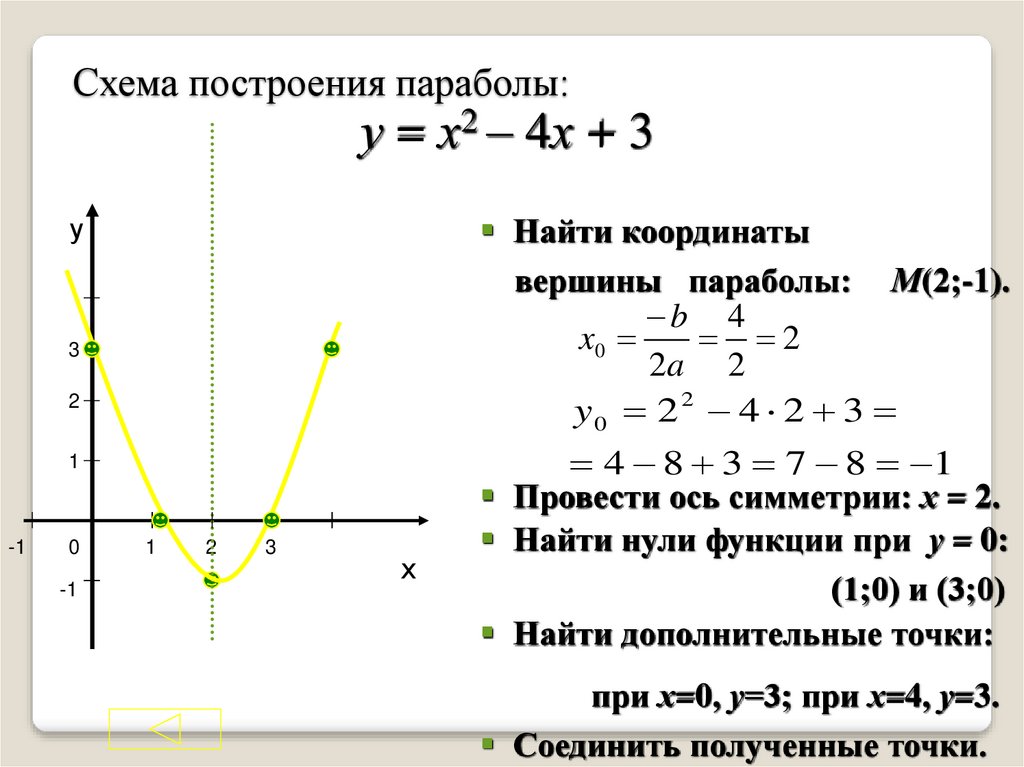 И чем больше электронов
добавляется в систему, тем больше происходит сцеплений, и тем выше
вычислительные ресурсы, которые требуются для изучения такой системы.
И чем больше электронов
добавляется в систему, тем больше происходит сцеплений, и тем выше
вычислительные ресурсы, которые требуются для изучения такой системы. Количество таких уравнений в итоге удалось низвести
до четырех.
Количество таких уравнений в итоге удалось низвести
до четырех. По
словам Ди Санте, существуют очень интересные возможности использовать данный
метод в других областях, где используются ренормализационные группы, в том
числе космологии и неврологии.
По
словам Ди Санте, существуют очень интересные возможности использовать данный
метод в других областях, где используются ренормализационные группы, в том
числе космологии и неврологии. д.».
д.».
 Более того — и именно это, на мой взгляд, делает калькулятор действительно стоящим — система выводит список с константами, которые вы можете иметь в виду. Вы имели в виду «е» как массу электрона или его заряд? Выберите правильную константу и правильно используйте ее для своих расчетов.
Более того — и именно это, на мой взгляд, делает калькулятор действительно стоящим — система выводит список с константами, которые вы можете иметь в виду. Вы имели в виду «е» как массу электрона или его заряд? Выберите правильную константу и правильно используйте ее для своих расчетов. Раукин!
Раукин!
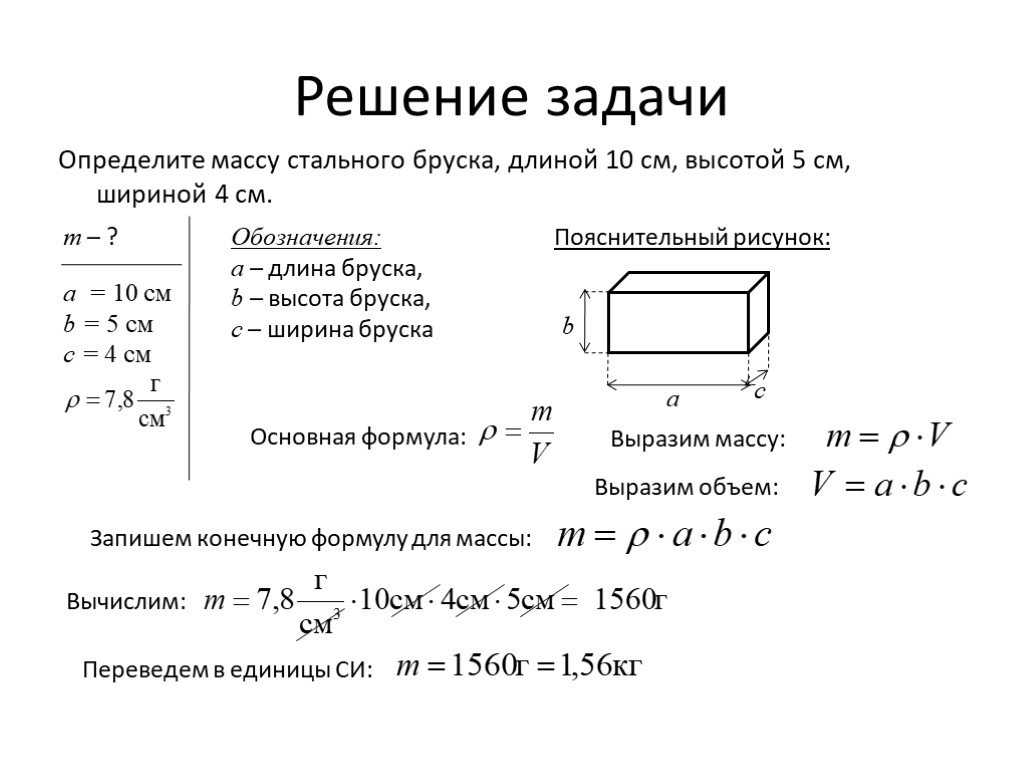



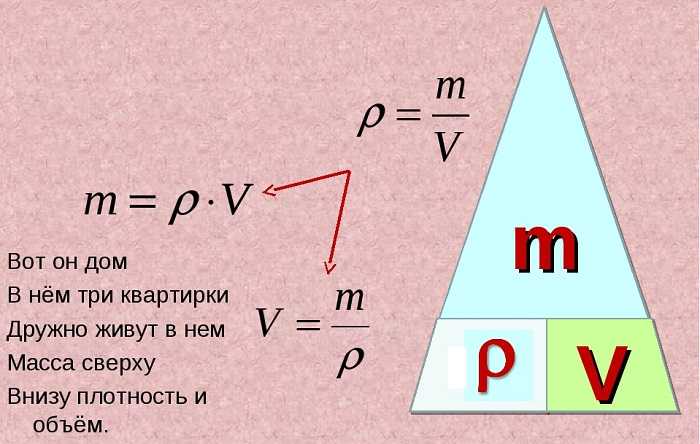
 0 x 10 3 kg/m 3
0 x 10 3 kg/m 3  Хассий — это химический элемент с символом Hs и атомным номером 108. Это синтетический элемент (впервые синтезированный в Хассе в Германии) и радиоактивный. Самый стабильный известный изотоп, 269 Hs , имеет период полураспада примерно 9,7 секунды. Расчетная плотность 40,7 x 10 3 кг/м 3 . Плотность хассия обусловлена его высоким атомным весом и значительным уменьшением ионных радиусов элементов ряда лантанидов, известных как лантанидов и актиноидов, сжатие .
Хассий — это химический элемент с символом Hs и атомным номером 108. Это синтетический элемент (впервые синтезированный в Хассе в Германии) и радиоактивный. Самый стабильный известный изотоп, 269 Hs , имеет период полураспада примерно 9,7 секунды. Расчетная плотность 40,7 x 10 3 кг/м 3 . Плотность хассия обусловлена его высоким атомным весом и значительным уменьшением ионных радиусов элементов ряда лантанидов, известных как лантанидов и актиноидов, сжатие . Увеличение давления всегда увеличивает плотность материала. Влияние давления на плотность жидкостей и твердых тел очень мало. С другой стороны, плотность газов сильно зависит от давления. Это выражается сжимаемостью . Сжимаемость измеряет относительное изменение объема жидкости или твердого вещества в ответ на изменение давления.
Увеличение давления всегда увеличивает плотность материала. Влияние давления на плотность жидкостей и твердых тел очень мало. С другой стороны, плотность газов сильно зависит от давления. Это выражается сжимаемостью . Сжимаемость измеряет относительное изменение объема жидкости или твердого вещества в ответ на изменение давления.
 Это объемы ядер, а атомные ядра (протоны и нейтроны) содержат около 99,95% массы атома.
Это объемы ядер, а атомные ядра (протоны и нейтроны) содержат около 99,95% массы атома. Вода (хладагент) нагревается в активной зоне реактора примерно до 325°C (617°F) по мере прохождения воды через активную зону. Как видно, реактор содержит недогретые теплоносители примерно на 25°C (расстояние от точки насыщения). Это высокое давление поддерживается компенсатором давления, отдельным сосудом, подключенным к первому контуру (горячая ветвь) и частично заполненным водой (частично насыщенным паром), которая нагревается до температура насыщения (точка кипения) для желаемого давления с помощью погружных электрических нагревателей . Температуру в компенсаторе давления можно поддерживать на уровне 350 °C. Около 60% объема компенсатора занимает сжатая вода при нормальных условиях, а около 40% объема занимает насыщенный пар .
Вода (хладагент) нагревается в активной зоне реактора примерно до 325°C (617°F) по мере прохождения воды через активную зону. Как видно, реактор содержит недогретые теплоносители примерно на 25°C (расстояние от точки насыщения). Это высокое давление поддерживается компенсатором давления, отдельным сосудом, подключенным к первому контуру (горячая ветвь) и частично заполненным водой (частично насыщенным паром), которая нагревается до температура насыщения (точка кипения) для желаемого давления с помощью погружных электрических нагревателей . Температуру в компенсаторе давления можно поддерживать на уровне 350 °C. Около 60% объема компенсатора занимает сжатая вода при нормальных условиях, а около 40% объема занимает насыщенный пар .
 Плотность жидкой (сжатой) воды как функция температуры воды
Плотность жидкой (сжатой) воды как функция температуры воды Эти эффекты должны контролироваться системой контроля уровня компенсатора давления.
Эти эффекты должны контролироваться системой контроля уровня компенсатора давления. Контрольный объем представляет собой воображаемую поверхность 9.0004, в котором содержится интересующий том. Контрольный объем может быть неподвижным или подвижным, жестким или деформируемым. Для определения всех сил, действующих на поверхности контрольного объема, необходимо решить законы сохранения в этом контрольном объеме.
Контрольный объем представляет собой воображаемую поверхность 9.0004, в котором содержится интересующий том. Контрольный объем может быть неподвижным или подвижным, жестким или деформируемым. Для определения всех сил, действующих на поверхности контрольного объема, необходимо решить законы сохранения в этом контрольном объеме.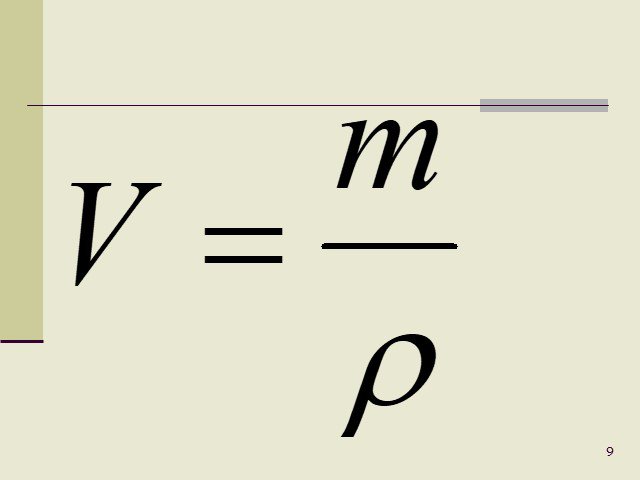 Это происходит при атмосферном давлении, а массовый расход равен Q =1 м 3 /с .
Это происходит при атмосферном давлении, а массовый расход равен Q =1 м 3 /с .
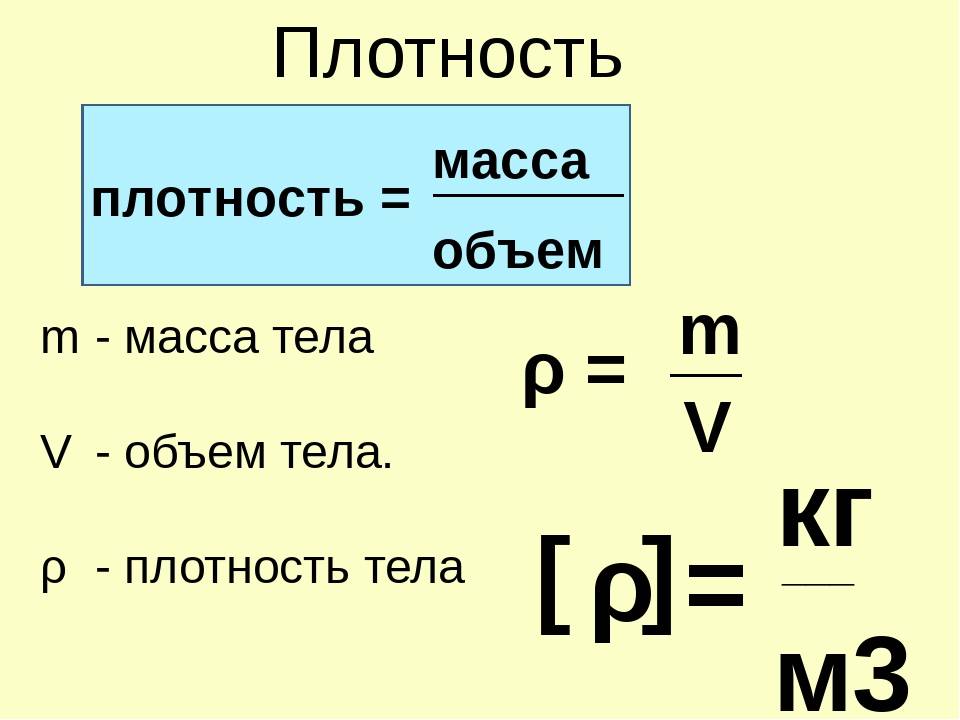 m — масса, d — плотность.
m — масса, d — плотность. 3
3
 Рекомендуем вам попробовать свои силы и поработать над заданиями самостоятельно. Имея на руках готовое решение задач, можете проработать проблемные вопросы, устраняя пробелы в знаниях.
Рекомендуем вам попробовать свои силы и поработать над заданиями самостоятельно. Имея на руках готовое решение задач, можете проработать проблемные вопросы, устраняя пробелы в знаниях.

 Здесь необходимо пользоваться большим числом законов и формул, вводить дополнительные обоснования в процессе решения. Способ решения задачи надо выбрать самостоятельно.
Здесь необходимо пользоваться большим числом законов и формул, вводить дополнительные обоснования в процессе решения. Способ решения задачи надо выбрать самостоятельно.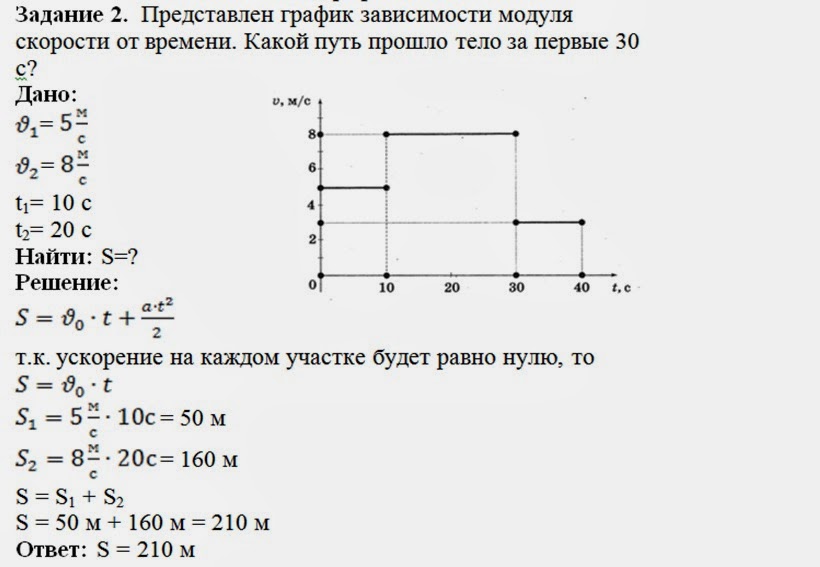 Объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков
Объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков
 Планетарная модель атома. Нуклонная модель ядра. Ядерные реакции.
Планетарная модель атома. Нуклонная модель ядра. Ядерные реакции. Квантовая физика. Расчетная задача
Квантовая физика. Расчетная задача сайт
сайт


 Как только они решат любую из них, они сразу же получат другую.
Как только они решат любую из них, они сразу же получат другую.
 Все звезды кажутся одинаково далёкими от нас, но истинное расстояние до них различно, и определить его можно только путем очень точных измерений и расчетов. Из-за осевого вращения Земли, звезды нам кажутся перемещающимися по небу, но при внимательном наблюдении можно заметить, что Полярная звезда почти не меняет своего положения относительно горизонта. Другие же звезды описывают в течении суток полный круг с центром вблизи Полярной. Это можно легко проверить, проведем небольшой опыт. Необходимо закрепить на штативе фотоаппарат, навести его на полярную звезду, и поставить длительную выдержку. В результате, мы получим фото, на котором увидим концентрические дуги – следы путей звезд. Общий центр этих дуг – точка, которая остается неподвижной при суточном движении звезд, условно называется северным полюсом мира. Диаметрально противоположная ему точка называется южным полюсом мира. Вращение звёзд происходит с Востока на Запад.
История астрономии
С тех самых пор, когда люди стали объединяться в группы, возникало множество проблем и вопросов, связанных с окружающим миром и природными явлениями, которые, так или иначе, влияли на жизнь человека.
Все звезды кажутся одинаково далёкими от нас, но истинное расстояние до них различно, и определить его можно только путем очень точных измерений и расчетов. Из-за осевого вращения Земли, звезды нам кажутся перемещающимися по небу, но при внимательном наблюдении можно заметить, что Полярная звезда почти не меняет своего положения относительно горизонта. Другие же звезды описывают в течении суток полный круг с центром вблизи Полярной. Это можно легко проверить, проведем небольшой опыт. Необходимо закрепить на штативе фотоаппарат, навести его на полярную звезду, и поставить длительную выдержку. В результате, мы получим фото, на котором увидим концентрические дуги – следы путей звезд. Общий центр этих дуг – точка, которая остается неподвижной при суточном движении звезд, условно называется северным полюсом мира. Диаметрально противоположная ему точка называется южным полюсом мира. Вращение звёзд происходит с Востока на Запад.
История астрономии
С тех самых пор, когда люди стали объединяться в группы, возникало множество проблем и вопросов, связанных с окружающим миром и природными явлениями, которые, так или иначе, влияли на жизнь человека. Вплоть до XIX века, астрономия была ограничена рамками познаний лишь в пределах Солнечной системы, объекты, находившиеся за её пределами и тем более за пределами нашей Галактики, были недосягаемы для изучения, и представления о них были лишь умозаключительными. Историческое развитие в астрономии заключается в том, что она формировалась, как наука вместе с изменяющейся в разные периоды общественной жизнью и культурой. В каждой народности были свои культура, мифы и обычаи, свои первооткрыватели, которые вносили вклад, делая открытия и давая объяснения тем или иным событиям, связанным с проявлениями природы и окружающего мира. Астрономия была необходима для охотников и мореплавателей, знание о расположении звёзд давало возможность для ориентации и навигации. Но для этого были необходимы длительные и регулярные наблюдения за светилами. Несмотря на то, что знание древних египтян о небесных светилах отставало от вавилонских, в задаче счёта времени жрецы Египта ушли вперёд. С развитие земледелия, возникает календарь (Рис.
Вплоть до XIX века, астрономия была ограничена рамками познаний лишь в пределах Солнечной системы, объекты, находившиеся за её пределами и тем более за пределами нашей Галактики, были недосягаемы для изучения, и представления о них были лишь умозаключительными. Историческое развитие в астрономии заключается в том, что она формировалась, как наука вместе с изменяющейся в разные периоды общественной жизнью и культурой. В каждой народности были свои культура, мифы и обычаи, свои первооткрыватели, которые вносили вклад, делая открытия и давая объяснения тем или иным событиям, связанным с проявлениями природы и окружающего мира. Астрономия была необходима для охотников и мореплавателей, знание о расположении звёзд давало возможность для ориентации и навигации. Но для этого были необходимы длительные и регулярные наблюдения за светилами. Несмотря на то, что знание древних египтян о небесных светилах отставало от вавилонских, в задаче счёта времени жрецы Египта ушли вперёд. С развитие земледелия, возникает календарь (Рис. 2), в котором год состоял из 12 месяцев, а месяц из 30 дней с добавочными 5 днями. Впоследствии этот календарь был положен в основу юлианского календаря, созданного в эпоху Древнего Рима.
Египтяне установили продолжительность года и создали систему летоисчисления.
…«Мир не только сфера, — говорит Платон. — Но сфера эта совершенна; Творец позаботился о том, чтобы поверхность ее была абсолютно гладкой, и это не без причин…»…
Длительные наблюдения светил помогли создать календарь, но привели к вопросу, который долгое время не находил ответа, что же находится в центре Земля или Солнце? Вопрос повис на многие столетия.
К VI в. до н.э. развитие культуры и науки в Европе способствовали созданию философских школ. Так известный древнегреческий философ и математик Пифагор (570-490 г. до н.э.) основал религиозно-философскую школу пифагорейцев. Он связывал сущность мира с соотношениями между числами. Пифагор считал, что Земля шарообразна и находится в центре, а Солнце, Луна и планеты вращаются вокруг неё.
2), в котором год состоял из 12 месяцев, а месяц из 30 дней с добавочными 5 днями. Впоследствии этот календарь был положен в основу юлианского календаря, созданного в эпоху Древнего Рима.
Египтяне установили продолжительность года и создали систему летоисчисления.
…«Мир не только сфера, — говорит Платон. — Но сфера эта совершенна; Творец позаботился о том, чтобы поверхность ее была абсолютно гладкой, и это не без причин…»…
Длительные наблюдения светил помогли создать календарь, но привели к вопросу, который долгое время не находил ответа, что же находится в центре Земля или Солнце? Вопрос повис на многие столетия.
К VI в. до н.э. развитие культуры и науки в Европе способствовали созданию философских школ. Так известный древнегреческий философ и математик Пифагор (570-490 г. до н.э.) основал религиозно-философскую школу пифагорейцев. Он связывал сущность мира с соотношениями между числами. Пифагор считал, что Земля шарообразна и находится в центре, а Солнце, Луна и планеты вращаются вокруг неё. Т.е. он был приверженцем геоцентрической системы мира.
Вопросов, которые бы решала сферическая астрономия очень много, помимо центра мира, неразрешимым вопросом было узнать расстояния до этих светил. Аристарх Самосский (310-230 гг. до н.э.) внёс огромный вклад в науку, он первый, кто задался вопросом о размерах и расстоянии до Луны и Солнца. Из всех сочинений Аристарха Самосского до нас дошло только одно, «О величинах и расстояниях Солнца и Луны». Поставив перед собой сложные задачи, он сам пытался их разрешить. К тому времени уже было представление о том, что Луна вращается вокруг Земли, во время затмений Луна заходит в тень Земли. Аристарх в доказательство своих теорий пользовался геометрическими теоремами, а условие теорем называл гипотезами.
В эпоху средневековья с рассветом культуры ислама, на востоке происходит большой научный подъём. Правители халифата были образованными людьми, и они способствовали развитию науки и образования для поддержания и развитости культуры в обществе.
Т.е. он был приверженцем геоцентрической системы мира.
Вопросов, которые бы решала сферическая астрономия очень много, помимо центра мира, неразрешимым вопросом было узнать расстояния до этих светил. Аристарх Самосский (310-230 гг. до н.э.) внёс огромный вклад в науку, он первый, кто задался вопросом о размерах и расстоянии до Луны и Солнца. Из всех сочинений Аристарха Самосского до нас дошло только одно, «О величинах и расстояниях Солнца и Луны». Поставив перед собой сложные задачи, он сам пытался их разрешить. К тому времени уже было представление о том, что Луна вращается вокруг Земли, во время затмений Луна заходит в тень Земли. Аристарх в доказательство своих теорий пользовался геометрическими теоремами, а условие теорем называл гипотезами.
В эпоху средневековья с рассветом культуры ислама, на востоке происходит большой научный подъём. Правители халифата были образованными людьми, и они способствовали развитию науки и образования для поддержания и развитости культуры в обществе.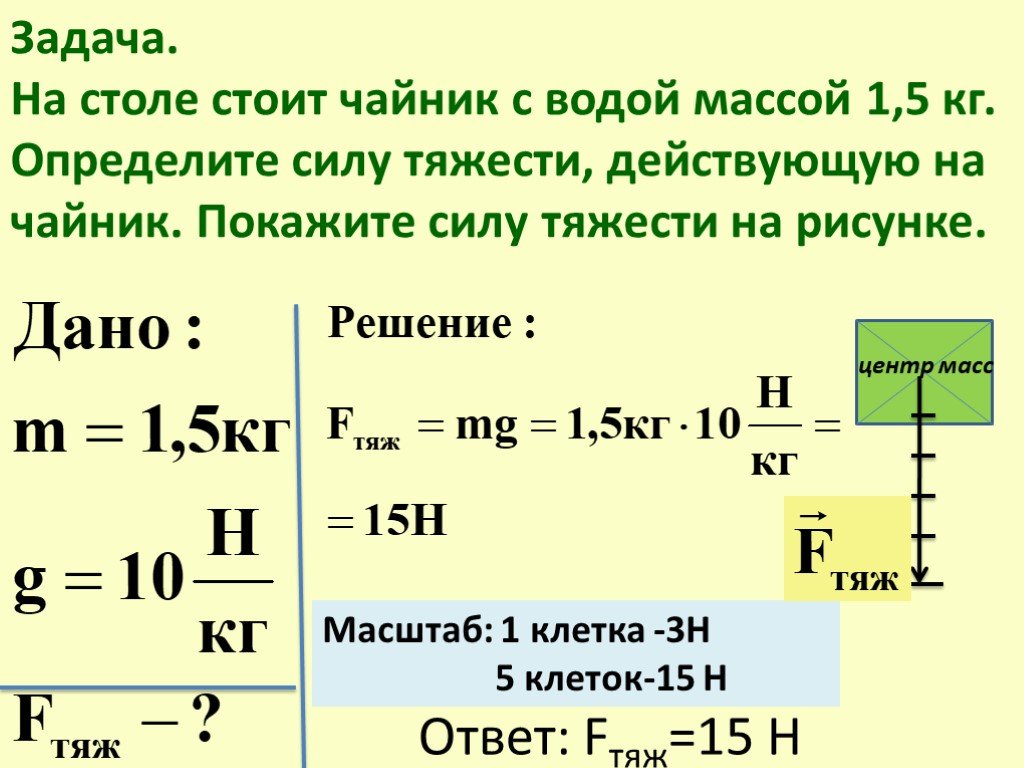 Астрономия и медицина были приоритетными науками. Вначале IX в. Аль-Мамун создал в Багдаде «Дом Мудрости» в котором находилась огромная библиотека и обсерватория. Он был похож на созданный в Александрии «Музей», который так же является прообразом «Академии Наук». Там учёные разных национальностей и конфессий занимались изучением древних сочинений – философии, астрономии, медицины, а так же занимались переводом литературы на арабский язык. Для решения сферических треугольников в IX-X веках исламскими математиками и астрономами был создан математический аппарат – сферическая тригонометрия — и инструмент, моделирующий преобразование координат – астролябия. Современной усовершенствованной астролябией является подвижная карта неба.
Классик персидской литературы Омар Хайям (1048 – 1122 гг. н.э.), автор знаменитых четверостиший – рубай, был астрономам. По его предложению был введён на Востоке один из самых точных календарей с високосными годами. Ошибка календаря была ничтожно малой – сутки за 4 500 лет.
Астрономия и медицина были приоритетными науками. Вначале IX в. Аль-Мамун создал в Багдаде «Дом Мудрости» в котором находилась огромная библиотека и обсерватория. Он был похож на созданный в Александрии «Музей», который так же является прообразом «Академии Наук». Там учёные разных национальностей и конфессий занимались изучением древних сочинений – философии, астрономии, медицины, а так же занимались переводом литературы на арабский язык. Для решения сферических треугольников в IX-X веках исламскими математиками и астрономами был создан математический аппарат – сферическая тригонометрия — и инструмент, моделирующий преобразование координат – астролябия. Современной усовершенствованной астролябией является подвижная карта неба.
Классик персидской литературы Омар Хайям (1048 – 1122 гг. н.э.), автор знаменитых четверостиший – рубай, был астрономам. По его предложению был введён на Востоке один из самых точных календарей с високосными годами. Ошибка календаря была ничтожно малой – сутки за 4 500 лет. Внук Тимура Улугбек (1394-1449 гг. н.э.) в 15 лет стал правителем Самарканда и прилегавших областей. При нём были сооружены грандиозные здания учебных заведений (Медресе). Он, с раннего детства пользуясь огромной библиотекой своего деда для самообразования, и оказался просвещённым правителем. В построенных в 1420 г. зданиях Медресе он основал университет, для преподавания в который были приглашены известные учёные, в том числе и астрономы. Через несколько лет, недалеко от Самарканда была создана большая обсерватория «Дворец наук», главным инструментом которой был огромный квадрант (по некоторым сведениям секстант). Часть его находилась в высеченной в скале траншее, а другая часть снаружи. Наземная часть дуги возвышалась над поверхностью земли приблизительно на двадцать метров, а глубина траншеи, в которой расположена сохранившаяся до нашего времени часть дуги (от 57 до 80 ), равна одиннадцати метрам. Квадрант размещался в плоскости меридиана и использовался для наблюдений кульминации и измерении угловых расстояний Солнца, Луны, планет и опорных звёзд.
Внук Тимура Улугбек (1394-1449 гг. н.э.) в 15 лет стал правителем Самарканда и прилегавших областей. При нём были сооружены грандиозные здания учебных заведений (Медресе). Он, с раннего детства пользуясь огромной библиотекой своего деда для самообразования, и оказался просвещённым правителем. В построенных в 1420 г. зданиях Медресе он основал университет, для преподавания в который были приглашены известные учёные, в том числе и астрономы. Через несколько лет, недалеко от Самарканда была создана большая обсерватория «Дворец наук», главным инструментом которой был огромный квадрант (по некоторым сведениям секстант). Часть его находилась в высеченной в скале траншее, а другая часть снаружи. Наземная часть дуги возвышалась над поверхностью земли приблизительно на двадцать метров, а глубина траншеи, в которой расположена сохранившаяся до нашего времени часть дуги (от 57 до 80 ), равна одиннадцати метрам. Квадрант размещался в плоскости меридиана и использовался для наблюдений кульминации и измерении угловых расстояний Солнца, Луны, планет и опорных звёзд. С одной стороны, если сдал данный предмет, то открывается колоссальный выбор всевозможных специальностей и направлений, и даже таких, где особенно она и не нужна, с другой стороны, если сдаешь слабо, набирая в районе 50 баллов или даже меньше, то высока вероятность дальнейшего отчисления после первой же сессии. Поэтому выбор должен быть по-настоящему осознанный. Не сказать, что в школьном курсе физики очень много теории, как например, по биологии или истории. В ЕГЭ по истории логика особенно-то и не нужна, просто учи себе, зубри, а вот физику надо понимать, уметь оперировать базовыми формулами, по которым затем выстраивается работа над задачами. Если раньше все сводилось к заучиванию формул и штудированию учебников, то сейчас есть огромное количество цифрового контента (в первую очередь видео). Полюбить физику стало проще!
С одной стороны, если сдал данный предмет, то открывается колоссальный выбор всевозможных специальностей и направлений, и даже таких, где особенно она и не нужна, с другой стороны, если сдаешь слабо, набирая в районе 50 баллов или даже меньше, то высока вероятность дальнейшего отчисления после первой же сессии. Поэтому выбор должен быть по-настоящему осознанный. Не сказать, что в школьном курсе физики очень много теории, как например, по биологии или истории. В ЕГЭ по истории логика особенно-то и не нужна, просто учи себе, зубри, а вот физику надо понимать, уметь оперировать базовыми формулами, по которым затем выстраивается работа над задачами. Если раньше все сводилось к заучиванию формул и штудированию учебников, то сейчас есть огромное количество цифрового контента (в первую очередь видео). Полюбить физику стало проще!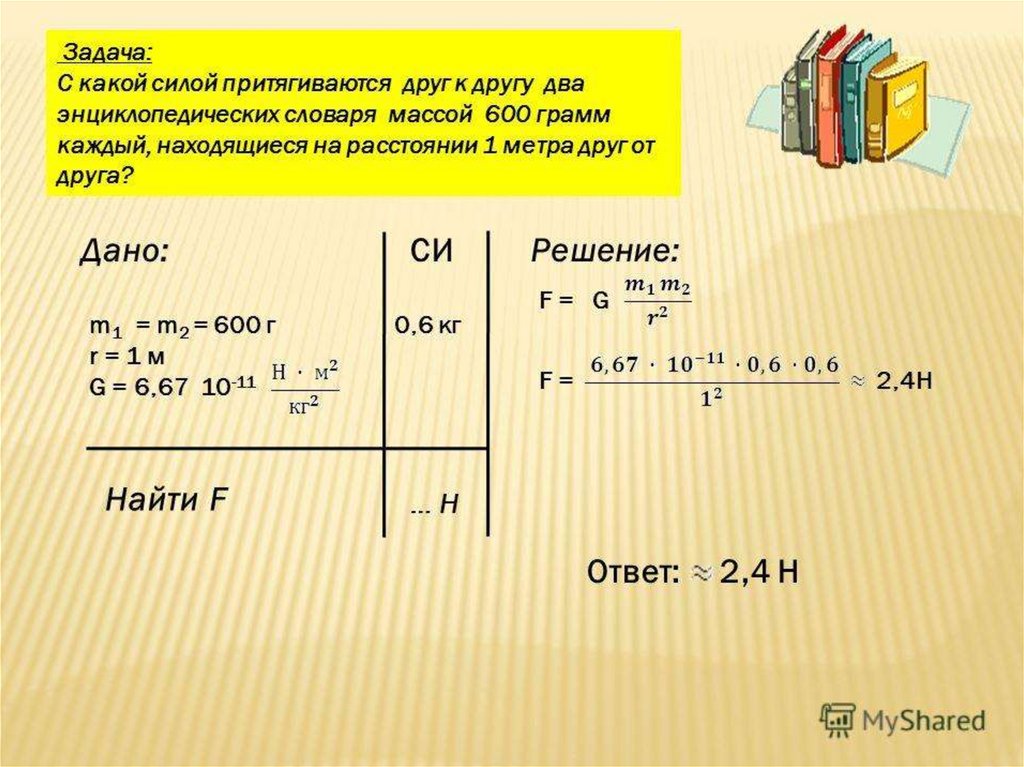 Из них 13 заданий с записью ответа в виде числа, слова или двух чисел, 10 заданий на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр.
Из них 13 заданий с записью ответа в виде числа, слова или двух чисел, 10 заданий на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр.



 Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.
Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным. Поэтому нельзя за …
Поэтому нельзя за … Хорошее определение это …
Хорошее определение это … В десятичной системе …
В десятичной системе …
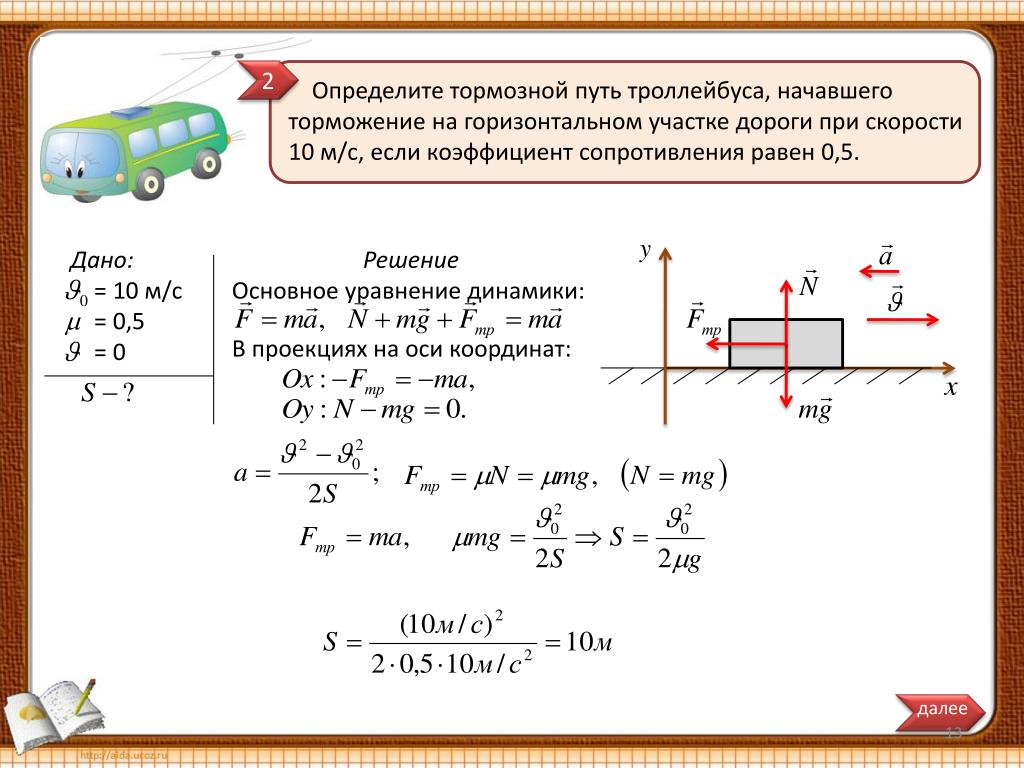 Четвертая величина будет рассчитана после нажатия на кнопку Рассчитать. Количество можно ввести в молях или указать молярную массу и массу газа. Для определения молярной массы любого газа можно использовать калькулятор молярной массы. Если нужно определить молярную массу смеси газов, например, сухого воздуха, нужно определить молярные массы каждого газа и умножить их на процентное содержание по массе каждого газа в воздухе.
Четвертая величина будет рассчитана после нажатия на кнопку Рассчитать. Количество можно ввести в молях или указать молярную массу и массу газа. Для определения молярной массы любого газа можно использовать калькулятор молярной массы. Если нужно определить молярную массу смеси газов, например, сухого воздуха, нужно определить молярные массы каждого газа и умножить их на процентное содержание по массе каждого газа в воздухе. Определить среднюю молярную массу воздуха.
Определить среднюю молярную массу воздуха.

 Один моль любого вещества в граммах численно равен средней массы одной молекулы в соединении, выраженной в атомных единицах массы. Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
Один моль любого вещества в граммах численно равен средней массы одной молекулы в соединении, выраженной в атомных единицах массы. Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра. Постоянная в точности равна 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Универсальная газовая постоянная также определяется как произведение числа Авогадро NA и постоянной Больцмана k:
Постоянная в точности равна 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Универсальная газовая постоянная также определяется как произведение числа Авогадро NA и постоянной Больцмана k: Подставив удельную газовую постоянную в уравнение состояния идеального газа, получим:
Подставив удельную газовую постоянную в уравнение состояния идеального газа, получим:
 Это уравнение показывает, что, если количество газа увеличивается, объем газа пропорционально растет. Иными словами, количество атомов или молекул газа не зависит от их размеров или от молярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, который опубликовал гипотезу об отношениях объема газа и его количества в молях в 1811 году. Число Авогадро также носит его имя.
Это уравнение показывает, что, если количество газа увеличивается, объем газа пропорционально растет. Иными словами, количество атомов или молекул газа не зависит от их размеров или от молярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, который опубликовал гипотезу об отношениях объема газа и его количества в молях в 1811 году. Число Авогадро также носит его имя. Поэтому этот закон в литературе не на английском языке часто называют законом Гей-Люссака. В русскоязычной литературе закон носит имя Гей-Люссака. Итальянцы называют этот закон первым законом Гей-Люссака (ит. prima legge di Gay-Lussac).
Поэтому этот закон в литературе не на английском языке часто называют законом Гей-Люссака. В русскоязычной литературе закон носит имя Гей-Люссака. Итальянцы называют этот закон первым законом Гей-Люссака (ит. prima legge di Gay-Lussac). Итальянцы называют этот закон вторым законом Вольта–Гей-Люссака (ит. seconda legge di Volta – Gay-Lussac), потому что итальянец Алессандро Вольта независимо проводил исследования газов и получил аналогичные результаты.
Итальянцы называют этот закон вторым законом Вольта–Гей-Люссака (ит. seconda legge di Volta – Gay-Lussac), потому что итальянец Алессандро Вольта независимо проводил исследования газов и получил аналогичные результаты. Цель этой статьи — помочь вам избежать этих ошибок.
Цель этой статьи — помочь вам избежать этих ошибок. Ну и какой толк от этих пятёрок?
Ну и какой толк от этих пятёрок?

 Хотя использование этой веб-страницы не ограничивается физикой
студенты, концепции, рассматриваемые здесь, как правило, вызывают проблемы, стоящие перед физикой
ученики.
Хотя использование этой веб-страницы не ограничивается физикой
студенты, концепции, рассматриваемые здесь, как правило, вызывают проблемы, стоящие перед физикой
ученики.
 1
x 10 6 + 4,2 x 10 5
1
x 10 6 + 4,2 x 10 5  Вычислите электрическую силу между зарядами. ответ
Вычислите электрическую силу между зарядами. ответ 9] (степень) заключается в том, что калькуляторы TI 83 делают
не отличать научное обозначение от умножения и деления. Это становится проблематичным при разделении
числа в научной записи. В качестве
пример посмотрите на вопрос 3 из примера задач по физике.
9] (степень) заключается в том, что калькуляторы TI 83 делают
не отличать научное обозначение от умножения и деления. Это становится проблематичным при разделении
числа в научной записи. В качестве
пример посмотрите на вопрос 3 из примера задач по физике. Много
учащиеся используют калькуляторы Texas Instrument (TI 83 и TI 83+) в качестве инструмента для
решать проблемы, и нам нужно прояснить проблемы, которые студенты имеют в
используя этот инструмент. ТИ
калькуляторы не используют здравый смысл при выполнении расчетов, поэтому
студенты должны правильно ввести данные, чтобы получить правильные результаты.
Много
учащиеся используют калькуляторы Texas Instrument (TI 83 и TI 83+) в качестве инструмента для
решать проблемы, и нам нужно прояснить проблемы, которые студенты имеют в
используя этот инструмент. ТИ
калькуляторы не используют здравый смысл при выполнении расчетов, поэтому
студенты должны правильно ввести данные, чтобы получить правильные результаты.