Как легко выучить формулы по физике для ЕГЭ 2023 в 11 классе — 4 способа запоминания физических формул из кодификатора
В кодификаторе ЕГЭ по физике около 180 формул. Сначала создаётся ощущение, что в течение года можно разбить формулы по блокам и изучать их в спокойном темпе. Однако это не очень хорошая идея: подготовка к ЕГЭ должна быть системной, зубрёжка не поможет. В этой статье преподавательница физики в Вебиуме Снежа Планк рассказывает, как правильно учить формулы по физике.
Снежа Планк, преподавательница физики в Вебиуме
Некоторые формулы мы выводим из задач и со временем понимаем, откуда появлялись те или иные величины. Но есть базовые формулы, которые невозможно вывести в рамках школьной программы по физике. Поэтому приходится их запоминать.
Метод 1: придумывайте ассоциации
Например, формула силы Ампера F = B * I * L * sina = Ампер бил сына.
На курсе в Вебиуме мы с ребятами запоминали формулу напряженности и разницу потенциалов U = E * d словом «еда». А при нахождении гидростатического давления нужно обязательно кому-то родить:
А при нахождении гидростатического давления нужно обязательно кому-то родить:
p = p*g*h — «ро жэ аш», рожаешь.
Если вы умеете рисовать, то можете изображать свои ассоциации. Написали формулу, придумали ассоциацию и нарисовали её.
Формулу циклической частоты мы запоминали со студентами как «две птицы», поскольку «омега» похожа на птичку. И такую иллюстрацию сможет нарисовать каждый.
Как не потерять баллы на лёгких заданиях и избежать ошибок в ЕГЭ по физике, рассказали в этой статье.
Метод 2: сделайте карточки с формулами
Сделайте карточки и развесьте их по всей квартире. Например, идёте ночью к холодильнику и повторяете кпд тепловой машины. Ставите разогревать еду в микроволновке — а там у вас формула электромагнитной волны.
Может ли девушка получить специальность инженера и получить работу в строительной компании? Снежа рассказала о своём профессиональном пути.
Метод 3: используйте мнемонические правила
Чтобы запомнить, в каком порядке идёт увеличение частоты волн видимого света, выучите фразу «Каждый охотник желает знать, где сидит фазан!». Самая высокая частота у фиолетового цвета, а у самая низкая — у красного.
Сделали подборку сборников и пособий для подготовки к ЕГЭ по физике.
Метод 4: используйте метод Фейнмана
Представьте, что вы объясняете тему восьмилетнему ребёнку. Вы не можете использовать терминологию, иначе он вас не поймёт. Придётся описывать формулу своими словами: максимально просто и доступно.
Например, опишем этим методом формулу мощности. Представьте, вы поехали отдыхать на дачу к бабушке. Но приехали в самый неудачный момент — пора выкапывать картошку. Утром вы начинаете усердно копать картошку, то есть, заниматься какой-то работой. Вы копали в течение двух часов. В итоге, бабушка сказала, что вы «супер мощная машина по выкапыванию картошки».
Для формулы мощности необходимо понять, какую работу вы выполняете в единицу времени.
Если вы только начинаете путь подготовки к ЕГЭ по физике, то первым делом изучите демоверсию. А наш подробный гайд по экзамену поможет вам стать высокобалльником в этом году.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
определения, правила, таблица с пояснениями, примеры
Содержание:
- Физика для 7-9 класса — какие основные темы изучаются
-
Все формулы по физике за 7 класс
- Формула для нахождения скорости равномерного движения
- Формула средней скорость неравномерного движения
- Формула плотности вещества
- Формула силы тяжести
- Формула для нахождения равнодействующих сил, которые направлены в единую сторону
- Формула для веса тела
- Формула для вычисления давления
- Формула для измерения давления жидкости
- Формула силы Архимеда
-
Формулы по физике за 8 класс
- Формула для вычисления количества теплоты при охлаждении (нагревании)
- Формула количества теплоты при сгорании топлива
- Формула количество теплоты плавления (кристаллизации)
- Формула КПД теплового двигателя
- Формула силы тока
- Формула электрического напряжения
- Формула закона Ома для участка цепи
- Формула последовательного соединения проводников
- Формула параллельного соединения проводников
- Формула мощности электрического тока
- Формула для закона преломления света
-
Формулы по физике за 9 класс
- Формула проекции вектора перемещения
- Формула скорости равномерного движения
- Формула движения тела по окружности
- Закон всемирного притяжения
- Формула импульса тела
- Формула связи между периодом и частотой колебаний
- Формула скорости волны
- Формула электрической емкости конденсатора
- Формула энергии связи (или формула Эйнштейна)
Содержание
- Физика для 7-9 класса — какие основные темы изучаются
-
Все формулы по физике за 7 класс
- Формула для нахождения скорости равномерного движения
- Формула средней скорость неравномерного движения
- Формула плотности вещества
- Формула силы тяжести
- Формула для нахождения равнодействующих сил, которые направлены в единую сторону
- Формула для веса тела
- Формула для вычисления давления
- Формула для измерения давления жидкости
- Формула силы Архимеда
-
Формулы по физике за 8 класс
- Формула для вычисления количества теплоты при охлаждении (нагревании)
- Формула количества теплоты при сгорании топлива
- Формула количество теплоты плавления (кристаллизации)
- Формула КПД теплового двигателя
- Формула силы тока
- Формула электрического напряжения
- Формула закона Ома для участка цепи
- Формула последовательного соединения проводников
- Формула параллельного соединения проводников
- Формула мощности электрического тока
- Формула для закона преломления света
-
Формулы по физике за 9 класс
- Формула проекции вектора перемещения
- Формула скорости равномерного движения
- Формула движения тела по окружности
- Закон всемирного притяжения
- Формула импульса тела
- Формула связи между периодом и частотой колебаний
- Формула скорости волны
- Формула электрической емкости конденсатора
- Формула энергии связи (или формула Эйнштейна)
Физика для 7-9 класса — какие основные темы изучаются
Физика — одна из естественных наук, изучающая общие и фундаментальные закономерности структуры, развития и эволюции мира вокруг нас. Изучением физики занимались многие известные ученые. Имена самых известных физиков: Альберт Эйнштейн, Исаак Ньютон, Ж.И. Алферов, Л.Д. Ландау, Никола Тесла и многие другие.
Изучением физики занимались многие известные ученые. Имена самых известных физиков: Альберт Эйнштейн, Исаак Ньютон, Ж.И. Алферов, Л.Д. Ландау, Никола Тесла и многие другие.
Так выглядел Никола Тесла (открытия в области электричества):
Источник: ru.wikipedia.orgПрактически все физические задачи, явления рассчитывают при помощи формул. Рассмотрим самые основные формулы по физике за 7-9 классы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Все формулы по физике за 7 класс
В 7 классе ученики школы знакомятся с формулами для вычисления следующих физических величин: скорость равномерного движения; плотность вещества; средняя скорость неравномерного движения; сила тяжести; равнодействующая сила, которая направлена в одну сторону; вес тела; давление; давление жидкости; сила Архимеда.
Формула для нахождения скорости равномерного движения
Скорость равномерного прямолинейного движения — неизменяемая скорость объекта в процессе движения по прямой линии.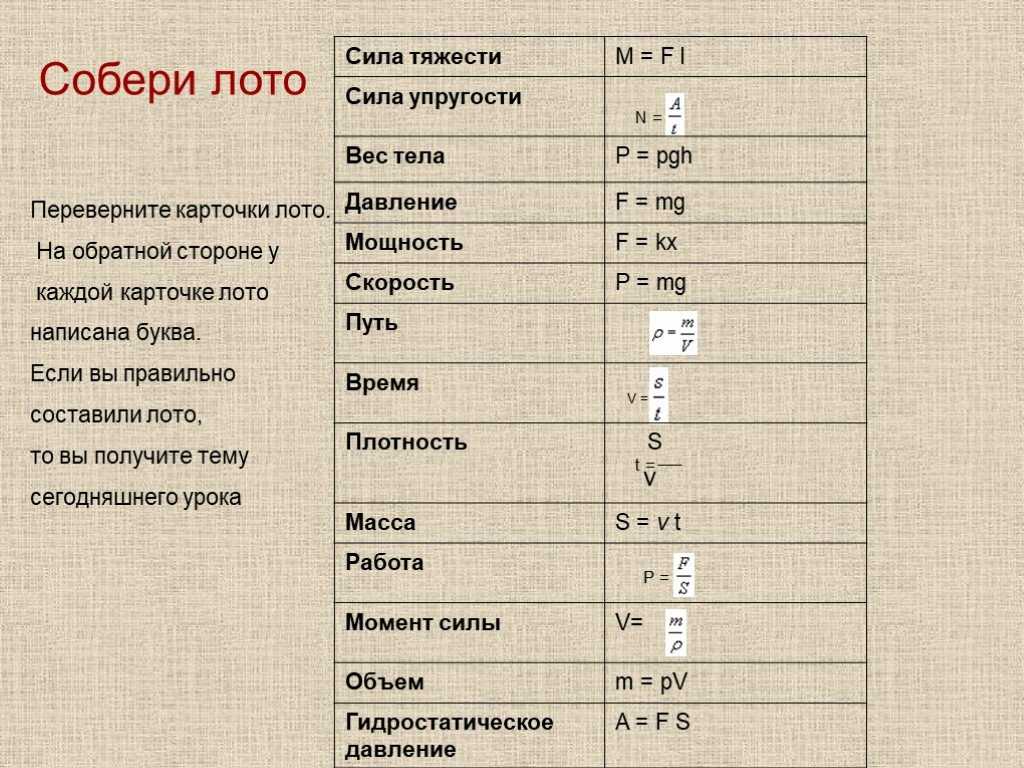 Такая скорость будет одинаковой в каждый момент движения тела.
Такая скорость будет одинаковой в каждый момент движения тела.
Рассчитать скорость равномерного движения можно так:
Формула 1
\(V=\frac{S}{t}\)
В данной формуле V является скоростью тела, которую ищем, показатель S является путем, который проходит объект, а t является временем, за которое путь был пройден.
Скорость обычно измеряют в километрах в час (обозначают как км/ч) в случае больших расстояний, а в случае маленьких — в метрах в секунду (обозначают как м/с).
Формула средней скорость неравномерного движения
Средняя скорость — скорость, которой мог бы обладать объект, если бы смог преодолеть тот же путь за это же время при условии равномерного движения.
Средняя скорость зависит от параметров, которые применяются к скорость равномерного движения: t и S. Для расчета средней скорости движения необходимо использовать следующую формулу:
Формула 2
\(V=\frac{S_{1}+S_{2}}{t_{1}+t_{2}} S_{1}\)
В данной формуле V будет искомой средней скоростью, \(S_{1}\), \(S_{2}\) — участники пути, из которых складывается полноценный путь тела, \(t_{1}\) — время, которое тело потратило на преодоление первого участка пути, а \(t_{2}\) — время, которое тело потратило на преодоление второго участка пути. Среднюю скорость изменяют в километрах в час.
Среднюю скорость изменяют в километрах в час.
Формула плотности вещества
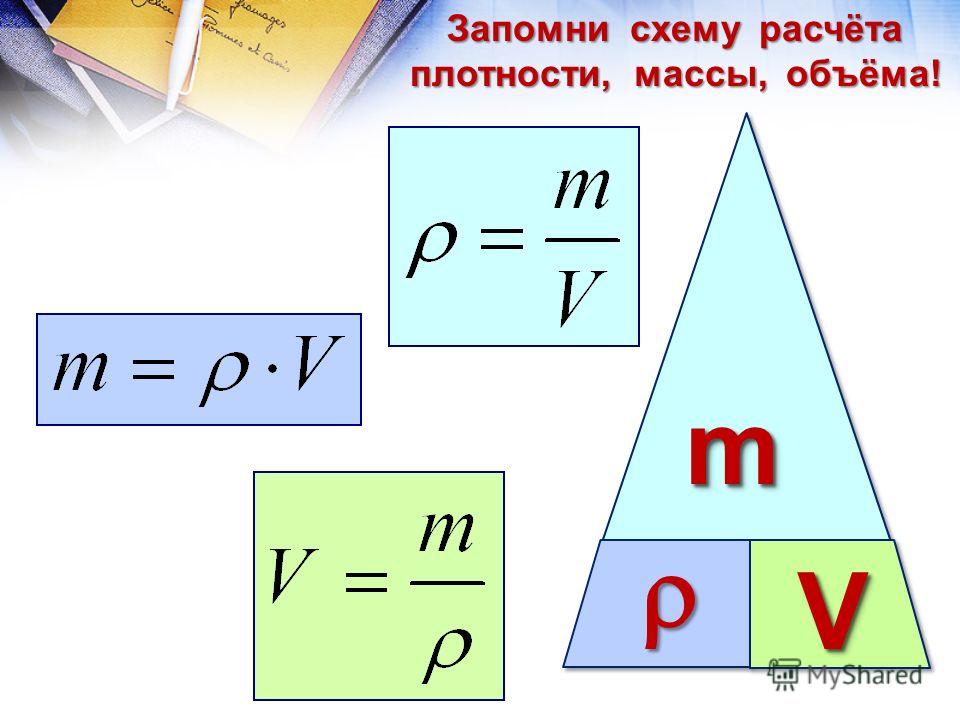
Плотность вещества — физическое значение, которое указывает на зависимость массы вещества от объема вещества. Формула для вычисления плотности вещества будет следующей:
\(p=\frac{m}{V}\)
В данной формуле p будет плотностью, m будет массой вещества, а V является объемом вещества. Единицами измерения плотности является килограмм на кубический метр.
Формула силы тяжести
Сила тяжести — такая сила, при помощи которой все тела на планете Земля притягиваются к поверхности.
Можно вычислить по формуле:
\(F=g\times{m}\)
Здесь F будет силой тяжести, m — массой тела, g будет являться коэффициентом силы тяжести (он равен 9,8 метров в секунду). Единицей измерения силы тяжести является ньютон.
Формула для нахождения равнодействующих сил, которые направлены в единую сторону
Равнодействующая сила — векторная сумма сил, которые действуют на объект или частицу.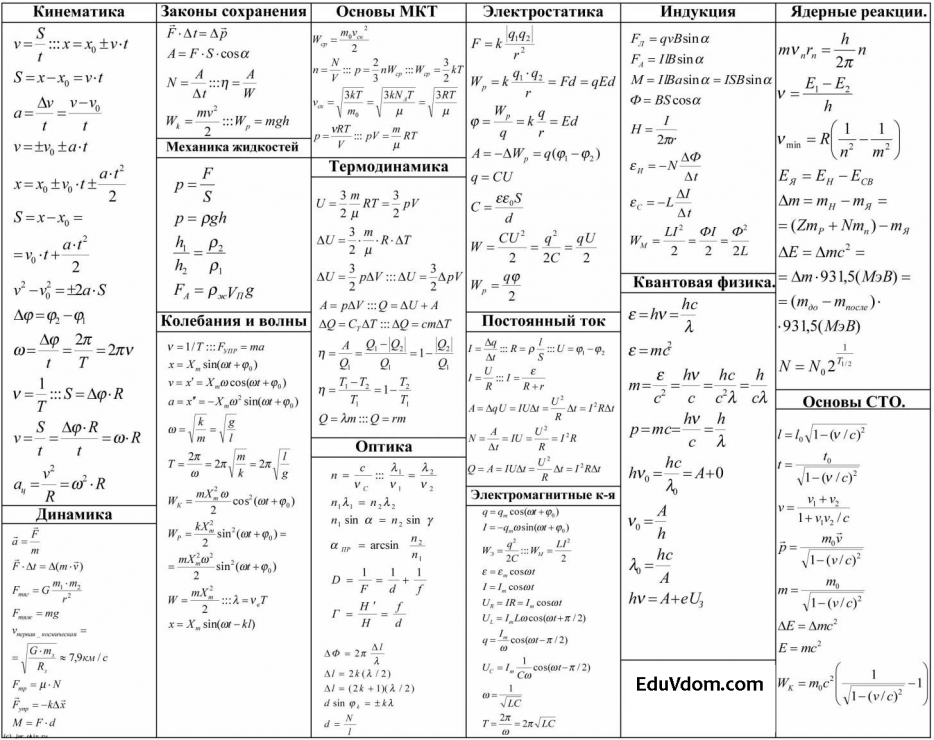
Если силы, которые воздействуют на объект, направляются по единой прямой в одну сторону, равнодействующая данных сил будет направлена в такую же сторону, модуль этой силы будет равняться сумме модулей данных сил.
Равнодействующую силу можно вычислить по формуле:
\(R=F_{1}+F_{2}\)
В данной формуле R является равнодействующей сил \(F_{1}\) и \(F_{2}\), которые воздействуют на объект. Единица измерения — Ньютоны.
Формула для веса тела
Вес тела — сила, с которой объект влияет на подвес или опору под ним из-за притяжения к поверхности Земли.
Вес тела вычисляют по такой формуле:
\(F=g\times{m}.\)
Единицы измерения веса тела — Ньютоны.
Формула для вычисления давления
Давление — физическая величина, которая характеризует величину воздействия силы, которая действует перпендикулярно поверхности на площадь данной поверхности.
Формула давления:
\(P=\frac{F}{S}\)
В данной формуле P является давлением, F — силой, которая направлена перпендикулярно площади поверхности, S является площадью поверхности, на которую влияет сила.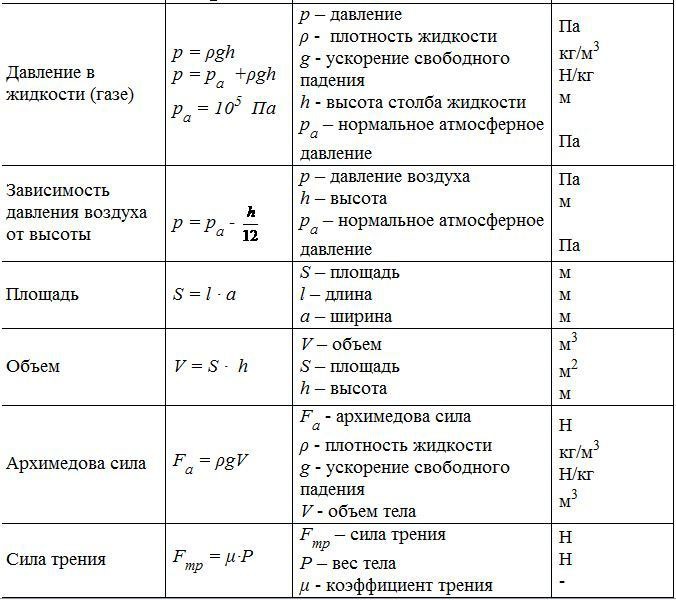 Единицей измерения давления являются паскали.
Единицей измерения давления являются паскали.
Формула для измерения давления жидкости
Обычно величина давления в газе или жидкости напрямую зависит от двух факторов:
- От уровня газа или жидкости в сосуде.
- От уровня плотности газа или жидкости. Чем больше показатель плотности, тем больше будет показатель давления.
Формула для вычисления давления жидкости выглядит так:
Формула 3
\(P=p\times{g}\times{h}\)
В данной формуле P является давлением в жидкости, p является плотностью жидкости, g является коэффициентом силы тяжести, который равен 9,8 метров в секунду, h является высотой столба жидкости в емкости. Единицей измерения давления в жидкости является паскаль.
Примечание 1
По закону Паскаля давление в газах и жидкости передает одинаково по всем направлениям.
Формула силы Архимеда
Сила Архимеда — сила выталкивания, которая воздействует на объект, который погружают в газ или жидкость. Данная сила постоянно направлена вверх, равна весу жидкости по модулю.
Данная сила постоянно направлена вверх, равна весу жидкости по модулю.
Формула силы Архимеда выглядит так:
\(F_{a}=p\times{g}\times{V}\)
В данной формуле \(F_{a}\) является силой Архимеда, p является плотностью газа или жидкости, g является коэффициентом силы тяжести, а V является объемом объекта, который погружен в жидкость. Единицей измерения силы Архимеда является ньютон.
Формулы по физике за 8 класс
В 8 классе ученики знакомятся с формулами, с помощью которых можно вычислить следующие величины: количество теплоты в случае нагревания (или охлаждения), количество теплоты в случае сгорания топлива, количество теплоты в случае плавления (кристаллизации), коэффициент полезного действия (КПД) теплового двигателя, сила тока, электрическое напряжение, закон Ома для определенного участка цепи, последовательное соединение проводников, параллельное соединение проводников, мощность электрического тока, а также закон преломления света.
Формула для вычисления количества теплоты при охлаждении (нагревании)
Количество теплоты — физическая величина, которая характеризуется количественным значением энергии, которую объект получает в случае нагревания и отдает в случае охлаждения.
Формула количества теплоты:
\(Q=c\times{m}\times{\triangle{t}}\)
В данной формуле Q является количеством теплоты, m — массой тела объекта, c — показатель удельной теплоемкости вещества, из которого состоит объект, \(\triangle{t}\) является показателем изменения температуры тела объекта. Единицей измерения являются джоули.
Примечание 2
Если Q>0, тогда происходит процесс нагревания, а если Q<0, тогда тело остывает.
Формула количества теплоты при сгорании топлива
Количество теплоты при сгорании топлива — физическая величина, равная количеству энергии, которая выделяется в случае полного сгорания топлива.
\(Q=q\times{m}\)
В данной формуле Q является количеством теплоты в процессе сгорания топлива, q является удельной теплотой сгорания топлива (то есть количество энергии, которое выделяется в случае сгорания килограмма топлива), m является массой топлива. Единицей измерения являются джоули.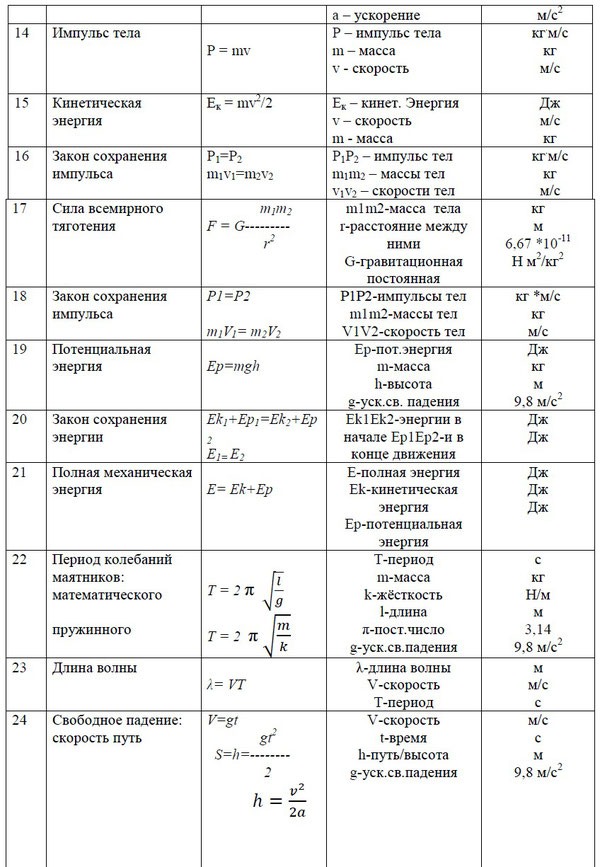
Формула количество теплоты плавления (кристаллизации)
Количество теплоты плавления или кристаллизации — количества теплоты, которое нужно для плавления объекта, который находится в условиях температуры плавления и нормальном атмосферном давлении.
Формула вычисления количества теплоты плавления такова:
\(Q=\lambda\times{m}\)
Формула вычисления количества теплоты кристаллизации такова:
\(Q=-\lambda\times{m}\)
В данных формулах Q будет количество теплоты плавления\кристаллизации, m будет массой тела, \(\lambda\) будет удельной теплотой плавления (то есть такой величиной теплоты, которая нужна для плавления килограмма вещества). Единицей измерения этой формулы является джоуль.
Формула КПД теплового двигателя
КПД (или же коэффициент полезного действия) теплового двигателя — знаковый показатель, который зависит от работы, которая совершается двигателем за единый цикл, а также количества теплоты, которое получает объект от нагревателя.
Формула КПД такова:
\(\eta=\frac{A}{Q_{1}}\times100%\]\)
В данной формуле \(\eta\) является КПД, A является полезной работой, \(Q_{1}\) является количеством теплоты, которое тело получило от нагревателя.
Существует и другой тип формулы:
Формула 4
\(\eta=\frac{Q_{1}-Q_{2}}{Q_{1}}\times100%\)
В данной формуле \(Q_{1}\) является количеством теплоты, которое получает тело от нагревателя, \(Q_{2}\) является количеством теплоты, которое отдается холодильнику. КПД измеряют обычно в процентах.
Формула силы тока
Сила тока — физическая величина, характеризующая заряд, который проходит через проводник за единицу времени.
Формула силы тока такова:
\(I=\frac{q}{\triangle{t}}\)
В данной формуле I является силой тока в проводнике, q является электрическим зарядом, который проходит через поперечное сечение проводника, а \(\triangle{t}\) является временем прохождения заряда. Единицей измерения силы тока является ампер.
Единицей измерения силы тока является ампер.
Формула электрического напряжения
Электрическое напряжение — физическая величина, которая характеризует действие электрического поля на заряженные частицы.
Формула для нахождения электрического напряжения:
\(U=\frac{A}{q}\)
В данной формуле U является напряжением на участке цепи, A является работой электрического поля, q является величиной заряда на участке цепи. Единицей измерения являются вольты.
Формула закона Ома для участка цепи
Теорема
Закон Ома сформулирован так: сила тока на конкретном участке электрической цепи прямо пропорционально напряжению на данном участке, а также обратно пропорциональна сопротивлению данного участка электрической цепи.
Формула закона Ома такова:
\(I=\frac{U}{R}\)
В данной формуле I является сила тока на конкретном участке цепи, U является напряжением на данной участке электрической цепи, R является сопротивлением конкретного участка электрической цепи. Единицей измерения является ампер.
Единицей измерения является ампер.
Формула последовательного соединения проводников
Последовательное соединение проводников в электрической цепи — соединение элементов, при котором конец одного элемента соединяется с началом другого.
Для последовательного соединения характерны закономерности, при помощи которых можно вычислить главные параметры электрической цепи, такие как сила тока, сопротивление и напряжения.
формула 5
Теорема
\(I=I_{1}=I_{2}\)
\(U=U_{1}+U_{2}\)
\(R=R_{1}+R_{2}\)
В данных формулах \(I_{1},U_{1},R_{1}\) является электрическими характеристиками первого участка цепи, а \(I_{2},U_{2},R_{2}\) является электрическими характеристиками второго участка цепи. Единицами измерения силы тока является ампер, напряжения — вольт, сопротивления — ом.
Формула параллельного соединения проводников
Параллельное соединение — вид соединения проводников, при котором начала проводников присоединяются к единой точке цепи, концы — к иной точке цепи.
В случае параллельного соединения основными характеристики электрической цепи вычисляются по таким формулам:
\(I=I_{1}+I_{2}\)
\(U=U_{1}=U_{2}\)
\(R=\frac{R_{1}\times{R_{2}}}{R_{1}+R_{2}}\)
В данной формуле \(I_{1},U_{1},R_{1}\) являются электрические характеристики первого участка цепи, а \(I_{2},U_{2},R_{2}\) являются электрические характеристики второго участка цепи. Единицы измерения: ампер, вольт и ом соответственно.
Формула мощности электрического тока
Мощность электрического тока — физическая величина, которая определяет, какую работу совершит ток за конкретный промежуток времени.
Мощность тока можно вычислить по следующей формуле:
\(P=\frac{A}{t}\)
В данной формуле P является мощностью тока, A является работой электрического тока на участке цепи, t является временем, в течение которого электрический ток совершал определенную работу.
Есть и другой вариант данной формулы:
Формула 6
\(P=I\times{U}\)
В данной формуле I является силой тока, U является электрическим напряжением на участке цепи. Единицей измерения является ватт.
Единицей измерения является ватт.
Формула для закона преломления света
Луч падающий и преломленный, плюс перпендикуляр к границе раздела двух сред, находятся в единой плоскости, причем отношение синуса угла падения к синусу угла преломления будет значением постоянной для таких сред — относительный показатель преломления \(n_{21}\).
Формула закона преломления света:
\(n_{21}=\frac{\sin\alpha}{\sin\beta}\)
Формулы по физике за 9 класс
В программе 9 класса школьникам необходимы формулы для вычисления следующих тем: проекция вектора перемещения; скорость равномерного движения; уравнение движения (то есть зависимость координаты от времени) в случае равномерного движения; движение тела по окружности; закон всемирного тяготения; импульс тела; связь между частотой и периодом колебания; скорость волны; электрическая емкость конденсатора; энергия связи (формула Альберта Эйнштейна).
Формула проекции вектора перемещения
Проекция вектора перемещения на ось будет равняться разности между начальной и конечной координатами тела по определенной оси.
Формула скорости равномерного движения
Скорость равномерного прямолинейного движения — постоянная векторная величина, равная отношению перемещения объекта ко времени, за которое произошло перемещение.
Расчет скорости равномерного прямолинейного движения производят по следующей формуле:
\(\overrightarrow{V}=\frac{\overrightarrow{S}}{t}\)
В данной формуле \(\overrightarrow{V}\) является скоростью тела, \(\overrightarrow{S}\) является путем, который объект проходит, а t — время, за которое тело проходит конкретный путь.
Обратите внимание, что вектор скорость всегда направляется в сторону движения. Единицей измерения скорости равномерного прямолинейного движения являются метры в секунду или километры в час.
Выражение движения (при зависимости координаты от времени) при равномерном движении
Формула 7
Уравнение облагает следующим видом: \(x=x_{0}+vt\). {-11}\). Единицы измерения — Ньютоны.
{-11}\). Единицы измерения — Ньютоны.
Формула импульса тела
Импульс тела — векторная физическая величина, равная произведению массы тела на скорость тела.
Формула импульса:
\(\overrightarrow{p}=m\times\overrightarrow{V}\)
В формуле \(\overrightarrow{p}\) является импульсом тела, m является массой тела, \(\overrightarrow{V}\) является скоростью движения. Единица измерения — кг на мс.
Формула связи между периодом и частотой колебаний
Период — время единичного полного колебания. Частота — количество полных колебаний за единицу времени (берется одна секунда). Период и частота свободных колебаний нитяного маятника зависит от длины нити маятника.
Между частотой и периодом колебаний есть обратно-пропорциональная зависимость: чем больше будет период колебаний, тем меньше значение частоты, и наоборот.
Формула:
\(T=\frac{1}{v}\)
\(v=\frac{1}{t}\)
В данных формулах T является периодом колебаний, а v является частотой колебаний. Единица измерения частоты — герц, периода — секунда.
Единица измерения частоты — герц, периода — секунда.
Формула скорости волны
Скорость волны — скорость распространения колебаний в условиях упругой среды.
Рассчитывается по формуле:
\(V=\lambda\times{v}\)
В данной формуле V является скоростью волны, \(\lambda\) является длиной волны, а v является частотой волны. Измеряется в метрах в секунду.
Формула электрической емкости конденсатора
Конденсатор — это два проводника, которые находятся на малом расстоянии друг от друга, разделяются слоем диэлектрика. Электроемкость — это физическая величина, которая характеризует умение проводника накапливать некоторое количество электрического заряда.
Электроемкость конденсатора зависит от нескольких параметров. Среди них размер проводников, форма проводников, расстояния между проводниками, электрические свойства диэлектрика. Электрическая емкость конденсатора никак не зависит от размера заряда, напряжения и материала проводников. {2}}\)
{2}}\)
В данной формуле \(\triangle{m}\) является дефектом массы ядра, а c является скоростью света в вакууме.
Все формулы за 7-9 классы в виде таблицы:
Источник: fgoskomplekt.ruНасколько полезной была для вас статья?
У этой статьи пока нет оценок.
19.4 Электроэнергетика — Физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Давать определение электрической мощности и описывать уравнение электрической мощности
- Расчет электрической мощности в цепях резисторов, соединенных последовательно, параллельно и комплексно
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (5) Научные понятия. Учащийся знает природу сил в физическом мире. Ожидается, что студент:
- (Ж)
проектировать, конструировать и рассчитывать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.

- (Ж)
проектировать, конструировать и рассчитывать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.
Кроме того, руководство по физике для средней школы рассматривает содержание этого раздела лабораторной работы под названием «Работа, энергия и мощность в цепях», а также следующие стандарты:
- (6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
- (С) рассчитать механическую энергию, мощность, генерируемую внутри, приложенный к ней импульс и импульс физической системы.
Основные термины раздела
| электроэнергия |
Энергия у многих ассоциируется с электричеством. Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи являются наглядными примерами электроснабжения. Мы также используем электроэнергию, чтобы заводить автомобили, компьютеры или освещать дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность – это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это значит, но и какие факторы определяют электрическую мощность.
Мощность — это скорость передачи энергии любого типа; электрическая мощность – это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это значит, но и какие факторы определяют электрическую мощность.
Для начала давайте подумаем об лампочках, которые часто характеризуются номинальной мощностью в ваттах. Сравним лампочку мощностью 25 Вт с лампочкой мощностью 60 Вт (см. рис. 19.20). Хотя оба работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходная мощность электрической цепи определяется не напряжением, а чем-то иным.
Лампы накаливания, такие как две, показанные на рис. 19.20, по существу представляют собой резисторы, которые нагреваются, когда через них проходит ток, и нагреваются настолько, что излучают видимый и невидимый свет. Таким образом, две лампочки на фотографии можно рассматривать как два разных резистора. В простой цепи, такой как лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, как и напряжение, должен определять мощность.
Рисунок 19.20 Слева лампочка на 25 Вт, а справа лампочка на 60 Вт. Почему их выходная мощность различна, несмотря на то, что они работают на одном и том же напряжении?
Формулу мощности можно найти с помощью размерного анализа. Рассмотрим единицы мощности. В системе СИ мощность указывается в ваттах (Вт), что представляет собой энергию в единицу времени, или Дж/с
Вт=Джс.Вт=Джс.
19,47
Вспомним теперь, что напряжение — это потенциальная энергия на единицу заряда, а это означает, что единицы измерения напряжения составляют Дж/Кл
В=ДК.В=ДК.
19,48
Мы можем переписать это уравнение как J=V×CJ=V×C и подставить его в уравнение для ватт, чтобы получить
W=Js=V×Cs=V×Cs.W=Js=V× Cs=V×Cs.
Но кулон в секунду (Кл/с) — это электрический ток, который мы можем видеть из определения электрического тока, I=ΔQΔtI=ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или
Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или
П=IV.П=IV.
Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .
Например, рассмотрим схему на рис. 19.21. По закону Ома ток, протекающий через цепь, равен
I=VR=12V100Ω=0,12A.I=VR=12V100Ω=0,12A.
19,49
Таким образом, мощность, потребляемая схемой, равна
P=VI=(12 В)(0,12 А)=1,4 Вт. P=VI=(12 В)(0,12 А)=1,4 Вт.
19,50
Куда уходит эта сила? В этой схеме мощность идет в основном на нагрев резистора в этой цепи.
Рисунок 19.21 Простая схема, потребляющая электроэнергию.
При расчете мощности в цепи на рис. 19.21 мы использовали сопротивление и закон Ома для определения силы тока. Закон Ома дает ток: I=V/RI=V/R, который мы можем подставить в уравнение для электрической мощности, чтобы получить
P=IV=(VR)V=V2RP. P=IV=(VR)V= В2Р.
P=IV=(VR)V= В2Р.
Мощность определяется только напряжением и сопротивлением.
Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электрической мощности и получить выражение для мощности только через ток и сопротивление. Если мы запишем закон Ома как V=IRV=IR и используя это, чтобы исключить V в уравнении P=IVP=IV, мы получаем
P=IV=I(IR)=I2R.P=IV=I(IR)=I2R.
Мощность определяется только током и сопротивлением.
Таким образом, комбинируя закон Ома с уравнением P=IVP=IV для электрической мощности, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (а не емкость или что-то еще), ток и напряжение. Это означает, что физической характеристикой цепи, которая определяет, сколько мощности она рассеивает, является ее сопротивление. Любые конденсаторы в цепи не рассеивают электроэнергию — напротив, конденсаторы либо накапливают электроэнергию, либо отдают ее обратно в цепь.
Чтобы понять, как связаны между собой напряжение, сопротивление, ток и мощность, рассмотрите рисунок 19.22, на котором показано колесо формул . Величины в центральной четверти окружности равны количествам в соответствующей внешней четверти окружности. Например, чтобы выразить потенциал V через мощность и ток, мы видим из круга формул, что V=P/IV=P/I.
Рисунок 19.22 Колесо формул показывает, как связаны вольты, сопротивление, ток и мощность. Количества во внутренних четвертях кругов равны количествам в соответствующих внешних четвертях кругов.
Рабочий пример
Найдите сопротивление лампочки
Типичная старая лампочка накаливания имела мощность 60 Вт. Если предположить, что на лампочку подается напряжение 120 В, какова сила тока через лампочку?
Стратегия
Нам известны напряжение и выходная мощность простой цепи, содержащей лампочку, поэтому мы можем использовать уравнение P=IVP=IV, чтобы найти ток I , протекающий через лампочку.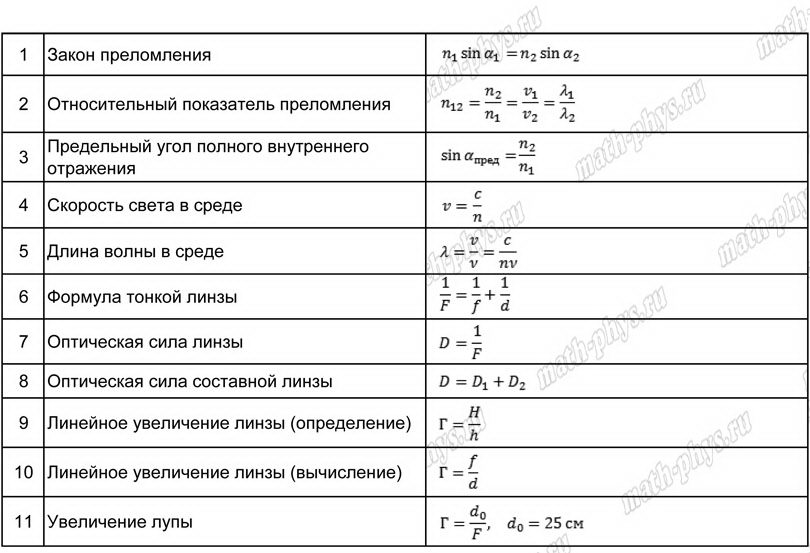
Решение
Решение P=IVP=IV для тока и вставка заданных значений напряжения и мощности дает
P=IVI=PV=60W120V=0,50A.P=IVI=PV=60W120V=0,50A.
19,51
Таким образом, через лампочку проходит полампера, когда на нее подается напряжение 120 В.
Обсуждение
Это значительный ток. Напомним, что бытовая электроэнергия является переменным, а не постоянным током, поэтому 120 В, подаваемые из бытовых розеток, представляют собой переменную, а не постоянную мощность. 120 В — это фактически усредненная по времени мощность, выдаваемая такими розетками. Таким образом, средний ток, проходящий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.
Рабочий пример
Грелки для ботинок
Чтобы согреть ботинки в холодные дни, вы решили вшить в стельку ботинок схему с резисторами. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите питать их от двух 9-вольтовых батарей (соединенных последовательно). Какое общее сопротивление вы должны оказывать на каждую стельку?
Какое общее сопротивление вы должны оказывать на каждую стельку?
Стратегия
Мы знаем желаемую мощность и напряжение (18 В, потому что у нас есть две 9-вольтовые батареи, соединенные последовательно), поэтому мы можем использовать уравнение P=V2/RP=V2/R, чтобы найти необходимое сопротивление.
Решение
Решая P=V2/RP=V2/R для сопротивления и подставляя данные напряжения и мощности, мы получаем
P=V2RR=V2P=(18V)210W=32Ω.P=V2RR=V2P=(18V )210 Вт=32 Ом.
19,52
Таким образом, общее сопротивление в каждой стельке должно быть 32 Ом.Ом.
Обсуждение
Давайте посмотрим, какой ток будет проходить по этой цепи. У нас есть 18 В, приложенные к сопротивлению 32 Ом, поэтому закон Ома дает
I=VR=18V32Ω=0,56A.I=VR=18V32Ω=0,56A.
19,53
Все аккумуляторы имеют маркировку, на которой указано, сколько заряда они могут обеспечить (в пересчете на ток, умноженный на время). Типичная щелочная батарея 9 В может обеспечить заряд 565 мА⋅чмА⋅ч.
(таким образом, две 9-вольтовые батареи обеспечивают 1130 мА⋅чмА⋅ч ), поэтому эта система отопления будет работать в течение времени
Типичная щелочная батарея 9 В может обеспечить заряд 565 мА⋅чмА⋅ч.
(таким образом, две 9-вольтовые батареи обеспечивают 1130 мА⋅чмА⋅ч ), поэтому эта система отопления будет работать в течение времени
t=1130×10−3A⋅ч0,56A=2,0ч.t=1130×10−3A⋅ч0. 56А=2,0ч.
19,54
Рабочий пример
Питание через ветвь цепи
Сопротивление каждого резистора в схеме ниже составляет 30 Ом. Какая мощность рассеивается на средней ветви цепи?
Стратегия
Средняя ветвь схемы содержит последовательно соединенные резисторы R3 и R5R3 и R5. Напряжение на этой ветви составляет 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем с помощью P=V2/RP=V2/R найдем мощность, рассеиваемую в ветви.
Решение
Эквивалентное сопротивление равно Rmiddle=R3+R5=30Ω+30Ω=60ΩRmiddle=R3+R5=30Ω+30Ω=60Ω . Мощность, рассеиваемая средней ветвью цепи, составляет
Pmiddle=V2Rmiddle=(12В)260Ом=2,4Вт. Pmiddle=V2Rmiddle=(12В)260Ом=2,4Вт.
Pmiddle=V2Rmiddle=(12В)260Ом=2,4Вт.
19,55
Обсуждение
Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, выдаваемой батареей. Во-первых, эквивалентное сопротивление левой ветви составляет
Rleft=11/R1+1/R2+R4=11/30Ω+1/30Ω+30Ω=45Ω.Rleft=11/R1+1/R2+R4=11/ 30 Ом + 1/30 Ом + 30 Ом = 45 Ом.
19,56
Мощность через левую ветвь
Pleft=V2Rleft=(12В)245Ом=3,2Вт.Pleft=V2Rleft=(12В)245Ом=3,2Вт.
19,57
Правая ветвь содержит только R6R6, поэтому эквивалентное сопротивление Rright=R6=30ΩRright=R6=30Ω . Мощность через правую ветвь составляет
Pright=V2Rright=(12В)230Ом=4,8Вт.Pright=V2Rright=(12В)230Ом=4,8Вт.
19,58
Общая мощность, рассеиваемая цепью, представляет собой сумму мощностей, рассеиваемых в каждой ветви.
P=Pleft+Pmiddle+Pright=2,4W+3,2W+4,8W=10,4WP=Pleft+Pmiddle+Pright=2,4W+3,2W+4,8W=10,4W
19,59
Мощность, обеспечиваемая аккумулятором
П=IV. П=IV.
П=IV.
19,60
где I — общий ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить I . Ответвления вносят токи
0,40А.
19,61
Суммарный ток равен
I=Iлевый+Iсредний+Iправый=0,2667A+0,20A+0,40A=0,87A.I=Iлевый+Iсредний+Iправый=0,2667A+0,20A+0,40A=0,87A.
19,62
и мощность, обеспечиваемая аккумулятором, равна
P=IV=(0,87A)(12В)=10,4Вт.P=IV=(0,87А)(12В)=10,4Вт.
19,63
Это та же мощность, которая рассеивается на резисторах цепи, что показывает, что в этой цепи сохраняется энергия.
Практические задачи
16.
Какова формула мощности, рассеиваемой на резисторе?
- Формула мощности, рассеиваемой на резисторе: P=IV.
 P=IV.
P=IV. - Формула для мощности, рассеиваемой на резисторе: P=VI.P=VI.
- Формула для мощности, рассеиваемой на резисторе: P = IV .
- Формула для мощности, рассеиваемой на резисторе: P = I 2 В .
17.
Какова формула для мощности, рассеиваемой резистором, с учетом его сопротивления и напряжения на нем?
- Формула для мощности, рассеиваемой на резисторе: P=RV2P=RV2
- Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
- Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
- Формула для мощности, рассеиваемой на резисторе: P=I2RP=I2R
Проверьте свое понимание
18.
Какие элементы схемы рассеивают мощность?
- конденсаторы
- катушки индуктивности
- идеальные переключатели
- резисторы
19.
Объясните словами уравнение для мощности, рассеиваемой на данном сопротивлении.
Электрическая мощность пропорциональна току через резистор, умноженному на квадрат напряжения на резисторе.
Электрическая мощность пропорциональна квадрату тока через резистор, умноженному на напряжение на резисторе.
Электрическая мощность пропорциональна току через резистор, деленному на напряжение на резисторе.
Электрическая мощность пропорциональна току через резистор, умноженному на напряжение на резисторе.

Сила (физика): определение, формула, единицы измерения, как найти (с примерами)
Бодибилдер и пятиклассник могли бы поднять все книги с полки на лестничный пролет, но это вряд ли выполнить задание за одинаковое время. Бодибилдер, вероятно, будет быстрее, потому что у него выше 9 баллов.0341 номинальная мощность , чем у пятиклассника.
Точно так же гоночный автомобиль с высокой мощностью лошадиных сил сможет проехать дальше намного быстрее, чем, ну, в общем, лошадь.
TL;DR (слишком длинно, не читал)
Мощность — это мера того, сколько работы выполняется за интервал времени.
Небольшое примечание о лошадиных силах: этот термин предназначен для сравнения мощности парового двигателя с мощностью лошади, так как двигатель мощностью 700 лошадиных сил может выполнять примерно в 700 раз больше работы, чем одна лошадь. Это восходит к тому времени, когда паровые двигатели были новыми, и один из самых выдающихся изобретателей, работавших над повышением их эффективности, Джеймс Уатт придумал этот термин, чтобы убедить среднего человека в их ценности.
Формулы для мощности
Существует два способа расчета мощности в зависимости от доступной информации. Кроме того, есть две единицы мощности, которые одинаково действительны.
1. Мощность в пересчете на работу и время:
P=\frac{W}{t}
Где работа Вт измеряется в ньютон-метрах (Нм), а время t измеряется в секундах (с).
2. Мощность по силе и скорости:
P=Fv
Где сила F в ньютонах (Н), а скорость v в метрах в секунду (м/с).
Эти уравнения не являются случайно эквивалентными. Второе уравнение может быть получено из первого следующим образом:
Обратите внимание, что работа это то же самое, что сила, умноженная на перемещение:
W=Fd
Подставьте это в первое уравнение мощности:
Затем, поскольку перемещение в любую единицу времени равно скорости (v = d/t), перепишите термины в конце как v , чтобы получить уравнение второй степени.
Единицы мощности
Единица мощности в системе СИ p обычно представлена как Вт (Вт) , названная в честь того же Джеймса Уатта, который разработал двигатели и сравнил их с лошадьми. На бирках лампочек и других бытовых приборов обычно указывается эта единица.
Однако вторая формула мощности приводит к другой единице измерения. Сила, умноженная на скорость, измеряется в ньютон-метрах в секунду (Нм/с). Затем, поскольку единица энергии джоуль также определяется как один ньютон-метр (Нм), первая часть этого может быть вместо этого переписана как джоуль, что приводит к второй единице мощности в системе СИ:0405 Джоулей в секунду (Дж/с).
Мощность может измеряться в ваттах (Вт) или джоулях в секунду (Дж/с).
Как стать могущественным
Принимая во внимание определение силы и два способа ее получения, можно найти несколько способов увеличить силу чего-либо та же работа выполняется быстрее (уменьшение t или увеличение t ). Мощный автомобиль силен и быстрые, а слабый ни то, ни другое. Чем легче и быстрее можно выполнить работу , тем мощнее сущность, выполняющая работу.
Мощный автомобиль силен и быстрые, а слабый ни то, ни другое. Чем легче и быстрее можно выполнить работу , тем мощнее сущность, выполняющая работу.
Как повысить мощность: сделать больше за более короткий период времени.
Это также означает, что очень мощная машина, скажем, мускулистый бодибилдер, все еще может не хватать мощности . Человек, который может поднять очень тяжелый груз, но только очень медленно, менее силен, чем тот, кто может поднять его быстро.
Точно так же очень быстрая машина или человек, который мало что делает, кто-то быстро вертится на месте, но никуда не двигается, на самом деле не обладает силой.
Пример расчета мощности
1. Усэйн Болт выработал около 25 Вт энергии в своем рекордном спринте на 100 м, который длился 9,58 секунды. Сколько работы он сделал?
Поскольку P и t даны, а W неизвестно, используйте первое уравнение:
P=\frac{W}{t}\implies 25=\frac{ Вт}{9. 58}\implies W=239.5\text{ Нм}
58}\implies W=239.5\text{ Нм}
2. С какой средней силой он отталкивался от земли во время бега?
Так как работа в Нм уже известна, как и перемещение в метрах, деление на длину пробега даст силу (иными словами, работа равно силе, умноженной на перемещение: W = F × d):
\frac{239,5}{100}=2,395\text{ N}
6 секунд, чтобы подняться по 3-метровой лестнице?
В этой задаче заданы перемещение и время, что позволяет быстро рассчитать скорость:
v=\frac{d}{t}=\frac{3}{6}=0,5\text{ м/с}
Во втором уравнении мощности есть скорость, но также и сила. Человек, взбегающий по лестнице, пытается противостоять силе тяжести. Итак, силу в этом случае можно найти, используя их массу и ускорение свободного падения, которое на Земле всегда равно 9,8 м/с 2 .
F_{грав}=мг=48\умножить на 9.8=470,4\text{ N}
Теперь сила и скорость вписываются во вторую формулу для мощности:
=Fv=470,4\times 0,5 = 235,2\text{ Дж/с}
Обратите внимание на решение оставить единицы измерения здесь как Дж / с, а не Вт является произвольным. Столь же приемлемым ответом является 235,2 Вт.
Столь же приемлемым ответом является 235,2 Вт.
4. Одна лошадиная сила в единицах СИ составляет около 746 Вт, что основано на нагрузке, которую здоровая лошадь могла бы нести в течение одной минуты. Какую работу за это время выполнила лошадь?
Единственный шаг перед подстановкой значений мощности и времени в первое уравнение — убедиться, что время указано в правильных единицах СИ (секунды), переписав одну минуту как 60 секунд. Тогда:
P=\frac{W}{t}\implies 746=\frac{W}{60}\implies W=44 670\text{ Нм}
Киловатты и электричество
Многие электроэнергетические компании взимают плату с клиентов исходя из их киловатт-часов использования. Чтобы понять значение этой общей единицы электрической мощности, начните с разбивки единиц.
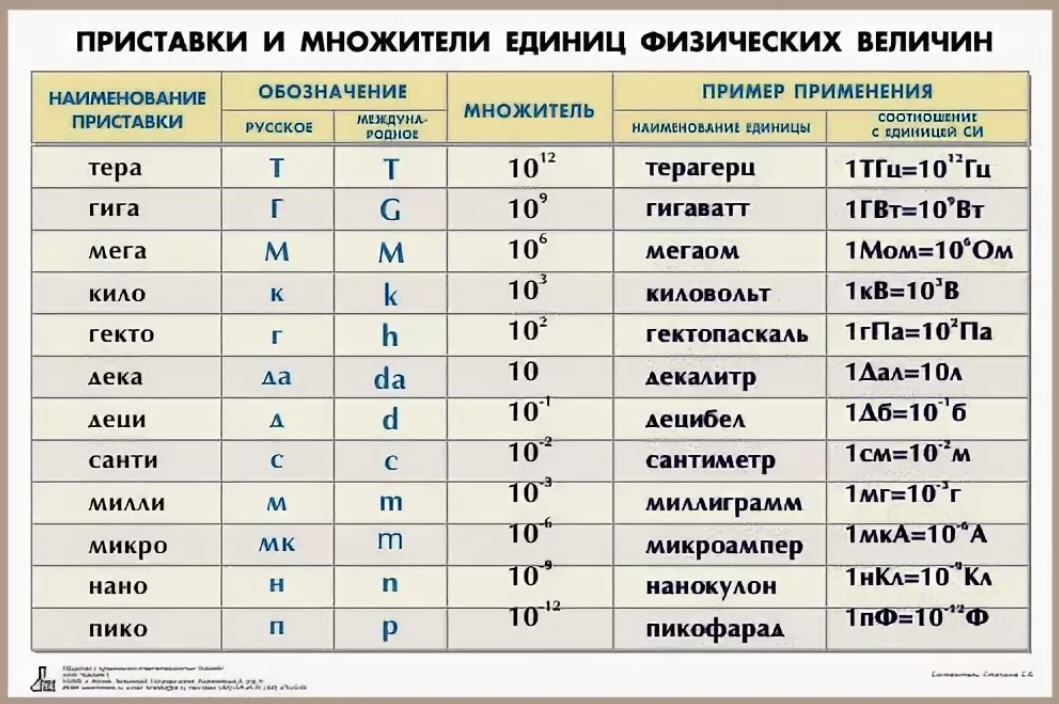
Префикс кило означает 1000, поэтому киловатт (кВт) равен 1000 Вт. Таким образом, киловатт-час (кВтч) — это количество киловатт, израсходованных за один час.
Чтобы подсчитать киловатт-часы, умножьте количество киловатт на использованные часы. Таким образом, если кто-то использует 100-ваттную лампочку в течение 10 часов, он израсходует в общей сложности 1000 ватт-часов или 1 кВтч электроэнергии.
Киловатт-час Примеры задач
1. Электроэнергетическая компания взимает 0,12 доллара за киловатт-час. Очень мощный пылесос мощностью 3000 Вт используется в течение 30 минут. Во сколько домовладельцам обходится это количество энергии?
3000 Вт = 3 кВт
30 минут = 0,5 часа
3\text{ кВт}\times 0,5\text{ ч}= 1,5\text{ кВтч}\text{ и }1,5\text{ кВтч}\times 0,12\text{доллар/кВтч} = \$0,18
2. Та же коммунальная служба начисляет домохозяйству 10 долларов за каждые 4 кВтч электроэнергии, возвращаемой в сеть. Солнце дает около 1000 Вт энергии на квадратный метр. Если солнечная батарея площадью два квадратных метра в доме собирает энергию в течение 8 часов, сколько денег она приносит?
Учитывая информацию в задаче, солнечная батарея должна быть в состоянии собрать 2000 Вт от Солнца, или 2 кВт.


 P=IV.
P=IV.
 За вас всё сделает умных программный алгоритм. Попробуйте использоваться описанные ниже приложения.
За вас всё сделает умных программный алгоритм. Попробуйте использоваться описанные ниже приложения. Попробуйте с этим приложением решить свою задачу, найдя готовый ответ в Интернете. Кроме этого Google Lens умеет различать и другие предметы на фото, такие как: насекомые, архитектурные объекты, текст на любом языке и переводит его, узнаёт товары на фото и помогает их найти. После решения задач по физике вам пригодится эта программа для поиска в сети любых предметов.
Попробуйте с этим приложением решить свою задачу, найдя готовый ответ в Интернете. Кроме этого Google Lens умеет различать и другие предметы на фото, такие как: насекомые, архитектурные объекты, текст на любом языке и переводит его, узнаёт товары на фото и помогает их найти. После решения задач по физике вам пригодится эта программа для поиска в сети любых предметов. Из них вы сможете выбрать подходящую категорию, чтобы поиск был более точным по вашему запросу. А справа в окне находится кнопка «Фильтры». С их помощью можно корректировать результаты поиска и выбирать по необходимости. Используйте сразу несколько разных приложений и фото, чтобы найти подходящий ответ на задачу по физике. Попробуйте применять разные поисковые системы, включая те, на которых нет возможности искать по картинке.
Из них вы сможете выбрать подходящую категорию, чтобы поиск был более точным по вашему запросу. А справа в окне находится кнопка «Фильтры». С их помощью можно корректировать результаты поиска и выбирать по необходимости. Используйте сразу несколько разных приложений и фото, чтобы найти подходящий ответ на задачу по физике. Попробуйте применять разные поисковые системы, включая те, на которых нет возможности искать по картинке. Удобный и простой интерфейс: в верхних вкладках выбирайте то, что вам нужно.
Удобный и простой интерфейс: в верхних вкладках выбирайте то, что вам нужно. Можно поступить другим способом: сначала узнать решение, а затем разобраться в самой задаче. А если вы не знаете, где его взять, то подсказываем — в Google Play. В данном приложении есть строка поиска, по которой можно найти всё, что угодно по предмету по фото. Введите название формулы в поисковой строке или часть условия задания. А приложение попытается вам помочь.
Можно поступить другим способом: сначала узнать решение, а затем разобраться в самой задаче. А если вы не знаете, где его взять, то подсказываем — в Google Play. В данном приложении есть строка поиска, по которой можно найти всё, что угодно по предмету по фото. Введите название формулы в поисковой строке или часть условия задания. А приложение попытается вам помочь. Встроены языки: русский, украинский, казахский, румынский, белорусский, молдавский и другие.
Встроены языки: русский, украинский, казахский, румынский, белорусский, молдавский и другие. Они удерживаются в круговом ускорителе сверхпроводящими дипольными магнитами 1232. Насколько силен магический …
Они удерживаются в круговом ускорителе сверхпроводящими дипольными магнитами 1232. Насколько силен магический … И наоборот, потенциал …
И наоборот, потенциал … Любой провод с током создает вокруг себя магнитное поле, но …
Любой провод с током создает вокруг себя магнитное поле, но … Объяснение: В двоичной системе каждая цифра может быть одним из двух значений: 0 и 1. Это две возможности («би» на латыни означает «дважды»). В десятичной системе …
Объяснение: В двоичной системе каждая цифра может быть одним из двух значений: 0 и 1. Это две возможности («би» на латыни означает «дважды»). В десятичной системе …
 Мы рассмотрели различные типы вентиляторов, что означает CFM, как найти массовый расход и познакомим вас с уравнением массового расхода и т. д. в одном месте.
Мы рассмотрели различные типы вентиляторов, что означает CFM, как найти массовый расход и познакомим вас с уравнением массового расхода и т. д. в одном месте. д. уродливые, шумные, но мощные и с оптимизированной производительностью. Они обычно используются в горячих местах и холодных помещениях. Поскольку они скрыты, они не служат никакой эстетической цели.
д. уродливые, шумные, но мощные и с оптимизированной производительностью. Они обычно используются в горячих местах и холодных помещениях. Поскольку они скрыты, они не служат никакой эстетической цели.


 Шпаргалка с формулами. Всё, что тебе нужно вызубрить, находится здесь.
Шпаргалка с формулами. Всё, что тебе нужно вызубрить, находится здесь. С 3 по 5 июня.
С 3 по 5 июня.
 Банк заданий ФИПИ.
Банк заданий ФИПИ.
 Занималась с детьми 7-9 классов, веду подготовку к олимпиадам (10 класс). Была куратором группы проекта от CERN Beamline4Schools.Работа «Исследование Черенковского излучения» вошла в ТОП-20 по миру.
Занималась с детьми 7-9 классов, веду подготовку к олимпиадам (10 класс). Была куратором группы проекта от CERN Beamline4Schools.Работа «Исследование Черенковского излучения» вошла в ТОП-20 по миру. Они соответствуют реальному опыту учеников.
Они соответствуют реальному опыту учеников.


 Я бы поставил 5, но он мог бы течь немного мягче.
Я бы поставил 5, но он мог бы течь немного мягче. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Для получения дополнительной информации см. политику конфиденциальности разработчика. По иронии судьбы, эти прекрасные «песни Земли» могут быть ответственны за распространение смертоносного электро в…
По иронии судьбы, эти прекрасные «песни Земли» могут быть ответственны за распространение смертоносного электро в… Какова скорость спутника на орбите?
Геостационарный о…
Какова скорость спутника на орбите?
Геостационарный о… ..
..
 Используйте этот простой инструмент для решения физической задачи, связанной со столкновением…
Используйте этот простой инструмент для решения физической задачи, связанной со столкновением… Йо-йо в космосе
Йо-йо в космосе  Жидкий азот используется в прозрачном стекле D…
Жидкий азот используется в прозрачном стекле D… ..
.. Это может…
Это может… ..
.. Система, использовавшаяся в классической древности
был слегка изменен в середине…
Система, использовавшаяся в классической древности
был слегка изменен в середине… ..
.. …
… Вы можете использовать этот инструмент для прохождения лучей света из одной среды в другую. Просто введите известные вам значения…
Вы можете использовать этот инструмент для прохождения лучей света из одной среды в другую. Просто введите известные вам значения… ..
.. ..
.. ..
..

 3).
3). 4. Спутник на круговой орбите.
4. Спутник на круговой орбите. Также вы можете воспользоваться другими материалами из данного раздела.
Также вы можете воспользоваться другими материалами из данного раздела. На широте Москвы g = 9,81523 м/с2. Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с2 или даже 10 м/с2.
На широте Москвы g = 9,81523 м/с2. Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с2 или даже 10 м/с2.
 е. тело достигает высшей точки подъема. Зависимость координаты y от времени t выражается формулой
y=υ0t-gt22.
е. тело достигает высшей точки подъема. Зависимость координаты y от времени t выражается формулой
y=υ0t-gt22.
 На рис. 1.5.2 изображен вектор начальной скорости υ→0 тела и его проекции на координатные оси.
На рис. 1.5.2 изображен вектор начальной скорости υ→0 тела и его проекции на координатные оси. В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела.
В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела.

 Какова единица ускорения свободного падения?
Какова единица ускорения свободного падения?  По состоянию на 8 апреля 2022 г.
По состоянию на 8 апреля 2022 г. Прежде чем раскрыть свой парашют, Феликс преодолел звуковой барьер, а также установил многочисленные мировые рекорды. В этой статье мы обсудим, что заставило Феликса достичь такой скорости — гравитационное ускорение: его значение, формула, единицы измерения и расчет, — а также рассмотрим некоторые примеры гравитационного ускорения.
Прежде чем раскрыть свой парашют, Феликс преодолел звуковой барьер, а также установил многочисленные мировые рекорды. В этой статье мы обсудим, что заставило Феликса достичь такой скорости — гравитационное ускорение: его значение, формула, единицы измерения и расчет, — а также рассмотрим некоторые примеры гравитационного ускорения.
 2}\\$$ 92\,kg}}\) , а \(r\) — расстояние между центрами масс тел. Как видим, сила тяжести прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их центрами масс. Когда мы говорим о такой планете, как Земля, притягивающей обычный объект, мы часто ссылаемся на гравитационную силу как на вес этого объекта.
2}\\$$ 92\,kg}}\) , а \(r\) — расстояние между центрами масс тел. Как видим, сила тяжести прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их центрами масс. Когда мы говорим о такой планете, как Земля, притягивающей обычный объект, мы часто ссылаемся на гравитационную силу как на вес этого объекта. Это настолько полезно, что мы определяем физическую величину, относящуюся именно к ней: напряженность гравитационного поля.
Это настолько полезно, что мы определяем физическую величину, относящуюся именно к ней: напряженность гравитационного поля. Однако здесь есть оговорка. Земля не идеально сферическая! Его радиус меняется в зависимости от того, где мы находимся. Из-за формы Земли значение гравитационного ускорения на полюсах отличается от на экваторе. В то время как сила тяжести на экваторе составляет около \(92.}\end{align*}$$
Однако здесь есть оговорка. Земля не идеально сферическая! Его радиус меняется в зависимости от того, где мы находимся. Из-за формы Земли значение гравитационного ускорения на полюсах отличается от на экваторе. В то время как сила тяжести на экваторе составляет около \(92.}\end{align*}$$
 1
1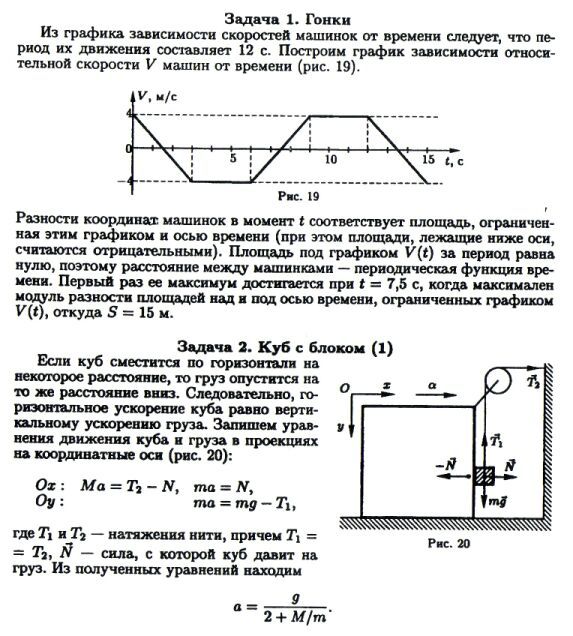 4
4 Работа и мощность тока
Работа и мощность тока 1
1 1
1 3
3 Ю.Замятнина для 7, 8 и 9 класса можно приобрести в магазине МФТИ (1 этаж) и в интернет магазинах Физматкнига и Карандаш
Ю.Замятнина для 7, 8 и 9 класса можно приобрести в магазине МФТИ (1 этаж) и в интернет магазинах Физматкнига и Карандаш Калькуляторы запрещены»
Калькуляторы запрещены»  Первым в этой серии является Американский пригласительный экзамен по математике (AIME), за которым следуют Математическая олимпиада США и Юношеская математическая олимпиада (USAMO и USAJMO). Лучшие участники из USA(J)MO приглашаются на программу математической олимпиады летом после соревнований. Затем участники программы математической олимпиады имеют право быть отобранными следующим летом в состав команды из шести человек, которая будет представлять Соединенные Штаты Америки в ИМО».
Первым в этой серии является Американский пригласительный экзамен по математике (AIME), за которым следуют Математическая олимпиада США и Юношеская математическая олимпиада (USAMO и USAJMO). Лучшие участники из USA(J)MO приглашаются на программу математической олимпиады летом после соревнований. Затем участники программы математической олимпиады имеют право быть отобранными следующим летом в состав команды из шести человек, которая будет представлять Соединенные Штаты Америки в ИМО». 
 Занятия на олимпиаде по физике готовят учащихся к участию в квалификационных экзаменах US Physics Bowl и олимпиады по физике в США.
Занятия на олимпиаде по физике готовят учащихся к участию в квалификационных экзаменах US Physics Bowl и олимпиады по физике в США. Мы уникальным образом интегрировали учебную программу AP Physics с экзаменом олимпиады по физике, чтобы добиться наилучшего взаимодействия в обучении и усилиях.
Мы уникальным образом интегрировали учебную программу AP Physics с экзаменом олимпиады по физике, чтобы добиться наилучшего взаимодействия в обучении и усилиях.
 Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
 Мощность:
Мощность: Это приложение поддерживает английский, вьетнамский, китайский (традиционный/упрощенный), турецкий, испанский, немецкий, французский, португальский, русский, индонезийский, персидский, итальянский, хинди и арабский язык. Скоро появятся новые языки.
Это приложение поддерживает английский, вьетнамский, китайский (традиционный/упрощенный), турецкий, испанский, немецкий, французский, португальский, русский, индонезийский, персидский, итальянский, хинди и арабский язык. Скоро появятся новые языки.  поддержка
поддержка

 Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:
Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как: {2}x(t)=0\)
{2}x(t)=0\) Необходимо определить, каковы период и частота колебаний шарика.
Необходимо определить, каковы период и частота колебаний шарика.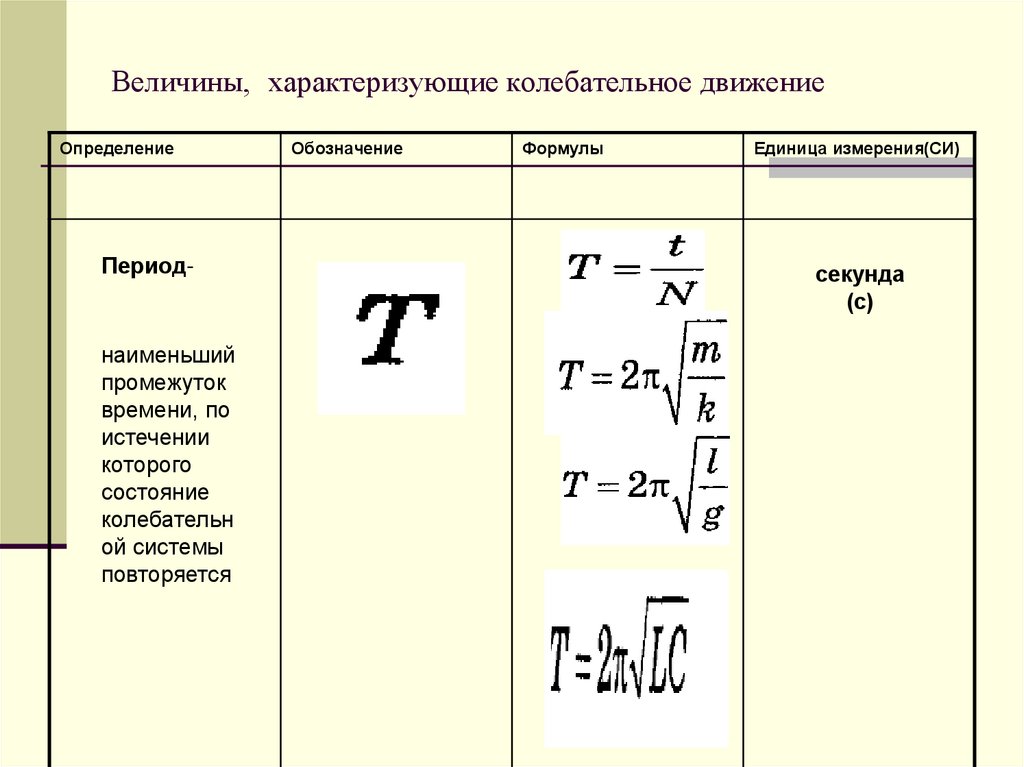 {2}}\approx 0.16\)
{2}}\approx 0.16\)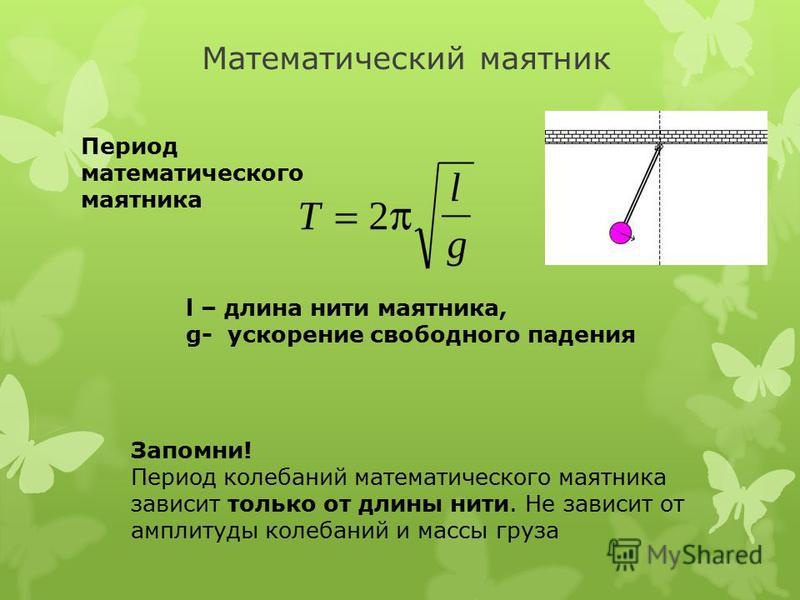
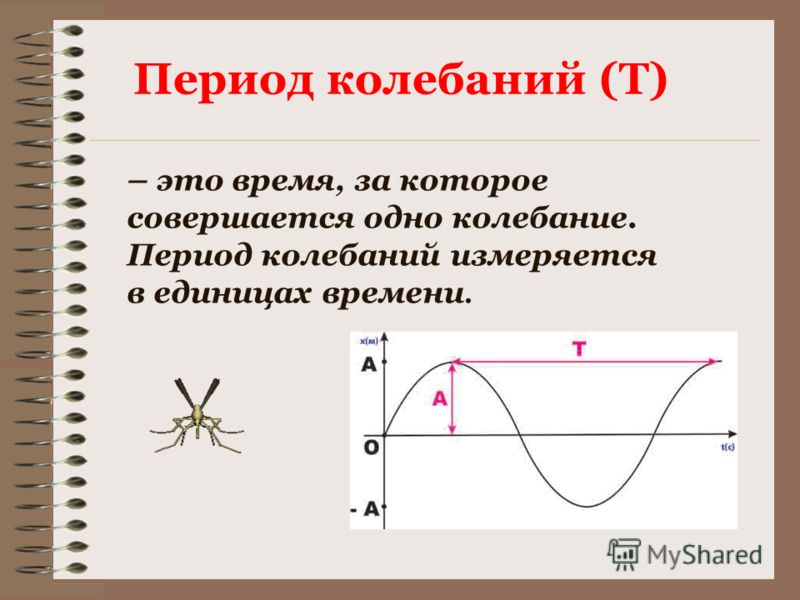 {-6}$ нс (период рентгеновского излучения) и до 250 млн. лет (время обращения Солнечной Системы вокруг центра нашей галактики).
{-6}$ нс (период рентгеновского излучения) и до 250 млн. лет (время обращения Солнечной Системы вокруг центра нашей галактики). Время, за которое колебательная система совершает полный цикл, называется ее период .
Время, за которое колебательная система совершает полный цикл, называется ее период .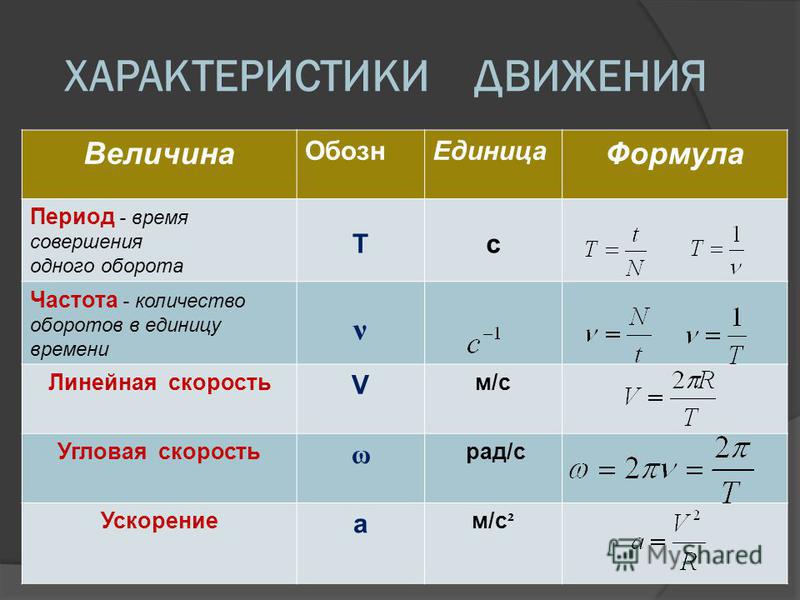



 Однако, поскольку волна распространяется через среду или пространство, колебания растягиваются вдоль направления движения. Длина волны определяется как поперечное расстояние между любыми двумя одинаковыми точками цикла колебаний, обычно точками максимальной амплитуды по одну сторону от положения равновесия.
Однако, поскольку волна распространяется через среду или пространство, колебания растягиваются вдоль направления движения. Длина волны определяется как поперечное расстояние между любыми двумя одинаковыми точками цикла колебаний, обычно точками максимальной амплитуды по одну сторону от положения равновесия.
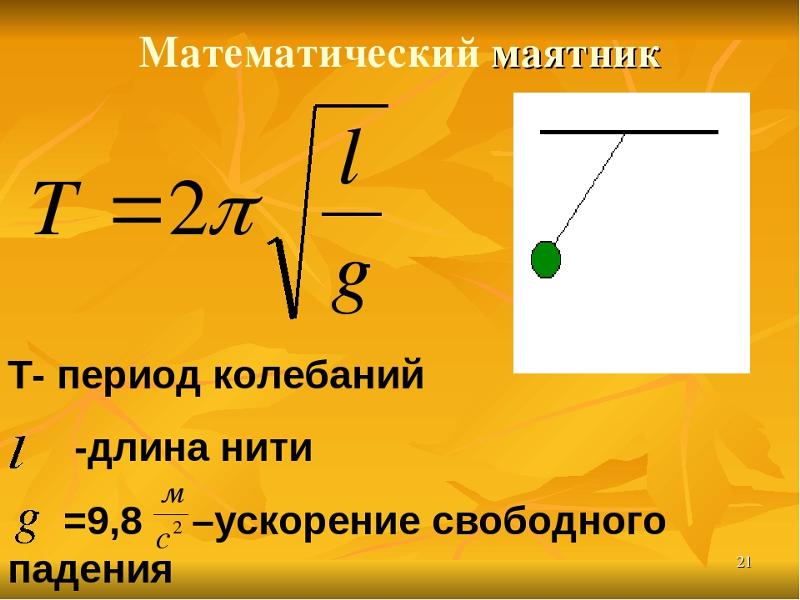
 Эти вопросы связаны со свойством, называемым периодом маятника.
Эти вопросы связаны со свойством, называемым периодом маятника. Теперь, когда мы понимаем, что мы подразумеваем под маятником, нам нужна еще одна информация, а именно, что мы подразумеваем под периодом.
Теперь, когда мы понимаем, что мы подразумеваем под маятником, нам нужна еще одна информация, а именно, что мы подразумеваем под периодом.
 То же самое испытывает груз нашего маятника: сила, действующая на груз 1, который в два раза массивнее, чем на груз 2, в два раза больше, но и сам груз в два раза тяжелее, чем груз 2. Таким образом, груз 1 в два раза так же трудно переместить, как и боб 2, поэтому ускорение обоих бобов будет одинаковым (опять же на a=F/m). Следовательно, период маятника не зависит от массы груза.
То же самое испытывает груз нашего маятника: сила, действующая на груз 1, который в два раза массивнее, чем на груз 2, в два раза больше, но и сам груз в два раза тяжелее, чем груз 2. Таким образом, груз 1 в два раза так же трудно переместить, как и боб 2, поэтому ускорение обоих бобов будет одинаковым (опять же на a=F/m). Следовательно, период маятника не зависит от массы груза.
 Это примерно — мг θ из-за малой амплитуды маятника. Итак, ускорение боба составляет а=F/m=-gθ.
Это примерно — мг θ из-за малой амплитуды маятника. Итак, ускорение боба составляет а=F/m=-gθ.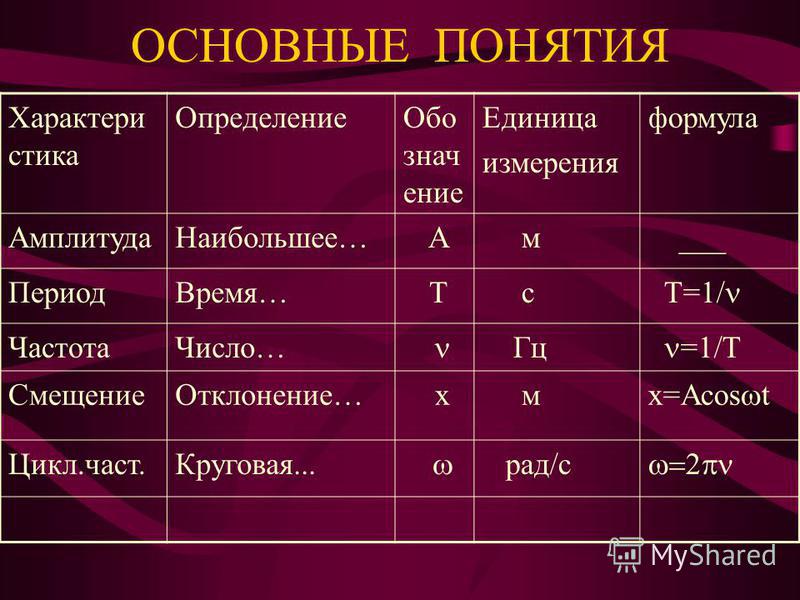 е. с небольшой амплитудой?
е. с небольшой амплитудой?

 Записывается это формула как V = h * S, при этом S является произведением сторон прямоугольника.
Записывается это формула как V = h * S, при этом S является произведением сторон прямоугольника. Используя законы умножения, чтобы узнать, сколько же поместится в середине фигуры таких площадей, нужно основание умножить на высоту. То есть и получается доказываемая формула: V = S * h.
Используя законы умножения, чтобы узнать, сколько же поместится в середине фигуры таких площадей, нужно основание умножить на высоту. То есть и получается доказываемая формула: V = S * h. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.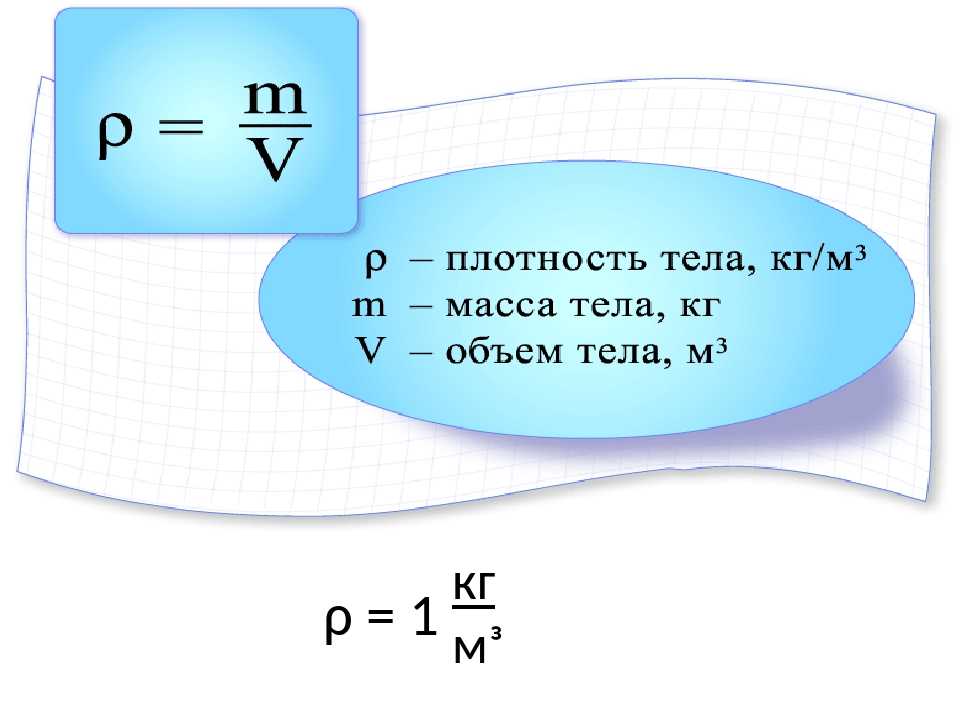




 Масса пустой канистры 1 кг, заполненной – 13 кг. Чему равна плотность жидкости.
Масса пустой канистры 1 кг, заполненной – 13 кг. Чему равна плотность жидкости. Примерно вот такую картофелину я вам принесла на урок. Давайте, определим ее объем. Вот только в мензурку, да и в отливной стакан она не войдет. Ваши предложения?
Примерно вот такую картофелину я вам принесла на урок. Давайте, определим ее объем. Вот только в мензурку, да и в отливной стакан она не войдет. Ваши предложения? Определите его объем, если плотность дуба 800 кг/м3.
Определите его объем, если плотность дуба 800 кг/м3. Этот калькулятор также может определить либо плотность, либо массу жидкости, если известны другие переменные.
Этот калькулятор также может определить либо плотность, либо массу жидкости, если известны другие переменные.
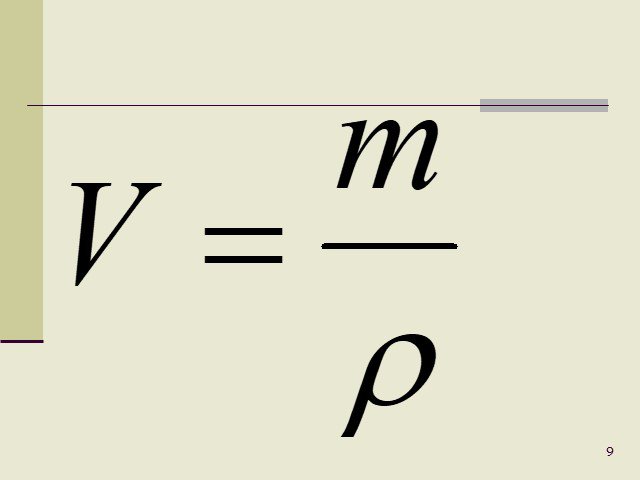
 Это всего лишь оценка, но она будет хорошей. Уравнение довольно простое. Количество атомов ЛЮБОГО вещества в объеме:
Это всего лишь оценка, но она будет хорошей. Уравнение довольно простое. Количество атомов ЛЮБОГО вещества в объеме:


 А вот значения гравитационного потенциала можно изменить на любую постоянную величину — градиент останется тем же. В те времена это выглядело тривиальным следствием математического формализма, не имеющим отношения к реальной физике.
А вот значения гравитационного потенциала можно изменить на любую постоянную величину — градиент останется тем же. В те времена это выглядело тривиальным следствием математического формализма, не имеющим отношения к реальной физике. Если такое допустить, теория рассыпется, потеряет самосогласованность. А в теории с правильно подобранной калибровочной симметрией эта проблема не возникает, лишние поляризации оттуда уходят. Аналогичная ситуация имеет место и в теории глюонного поля, переносящего сильные взаимодействия, и в теории слабого взаимодействия, переносящего промежуточные векторные бозоны. Все эти частицы имеют единичный спин, и у всех возникают неприемлемые состояния, которые не исчезают сами по себе, однако изгоняются калибровочной симметрией».
Если такое допустить, теория рассыпется, потеряет самосогласованность. А в теории с правильно подобранной калибровочной симметрией эта проблема не возникает, лишние поляризации оттуда уходят. Аналогичная ситуация имеет место и в теории глюонного поля, переносящего сильные взаимодействия, и в теории слабого взаимодействия, переносящего промежуточные векторные бозоны. Все эти частицы имеют единичный спин, и у всех возникают неприемлемые состояния, которые не исчезают сами по себе, однако изгоняются калибровочной симметрией». Однако они становятся неоднозначными, поскольку одному и тому же полю могут соответствовать разные потенциалы. Например, к векторному потенциалу можно добавить любой постоянный вектор, а к скалярному — любое число.
Однако они становятся неоднозначными, поскольку одному и тому же полю могут соответствовать разные потенциалы. Например, к векторному потенциалу можно добавить любой постоянный вектор, а к скалярному — любое число. В квантовой электродинамике такая инвариантность, в соответствии с теоремой Нётер, влечет за собой закон сохранения электрического заряда. Таким образом, калибровочная инвариантность, несмотря на свой вроде бы формальный характер, открывает возможность заключений, имеющих прямой физический смысл!
В квантовой электродинамике такая инвариантность, в соответствии с теоремой Нётер, влечет за собой закон сохранения электрического заряда. Таким образом, калибровочная инвариантность, несмотря на свой вроде бы формальный характер, открывает возможность заключений, имеющих прямой физический смысл! Калибровочная инвариантность — и как идея, и как термин — пришла в теоретическую физику иным путем. Чтобы понять, как это произошло, обратимся к работам Вейля.
Калибровочная инвариантность — и как идея, и как термин — пришла в теоретическую физику иным путем. Чтобы понять, как это произошло, обратимся к работам Вейля.
 Калибровочные преобразования на первый взгляд кажутся абстрактными, но они приводят к существованию различных калибровочных полей, связанных с математическим понятием групп симметрии. В группе U(1) только один фазовый угол, в Стандартной модели ему соответствует один бозон (электромагнитного взаимодействия – фотон), группа SU(2) имеет три фазовых угла (в СМ – три бозона слабого взаимодействия), SU(3) – восемь фазовых углов (восемь бозонов сильного взаимодействия — глюонов).
Калибровочные преобразования на первый взгляд кажутся абстрактными, но они приводят к существованию различных калибровочных полей, связанных с математическим понятием групп симметрии. В группе U(1) только один фазовый угол, в Стандартной модели ему соответствует один бозон (электромагнитного взаимодействия – фотон), группа SU(2) имеет три фазовых угла (в СМ – три бозона слабого взаимодействия), SU(3) – восемь фазовых углов (восемь бозонов сильного взаимодействия — глюонов).
 Если частица заряжена и, следовательно, подчиняется действию электромагнитного поля, возможность произвольной смены фазового множителя обеспечивается соответствующим изменением электромагнитных потенциалов. Инвариантность уравнения движения частицы относительно выбора фазы волновой функции автоматически приводит к калибровочной инвариантности полевых уравнений.
Если частица заряжена и, следовательно, подчиняется действию электромагнитного поля, возможность произвольной смены фазового множителя обеспечивается соответствующим изменением электромагнитных потенциалов. Инвариантность уравнения движения частицы относительно выбора фазы волновой функции автоматически приводит к калибровочной инвариантности полевых уравнений. Объединенная калибровочная теория слабых и электромагнитных взаимодействий была развита Стивеном Вайнбергом и Абдусом Саламом во второй половине 1960-х годов и окончательно доработана лишь в начале 1970-х. А потом настала очередь и внутриядерных сил. Как раз тогда экспериментаторы показали, что на очень малых дистанциях взаимодействие между кварками не растет, а слабеет. Это явление назвали асимптотической свободой, и поначалу оно не находило разумного объяснения. Однако трое физиков-теоретиков — Дэвид Гросс, Фрэнк Вильчек и Дэвид Политцер — вскоре показали, что в калибровочных моделях глюонных полей асимптотическая свобода возникает естественным образом. Отсюда было недалеко до объединения теорий электрослабых и сильных взаимодействий в единую теоретическую конструкцию, которую назвали Стандартной моделью».
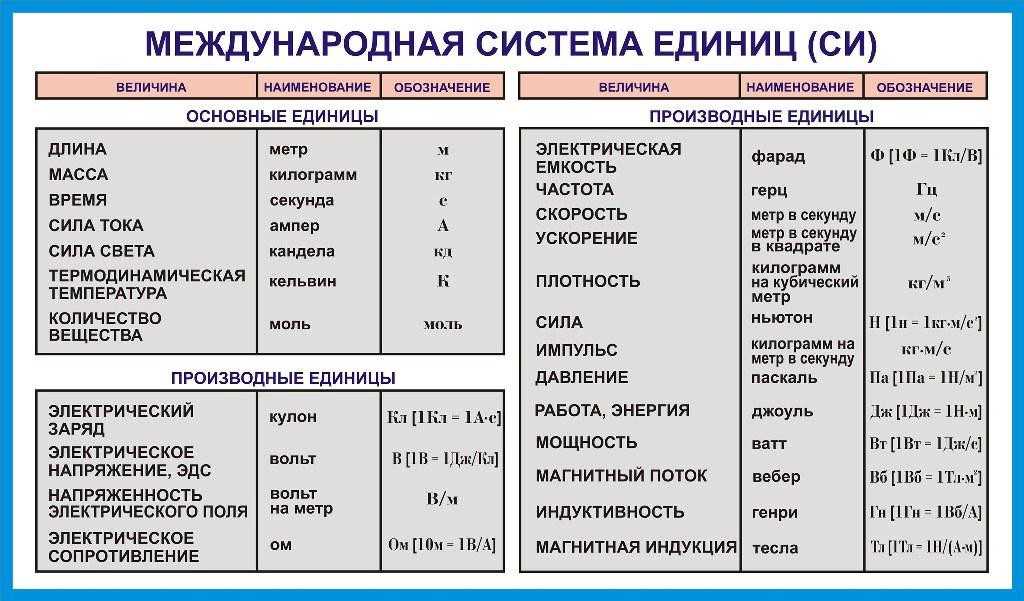
Объединенная калибровочная теория слабых и электромагнитных взаимодействий была развита Стивеном Вайнбергом и Абдусом Саламом во второй половине 1960-х годов и окончательно доработана лишь в начале 1970-х. А потом настала очередь и внутриядерных сил. Как раз тогда экспериментаторы показали, что на очень малых дистанциях взаимодействие между кварками не растет, а слабеет. Это явление назвали асимптотической свободой, и поначалу оно не находило разумного объяснения. Однако трое физиков-теоретиков — Дэвид Гросс, Фрэнк Вильчек и Дэвид Политцер — вскоре показали, что в калибровочных моделях глюонных полей асимптотическая свобода возникает естественным образом. Отсюда было недалеко до объединения теорий электрослабых и сильных взаимодействий в единую теоретическую конструкцию, которую назвали Стандартной моделью». Чтобы сделать их более удобными для пользователей, а также более простыми в использовании и запоминании, мы часто используем обозначения/символы для представления этих физических величин. Эти обозначения/символы, которые мы используем для представления физических величин при решении связанных с ними задач или для других целей, являются символами.
Чтобы сделать их более удобными для пользователей, а также более простыми в использовании и запоминании, мы часто используем обозначения/символы для представления этих физических величин. Эти обозначения/символы, которые мы используем для представления физических величин при решении связанных с ними задач или для других целей, являются символами. Иногда символ может быть первой буквой физических величин, которые они представляют, например «d», что означает расстояние. В других случаях они могут быть совершенно не связаны с названием физических величин, например, c символизирует скорость света. Они также могут быть в виде греческих символов, таких как λ, что означает длину волны.
Иногда символ может быть первой буквой физических величин, которые они представляют, например «d», что означает расстояние. В других случаях они могут быть совершенно не связаны с названием физических величин, например, c символизирует скорость света. Они также могут быть в виде греческих символов, таких как λ, что означает длину волны.
 0003
0003 m/s
m/s м2/с
м2/с Номер
Номер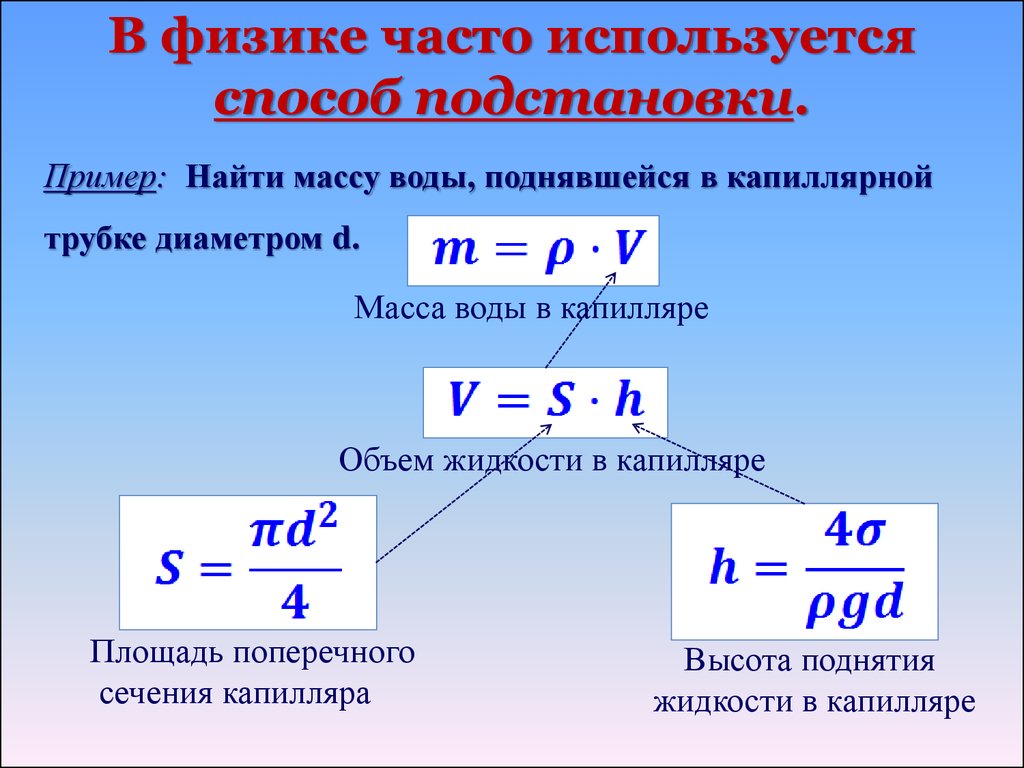 K
K 27 SI
27 SI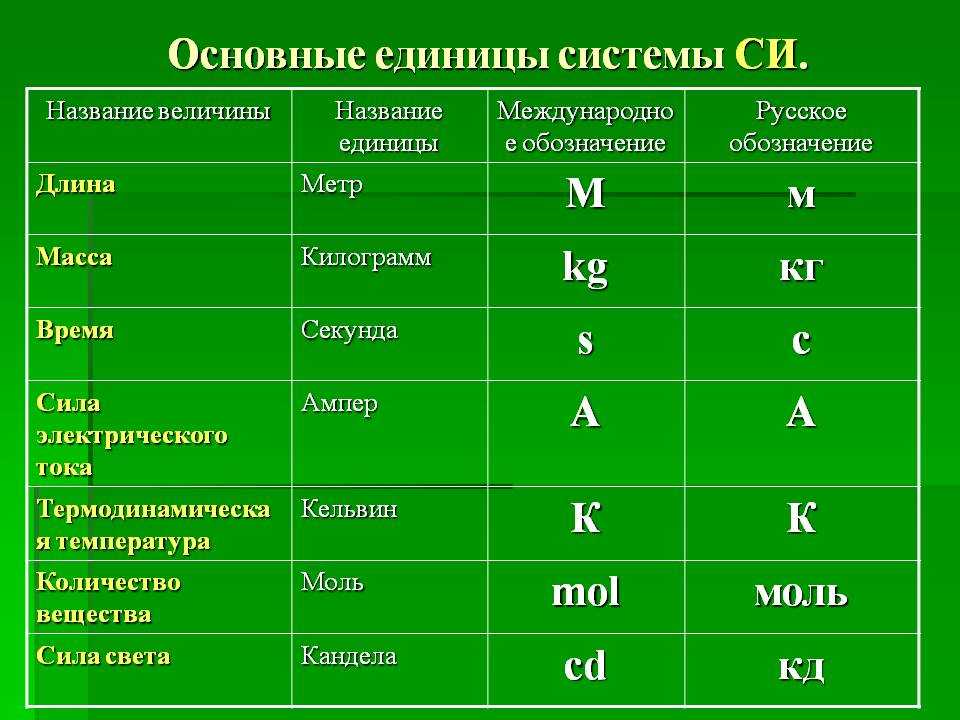 C)
C)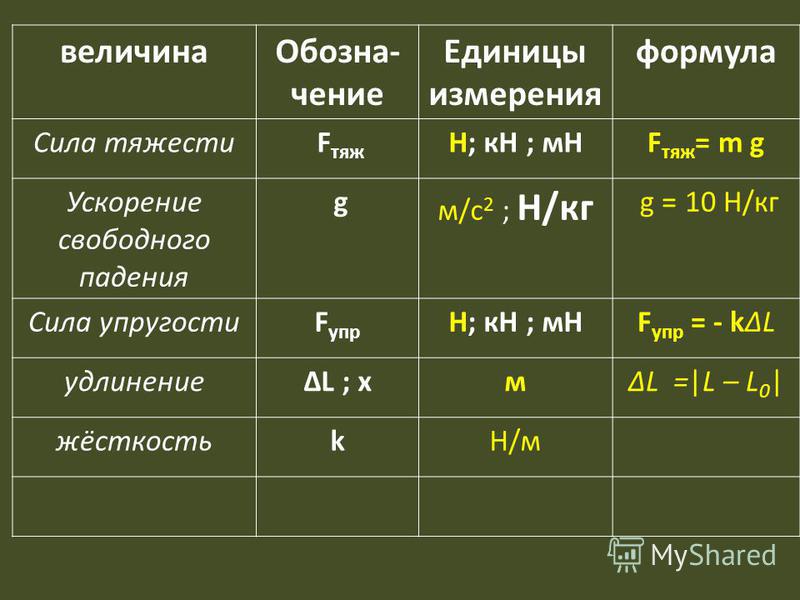 Обозначения упрощают представление величин.
Обозначения упрощают представление величин.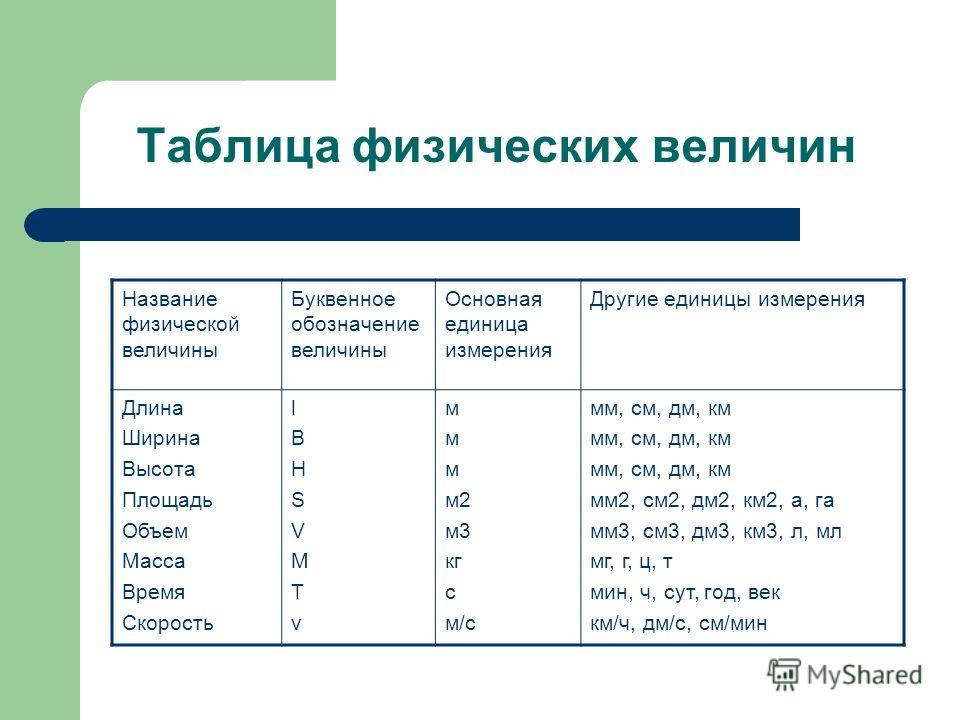
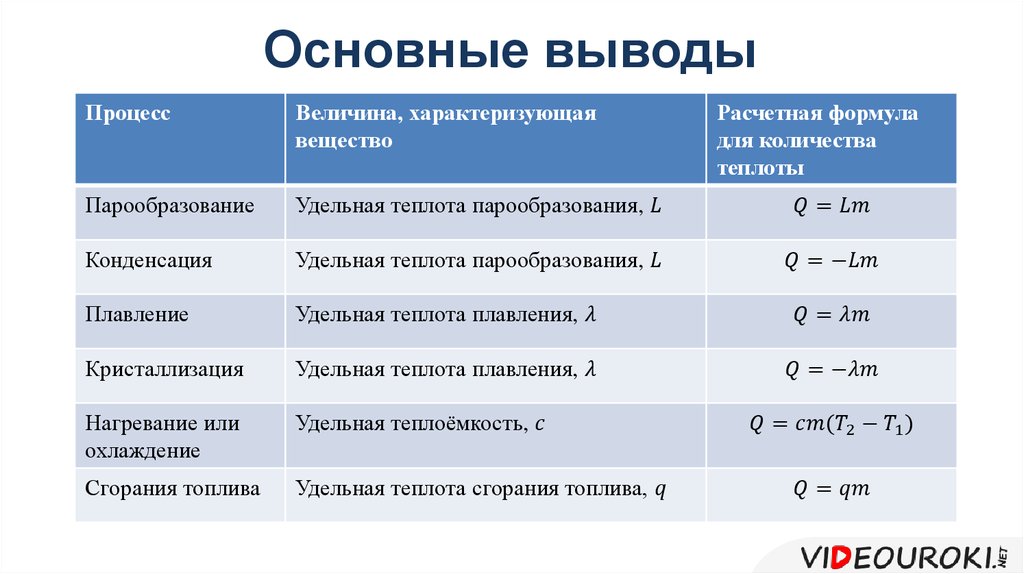

 В отличие от молекулярно-кинетической теории, в термодинамике не учитывается внутреннее строение веществ и микропараметры.
В отличие от молекулярно-кинетической теории, в термодинамике не учитывается внутреннее строение веществ и микропараметры. Для нагревания 1кг стекла или 1кг воды требуется различное количество энергии. Удельная теплоемкость — известная, уже вычисленная для всех веществ величина, значение смотреть в физических таблицах.
Для нагревания 1кг стекла или 1кг воды требуется различное количество энергии. Удельная теплоемкость — известная, уже вычисленная для всех веществ величина, значение смотреть в физических таблицах.
 Давайте подробнее рассмотрим концепцию электрического заряда,
Давайте подробнее рассмотрим концепцию электрического заряда,
