Формула в физике периода: Физика: формула периода колебаний

формула расчета, как найти для физического маятника

Содержание:

• Что такое колебательный процесс 
• Определение периода колебаний, формула
  • Как найти период для физического маятника
• Примеры решений

Содержание

• Что такое колебательный процесс 
• Определение периода колебаний, формула
  • Как найти период для физического маятника
• Примеры решений

Что такое колебательный процесс 

Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.

Систему, совершающую колебания, называют колебательной системой или осциллятором.

Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.

Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.

При механических колебаниях, которые относят к категории вынужденных:

\(F=F_{0}\cos \cot\)

Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.

Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.

Определение периода колебаний, формула

Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:

\(x(t)=A\times \cos \left(\omega _{0}t+\phi _{0} \right)\)

Где \(x(t)\) является отклонением колеблющейся физической величины от равновесного значения;

А представляет собой амплитуду гармонических колебаний;

\(\omega _{0}\) равно циклической или круговой частоте колебаний;

\(\phi _{0}\) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;

\(cp(t)=(co_{0}t+cp_{0})\) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.

В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:

\(\cos \left(\alpha +2\pi \right)=\cos \alpha,\)

то х остается без изменений при фазе колебаний, получающей приращение в $$2\pi$$

Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.

В этом случае фаза будет увеличена на \(2\pi:\)

\(\omega _{0}(t+T)+\phi _{0}=\left(\omega _{0}t+\phi _{0} \right)+2\pi\)

Из данного равенства можно вычислить период колебаний:

\(T=\frac{2\pi }{\omega _{0}}\)

Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:

\(v=\frac{\omega _{0}}{2\pi}\)

 

На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.

{2}x(t)=0\)

Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:

\(\omega =\sqrt{\frac{mgl}{J}}\)

В таком случае для расчета периода колебаний математического маятника будет использоваться формула:

\(T =\frac{2\pi }{\omega }=2\pi \sqrt{\frac{J}{mgl}}\)

Исходя из расчетов, можно сделать следующие выводы:

1. Период пружинного маятника \(T =2\pi \sqrt{\frac{m}{k}}\)
2. Период математического маятника \(T =2\pi \sqrt{\frac{L}{g}}\)
3. Период крутильного маятника \(T =2\pi \sqrt{\frac{I}{K}}\)

В приведенных формулах:

• T — период физического маятника;
• J — момент силы маятника относительно оси вращения;
• l — расстояние от оси вращения до центра масс;
• m — масса маятника;
• g=9.8 — ускорение свободного падения.

Примеры решений

Задача № 1

Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.

Решение

\(T =\frac{t}{N}=\frac{120}{60}=2\)

\(V=\frac{1}{T}=\frac{1}{2}=0.5\)

Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.

Задача № 2

Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.

 

Решение

А = 20

Т = 0,8

\(V=\frac{1}{T}=\frac{1}{0,8}=1,25\)

\(x(t)=A\sin 2\pi Vt=0.2\sin 2\pi \times 1.25t=0.2\sin 2.5\pi t\)

Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: \(x(t)=0.2\sin 2.5\pi t\)

Задача № 3

Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны.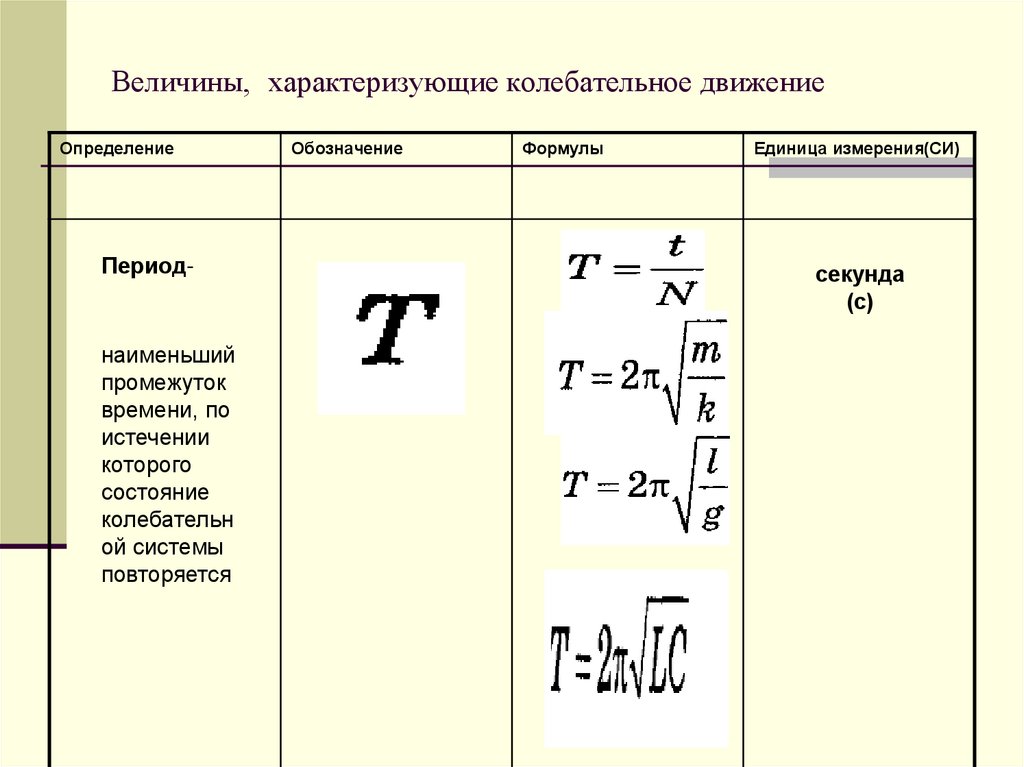 {2}}\approx 0.16\)

Ответ: длина математического маятника примерно составляет 0,16 метра.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Период колебаний – формула определения, расчет

4.8

Средняя оценка: 4.8

Всего получено оценок: 123.

4.8

Средняя оценка: 4.8

Всего получено оценок: 123.

Важнейшим параметром, требуемым при расчетах колебательных и волновых процессов, является период колебаний. Он входит во многие формулы, и является одним из базовых. Рассмотрим это понятие.

Колебательный процесс

Одними из самых частых процессов в Природе являются колебательные. Как правило, любой колебательный процесс состоит в том, что некоторый параметр рассматриваемой системы изменяет свое значение, периодически отклоняясь то в одну, то в другую сторону от некоторого положения равновесия.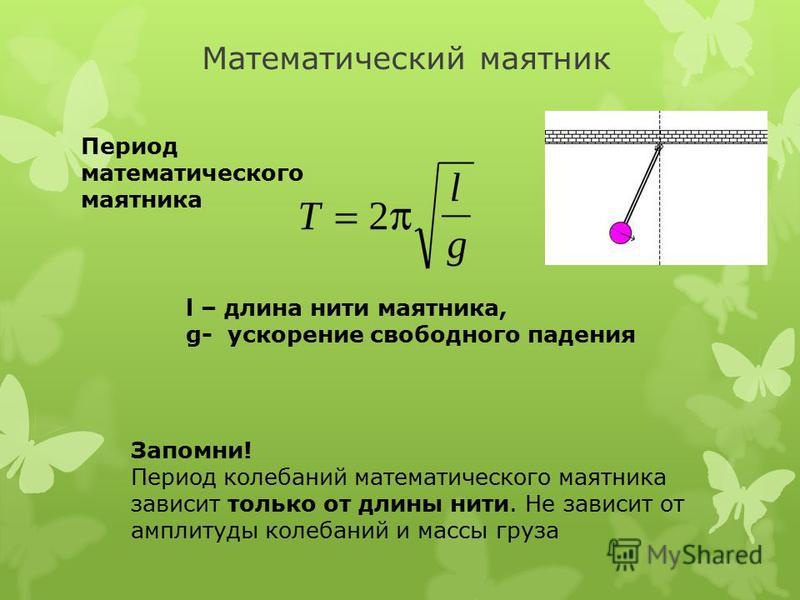

Рис. 1. Колебательные процессы в природе.

Колебания маятника

Простейший пример колебательного процесса – маятник, легкая нить с грузом на конце. Отклоним его от равновесия в крайнее положение, а потом отпустим (чтобы уменьшить влияние трения, отклонение должно быть намного меньше длины нити).

Груз, начнет движение к противоположной крайней точке. Здесь его скорость упадет до нуля, и он качнется в обратную сторону до начального положения. (Реальный маятник имеет потери на трение, и немного не дойдет до начальной точки, но этим небольшим отклонением можно пренебречь).

Рис. 2. Колебания маятника.

Полное движение, которое начинается от начальной точки и продолжается до ближайшего возвращение в нее, называется колебанием.

Период колебаний

Если сравнить несколько последовательных колебаний, то можно заметить, что они очень похожи. При этом каждое колебание длится одно и то же время.

Время за которое происходит одно колебание, называется периодом колебаний.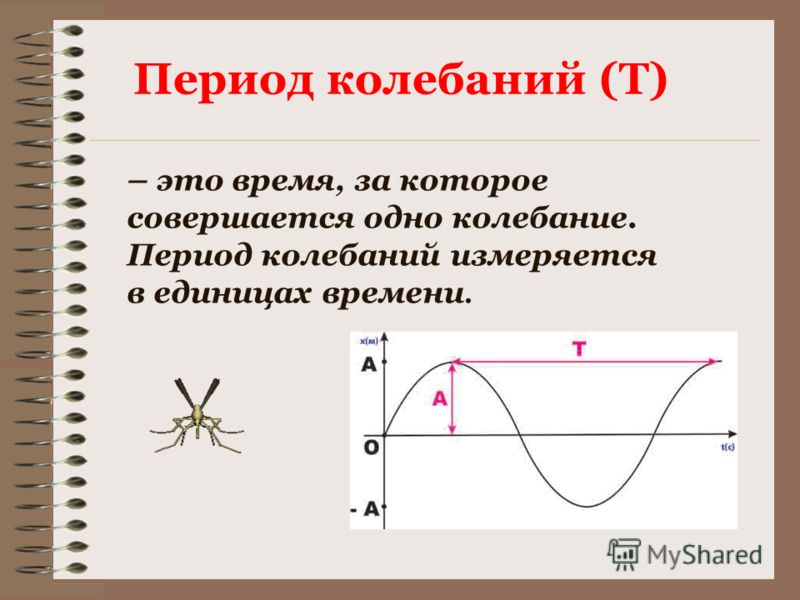 {-6}$ нс (период рентгеновского излучения) и до 250 млн. лет (время обращения Солнечной Системы вокруг центра нашей галактики).

Что мы узнали?

Одно колебание маятника (или другого колеблющегося объекта) – это движение от точки максимального отклонения и до возвращения в эту точку. Время, за которое совершается одно колебание, называется периодом колебаний.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Егор Князев

  5/5

Оценка доклада

4.8

Средняя оценка: 4.8

Всего получено оценок: 123.

---

А какая ваша оценка?

Как рассчитать период движения в физике

Мир природы полон примеров периодического движения, от орбит планет вокруг Солнца до электромагнитных колебаний фотонов и биения нашего собственного сердца.

Все эти колебания связаны с завершением цикла, будь то возвращение тела на орбиту в исходную точку, возвращение вибрирующей пружины в точку равновесия или расширение и сокращение сердцебиения. Время, за которое колебательная система совершает полный цикл, называется ее период ​.

Период системы — это мера времени, и в физике он обычно обозначается заглавной буквой ​ T ​. Период измеряется в единицах времени, соответствующих данной системе, но чаще всего используются секунды. Секунда — это единица времени, первоначально основанная на вращении Земли вокруг своей оси и на ее орбите вокруг Солнца, хотя современное определение основано на колебаниях атома цезия-133, а не на каком-либо астрономическом явлении.

Периоды некоторых систем интуитивно понятны, например, вращение Земли, равное дню, или (по определению) 86 400 секунд. Вы можете рассчитать периоды некоторых других систем, таких как колеблющаяся пружина, используя характеристики системы, такие как масса и жесткость пружины.

Когда дело доходит до колебаний света, все становится немного сложнее, потому что фотоны движутся в поперечном пространстве, пока они вибрируют, поэтому длина волны является более полезной величиной, чем период.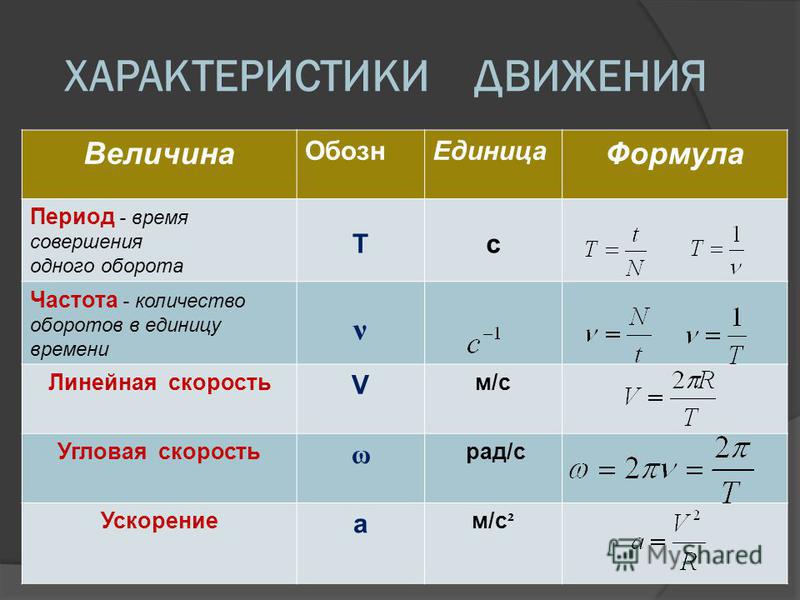

Период обратно пропорционален частоте

Период – это время, необходимое колебательной системе для завершения цикла, тогда как ​ частота (​ f ​) ​ – это количество циклов, которое система может совершить завершить в заданный период времени. Например, Земля вращается один раз в сутки, поэтому период равен 1 дню, а частота также равна 1 обороту в сутки. Если вы установите стандарт времени на годы, период составит 1/365 года, а частота — 365 циклов в год. Период и частота являются обратными величинами:

T = \frac{1}{f}

В расчетах, связанных с атомными и электромагнитными явлениями, частота в физике обычно измеряется в циклах в секунду, также называемых Герцами (Гц), с ⁻¹ или 1/сек. . При рассмотрении вращающихся тел в макроскопическом мире число оборотов в минуту (об/мин) также является общепринятой единицей. Период может измеряться в секундах, минутах или любом другом подходящем периоде времени.

Период простого гармонического осциллятора

Самым основным типом периодического движения является движение простого гармонического осциллятора, который определяется как движение, которое всегда испытывает ускорение, пропорциональное его расстоянию от положения равновесия и направленное к равновесию позиция. В отсутствие сил трения и маятник, и груз, прикрепленный к пружине, могут быть простыми гармоническими осцилляторами.

Колебания массы на пружине или маятнике можно сравнить с движением тела, вращающегося с равномерным движением по круговой траектории с радиусом ​ r ​. Если угловая скорость тела, движущегося по окружности, равна ω, его угловое смещение ( θ ) от начальной точки в любой момент времени t равно θ ​ = ωt ​, и компоненты его положения x и y равны x = r ​ cos(​ ωt ​) и ​ y ​ = ​ r ​ sin(​ ωt ​).

Многие осцилляторы движутся только в одном измерении, и если они движутся горизонтально, то движутся в направлении ​ x ​. Если амплитуда, которая дальше всего отходит от положения равновесия, равна A , то положение в любой момент времени t равно x = A cos( ωt ​). Здесь ω известно как угловая частота и связано с частотой колебаний ( f ​) уравнением ​ ω ​ = 2π​ f ​. Поскольку ​ f ​ = 1/​ T ​, период колебаний можно записать так:

T = \frac{2π}{ω}

Пружины и маятники: уравнения периода по закону Гука на массу пружины действует восстанавливающая сила ​ F ​ = −​ k x ​, где ​ k ​ – характеристика пружины, известная как жесткость пружины, и ​ x — смещение. Знак минус указывает, что сила всегда направлена ​​против направления перемещения. Согласно второму закону Ньютона эта сила также равна массе тела ( м ), умноженной на его ускорение ( a ), поэтому ma = − kx .

Для объекта, колеблющегося с угловой частотой ω , ускорение равно − Aω ² cos ωt или, упрощенно, − ω ​ ² ​ x ​. Теперь вы можете написать м ( − ω ² x ​) = − kx , удалить x и получить √ 1 ω 90 к ​/​ м ​). Тогда период колебаний массы на пружине равен:

T = 2π\sqrt{\frac{m}{k}}

Аналогичные рассуждения можно применить к простому маятнику, на котором вся масса центрируется на конце строки. Если длина строки равна L ​, уравнение периода в физике для малоуглового маятника (т.е. такого, в котором максимальное угловое смещение от положения равновесия мало), которое оказывается не зависящим от массы, равно

T = 2π\sqrt{ \frac{L}{g}}

где ​ g ​ — ускорение свободного падения.

Период и длина волны волны

Подобно простому осциллятору, волна имеет точку равновесия и максимальную амплитуду по обе стороны от точки равновесия.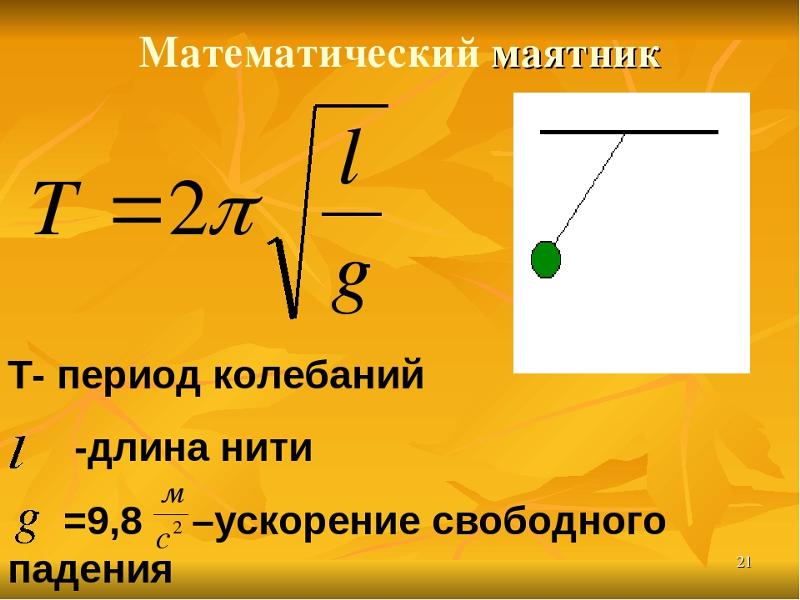 Однако, поскольку волна распространяется через среду или пространство, колебания растягиваются вдоль направления движения. Длина волны определяется как поперечное расстояние между любыми двумя одинаковыми точками цикла колебаний, обычно точками максимальной амплитуды по одну сторону от положения равновесия.

Период волны — это время, за которое одна полная длина волны проходит контрольную точку, тогда как частота волны — это количество длин волн, которые проходят контрольную точку за заданный период времени. Когда период времени равен одной секунде, частота может быть выражена в циклах в секунду (Герцах), а период выражен в секундах.

Период волны зависит от скорости ее движения и длины волны (​ λ ​). Волна проходит расстояние в одну длину волны за один период, поэтому формула скорости волны равна 9.0009 v ​ = ​ λ ​/​ T ​, где ​ v ​ — скорость. Выразив период через другие величины, вы получите:

T = \frac{λ}{v}

Например, если волны на озере разделены 10 футами и движутся со скоростью 5 футов в секунду, период каждой волны 10/5 = 2 секунды.

Использование формулы скорости волны

Все электромагнитное излучение, одним из видов которого является видимый свет, распространяется с постоянной скоростью, обозначаемой буквой ​ c ​, через вакуум. Вы можете написать формулу скорости волны, используя это значение, и поступая так, как обычно делают физики, заменив период волны на ее частоту. Формула принимает вид:

c = \frac{λ}{T} = f × λ

Поскольку c является константой, это уравнение позволяет вычислить длину волны света, если известна его частота и наоборот. наоборот Частота всегда выражается в герцах, а поскольку длина волны света чрезвычайно мала, физики измеряют ее в ангстремах (Å), где один ангстрем равен 10 ⁻¹⁰ метров.

Период маятника: значение, формула и частота

Когда что-то свободно свисает с потолка, и вы толкаете его, оно начинает раскачиваться взад и вперед. Но как быстро он будет качаться и почему? Это то, на что мы действительно можем ответить, и есть довольно простая формула, чтобы понять это. Эти вопросы связаны со свойством, называемым периодом маятника.

Значение периода маятника

Чтобы понять, что такое период маятника, нам нужно знать значение двух вещей: периода и маятника.

Маятник представляет собой систему, состоящую из объекта определенной массы, подвешенного на стержне или шнуре к неподвижной оси. Висячий объект называется боб .

Маятник будет качаться вперед и назад, и максимальное значение, которое принимает угол θ шнура с вертикалью, называется амплитудой . Эта ситуация на самом деле довольно сложная, и в этой статье мы будем говорить только о простой версии маятника.

Простой маятник — это маятник, в котором стержень или шнур не имеют массы, а ось не имеет трения.

На рисунке ниже изображен простой маятник.

Простой маятник, адаптированный из изображения Chetvorno (Public Domain).

В этой статье всякий раз, когда мы говорим о маятнике, мы имеем в виду простой маятник с небольшой амплитудой. Теперь, когда мы понимаем, что мы подразумеваем под маятником, нам нужна еще одна информация, а именно, что мы подразумеваем под периодом.

период маятника — это продолжительность одного полного колебания боба.

Например, продолжительность времени между двумя последовательными ситуациями, в которых груз маятника находится полностью вправо, составляет один период маятника.

Влияние длины на период маятника

Длина шнура маятника влияет на период маятника, которому он принадлежит. Это утверждение довольно убедительно, если мы просто посмотрим на несколько повседневных примеров.

Некоторые елочные игрушки являются хорошими примерами маятника. Эти маленькие украшения имеют небольшую длину шнура в пару сантиметров и небольшие периоды менее полсекунды (быстро раскачиваются).

Качели для детской площадки являются примером маятника с длиной шнура в несколько метров. Период этих колебаний часто превышает 3 секунды.

Набор колебаний, из которых левое будет иметь более короткий период, чем правое, Wikimedia Commons (Public Domain).

Таким образом, чем длиннее шнур, тем больше период маятника.

Другие факторы, влияющие на период маятника

Есть два других фактора, влияющих на период маятника: ускорение свободного падения и амплитуда маятника. Поскольку мы говорим только о маятниках с малыми амплитудами, единственный другой фактор, который мы должны учитывать, — это гравитационное ускорение. С очень малым гравитационным ускорением мы можем представить, как вещи разыгрываются в замедленном темпе. Таким образом, мы ожидаем, что чем больше ускорение свободного падения, тем быстрее качается маятник и тем меньше период маятника.

Но подождите, почему масса шарика не влияет на период маятника? Это очень похоже на тот факт, что масса объекта не влияет на скорость его падения: если масса удваивается, сила тяжести, действующая на него, также удваивается, но ускорение остается прежним: а=F/m. То же самое испытывает груз нашего маятника: сила, действующая на груз 1, который в два раза массивнее, чем на груз 2, в два раза больше, но и сам груз в два раза тяжелее, чем груз 2. Таким образом, груз 1 в два раза так же трудно переместить, как и боб 2, поэтому ускорение обоих бобов будет одинаковым (опять же на a=F/m). Следовательно, период маятника не зависит от массы груза.

Вы можете экспериментально проверить это, подойдя к качелям на игровой площадке и измерив период качания, когда на них кто-то находится и когда на них никого нет. Два измеренных периода окажутся одинаковыми: масса шарика не влияет на период колебания.

Формула периода маятника

Если длина шнура маятника и g ускорение свободного падения, то формула периода T маятника:

T=2πlg

Мы видим, что были правы в своих предсказаниях. Большая длина шнура маятника и меньшее гравитационное ускорение вызывают больший период маятника, а масса груза вообще не влияет на период маятника.

Это хорошее короткое упражнение, чтобы проверить правильность единиц измерения в этом уравнении.

Схема простого маятника с малой амплитудой с указанием соответствующих величин, Арьян ван Дензен — StudySmarter.

Немного посчитав, мы можем вывести формулу для периода маятника. Нам нужно измерять углы в радианах, чтобы для малых углов мы имели примерно sin( θ ) = θ . Единственные результирующие силы, действующие на груз массой м , — это горизонтальные силы, а единственная горизонтальная сила, которую мы можем найти, — это горизонтальная часть натяжения шнура.

Общее натяжение шнура примерно равно вертикальной составляющей натяжения, поскольку амплитуда маятника мала. Эта вертикальная составляющая равна направленной вниз силе на груз (поскольку на груз нет чистой вертикальной силы), что составляет его вес мг .

Тогда горизонтальная часть напряжения равна — мг sin( θ ) (со знаком минус, потому что ускорение направлено в сторону, противоположную его положению, которое мы принимаем за положительное). Это примерно — мг θ из-за малой амплитуды маятника. Итак, ускорение боба составляет а=F/m=-gθ.

Ускорение также измеряется как вторая производная по времени от его горизонтального положения, что примерно равно a=d2xdt2=d2(lθ)dt2. Butlis постоянная, так что уравнение теперь имеет вид ld2θdt2=a=-gθ, где мы должны найти угол θ как функция времени t . Решение этого уравнения (как вы можете проверить) есть θ=Asinglt, где A — амплитуда маятника. Мы видим, что θ равно A через каждые 2πl единиц времени, поэтому период маятника равен T=2πlg. Этот вывод ясно показывает, откуда берутся все факторы, влияющие на период маятника.

Делаем вывод, что на Земле единственным фактором, влияющим на период маятника, является длина шнура маятника.

Вычисление периода маятника

Предположим, мы можем рассматривать детские качели как простой маятник. Каков период качелей, седло которых расположено на 4 м ниже оси вращения, если мы позволим им раскачиваться только плавно, т.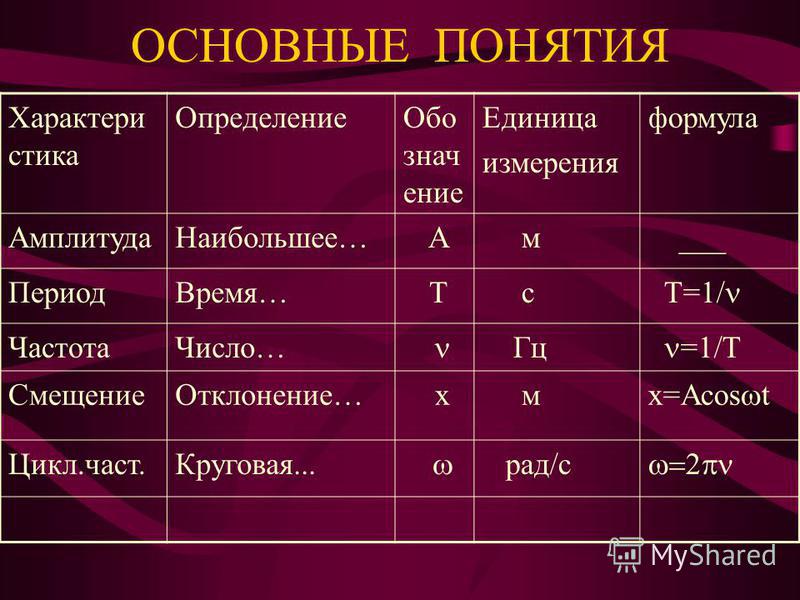 е. с небольшой амплитудой?

Мы знаем, что г = 10 м/с ² и что l=4м. Затем период T этого маятника рассчитывается как:

T=2πlg=2π4m10m/s2=4s.

Это действительно то, что мы знаем из собственного опыта.

Предположим, мы можем рассматривать сережку как простой маятник. Если кто-то идет, он лишь немного толкает сережку, вызывая небольшую амплитуду. Каков срок службы такой серьги, если длина шнура 1 см?

Период этого маятника рассчитывается следующим образом:

T=2πlg=2π0,01м10м/с2=0,2с.

Это также то, что мы знаем из опыта: маленький маятник качается очень быстро.

Частота маятника

Частота (часто обозначаемый как f ) системы всегда является обратным периоду этой системы.

Следовательно, частота маятника определяется как:

f=12πgl.

Помните, что стандартной единицей измерения частоты является герц (Гц), который является обратным значением секунды.