Как найти h в физике? – Обзоры Вики
h = v 0 y 2 2 г . Это уравнение определяет максимальную высоту снаряда над его стартовой позицией и зависит только от вертикальной составляющей начальной скорости.
Отсюда, как найти H треугольника? Заданная площадь треугольника
площадь = с*ч/2 , где b — основание, h — высота. поэтому h = 2 * площадь / b.
Дополнительно Как рассчитать кинетическую энергию? В классической механике кинетическая энергия (КЭ) равна равна половине массы объекта (1/2 * м), умноженной на квадрат скорости. Например, если объект массой 10 кг (m = 10 кг) движется со скоростью 5 метров в секунду (v = 5 м / с), кинетическая энергия равна 125 Джоулей, или (1 / 2 * 10 кг) * 5 м / с2.
Какова формула веса? Вес – это мера силы гравитации, притягивающей объект. Это зависит от массы объекта и ускорения свободного падения, которое составляет 9. 8 м/с.2 на земле. Формула для расчета веса: F = м × 9.8 м / с2, где F — вес объекта в Ньютонах (Н), а m — масса объекта в килограммах.
8 м/с.2 на земле. Формула для расчета веса: F = м × 9.8 м / с2, где F — вес объекта в Ньютонах (Н), а m — масса объекта в килограммах.
Как найти недостающую длину треугольника?
Как мне узнать, есть ли у меня SOH CAH TOA? SOHCAHTOA — это мнемоническое устройство, помогающее запомнить, какое соотношение соответствует какой функции.
- SOH = Синус противоположен гипотенузе.
- CAH = косинус смежен с гипотенузой.
- TOA = Касательная противоположна соседнему.
Как найти недостающую высоту треугольника? Высота треугольника, также называемая его высотой, может быть решена с помощью простой формулы с использованием длины основания и площади.
- h = 2Тб.
- с = р2.
- ч = абс.
- h a = √ (a² — (0.
 2 / 2 м где p — импульс объекта, а m — масса объекта. Так что здесь и должны быть заданы импульс и масса объекта.
2 / 2 м где p — импульс объекта, а m — масса объекта. Так что здесь и должны быть заданы импульс и масса объекта.Как рассчитать кинетическую и потенциальную энергию?
Как рассчитать вес по размеру? Умножьте длину на ширину на высоту, чтобы получить кубические дюймы (см). Чтобы получить размерный вес в килограммах, разделите результат в кубических дюймах на 366. Чтобы получить размерный вес в фунтах, разделите результат в кубических дюймах на 166.
Что такое % масс в химии? вес.% означает весовые проценты который иногда записывается как w/w, т.е. [вес растворенного вещества/вес растворителя*100 = процент растворенного вещества в растворе]. В вашем случае 25% тетраметиламмония в метаноле означает, что на каждые 25 г метанола приходится 100 г тетраметиламмония.
Как перевести килограммы в ньютоны?
N — сила в ньютоне.
 Kg — масса в килограммах.
Kg — масса в килограммах.
…
Кг и Ньютон.Ценности Кг в Ньютон 1 кг = 9.81 Н Ньютон в кг 1N = 0.10197 кг Как найти две недостающие стороны треугольника? Учитывая две стороны
- если сторона a — недостающая сторона, преобразовать уравнение к форме, когда a находится на одной стороне, и извлечь квадратный корень: a = √ (c² — b²)
- если нога b неизвестна, то. b = √ (c² — a²)
- если гипотенуза c отсутствует, формула имеет вид. c = √ (a² + b²)
Как вы решаете треугольники?
Как найти длину третьей стороны треугольника? Ты можешь использовать Теорема Пифагора найти длину гипотенузы прямоугольного треугольника, если известны длины двух других сторон треугольника, называемых катетами.
 Иными словами, если вы знаете длины a и b, вы можете найти c.
Иными словами, если вы знаете длины a и b, вы можете найти c.Работает ли Sohcahtoa на всех треугольниках?
A: Да, это относится только к прямоугольным треугольникам. Если у нас есть наклонный треугольник, мы не можем предположить, что эти триггерные отношения будут работать. У нас есть и другие методы, которые мы узнаем в математическом анализе и тригонометрии, такие как законы синусов и косинусов для обработки этих случаев.
Как найти гипотенузу?
Гипотенуза называется самой длинной стороной прямоугольного треугольника. Чтобы найти самую длинную сторону, мы используем формулу гипотенузы, которая легко выводится из теоремы Пифагора (Гипотенуза)2 = (База)2 + (Высота)2. Формула гипотенузы = √ ((основание)2 + (высота)2) (или) c = √ (a2 + b2).

Какова формула высоты в физике? – Обзоры Вики
h = v 0 y 2 2 г. h = v 0 y 2 2 г . Это уравнение определяет максимальную высоту снаряда над его стартовой позицией и зависит только от вертикальной составляющей начальной скорости.
Точно так же, как вы находите высоту в физике со временем? Решите для высоты
Это говорит о том, что высота снаряда (h) равна равной сумме двух произведений — его начальной скорости и времени, в течение которого находится в воздухе, а ускорение постоянное и половина времени в квадрате.
Какова формула максимальной высоты? Максимальная высота h, достигнутая снарядом, равна половине высоты H — высоты этого треугольника. = H u2013 ½H н/д h = H / 2, что и является желаемым результатом.
Во-вторых, как мне найти высоту объекта? Высота объекта рассчитывается по измерение расстояния от объекта и угла подъема вершины объекта.
 Тангенс угла — это высота объекта, деленная на расстояние от объекта. Таким образом, высота найдена.
Тангенс угла — это высота объекта, деленная на расстояние от объекта. Таким образом, высота найдена.Как найти высоту, зная начальную скорость и время?
Максимальная высота объекта с учетом начального угла запуска и начальной скорости определяется с помощью:h = v2isin2θi2g h = vi 2 sin 2 θ i 2 g . Время полета объекта при заданном начальном угле запуска и начальной скорости определяется по формуле: T = 2visinθg T = 2 vi sin .
тогда Как найти максимальную высоту, на которую поднялся мяч? Полное тематическое исследование:
- Максимальная высота, достигнутая им, будет = v1 2 /2g= (98 х 98)/(2 х 9.8) метр = 490 метров.
- Время, необходимое для достижения высшей точки = v1/g = 98/9.8 секунды = 10 секунд.
- Скорость в высшей точке = 0.
Как найти высоту через массу и работу? Работа — это сила, действующая на объект, умноженная на расстояние, на котором действует сила: W = Fx, где W — работа в Нм = Джоуль.
 Работа, совершенная для подъема тела массой на мою высоту h: W = Fgh = mgh.
Работа, совершенная для подъема тела массой на мою высоту h: W = Fgh = mgh.Как рассчитать свой общий рост?
Вот популярный пример:
- Добавьте рост матери и отца в дюймах или сантиметрах.
- Добавьте 5 дюймов (13 сантиметров) для мальчиков или вычтите 5 дюймов (13 сантиметров) для девочек.
- Разделите на два.
Как рассчитать высоту здания? Высота здания измеряется как расстояние по вертикали от среднего конечного уклона до высшей точки настила плоской кровли, или линии настила мансардной крыши, или средней высоты самого высокого фронтона скатной или вальмовой крыши.
На какую максимальную высоту подбрасывает мяч калькулятор?
Введите общую скорость и угол запуска в формулу h = V₀² * sin (α) ² / (2 * g) для расчета максимальной высоты.
Какова высота мяча через 5 секунд? Средняя скорость 25 м/с, значит, за 5 секунд он падает. 125 метров.
Как найти высоту в науке?
Потенциальная энергия тела массы m на высоте h в гравитационном поле g равна mgh.
 2/2г = ч.
2/2г = ч.Как найти высоту через массу и время?
Калькулятор использует стандартную формулу из физики Ньютона, чтобы вычислить, сколько времени осталось до того, как падающий объект разобьется:
- Сила тяжести, g = 9.8 м / с 2 …
- Время до splat: sqrt (2 * height / 9.8)…
- Скорость во время splat: sqrt (2 * g * height)…
- Энергия в момент времени: 1/2 * масса * скорость 2 = масса * г * высота.
Как найти высоту с учетом гравитации и времени? Свободное падение означает, что объект падает свободно без каких-либо сил, действующих на него, кроме силы тяжести, определенной постоянной, g = -9.8 м/с.2. Расстояние, на которое падает объект, или высота, h, равно 1/2 силы тяжести x квадрат времени падения. Скорость определяется как сила тяжести x время.
Какой рост 5 футов 7 дюймов? Пять футов семь дюймов (5 футов 7 дюймов) равно 170.18 см . Это потому, что в футе 30.
 48 см.
48 см.
…
5′ 7″ в см.Ноги и дюймы сантиметров Метров 5 футов 7 дюймов 170.18 см 1.7 m 5 футов 8 дюймов 172.72 см 1.73 m 5 футов 9 дюймов 175.26 см 1.75 m Какой рост у 14-летнего ребенка?
Для американских мужчин от 20 лет средний рост с поправкой на возраст составляет 69.1 см, или чуть более 175.4 футов 5 дюймов.
…
Рост по возрасту.Age (years) 50-й процентиль роста для мальчиков (дюймы и сантиметры) 13 61.4 дюйма (156 см) 14 64.6 дюйма ( 164 см) 15 66.9 дюйма (170 см) 16 68.3 дюйма (173.  5 см)
5 см)Какой рост должен быть у 13-летней девочки? Рост по возрасту
Age (years) 50-й процентиль роста для девочек (дюймы и сантиметры) 11 56.7 дюйма (144 см) 12 59.4 дюйма (151 см) 13 61.8 дюйма ( 157 см) 14 63.2 дюйма (160.5 см) Какая высота у 4-этажного дома?
Также по действующему стандарту 4-этажное здание может быть на большинство 62 футов или в среднем 15.5 футов на этаж. И, в соответствии с текущим стандартом, 3-этажное здание может быть не более 50 футов или в среднем 16.67 футов на этаж.
Как найти максимальную высоту на калькуляторе? Как найти максимальную высоту снаряда?
- если α = 90 °, то формула упрощается до: hmax = h + V₀² / (2 * g) и время полета является самым длинным.
 …
… - если α = 45 °, то уравнение можно записать как:…
- если α = 0 °, то вертикальная скорость равна 0 (Vy = 0), и это случай горизонтального движения снаряда.
Сколько времени нужно, чтобы мяч достиг максимальной высоты?
Он принимает около 88 секунд чтобы пушечное ядро достигло максимальной высоты (без учета сопротивления воздуха). У вас есть 176 секунд, или 2 минуты 56 секунд, пока пушечное ядро не уничтожит пушку, которая его выпустила.
На какой высоте находится мяч через 3 секунды?
Через 3 секунды высота мяча составит 150 ноги.
Как найти начальную высоту? Начальная скорость, v0 = 200 фут / сек, а начальная высота h0 = 0 (поскольку запускается с земли). Формула: h = -16t2 + 200т + 0 у.е.
Как найти высоту по химии?
Разделите объем цилиндра на квадрат радиуса, умноженный на пи.
 , чтобы вычислить его высоту. В этом примере объем цилиндра равен 300, а радиус равен 3.
, чтобы вычислить его высоту. В этом примере объем цилиндра равен 300, а радиус равен 3.Постоянная Планка — значение, формула, символ, приложения и примеры
Изначально считалось, что энергия непрерывна. Однако после долгих исследований Макс Планк пришел к выводу, что энергия по своей природе не непрерывна, а дискретна и состоит из небольших пакетов, на которые указывают маленькие невидимые частицы, называемые фотонами. Эти частицы несут энергию, и эта энергия, которая была перенесена, определяется постоянной Планка. Чтобы узнать больше о постоянной Планка — значении, формуле, символе, приложениях и примерах, студенты теперь могут узнать больше об этом через Vedantu.
Энергия, которая высвобождается в виде пакетов или фрагментов прерывистым образом, известна как фотоны, где энергия каждого фотона прямо пропорциональна частоте, т. е. Е, и зависит от f.
E ∝ f, E = k x h x u….(1) (k – число фотонов, целое число)
Здесь h называется постоянной Планка.

На этой странице мы узнаем о следующем:
постоянная Планка
Значение постоянной Планка
Вывод формулы постоянной Планка в единицах МКС и СГС
Единицы постоянной Планка и размерная формула символ константы
Применение постоянной Планка с примерами
Наглядные примеры для понимания основ этой темы.
В чем суть квантовой теории Планка?
Немецкий физик-теоретик доктор Макс Планк выдвинул теорию, известную как квантовая теория Планка. Эта теория утверждает: Энергия, излучаемая или свернутая, не вечна, а находится в форме пакетов, называемых квантами.
 Эта энергия известна как «квант энергии». Для одного пакета мы называем это квантами, где кванты — это целочисленное значение, в отличие от непрерывного энергоснабжения, которое имеет переменные значения: 1 или 1,1 или 1,2…
Эта энергия известна как «квант энергии». Для одного пакета мы называем это квантами, где кванты — это целочисленное значение, в отличие от непрерывного энергоснабжения, которое имеет переменные значения: 1 или 1,1 или 1,2…Пакеты — это единицы энергии, и в общем смысле они называются квантами, тогда как фотоны — это термин, используемый для пакетов в терминах видимого света.
Рассмотрим это уравнение:
E = h x c/λ….(2)
h = 6,626 x 10⁻³⁴
c = 3 x 10⁸ м/с
Поместите это значение в приведенное выше уравнение (2)
(6,626 х 10⁻³⁴) * (3 х 10⁸)/λ
(19,878 х 10⁻²⁶)/λ ∽ (2 х 10²⁵)/λ
Получаем,
М = (2 х 10²⁵)/ λ
Это значение энергии одного фотона, а для «k» фотонов оно будет:
E = (k x 2 x 10²⁵)/λ
метров.
 Если λ дано в любой другой единице измерения, скажем, в ангстремах, просто мы можем преобразовать 1 ангстрем в метры (1 ангстрем = 10⁻¹⁰м), где h — постоянная Планка, а h — энергия кванта электромагнитного излучения, деленная на его частота.
Если λ дано в любой другой единице измерения, скажем, в ангстремах, просто мы можем преобразовать 1 ангстрем в метры (1 ангстрем = 10⁻¹⁰м), где h — постоянная Планка, а h — энергия кванта электромагнитного излучения, деленная на его частота.Постоянная Планка h измеряется в джоулях-секундах в системе СИ.
h = 6,626 x 10⁻³⁴
и электронвольт или (эВ) в системе М.К.С.
1 эВ = 1,6 x 10⁻¹⁹ Дж
E = (12400/λ) эВ для λ в Å.
E = (1240/λ) эВ для λ в нм.
Значение для λ при E = 4,13 В
E = 12400/λ
4,13 = 12400/λ
90 068λ = 12400/4,13 = 3000 Å
Эксперименты, использованные для определения постоянной Планка:
Для определения постоянной Планка использовались два эксперимента, которые можно представить следующим образом:
1.
 Весы Кибла
Весы Кибла2. Рентгеновская плотность кристаллов метод
Весы Киббла:
Это точные весы, названные в честь изобретателя Брайана Киббла в 1975 году. Они предназначены для уравнивания одной из возникающих сил с другой. В этом случае вес пробной массы точно уравновешивается силой, возникающей при пропускании электрического тока через катушку с проволокой, погруженную в окружающее магнитное поле.
Метод рентгеновской плотности кристаллов:
Этот метод является основным методом, используемым для определения постоянной Планка. Здесь используются кристаллы кремния, которые доступны в полупроводниковой промышленности высокого качества и чистоты.
Что особенного в постоянной Планка?
Черное тело — идеализированное физическое тело, поглощающее все электромагнитное излучение.
 При нагревании он отражает падающий на него свет, но тоже с различной длиной волны.
При нагревании он отражает падающий на него свет, но тоже с различной длиной волны.(Изображение будет загружено в ближайшее время)
(Изображение будет загружено в ближайшее время)
Здесь на этом графике мы можем наблюдать, что меньше длина волны, меньше излучение волн, затем наступает время, когда мы получаем максимум длина волны, Vmax, что означает максимальное излучение.
Vmax — это положение, показанное пиком на графике в видимом свете.
Здесь происходит то, что когда мы идем дальше, длина волны продолжает увеличиваться, но излучение волн продолжает уменьшаться и продолжается дальше, мы видим, что излучение волн незначительно, но не равно нулю. (Излучаются все длины волн любого количества и независимо от частоты).
Но из теоретических выводов вы, должно быть, заметили на кривой, что от начала до точки, когда длина волны максимальна, график демонстрирует симметрию, но что происходит после этого? Излучение волн максимально, даже когда длина волны меньше.

Есть большая разница, когда длина волны меньше. Модификация вышеупомянутой концепции была предложена великим немецким физиком-теоретиком по имени доктор Макс Планк.
Где он рассматривал свет как форму «k» количества кусков или пакетов, называемых фотонами по соотношению.
E = k x h x f, где k число фотонов.
После его экспериментов экспериментальные и теоретические кривые, которые не были симметричны друг другу, стали симметричными, что свидетельствует о том, что теория, данная доктором Планком, была правильной.
РезюмеПри нагревании железного стержня излучается свет всех длин волн, но человеческий глаз может воспринимать только тот свет, который имеет максимальную длину волны Vmax.
Мы оцениваем температуру звезд, наблюдая за Vmax излучаемого света.

4.3 Движение снарядов — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Используйте одномерное движение в перпендикулярных направлениях для анализа движения снаряда.
- Рассчитайте дальность, время полета и максимальную высоту снаряда, который запускается и поражает плоскую горизонтальную поверхность.
- Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
- Рассчитать траекторию снаряда.
Снарядное движение — это движение объекта, брошенного или отброшенного в воздух, с ускорением только под действием силы тяжести. Применения движения снаряда в физике и технике многочисленны. Некоторые примеры включают метеоры, когда они входят в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядов и их путь называется траекторией.
 Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.Наиболее важным фактом, который следует здесь помнить, является то, что движения вдоль перпендикулярных осей являются независимыми и поэтому могут быть проанализированы отдельно. Мы обсуждали этот факт в разделе «Векторы смещения и скорости», где увидели, что вертикальное и горизонтальное движения независимы. Ключом к анализу двумерного движения снаряда является разбиение его на два движения: одно по горизонтальной оси, а другое по вертикальной. (Этот выбор осей является наиболее разумным, потому что ускорение, вызванное силой тяжести, является вертикальным; таким образом, нет никакого ускорения вдоль горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось x — ось и вертикальная ось y — ось.
 Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. На рис. 4.11 показано обозначение перемещения, где мы определяем s→s→ как полное перемещение, а x→x→ и y→y→ — его составляющие векторы вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , x и и .
Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. На рис. 4.11 показано обозначение перемещения, где мы определяем s→s→ как полное перемещение, а x→x→ и y→y→ — его составляющие векторы вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , x и и .Рисунок 4.11 Полное перемещение с футбольного мяча в точке на его пути. Вектор s→s→ имеет компоненты x→x→ и y→y→ вдоль горизонтальной и вертикальной осей. Его величина составляет s , и он составляет угол Φ с горизонтом.
Чтобы полностью описать движение снаряда, мы должны включить скорость и ускорение, а также перемещение. Мы должны найти их компоненты по х- и и -оси.
 Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми:
Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми:с2).
Поскольку гравитация вертикальна, ax=0.ax=0. Если ax=0,ax=0, это означает, что начальная скорость в направлении x равна конечной скорости в направлении x , или vx=v0x.vx=v0x. С этими условиями на ускорение и скорость мы можем записать кинематическое уравнение 4.11 через уравнение 4.18 для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из движения с постоянным ускорением. Кинематические уравнения движения в однородном гравитационном поле переходят в кинематические уравнения с ay=−g,ax=0:ay=−g,ax=0:
Горизонтальное движение
v0x=vx,x=x0+vxtv0x=vx,x=x0+vxt
4.19
Вертикальное движение
y=y0+12(v0y+vy)ty=y0+12 (v0y+ vy)t
4.
 20
20vy=v0y-gtvy=v0y-gt
4.21
y=y0+v0yt-12gt2y=y0+v0yt-12gt2
4.22
vy2=v0y2−2g(y−y0) vy2=v0y2−2g(y−y0)
4,23
Используя эту систему уравнений, мы можем анализировать движение снаряда, учитывая некоторые важные моменты.
Стратегия решения проблем
Движение снаряда
- Разложите движение на горизонтальную и вертикальную составляющие по осям x и y . Величины компонент смещения s→s→ по этим осям равны x и y. Значения компонентов скорости v→v→ равны vx=vcosθandvy=vsinθ,vx=vcosθandvy=vsinθ, где v — модуль скорости, а θ — ее направление относительно горизонтали, как показано на Рисунок 4.
 12.
12. - Рассматривайте движение как два независимых одномерных движения: одно по горизонтали, а другое по вертикали. Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
- Найдите неизвестные в двух отдельных движениях: горизонтальном и вертикальном. Обратите внимание, что единственной общей переменной между движениями является время t . Процедуры решения задач здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.
- Рекомбинируйте величины в горизонтальном и вертикальном направлениях, чтобы найти полное перемещение s→s→ и скорость v→.v→. Найдите величину и направление смещения и скорости, используя
s=x2+y2,Φ=tan−1(y/x),v=vx2+vy2,s=x2+y2,Φ=tan−1(y/ x),v=vx2+vy2,
, где Φ — направление перемещения s→.s→.
Рисунок 4.12 (а) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения вдоль вертикальной и горизонтальной осей.
 (b) Горизонтальное движение простое, потому что ax=0ax=0, а vxvx — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (г) x и y движений рекомбинируются, чтобы получить общую скорость в любой заданной точке траектории.
(b) Горизонтальное движение простое, потому что ax=0ax=0, а vxvx — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (г) x и y движений рекомбинируются, чтобы получить общую скорость в любой заданной точке траектории.Пример 4.7
Снаряд фейерверка взрывается высоко и прочь
Во время фейерверка снаряд взлетает в воздух с начальной скоростью 70,0 м/с под углом 75,0°75,0° над горизонтом, как показано на рис. 4.13. Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей высшей точки над землей. а) Вычислите высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? в) Чему равно горизонтальное перемещение снаряда при взрыве? г) Чему равно полное перемещение от точки запуска до высшей точки?
Рисунок 4.
 13
Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
13
Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.Стратегия
Движение можно разбить на горизонтальное и вертикальное движения, в которых ax=0ax=0 и ay=-g.ay=-g. Затем мы можем определить x0x0 и y0y0 равными нулю и найти нужные величины.
Раствор
(а) Под «высотой» мы подразумеваем высоту или вертикальное положение y над начальной точкой. Высшая точка любой траектории, называемая вершиной , достигается, когда vy=0.vy=0. Поскольку мы знаем начальную и конечную скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
vy2=v0y2−2g(y−y0).vy2=v0y2−2g(y−y0).
Поскольку y0y0 и vyvy равны нулю, уравнение упрощается до
0=v0y2−2gy.
 0=v0y2−2gy.
0=v0y2−2gy.Решение для y дает
y=v0y22g.y=v0y22g.
Теперь мы должны найти v0y,v0y, составляющую начальной скорости в направлении y . Она определяется как v0y=v0sinθ0,v0y=v0sinθ0, где v0v0 — начальная скорость 70,0 м/с, а θ0=75°θ0=75° — начальный угол. Таким образом,
v0y=v0sinθ=(70,0 м/с)sin75°=67,6 м/sv0y=v0sinθ=(70,0 м/с)sin75°=67,6 м/с
и y равно
y =(67,6 м/с)22(9,80 м/с2).y=(67,6 м/с)22(9,80 м/с2).
Таким образом, имеем
y=233m.y=233m.
Обратите внимание, что, поскольку значение up положительно, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение, вызванное силой тяжести, отрицательно. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м/с достигает максимальной высоты 233 м (без учета сопротивления воздуха).
 Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты.
Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты.(b) Как и во многих задачах по физике, существует несколько способов решения для времени, когда снаряд достигает своей высшей точки. В этом случае проще всего использовать vy=v0y-gt.vy=v0y-gt. Поскольку vy=0vy=0 на вершине, это уравнение сводится к простому виду м/с9,80 м/с2=6,90 с.
Это время подходит и для больших фейерверков. Если вы можете увидеть запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется. Другой способ найти время — использовать y=y0+12(v0y+vy)t.y=y0+12(v0y+vy)t. Это оставлено вам в качестве упражнения для выполнения.
(c) Поскольку сопротивлением воздуха можно пренебречь, ax=0ax=0, а горизонтальная скорость постоянна, как обсуждалось ранее.
 Горизонтальное смещение представляет собой произведение горизонтальной скорости на время по формуле x=x0+vxt,x=x0+vxt, где x0x0 равно нулю. Таким образом,
Горизонтальное смещение представляет собой произведение горизонтальной скорости на время по формуле x=x0+vxt,x=x0+vxt, где x0x0 равно нулю. Таким образом,x=vxt,x=vxt,
, где vxvx — x -компонента скорости, которая определяется выражением
vx=v0cosθ=(70,0 м/с)cos75°=18,1 м/с .vx=v0cosθ=(70,0 м/с)cos75°=18,1 м/с.
Время t для обоих движений одинаково, поэтому x равно
x=(18,1 м/с)6,90 с=125 м.x=(18,1 м/с)6,90 с=125 м.
Горизонтальное движение с постоянной скоростью при отсутствии сопротивления воздуха. Найденное здесь горизонтальное смещение может быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, большое влияние оказывает сопротивление воздуха, и многие осколки приземляются прямо под ним.
(d) Горизонтальная и вертикальная составляющие смещения были только что рассчитаны, поэтому все, что здесь нужно, это найти величину и направление смещения в самой высокой точке: 9
|s→|=1252+2332=264м|s→|=1252+2332=264м
Φ=tan−1(233125)=61,8°.
 Φ=tan−1(233125)=61,8°.
Φ=tan−1(233125)=61,8°.Обратите внимание, что угол вектора смещения меньше начального угла запуска. Чтобы понять, почему это так, просмотрите рисунок 4.11, на котором показана кривизна траектории по направлению к уровню земли.
При решении примера 4.7(а) выражение, которое мы нашли для y , справедливо для любого движения снаряда, когда сопротивлением воздуха можно пренебречь. Назовите максимальную высоту г = ч . Тогда
ч=v0y22g.h=v0y22g.
Это уравнение определяет максимальную высоту снаряда над точкой его запуска и зависит только от вертикальной составляющей начальной скорости.
Проверьте свое понимание 4.3
Камень брошен горизонтально со скалы высотой 100,0 м 100,0 м со скоростью 15,0 м/с. (a) Определите начало системы координат. б) Какое уравнение описывает горизонтальное движение? в) Какие уравнения описывают вертикальное движение? г) Какова скорость камня в момент удара?
Пример 4,8
Расчет движения снаряда: теннисист
Теннисист выиграл матч на стадионе имени Артура Эша и ударил мячом по трибунам со скоростью 30 м/с и под углом 45°45° над горизонтом (рис.
 4.14). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?
4.14). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?Рисунок 4.14 Траектория попадания теннисного мяча в трибуны.
Стратегия
Опять же, разложение этого двумерного движения на два независимых одномерных движения позволяет нам найти нужные величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением. Таким образом, мы сначала решаем для t . Пока мяч поднимается и падает вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается конечная скорость. Таким образом, мы рекомбинируем результаты по вертикали и горизонтали, чтобы получить v→v→ в последний момент времени t , определенные в первой части примера.
Раствор
(a) Пока мяч находится в воздухе, он поднимается, а затем падает в конечное положение на 10,0 м выше начальной высоты.
 Мы можем найти время для этого, используя уравнение 4.22:
Мы можем найти время для этого, используя уравнение 4.22:y=y0+v0yt−12gt2.y=y0+v0yt−12gt2.
Если принять начальное положение y0y0 равным нулю, то конечное положение будет y = 10 м. Начальная вертикальная скорость – это вертикальная составляющая начальной скорости:
v0y=v0sinθ0=(30,0 м/с)sin45°=21,2 м/с.v0y=v0sinθ0=(30,0 м/с)sin45°=21,2 м/с.
Подстановка в уравнение 4.22 вместо y дает нам
10,0 м = (21,2 м/с)t−(4,90 м/с2)t2,10,0 м=(21,2 м/с)t−(4,90 м/с2) т2.
Перестановка членов дает квадратное уравнение в t :
(4,90 м/с2)t2−(21,2 м/с)t+10,0 м=0,(4,90 м/с2)t2−(21,2 м/с) т+10,0м=0.
Использование квадратичной формулы дает t = 3,79 с и t = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории — один раз по пути вверх и один раз по пути вниз — мы принимаем более длинное решение для времени, которое требуется мячу, чтобы достичь зрителя:
t=3,79 с.
 t=3,79 с.
t=3,79 с.Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м выше начальной высоты, находится в воздухе 3,79 с.
(б) Мы можем найти конечные горизонтальную и вертикальную скорости vxvx и vyvy, используя результат (а). Затем мы можем объединить их, чтобы найти модуль полного вектора скорости v→v→ и угол θθ, который он образует с горизонтом. Поскольку vxvx является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем и начальную скорость, и начальный угол. Следовательно,
vx=v0cosθ0=(30 м/с)cos45°=21,2 м/с.vx=v0cosθ0=(30 м/с)cos45°=21,2 м/с.
Конечная вертикальная скорость определяется уравнением 4.21:
vy=v0y-gt.vy=v0y-gt.
Поскольку v0yv0y было найдено в части (a) равным 21,2 м/с, мы имеем
vy=21,2 м/с−9,8 м/с2(3,79 с)=−15,9 м/с.vy=21,2 м/с −9,8 м/с2(3,79 с)=−15,9 м/с.

Величина конечной скорости v→v→ равна
v=vx2+vy2=(21,2м/с)2+(−15,9м/с)2=26,5м/с.v=vx2+vy2=(21,2м /с)2+(−15,9 м/с)2=26,5 м/с.
Направление θvθv находится с помощью арктангенса:
θv=tan-1(vyvx)=tan-1(-15,921,2)=36,9° ниже горизонта. θv=tan-1(vyvx)=tan-1(-15,921,2)=36,9° ниже горизонт.
Значение
(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м выше начальной высоты, находится в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость на 36,9°36,9° ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется в точку по другую сторону от вершины траектории и, следовательно, имеет отрицательное значение 9.0223 y составляющая скорости. Величина скорости меньше, чем величина начальной скорости, которую мы ожидаем, поскольку она воздействует на высоту 10,0 м над уровнем запуска.

Время полета, траектория и дальность
Интерес представляют время полета, траектория и дальность полета снаряда, запущенного на плоской горизонтальной поверхности и упавшего на эту же поверхность. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах.
Время полета
Мы можем определить время полета снаряда, который одновременно запускается и ударяется о плоскую горизонтальную поверхность, выполняя некоторые манипуляции с кинематическими уравнениями. Заметим, что положение и перемещение в и должны быть равны нулю при запуске и при ударе о ровную поверхность. Таким образом, мы устанавливаем смещение в y равным нулю и находим
y−y0=v0yt−12gt2=(v0sinθ0)t−12gt2=0.y−y0=v0yt−12gt2=(v0sinθ0)t−12gt2=0.
Факторинг, у нас
t(v0sinθ0−gt2)=0.t(v0sinθ0−gt2)=0.
Решение для t дает нам
Ttof=2(v0sinθ0)g.
 Ttof=2(v0sinθ0)g.
Ttof=2(v0sinθ0)g.4,24
Это время полета снаряда, выпущенного и ударившегося о плоскую горизонтальную поверхность. Уравнение 4.24 неприменимо, когда снаряд приземляется на другой высоте, чем он был запущен, как мы видели в примере 4.8, где теннисист отбивает мяч в трибуны. Другое решение, t = 0, соответствует моменту запуска. Время полета линейно пропорционально начальной скорости в y направление и обратно пропорционально g . Таким образом, на Луне, где гравитация составляет одну шестую от земной, снаряд, запущенный с той же скоростью, что и на Земле, будет находиться в воздухе в шесть раз дольше.
Траектория
Траекторию снаряда можно найти, исключив переменную времени t из кинематических уравнений для произвольных t и решив y ( x ).
 Мы берем x0=y0=0x0=y0=0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для x дает
Мы берем x0=y0=0x0=y0=0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для x даетх=v0xt⇒t=xv0x=xv0cosθ0.x=v0xt⇒t=xv0x=xv0cosθ0.
Подстановка выражения для t в уравнение для положения y=(v0sinθ0)t−12gt2y=(v0sinθ0)t−12gt2 дает
y=(v0sinθ0)(xv0cosθ0)−12g(xv0cosθ0)2.y=(v0sinθ0)(xv0cosθ0)−12g(xv0cosθ0)2.
Переставляем члены, имеем
y=(tanθ0)x−[g2(v0cosθ0)2]x2.y=(tanθ0)x−[g2(v0cosθ0)2]x2.
4,25
Это уравнение траектории имеет вид y=ax+bx2,y=ax+bx2, которое представляет собой уравнение параболы с коэффициентами
a=tanθ0,b=−g2(v0cosθ0)2.a=tanθ0,b=−g2(v0cosθ0)2.
Диапазон
Из уравнения траектории мы также можем найти дальность или горизонтальное расстояние, пройденное снарядом. Факторинг Уравнение 4.25, мы имеем
y=x[tanθ0−g2(v0cosθ0)2x].y=x[tanθ0−g2(v0cosθ0)2x].

Позиция y равна нулю как для точки запуска, так и для точки удара, так как мы снова рассматриваем только плоскую горизонтальную поверхность. Установка y = 0 в этом уравнении дает решения х = 0, что соответствует точке запуска, и
х=2v02sinθ0cosθ0g,x=2v02sinθ0cosθ0g,
, соответствующий точке удара. Используя тригонометрическое тождество 2sinθcosθ=sin2θ2sinθcosθ=sin2θ и установив для диапазона x = R , мы находим
R=v02sin2θ0g.R=v02sin2θ0g.
4,26
Обратите особое внимание на то, что уравнение 4.26 справедливо только для запуска и удара о горизонтальную поверхность. Мы видим, что размах прямо пропорционален квадрату начальной скорости v0v0 и sin2θ0sin2θ0 и обратно пропорционален ускорению свободного падения. Таким образом, на Луне дальность была бы в шесть раз больше, чем на Земле, при той же начальной скорости.
 Кроме того, из коэффициента sin2θ0sin2θ0 мы видим, что диапазон максимален при 45°.45°. Эти результаты показаны на рис. 4.15. В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (b) мы видим, что диапазон максимален при 45°.45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют 90°.90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
Кроме того, из коэффициента sin2θ0sin2θ0 мы видим, что диапазон максимален при 45°.45°. Эти результаты показаны на рис. 4.15. В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (b) мы видим, что диапазон максимален при 45°.45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют 90°.90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.Рисунок 4.15 Траектории снарядов на ровной местности. (а) Чем больше начальная скорость v0,v0, тем больше диапазон для данного начального угла. (б) Влияние начального угла θ0θ0 на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон одинаковый для начальных углов 15°15° и 75°,75°, хотя максимальная высота этих путей различна.

Пример 4.9
Сравнение ударов по гольфу
Игрок в гольф оказывается в двух разных ситуациях на разных лунках. На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и дать ему вылететь на грин. Он направляет удар низко к земле под углом 30 ° 30 ° к горизонтали, чтобы мяч мог катиться после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным количеством качения после удара. Здесь он направляет выстрел под углом 70°70° к горизонтали, чтобы свести к минимуму перекатывание после удара. Оба выстрела попали в ровную поверхность.
а) Какова начальная скорость мяча у второй лунки?
(b) Какова начальная скорость мяча у четвертой лунки?
(c) Напишите уравнение траектории для обоих случаев.
(d) Нарисуйте траектории.
Стратегия
Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (а), так и для (б).
 Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.Решение
(а) R=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(30°))=31,9 м/сR=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(30° ))=31,9 м/с
(б) R=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(70°))=37,0 м/сR=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(70° ))=37,0 м/с
(c)
y=x[tanθ0−g2(v0cosθ0)2x]Второе отверстие: y=x[tan30°−9,8 м/с22[(31,9 м/с)(cos30°) ]2x]=0,58x−0,0064×2Четвертое отверстие:y=x[tan70°−9,8 м/с22[(37,0 м/с)(cos70°)]2x]=2,75x−0,0306x2y=x[tanθ0−g2(v0cosθ0 )2x]Второе отверстие:y=x[tan30°−90,8 м/с22[(31,9 м/с)(cos30°)]2x]=0,58x−0,0064×2Четвертое отверстие:y=x[tan70°−9,8 м/с22[(37,0 м/с)(cos70°)]2x ]=2,75x−0,0306×2(d) Используя графическую утилиту, мы можем сравнить две траектории, показанные на рис. 4.16.
Рисунок 4.16 Две траектории мяча для гольфа с дальностью 90 м.
 Точки удара обоих находятся на том же уровне, что и точка запуска.
Точки удара обоих находятся на том же уровне, что и точка запуска.Значение
Начальная скорость выстрела под углом 70°70° больше, чем начальная скорость выстрела под углом 30°.30°. Обратите внимание на рис. 4.16, что если бы два снаряда были запущены с одинаковой скоростью, но под разными углами, снаряды имели бы одинаковую дальность, пока углы были бы меньше 90°.90°. Углы запуска в этом примере складываются, чтобы получить число больше 90°,90°. Таким образом, выстрел под углом 70°70° должен иметь большую стартовую скорость, чтобы достичь 90 м, иначе он попадет на более короткое расстояние.
Проверьте свое понимание 4.4
Если бы два удара для гольфа в примере 4.9 были произведены с одинаковой скоростью, какой удар имел бы наибольшую дальность?
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что R очень мала по сравнению с окружностью Земли.
 Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рис. 4.17, основанном на рисунке Ньютона.0223 Принципы. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».
Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рис. 4.17, основанном на рисунке Ньютона.0223 Принципы. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».

 2 / 2 м где p — импульс объекта, а m — масса объекта. Так что здесь и должны быть заданы импульс и масса объекта.
2 / 2 м где p — импульс объекта, а m — масса объекта. Так что здесь и должны быть заданы импульс и масса объекта. Kg — масса в килограммах.
Kg — масса в килограммах.  Иными словами, если вы знаете длины a и b, вы можете найти c.
Иными словами, если вы знаете длины a и b, вы можете найти c.
 Тангенс угла — это высота объекта, деленная на расстояние от объекта. Таким образом, высота найдена.
Тангенс угла — это высота объекта, деленная на расстояние от объекта. Таким образом, высота найдена. Работа, совершенная для подъема тела массой на мою высоту h: W = Fgh = mgh.
Работа, совершенная для подъема тела массой на мою высоту h: W = Fgh = mgh. 2/2г = ч.
2/2г = ч. 48 см.
48 см.  5 см)
5 см) …
… , чтобы вычислить его высоту. В этом примере объем цилиндра равен 300, а радиус равен 3.
, чтобы вычислить его высоту. В этом примере объем цилиндра равен 300, а радиус равен 3.
 Эта энергия известна как «квант энергии». Для одного пакета мы называем это квантами, где кванты — это целочисленное значение, в отличие от непрерывного энергоснабжения, которое имеет переменные значения: 1 или 1,1 или 1,2…
Эта энергия известна как «квант энергии». Для одного пакета мы называем это квантами, где кванты — это целочисленное значение, в отличие от непрерывного энергоснабжения, которое имеет переменные значения: 1 или 1,1 или 1,2… Если λ дано в любой другой единице измерения, скажем, в ангстремах, просто мы можем преобразовать 1 ангстрем в метры (1 ангстрем = 10⁻¹⁰м), где h — постоянная Планка, а h — энергия кванта электромагнитного излучения, деленная на его частота.
Если λ дано в любой другой единице измерения, скажем, в ангстремах, просто мы можем преобразовать 1 ангстрем в метры (1 ангстрем = 10⁻¹⁰м), где h — постоянная Планка, а h — энергия кванта электромагнитного излучения, деленная на его частота. Весы Кибла
Весы Кибла При нагревании он отражает падающий на него свет, но тоже с различной длиной волны.
При нагревании он отражает падающий на него свет, но тоже с различной длиной волны.

 Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха. Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. На рис. 4.11 показано обозначение перемещения, где мы определяем s→s→ как полное перемещение, а x→x→ и y→y→ — его составляющие векторы вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , x и и .
Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. На рис. 4.11 показано обозначение перемещения, где мы определяем s→s→ как полное перемещение, а x→x→ и y→y→ — его составляющие векторы вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , x и и . Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми:
Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми: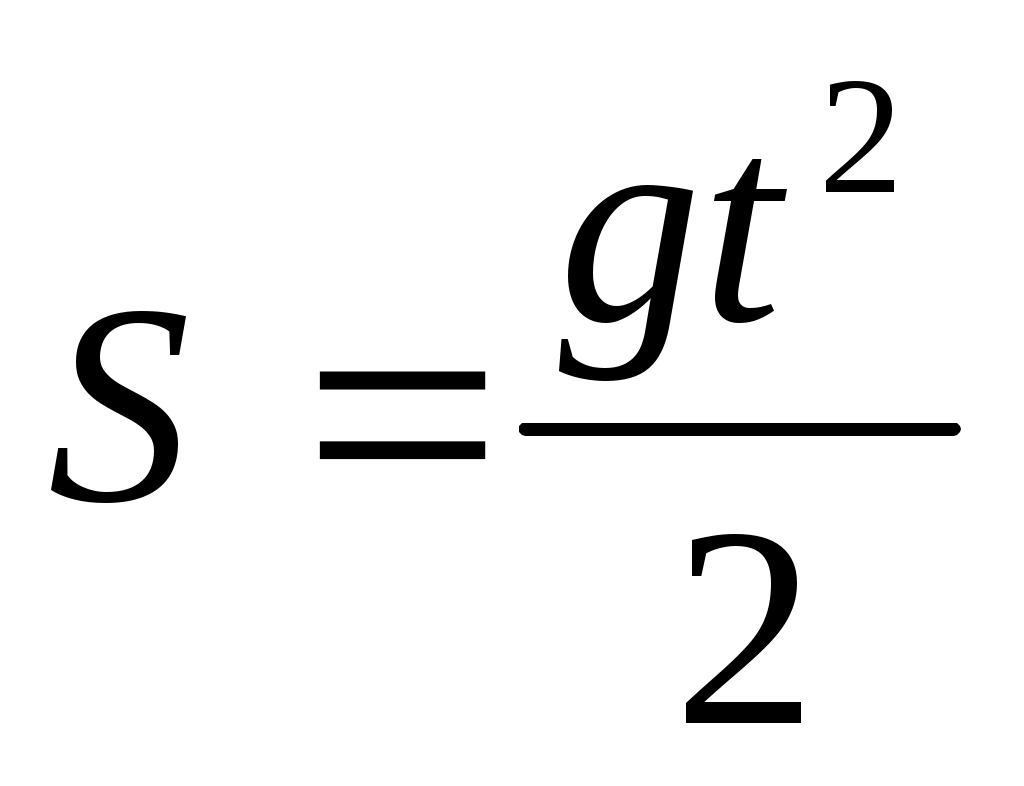 20
20 12.
12. (b) Горизонтальное движение простое, потому что ax=0ax=0, а vxvx — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (г) x и y движений рекомбинируются, чтобы получить общую скорость в любой заданной точке траектории.
(b) Горизонтальное движение простое, потому что ax=0ax=0, а vxvx — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (г) x и y движений рекомбинируются, чтобы получить общую скорость в любой заданной точке траектории. 13
Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
13
Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали. 0=v0y2−2gy.
0=v0y2−2gy. Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты.
Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты. Горизонтальное смещение представляет собой произведение горизонтальной скорости на время по формуле x=x0+vxt,x=x0+vxt, где x0x0 равно нулю. Таким образом,
Горизонтальное смещение представляет собой произведение горизонтальной скорости на время по формуле x=x0+vxt,x=x0+vxt, где x0x0 равно нулю. Таким образом, Φ=tan−1(233125)=61,8°.
Φ=tan−1(233125)=61,8°.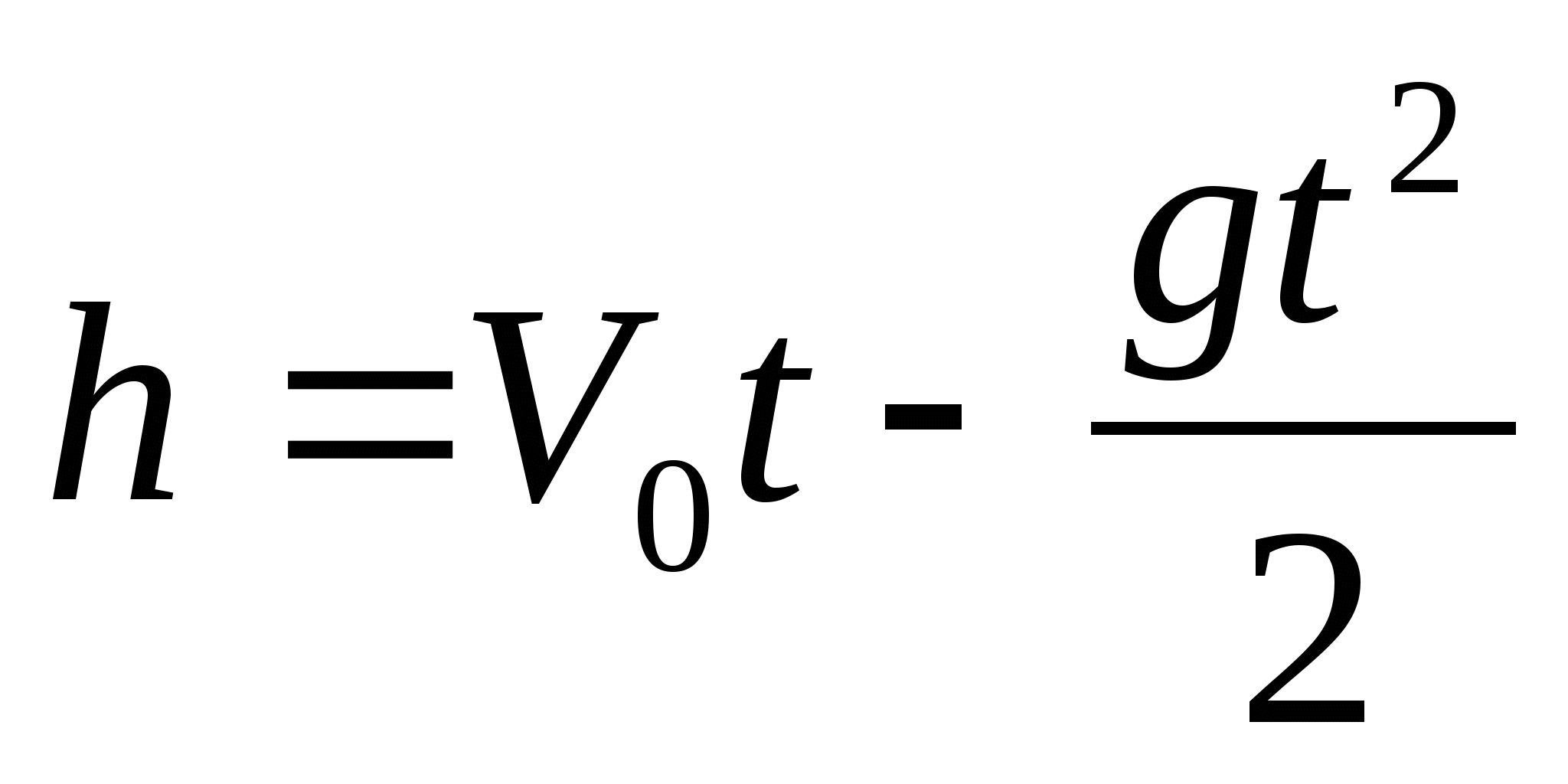 4.14). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?
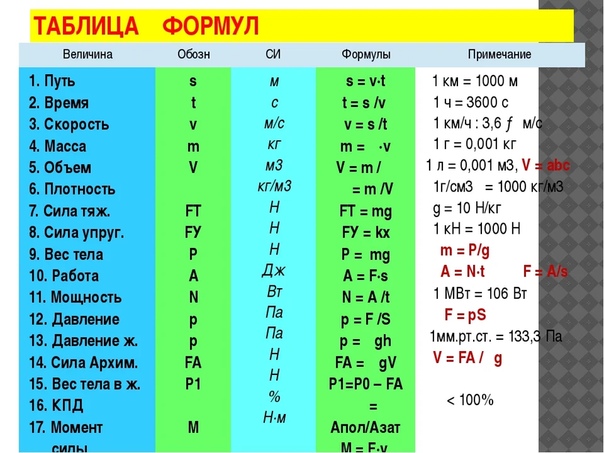
4.14). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара? Мы можем найти время для этого, используя уравнение 4.22:
Мы можем найти время для этого, используя уравнение 4.22: t=3,79 с.
t=3,79 с.

 Ttof=2(v0sinθ0)g.
Ttof=2(v0sinθ0)g. Мы берем x0=y0=0x0=y0=0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для x дает
Мы берем x0=y0=0x0=y0=0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для x дает
 Кроме того, из коэффициента sin2θ0sin2θ0 мы видим, что диапазон максимален при 45°.45°. Эти результаты показаны на рис. 4.15. В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (b) мы видим, что диапазон максимален при 45°.45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют 90°.90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
Кроме того, из коэффициента sin2θ0sin2θ0 мы видим, что диапазон максимален при 45°.45°. Эти результаты показаны на рис. 4.15. В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (b) мы видим, что диапазон максимален при 45°.45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют 90°.90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
 Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории. Точки удара обоих находятся на том же уровне, что и точка запуска.
Точки удара обоих находятся на том же уровне, что и точка запуска. Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рис. 4.17, основанном на рисунке Ньютона.0223 Принципы. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».
Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рис. 4.17, основанном на рисунке Ньютона.0223 Принципы. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».
 3 кг
3 кг Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов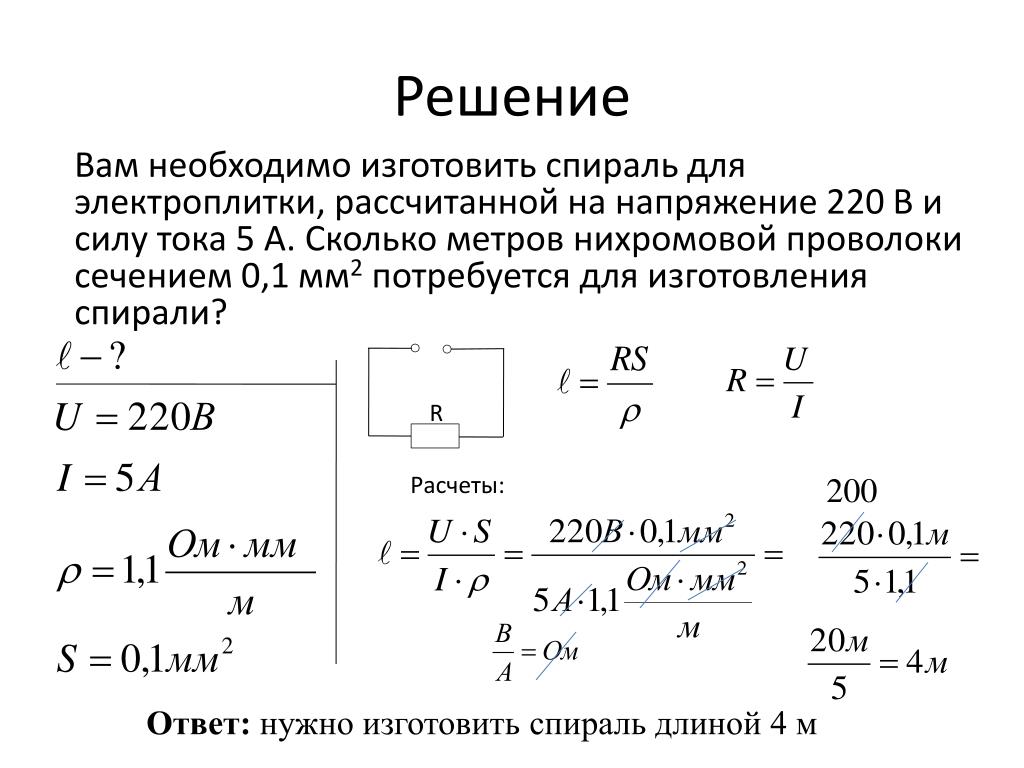 Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ. М.Онджеля, г. Бугульма
М.Онджеля, г. Бугульма Физика как учебная дисциплина отлично поддается процессу компьютеризации. Информационные технологии в процессе обучения физики можно использовать для изучения теоретического материала, тренинга, в качестве средства моделирования и визуализации, а также при решении физических задач.
Физика как учебная дисциплина отлично поддается процессу компьютеризации. Информационные технологии в процессе обучения физики можно использовать для изучения теоретического материала, тренинга, в качестве средства моделирования и визуализации, а также при решении физических задач.
 В конце каждого раздела физики находятся контрольные тесты и задачи, которые разделены на три уровня сложности.
В конце каждого раздела физики находятся контрольные тесты и задачи, которые разделены на три уровня сложности.
 Калькулятор представит подробное решение с различными комментариями, в котором учащийся сможет полностью разобраться.
Калькулятор представит подробное решение с различными комментариями, в котором учащийся сможет полностью разобраться. Т. Решение задач по физике с использованием программы Mathcad / Н. Т. Авласевич, Ж. В. Царикович // Образовательная среда сегодня: стратегии развития: материалы VIII Междунар. науч.–практ. конф. — Чебоксары: ЦНС «Интерактив плюс», 2016. — № 4. — С. 85-88.
Т. Решение задач по физике с использованием программы Mathcad / Н. Т. Авласевич, Ж. В. Царикович // Образовательная среда сегодня: стратегии развития: материалы VIII Междунар. науч.–практ. конф. — Чебоксары: ЦНС «Интерактив плюс», 2016. — № 4. — С. 85-88. 2023 г.
2023 г. Воспользуйтесь пошаговой процедурой, упомянутой ниже, чтобы решить вопросы смещения.
Воспользуйтесь пошаговой процедурой, упомянутой ниже, чтобы решить вопросы смещения. Что такое перемещение объекта?
Что такое перемещение объекта? 

 Знаете ли вы, что существует существенная разница между скоростью и скоростью? Мы написали об этом с точки зрения физика в тексте ниже.
Знаете ли вы, что существует существенная разница между скоростью и скоростью? Мы написали об этом с точки зрения физика в тексте ниже. Когда объект имеет только угловую скорость, он не смещается (расстояние равно нулю), и вы не можете использовать формулу средней скорости.
Когда объект имеет только угловую скорость, он не смещается (расстояние равно нулю), и вы не можете использовать формулу средней скорости. ..
..  Первое определяется разницей между конечным и начальным положением и направлением движения, а второе требует только пройденного расстояния. Другими словами, скорость — это вектор (с величиной и направлением), а скорость — скаляр (только с величиной).
Первое определяется разницей между конечным и начальным положением и направлением движения, а второе требует только пройденного расстояния. Другими словами, скорость — это вектор (с величиной и направлением), а скорость — скаляр (только с величиной).
 Конечная скорость возникает в жидкостях (например, в воздухе или воде) и зависит от плотности жидкости. Знание того, как рассчитать скорость, также имеет особое значение в астрофизике, поскольку результаты должны быть очень точными.
Конечная скорость возникает в жидкостях (например, в воздухе или воде) и зависит от плотности жидкости. Знание того, как рассчитать скорость, также имеет особое значение в астрофизике, поскольку результаты должны быть очень точными. Для европейского вида это будет примерно 11 м/с, или 24 мили в час . Если вы ищете нашего знакомого африканского птичьего полета, то, боюсь, вам не повезло, присяжные еще не вынесены.
Для европейского вида это будет примерно 11 м/с, или 24 мили в час . Если вы ищете нашего знакомого африканского птичьего полета, то, боюсь, вам не повезло, присяжные еще не вынесены. Это время изменится, если человек изменит положение тела.
Это время изменится, если человек изменит положение тела.




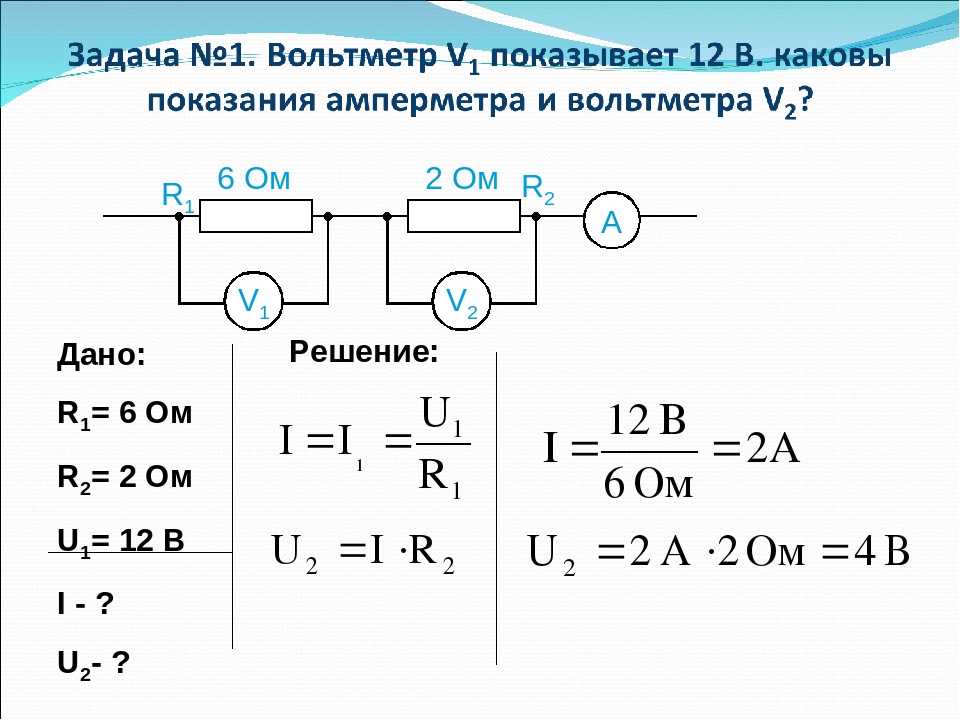 нашли 17 слитков серебра общей массой 3,5 кг при температуре 5 °С. Какова удельная теплота плавления серебра, если для переплавки потребовалось 254 г газа удельной теплотой сгорания 45 МДж/кг? Потерями пренебречь.
нашли 17 слитков серебра общей массой 3,5 кг при температуре 5 °С. Какова удельная теплота плавления серебра, если для переплавки потребовалось 254 г газа удельной теплотой сгорания 45 МДж/кг? Потерями пренебречь.

 Он считается самым крупным, из сохранившихся в мире. На сколько градусов он нагреется, если получит 18 720 Дж тепла? Удельная теплоемкость золота 0,13 кДж/(кг • К).
Он считается самым крупным, из сохранившихся в мире. На сколько градусов он нагреется, если получит 18 720 Дж тепла? Удельная теплоемкость золота 0,13 кДж/(кг • К). При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока. 3}$.
3}$.

 3$
3$ 3 \frac{Дж}{\degree C}} \approx 22.3 \degree C$.
3 \frac{Дж}{\degree C}} \approx 22.3 \degree C$. Эти энергии будут численно равны друг другу, но противоположны по знаку:
Эти энергии будут численно равны друг другу, но противоположны по знаку:
 Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды. Остывание происходит за $9 \space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 \space мин$ будет равно:
Остывание происходит за $9 \space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 \space мин$ будет равно: е., в окружающую среду рассеивается $\frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
е., в окружающую среду рассеивается $\frac{1}{4}$ часть энергии, сообщаемая воде в чайнике. Вам предлагается прочитать каждую задачу и попрактиковаться в использовании стратегии при решении задачи. Затем нажмите кнопку, чтобы проверить ответ, или воспользуйтесь ссылкой для просмотра решения.
Вам предлагается прочитать каждую задачу и попрактиковаться в использовании стратегии при решении задачи. Затем нажмите кнопку, чтобы проверить ответ, или воспользуйтесь ссылкой для просмотра решения.  Определите время падения пера на поверхность Луны.
Определите время падения пера на поверхность Луны.
 Пуля проникает на расстояние 0,0621 м. Определить ускорение пули при движении в глину. (Предположим, что ускорение равномерное.)
Пуля проникает на расстояние 0,0621 м. Определить ускорение пули при движении в глину. (Предположим, что ускорение равномерное.)

 )
) )
) Недавно мы переработали и улучшили Калькулятор. Версия 2 теперь ЖИВАЯ! Мы увеличили количество задач более чем в три раза, разбили каждую часть на несколько небольших однотематических наборов задач и использовали генератор случайных чисел для предоставления числовой информации по каждой задаче. Ответы учащихся оцениваются автоматически, а обратная связь осуществляется мгновенно. И мы сохранили такое же обязательство предоставлять помощь через ссылки на существующие ресурсы. В то время как БЕСПЛАТНАЯ версия делает все вышеперечисленное, учителя с подпиской на Task Tracker могут пойти еще дальше. Они могут модифицировать наши готовые наборы задач, писать свои собственные задачи с помощью нашего простого в использовании Конструктора задач и использовать планшет для разработки собственной программы, выражающей их акцент на использовании математики в физике.
Недавно мы переработали и улучшили Калькулятор. Версия 2 теперь ЖИВАЯ! Мы увеличили количество задач более чем в три раза, разбили каждую часть на несколько небольших однотематических наборов задач и использовали генератор случайных чисел для предоставления числовой информации по каждой задаче. Ответы учащихся оцениваются автоматически, а обратная связь осуществляется мгновенно. И мы сохранили такое же обязательство предоставлять помощь через ссылки на существующие ресурсы. В то время как БЕСПЛАТНАЯ версия делает все вышеперечисленное, учителя с подпиской на Task Tracker могут пойти еще дальше. Они могут модифицировать наши готовые наборы задач, писать свои собственные задачи с помощью нашего простого в использовании Конструктора задач и использовать планшет для разработки собственной программы, выражающей их акцент на использовании математики в физике.
 Определить работу, совершенную Ламаром при подъеме становой тяги 300 кг на высоту 0,90 м над землей.
Определить работу, совершенную Ламаром при подъеме становой тяги 300 кг на высоту 0,90 м над землей.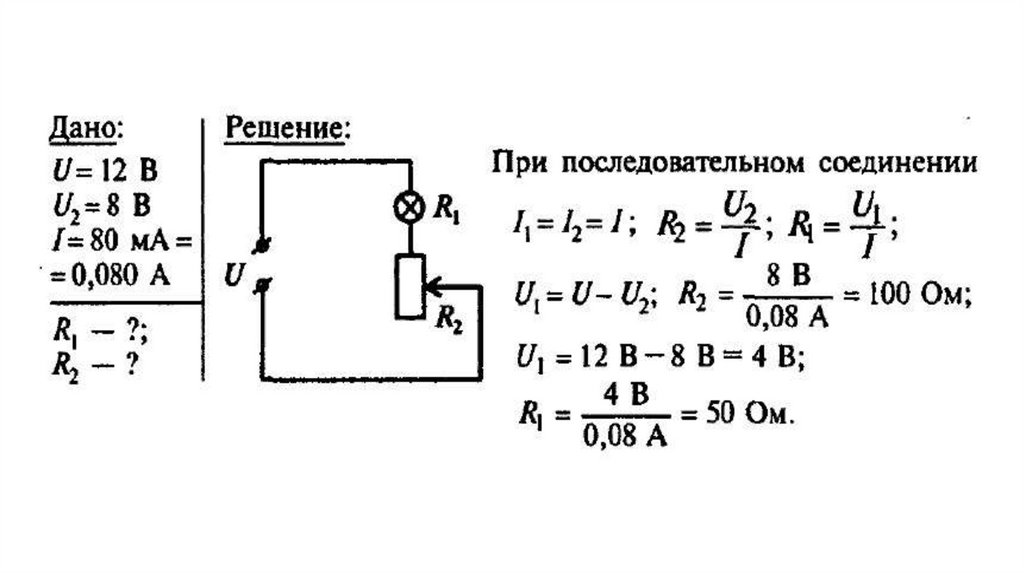
 Один из буксирных тросов приводится в действие двигателем мощностью 22 кВт, который тянет лыжников по обледенелому склону 14° с постоянной скоростью. Предположим, что 18 лыжников со средней массой 48 кг держатся за веревку и предположим, что мотор работает на полную мощность.
Один из буксирных тросов приводится в действие двигателем мощностью 22 кВт, который тянет лыжников по обледенелому склону 14° с постоянной скоростью. Предположим, что 18 лыжников со средней массой 48 кг держатся за веревку и предположим, что мотор работает на полную мощность.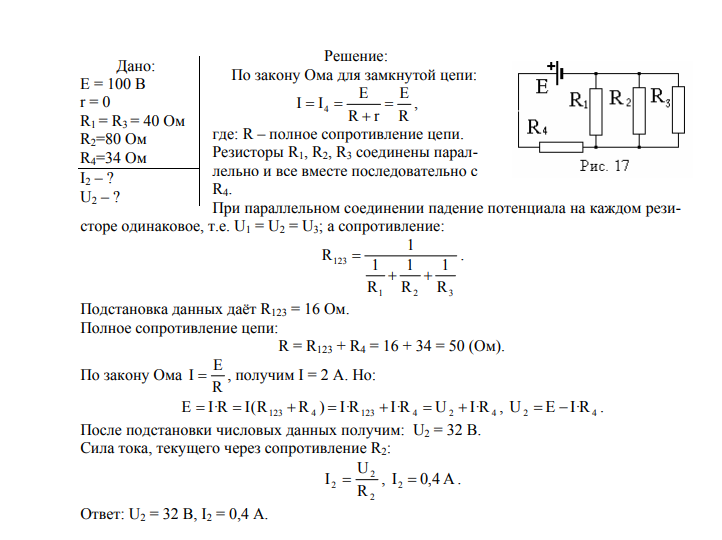 Какой кинетической энергией был бы велосипед, если бы он имел …
Какой кинетической энергией был бы велосипед, если бы он имел … Он движется со скоростью 23,4 м/с на высоте 44,6 метра над землей. Определить полную механическую энергию Ли Бен Фардеста.
Он движется со скоростью 23,4 м/с на высоте 44,6 метра над землей. Определить полную механическую энергию Ли Бен Фардеста. Примите пренебрежимо малое сопротивление воздуха во время движения. Используйте эту информацию для заполнения таблицы.
Примите пренебрежимо малое сопротивление воздуха во время движения. Используйте эту информацию для заполнения таблицы. Она движется со скоростью 16 м/с по гребню лыжной горки, расположенной на высоте 34 м над уровнем земли в конце трассы.
Она движется со скоростью 16 м/с по гребню лыжной горки, расположенной на высоте 34 м над уровнем земли в конце трассы. Определите потенциальную энергию Николаса в верхней части слайда.
Определите потенциальную энергию Николаса в верхней части слайда.  Определите потенциальную энергию Имы в верхней части петли.
Определите потенциальную энергию Имы в верхней части петли.  Он наполняет кувшин колой, ставит его на прилавок и толкает кувшин весом 2,6 кг вперед с усилием 8,8 Н на расстояние 48 см, чтобы отправить его покупателю в конце прилавка. Коэффициент трения между кувшином и столешницей равен 0,28.
Он наполняет кувшин колой, ставит его на прилавок и толкает кувшин весом 2,6 кг вперед с усилием 8,8 Н на расстояние 48 см, чтобы отправить его покупателю в конце прилавка. Коэффициент трения между кувшином и столешницей равен 0,28. Он садится в машину, пристегивается ремнями и готовится к волнениям дня. Какова кинетическая энергия Джерома до периода ускорения?
Он садится в машину, пристегивается ремнями и готовится к волнениям дня. Какова кинетическая энергия Джерома до периода ускорения?  Пейдж бросает мяч, совершая над ним работу 9,89 Дж.
Пейдж бросает мяч, совершая над ним работу 9,89 Дж. Вместо этого он потерял равновесие, кувыркнулся и кувыркнулся со склона в плотную толпу. В течение почти 30 лет после этого кадры этого события были включены во вступление к печально известному спортивному шоу ABC, и Винко стал известен как 9-й.1808 агония поражения икона.
Вместо этого он потерял равновесие, кувыркнулся и кувыркнулся со склона в плотную толпу. В течение почти 30 лет после этого кадры этого события были включены во вступление к печально известному спортивному шоу ABC, и Винко стал известен как 9-й.1808 агония поражения икона. Если бы такая подача была направлена вертикально вверх с той же скоростью, то на какой высоте оно путешествовало?
Если бы такая подача была направлена вертикально вверх с той же скоростью, то на какой высоте оно путешествовало? Тормозная система резко разгоняет 328-килограммовый автомобиль (включая массу гонщика) до скорости 2,9 м/с на дистанции 5,55 метра. Определите тормозную силу, действующую на автомобиль Диззи.
Тормозная система резко разгоняет 328-килограммовый автомобиль (включая массу гонщика) до скорости 2,9 м/с на дистанции 5,55 метра. Определите тормозную силу, действующую на автомобиль Диззи. Она берет 3-летнюю Эллисон в соседний парк и усаживает ее на детские качели. Гвен тянет 1,8-метровую цепь назад, образуя угол 26° с вертикалью, и отпускает 14-килограммовую Эллисон (включая поворотный груз). Предполагая, что трение и сопротивление воздуха пренебрежимо малы, определите скорость Эллисон в самой нижней точке траектории.
Она берет 3-летнюю Эллисон в соседний парк и усаживает ее на детские качели. Гвен тянет 1,8-метровую цепь назад, образуя угол 26° с вертикалью, и отпускает 14-килограммовую Эллисон (включая поворотный груз). Предполагая, что трение и сопротивление воздуха пренебрежимо малы, определите скорость Эллисон в самой нижней точке траектории.
 После опускания в воду, имеющую температуру 10 °C, тела, нагретого до 100 °C, через некоторое время установилась общая температура 40 °C. Какой станет температура воды, если, не вынимая тела, в воду опустить еще одно такое же тело, нагретое до 100 °C? Теплоемкостью калориметра и испарением воды пренебречь. [ t = 55 °C ]
После опускания в воду, имеющую температуру 10 °C, тела, нагретого до 100 °C, через некоторое время установилась общая температура 40 °C. Какой станет температура воды, если, не вынимая тела, в воду опустить еще одно такое же тело, нагретое до 100 °C? Теплоемкостью калориметра и испарением воды пренебречь. [ t = 55 °C ] Электрокипятильник со спиралью сопротивлением 160 Ом поместили в сосуд, содержащий 0,50 л воды при 20 °C и включили в сеть напряжением 220 В. Через 20 минут кипятильник выключили. Сколько воды выкипело? Считать, что вся подводимая теплота пошла на нагревание воды. [ m = 85 г ]
Электрокипятильник со спиралью сопротивлением 160 Ом поместили в сосуд, содержащий 0,50 л воды при 20 °C и включили в сеть напряжением 220 В. Через 20 минут кипятильник выключили. Сколько воды выкипело? Считать, что вся подводимая теплота пошла на нагревание воды. [ m = 85 г ] Тогда из того же ведра зачерпнули еще некоторое количество воды и долили в кастрюлю. При этом температура воды в кастрюле понизилась на 12 °С. Через 5 минут после этого вода в кастрюле закипела. Какова температура воды в вере. Теплообмен воды с внешней средой не учитывать. [ t = 16 °C ]
Тогда из того же ведра зачерпнули еще некоторое количество воды и долили в кастрюлю. При этом температура воды в кастрюле понизилась на 12 °С. Через 5 минут после этого вода в кастрюле закипела. Какова температура воды в вере. Теплообмен воды с внешней средой не учитывать. [ t = 16 °C ] Температура воды в первом стакане через время t1 = 2 мин увеличилась на Δt = 1 °C. Через какое время после заполнения второй стакан нагреется до той же температуры? Удельная теплота плавления льда λ = 336 Дж/г, теплоемкость воды c = 4,2 Дж/(г×К). Теплоемкостью стаканов пренебречь. [ τ2 = 10 мин ]
Температура воды в первом стакане через время t1 = 2 мин увеличилась на Δt = 1 °C. Через какое время после заполнения второй стакан нагреется до той же температуры? Удельная теплота плавления льда λ = 336 Дж/г, теплоемкость воды c = 4,2 Дж/(г×К). Теплоемкостью стаканов пренебречь. [ τ2 = 10 мин ] Считать, что шарик погрузился в лед полностью. Удельная теплоемкость железа 460 Дж/(кг × °С), удельная теплота плавления льда 3,3×105 Дж/кг, плотность льда 900 кг/м3.
Считать, что шарик погрузился в лед полностью. Удельная теплоемкость железа 460 Дж/(кг × °С), удельная теплота плавления льда 3,3×105 Дж/кг, плотность льда 900 кг/м3. Начальные температуры воды – 40 °С, льда – (−20 °С). Масса воды в калориметре была 1,2 кг. Определите объемное содержание свинца в куске льда. Теплоемкостью калориметра пренебречь. Удельная теплоемкость воды 4,2×103 Дж/(кг×°C), льда 2,1×103 Дж/(кг×°C), свинца 138 Дж/(кг×°C). Плотность льда 900 кг/м3, свинца 11,3×103 кг/м3. Удельная теплота плавления льда 3,35×105 Дж/кг. [ η ≈ 0,8 % ]
Начальные температуры воды – 40 °С, льда – (−20 °С). Масса воды в калориметре была 1,2 кг. Определите объемное содержание свинца в куске льда. Теплоемкостью калориметра пренебречь. Удельная теплоемкость воды 4,2×103 Дж/(кг×°C), льда 2,1×103 Дж/(кг×°C), свинца 138 Дж/(кг×°C). Плотность льда 900 кг/м3, свинца 11,3×103 кг/м3. Удельная теплота плавления льда 3,35×105 Дж/кг. [ η ≈ 0,8 % ] Из ведра налили в кастрюлю некоторое количество воды, затем поставили кастрюлю на нагреватель и через 30 минут вода в ней закипела. Тогда из того же ведра зачерпнули еще некоторое количество воды и долили в кастрюлю. При этом температура воды в кастрюле понизилась на 12 °С. Через 5 минут после этого вода в кастрюле закипела. Какова температура воды в ведре? Теплообмен воды с внешней средой не учитывать. [ t1 = 16 °С]
Из ведра налили в кастрюлю некоторое количество воды, затем поставили кастрюлю на нагреватель и через 30 минут вода в ней закипела. Тогда из того же ведра зачерпнули еще некоторое количество воды и долили в кастрюлю. При этом температура воды в кастрюле понизилась на 12 °С. Через 5 минут после этого вода в кастрюле закипела. Какова температура воды в ведре? Теплообмен воды с внешней средой не учитывать. [ t1 = 16 °С]
 В таких тестах учащиеся должны решить поставленные вопросы. В зависимости от решения задачи студент награждается оценками и похвалами. Для поддержки в этой конкретной ситуации существует несколько коучинговых центров и веб-сайтов, которые оказывают необходимую поддержку.
В таких тестах учащиеся должны решить поставленные вопросы. В зависимости от решения задачи студент награждается оценками и похвалами. Для поддержки в этой конкретной ситуации существует несколько коучинговых центров и веб-сайтов, которые оказывают необходимую поддержку.

 Вопросы олимпиады по математике для класса 3
Вопросы олимпиады по математике для класса 3 Математическая олимпиада для 4-го класса с предыдущими вопросами поможет учащимся повысить и улучшить свои навыки решения задач. Учащиеся могут с уверенностью ответить на несколько вопросов, которые они получат на этой олимпиаде по математике для класса 4. Эти вопросы IMO для класса 4 содержат вопросы на основе MCQ, которые включают математические рассуждения и логические рассуждения. Справедливо практиковать различные типы вопросов, которые могут отсутствовать в школьных учебниках.
Математическая олимпиада для 4-го класса с предыдущими вопросами поможет учащимся повысить и улучшить свои навыки решения задач. Учащиеся могут с уверенностью ответить на несколько вопросов, которые они получат на этой олимпиаде по математике для класса 4. Эти вопросы IMO для класса 4 содержат вопросы на основе MCQ, которые включают математические рассуждения и логические рассуждения. Справедливо практиковать различные типы вопросов, которые могут отсутствовать в школьных учебниках.
 Многие «математические олимпиады», проводимые предприятиями в нашей стране, «жестче», чем школьные тесты и экзамены.
Многие «математические олимпиады», проводимые предприятиями в нашей стране, «жестче», чем школьные тесты и экзамены. Взгляните на эти советы, которые помогут вам лучше подготовиться. Несмотря на то, что эти советы полезны, они не могут заменить практику, что более важно.
Взгляните на эти советы, которые помогут вам лучше подготовиться. Несмотря на то, что эти советы полезны, они не могут заменить практику, что более важно. Математическая олимпиада Вопросы для 11-го класса
Математическая олимпиада Вопросы для 11-го класса Что-то настораживает в том, что даже самые способные ученики могут испытывать стресс и терять концентрацию. Студентам с выдающимися академическими показателями также сложно хорошо сдать такие тесты.
Что-то настораживает в том, что даже самые способные ученики могут испытывать стресс и терять концентрацию. Студентам с выдающимися академическими показателями также сложно хорошо сдать такие тесты. Обычно это двухуровневый экзамен.
Обычно это двухуровневый экзамен.
 Разработка схемы навыков отражается в анализе успеваемости на индивидуальном уровне, уровне класса, школы и страны с помощью графического отчета, доступного для всех.
Разработка схемы навыков отражается в анализе успеваемости на индивидуальном уровне, уровне класса, школы и страны с помощью графического отчета, доступного для всех. NIMO обещает сделать математику более увлекательной, представляя интерактивные мероприятия, такие как интерактивные олимпиады, мастер-классы и семинары. Учебники по математике и ежегодная электронная газета.
NIMO обещает сделать математику более увлекательной, представляя интерактивные мероприятия, такие как интерактивные олимпиады, мастер-классы и семинары. Учебники по математике и ежегодная электронная газета. д.
д. Эта программа является одной из основных инициатив, предпринятых NBHM. Его основная цель — выявление математических талантов среди доуниверситетских студентов страны.
Эта программа является одной из основных инициатив, предпринятых NBHM. Его основная цель — выявление математических талантов среди доуниверситетских студентов страны. Пробные тесты можно пройти 3 раза. Экзамен будет представлять собой тест типа MCQ. Учащиеся 2-11 классов должны выполнить тест за 60 минут, а ученики 1 класса — за 45 минут. Кроме того, учебная программа для классов с 3-го по 11-й будет охватывать темы двух предыдущих классов, пройденных учащимся, в то время как учебная программа 2-го класса охватывает темы 1-го класса. Учебная программа 1-го класса охватывает темы дошкольных классов.
Пробные тесты можно пройти 3 раза. Экзамен будет представлять собой тест типа MCQ. Учащиеся 2-11 классов должны выполнить тест за 60 минут, а ученики 1 класса — за 45 минут. Кроме того, учебная программа для классов с 3-го по 11-й будет охватывать темы двух предыдущих классов, пройденных учащимся, в то время как учебная программа 2-го класса охватывает темы 1-го класса. Учебная программа 1-го класса охватывает темы дошкольных классов. Он открыт для учащихся с 1 по 10 класс. Все вопросы, задаваемые на этих экзаменах, представляют собой вопросы с несколькими вариантами ответов. Экзамен на олимпиаде также служит основой для получения учащимися хороших результатов в учебе. Это дает учащимся преимущество перед другими в решении каверзных вопросов.
Он открыт для учащихся с 1 по 10 класс. Все вопросы, задаваемые на этих экзаменах, представляют собой вопросы с несколькими вариантами ответов. Экзамен на олимпиаде также служит основой для получения учащимися хороших результатов в учебе. Это дает учащимся преимущество перед другими в решении каверзных вопросов. Элемент, который делает математику более интересной, заключается в том, что это практический предмет и содержит различные формы задач. Международная математическая олимпиада — это платформа, которая помогает учащимся усвоить основы, быстро понять концепции и узнать что-то новое. Итак, если вы хотите больше узнать о математике, вам следует принять участие в Международной олимпиаде по математике, а для подготовки вы также можете воспользоваться помощью Математические формулы для справки.
Элемент, который делает математику более интересной, заключается в том, что это практический предмет и содержит различные формы задач. Международная математическая олимпиада — это платформа, которая помогает учащимся усвоить основы, быстро понять концепции и узнать что-то новое. Итак, если вы хотите больше узнать о математике, вам следует принять участие в Международной олимпиаде по математике, а для подготовки вы также можете воспользоваться помощью Математические формулы для справки.



 Одной из характеристик автомобиля является время t его разгона с места до скорости 100 км/ ч. Два автомобиля имеют такое время разгона, что t1 = 2t2. Ускорение первого автомобиля по отношению к ускорению второго автомобиля:
Одной из характеристик автомобиля является время t его разгона с места до скорости 100 км/ ч. Два автомобиля имеют такое время разгона, что t1 = 2t2. Ускорение первого автомобиля по отношению к ускорению второго автомобиля: Один кирпич положили на другой и подбросили вертикально вверх. Когда сила давления верхнего кирпича на нижний будет равна нулю? (Сопротивлением воздуха пренебречь.)
Один кирпич положили на другой и подбросили вертикально вверх. Когда сила давления верхнего кирпича на нижний будет равна нулю? (Сопротивлением воздуха пренебречь.) Наибольшее отклонение тела от положения равновесия-это:
Наибольшее отклонение тела от положения равновесия-это: С какой силой притягиваются два корабля массами по 10000 т, находящиеся на расстоянии 1 км один от другого?
С какой силой притягиваются два корабля массами по 10000 т, находящиеся на расстоянии 1 км один от другого?
 Пособие содержит 12 вариантов типовых тестовых заданий по физике, составленных с учётом всех особенностей и требований Единого государственного экзамена. В сборнике даны ответы на все варианты тестов, подробные решения заданий и приведены образцы бланков, используемых на ЕГЭ для записи ответов и решений. Пособие предназначено учителям для подготовки учащихся к сдаче Единого государственного экзамена по физике, а также учащимся-старшеклассникам для самоподготовки и самоконтроля.
Пособие содержит 12 вариантов типовых тестовых заданий по физике, составленных с учётом всех особенностей и требований Единого государственного экзамена. В сборнике даны ответы на все варианты тестов, подробные решения заданий и приведены образцы бланков, используемых на ЕГЭ для записи ответов и решений. Пособие предназначено учителям для подготовки учащихся к сдаче Единого государственного экзамена по физике, а также учащимся-старшеклассникам для самоподготовки и самоконтроля. 00-20.00 Вс: 10.00-19.00
00-20.00 Вс: 10.00-19.00 Этот раздел, наполненный интерактивными элементами, является идеальным инструментом для того, чтобы заставить учащихся задуматься о значении понятий. Идеально подходит для учащихся и аудиторий 1 : 1, использующих iPad, Chromebook и т. п. А для типов химии мы добавили большую коллекцию конструкторов концепций химии.
Этот раздел, наполненный интерактивными элементами, является идеальным инструментом для того, чтобы заставить учащихся задуматься о значении понятий. Идеально подходит для учащихся и аудиторий 1 : 1, использующих iPad, Chromebook и т. п. А для типов химии мы добавили большую коллекцию конструкторов концепций химии. Наша новейшая версия включает >2500 задач по физике и химии, организованных в >250 готовых к использованию наборов задач. Числовая информация генерируется случайным образом. Поле для ответов позволяет учащимся решать и проверять свои ответы. Большинство проблем сопровождаются звуковым сопровождением, в котором объясняется, как решить аналогичную проблему, и подчеркиваются привычки, которые можно использовать для решения любой проблемы. Учителя с учетными записями Task Tracker могут изменять задачи и наборы задач и даже создавать свои собственные задачи. Task Tracker также позволяет учителям ставить задачи своим ученикам и отслеживать их прогресс.
Наша новейшая версия включает >2500 задач по физике и химии, организованных в >250 готовых к использованию наборов задач. Числовая информация генерируется случайным образом. Поле для ответов позволяет учащимся решать и проверять свои ответы. Большинство проблем сопровождаются звуковым сопровождением, в котором объясняется, как решить аналогичную проблему, и подчеркиваются привычки, которые можно использовать для решения любой проблемы. Учителя с учетными записями Task Tracker могут изменять задачи и наборы задач и даже создавать свои собственные задачи. Task Tracker также позволяет учителям ставить задачи своим ученикам и отслеживать их прогресс. Большинство симов сопровождаются средством проверки концепций. У некоторых симов есть встроенный в симуляцию код Task Tracker. Не у всех симов будет средство проверки концепции. Средства проверки концепций можно использовать как с учетной записью системы отслеживания задач, так и без нее.
Большинство симов сопровождаются средством проверки концепций. У некоторых симов есть встроенный в симуляцию код Task Tracker. Не у всех симов будет средство проверки концепции. Средства проверки концепций можно использовать как с учетной записью системы отслеживания задач, так и без нее.
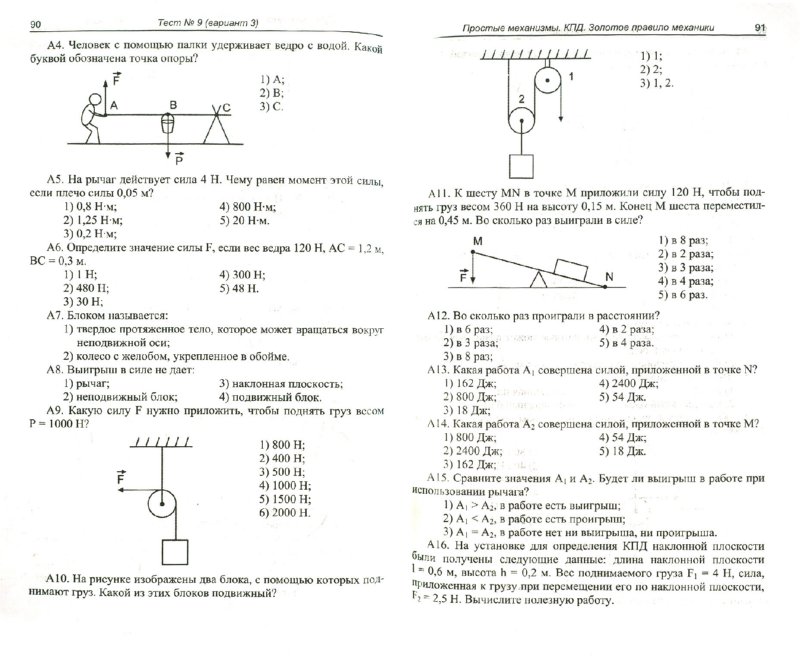 Например, вы можете не получить баллы за ответ на часть а, но получить полный балл за части б, в или г. Если ответ на более позднюю часть вопроса зависит от ответа на более раннюю часть, вы все равно можете получить полный балл за более позднюю часть, даже если этот более ранний ответ неверен.
Например, вы можете не получить баллы за ответ на часть а, но получить полный балл за части б, в или г. Если ответ на более позднюю часть вопроса зависит от ответа на более раннюю часть, вы все равно можете получить полный балл за более позднюю часть, даже если этот более ранний ответ неверен. е. писать много уравнений или списков терминов в надежде, что среди них будет правильный, чтобы вы могли получить частичное признание. Для экзаменов, требующих 2 или 3 примеров или уравнений, будут оцениваться только первые 2 или 3 примера.
е. писать много уравнений или списков терминов в надежде, что среди них будет правильный, чтобы вы могли получить частичное признание. Для экзаменов, требующих 2 или 3 примеров или уравнений, будут оцениваться только первые 2 или 3 примера.


 Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква .
Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква .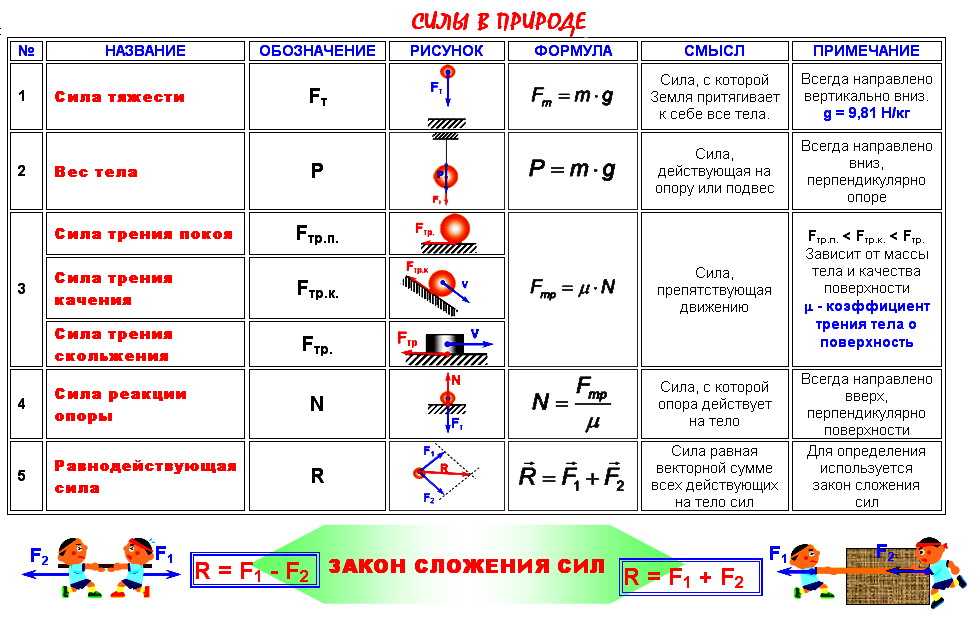 Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы concentration), первая радиационная постоянная, Вторая радиационная постоянная
concentration), первая радиационная постоянная, Вторая радиационная постоянная Dicke)
Dicke) fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения
fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials)
Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона
kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка
massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка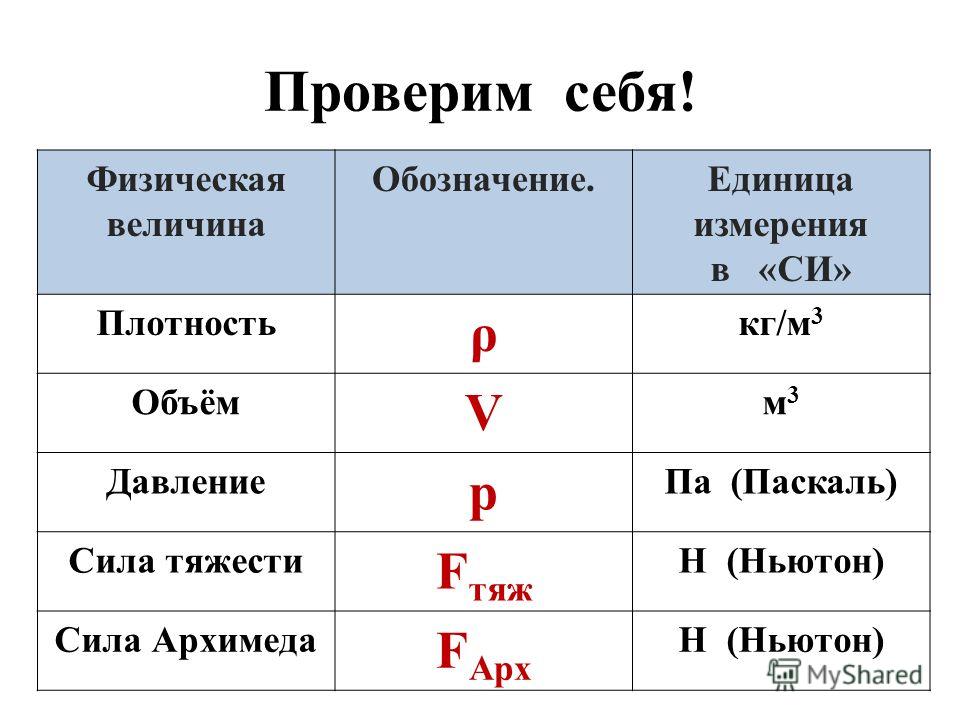 petere), протон (англ. proton), дипольный момент, волновой параметр
petere), протон (англ. proton), дипольный момент, волновой параметр radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние
radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние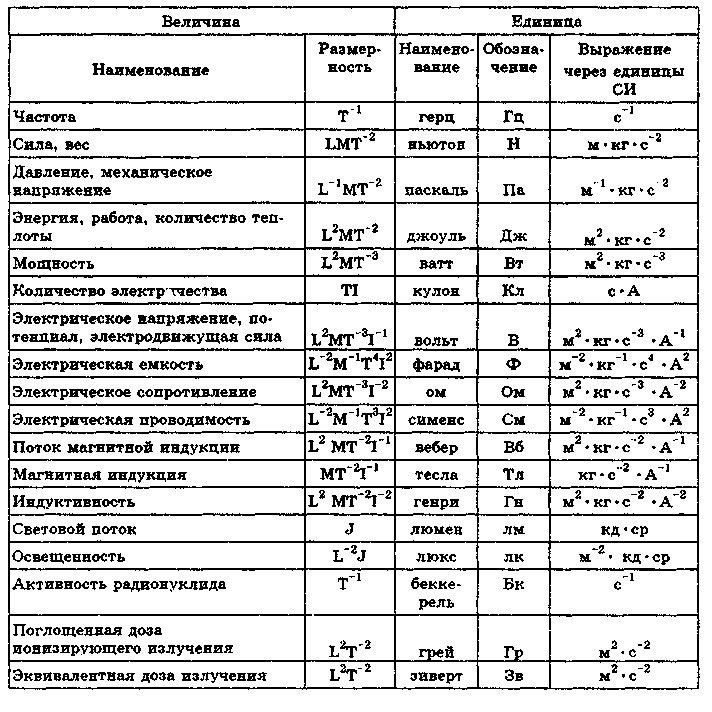 tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время
tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление, угловое увеличение, волновое сопротивление вакуума
Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление, угловое увеличение, волновое сопротивление вакуума
 ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект
), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон
14159…, пи-связь, пи-плюс мезон, пи-ноль мезон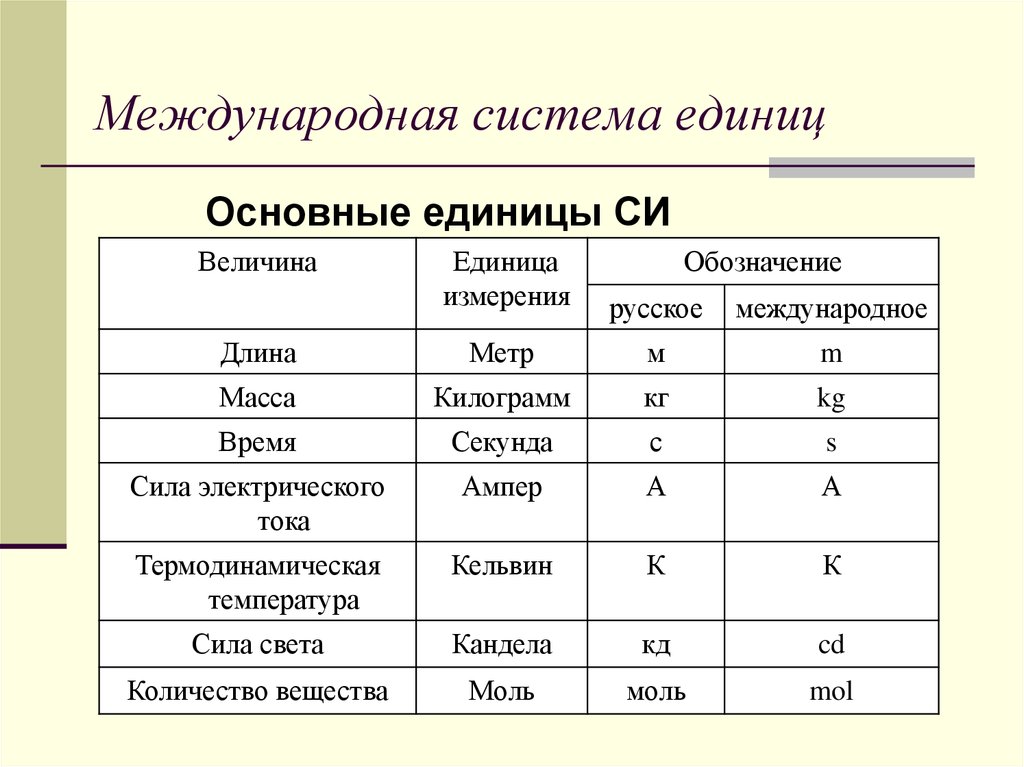 Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.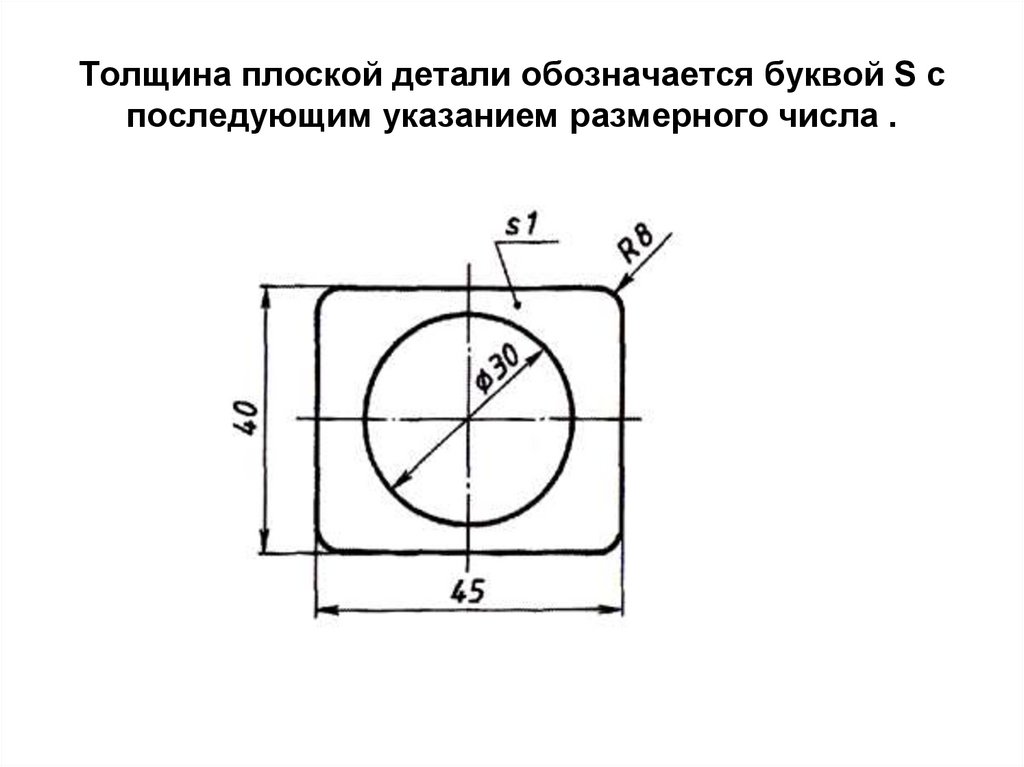 Например, f(x, y) означает, что величина f является функцией x и y.
Например, f(x, y) означает, что величина f является функцией x и y.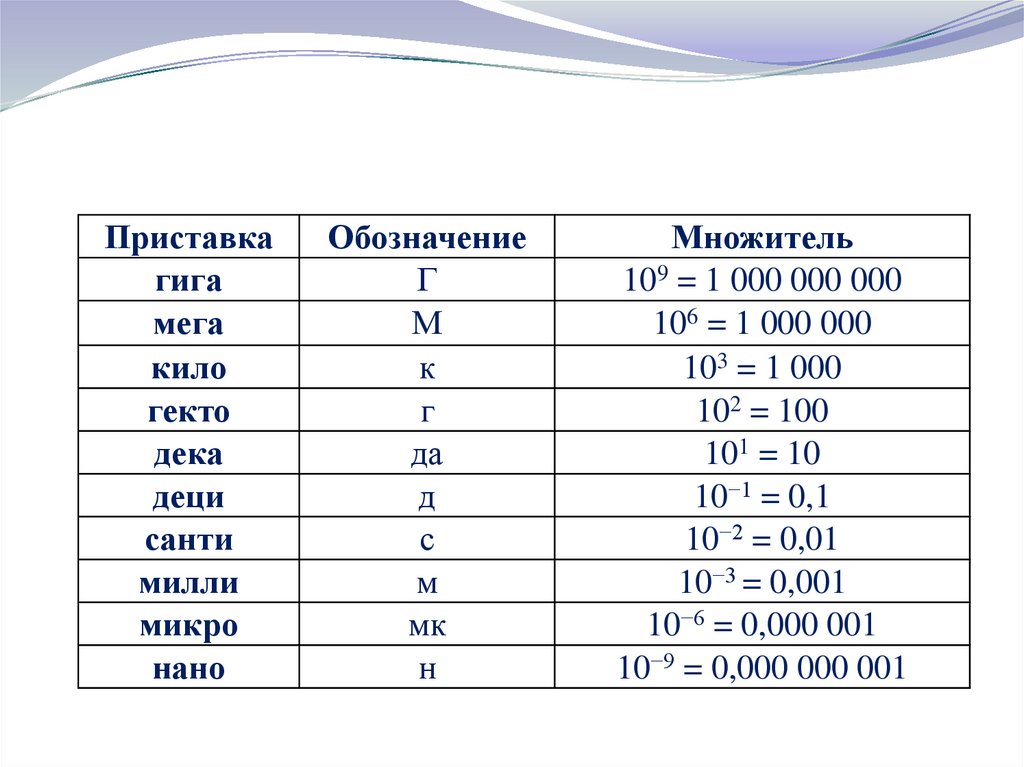 Обычно нижний индекс обозначает характерный признак величины, например ее порядковый номер, тип, проекцию и т. п.. Верхний индекс обозначает степень кроме случаев когда величина является тензором.
Обычно нижний индекс обозначает характерный признак величины, например ее порядковый номер, тип, проекцию и т. п.. Верхний индекс обозначает степень кроме случаев когда величина является тензором. Теоретик электромагнетизма называл величины в своих уравнениях по алфавиту: A, B, C, D, E, F, G, H. В этой последовательности A было векторным потенциалаом, С — током, B — вектором магнитной индукции, D — вектором электрической идукции, а H — напряженностью магнитного поля. Подробное объяснение по ссылке а также в Mark P. Silverman, Waves and Grains, p. 205—206, Princeton University Press, New Jersey, 1998.
Теоретик электромагнетизма называл величины в своих уравнениях по алфавиту: A, B, C, D, E, F, G, H. В этой последовательности A было векторным потенциалаом, С — током, B — вектором магнитной индукции, D — вектором электрической идукции, а H — напряженностью магнитного поля. Подробное объяснение по ссылке а также в Mark P. Silverman, Waves and Grains, p. 205—206, Princeton University Press, New Jersey, 1998. Poggendorff’s Annalen der Physick, LXXIX (Dover Reprint). ISBN 0-486-59065-8.
Poggendorff’s Annalen der Physick, LXXIX (Dover Reprint). ISBN 0-486-59065-8. Современная наука утверждает, что всего в природе существует 92 различных атома, ещё около 2Ь атомов новых элементов учёные искусственно создали в своих лабораториях. Все атомы систематизированы на основе периодического закона, открытого Д. И Менделеевым.
Современная наука утверждает, что всего в природе существует 92 различных атома, ещё около 2Ь атомов новых элементов учёные искусственно создали в своих лабораториях. Все атомы систематизированы на основе периодического закона, открытого Д. И Менделеевым. Например, молекула воды всегда одна и та же: и в воде, и в снежинке, и в паре.
Например, молекула воды всегда одна и та же: и в воде, и в снежинке, и в паре. Учитывая значения, полученные в этом опыте, получаем
Учитывая значения, полученные в этом опыте, получаем Только при помощи электронного микроскопа удалось сфотографировать наиболее крупные из них.
Только при помощи электронного микроскопа удалось сфотографировать наиболее крупные из них.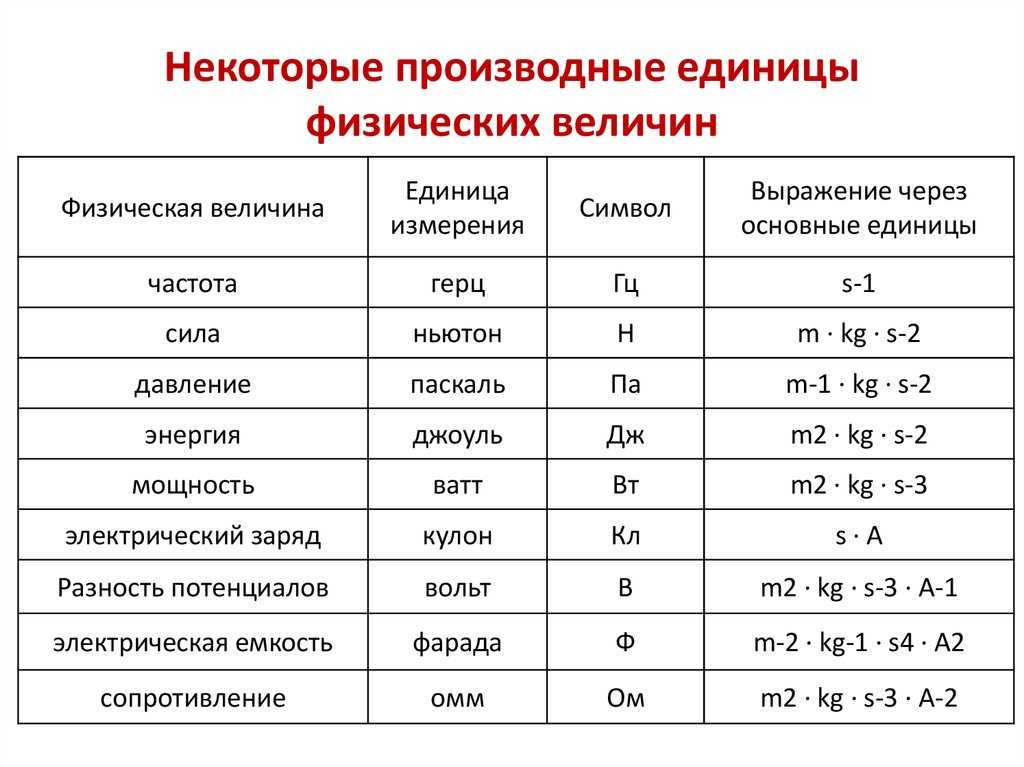
 д.
д. В виде угла θ si =3,26239 рад ± 2 мкрад; как импульс θ si =3,2623
В виде угла θ si =3,26239 рад ± 2 мкрад; как импульс θ si =3,2623
 Дж. Фикссен, Температура космического микроволнового фона, (2009), arXiv: 0911.1955, doi: 10.1088/0004-637X/707/2/916.
Дж. Фикссен, Температура космического микроволнового фона, (2009), arXiv: 0911.1955, doi: 10.1088/0004-637X/707/2/916.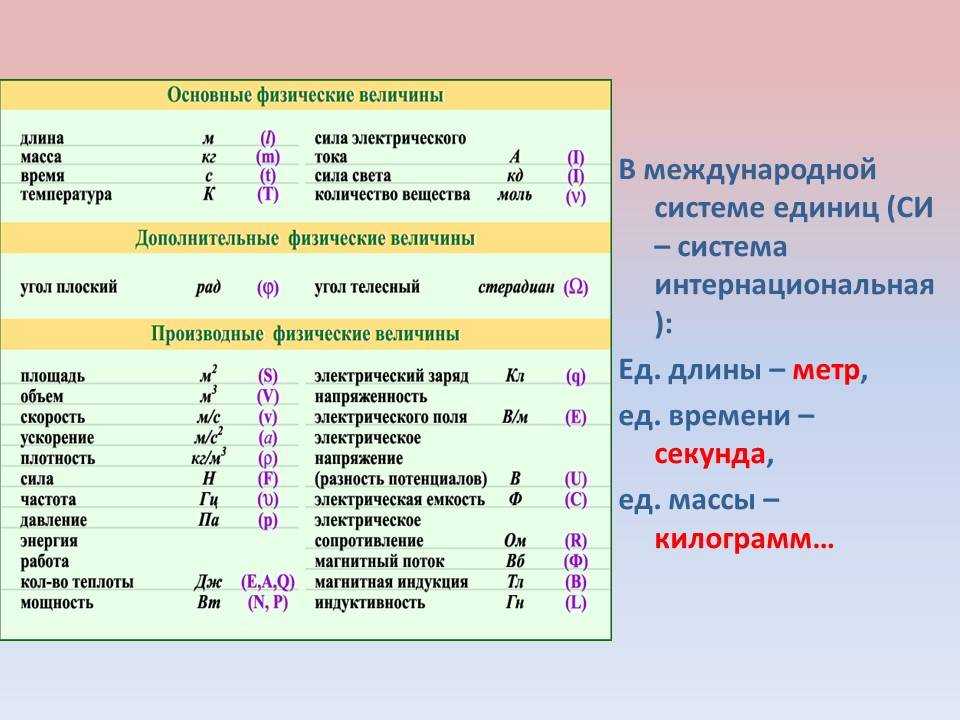 Это достигается с помощью процесса, известного как масштабирование.
Это достигается с помощью процесса, известного как масштабирование.
 А зная общую аккрецированную массу, которая затем будет составлять реликтовое излучение, и зная выражения для диаметра и возраста Вселенной, а также результирующую плотность, мы можем определить температуру реликтового излучения.
А зная общую аккрецированную массу, которая затем будет составлять реликтовое излучение, и зная выражения для диаметра и возраста Вселенной, а также результирующую плотность, мы можем определить температуру реликтового излучения. Выражение обеспечивает новый способ понимания Вселенной как системы как внешне, так и внутренне, ее свойств и конструкции в отношении нашего понимания массы.
Выражение обеспечивает новый способ понимания Вселенной как системы как внешне, так и внутренне, ее свойств и конструкции в отношении нашего понимания массы.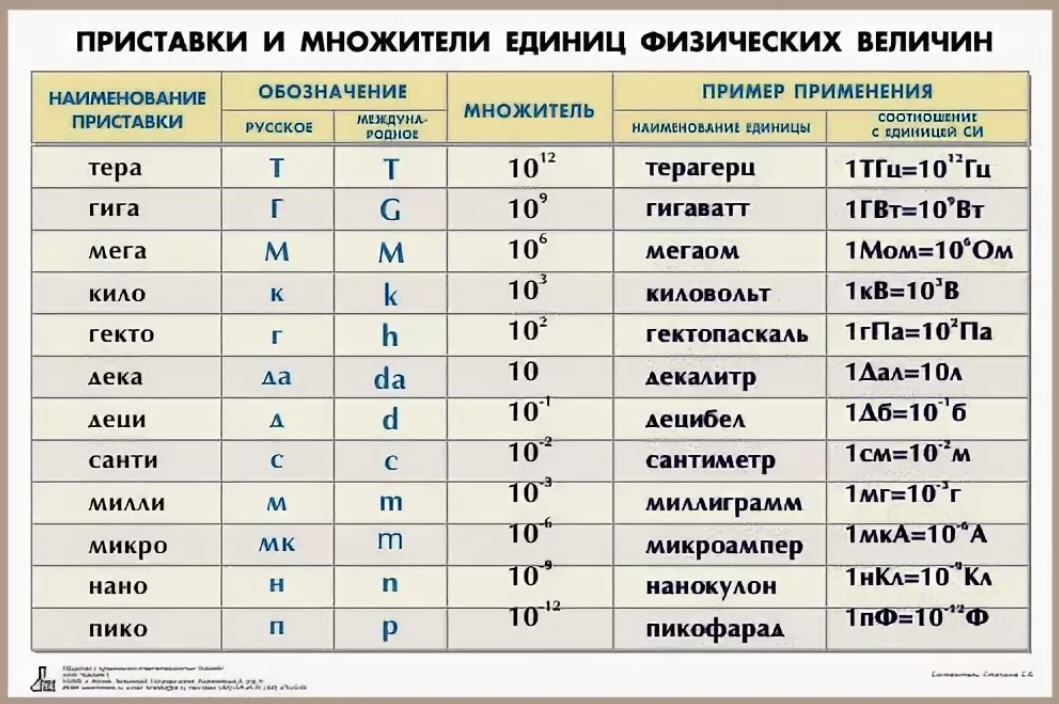
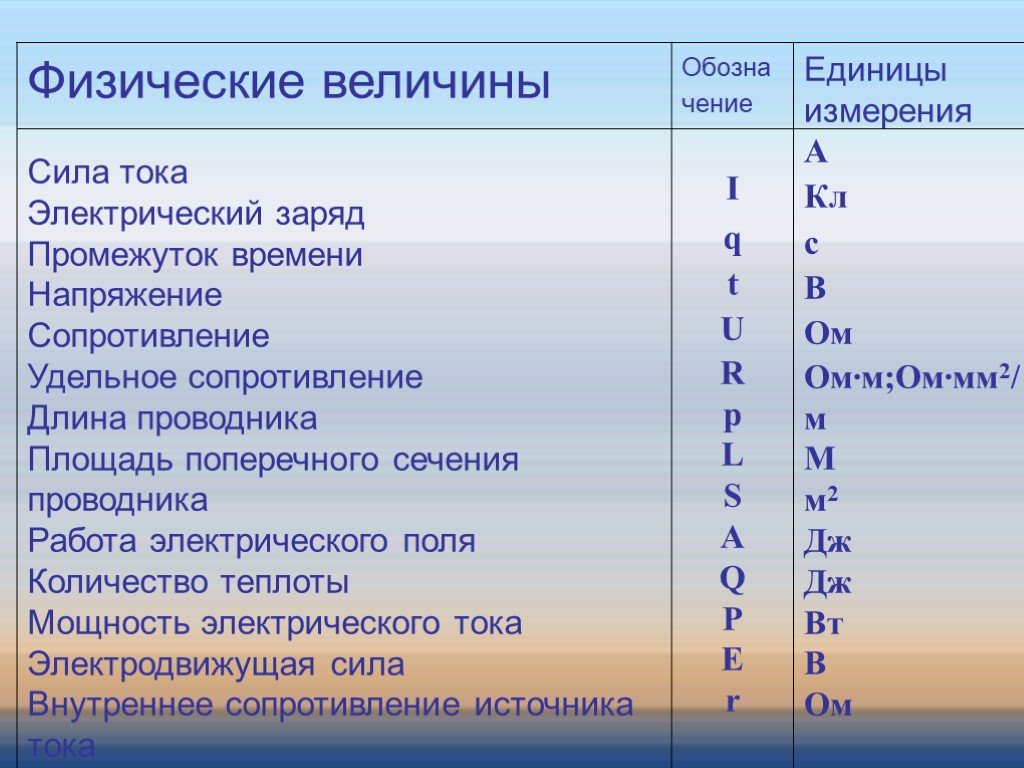 для оценки частичных площадей требовалась оценка площади, но мы могли измерить площадь в миллиметрах, чтобы получить очень точное измерение. Затем мы использовали logger pro для построения графика всех данных, которые мы собираем. Мы обнаружили, что один из графиков был линейным, и мы оставили эту линию в покое, но другой был в форме параболы с верхним отверстием, поэтому мы возвели в квадрат независимую переменную, чтобы найти линейное соответствие для данных.
для оценки частичных площадей требовалась оценка площади, но мы могли измерить площадь в миллиметрах, чтобы получить очень точное измерение. Затем мы использовали logger pro для построения графика всех данных, которые мы собираем. Мы обнаружили, что один из графиков был линейным, и мы оставили эту линию в покое, но другой был в форме параболы с верхним отверстием, поэтому мы возвели в квадрат независимую переменную, чтобы найти линейное соответствие для данных.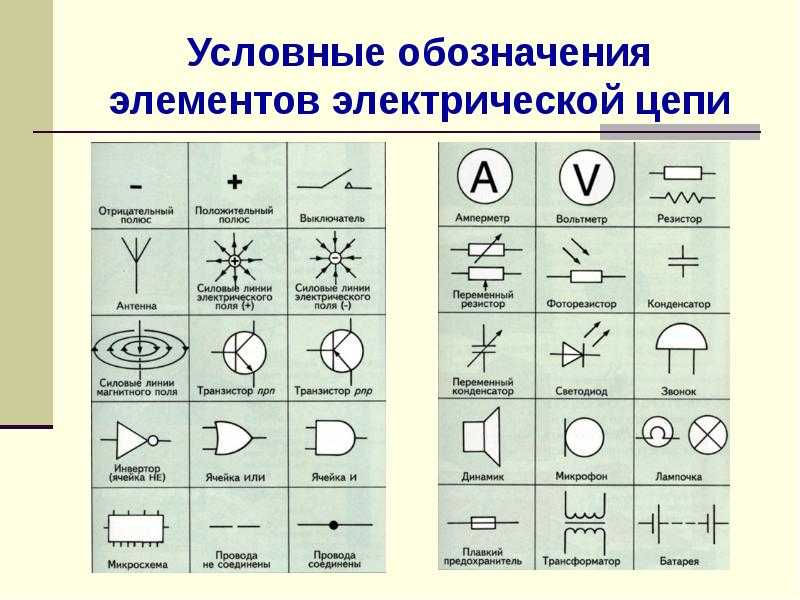 В этом уравнении также была точка пересечения y, но она была незначительной, поэтому мы решили не включать ее.
В этом уравнении также была точка пересечения y, но она была незначительной, поэтому мы решили не включать ее.
 Работа и мощность тока
Работа и мощность тока 1
1 1
1 3
3 Время движения одного поезда мимо другого — это промежуток времени от момента, когда поровнялись их «головы», до момента, когда поравнялись их «хвосты».
Время движения одного поезда мимо другого — это промежуток времени от момента, когда поровнялись их «головы», до момента, когда поравнялись их «хвосты». канатоходец прошел над Ниагарским водопадом по стальной проволоке диаметром 76 мм и массой 11 848 кг.
канатоходец прошел над Ниагарским водопадом по стальной проволоке диаметром 76 мм и массой 11 848 кг.



 4: Вредные микроорганизмы
4: Вредные микроорганизмы 2: Нефть
2: Нефть 9: Красная книга
9: Красная книга 2: Изменения в период полового созревания
2: Изменения в период полового созревания 9: Давление, оказываемое жидкостями и газами
9: Давление, оказываемое жидкостями и газами 2: Химические эффекты электрического тока
2: Химические эффекты электрического тока 10: Что такое система Брайля?
10: Что такое система Брайля? Планируйте свое время
Планируйте свое время Когда вы освободитесь и ляжете на кровать перед сном, вспомните, какие темы вы выучили за день. Спросите себя, какой урок требует большего внимания, чтобы вы могли спланировать занятия на следующий день.
Когда вы освободитесь и ляжете на кровать перед сном, вспомните, какие темы вы выучили за день. Спросите себя, какой урок требует большего внимания, чтобы вы могли спланировать занятия на следующий день.
 Хорошо управляйте своим временем и выполняйте учебный план вовремя.
Хорошо управляйте своим временем и выполняйте учебный план вовремя. Мы сосредоточены на научных исследованиях, решении проблем и лучшем понимании нашего физического мира. Изучая физику на раннем этапе, учащиеся имеют больше возможностей участвовать в научных исследованиях в старших классах и участвовать в конкурсных летних программах, основанных на исследованиях.
Мы сосредоточены на научных исследованиях, решении проблем и лучшем понимании нашего физического мира. Изучая физику на раннем этапе, учащиеся имеют больше возможностей участвовать в научных исследованиях в старших классах и участвовать в конкурсных летних программах, основанных на исследованиях.


 2}=25\)
2}=25\)
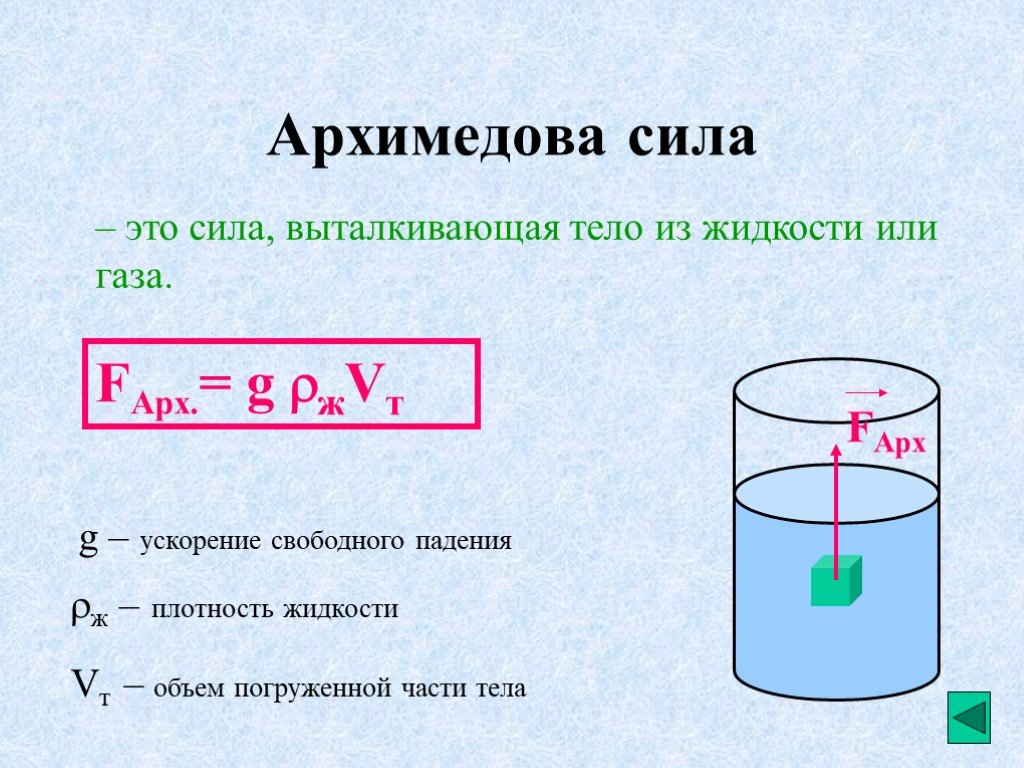
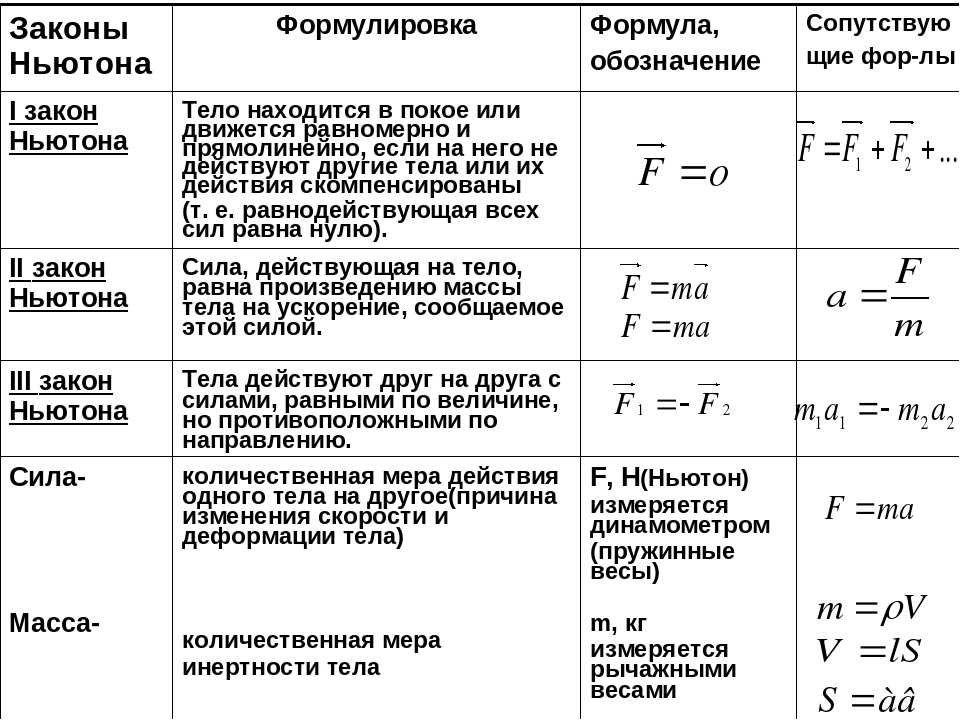 2\cdot \rho\right)=8\cdot 75=600 \ {\small{\text{грамм}}}\)
2\cdot \rho\right)=8\cdot 75=600 \ {\small{\text{грамм}}}\) 3 \quad\Rightarrow\quad \dfrac{R_1}{R_2}=\sqrt[3]{343}=7\)
3 \quad\Rightarrow\quad \dfrac{R_1}{R_2}=\sqrt[3]{343}=7\)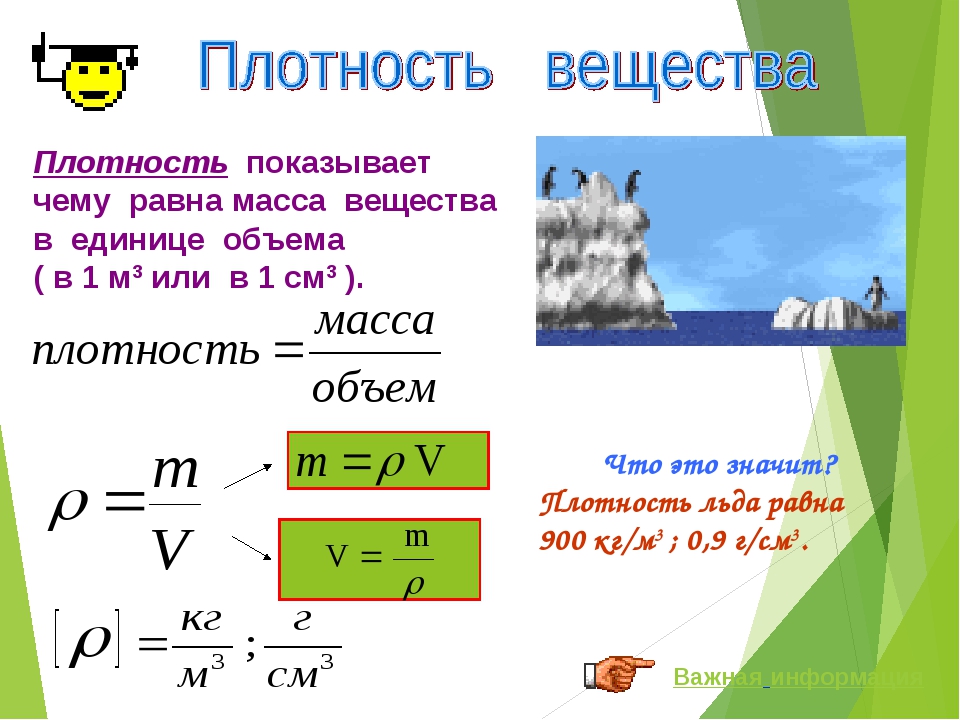 3=27\)
3=27\)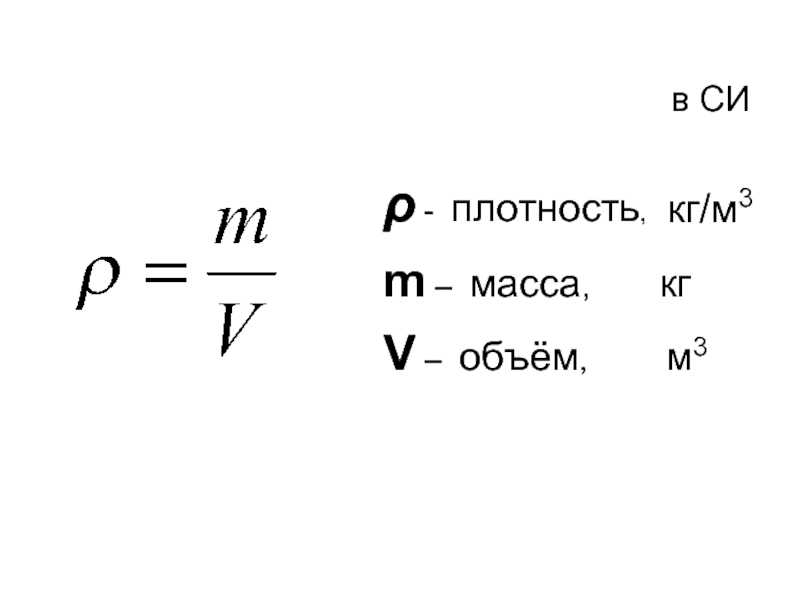 Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.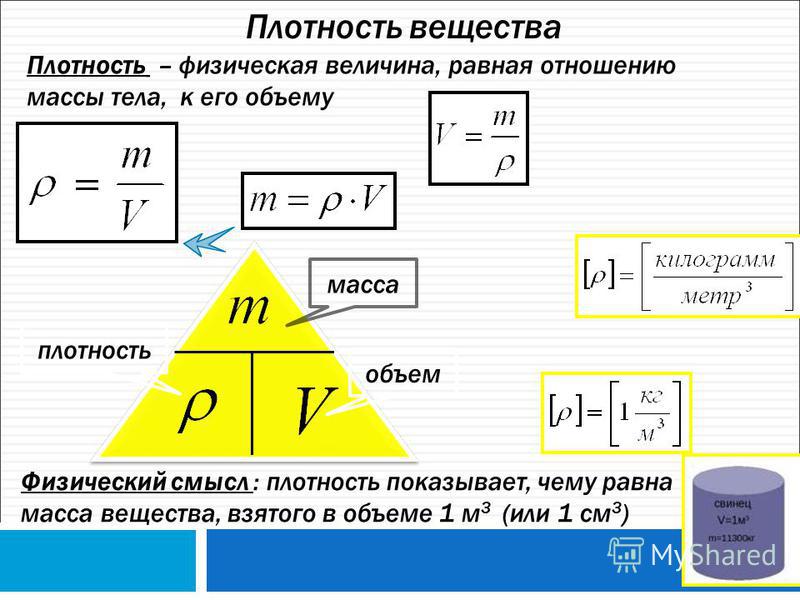


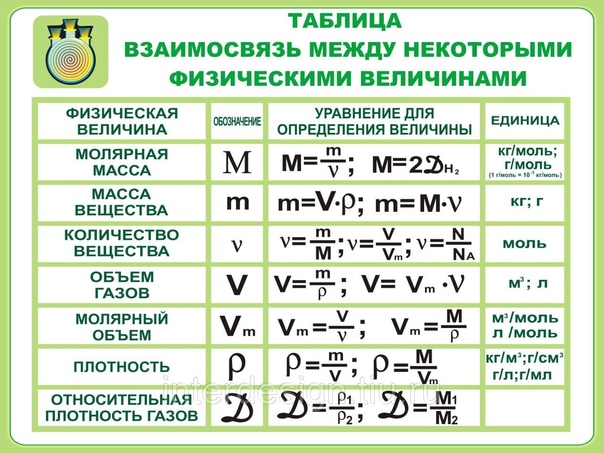
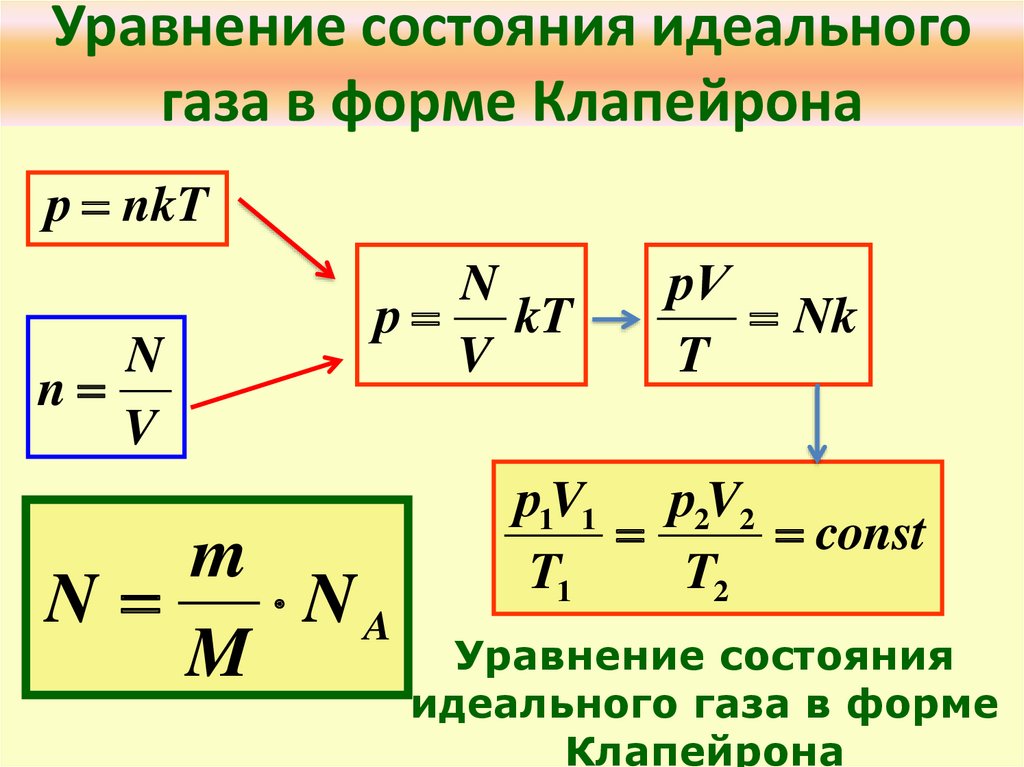
 Плотность прямо пропорциональна массе и обратно пропорциональна объему.
Плотность прямо пропорциональна массе и обратно пропорциональна объему.
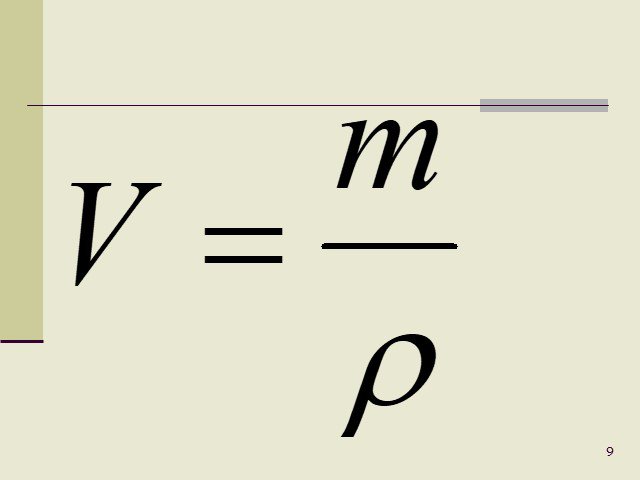
 Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».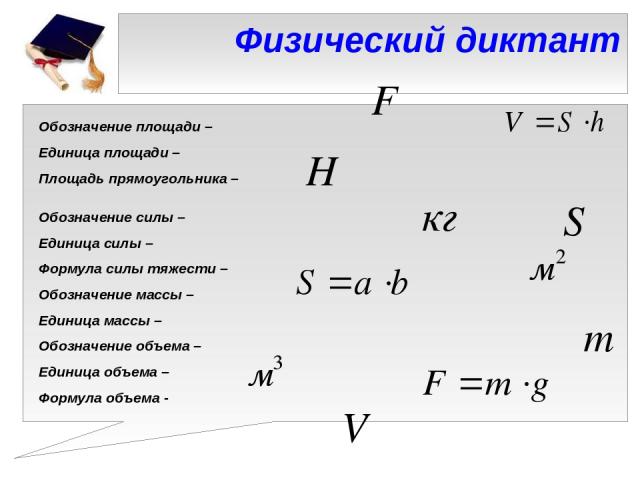










 ширина)
ширина) Сколько литров воды можно налить в бак данных размеров?
Сколько литров воды можно налить в бак данных размеров?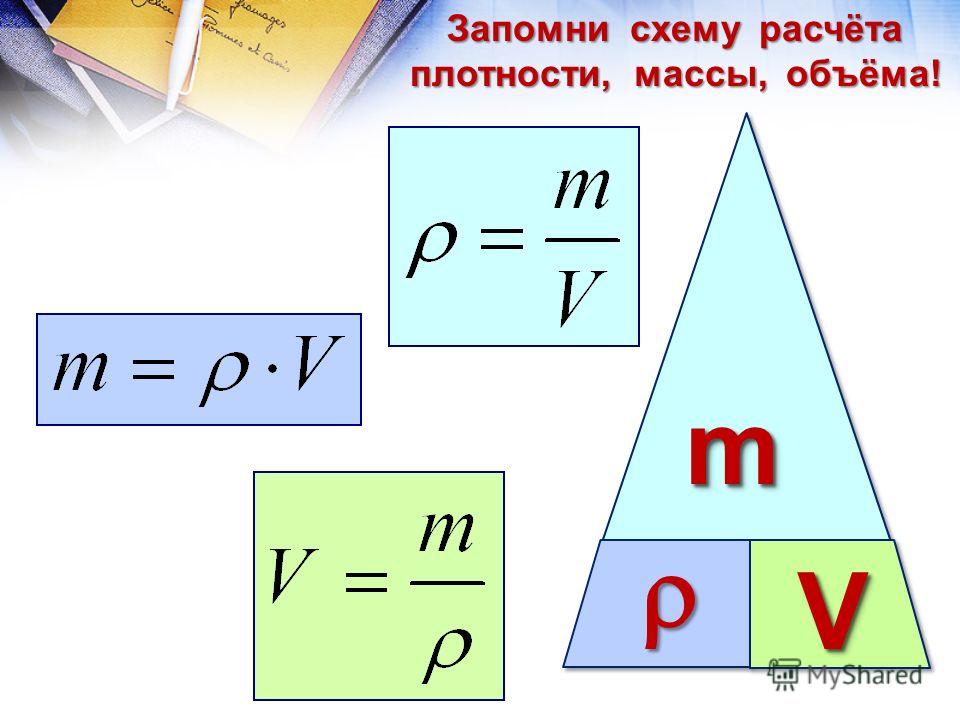 Объем является производной величиной и выражает трехмерную протяженность объекта . Объем часто количественно измеряется с использованием производной единицы СИ, кубических метров .
Объем является производной величиной и выражает трехмерную протяженность объекта . Объем часто количественно измеряется с использованием производной единицы СИ, кубических метров . Стандартная единица измерения удельных объемов в системе СИ — кубический метр на килограмм (м 3 /кг). Стандартной единицей измерения в английской системе является кубический фут на фунт массы (фут 3 /фунт).
Стандартная единица измерения удельных объемов в системе СИ — кубический метр на килограмм (м 3 /кг). Стандартной единицей измерения в английской системе является кубический фут на фунт массы (фут 3 /фунт). вещество. Самый плотный материал , обнаруженный на Земле, — это металлический осмий . Тем не менее, его плотность бледнеет по сравнению с плотностью экзотических астрономических объектов, таких как белые карлики и .0290 нейтронных звезд .
вещество. Самый плотный материал , обнаруженный на Земле, — это металлический осмий . Тем не менее, его плотность бледнеет по сравнению с плотностью экзотических астрономических объектов, таких как белые карлики и .0290 нейтронных звезд . Но ученые обнаружили следовые количества встречающегося в природе плутония.
Но ученые обнаружили следовые количества встречающегося в природе плутония.
 Изменение объема материала при изменении температуры определяется следующим соотношением:
Изменение объема материала при изменении температуры определяется следующим соотношением: Радиусы ядер можно рассчитать по следующей формуле, предполагая сферическую форму:
Радиусы ядер можно рассчитать по следующей формуле, предполагая сферическую форму: Радиус Ван-дер-Ваальса, r w , атома — это радиус воображаемой твердой сферы, представляющий расстояние наибольшего сближения для другого атома. Атом урана имеет объем около 26,9 × 10 −30 м 3 , принимая сферическую форму. Но это «огромное» пространство занято в основном электронами, потому что ядро занимает лишь около 1721×10 −45 м 3 место. Эти электроны вместе весят лишь часть (скажем, 0,05%) всего атома.
Радиус Ван-дер-Ваальса, r w , атома — это радиус воображаемой твердой сферы, представляющий расстояние наибольшего сближения для другого атома. Атом урана имеет объем около 26,9 × 10 −30 м 3 , принимая сферическую форму. Но это «огромное» пространство занято в основном электронами, потому что ядро занимает лишь около 1721×10 −45 м 3 место. Эти электроны вместе весят лишь часть (скажем, 0,05%) всего атома. Поэтому пространство в атоме (между электронами и атомным ядром) не пусто. Тем не менее, он заполнен функцией плотности вероятности электронов (обычно известной как «электронное облако »).
Поэтому пространство в атоме (между электронами и атомным ядром) не пусто. Тем не менее, он заполнен функцией плотности вероятности электронов (обычно известной как «электронное облако »).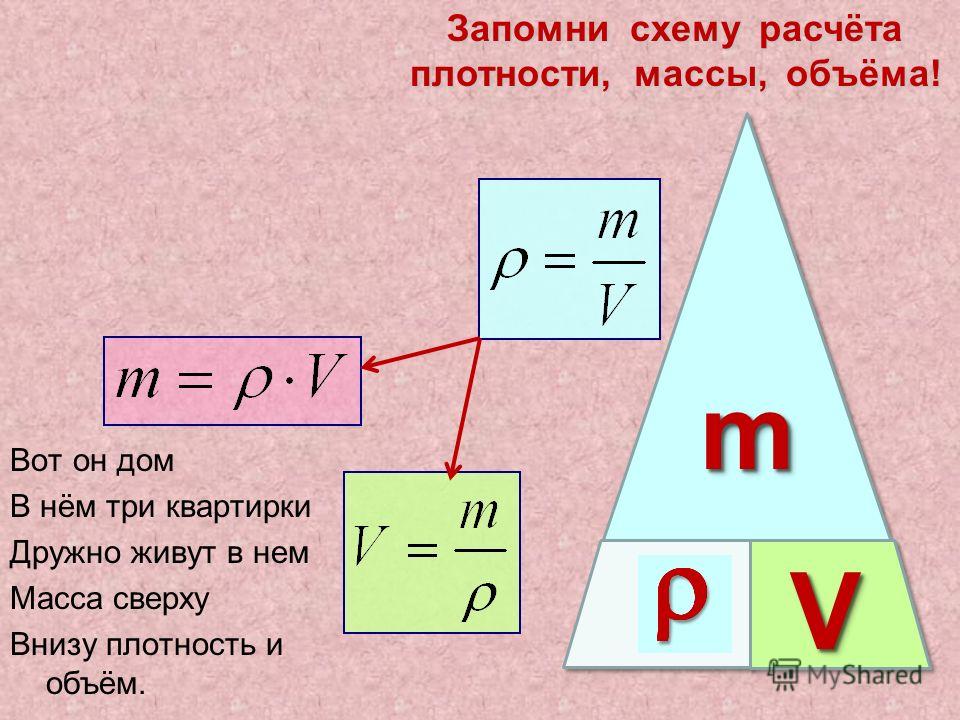
 Около 60% объема компенсатора давления занимает сжатая вода при нормальных условиях, а около 40% объема занимает насыщенный пар .
Около 60% объема компенсатора давления занимает сжатая вода при нормальных условиях, а около 40% объема занимает насыщенный пар . Это явление известно как тепловое расширение . Изменение объема материала, подвергающегося изменению температуры, определяется следующим соотношением:
Это явление известно как тепловое расширение . Изменение объема материала, подвергающегося изменению температуры, определяется следующим соотношением: Эти изменения естественным образом отражаются в изменении уровня воды в компенсаторе давления. При постепенном снижении средней температуры теплоносителя реактора общий объем воды также уменьшается, что снижает уровень компенсатора давления. При постепенном наборе нагрузки увеличение средней температуры теплоносителя реактора вызывает расширение общего объема воды, повышая уровень компенсатора давления. Эти эффекты должны контролироваться системой контроля уровня компенсатора давления.
Эти изменения естественным образом отражаются в изменении уровня воды в компенсаторе давления. При постепенном снижении средней температуры теплоносителя реактора общий объем воды также уменьшается, что снижает уровень компенсатора давления. При постепенном наборе нагрузки увеличение средней температуры теплоносителя реактора вызывает расширение общего объема воды, повышая уровень компенсатора давления. Эти эффекты должны контролироваться системой контроля уровня компенсатора давления. В этом анализе будет рассматриваться струйная трубка ( контрольный объем ), как мы делали для уравнения Бернулли. В этом контрольном объеме , любое изменение импульса жидкости в контрольном объеме происходит из-за действия внешних сил на жидкость внутри объема.
В этом анализе будет рассматриваться струйная трубка ( контрольный объем ), как мы делали для уравнения Бернулли. В этом контрольном объеме , любое изменение импульса жидкости в контрольном объеме происходит из-за действия внешних сил на жидкость внутри объема. Этот объем может быть статичным, подвижным и даже деформироваться во время течения. Чтобы решить любую задачу, мы должны решить основные законы сохранения в этом томе. Очень важно знать все относительные скорости потока к поверхности управления. Поэтому очень важно точно определить границы контрольного объема при анализе.
Этот объем может быть статичным, подвижным и даже деформироваться во время течения. Чтобы решить любую задачу, мы должны решить основные законы сохранения в этом томе. Очень важно знать все относительные скорости потока к поверхности управления. Поэтому очень важно точно определить границы контрольного объема при анализе.
 Какова масса копии, если масса оригинала равна 50 кг? (Плотность снега в обоих снеговиках одинаковая.) (9 баллов)
Какова масса копии, если масса оригинала равна 50 кг? (Плотность снега в обоих снеговиках одинаковая.) (9 баллов) Общее время движения велосипедиста t= t₁+ t₂. Таким образом можно записать:
Общее время движения велосипедиста t= t₁+ t₂. Таким образом можно записать:  Затем поместить его в теплое помещение. В помещении в результате конденсации пара бидон покроется капельками воды. По мере нагревания бидона в теплом помещении вода на нем будет испаряться. Так как масса воздуха и паров бензина в верхней части его значительно меньше массы керосина, находящегося в нижней части бидона, то при нагревании бидона в тёплом помещении испарение будет происходить быстрее с верхней части его. В результате в какой-то момент времени можно будет наблюдать резкую границу между сухой поверхностью бидона и частью его, еще покрытой капельками воды. Эта граница и укажет на уровень керосина в бидоне.
Затем поместить его в теплое помещение. В помещении в результате конденсации пара бидон покроется капельками воды. По мере нагревания бидона в теплом помещении вода на нем будет испаряться. Так как масса воздуха и паров бензина в верхней части его значительно меньше массы керосина, находящегося в нижней части бидона, то при нагревании бидона в тёплом помещении испарение будет происходить быстрее с верхней части его. В результате в какой-то момент времени можно будет наблюдать резкую границу между сухой поверхностью бидона и частью его, еще покрытой капельками воды. Эта граница и укажет на уровень керосина в бидоне.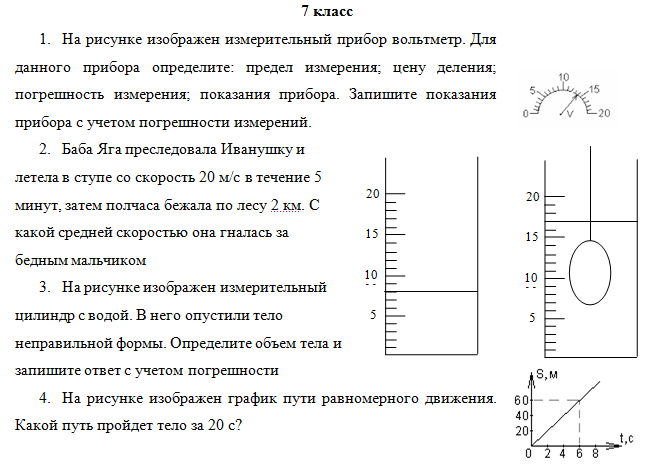 Рекомендации относительно уровня каждой темы в рамках программы можно найти в прошлых вопросах IPhO.
Рекомендации относительно уровня каждой темы в рамках программы можно найти в прошлых вопросах IPhO.
 5% лучших могут быть приглашены на участие в USAPhO в формате бесплатных ответов. Лучшие участники могут быть приглашены в лагерь олимпиады по физике в США, где может быть сделан окончательный выбор.
5% лучших могут быть приглашены на участие в USAPhO в формате бесплатных ответов. Лучшие участники могут быть приглашены в лагерь олимпиады по физике в США, где может быть сделан окончательный выбор.  Использование калькуляторов запрещено»
Использование калькуляторов запрещено»  Первым в этой серии является Американский пригласительный экзамен по математике (AIME), за которым следуют Математическая олимпиада США и Юношеская математическая олимпиада (USAMO и USAJMO). Лучшие участники из USA(J)MO приглашаются на программу математической олимпиады летом после соревнований. Затем участники программы математической олимпиады имеют право быть отобранными следующим летом в состав команды из шести человек, которая будет представлять Соединенные Штаты Америки в ИМО».
Первым в этой серии является Американский пригласительный экзамен по математике (AIME), за которым следуют Математическая олимпиада США и Юношеская математическая олимпиада (USAMO и USAJMO). Лучшие участники из USA(J)MO приглашаются на программу математической олимпиады летом после соревнований. Затем участники программы математической олимпиады имеют право быть отобранными следующим летом в состав команды из шести человек, которая будет представлять Соединенные Штаты Америки в ИМО».