Момент силы — как найти? В чем измеряется? Формулы
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, является мерой действия тела на другое тело.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный.
В данном случае результат выражается в направлении движения.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила — это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте.
Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Правило равновесия рычага Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил. F1, F2 — силы, действующие на рычаг l1, l2 — плечи этих сил |
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.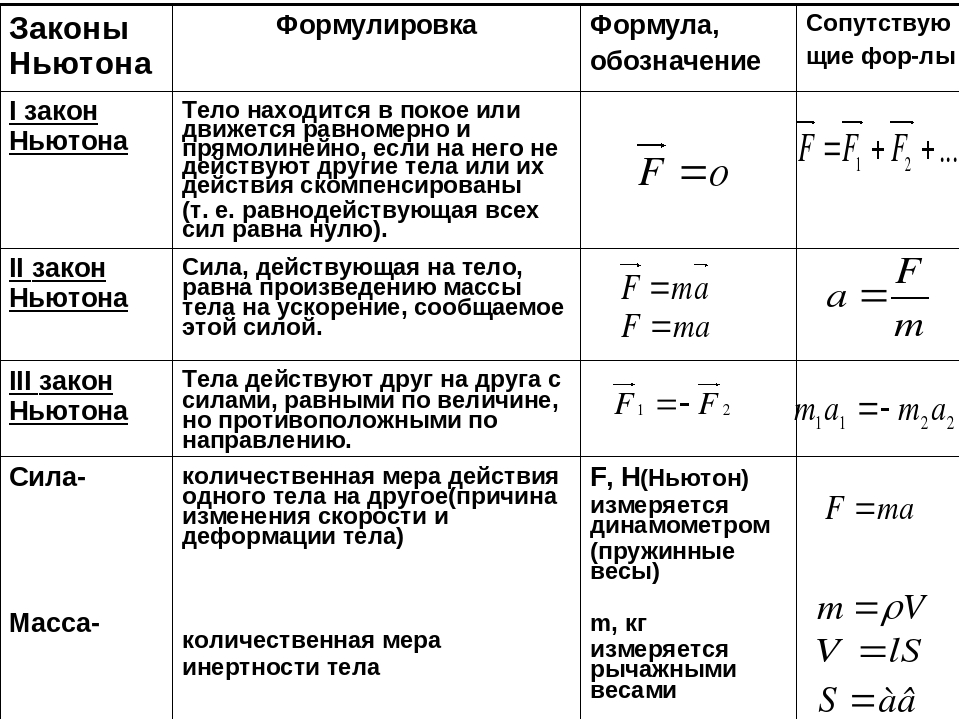
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
M = Fl M — момент силы [Н*м] |
Для примера представьте, что вы забыли, как открывать двери. Стоите перед дверью и раздумываете, как легче это сделать.
Для начала приложим силу к краю двери — туда, где самый длинный рычаг.
Открылась!
А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придется приложить силу большего значения.
Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.
Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
МА=F×AB=F×3м
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
MB=F×cos30×AB=F×cos30×3м
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
MB=F×3м
Правило моментов
Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м] M’1 + M’2 +…+ M’n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м] |
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом: — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке.
Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага:
где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага
Отсюда
Ответ: Масса груза равна 0,3 кг
Задача 4 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии.
Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
youtube.com/embed/OctfStSExzo» title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»» ssmarticle=»»/>
Второй закон Ньютона просто и понятно: определение и формула
Основные понятия: сила, ускорение, масса– В чем сила брат?
– В Ньютонах брат.
С этой шутки можно начать, а точнее продолжить нашу статью о законах Ньютона, на которых, словно на трех слонах стоят основы классической механики. О первом законе Ньютона мы уже писали, и сегодня очередь за вторым законом имени великого английского физика. В чем его суть, как звучит второй закон Ньютона и какая его формула, об этом читайте далее.
Основные понятия: сила, ускорение, масса
Именно с открытием второго закона Ньютона его имя стало ассоциироваться с физическим понятием силы.
Впрочем, сила стала не только ассоциироваться, но и измеряться в ньютонах. Да и сам второй закон тесно связан с понятием силы, а также скорости, и ускорения, а еще массы. Но обо всем по порядку.
Что такое сила в физике? Сила это некая физическая величина, обязательно имеющая свое направление (вектор), которая является мерой действия на тело. Обозначается сила литерой F. Измерить величину силы можно при помощи специального прибора – динамометра. Обычно он состоит из пружины, связанной со стрелочным указателем. Если пружину растянуть, то произойдет отклонение стрелки, которая покажет количественную характеристику силы F.
Вот так выглядит динамометр, измеритель силы. Впрочем, существуют разные разновидности этого прибора. Обычно на тело при движении действует сразу несколько сил (к тому же имеющих разную направленность или вектор): сила гравитации, сила трения и т. д.
В прошлой статье о первом законе у нас в качестве примера фигурировала некая тележка.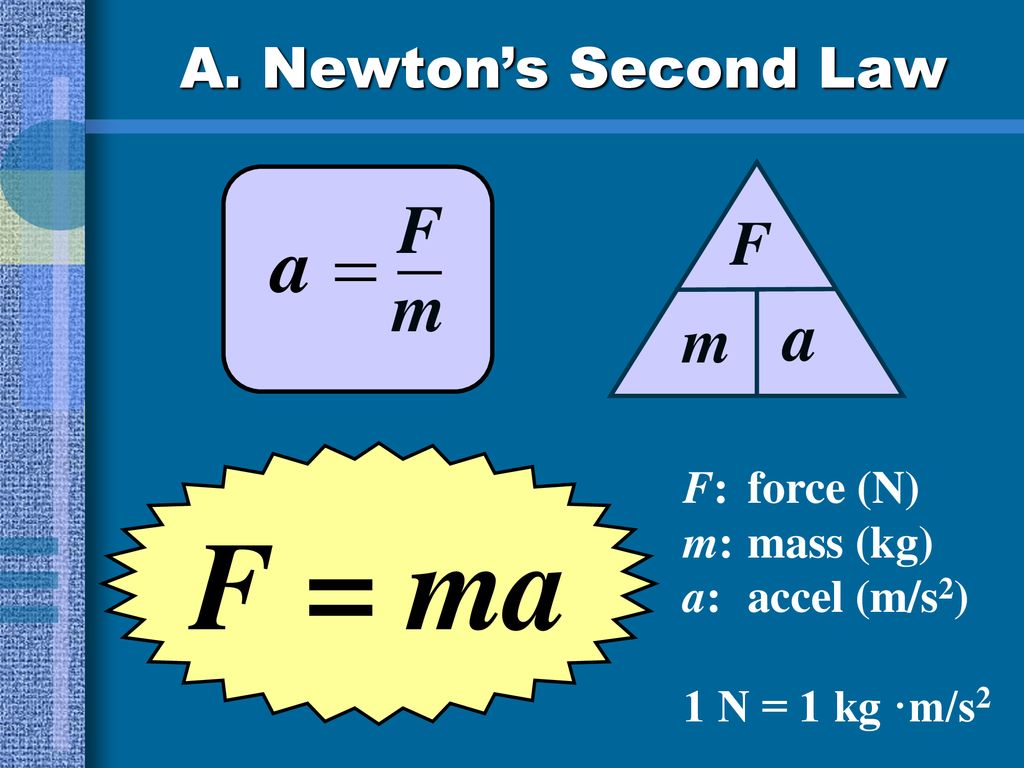
Если приложить силу к этой тележке она станет катиться, и если представить, что на тележку не действуют никакие другие силы, то она будет катиться бесконечно. Бесконечно тележки катиться могут только в придуманной Ньютоном инерциальной системе отсчета (ИСО), существующей лишь теоретически. На практике же мы прекрасно понимаем, что тележка покатится лишь какое-то время и вскоре остановится. А значит, ее скорость изменится, от некоего значения до нуля.
То как меняется скорость в течение времени, называется ускорением (его принято обозначать литерой a). На практике в реальной жизни все тела движутся с ускорением, причем если скорость нарастает, или убывает равномерно, то такое движение называется равноускоренным. Примером такого движение может быть падение любого тела вниз, оно будет падать с одинаковым ускорением, формируемым земной гравитацией g.
И напоследок на характеристику движения любого тела влияет его масса, которую принято обозначать литерой m. В физике масса часто является мерой инертности тела, то есть чем больше масса того или иного тела, тем труднее его сдвинуть с места, но уже сдвинув, его опять таки труднее остановить.
Определение
Если первый закон Ньютона в свое время пытался объяснить то, как работает небесная механика, каким образом планеты непрерывно движутся вокруг Солнца (и не падают на него), то второй закон в этом плане более приземлен, он объясняет движение тел тут, на Земле. По сути это основной закон динамики, базовой закон физической природы.
Существует несколько классических определений второго закона Ньютона: первое из них гласит: сила, оказывающая воздействие на тело, равна произведению массы тела на сообщаемое данной силой ускорение.
Второе определение идет не от силы, а от ускорения, оно гласит: ускорение тела прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Формула
Первое приведенное нами определение можно записать классической формулой:
F = ma
Где F – сила, действующая на тело, m – его масса, а – ускорение.
Для второго определения уравнение будет следующим:
a = F/m
Иными словами, чем больше сила, действующая на тело, тем больше его ускорения, и наоборот, чем больше масса тела, тем его ускорение будет меньшим.
По сути, мы пересказали суть второго закона Ньютона своими словами.
Равнодействующая сила
Как мы писали выше, на практике в реальной жизни на каждое физическое тело действует не одна, а несколько сил, причем с разными направлениями. Какое же отражения во втором законе Ньютона находит действия разных сил, обозначим их F1, F2, F3. Так вот если на тело действует несколько сил, то в формуле второго закона фигурирует равнодействующая сила F, которая высчитывается по формуле:
F = F1 + F2 + F3.
Если же равнодействующая сила будет равна нулю, то тело будет пребывать в состоянии покоя, либо равномерного прямолинейного движения.
Рекомендованная литература и полезные ссылки
- Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977.
- Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974.
- Crowell, Benjamin (2011), Light and Matter (2011, Light and Matter), especially at Section 4.
2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law. - Feynman, R. P. (англ.)русск.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics (неопр.). — 2nd. — Pearson/Addison-Wesley, 2005. — Т. Vol. 1. — ISBN 0-8053-9049-9.
2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.Видео
И в завершении образовательное видео по теме нашей статьи.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.
Страница про автора
Масса | Определение, единицы и факты
вес и расстояние от Земли
Посмотреть все СМИ
- Ключевые люди:
- Субрахманьян Чандрасекар
- Похожие темы:
- сохранение массы плотность Предел массы Эддингтона релятивистская масса уменьшенная масса
Просмотреть весь связанный контент →
масса , в физике количественная мера инерции, фундаментальное свойство всей материи.
По сути, это сопротивление, которое материя оказывает изменению своей скорости или положения при приложении силы. Чем больше масса тела, тем меньше изменение, производимое приложенной силой. Единицей массы в Международной системе единиц (СИ) является килограмм, который определяется через постоянную Планка, которая равна 6,62607015 × 10 −34 джоулей в секунду. Один джоуль равен одному килограмму, умноженному на квадратный метр на секунду в квадрате. Поскольку секунда и метр уже определены в терминах других физических констант, килограмм определяется точными измерениями постоянной Планка. (до 2019 г.килограмм определялся платино-иридиевым цилиндром, называемым международным прототипом килограмма, хранящимся в Международном бюро мер и весов в Севре, Франция.) В английской системе измерения единицей массы является порция, масса которой уровень моря 32,17 фунта.
Вес, хотя и связан с массой, тем не менее отличается от последней. Вес, по сути, представляет собой силу, действующую на вещество гравитационным притяжением Земли, и поэтому он немного варьируется от места к месту.
Напротив, масса остается постоянной независимо от ее положения при обычных обстоятельствах. Спутник, запущенный в космос, например, весит тем меньше, чем дальше он удаляется от Земли. Однако его масса остается прежней.
Еще из Британники
Галактика Млечный Путь: Масса
В соответствии с принципом сохранения массы масса объекта или набора объектов никогда не меняется, как бы ни перестраивались составные части. Если тело разделить на части, то вместе с частями делится и масса, так что сумма масс отдельных частей равна первоначальной массе. Или, если частицы соединены вместе, масса композита равна сумме масс составляющих частиц. Однако этот принцип не всегда верен.
С появлением специальной теории относительности Эйнштейна в 1905 году понятие массы подверглось радикальному пересмотру. Масса потеряла свою абсолютность. Было замечено, что масса объекта эквивалентна энергии, взаимопревращается с энергией и значительно увеличивается при чрезвычайно высоких скоростях, близких к скорости света (около 3 × 10 8 метров в секунду, или 186 000 миль в секунду).
Под полной энергией объекта понималась его масса покоя, а также увеличение его массы, вызванное высокой скоростью. Было обнаружено, что масса покоя атомного ядра значительно меньше суммы масс покоя составляющих его нейтронов и протонов. Масса больше не считалась постоянной или неизменной. Как в химических, так и в ядерных реакциях происходит некоторая конверсия между массой и энергией, так что продукты обычно имеют меньшую или большую массу, чем реагенты. Разница в массе для обычных химических реакций настолько незначительна, что закон сохранения массы можно использовать в качестве практического принципа для предсказания массы продуктов. Однако закон сохранения массы недействителен для поведения масс, активно участвующих в ядерных реакторах, ускорителях частиц и в термоядерных реакциях на Солнце и в звездах. Новый принцип сохранения — сохранение массы-энергии. См. также энергия, сохранение; энергия; Соотношение массы и энергии Эйнштейна.
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Эриком Грегерсеном.
| Ознакомьтесь с семью определяющими константами СИ. Определения основных единиц СИ Моль, символ моль, является единицей СИ количества вещества. Один моль содержит ровно 6,022 140 76 x 10 23 элементарных частиц. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Следующие семь определений базовых единиц СИ основаны на Брошюре SI BIPM (9-е издание).
Это число представляет собой фиксированное числовое значение постоянной Авогадро, N A , выраженное в единицах моль -1 , и называется числом Авогадро.
Количество вещества, символ n , системы является мерой количества определенных элементарных объектов. Элементарным объектом может быть атом, молекула, ион, электрон, любая другая частица или определенная группа частиц.