Кинематика | Формулы по физике
Путь, время, скорость
Найти
Известно, что:
Svt =
Вычислить ‘S’Равномерное движение
Найти
Известно, что:
xx_0vt =
Вычислить ‘x’Равномерно ускоренное движение: ускорение
Найти
Известно, что:
avv0t =
Вычислить ‘a’Равномерно ускоренное движение: скорость
Найти
Известно, что:
vv0at =
Вычислить ‘v’Равномерно ускоренное движение: путь
Найти
Известно, что:
svta =
Вычислить ‘s’Равномерно ускоренное движение: координата
Найти
Известно, что:
xx0vta =
Вычислить ‘x’Высота тела, брошенного вертикально вверх (вниз)
Найти
Известно, что:
hh0v0tg = Вычислить ‘h’Скорость тела, брошенного вертикально вверх (вниз)
Найти
Известно, что:
vv0gt =
Вычислить ‘v’Скорость, ускорение, время
Найти
Известно, что:
vat =
Вычислить ‘v’Скорость свободно падающего тела
Найти
Известно, что:
vgt =
Вычислить ‘v’Центростремительное ускорение
Найти
Известно, что:
avR =
Вычислить ‘a’Угловая скорость
Найти
Известно, что:
ωφt =
Вычислить ‘ω’Равномерное круговое движение
Найти
Известно, что:
lRφ =
Вычислить ‘l’Равномерное круговое движение: линейная скорость
Найти
Известно, что:
vRω = Вычислить ‘v’Период вращения
Найти
Известно, что:
TtN =
Вычислить ‘T’Период вращения
Найти
Известно, что:
TπRv =
Вычислить ‘T’Период вращения
Найти
Известно, что:
Tπω =
Вычислить ‘T’Центростремительное ускорение
Найти
Известно, что:
aπRT =
Вычислить ‘a’Центростремительное ускорение
Найти
Известно, что:
aπRn =
Вычислить ‘a’Частота вращения
Найти
Известно, что:
nT =
Вычислить ‘n’Центростремительное ускорение
Найти
Известно, что:
aωR =
Вычислить ‘a’ Дальность броска тела, брошенного под углом к горизонтуНайти
Известно, что:
xv0tα =
Вычислить ‘x’Высота подъема тела, брошенного под углом к горизонту
Найти
Известно, что:
yv0tαg =
Вычислить ‘y’Вертикальная скорость тела, брошенного под углом к горизонту
Найти
Известно, что:
v_yv0αgt =
Вычислить ‘v_y’Максимальная высота подъема тела, брошенного под углом к горизонту
Найти
Известно, что:
h_максv0αg =
Вычислить ‘h_макс’Общее время движения тела, брошенного под углом к горизонту
Найти
Известно, что:
tv0αg =
Вычислить ‘t’Максимальная дальность броска тела, брошенного под углом к горизонту
Найти
Известно, что:
s_максv0g =
Вычислить ‘s_макс’Дальность броска тела, брошенного горизонтально
Найти
Известно, что:
xx0vt =
Вычислить ‘x’Высота подъема тела, брошенного горизонтально
Найти
Известно, что:
yy0gt =
Вычислить ‘y’Общее время движения тела, брошенного горизонтально
Найти
Известно, что:
t_максhg =
Вычислить ‘t_макс’Формулы по физике 11 класса.
 Все формулы по физике за 11 класс с пояснениями и определениями
Все формулы по физике за 11 класс с пояснениями и определениями| Закон | Формула | Единицы измерения | |
|---|---|---|---|
| Формула расчета силы Ампера | FA = B I L sinα | Закон Ампера: сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником. | FA – сила Ампера, [Н] В – магнитная индукция, [Тл] I – сила тока, [А] L – длина проводника, [м] |
| Формула расчета силы Лоренца | Fл= q B υ sinα | Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы. | Fл – сила Лоренца, [Н] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с] |
| Формула радиуса движения частицы в магнитном поле | r= mυ/qB | r – радиус окружности, по которой движется частица в магнитном поле, [м] m – масса частицы, [кг] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с] | |
| Формула для вычисления магнитного потока | Ф = B S cosα | Ф – магнитный поток, [Вб] В – магнитная индукция, [Тл] S – площадь контура, [м2] | |
| Формула для вычисления величины заряда | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Закон Ома для участка цепи | I = U/R | Закон Ома — сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления удельного сопротивления проводника | R = ρ L/S ρ = R S/L | Удельное сопротивление – величина, характеризующая электрические свойства вещества, из которого изготовлен проводник. | ρ – удельное сопротивление вещества, [Ом·мм2/м] R – сопротивление, [Ом] S – площадь поперечного сечения проводника, [ммБ2] L – длина проводника, [м] |
| Законы последовательного соединения проводников | I = I1 = I2 U = U1 + U2 Rобщ = R1 + R2 | Последовательным соединением называется соединение, когда элементы идут друг за другом. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Законы параллельного соединения проводников | U = U1 = U2 I = I1 + I2 1/Rобщ =1/R1 +1/R2 | Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления величины заряда. | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула для нахождения работы электрического тока. | A = Uq A = UIt | Работа – это величина, которая характеризует превращение энергии из одного вида в другой, т.е. показывает, как энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д. Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле. | A – работа электрического тока, [Дж] U – напряжение на концах участка, [В] q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула электрической мощности | P = A/t P = UI P = U2/R | Мощность – работа, выполненная в единицу времени. | P – электрическая мощность, [Вт] A – работа электрического тока, [Дж] t – время, [c] U – напряжение на концах участка, [В] I – сила тока, [А] R – сопротивление, [Ом] |
| Формула закона Джоуля-Ленца | Q=I2Rt | Закон Джоуля-Ленца при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику. | Q – количество теплоты, [Дж] I – сила тока, [А]; t – время, [с]. R – сопротивление, [Ом]. |
| ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ | |||
| Закон отражения света | Луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, при этом угол падения луча равен углу отражения луча. | ||
| Закон преломления | sinα/sinγ = n2/n1 | При увеличении угла падения увеличивается и угол преломления, то есть при угле падения, близком к 90°, преломлённый луч практически исчезает, а вся энергия падающего луча переходит в энергию отражённого. | n – показатель преломления одного вещества относительно другого |
| Формула вычисления абсолютного показателя преломления вещества | n = c/v | Абсолютный показатель преломления вещества – величина, равная отношению скорости света в вакууме к скорости света в данной среде. | n – абсолютный показатель преломления вещества c – скорость света в вакууме, [м/с] v – скорость света в данной среде, [м/с] |
| Закон Снеллиуса | sinα/sinγ = v1/v2=n | Закон Снеллиуса (закон преломления света): отношение синуса угла падения к синусу угла преломления есть величина постоянная. | |
| Показатель преломления среды | sinα/sinγ = n | Отношение синуса угла падения к синусу угла преломления есть величина постоянная. | n – показатель преломления среды |
| Преломляющий угол призмы | δ = α(n – 1) | δ – угол отклонения α – угол падения n – показатель преломления среды | |
| Линейное увеличение оптической системы | Г = H/h | Г – линейное увеличение оптической системы H – размер изображения, [м] h – размер предмета, [м] | |
| Формула оптической силы линзы | D = 1/F | Оптическая сила линзы – способность линзы преломлять лучи. | D – оптическая сила линзы, [дптр] F – фокусное расстояние линзы, [м] |
| Формула тонкой линзы | 1/F = 1/d+1/f | F – фокусное расстояние линзы, [м] d – расстояние от предмета до линзы, [м] f – расстояние от линзы до изображения, [м] | |
| Максимальная результирующая интенсивность | Δt = mT | Δt – максимальная результирующая интенсивность Т – период колебании, [с] | |
| Минимальная результирующая интенсивность | Δt = (2m + 1)T/2 | Δt – минимальная результирующая интенсивность Т – период колебании, [с] | |
| Геометрическая разность хода интерферирующих волн | Δ = mλ | Δ – геометрическая разность хода интерферирующих волн λ – длина волны, [м] | |
| Условие интерференционного минимума | Δ = (2m + 1)λ/2 | λ – длина волны, [м] | |
| Условие дифракционного минимума на щели | Asinα = m λ | A – ширина щели, [м] λ – длина волны, [м] | |
| Условие главных максимумов при дифракции | dsinα = m λ | d – период решетки λ – длина волны, [м] | |
| Энергия кванта излучения | E = hϑ | Е – энергия кванта излучения, [Дж] ϑ – частота излучения h – постоянная Планка | |
| Закон смещения Вина | λT = b | b – постоянная Вина λ – длина волны, [м] Т – температура черного тела | |
| Закон Стефана-Больцмана | R = ϭT4 | ϭ – постоянная Стефана-Больцмана Т – абсолютная температура черного тела R – интегральная светимость абсолютно черного тела | |
| Уравнение Эйнштейна для фотоэффекта | А – работа выхода, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с] ϑ – частота излучения h – постоянная Планка | ||
| ФИЗИКА ВЫСОКИХ ЭНЕРГИИ | |||
| Массовое число | M = Z + N | M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов | |
| Формула массы ядра | МЯ = МА – Z me | MЯ – масса ядра, [кг] МА – масса изотопа , [кг] me – масса электрона, [кг] | |
| Формула дефекта масс | ∆m = Zmp+ Nmn – MЯ | Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида. | ∆m – дефект масс, [кг] mp – масса протона, [кг] mn – масса нейтрона, [кг] |
| Формула энергии связи | Есвязи = ∆m c2 | Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны). | Есвязи – энергия связи, [Дж] m – масса, [кг] с = 3·108м/с – скорость света |
| Закон радиоактивного распада | N = N02 –t/T1/2 | N0 – первоначальное количество ядер N – конечное количество ядер T – период полураспада, [c] t – время, [c] | |
| Доза поглощенного излучения | D = E/m | D – доза поглощенного излучения, [Гр] E – энергия излучения, [Дж] m – масса тела, [кг] | |
| Эквивалентная доза поглощенного излучения | H = Dk | H – эквивалентная доза поглощенного излучения, [Зв] D – доза поглощенного излучения, [Гр] k – коэффициент качества | |
Быстро найти нужную формулу для расчета онлайн.
 Геометрия. Алгебра.
Геометрия. Алгебра.h — высота на которую опустилось тело за время t
S — расстояние по горизонтали, пройденное телом за время t
V — скорость тела, направленная по касательной к траектории движения, через время t
Vo — начальная скорость тела, которая является составляющей скорости V и направленна по горизонтали (не меняется со временем)
Vg — составляющая скорости V, направленная по вертикали вниз, возникает под воздействием силы тяжести и в начале броска равна нулю
t — время падения тела на высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
Используя теорему Пифагора, по формуле, находим численное значение скорости V, а по правилу сложения векторов, можем определить направление , которое всегда будет по касательной к траектории движения :
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vo):
Формула расстояния по горизонтали, которое пролетело тело при падении (S):
Формула высоты, на которую опустилось тело при падении (h):
Формула времени падения тела (t):
Рейтинг: 5 / 5
hmax — максимальная высота
Smax — максимальная дальность полета, если бросок и падение на одном уровне
Sh — расстояние пройденное по горизонтали до момента максимального подъема
tmax — время всего полета
th — время за которое тело поднялось на максимальную высоту
Vo — начальная скорость тела
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для расчета максимальной высоты достигнутое телом, если даны, начальная скорость Vo и угол α под которым брошено тело.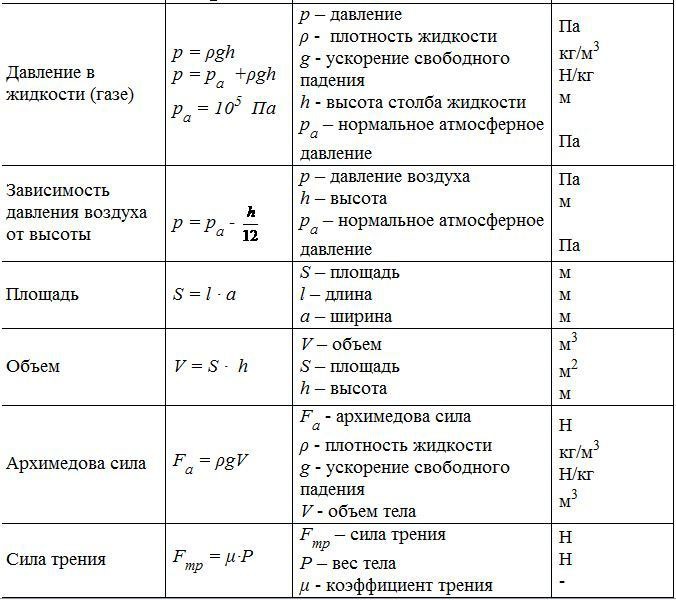 :
:
Формула для вычисления максимальной высоты, если известны, максимальное расстояние S max или расстояние по горизонтали при максимальной высоте Sh и угол α под которым брошено тело. :
По этой формуле, можно определить максимальную высоту, если известно время th за которое тело поднялось на эту высоту. :
Формула для расчета максимальной дальности полета, если даны, начальная скорость броска Vo и угол α под которым брошено тело. :
или известны максимальная высота hmax и угол α под которым брошено тело. :
:
Формула для нахождения расстояния по горизонтали при максимальной высоте, если даны, начальная скорость броска Vo и угол α под которым брошено тело. :
или известны максимальная высота hmax и угол α под которым брошено тело. :
* т. к. траектория движения симметрична относительно линии максимальной высоты, то расстояние Sh ровно в два раза, меньше максимальной дальности броска Smax
Формула для определения времени затраченного на весь полет, если даны, начальная скорость Vo и угол α под которым брошено тело или если известна только максимальная высота hmax :
* т. к. траектория движения симметрична относительно линии максимальной высоты, то время максимального подъема th ровно в два раза, меньше максимального времени tmax
к. траектория движения симметрична относительно линии максимальной высоты, то время максимального подъема th ровно в два раза, меньше максимального времени tmax
Формула для определения времени за которое тело поднялось на максимальную высоту, если даны, начальная скорость Vo и угол α под которым брошено тело или если известна только максимальная высота hmax :
Рейтинг: 5 / 5
1. Определить, на какой высоте находится тело, в любой точке траектории движения
h — высота тела в момент времени t
hну — высота ниже уровня броска (принимает отрицательное значение)
S — дальность полета по горизонтали
t — время полета
Vo — начальная скорость тела
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для определения значения высоты тела в момент времени t
Формула для определения значения высоты тела через расстояние S по горизонтали
hну — высота ниже уровня броска, принимает отрицательное значение
2.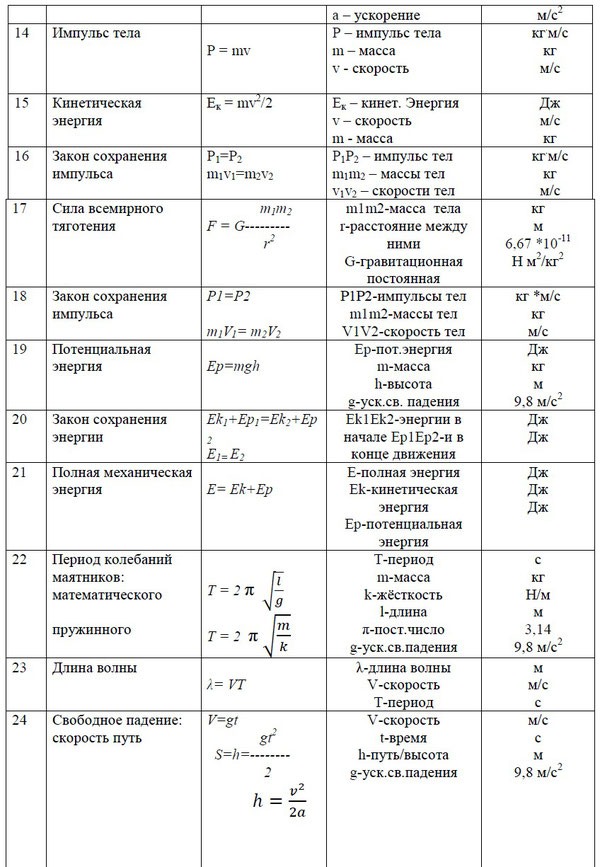 Найти максимальную высоту, на которую поднялось тело
Найти максимальную высоту, на которую поднялось тело
hmax — максимальная высота
Smax — максимальная дальность полета, если бросок и падение на одном уровне
Sh — расстояние пройденное по горизонтали до момента максимального подъема
tmax — время всего полета
th — время за которое тело поднялось на максимальную высоту
Vo — начальная скорость тела
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для расчета максимальной высоты достигнутое телом, если даны, начальная скорость Vo и угол α под которым брошено тело. :
Формула для вычисления максимальной высоты, если известны, максимальное расстояние S max или расстояние по горизонтали при максимальной высоте Sh и угол α под которым брошено тело.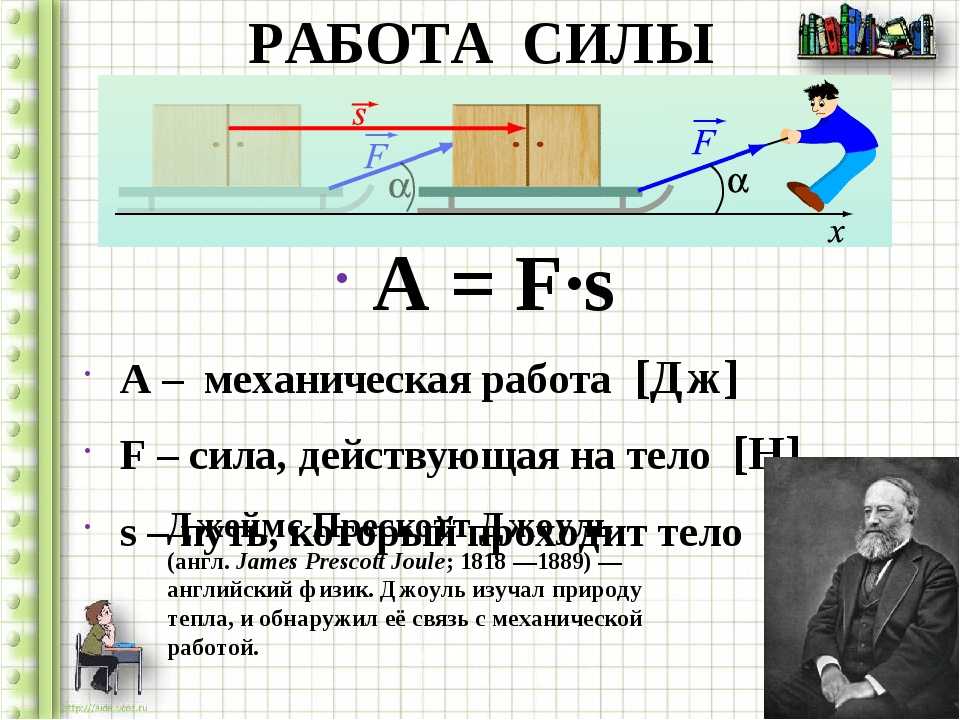 :
:
По этой формуле, можно определить максимальную высоту, если известно время th за которое тело поднялось на эту высоту. :
Рейтинг: 0 / 5
1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
h max — максимальная высота достигнутая телом за время t
Vк — конечная скорость тела на пике, равная нулю
Vн — начальная скорость тела
t — время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула максимальной высоты (h max):
Формула времени за которое тело достигло максимальную высоту (t):
2.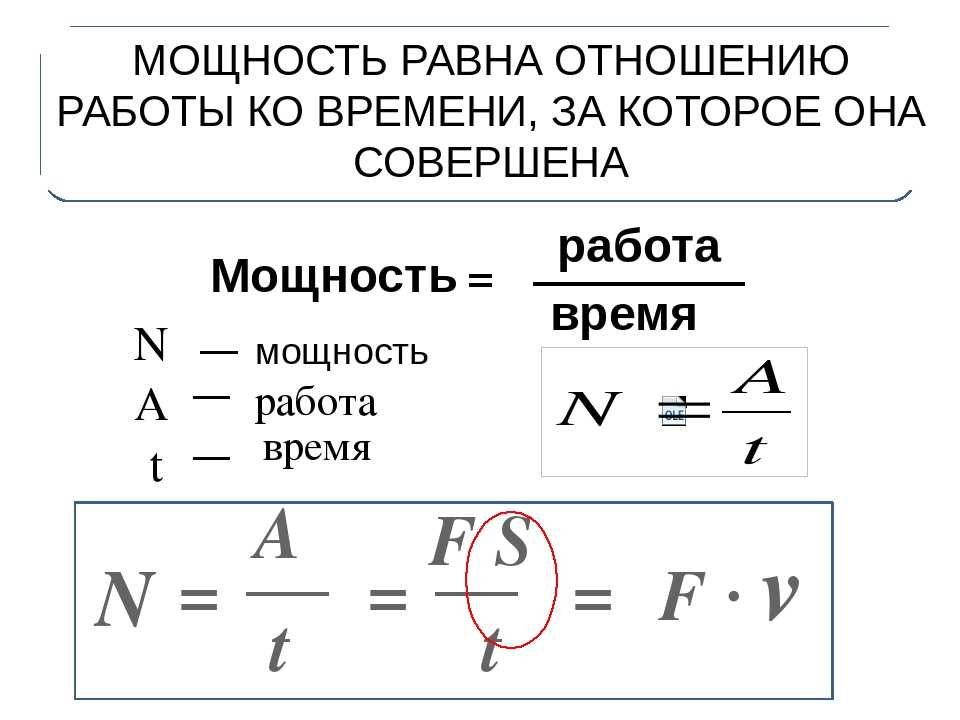 Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h — расстояние пройденное телом за время t
Vн — начальная скорость тела
V — скорость тела в момент времени t
t — время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
Формулы времени, за которое тело достигло высоту h (t):
Рейтинг: 5 / 5
1. Формулы скорости, высоты, времени
Формулы скорости, высоты, времени
h — раcстояние пройденное телом за время t
Vo — начальная скорость тела
Vk — конечная скорость тела в момент времени t
t — время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула конечной скорости тела (V):
Формула начальной скорости тела (Vo):
Формула расстояния, которое пролетело тело при падении (h):
Формула времени падения тела (t):
2. Формулы координаты тела, если направление оси OY совпадает с направлением скорости V
h — раcстояние пройденное телом за время t
Vo — начальная скорость тела
Vk — конечная скорость тела в момент времени t
t — время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Yo , Yк — начальная и конечная координаты тела на оси OY
Формулы конечной координаты тела (Yк ):
3.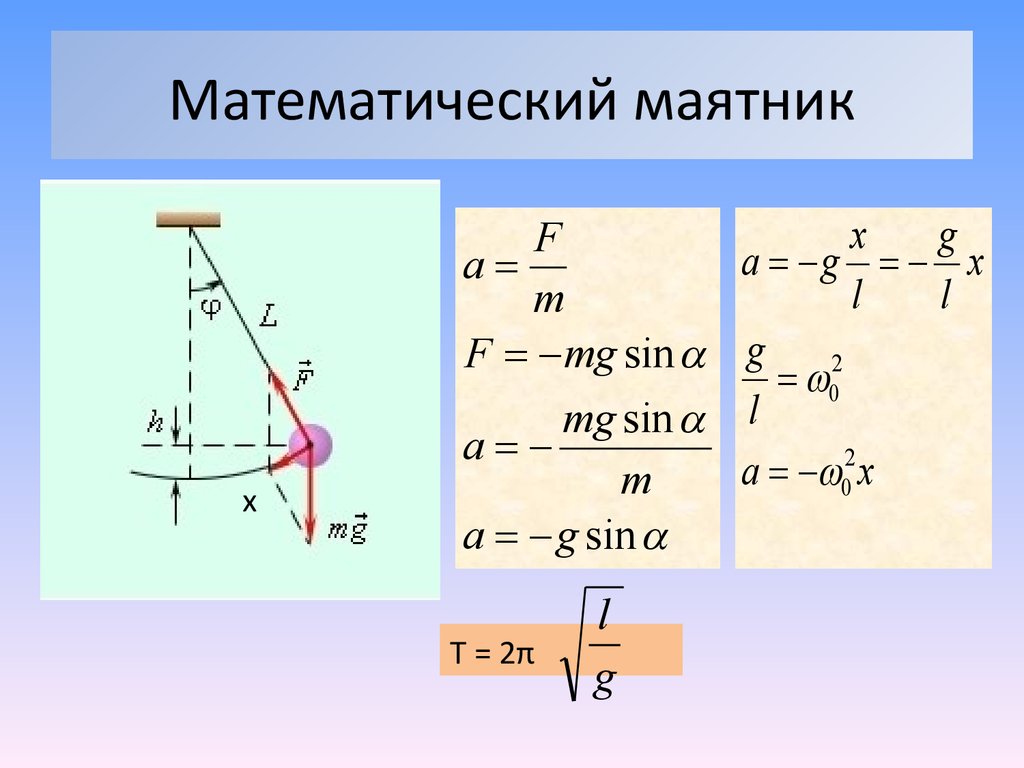 Формулы координаты тела, если направление оси OY не совпадает с направлением скорости V
Формулы координаты тела, если направление оси OY не совпадает с направлением скорости V
h — раcстояние пройденное телом за время t
Vo — начальная скорость тела
Vk — конечная скорость тела в момент времени t
t — время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Yo , Yк — начальная и конечная координаты тела на оси OY
Формулы конечной координаты тела (Yк):
Рейтинг: 1 / 5
1. Формулы скорости, высоты, времени в условиях свободного падения при начальной скорости равной нулю
h — раcстояние пройденное телом за время t
V — скорость тела в момент времени t
t — время падения за которое тело пролетело расстояние или опустилось на высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула скорости тела в определенный момент времени или на определенной высоте (V):
Формула высоты, на которую опустилось тело или расстояния, которое пролетело тело при падении (h):
Формула времени свободного падения тела вертикально вниз (t):
2. Формулы координаты тела, если направление оси OY совпадает с направлением скорости падующего тела V
Формулы координаты тела, если направление оси OY совпадает с направлением скорости падующего тела V
h — раcстояние пройденное телом за время t
V — скорость тела в момент времени t
t — время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Yo , Yк — начальная и конечная координаты тела на оси OY
Формулы конечной координаты тела (Yк):
3. Формулы координаты тела, если направление оси OY не совпадает с направлением скорости V
h — раcстояние пройденное телом за время t
V — скорость тела в момент времени t
t — время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Yo , Yк — начальная и конечная координаты тела на оси OY
Формулы конечной координаты тела (Yк):
Рейтинг: 0 / 5
1. Найти время полета тела на определенной высоте
Найти время полета тела на определенной высоте
hв — высота на восходящем участке траектории
hн — высота на нисходящем участке траектории
t — время в момент которого тело находится на высоте hв или hн
Vo — начальная скорость тела
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для определения значения времени, за которое тело поднялось на определенную высоту, на восходящем участке траектории
Формула для определения значения времени, за которое тело поднялось на определенную высоту, на нисходящем участке траектории
Таким образом, одному значению высоты будет соответствовать два значения времени, одно при подъеме, второе при падении.
2. Найти время полета тела пролетевшее определенное расстояние
S — расстояние пройденное по горизонтали
t — время за которое тело прошло расстояние S
Vo — начальная скорость тела
Vx — проекция начальной скорости на ось OX
Vy — проекция начальной скорости на ось OY
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для определения значения времени, за которое пройдено определенное расстояние
3. Значение времени при максимальных значениях высоты и дальности
Smax — максимальная дальность по горизонтали
hmax — максимальная высота
tmax — время всего полета
th — время за которое тело поднялось на максимальную высоту
Vo — начальная скорость тела
Vx — проекция начальной скорости на ось OX
Vy — проекция начальной скорости на ось OY
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для определения значения времени, затраченное на весь полет, если известна начальная скорость или ее проекции
Формула для определения значения времени, на максимальной высоте
Т. к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно — время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту
к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно — время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту
Рейтинг: 0 / 5
физика для 7 класса: что такое работа, кпд, время и другие основные понятия предмета
Здравствуйте, дорогие друзья! Сегодня мы рассмотрим основные понятия физики и формулы, которые входят в программу учебника Физика 7 класс. Мы пройдем вкратце весь путь познания в области физики от таких базовых понятий, как объем и масса, до коэффициента полезного действия.
Количественные характеристики тела
Основные понятия физики – суть всех понятий, которые прямо или косвенно описывают природу явлений. Из количественных характеристик тела можно отметить его объем и массу. Приведем определение.
Объем представляет собой показатель того, сколько место занимает тело в пространстве. Уточним, что, если, к примеру, полая сфера и шар одинакового радиуса находятся в пространстве, то это не означает, что обе фигуры занимают в пространстве одинаковое количество места. Поясним это подробнее.
Поясним это подробнее.
Полая сфера только на первый взгляд занимает столько же места, сколько шар, на деле их объемы различны – внутри сферы пустота, поэтому, рассчитывая объем, необходимо понимать, что объем воздуха внутри не входит в общую формулу.
[stop]Важно! Объем – величина, которая характеризует исключительно место, занимаемое телом. Объем не отражает суть влияние тела на само пространство и на другие тела. Тела одинаковой формы и размеров из совершенно различных материалов будут иметь одинаковые объемы. Формула объема также будет одинакова, как и его численное значение.[/stop]
Для того чтобы характеризовать понятие объема, вспомним о том, каким образом мы измеряли размеры фигур на плоскости. Для этого мы пользовались понятием площадь. У плоских фигур не может быть объема, у объемных фигур может быть площадь, она называется площадью поверхности. Роль объема в физике очень велика, так как она отражает суть его размеров.
Приведем формулы некоторых фигур:
Формула объема параллелепипеда:
V = abc,
где abc – стороны.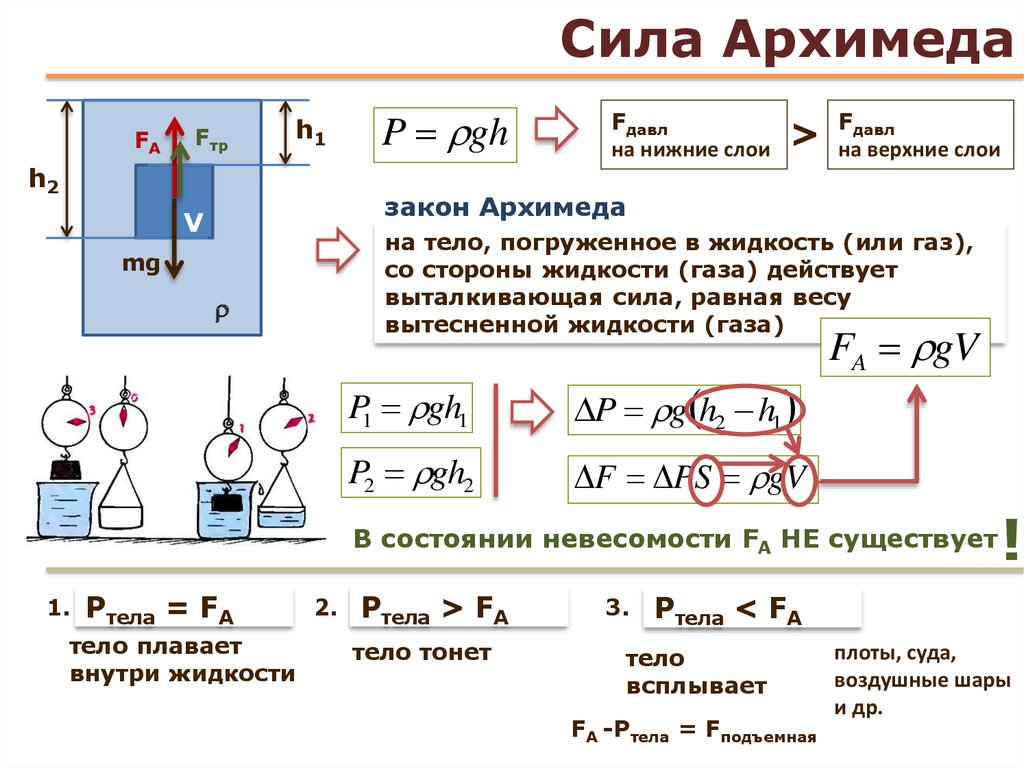
Пирамиды:
,
где S – основание, Н – высота.
Конуса:
,
где R – радиус основания, Н – высота.
Цилиндра:
?=?,
где R – радиус основания, Н – высота.
Говоря о массе, необходимо помнить, что эта физическая величина, в отличие от объема, как раз отражает влияние тела на окружающие тела. Масса представляет собой меру инерции тела, это физическая величина, которая определяет его гравитационные характеристики.
Не следует путать вес с массой, поскольку вес – это сила, и она зависит от гравитационных условий, в котором тело «взвешивается».
Путь, время, скорость, ускорение
При движении тела оно проходит множество точек. Совокупность этих точек называется траекторией. Вектор между началом движения и концом называется перемещением. Если тело движется равномерно и прямолинейно, то перемещение, путь и расстояния равны.
При движении с постоянной скоростью тело проходит за равные промежутки времени равные отрезки пути. Его путь можно отметить формулой:
Его путь можно отметить формулой:
S = vt, где:
v – скорость тела, t – время его пути. Понятие скорости в физике является одним из самых базовых, поскольку отражает общую тенденцию движущегося тела.
Если в течение времени t1 тело прошло расстояние S1, затем, изменив свою скорость, прошло расстояние S2 за время t2, то есть смысл говорить о таком понятии, как средняя скорость.
Явление средней скорости в общем понимании можно рассматривать как среднее арифметическое двух его скоростей:
.
Если тело обе части пути проходило одно и то же расстояние S, то формула времени принимает вид:
.
Запишем время как отношение расстояния к скорости:
.
Тогда из этого соотношения можно получить выражение для средней скорости:
.
Если тело движется не с постоянной скоростью, но в течение одинаковых промежутков времени, его скорость одинаково меняется, то есть смысл говорить о равноускоренном движении (либо равнозамедленном, если скорость снижается, т.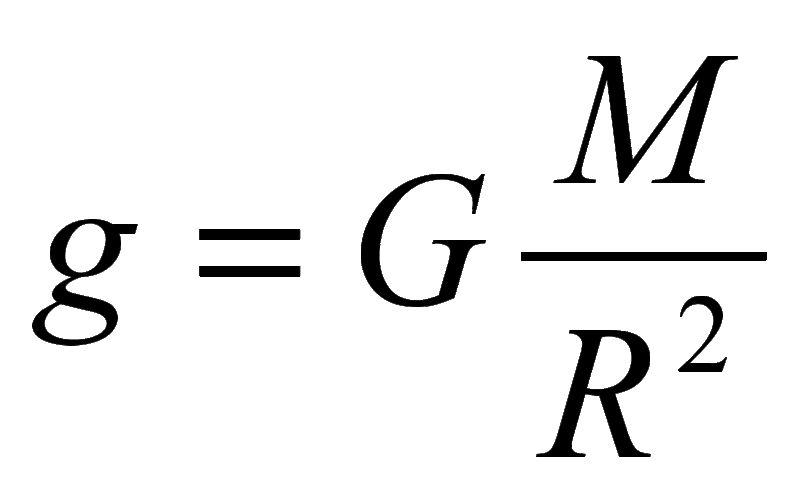 е. тело тормозит).
е. тело тормозит).
[stop]Важно! Именно равноускоренно двигаются все падающие тела. Ускорение соответствует ускорению свободного падения.[/stop]
Введем понятие ускорения. Если тело двигалось со скоростью v0, спустя время t оно начало двигаться со скоростью v, то ускорением называется величина, равная:
В математике подобное отношение также называют производной скорости по времени. Зависимость скорости от каждого момента времени легко получить, отделив из формулы ускорения скорость:
.
Изобразим график зависимости скорости от времени:
Очевидно, что графиком является прямая, причем тангенсом угла наклона этой прямой будет ускорение.
Площадь трапеции под графиком – расстояние, которое прошло тело. Вычислить эту площадь довольно просто, нам известно, что площадь трапеции является полусуммой ее оснований, умноженной на высоту. Одно основание трапеции равно v0 (как раз место, где прямая пересекает координату скорости), второе основание равно v. Высотой трапеции является ее сторона – время, т.е. t. Таким образом, площадь трапеции (пройденное расстояние) будет равна:
Высотой трапеции является ее сторона – время, т.е. t. Таким образом, площадь трапеции (пройденное расстояние) будет равна:
.
Поскольку v = v0 + at, получаем:
.
Таким образом, при равноускоренном движении расстояние равно:
.
В случае, если речь идет о свободном падении, то вместо ускорения во все формулы должно быть поставлено ускорение свободного падения g=9,81 м/с2.
v = v0 + gt;
Если начальная скорость равна нулю, то:
.
Графиком зависимости пути от времени будет парабола (поскольку зависимость квадратичная):
Постараемся найти формулу времени для разных типов движений:
При равномерном движении:
.
При равноускоренном движении:
.
Расчет скорости, пути и времени движения
Вес, сила
Если кинематика занимается изучением того, как именно двигаются тела, то динамика подходит к понятию движения более глубоко – она изучают, почему они двигаются именно так. Здесь появляется понятие силы. Что такое сила в динамике? Данная физическая величина численно отражает уровень воздействия одного тела на другое. Измеряется она в ньютонах.
Что такое сила в динамике? Данная физическая величина численно отражает уровень воздействия одного тела на другое. Измеряется она в ньютонах.
Больше всего физического смысла данной величины отражается в главных четырех законах, которые носят названия «Три закона Ньютона» и «Закон всемирного тяготения«.
Первый закон Ньютона гласит, что если сумма всех сил равна нулю, то тело движется равномерно. Не стоит путать «сумма всех сил равна нулю» и «на тело не действуют никакие силы».
Знаменитый второй закон Ньютона устанавливает связь между динамической величиной силы, импульса и ускорения:
,
.
При постоянной массе:
F = ma.
В частности, если ускорение представляет собой ускорение свободного падения g, то сила превращается в вес:
Р = mg
Здесь мы на минуту остановимся и постараемся при помощи этих двух законов Ньютона усвоить несколько важных понятий.
Первый закон Ньютона гласит, что лежащее на поверхности тело хотя и находится в состоянии покоя (относительно земли), тем не менее, на него действуют две силы. Вес:
Вес:
Р = mg
И нормаль (сила реакции опоры). Сумма этих сил равна нулю. Формула первого закона Ньютона может выглядеть таким образом:
Если .
Вес является величиной относительной с точки зрения планет, на которых находятся тела. Например, часто можно услышать ошибочное высказывание: «масса тела на Луне меньше, чем на Земле». Это не так. Массы на всех планетах одинаковые, а вот вес разный, поскольку различается ускорение свободного падения. Именно поэтому космонавты на Луне с такой легкостью подпрыгивали – их вес на Луне был значительно ниже, чем на Земле, ведь Луна их притягивала к себе не так сильно, как Земля.
Третий закон Ньютона гласит, что сила действия равна силе противодействия. Иными словами, чем сильнее мы давим на тело, тем сильнее оно давит на нас. Этот закон отражает равенство силы тяжести и нормали.
.
,
где Fi — сила инерции.
Если есть система тел, то скорость центра масс системы равна:
.
Три закона Ньютона
Закон всемирного тяготения, который еще называют четвертым законом Ньютона, гласит:
,
где G – гравитационная постоянная, m1, m2 – массы притягивающихся тел.
Если в левой части этого равенства указать вес, то получаем формулу для ускорения свободного падения тел на любой планете:
.
Также, из закона всемирного тяготения выводится понятие первой космической скорости, т.е. скорости, при которой тело покидает гравитационное поле. Именно до этой скорости (на Земле она равна 7,9 км/с) разгоняют ракеты, которые необходимо вывести на орбиту.
Первая космическая скорость:
.
Вернемся к понятию веса.
Если тело находится в состоянии покоя, то вес равен:
Р = mg
Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:
Р = m(g+a)
Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:
Р = m(g-a)
Эта формула наглядно показывает, что в падающем лифте, где а = g, вес тела будет равен нулю, т.е. тело испытает невесомость.
Если тело движется по выпуклой траектории, то ускорение, действующее на него, – центробежное, а значит вес:
Р=m(g-v2/r).
Если тело движется по вогнутой траектории, то ускорение действующее на него — тоже центробежное и направлена от центра, а значит вес:
Р=m(g+v2/r).
Формула силы трения:
,
где — коэффициент трения, N — нормаль (реакция опоры).
Таким образом, мы познакомились уже с несколькими видами сил – вес (сила тяжести), сила трения, центробежная сила, сила всемирного тяготения (которая является по сути тем же весом, только в более общей форме).
Рассмотрим еще одну силу, которая имеет место в случае деформаций. Она называется силой упругости. Закон Гука для малых деформаций (сжатий или растяжений) гласит, что сила, действующая на тело, длину которого деформировали на х, равна:
Fупр = –kx.
Из этого закона вытекает ряд следствий, например модуль Юнга, который выступает коэффициентом пропорциональности в связи между нормальным напряжением и относительным изменением длины:
.
Центробежная сила
Энергия, работа, мощность, полезное действие
Для того чтобы описывать различные формы взаимодействия материи и ее движение, вводится физическая величина энергия. Если тело прошло расстояние S из-за того, что на него в это время действовала сила F, то энергия этого движения называет работой этого тела. Формула работы записывается таким образом (произведение силы и пройденного пути):
Если тело прошло расстояние S из-за того, что на него в это время действовала сила F, то энергия этого движения называет работой этого тела. Формула работы записывается таким образом (произведение силы и пройденного пути):
A = FS
Если тело движется со скоростью v, то тело обладает энергией, которая называется кинетической:
.
Если тело приподняли на высоту h, то оно обладает в точке подъеме потенциальной энергией:
E = mgh/.
[stop]Важно ! По сути, потенциальная энергия представляет собой работу силы тяжести. Если сила тяжести mg, а путь, пройденный телом, – высота h, на которую его подняли, то работа A = F[/stop]S = mgh.
При падении тела с высоты Н его потенциальная энергия превращается в кинетическую.
Закон сохранения энергии гласит, что в замкнутых системах энергия сохраняется. Таким образом, если тело подняли на высоту h и отпустили, то скорость, с которой оно будет приземляться, можно вычислить из закона сохранения:
.
Отсюда:
.
Остановимся подробнее на двух законах сохранения: законе сохранения энергии и импульса.
Импульс в замкнутых системах сохраняется, энергия в замкнутых системах сохраняется. В паре эти два закона могут разрешить бесконечное количество задач. Рассмотрим пример.
Кинетическая энергия
Задача на закон сохранения энергии и импульса
Задача. Идеально упругий шарик массой m движется со скоростью v и ударяется о покоящийся шарик массой M. Удар будет центральный, т.е. траектория шарика и ось между их центрами – одна и та же линия.
Какая будет скорость u шарика массой M и скорость v1 шарика массой m после удара?
Решение:
Первый шарик до столкновения обладал импульсом mv. Второй шарик находился в состоянии покоя, т.е. его импульс был равен M∙0 = 0.
Таким образом, в системе двух шариков суммарный импульс до столкновения был равен:
.
После столкновения импульс первого шарика стал равен mv1, а импульс второго шарика составил Mu. Тогда суммарный импульс системы двух шариков после удара равен:
Тогда суммарный импульс системы двух шариков после удара равен:
Согласно закону сохранения импульса Р = Р1, а именно:
(1).
Теперь рассмотрим энергии. Кинетическая энергия первого шарика до удара составила . Кинетическая энергия второго шарика равна нулю. После удара первый шарик имеет кинетическую энергию . Второй шарик после удара обладает энергией:.
Согласно закону сохранения энергии:
.
Сократив двойки в знаменателях, получаем:
(2).
Получаем систему из двух выражений (1) и (2).
(*).
Из первого уравнения можем получить выражение для скорости первого шарика после удара:
(3).
Найдем квадрат этой скорости:
.
Найдем значение выражения:
.
Теперь можно подставить это выражение во второе уравнение системы (*):
.
Упрощаем выражение:
.
Выводим квадрат скорости u за скобки:
.
Сокращаем на u:
.
Таким образом, скорость второго шарика после удара составляет:
.
Подставив это в выражение (3), можем найти скорость первого шарика после удара:
.
Это был один из немногих примеров того, каким образом при помощи двух законов сохранения находить величины.
Траты энергии. КПД
Однако, говоря об энергии, следует помнить о ее тратах. Например, если во время работы какой-либо физической системы (движущееся тело или тепловая машина) затраченная энергия Q привела к тому, что система произвела полезную энергию A, то говорят о так называемом коэффициенте полезного действия (КПД). КПД измеряется в процентах, которые численно отображают отношение полезной энергии (которую дает система) ко всей суммарно использованной.
Формулу КПД записывают в таком виде:
,
либо, если в процентах:
.
КПД всегда меньше единицы, поскольку полезная работа не может быть больше суммарной, а закон сохранения энергии должен соблюдаться.
Не существует КПД 100%, поскольку траты (даже самые малые) есть в любых системах.
Скорость движения
youtube.com/embed/z9kl8R78PJE» frameborder=»0″ allowfullscreen=»allowfullscreen»>
Сила тяжести — вес тела — 7 класс
Формула давления — примеры и условия расчетов » Kupuk.net
Термодинамическая величина зависит от силы, воздействующей на площадь поверхности. Для расчёта применяется формула давления газа, воды, твёрдого тела (Р = mg / S, где р — давление, m — масса, g — ускоренное падение, S — площадь). Явление не зависит от ёмкости сосуда, поэтому считается интенсивным показателем. В условиях равновесия Р одинаково для каждой точки системы. На основе закона работают приборы, по которым определяется р.
Точные науки
Единица измерения давления в физике и химии — буква «Р» (перевод на латинский — «pressūra). Если наблюдается равновесие внутри и снаружи стенок цилиндра, показатель обозначается «П». По международной системе используются Паскали. Используя формулу давления жидкости и силу, можно прийти к выводу, что 1 Па=1 Н/ 1 кв. м. Так как единица мала, применять её в расчётах сложно.
По международной системе используются Паскали. Используя формулу давления жидкости и силу, можно прийти к выводу, что 1 Па=1 Н/ 1 кв. м. Так как единица мала, применять её в расчётах сложно.
Из таблицы стандартных конвертеров в физике чаще используются обозначения:
Для определения давления используется сила и площадь: Р = mg / S. Существует зависимость величины от объёма и массы. Для показателя характерно следующее свойство: чем меньше площадь, тем большая сила оказывается на тело. Если давление не изменяется, но увеличивается S, тогда искомый показатель уменьшается.
Главные формулы
При изменении условия агрегатного состояния вещества наблюдаются отличные друг от друга свойства. С учётом этого принципа определяется способ вычисления Р. Для гидростатического состояния используется формула: Р = pgh, где:
С учётом этого принципа определяется способ вычисления Р. Для гидростатического состояния используется формула: Р = pgh, где:
- р — плотность;
- g — ускорение;
- h — высота.
Гидростатика применяется к газам. Исключение — вычисление АД. Это объясняется разностью высот и плотностей воздушных масс. От глубины погружения предмета либо объекта зависит значение Р вещества. Так как сила F вычисляется путём умножения m на g, а масса воды — p на V, идеальным вариантом для расчёта давления считается выражение: P = pVg / S. Формула применяется на онлайн-ресурсах, где можно решать задачи по физике и химии.
Если площадь записать в виде S= V/h, тогда Р= pgh. Давление в воде либо иной жидкости вычисляется с учётом изменения верхнего слоя. Это приводит к образованию другого Р. Чтобы найти абсолютную силу, используется формула:
Р = Р0 + 2QH, где:
- Р0 — давление неизменяемого слоя;
- Q — поверхность натяжения жидкого вещества;
- H — среднее значение.

Последний показатель должен сообщаться между первыми двумя, поэтому он считается усреднённым. Для определения значения используются радиусы кривизны: ½ (1/R1+ 1/R2). Каждый вид газа оказывает особенное парциальное давление. Для идеального состояния характерна сумма Р каждого отдельного компонента смеси. Частая ошибка, которую допускают школьники при вычислении давления воздуха — применение только кислорода. Но воздух представлен в виде различных газов:
- аргон;
- азот.
Для нахождения давления воздушных масс используется формула P=P1+P2+P3…
Виды величины
Давление может быть различным (избыточным, барометрическим). Абсолютное понятие характерно для вещества либо объекта, на которое не оказывают влияния иные газы. Показатель измеряется в Паскалях. Он вычисляется по следующему калькулятору: нормальное Р = Р2 + Р3 или Р = Р2 — Р4.
Начало отсчёта идёт от планеты Земля, силы внутри сосуда, из которого удалён воздух. Величина используется во многих термодинамических формулах. Для определения гравитации используется понятие барометрическое либо атмосферное давление. Оно изменяется с учётом температуры атмосферы, времени, высоты.
Величина используется во многих термодинамических формулах. Для определения гравитации используется понятие барометрическое либо атмосферное давление. Оно изменяется с учётом температуры атмосферы, времени, высоты.
В норме показатель равняется 760 мм рт. ст., при этом температура должна соответствовать нулю по Цельсию. Чем выше находится объект от Земли, тем ниже оказывается на него давление. Значение уменьшается на 100 Па через каждый восьмой километр.
В горах вода закипает быстрее, чем в домашних условиях: давление воздействует на температуру кипения. Если оно снижается, уменьшается t. Зависимость сохраняется и в обратном порядке. На подобном свойстве функционируют некоторые кухонные приборы: скороварка, автоклав. При повышении номинального Р внутри поднимается температура.
Для расчётов применяется стандартная формула, где используются переменные:
- плотность воздушных масс вблизи уровня Земли;
- высота;
- ускорение;
- температура;
- молярная масса.

Если количество частиц задано в молях, используется формула с постоянной величиной К. При проведении расчётов учитывается вероятность изменения температуры, что связано со сменой погоды, набором высоты, географической широтой. Если из атмосферного Р вычесть измеренное, получится избыточная сила. С учётом результата изменяется название показателя:
- положительный — манометрический;
- отрицательный — вакуумметрический.
Последнее значение не может превышать барометрический уровень. Разница давлений в разных точках называется дифференциальным явлением. Его используют, чтобы определить Р на определённом оборудовании. Такое понятие используется в нефтедобывающей отрасли.
Решение задач
В задачах по физике формулы давления могут выглядеть по-разному. Задача первая: нужно найти Р, оказываемое телом на судно и грунт под водой, когда водолаз находится в движении. Человек весит со снаряжением на суше 180 кг. Площадь стопы равняется 360 кв. см. Сила, с которой человек воздействует на судно равно 180/360 = 0.5 (кгс/см). Используя таблицу, величину можно перевести в Па. Получится 49 кПа. На грунт под водой оказывается сила в 2,46 кПа.
Задача первая: нужно найти Р, оказываемое телом на судно и грунт под водой, когда водолаз находится в движении. Человек весит со снаряжением на суше 180 кг. Площадь стопы равняется 360 кв. см. Сила, с которой человек воздействует на судно равно 180/360 = 0.5 (кгс/см). Используя таблицу, величину можно перевести в Па. Получится 49 кПа. На грунт под водой оказывается сила в 2,46 кПа.
Пример 2: нужно вычислить абсолютное Р воды, если глубина равна 150 м, сила — 765, а масса тела — 1,024 кгс/л. Решение: P = 765/735,6+1,024×150/10=16.4.
Пример 3: ёмкость баллона равна 40 л, давление в нём 150 кгс/см2. Нужно найти V свободных воздушных масс. Решение: начальное Р вычисляется следующим образом: 150+1 = 151 кгс/кв.см. Начальное V равно 40 литров. Свободное V вычисляется p1xнач V/p2=6.04 куб. м. Аналогичным способом решаются задачи, где нужно найти Р любой жидкости, твёрдого объекта, газового вещества.
youtube.com/embed/a4ckOyjz79o»/>Измерительные приборы
Можно сэкономить время на расчётах, воспользовавшись специальными приборами, функционирующими путём определения давления в соответствующей среде, что схоже с манометром. Их отличия между собой заключаются в инструкции по эксплуатации, сфере использования, точности, области применения.
Чтобы определить АД, понадобится манометр типа барометра. Для определения разряжения (Па меньше атмосферного) понадобится иная разновидность аппарата — вакуумметр. У человека показатель определяется с помощью сфигмоманометра. Большинство пациентов называют такое оборудование неинвазивным тонометром.
Подобные приборы классифицируются на следующие подвиды:
- ртутные механические;
- полуавтоматические;
- автоматические цифровые.
Их погрешность зависит от материалов, используемых в процессе производства и области измерения. Некоторые устройства одновременно измеряют давление и пульс. Они работают автоматически от батареек. За счёт наличия цифрового табло легко узнать результат. Более точными считаются механические.
Некоторые устройства одновременно измеряют давление и пульс. Они работают автоматически от батареек. За счёт наличия цифрового табло легко узнать результат. Более точными считаются механические.
Чтобы определить Р, понадобится надеть манжет на правую руку больного. Зажав механизм, производится накачка груши. Максимальный и минимальный пределы начинаются с появления, а затем с исчезновения характерного стука. Постепенно механизм ослабляется. Для получения точных данных потребуется опыт работы с механическим тонометром и внимательность. Если наблюдаются колебания давления в воздухе, понадобится дифнамометр либо манометр.
Как найти h в физике? – Обзоры Вики
h = v 0 y 2 2 г . Это уравнение определяет максимальную высоту снаряда над его стартовой позицией и зависит только от вертикальной составляющей начальной скорости.
Отсюда, как найти H треугольника? Заданная площадь треугольника
площадь = с*ч/2 , где b — основание, h — высота. поэтому h = 2 * площадь / b.
поэтому h = 2 * площадь / b.
Дополнительно Как рассчитать кинетическую энергию? В классической механике кинетическая энергия (КЭ) равна равна половине массы объекта (1/2 * м), умноженной на квадрат скорости. Например, если объект массой 10 кг (m = 10 кг) движется со скоростью 5 метров в секунду (v = 5 м / с), кинетическая энергия равна 125 Джоулей, или (1 / 2 * 10 кг) * 5 м / с2.
Какова формула веса? Вес – это мера силы гравитации, притягивающей объект. Это зависит от массы объекта и ускорения свободного падения, которое составляет 9.8 м/с.2 на земле. Формула для расчета веса: F = м × 9.8 м / с2, где F — вес объекта в Ньютонах (Н), а m — масса объекта в килограммах.
Как найти недостающую длину треугольника?
Как мне узнать, есть ли у меня SOH CAH TOA? SOHCAHTOA — это мнемоническое устройство, помогающее запомнить, какое соотношение соответствует какой функции. 2 / 2 м где p — импульс объекта, а m — масса объекта. Так что здесь и должны быть заданы импульс и масса объекта.
2 / 2 м где p — импульс объекта, а m — масса объекта. Так что здесь и должны быть заданы импульс и масса объекта.
Как рассчитать кинетическую и потенциальную энергию?
Как рассчитать вес по размеру? Умножьте длину на ширину на высоту, чтобы получить кубические дюймы (см). Чтобы получить размерный вес в килограммах, разделите результат в кубических дюймах на 366. Чтобы получить размерный вес в фунтах, разделите результат в кубических дюймах на 166.
Что такое % масс в химии? вес.% означает весовые проценты который иногда записывается как w/w, т.е. [вес растворенного вещества/вес растворителя*100 = процент растворенного вещества в растворе]. В вашем случае 25% тетраметиламмония в метаноле означает, что на каждые 25 г метанола приходится 100 г тетраметиламмония.
Как перевести килограммы в ньютоны?
N — сила в ньютоне.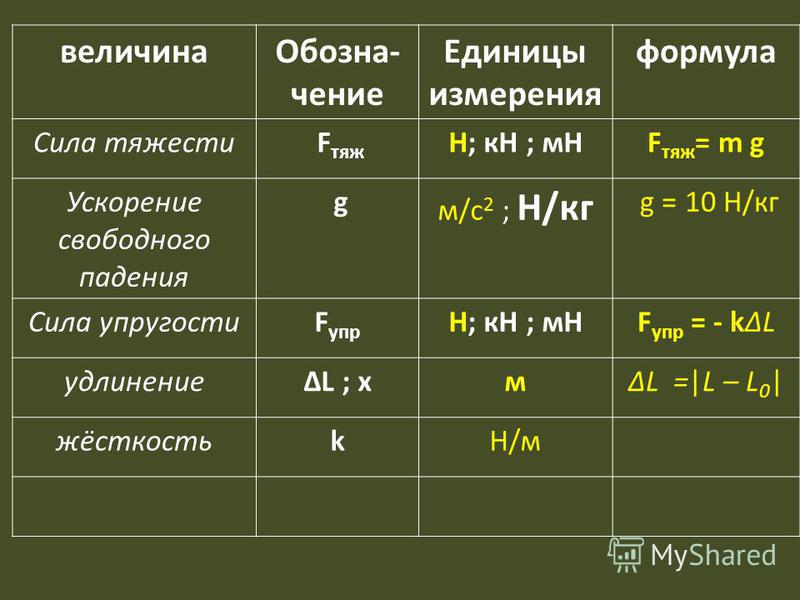 Kg — масса в килограммах.
Kg — масса в килограммах.
…
Кг и Ньютон.
| Ценности | |
|---|---|
| Кг в Ньютон | 1 кг = 9.81 Н |
| Ньютон в кг | 1N = 0.10197 кг |
Как найти две недостающие стороны треугольника? Учитывая две стороны
- если сторона a — недостающая сторона, преобразовать уравнение к форме, когда a находится на одной стороне, и извлечь квадратный корень: a = √ (c² — b²)
- если нога b неизвестна, то. b = √ (c² — a²)
- если гипотенуза c отсутствует, формула имеет вид. c = √ (a² + b²)
Как вы решаете треугольники?
Как найти длину третьей стороны треугольника? Ты можешь использовать Теорема Пифагора найти длину гипотенузы прямоугольного треугольника, если известны длины двух других сторон треугольника, называемых катетами. Иными словами, если вы знаете длины a и b, вы можете найти c.
Иными словами, если вы знаете длины a и b, вы можете найти c.
Работает ли Sohcahtoa на всех треугольниках?
A: Да, это относится только к прямоугольным треугольникам. Если у нас есть наклонный треугольник, мы не можем предположить, что эти триггерные отношения будут работать. У нас есть и другие методы, которые мы узнаем в математическом анализе и тригонометрии, такие как законы синусов и косинусов для обработки этих случаев.
Как найти гипотенузу?
Гипотенуза называется самой длинной стороной прямоугольного треугольника. Чтобы найти самую длинную сторону, мы используем формулу гипотенузы, которая легко выводится из теоремы Пифагора (Гипотенуза)2 = (База)2 + (Высота)2. Формула гипотенузы = √ ((основание)2 + (высота)2) (или) c = √ (a2 + b2).
4.3 Движение снарядов — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Используйте одномерное движение в перпендикулярных направлениях для анализа движения снаряда.
- Рассчитайте дальность, время полета и максимальную высоту снаряда, который запускается и поражает плоскую горизонтальную поверхность.
- Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
- Рассчитать траекторию снаряда.
Снарядное движение — это движение объекта, брошенного или отброшенного в воздух, с ускорением только под действием силы тяжести. Применения движения снаряда в физике и технике многочисленны. Некоторые примеры включают метеоры, когда они входят в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядов , а их путь называется траекторией. Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Наиболее важным фактом, который следует помнить, является то, что движений вдоль перпендикулярных осей являются независимыми и поэтому могут быть проанализированы отдельно. Мы обсуждали этот факт в разделе «Векторы смещения и скорости», где увидели, что вертикальное и горизонтальное движения независимы. Ключом к анализу двумерного движения снаряда является разбиение его на два движения: одно по горизонтальной оси, а другое по вертикальной. (Этот выбор осей является наиболее разумным, потому что ускорение, вызванное силой тяжести, является вертикальным; таким образом, нет никакого ускорения вдоль горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось x — ось и вертикальная ось y — ось. Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. На рис. 4.11 показано обозначение перемещения, где мы определяем s→s→ как полное перемещение, а x→x→ и y→y→ — его составляющие векторы вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , х и y .
Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. На рис. 4.11 показано обозначение перемещения, где мы определяем s→s→ как полное перемещение, а x→x→ и y→y→ — его составляющие векторы вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , х и y .
Рисунок 4.11 Полное перемещение с футбольного мяча в точке на его пути. Вектор s→s→ имеет компоненты x→x→ и y→y→ вдоль горизонтальной и вертикальной осей. Его величина составляет s , и он составляет угол Φ с горизонтом.
Чтобы полностью описать движение снаряда, мы должны включить скорость и ускорение, а также перемещение. Мы должны найти их компоненты по x- и y -оси. Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми:
Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми:
с2).
Поскольку гравитация вертикальна, ax=0.ax=0. Если ax=0,ax=0, это означает, что начальная скорость в направлении x равна конечной скорости в направлении x , или vx=v0x.vx=v0x. С этими условиями на ускорение и скорость мы можем записать кинематическое уравнение 4.11 через уравнение 4.18 для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из движения с постоянным ускорением. Кинематические уравнения движения в однородном гравитационном поле переходят в кинематические уравнения с ay=−g,ax=0:ay=−g,ax=0:
Горизонтальное движение
v0x=vx,x=x0+vxtv0x=vx,x=x0+vxt
4.19
Вертикальное движение
y=y0+12(v0y+vy)ty=y0+12(v0y+ vy) t
4,20
vy = v0y -gtvy = v0y -gt
4,21
y = y0+v0yt -12gt2y = y0+v0yt -12gt2
4,22
vy2 = v0y -2gt2
4,22
vy2 = v0y -2gt2
4,22
vy2gy2gt2
4,22
VY2GY2GT2
4,22
VY2GY2GT2
4,22
vyt -12gt2
vy2=v0y2−2g(y−y0)
4,23
Используя эту систему уравнений, мы можем анализировать движение снаряда, учитывая некоторые важные моменты.
Стратегия решения проблем
Движение снаряда
- Разделите движение на горизонтальную и вертикальную составляющие вдоль осей x и y . Величины компонент смещения s→s→ по этим осям равны x и лет. Величины компонентов скорости v→v→ равны vx=vcosθandvy=vsinθ,vx=vcosθandvy=vsinθ, где v — модуль скорости, а θ — ее направление относительно горизонтали, как показано на Рисунок 4.12.
- Рассматривайте движение как два независимых одномерных движения: одно по горизонтали, а другое по вертикали. Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
- Найдите неизвестные в двух отдельных движениях: горизонтальном и вертикальном. Обратите внимание, что единственной общей переменной между движениями является время t .
 Процедуры решения задач здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.
Процедуры решения задач здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах. - Рекомбинируйте величины в горизонтальном и вертикальном направлениях, чтобы найти полное перемещение s→s→ и скорость v→.v→. Найдите величину и направление смещения и скорости, используя
s=x2+y2,Φ=tan−1(y/x),v=vx2+vy2,s=x2+y2,Φ=tan−1(y/ x),v=vx2+vy2,
, где Φ — направление перемещения s→.s→.
Рисунок
4.12
(а) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения вдоль вертикальной и горизонтальной осей. (b) Горизонтальное движение простое, потому что ax=0ax=0, а vxvx — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости.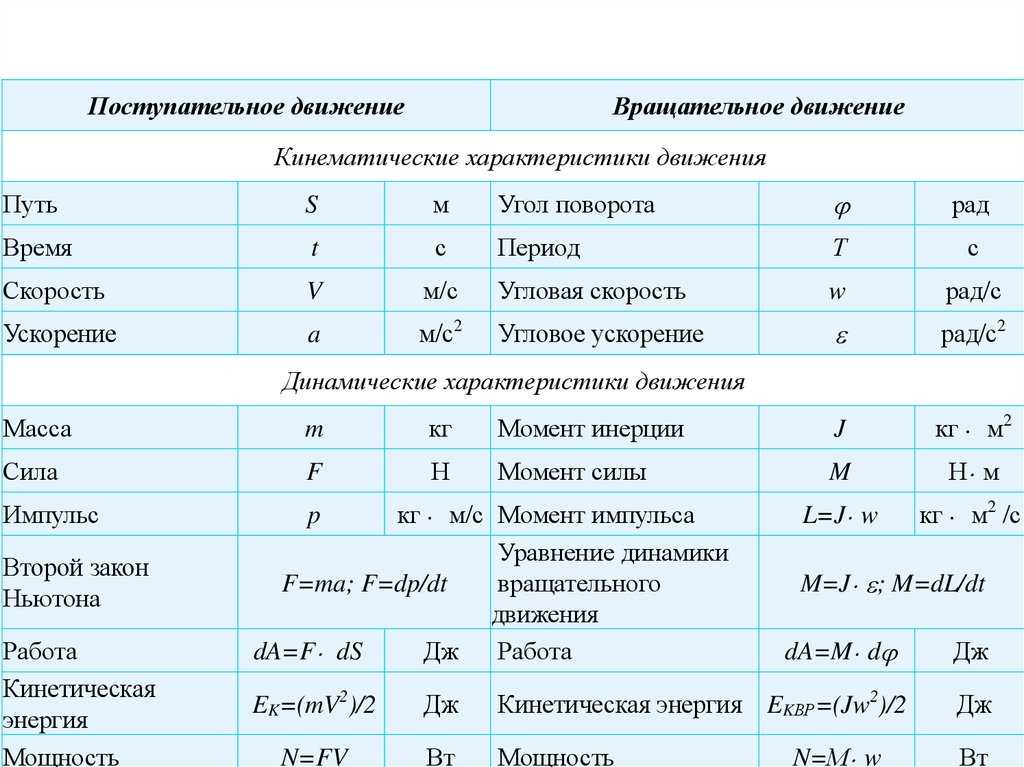 (г) x и y движений рекомбинируются для получения общей скорости в любой заданной точке траектории.
(г) x и y движений рекомбинируются для получения общей скорости в любой заданной точке траектории.
Пример 4.7
Снаряд фейерверка взрывается высоко и прочь
Во время фейерверка снаряд взлетает в воздух с начальной скоростью 70,0 м/с под углом 75,0°75,0° над горизонтом, как показано на рис. 4.13. Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей высшей точки над землей. а) Вычислите высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? в) Чему равно горизонтальное перемещение снаряда при взрыве? г) Чему равно полное перемещение от точки запуска до высшей точки?
Рисунок 4.13 Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
Стратегия
Движение можно разбить на горизонтальное и вертикальное движения, в которых ax=0ax=0 и ay=-g.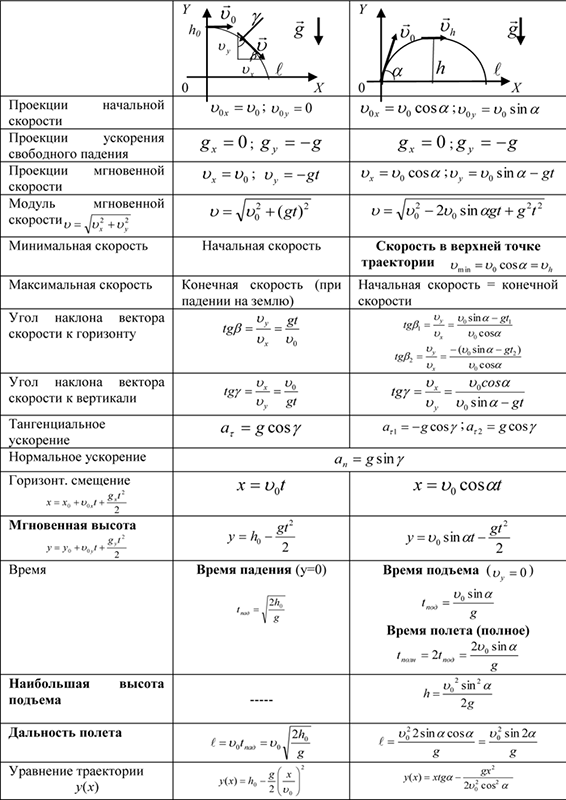 ay=-g. Затем мы можем определить x0x0 и y0y0 равными нулю и найти нужные величины.
ay=-g. Затем мы можем определить x0x0 и y0y0 равными нулю и найти нужные величины.
Раствор
(а) Под «высотой» мы подразумеваем высоту или вертикальное положение y выше начальной точки. Высшая точка любой траектории, называемая вершиной , достигается, когда vy=0.vy=0. Поскольку мы знаем начальную и конечную скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
vy2=v0y2−2g(y−y0).vy2=v0y2−2g(y−y0).
Поскольку y0y0 и vyvy равны нулю, уравнение упрощается до
0=v0y2−2gy.0=v0y2−2gy.
Решение для y дает
y=v0y22g.y=v0y22g.
Теперь мы должны найти v0y,v0y, составляющую начальной скорости в направлении y . Она определяется как v0y=v0sinθ0,v0y=v0sinθ0, где v0v0 — начальная скорость 70,0 м/с, а θ0=75°θ0=75° — начальный угол.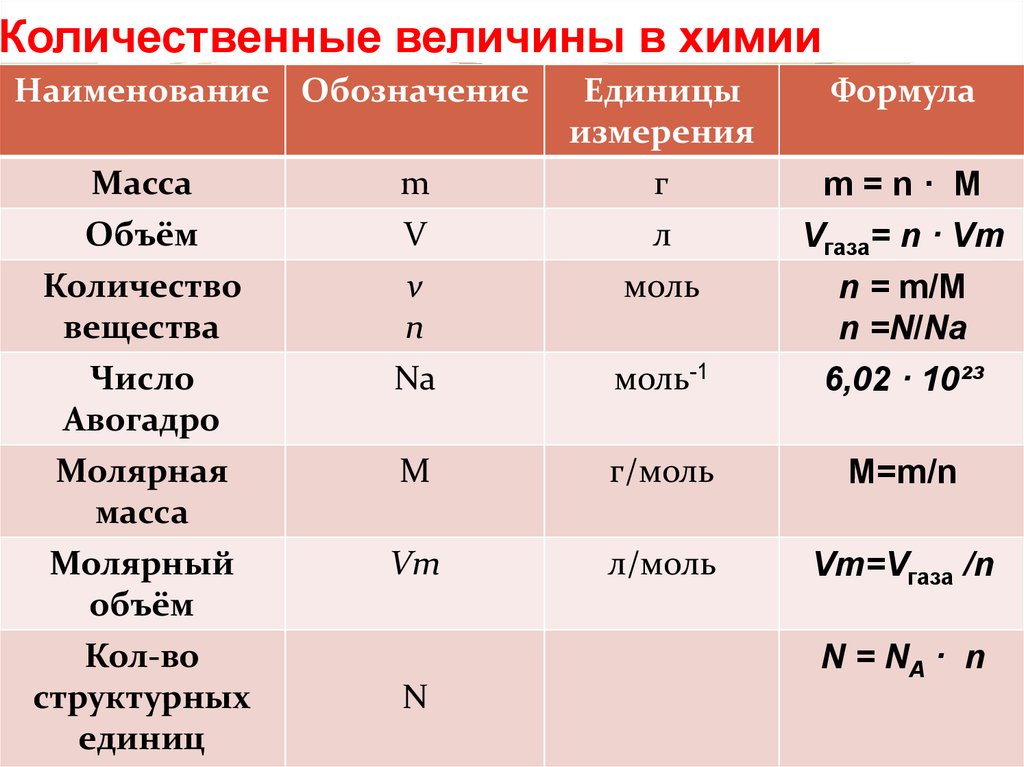 Таким образом,
Таким образом,
v0y=v0sinθ=(70,0 м/с)sin75°=67,6 м/sv0y=v0sinθ=(70,0 м/с)sin75°=67,6 м/с
и y равно
y=(67,6 м/с)22(9,80 м/с2).y=(67,6 м/с)22(9,80 м/с2).
Таким образом, имеем
y=233m.y=233m.
Обратите внимание, что, поскольку значение up положительно, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение от силы тяжести отрицательно. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м/с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты.
(b) Как и во многих физических задачах, существует более одного способа решения для времени, когда снаряд достигает своей высшей точки. В этом случае проще всего использовать vy=v0y-gt.vy=v0y-gt. Поскольку vy=0vy=0 на вершине, это уравнение сводится к простому виду м/с9,80 м/с2=6,90 с.
В этом случае проще всего использовать vy=v0y-gt.vy=v0y-gt. Поскольку vy=0vy=0 на вершине, это уравнение сводится к простому виду м/с9,80 м/с2=6,90 с.
Это время подходит и для больших фейерверков. Если вы можете увидеть запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется. Другой способ найти время — использовать y=y0+12(v0y+vy)t.y=y0+12(v0y+vy)t. Это оставлено вам в качестве упражнения для выполнения.
(c) Поскольку сопротивлением воздуха можно пренебречь, ax=0ax=0, а горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение представляет собой произведение горизонтальной скорости на время по формуле x=x0+vxt,x=x0+vxt, где x0x0 равно нулю. Таким образом,
x=vxt,x=vxt,
, где vxvx — составляющая скорости x , которая определяется выражением
vx=v0cosθ=(70,0 м/с)cos75°=18,1 м/с .vx=v0cosθ=(70,0 м/с)cos75°=18,1 м/с.
Время t для обоих движений одинаково, поэтому x равно
x=(18,1 м/с)6,90 с=125 м. x=(18,1 м/с)6,90 с=125 м.
x=(18,1 м/с)6,90 с=125 м.
Горизонтальное движение с постоянной скоростью при отсутствии сопротивления воздуха. Найденное здесь горизонтальное смещение может быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, большое влияние оказывает сопротивление воздуха, и многие осколки приземляются прямо под ним.
(d) Горизонтальная и вертикальная составляющие смещения были только что рассчитаны, поэтому все, что здесь нужно, это найти величину и направление смещения в самой высокой точке: 9
|с→|=1252+2332=264м|с→|=1252+2332=264м
Φ=tan−1(233125)=61,8°. Φ=tan−1(233125)=61,8°.
Обратите внимание, что угол вектора смещения меньше начального угла запуска. Чтобы понять, почему это так, просмотрите рисунок 4.11, на котором показана кривизна траектории по направлению к уровню земли.
При решении примера 4.7(а) выражение, которое мы нашли для y , справедливо для любого движения снаряда, когда сопротивлением воздуха можно пренебречь. Назовите максимальную высоту г = ч . Тогда
Назовите максимальную высоту г = ч . Тогда
ч=v0y22g.h=v0y22g.
Это уравнение определяет максимальную высоту снаряда над точкой старта и зависит только от вертикальной составляющей начальной скорости.
Проверьте свое понимание 4.3
Камень брошен горизонтально со скалы высотой 100,0 м 100,0 м со скоростью 15,0 м/с. (a) Определите начало системы координат. б) Какое уравнение описывает горизонтальное движение? в) Какие уравнения описывают вертикальное движение? г) Какова скорость камня в момент удара?
Пример 4,8
Расчет движения снаряда: теннисист
Теннисист выиграл матч на стадионе имени Артура Эша и ударил мячом по трибунам со скоростью 30 м/с и под углом 45°45° над горизонтом (рис. 4.14). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу.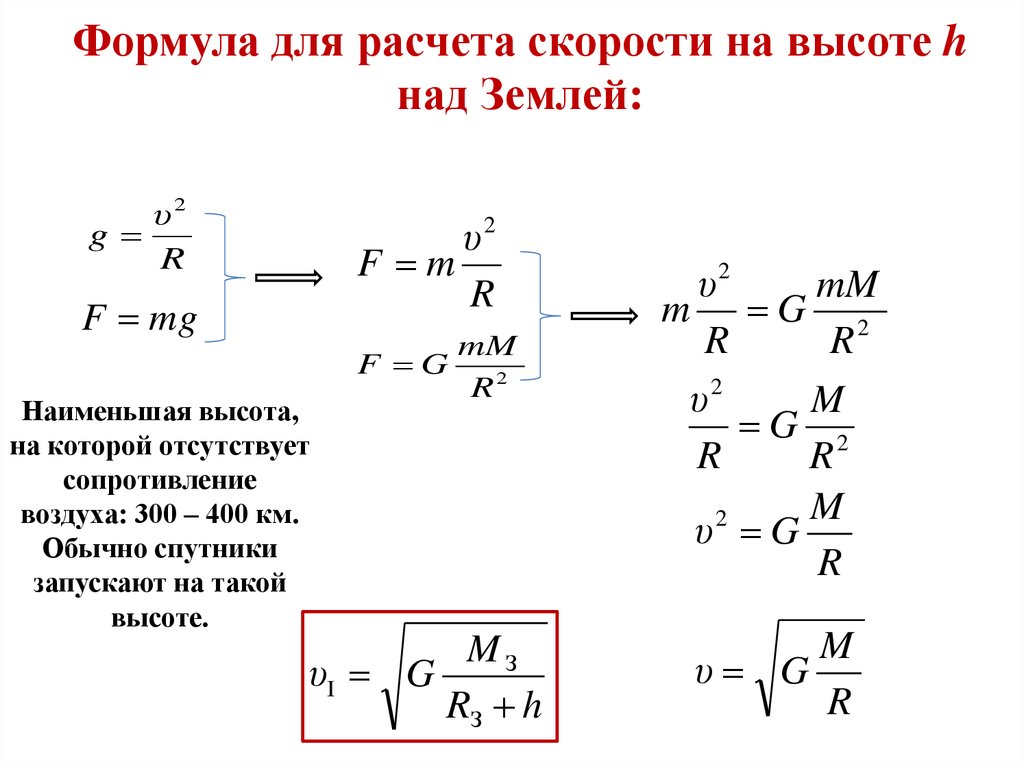 а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?
а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?
Рисунок 4.14 Траектория попадания теннисного мяча в трибуны.
Стратегия
Опять же, разложение этого двумерного движения на два независимых одномерных движения позволяет нам найти нужные величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением. Таким образом, мы сначала решим для t . Пока мяч поднимается и падает вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается конечная скорость. Таким образом, мы рекомбинируем результаты по вертикали и горизонтали, чтобы получить v→v→ в последний момент времени t , определенные в первой части примера.
Раствор
(a) Пока мяч находится в воздухе, он поднимается, а затем падает в конечное положение на 10,0 м выше начальной высоты. Мы можем найти время для этого, используя уравнение 4.22:
Мы можем найти время для этого, используя уравнение 4.22:
y=y0+v0yt−12gt2.y=y0+v0yt−12gt2.
Если принять начальное положение y0y0 равным нулю, то конечное положение будет y = 10 м. Начальная вертикальная скорость – это вертикальная составляющая начальной скорости:
v0y=v0sinθ0=(30,0 м/с)sin45°=21,2 м/с.v0y=v0sinθ0=(30,0 м/с)sin45°=21,2 м/с.
Подстановка в уравнение 4.22 вместо y дает нам
10,0 м=(21,2 м/с)t−(4,90 м/с2)t2,10,0 м=(21,2 м/с)t−(4,90 м/с2) т2.
Перестановка членов дает квадратное уравнение в t :
(4,90 м/с2)t2−(21,2 м/с)t+10,0 м=0,(4,90 м/с2)t2−(21,2 м/с) т+10,0м=0.
Использование квадратичной формулы дает t = 3,79 с и t = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории — один раз по пути вверх и один раз по пути вниз — мы принимаем более длинное решение для времени, которое требуется мячу, чтобы достичь зрителя:
t=3,79 с. t=3,79 с.
t=3,79 с.
Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м ниже начальной высоты, находится в воздухе 3,79 с.
(б) Мы можем найти конечные горизонтальную и вертикальную скорости vxvx и vyvy, используя результат (а). Затем мы можем объединить их, чтобы найти модуль полного вектора скорости v→v→ и угол θθ, который он образует с горизонтом. Поскольку vxvx является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем и начальную скорость, и начальный угол. Следовательно,
vx=v0cosθ0=(30 м/с)cos45°=21,2 м/с.vx=v0cosθ0=(30 м/с)cos45°=21,2 м/с.
Конечная вертикальная скорость определяется уравнением 4.21:
vy=v0y-gt.vy=v0y-gt.
Поскольку v0yv0y было найдено в части (a) равным 21,2 м/с, мы имеем
vy=21,2 м/с−9,8 м/с2(3,79 с)=−15,9 м/с.vy=21,2 м/с −9,8 м/с2(3,79 с)=−15,9 м/с.
Величина конечной скорости v→v→ равна
v=vx2+vy2=(21,2м/с)2+(−15,9м/с)2=26,5м/с.v=vx2+vy2=(21,2м /с)2+(−15,9 м/с)2=26,5 м/с.
Направление θvθv находится с помощью арктангенса:
θv=tan-1(vyvx)=tan-1(-15,921,2)=36,9° ниже горизонта. θv=tan-1(vyvx)=tan-1(-15,921,2)=36,9° ниже горизонт.
Значение
(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м выше начальной высоты, находится в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость на 36,9°36,9° ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется в точку по другую сторону от вершины траектории и, следовательно, имеет отрицательное значение 9.0019 y составляющая скорости. Величина скорости меньше, чем величина начальной скорости, которую мы ожидаем, поскольку она воздействует на высоту 10,0 м над уровнем запуска.
Время полета, траектория и дальность
Интерес представляют время полета, траектория и дальность полета снаряда, запущенного на плоской горизонтальной поверхности и упавшего на эту же поверхность. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах.
Время полета
Мы можем определить время полета снаряда, который одновременно запускается и ударяется о плоскую горизонтальную поверхность, выполняя некоторые манипуляции с кинематическими уравнениями. Заметим, что положение и перемещение в y должны быть равны нулю при запуске и при ударе о ровную поверхность. Таким образом, приравняем смещение в y к нулю и найдем
y−y0=v0yt−12gt2=(v0sinθ0)t−12gt2=0.y−y0=v0yt−12gt2=(v0sinθ0)t−12gt2=0.
Факторинг, у нас
t(v0sinθ0−gt2)=0.t(v0sinθ0−gt2)=0.
Решение для t дает нам
Ttof=2(v0sinθ0)g. Ttof=2(v0sinθ0)g.
Ttof=2(v0sinθ0)g.
4,24
Это время полета снаряда, выпущенного с ударом о плоскую горизонтальную поверхность. Уравнение 4.24 неприменимо, когда снаряд приземляется на другой высоте, чем он был запущен, как мы видели в примере 4.8, где теннисист отбивает мяч в трибуны. Другое решение, t = 0, соответствует моменту запуска. Время полета линейно пропорционально начальной скорости в y направление и обратно пропорционально g . Таким образом, на Луне, где гравитация составляет одну шестую от земной, снаряд, запущенный с той же скоростью, что и на Земле, будет находиться в воздухе в шесть раз дольше.
Траектория
Траекторию снаряда можно найти, исключив переменную времени t из кинематических уравнений для произвольных t и решив y ( x ). Мы берем x0=y0=0x0=y0=0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для х дает
Мы берем x0=y0=0x0=y0=0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для х дает
х=v0xt⇒t=xv0x=xv0cosθ0.x=v0xt⇒t=xv0x=xv0cosθ0.
Подстановка выражения для t в уравнение для положения y=(v0sinθ0)t−12gt2y=(v0sinθ0)t−12gt2 дает
y=(v0sinθ0)(xv0cosθ0)−12g(xv0cosθ0)2.y=(v0sinθ0)(xv0cosθ0)−12g(xv0cosθ0)2.
Переставляем члены, имеем
y=(tanθ0)x−[g2(v0cosθ0)2]x2.y=(tanθ0)x−[g2(v0cosθ0)2]x2.
4,25
Это уравнение траектории имеет вид y=ax+bx2,y=ax+bx2, которое представляет собой уравнение параболы с коэффициентами
a=tanθ0,b=−g2(v0cosθ0)2.a=tanθ0,b=−g2(v0cosθ0)2.
Диапазон
Из уравнения траектории мы также можем найти дальность или горизонтальное расстояние, пройденное снарядом. Факторинг Уравнение 4.25, мы имеем
y=x[tanθ0−g2(v0cosθ0)2x].y=x[tanθ0−g2(v0cosθ0)2x].
Позиция y равна нулю как для точки запуска, так и для точки удара, так как мы снова рассматриваем только плоскую горизонтальную поверхность. Установка y = 0 в этом уравнении дает решения х = 0, что соответствует точке запуска, и
х=2v02sinθ0cosθ0g,x=2v02sinθ0cosθ0g,
, соответствующий точке удара. Используя тригонометрическое тождество 2sinθcosθ=sin2θ2sinθcosθ=sin2θ и установив для диапазона x = R , мы находим
R=v02sin2θ0g.R=v02sin2θ0g.
4,26
Обратите внимание, что уравнение 4.26 справедливо только для запуска и удара о горизонтальную поверхность. Мы видим, что размах прямо пропорционален квадрату начальной скорости v0v0 и sin2θ0sin2θ0 и обратно пропорционален ускорению свободного падения. Таким образом, на Луне дальность была бы в шесть раз больше, чем на Земле, при той же начальной скорости. Кроме того, из коэффициента sin2θ0sin2θ0 мы видим, что диапазон максимален при 45°.45°. Эти результаты показаны на рис. 4.15. В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (b) мы видим, что диапазон максимален при 45°.45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют 90°.90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
Кроме того, из коэффициента sin2θ0sin2θ0 мы видим, что диапазон максимален при 45°.45°. Эти результаты показаны на рис. 4.15. В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (b) мы видим, что диапазон максимален при 45°.45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют 90°.90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
Рисунок
4.15
Траектории снарядов на ровной местности. (а) Чем больше начальная скорость v0,v0, тем больше диапазон для данного начального угла. (б) Влияние начального угла θ0θ0 на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон одинаковый для начальных углов 15°15° и 75°,75°, хотя максимальная высота этих путей различна.
Пример 4.9
Сравнение ударов по гольфу
Игрок в гольф оказывается в двух разных ситуациях на разных лунках. На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и дать ему вылететь на грин. Он направляет удар низко к земле под углом 30 ° 30 ° к горизонтали, чтобы мяч мог катиться после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным количеством качения после удара. Здесь он направляет выстрел под углом 70°70° к горизонтали, чтобы свести к минимуму качение после удара. Оба выстрела попали в ровную поверхность.
а) Какова начальная скорость мяча у второй лунки?
(б) Какова начальная скорость мяча у четвертой лунки?
(c) Напишите уравнение траектории для обоих случаев.
(d) Нарисуйте траектории.
Стратегия
Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (а), так и для (б). Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Раствор
(а) R=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(30°))=31,9 м/сR=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(30° ))=31,9 м/с
(б) R=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(70°))=37,0 м/сR=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(70° ))=37,0 м/с
(c)
y=x[tanθ0−g2(v0cosθ0)2x]Второе отверстие: y=x[tan30°−9,8 м/с22[(31,9 м/с)(cos30°) ]2x]=0,58x−0,0064×2Четвертое отверстие:y=x[tan70°−9,8 м/с22[(37,0 м/с)(cos70°)]2x]=2,75x−0,0306x2y=x[tanθ0−g2(v0cosθ0 )2x]Второе отверстие:y=x[tan30°−90,8 м/с22[(31,9 м/с)(cos30°)]2x]=0,58x−0,0064×2Четвертое отверстие:y=x[tan70°−9,8 м/с22[(37,0 м/с)(cos70°)]2x ]=2,75x−0,0306×2
(d) Используя графическую утилиту, мы можем сравнить две траектории, показанные на рис. 4.16.
Рисунок
4.16
Две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка запуска.
Точки удара обоих находятся на том же уровне, что и точка запуска.
Значение
Начальная скорость выстрела под углом 70°70° больше, чем начальная скорость выстрела под углом 30°.30°. Обратите внимание на рис. 4.16, что если бы два снаряда были запущены с одинаковой скоростью, но под разными углами, снаряды имели бы одинаковую дальность, пока углы были бы меньше 90°.90°. Углы запуска в этом примере складываются, чтобы получить число больше 90°,90°. Таким образом, выстрел под углом 70°70° должен иметь большую стартовую скорость, чтобы достичь 90 м, иначе он попадет на более короткое расстояние.
Проверьте свое понимание 4.4
Если бы два удара для гольфа в примере 4.9 были произведены с одинаковой скоростью, какой удар имел бы наибольшую дальность?
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что R очень мала по сравнению с окружностью Земли. Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рис. 4.17, основанном на рисунке Ньютона.0019 Принципы. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».
Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рис. 4.17, основанном на рисунке Ньютона.0019 Принципы. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».
Рисунок 4.17 Снаряд к спутнику. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости диапазон увеличивается и становится длиннее, чем он был бы на ровной поверхности, потому что Земля изгибается под его траекторией. При скорости 8000 м/с достигается орбита.
Постоянная Планка — значение, формула, символ, приложения и примеры
Изначально считалось, что энергия непрерывна. Однако после долгих исследований Макс Планк пришел к выводу, что энергия по своей природе не непрерывна, а дискретна и состоит из небольших пакетов, на которые указывают маленькие невидимые частицы, называемые фотонами. Эти частицы несут энергию, и эта энергия, которая была перенесена, определяется постоянной Планка. Чтобы узнать больше о постоянной Планка — значении, формуле, символе, приложениях и примерах, студенты теперь могут узнать больше об этом через Vedantu.
Энергия, которая высвобождается в виде пакетов или фрагментов прерывистым образом, известна как фотоны, где энергия каждого фотона прямо пропорциональна частоте, т. е. Е, и зависит от f.
е. Е, и зависит от f.
E ∝ f, E = k x h x u….(1) (k – число фотонов, целое число)
Здесь h называется постоянной Планка.
На этой странице мы узнаем о следующем:
постоянная Планка
Value of Planck’s constant
Deriving Planck’s constant formula in both MKS and CGS unit
Planck’s constant units and dimensional formula
Planck’s constant symbol
Applications of Planck’s constant with examples
Наглядные примеры для понимания основ этой темы.

В чем суть квантовой теории Планка?
Немецкий физик-теоретик доктор Макс Планк выдвинул теорию, известную как квантовая теория Планка. Эта теория утверждает: Энергия, излучаемая или свернутая, не вечна, а находится в форме пакетов, называемых квантами. Эта энергия известна как «квант энергии». Для одного пакета мы называем это квантами, где кванты — это целочисленное значение, в отличие от непрерывного энергоснабжения, которое имеет переменные значения: 1 или 1,1 или 1,2…
Пакеты — это единицы энергии, и в общем смысле они называются квантами, тогда как фотоны — это термин, используемый для пакетов в терминах видимого света.
Рассмотрим это уравнение:
E = h x c/λ….(2)
h = 6,626 x 10⁻³⁴
c = 3 x 10⁸ м/с
Подставьте это значение в приведенное выше уравнение 900(2)
(6,626 x 10⁻³⁴) * (3 x 10⁸)/λ
(19,878 x 10⁻²⁶)/λ ∽ (2 x 10²⁵)/λ
Получаем,
M = (2 x)10² λ
Это значение энергии одного фотона, а для «k» фотонов оно будет:
E = (k x 2 x 10²⁵)/λ |
Значение E рассчитывается только для длины волны λ, выраженной в метрах. Если λ дано в любой другой единице измерения, скажем, в ангстремах, просто мы можем преобразовать 1 ангстрем в метры (1 ангстрем = 10⁻¹⁰м), где h — постоянная Планка, а h — энергия кванта электромагнитного излучения, деленная на его частота.
Если λ дано в любой другой единице измерения, скажем, в ангстремах, просто мы можем преобразовать 1 ангстрем в метры (1 ангстрем = 10⁻¹⁰м), где h — постоянная Планка, а h — энергия кванта электромагнитного излучения, деленная на его частота.
Постоянная Планка h измеряется в джоулях-секундах в системе СИ.
h = 6,626 x 10⁻³⁴
и электронвольт или (эВ) в системе М.К.С.
1 эВ = 1,6 x 10⁻¹⁹ Дж
E = (12400/λ) эВ для λ в Å. E = (1240/λ) эВ для λ в нм. |
Value for λ when E = 4.13 V
E = 12400/λ
4.13 = 12400/λ
λ = 12400/4.13 = 3000 Å |
Эксперименты, использованные для определения постоянной Планка:
Для определения постоянной Планка использовались два эксперимента, которые можно представить следующим образом:
1. Весы Киббла
Весы Киббла
2. Рентгеновская плотность кристаллов метод
Весы Киббла:
Это точные весы, названные в честь изобретателя Брайана Киббла в 1975 году. Они предназначены для уравнивания одной из возникающих сил с другой. В этом случае вес пробной массы точно уравновешивается силой, возникающей при пропускании электрического тока через катушку с проволокой, погруженную в окружающее магнитное поле.
Метод рентгеновской плотности кристаллов:
Этот метод является основным методом, используемым для определения постоянной Планка. Здесь используются кристаллы кремния, которые доступны в полупроводниковой промышленности высокого качества и чистоты.
Что особенного в постоянной Планка?
Черное тело — идеализированное физическое тело, поглощающее все электромагнитное излучение. При нагревании он отражает падающий на него свет, но тоже с различной длиной волны.
При нагревании он отражает падающий на него свет, но тоже с различной длиной волны.
(Изображение будет загружено в ближайшее время)
(Изображение будет загружено в ближайшее время)
Здесь на этом графике мы можем наблюдать, что меньше длина волны, меньше излучение волн, затем наступает время, когда мы получаем максимум длина волны, Vmax, что означает максимальное излучение.
Vmax — это положение, показанное пиком на графике в видимом свете.
Здесь происходит то, что когда мы идем дальше, длина волны продолжает увеличиваться, но излучение волн продолжает уменьшаться и продолжается дальше, мы видим, что излучение волн ничтожно мало, но не равно нулю. (Излучаются все длины волн любого количества и независимо от частоты).
Но из теоретических выводов вы, должно быть, заметили на кривой, что от начала до точки, когда длина волны максимальна, график демонстрирует симметрию, но что происходит после этого? Излучение волн максимально, даже когда длина волны меньше.
Есть большая разница, когда длина волны меньше. Модификация вышеупомянутой концепции была предложена великим немецким физиком-теоретиком по имени доктор Макс Планк.
Где он рассматривал свет как форму «k» количества кусков или пакетов, называемых фотонами по соотношению.
E = k x h x f, где k число фотонов. |
После его экспериментов экспериментальные и теоретические кривые, которые не были симметричны друг другу, стали симметричными, что свидетельствует о том, что теория, данная доктором Планком, была правильной.
РезюмеПри нагревании железного стержня излучается свет всех длин волн, но человеческий глаз может воспринимать только тот свет, который имеет максимальную длину волны Vmax.
Мы оцениваем температуру звезд, наблюдая Vmax излучаемого света.

Объяснение урока: Кинетическая энергия фотоэлектронов
В этом объяснении мы узнаем, как рассчитать максимально возможную кинетическую энергию электронов, выбрасываемых с поверхности. металла за счет фотоэффекта.
Фотоэлектрический эффект представляет собой процесс ухода электронов с поверхности металла после поглощения электромагнитного излучения. Экспериментальная установка, используемая для наблюдения фотоэлектрического эффекта, показана на диаграмме ниже.
Две отдельные металлические пластины присоединены к цепи, к которой последовательно подключен амперметр. Металлические пластины заключены в
вакуумную камеру, чтобы воздух не влиял на эксперимент. Свет направляется на одну из металлических пластин. Если падающий свет
имеет достаточно большую энергию, электроны выбрасываются с поверхности металла. Эти выброшенные электроны известны как
«фотоэлектроны». Амперметр регистрирует ток, когда фотоэлектроны достигают соседней пластины.
Вспомните, что свет можно смоделировать как частицу. Частицы света известны как фотоны. Каждый фотон имеет дискретное количество энергия, 𝐸, описываемая формулой 𝐸=ℎ𝑓, где ℎ представляет постоянную Планка, а 𝑓 представляет частоту фотона.
Каждый отдельный падающий фотон передает энергию одному электрону на поверхности металла. Электрон покинет поверхность если у фотона достаточно большая энергия. Поскольку энергия фотона определяется частотой, амплитуда не имеет значения. световой волны — фотоэлектрический эффект индуцируется до тех пор, пока свет имеет достаточно высокую частоту. Отношение между энергией и частотой, а также независимость этих значений от амплитуды показана в таблице ниже.
Теперь, когда мы установили основы фотоэффекта, давайте более подробно рассмотрим передачу энергии между фотоны и электроны.
Напомним, что атомные ядра имеют электроны на дискретных энергетических уровнях. На каждом уровне электроны имеют разное количество энергии. которые удерживают их связанными с атомной системой; это количество энергии называется «работой выхода». Мы можем рассмотреть
работа выхода, обозначаемая 𝑊, как барьер, который удерживает электрон связанным с материалом. Если количество энергии
электрону передается больше работы выхода, барьер преодолевается и электрон освобождается от своей связи.
которые удерживают их связанными с атомной системой; это количество энергии называется «работой выхода». Мы можем рассмотреть
работа выхода, обозначаемая 𝑊, как барьер, который удерживает электрон связанным с материалом. Если количество энергии
электрону передается больше работы выхода, барьер преодолевается и электрон освобождается от своей связи.
Проводящие материалы, такие как металлы, имеют относительно низкую работу выхода. Таким образом, самые внешние электроны на поверхности металла могут несколько легко покидают материал, если они получают достаточно энергии. Это то, что происходит при фотоэффекте.
Если электрон получает количество энергии, превышающее работу выхода, оставшаяся энергия становится кинетической энергией электрона. электрон. Это можно наблюдать, поскольку фотоэлектроны часто покидают поверхность металла со значительными скоростями.
Мы можем определить максимальную кинетическую энергию фотоэлектрона, если мы знаем энергию, испускаемую фотоном и
работа выхода для поверхности металла. Количество кинетической энергии, которое имеет результирующий фотоэлектрон, равно энергии
что фотон перешел к ней за вычетом работы выхода, которую нужно было преодолеть.
Количество кинетической энергии, которое имеет результирующий фотоэлектрон, равно энергии
что фотон перешел к ней за вычетом работы выхода, которую нужно было преодолеть.
Определим эту связь формально.
Определение: максимальная кинетическая энергия фотоэлектрона при заданной частоте
Максимальная кинетическая энергия фотоэлектрона определяется выражением 𝐸=ℎ𝑓−𝑊,макс. где ℎ — постоянная Планка, 𝑓 — частота падающего фотона, а 𝑊 — работа выхода поверхности металла.
Мы попрактикуемся в использовании этого уравнения на следующем примере.
Пример 1. Расчет максимальной кинетической энергии фотоэлектронов
Полированная металлическая поверхность в вакууме освещается светом лазера, что приводит к испусканию электронов из
поверхность металла. Свет имеет частоту
2,00×10 Гц. Рабочая функция
металла 1,40 эВ. Какова максимальная кинетическая энергия этого
электроны могут иметь? Используйте значение
4,14×10 эВ⋅с для
постоянная Планка. Дайте ответ в электрон-вольтах.
Дайте ответ в электрон-вольтах.
Ответ
Начнем с того, что вспомним уравнение для максимальной кинетической энергии фотоэлектрона: 𝐸=ℎ𝑓−𝑊.max
Нам даны значения для ℎ, 𝑓 и 𝑊; подставляя их, имеем 𝐸=4,14×10⋅2,00×10−1,40=6,88.maxэВсГцэВэВ
Таким образом, мы нашли, что максимальная кинетическая энергия, которой могут обладать электроны, равна 6,88 эВ.
Часто бывает полезно нарисовать уравнение для максимальной кинетической энергии фотоэлектрона. График фотоэлектронной кинетики энергия в зависимости от частоты падающего фотона показана ниже.
Напомним, что для того, чтобы электрон был выброшен, падающий фотон должен иметь достаточно высокую частоту (и, следовательно, энергию), чтобы
преодолеть трудовую функцию. По этой причине мы записываем нулевую энергию фотоэлектронов для низкочастотного света, как показано на
горизонтальная часть графика. Это показывает, где падающий свет имеет слишком низкую энергию, чтобы удалить электроны, поэтому мы обнаруживаем
нет фотоэлектронов и нет кинетической энергии.
Однако при достаточно высокой частоте фотонов работа выхода преодолевается. Напомним, что работа выхода материала – это постоянное значение, поэтому после его преодоления кинетическая энергия фотоэлектронов увеличивается по мере того, как частота падающего фотона увеличивается. Таким образом, 𝐸max прямо пропорционально 𝑓, и соотношение линейный, как показано на наклонной, возрастающей части графика.
Мы можем определить определенные свойства аппарата, анализируя его график зависимости 𝐸max от 𝑓. В частности, нас интересует точка, в которой график отклоняется от горизонтальной оси, как выделено на рисунке ниже. Эта точка возникает при пороговом значении частоты, которое мы будем называть 𝑓.
Это определяет поворотный момент в эксперименте, когда фотоны передают ровно столько энергии, сколько необходимо для выброса электронов. Здесь «остаточная» кинетическая энергия фотоэлектронов равна нулю, так как энергия фотона
едва хватает для преодоления работы выхода.
Мы можем использовать эту информацию для экспериментального определения работы выхода материала. Для начала переставим формула максимальной кинетической энергии для решения для 𝑊: 𝑊=ℎ𝑓−𝐸.max
Напомним, что 𝐸=0max на пороговой частоте, 𝑓. Замена этих значения в, мы имеем 𝑊=ℎ𝑓.
Таким образом, на пороговой частоте работа выхода равна энергии падающего фотона. будем практиковать этот метод определения работы выхода в следующих нескольких примерах.
Пример 2. Определение работы выхода с помощью графика зависимости энергии электронов от энергии фотонов
Перестраиваемый лазер используется для освещения поверхности металла светом различной частоты. Выше определенного частота света, электроны испускаются с поверхности металла. График показывает максимальную кинетическую энергию испускаемых электронов против энергии фотонов. Какова работа выхода металла?
Ответить
Этот график иллюстрирует взаимосвязь между энергией падающего фотона и максимальной кинетической энергией фотоэлектрона. покидая поверхность металла. Вспомните уравнение, связывающее эти значения,
𝐸=ℎ𝑓−𝑊,макс.
где ℎ𝑓 описывает энергию падающего фотона с учетом его частоты, 𝑓 и планковского
постоянная, ℎ. Мы хотим найти работу выхода для этой металлической поверхности, поэтому изменим это уравнение следующим образом:
решить для 𝑊:
𝑊=ℎ𝑓−𝐸.max
покидая поверхность металла. Вспомните уравнение, связывающее эти значения,
𝐸=ℎ𝑓−𝑊,макс.
где ℎ𝑓 описывает энергию падающего фотона с учетом его частоты, 𝑓 и планковского
постоянная, ℎ. Мы хотим найти работу выхода для этой металлической поверхности, поэтому изменим это уравнение следующим образом:
решить для 𝑊:
𝑊=ℎ𝑓−𝐸.max
Мы можем использовать значения координат из любой точки на графике для подстановки в это уравнение. Как правило, самое простое указание на работать на «пороговой частоте» 𝑓, или горизонтальном пересечении графика, потому что 𝐸=0max в этот момент. Таким образом, мы можем исключить член 𝐸max в уравнении, и мы остаемся с 𝑊=ℎ𝑓.
Следовательно, энергия фотона в этой точке равна работе выхода материала.
График пересекает горизонтальную ось на уровне 2,6 эВ, поэтому мы нашли, что работа выхода металла равна 2,6 эВ.
Пример 3: Определение работы выхода с помощью графика зависимости энергии электронов от энергии фотонов
График показывает максимальную кинетическую энергию фотоэлектронов при освещении разных металлов светом разных
частоты.
- Какой металл имеет наименьшую работу выхода?
- Какой металл имеет наибольшую работу выхода?
Ответ
Часть 1
Напомним формулу максимальной кинетической энергии фотоэлектрона, 𝐸=ℎ𝑓−𝑊,макс. где 𝑊 — работа выхода, а ℎ𝑓 — значение энергии фотона, которое зависит от частота, 𝑓, и постоянная Планка, ℎ.
На этом графике показаны свойства пяти различных элементов. Все пять линий на графике имеют одинаковый наклон и отличаются только пересечением их горизонтальной оси.
Мы можем узнать об элементах по тому, где их графики пересекают горизонтальную ось, потому что это значение описывает, где падающие фотоны имеют достаточно энергии, чтобы преодолеть работу выхода. Таким образом, 𝐸=0max, но фотоэлектроны все еще создаются. Мы можем подставить это значение, чтобы определить связь между функцией выхода и энергия фотона: 0=ℎ𝑓−𝑊, или же ℎ𝑓=𝑊.
Следовательно, энергия фотона в этой точке равна работе выхода материала.
Меньшее значение точки пересечения горизонтальной оси означает, что для преодоления работы выхода требуется меньшее значение энергии фотона. Таким образом, мы можем сравнить величины работы выхода материалов, сравнив их пороговые значения энергии фотонов. Линия Цезия имеет наименьшее горизонтальное пересечение.
Таким образом, мы обнаружили, что у цезия самая низкая работа выхода.
Часть 2
Снова рассматривая график, мы видим, что платина является элементом с наибольшей энергией фотонов на пороге где 𝐸=0макс.
Следовательно, у платины самая высокая работа выхода.
Мы рассмотрели, как определить работу выхода материала по графику зависимости его кинетической энергии электронов от
частота падающего фотона. Теперь предположим, что мы хотим знать, как это связано с длиной волны падающего света, а не с частотой. Чтобы сделать это, мы должны разработать соотношение между частотой и длиной волны света, чтобы мы могли заменить
𝑓 из нашего уравнения и подставить 𝜆 в.
Мы можем связать частоту и длину волны, используя уравнение скорости волны для электромагнитной волны, 𝑐=𝜆𝑓, где 𝑐 — скорость света. Решая эту формулу для частоты, имеем 𝑓=𝑐𝜆.
Теперь вспомните уравнение кинетической энергии электрона, 𝑊=ℎ𝑓−𝐸.max
Наконец, мы можем заменить частоту: 𝑊=ℎ𝑐𝜆−𝐸.max
Это уравнение позволяет связать работу выхода и максимальную кинетическую энергию фотоэлектронов с длиной волны падающего света.
Мы можем преобразовать эту формулу, чтобы определить максимальную кинетическую энергию фотоэлектрона, учитывая длину волны падающего фотона, как указано ниже.
Определение: максимальная кинетическая энергия фотоэлектрона при заданной длине волны
Максимальная кинетическая энергия фотоэлектрона определяется выражением 𝐸=ℎ𝑐𝜆−𝑊,макс. где ℎ — постоянная Планка, 𝑐 — скорость света, 𝜆 — длина волны падающего фотона, а 𝑊 — работа выхода поверхности металла.
Обратите внимание, что в частотной форме уравнения 𝑓 появляется в числителе, допуская линейное
отношение между 𝑓 и 𝐸max. Напротив, в форме длины волны
уравнение, 𝜆 появляется в знаменателе, что означает, что график 𝐸max
против 𝜆 не имеет линейного наклона. Общий вид графика кинетической энергии электрона
относительно длины волны фотона нарисовано ниже.
Напротив, в форме длины волны
уравнение, 𝜆 появляется в знаменателе, что означает, что график 𝐸max
против 𝜆 не имеет линейного наклона. Общий вид графика кинетической энергии электрона
относительно длины волны фотона нарисовано ниже.
Обратите внимание, что фотоэлектроны не испускаются, когда длина волны фотона превышает определенное значение. Это потому, что по мере того, как мы увеличиваем длину волны падающего света, мы одновременно уменьшаем его частоту (и, следовательно, энергию). Давайте попрактикуемся используя это отношение в нескольких примерах.
Пример 4. Определение работы выхода с помощью графика зависимости энергии электронов от длины волны фотона
Перестраиваемый лазер используется для освещения поверхности металла светом с различной длиной волны. Когда длина волны
света короче определенного значения, электроны испускаются с поверхности металла. На графике показано
максимальная кинетическая энергия испускаемых электронов относительно длины волны фотонов.
- При какой максимальной длине волны света электроны будут испускаться с поверхности металла?
- Какова работа выхода металла? Используйте значение 4,14×10 эВ⋅с для постоянная Планка. Дайте ответ в электрон-вольтах до двух знаков после запятой.
Ответ
Часть 1
Для начала вспомним формулу максимальной кинетической энергии фотоэлектрона в зависимости от длины волны падающего фотона: 𝐸=ℎ𝑐𝜆−𝑊.max
Существует обратная зависимость между энергией фотона и длиной волны. Таким образом, выше определенной пороговой длины волны фотонам не хватает энергии, чтобы преодолеть барьер работы выхода и вызвать фотоэффект.
Эта точка видна на графике, где 𝐸=0макс. Длина волны в этой точке представляет
максимальная длина волны света, при которой электроны будут выброшены с поверхности. Эта точка расположена на
горизонтальная ось на 𝜆=300нм.
Таким образом, максимальная длина волны падающего света, при которой электроны испускаются с поверхности металла, равна 300 нм.
Часть 2
Напомним, что формула для работы выхода при заданной длине волны падающего фотона имеет вид 𝑊=ℎ𝑐𝜆−𝐸.max
Чтобы найти работу выхода металла, мы можем подставить значение горизонтальной точки пересечения графика в это уравнение. Мы должны преобразовать нанометры в метры, поэтому это пороговое значение длины волны равно 300=300×10 нм. При этой длине волны падающего света кинетическая энергия электрона равна нулю, поэтому мы исключим 𝐸max. Далее подставляем в значения постоянной Планка и скорости света, и мы можем вычислить работу выхода: 𝑊=4,14×10⋅3,0×10300×10=4,14.eVsmeVms
Таким образом, мы нашли, что работа выхода металла равна 4,14 эВ.
Пример 5. Расчет характеристик экспериментального устройства фотоэлектрического эффекта
На схеме показана электрическая цепь. Схема содержит анод и катод в вакуумной камере. Анод и катод
подключены к амперметру и аккумулятору последовательно. Катод изготовлен из никеля.
Схема содержит анод и катод в вакуумной камере. Анод и катод
подключены к амперметру и аккумулятору последовательно. Катод изготовлен из никеля.
- Свет различных длин волн используется для освещения никелевого катода. Когда длина волны света короче 248 нм, амперметр показывает показание 12,8 мА. Что это работа выхода никеля? Используйте значение 4,14×10 эВ⋅с для постоянная Планка. Дайте ответ с точностью до двух знаков после запятой.
- Первоначально лазер, использовавшийся для освещения катода, имел выходную мощность 64 мВт. Если бы это было увеличено до 128 мВт, какой бы ток в схема быть? Дайте ответ с точностью до одного десятичного знака.
Ответ
Часть 1
Начнем с того, что вспомним формулу для работы выхода при заданной длине волны падающего фотона,
𝑊=ℎ𝑐𝜆−𝐸. max
max
Мы знаем, что когда падающий свет имеет достаточно большую энергию, электроны будут испускаться с поверхности меди, вызывая амперметр для определения силы тока.
Здесь мы знаем, что амперметр определяет ток только тогда, когда длина волны падающего света меньше, чем 248 мА. На этой пороговой длине волны значение, которое мы будем называть 𝜆, падающие фотоны имеют достаточно энергии, чтобы преодолеть работу функциональный барьер. Таким образом, для фотоэлектронов не останется кинетической энергии, т. е. 𝐸=0max, поэтому формула принимает вид 𝑊=ℎ𝑐𝜆.
Для расчета работы выхода подставим значения постоянной Планка, скорости света и пороговая длина волны: 𝑊=4,14×10⋅3,0×10248×10=5,01.eVsmeVms
Таким образом, мы нашли, что работа выхода никеля составляет 5,01 эВ.
Часть 2
Мощность лазера дает количество энергии в секунду. Фотоны переносят энергию лазерного луча, поэтому, если лазер включен в два раза больше энергии
в секунду он испускает в два раза больше фотонов
в секунду. Напомним, один случай
фотон взаимодействует с одним электроном на поверхности металла. Таким образом, если на поверхность падает в два раза больше фотонов,
вдвое больше электронов, получающих энергию и покидающих поверхность.
Напомним, один случай
фотон взаимодействует с одним электроном на поверхности металла. Таким образом, если на поверхность падает в два раза больше фотонов,
вдвое больше электронов, получающих энергию и покидающих поверхность.
Таким образом, если мощность лазера удвоится, ток тоже удвоится. Поскольку амперметр первоначально обнаружил ток 12,8 мА, теперь он будет обнаруживать вдвое больше этого значения.
Таким образом, ток в цепи будет 25,6 мА.
Давайте закончим резюмированием некоторых важных понятий.
Ключевые положения
- Фотоэлектрический эффект — это явление удаления электронов с поверхности металла при освещении ее светом. Фотоэлектрон — это электрон, испускаемый с поверхности после получения энергии от падающего фотона.
- Работа выхода материала – это минимальное количество энергии, необходимое для удаления электрона с его поверхности.
и его значение можно найти из графика зависимости кинетической энергии электрона от энергии фотона.

- Энергия света пропорциональна его частоте и обратно пропорциональна длине волны.
- Мы можем связать работу выхода, 𝑊, и максимальную энергию электрона, 𝐸max, заданной частоты, 𝑓, используя формулу 𝐸=ℎ𝑓−𝑊max, где ℎ — постоянная Планка.
- Мы можем связать работу выхода, 𝑊, и максимальную энергию электрона, 𝐸max, заданной длины волны 𝜆, используя формулу 𝐸=ℎ𝑐𝜆−𝑊max, где ℎ — постоянная Планка, а 𝑐 — скорость света.
кинематических уравнений | PASCO
Что такое кинематические уравнения?
Кинематические уравнения представляют собой набор уравнений, описывающих движение объекта с постоянным ускорением. Уравнения кинематики требуют знания производных, скорости изменения и интегралов. Чтобы сосредоточиться на школьной физике, мы не будем рассматривать интегралы.
Когда мы используем кинематические уравнения, мы используем специальные обозначения для обозначения начальных и конечных измерений. Например, когда у нас есть начальное значение скорости, оно записывается как $ \Large\mathcal{v}_{\normalsize0} $.
Когда мы пишем конечную скорость, мы просто пишем $\Large\mathcal{v}$ без нижнего индекса.
Следовательно, изменение скорости объекта представляется уравнением $\Delta\Large\mathcal{v} = \mathcal{v} — \mathcal{v}_{\normalsize0} $.
Это обозначение также применимо к смещению и времени.
Это означает, что $ {\large x}_0 $ — это начальное положение, $ {\large x} $ — это конечное положение, $ {\large t}_0 $ — начальное время, а $ \large t $ — конечное время. .
Важно помнить, что начальное время, $ {\large t}_0 $, будет равно нулю для уравнений кинематики.
Поскольку временной интервал равен $ \Delta\mathcal{t} $ и $ {\mathcal{t}}_0 = 0{\normalsize{s}} $, мы знаем, что $ \Delta\mathcal{t} = \mathcal{ т} $.
Например, когда у нас есть начальное значение скорости, оно записывается как $ \Large\mathcal{v}_{\normalsize0} $.
Когда мы пишем конечную скорость, мы просто пишем $\Large\mathcal{v}$ без нижнего индекса.
Следовательно, изменение скорости объекта представляется уравнением $\Delta\Large\mathcal{v} = \mathcal{v} — \mathcal{v}_{\normalsize0} $.
Это обозначение также применимо к смещению и времени.
Это означает, что $ {\large x}_0 $ — это начальное положение, $ {\large x} $ — это конечное положение, $ {\large t}_0 $ — начальное время, а $ \large t $ — конечное время. .
Важно помнить, что начальное время, $ {\large t}_0 $, будет равно нулю для уравнений кинематики.
Поскольку временной интервал равен $ \Delta\mathcal{t} $ и $ {\mathcal{t}}_0 = 0{\normalsize{s}} $, мы знаем, что $ \Delta\mathcal{t} = \mathcal{ т} $.
Как выбрать правильное уравнение?
Кинематические уравнения могут применяться к множеству задач размерного движения, рассматривающих движение объекта с постоянным ускорением. При решении задач формула, которую мы выбираем, должна включать неизвестную переменную, а также три известные переменные.
В каждом из уравнений отсутствует одна переменная.
Это позволяет вам определить, какая переменная не задана или не запрошена в вашей задаче, прежде чем выбрать уравнение, в котором также отсутствует эта переменная.
Давайте посмотрим поближе.
При решении задач формула, которую мы выбираем, должна включать неизвестную переменную, а также три известные переменные.
В каждом из уравнений отсутствует одна переменная.
Это позволяет вам определить, какая переменная не задана или не запрошена в вашей задаче, прежде чем выбрать уравнение, в котором также отсутствует эта переменная.
Давайте посмотрим поближе.
Не хватает смещения? В этой формуле отсутствует $ \Delta{\large x} $, и ее следует использовать для задач, которые не включают или не требуют смещения.
$ \Large v = v_0 + \Large {at} $
Не хватает ускорения? Эта формула идеальна для задач, которые не включают или не требуют ускорение. Однако важно помнить, что иногда ускорение косвенно упоминается, например, когда объект находится в свободном падении (см. ниже).
$ \Большой\Дельта\большой х = \Большой (\фракция {v + v_0}{2}) \большой т $ 92 + \Large 2a\Delta{\large x} $
Скорость, ускорение и сопротивление воздуха
Когда мы используем уравнения кинематики, мы можем сделать некоторые математические предположения. Когда движущийся объект движется по воздуху, сопротивление воздуха замедляет скорость объекта.
К счастью, когда мы используем уравнения движения, мы предполагаем, что сопротивление воздуха достаточно незначительно, чтобы им можно было пренебречь.
Когда движущийся объект движется по воздуху, сопротивление воздуха замедляет скорость объекта.
К счастью, когда мы используем уравнения движения, мы предполагаем, что сопротивление воздуха достаточно незначительно, чтобы им можно было пренебречь.
Второе предположение, которое мы можем сделать при использовании этих уравнений, касается ускорения. Мы уже знаем, что ускорение для задач кинематики постоянно, а значит, среднее ускорение равно этому значению. Объекты в свободном падении или снаряды испытывают одинаковое ускорение, независимо от их массы. Это означает, что всякий раз, когда объект брошен, брошен или падает, он движется с постоянным нисходящим ускорением в 9 долларов.2$.
Поскольку уравнения кинематики используются, когда ускорение объекта постоянно, мы можем использовать простое уравнение для определения средней скорости объекта. Чтобы найти среднюю скорость, просто прибавьте начальную скорость к конечной скорости и разделите на 2.
$ \LARGE v_{ \textrm {среднее}} = \bar{v} = \frac {v_1 + v_2}{2} $ Это уравнение можно использовать только при постоянном ускорении
Когда объект движется прямолинейно вдоль оси x, мы можем использовать смещение объекта и временной интервал для определения средней скорости. Это уравнение учитывает начальное положение, конечное положение и временной интервал.
Это уравнение учитывает начальное положение, конечное положение и временной интервал.
$ \LARGE v_{ \textrm {среднее}} = \bar{v} = \frac {x_2 — x_1}{t_2 — t_1} = \frac {\Delta x}{\Delta t} $
Вы можете использовать наклон линии, касательной к излечению положение-время, чтобы определить скорость объекта. Скорость объекта в определенный момент времени называется мгновенной скоростью. Построение графика положение-время может помочь вам определить как мгновенную скорость, так и среднюю скорость. Точно так же построение графика зависимости скорости от времени может помочь вам определить мгновенное ускорение и среднее ускорение объекта, поскольку ускорение — это скорость изменения скорости. Однако, когда мы применяем это к уравнениям кинематики, которые имеют постоянное ускорение, мгновенное ускорение объекта будет равно его среднему ускорению.
Как вывести уравнения кинематики
Первое уравнение: $ \large v = v_0 + at $
1.) Чтобы начать вывод первого кинематического уравнения, мы должны сначала рассмотреть определение ускорения. $ \Large a = \frac {\Delta v}{\Delta t} $
$ \Large a = \frac {\Delta v}{\Delta t} $
2.) Мы знаем, что $ \Large \Delta v = v — v\normalsize{_0} $ , и когда мы это подставим, мы получим $ \Large a = \frac {v — v_0}{\Delta t} $
3.) Если мы решим для $\Large v $, уравнение станет $\Large v = v_0 + \Large a \Delta t $
4.) Мы можем обозначить интервал времени как для генерации первого кинематического уравнения.
$ \НАИБОЛЬШИЙ v = v_0 + в $
Второе уравнение: $ \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
Чтобы вывести это уравнение, рассмотрим график зависимости скорости от времени с постоянным ускорением. Наклон графика скорости можно интерпретировать как ускорение, а площадь под графиком равна смещению объекта $ \Delta x $ .
Здесь высота синего прямоугольника равна $\large v_0 $, а ширина $\large t $, поэтому площадь равна $\large v_0 t $.
Основание красного треугольника равно $ \large t $, а высота равна $ \large v — v_0 $, поэтому площадь красного треугольника равна $ \large \ frac {1}{2} t (v — v_0) $ . 2 $
92 $
2 $
92 $
Мы можем получить третье кинематическое уравнение, подставив первую кинематическую формулу во вторую формулу.
1.) Начните со второго кинематического уравнения. $ \large \frac {\Delta x}{t} = (\frac {\Large v + v_{\normalsize0}}{2}) $
2.) Подставляем первую кинематическую формулу вместо $\large v$. $ \Large v = v\normalsize{_0} + \Large в $
3.) После подстановки уравнение становится $ \large \frac {\Delta x}{t} = \frac {\Large (v_0 + at) + v_0}{2} $ 92 + 2а \Дельта х $
Четвертое кинематическое уравнение может быть получено с использованием первого и второго кинематических уравнений.
1.) Начните со второй кинематической формулы. $ \large \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
2.) Мы можем использовать первую кинематическую формулу, $ \Large \mathcal{v} = \mathcal{v}\normalsize{_0} + \large at $, чтобы найти время. $ \large t = \frac {\Large v — v _{\normalsize0}}{a} $
3.) Мы можем подставить наше выражение для времени во вторую кинематическую формулу. $ \large \Delta x = (\frac {\Large v + v_{\normalsize0}}{2}) (\frac {\Large v — v_{\normalsize0}}{\Large a}) $
92 + 2а \Дельта х $
$ \large \Delta x = (\frac {\Large v + v_{\normalsize0}}{2}) (\frac {\Large v — v_{\normalsize0}}{\Large a}) $
92 + 2а \Дельта х $
Решение задач для кинематических уравнений
При решении задач кинематики есть шаги, которым вы можете следовать, чтобы структурировать свой мыслительный процесс. Прочитав задачу, начертите схему и отметьте известные и неизвестные. Определите, что вас просят найти. Затем определите переменные, которые предоставляет проблема. Затем определите, какие уравнения связывают ваши известные переменные с неизвестной переменной. Затем можно приступать к решению.
Свободное падение 92)} = \large 5.1 \textrm m $
Беспроводная фотоворота и частокол
Беспроводной фотозатвор совершенствует конструкцию традиционных фотозатворов, чтобы предоставить учащимся данные о скорости в реальном времени и расширенные функции для большего количества приложений. Беспроводные интеллектуальные ворота позволяют учащимся собирать высокоточные данные о движении различных объектов — от исследований свободного падения и движения снарядов до маятников и столкновений тележек.
2.) Вы и ваш партнер расходитесь во мнениях относительно того, сможете ли вы заставить штакетник упасть на землю ровно за 1,0 с. Ваш напарник считает, что забор слишком легкий, чтобы его так быстро опустить, но вы убеждены, что это возможно. Предполагая, что ускорение является постоянным, а сопротивление воздуха пренебрежимо мало, с какой высоты вам нужно бросить штакетник, чтобы «умные ворота» зафиксировали его удар о землю ровно через 1,0 с? 92 = 4,9 \textrm м $
Линейное движение в одном измерении
1.) Ваш класс использует датчик движения и MatchGraph! изучать движение. Ваш партнер надевает коньки и удаляется от датчика движения со скоростью 5 м/с. Он останавливается через 23 м. Если торможение вашего партнера было постоянным, сколько времени ему потребовалось, чтобы остановиться?
Каковы заданные значения? $ \large v_0 = 5 \textrm {м/с} $ $ \large v_0 = 0 \textrm {м/с} $ $ \большой x — x_0 = 23 \textrm m $
Мы можем изменить формулу второй кинематики $ \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
Подставим наше уравнение вместо $\Delta x $ и перестроим уравнение. $ х — х_0 = \ гидроразрыва {1} {2} (v_0 + v) t $
$ х — х_0 = \ гидроразрыва {1} {2} (v_0 + v) t $
Подготовьте уравнение для решения $\large t$ и подставьте известные значения для решения.
$ \Large t = 2 (\frac {x — x_0}{v_0 + v}) = 2 (\frac {23 \textrm m}{5 \textrm {м/с} + 0 \textrm {м/с}} ) = \large 11.6 \textrm s $
Система тележки и гусеницы Dynamics
Dynamics Cart and Track Systems — это многоцелевые наборы оборудования, которые позволяют преподавателям демонстрировать и преподавать различные сложные темы физики в области кинематики и динамики.
С момента своего изобретения динамические системы PASCO стали незаменимыми инструментами в физических лабораториях по всему миру.
Наши динамические системы представляют собой комплексные решения для экспериментов, которые позволяют учащимся наблюдать, измерять и анализировать движение посредством практических экспериментов.
Независимо от того, являетесь ли вы новичком в динамических системах или хотите расширить возможности своих существующих систем, мы предлагаем ряд настраиваемых динамических систем в соответствии с вашим бюджетом и потребностями. 92 $
92 $
Линейное движение во втором измерении
Задачи, включающие наклонную плоскость, пандус или снаряд, потребуют от нас разделения движения на векторные компоненты $\small\overrightarrow{\normalsize x} $ и $\small \overrightarrow{\normalsize y} $.
Рассмотрим реактивный самолет с двумя перпендикулярными двигателями, которые двигают его вдоль осей x и y.
Когда работает только вертикальный двигатель, реактивный самолет движется вдоль оси y.
Точно так же, когда работает только горизонтально ориентированный двигатель, реактивный самолет движется вдоль оси x.
Когда оба двигателя включены, движение струи происходит как в направлении x, так и в направлении y, но ни x, ни y не влияют друг на друга.
По этой причине мы можем анализировать компоненты $\small\overrightarrow{\normalsize x}$ и $\small\overrightarrow{\normalsize y}$ для каждого вектора отдельно, признавая при этом, что они
связаны общей стоимостью $\large t$.
Направления компонентов можно передать, назначив каждому знак плюс или минус. 92 + 2a_yy $
92 + 2a_yy $
Мы можем представить векторные компоненты $\small\overrightarrow{\normalsize x} $ и $\small \overrightarrow{\normalsize y} $ с помощью диаграмм свободного тела — метод, обычно используемый для решения задач, связанных с законами Ньютона. Мы углубимся в это, когда будем изучать динамику. На данный момент важно понимать, что некоторые проблемы должны быть разбиты на компоненты x и y. Например, когда тележка спускается по пандусу, она испытывает движение в направлениях x и y. Его движение зависит от чистого ускорения в направлении x вдоль рампы. Поскольку есть компонент ускорения силы тяжести, который ускоряет тележку вниз по склону, часть ускорения силы тяжести является вертикальной. Ниже вы найдете векторную диаграмму Smart Cart, которая разбивает свое движение на компоненты x и y.
Величины составляющих смещения по осям равны x и y. Величины компонент скорости $ \large v $ равны
$ \large v_x = v\cos \Theta $ и $ \large v_y = v\sin \Theta $, где $ \large v $ — величина скорости, а theta — ее направление.
1.) Тележка Smart Cart высвобождается из состояния покоя на вершине 45-градусного пандуса длиной 5,0 м. Какова конечная скорость умной тележки, если ускорение постоянно, а трение пренебрежимо мало? 9{\circ})] (5,0 \textrm м) = 8,3 \textrm {м/с} $
Беспроводная умная тележка
Wireless Smart Cart — это динамическая тележка следующего поколения со встроенными датчиками, которые измеряют ее положение, скорость, ускорение, силу и вращение.
Полностью функциональная тележка Wireless Smart Cart с треком или без него предоставляет учащимся данные о движении в режиме реального времени, интерактивные графики и интуитивно понятные функции анализа на любом устройстве с подключением Bluetooth и программным обеспечением PASCO.
От вводных экспериментов с линейным и вращательным движением до законов Ньютона и столкновений нескольких тележек — Wireless Smart Cart расширяет возможности классических экспериментов и позволяет учащимся исследовать новый мир экспериментальных возможностей.
Векторный дисплей Smart Cart
Векторный дисплей Smart Cart дает новую жизнь векторным демонстрациям с живыми векторными дисплеями для скорости, ускорения и силы Smart Cart в движении. По мере движения тележки на векторном дисплее загораются стрелки, указывающие направление и величину движения тележки. Этот инновационный дизайн позволяет учащимся наблюдать за векторами скорости, силы и ускорения в режиме реального времени, когда тележка катится по склону, свободно падает, вращается или сталкивается с другой тележкой.
Узнайте больше о правильной настройке динамической тележки и гусеничной системы для вашего класса.
Движение снаряда
Снарядное движение возникает, когда единственное ускорение, испытываемое объектом в полете, вызвано гравитацией, которая тянет его вниз.
Объект в движении называется снарядом, а его путь известен как его траектория.
Горизонтальное расстояние, пройденное снарядом, называется его дальностью.
Конечное положение за вычетом начального положения снаряда называется его перемещением, с. В двумерных задачах движения снаряда часто предполагается, что сопротивление воздуха и трение пренебрежимо малы.
Поскольку движения вдоль перпендикулярной оси независимы, мы можем анализировать их отдельно, разбивая их на компоненты x и y.
Когда мы применяем кинематические уравнения для каждого компонента, мы используем нижние индексы x и y для обозначения отношения каждой переменной к осям x или y.
Для компонентов x и y ускорение постоянно, что позволяет нам использовать кинематические уравнения.
92 $
В двумерных задачах движения снаряда часто предполагается, что сопротивление воздуха и трение пренебрежимо малы.
Поскольку движения вдоль перпендикулярной оси независимы, мы можем анализировать их отдельно, разбивая их на компоненты x и y.
Когда мы применяем кинематические уравнения для каждого компонента, мы используем нижние индексы x и y для обозначения отношения каждой переменной к осям x или y.
Для компонентов x и y ускорение постоянно, что позволяет нам использовать кинематические уравнения.
92 $
Визуальное представление полного смещения, $\Large s $, летящего мяча в точке на его пути показано выше. Вектор $\Large s$, имеет вдоль осей компоненты $\Large x$ и $\Large y$. Его величина составляет угол $\Theta$ с горизонтом. Обратите внимание, что $\Large s $ и $\Large x $ могут обозначать смещение. Здесь мы используем $\Large s $, чтобы упростить идентификацию каждого вектора. Мы можем использовать ряд шагов для анализа движения снаряда.
Шаг 1: Разбейте движение на горизонтальные и вертикальные компоненты по осям x и y.
$ \large A_x = A\cos\Theta $$ \large A_y = A\sin\Theta $
Величины составляющих смещения по осям равны $\large x$ и $\large y$. Величины составляющих скорости, $\Large v $, являются $\Large v_x = v \normalsize \cos\Theta $ и $\Large v_y = v \normalsize \sin\Theta $, где $\Large v $ — величина скорости, а theta равна его направление. 9{-1} (v_y/v_x) $
Когда мы рассматриваем горизонтальную и вертикальную составляющие движения, мы находим горизонтальное движение простым, потому что $\large a_x = \normalsize 0 $ и $\large v_x $ является постоянным. Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. На его высоте вертикальная скорость объекта равна нулю. Когда он падает обратно, вертикальная скорость увеличивается по величине, но в направлении, противоположном его первоначальному пути. X- и y-движения рекомбинируются, чтобы найти полную скорость в любой заданной точке во время траектории снаряда.
Метательные установки
Продемонстрируйте независимость x- и y-движения, помогая учащимся развивать практические знания кинематических уравнений с помощью высокоточной и воспроизводимой мини-пусковой установки для снарядов PASCO. Мини-пусковая установка запускает снаряды с высокой повторяемостью, что позволяет учащимся исследовать движение снаряда, сравнивая влияние различных углов запуска и скорости на дальность полета снаряда.
Мини-пусковая установка запускает снаряды с высокой повторяемостью, что позволяет учащимся исследовать движение снаряда, сравнивая влияние различных углов запуска и скорости на дальность полета снаряда.1.) Предположим, вы используете гранатомет для запуска шарика горизонтально со стола со скоростью . Если стол имеет высоту 3,0 м, как далеко пролетит шарик, прежде чем Smart Gate замерит его удар о землю? 92} = 7,8 \textrm м $
2.) Умная тележка, оснащенная аксессуаром для баллистической тележки, движется по горизонтальной дорожке. Тележка запускает мяч с дорожки на уровне земли и ловит его на расстоянии 15 м. Горизонтальная составляющая скорости запуска равна $ \large v_{0x} = \normalsize +3.0 \textrm {м/с} $. Если предположить, что сопротивление воздуха или трение отсутствуют, какова вертикальная составляющая $ \large v_{0y} $ начальной скорости запуска?
Мы ищем $ \Large v_{0y} $ и наши известные значения: $ \Large v_{0x} = \normalsize +3. 0 \textrm {м/с} $ и $ \Large x = \normalsize 15 \textrm m $
92)(5,0 \textrm с) = 25,0 \textrm {м/с} $
0 \textrm {м/с} $ и $ \Large x = \normalsize 15 \textrm m $
92)(5,0 \textrm с) = 25,0 \textrm {м/с} $
Предлагаемые связанные темы
Вращательное движение
Кинематика вращательного движения описывает отношения между угловой скоростью, углом поворота, угловым ускорением и временем. Каждая из кинематических переменных для линейного движения имеет аналог вращательного движения. Подобно уравнениям линейной кинематики, уравнения вращательного движения используют нижние индексы для обозначения начальных значений и исключают нижние индексы для обозначения конечных значений. Ниже вы найдете уравнения вращательного движения и их уравнения поступательного, линейного движения. 92+2ах$
Прямолинейное движение заряженных частиц в магнитных полях
Первый закон движения Ньютона гласит, что если на объект не действует результирующая сила, то его скорость постоянна.
Когда скорость заряженной частицы параллельна магнитному полю, она не испытывает результирующей силы и движется в пространстве прямолинейно. Это называется прямолинейным движением.
Если вектор скорости не параллелен и не перпендикулярен магнитному полю, составляющая скорости, параллельная полю, останется постоянной.
Это называется прямолинейным движением.
Если вектор скорости не параллелен и не перпендикулярен магнитному полю, составляющая скорости, параллельная полю, останется постоянной.
Катящиеся объекты с различными моментами инерции
В одном классическом школьном вопросе по физике участвуют два цилиндра. Вопрос гласит: у вас есть два цилиндра, один полый и один сплошной, с одинаковыми массами и диаметрами. Если их обоих скатить вниз по склону, какой из цилиндров первым достигнет дна?
Когда мы катим объект, его кинетическая энергия принимает две формы: поступательную (прямолинейное движение) и вращательную (вращение). Поступательная энергия с постоянным ускорением
можно описать с помощью кинематических уравнений, но чтобы ответить на наш вопрос, мы должны сосредоточиться на инерции вращения. Вращательная инерция зависит не только от массы и вращательного
скорость объекта, но и от того, как масса распределяется вокруг оси вращения. Это означает, что обруч будет иметь большую инерцию вращения, чем цилиндр такой же массы при
та же угловая скорость, потому что масса в обруче движется быстрее из-за большего удаления его от оси вращения. 92$, где $I$ равен моменту инерции, $\large m$
равно массе объекта, а $ \large r $ равно радиусу. Если два цилиндра имеют разные диаметры, но равные массы, то цилиндр большего диаметра будет иметь
больший момент инерции. Теперь рассмотрим наш первоначальный вопрос. Полый цилиндр имеет ту же массу и диаметр, что и сплошной цилиндр, но его масса более «размазана», что
заставляет его иметь больший момент инерции. Итак, определяет ли величина момента инерции объекта, достигнет ли он дна первым? Не обязательно.
На самом деле, если вы катите два цилиндра вниз по склону, твердый цилиндр каждый раз будет достигать дна первым. Это может показаться нелогичным, потому что полый цилиндр имеет большую
момента инерции, но сплошной цилиндр или сфера всегда достигают дна раньше полого предмета, независимо от диаметра.
92$, где $I$ равен моменту инерции, $\large m$
равно массе объекта, а $ \large r $ равно радиусу. Если два цилиндра имеют разные диаметры, но равные массы, то цилиндр большего диаметра будет иметь
больший момент инерции. Теперь рассмотрим наш первоначальный вопрос. Полый цилиндр имеет ту же массу и диаметр, что и сплошной цилиндр, но его масса более «размазана», что
заставляет его иметь больший момент инерции. Итак, определяет ли величина момента инерции объекта, достигнет ли он дна первым? Не обязательно.
На самом деле, если вы катите два цилиндра вниз по склону, твердый цилиндр каждый раз будет достигать дна первым. Это может показаться нелогичным, потому что полый цилиндр имеет большую
момента инерции, но сплошной цилиндр или сфера всегда достигают дна раньше полого предмета, независимо от диаметра.
Планетарные орбиты (законы Кеплера)
В 16 веке немецкий астроном Иоганн Кеплер объявил свои три закона движения планет.
Законы гласят:
(1) Все планеты движутся вокруг Солнца по эллиптическим орбитам с Солнцем в одном из фокусов. (2) Радиус-вектор, соединяющий любую планету с Солнцем, заметает равные площади за равные промежутки времени.
(3) Квадраты сидерических периодов обращения планет прямо пропорциональны кубам их средних расстояний от Солнца.
(2) Радиус-вектор, соединяющий любую планету с Солнцем, заметает равные площади за равные промежутки времени.
(3) Квадраты сидерических периодов обращения планет прямо пропорциональны кубам их средних расстояний от Солнца.
Эти законы в конечном итоге помогли развитию законов Ньютона, когда он сформулировал закон всемирного тяготения, в котором он описал гравитацию между Землей и Луной, а также Солнцем и планетами. Ньютон пришел к выводу, что движение тел, подверженных действию центральной гравитационной силы, не всегда следует одним и тем же эллиптическим орбитам, заявленным первым законом Кеплера. Вместо этого их пути определяются общей энергией тела, что позволяет этим телам двигаться по гиперболическим или даже параболическим орбитам. Возможно, наиболее интересным аспектом законов Кеплера является то, что они также применимы ко всем другим силам обратных квадратов, включая электромагнитные силы внутри атома (с учетом релятивистских и квантовых эффектов).
Скорость убегания
Скорость убегания — это скорость, с которой должен двигаться объект, чтобы вырваться из гравитационного колодца планеты или луны и покинуть его без дальнейшего движения. Например, объект на Луне должен развить скорость 2,38 км/с, чтобы избежать гравитационного поля Луны.
Для сравнения, объекту на Солнце нужна скорость убегания 618 км/сек!
Например, объект на Луне должен развить скорость 2,38 км/с, чтобы избежать гравитационного поля Луны.
Для сравнения, объекту на Солнце нужна скорость убегания 618 км/сек!
Спутниковые орбиты
Спутники удерживаются в пределах трех типов околоземных орбит в космосе. Высокая околоземная орбита наиболее удалена от поверхности Земли и является местом расположения многих метеорологических спутников и спутников связи. Средняя или средняя околоземная орбита включает в себя навигационные и большинство специальных спутников, а низкая околоземная орбита — это место, где вращается большинство научных спутников. Расстояние между спутником и поверхностью Земли, также известное как высота орбиты, определяет орбитальную скорость спутника. Чем выше орбита спутника, тем медленнее он будет двигаться. Другие факторы, влияющие на орбиту спутника, включают эксцентриситет и наклонение.
Potential Energy by Ron Kurtus
SfC Home > Physics > Energy >
Рон Куртус
Потенциальная энергия — это состояние объекта или частицы, при котором они потенциально могут стать кинетической энергией или родственными формами энергии. Объект остается в состоянии равновесия, когда есть сила, пытающаяся сдвинуть материю, и равная другая сила, препятствующая этому движению.
Объект остается в состоянии равновесия, когда есть сила, пытающаяся сдвинуть материю, и равная другая сила, препятствующая этому движению.
Ослабление силы, препятствующей движению, или добавление внешней силы может превратить потенциальную энергию в кинетическую.
Хорошим примером такого равновесия является сила, сжимающая пружину, и внутренняя сила, пытающаяся растянуть пружину. Эта внутренняя сила считается потенциальной энергией сжатой пружины.
Распространенными типами потенциальной энергии являются упругая, гравитационная, химическая, электрическая и ядерная. Когда потенциальная энергия высвобождается, ее можно использовать для совершения работы.
Возможные вопросы:
- Каково состояние равновесия?
- Какие существуют виды потенциальной энергии?
- Как можно применить потенциальную энергию?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения
Равновесие и потенциальная энергия
Потенциальная энергия возникает при приложении к объекту двух равных сил в противоположных направлениях.
Сила вызывает ускорение
Когда вы прикладываете силу к объекту, он будет ускоряться, пока действует эта сила, согласно второму закону Ньютона и уравнению:
Ф = ма
где
- F — приложенная сила в ньютонах (Н)
- m — масса в килограммах (кг)
- a результирующее ускорение в метрах/секундах в квадрате (м/с 2 )
Примечание : 1 Н = 1 кг-м/с².
Сила сопротивления может привести к потенциальной энергии
Но это простое уравнение или соотношение исходят из предположения, что нет никаких других сил, препятствующих этому движению. Если есть какая-то сила, такая как трение, которая сопротивляется движению, ускорение будет:
а = (F — F r )/м
где F r сила сопротивления.
Теперь, если F r равно приложенной силе F , ускорение и движение будут равны нулю. Но если сила F все еще приложена, то существует потенциальная энергия, которая высвободится, как только F r будет отнята или уменьшена.
Но если сила F все еще приложена, то существует потенциальная энергия, которая высвободится, как только F r будет отнята или уменьшена.
Пример
Например, если вы находитесь в машине на холме, сила тяжести F g пытается скатить автомобиль с холма. Но если у вас есть тормоза, сила сопротивления F r сдерживает вас. F г – потенциальная энергия. Теперь, если вы медленно отпустите тормоза, эта потенциальная энергия изменится на кинетическую энергию, когда вы начнете катиться вниз по склону. Повторное нажатие на тормоз вернет вас в состояние потенциальной энергии, пока вы находитесь на холме.
Виды потенциальной энергии
Бывают ситуации, когда объект потенциально может начать движение и набрать кинетическую энергию. Часто на объект действуют силы, но этих сил еще недостаточно для перемещения объекта. Общие типы потенциальной энергии:
- Эластичный
- Гравитация
- Химическая
- Электрика
- Ядерный
Потенциальная энергия упругости
Когда вы сжимаете пружину, вы создаете потенциальную энергию. Сила сжатия пропорциональна сжатию по закону Гука. При отпускании пружины потенциальная энергия превращается в кинетическую. затем пружину можно использовать для приведения в движение какого-либо предмета.
Сила сжатия пропорциональна сжатию по закону Гука. При отпускании пружины потенциальная энергия превращается в кинетическую. затем пружину можно использовать для приведения в движение какого-либо предмета.
Воздушный шар является еще одним примером упругой потенциальной энергии, когда воздух сжимается внутри воздушного шара. Если разбить шарик иголкой, потенциальная энергия превратится в кинетическую энергию быстро движущихся молекул воздуха.
Потенциальная энергия гравитации
Объект, удерживаемый над землей, имеет потенциальную энергию, связанную с высотой, на которой он удерживается, согласно уравнению
PE = мгч
где:
- PE – потенциальная энергия в джоулях (Дж)
- м — масса объекта в кг
- г ускорение свободного падения (9,8 м/с²)
- h высота над землей или расстояние, на которое падает объект в м
- мгх составляет м раза г раза ч
Примечание : 1 Дж = 1 кг-м 2 /с 2
Если вы уроните объект, его потенциальная энергия станет кинетической энергией движения:
KE = ½ мВ²
где
- KE – кинетическая энергия в Дж или кг-м 2 /с 2
- v скорость в м/с
Так как PE = mgh и KE = ½ mv² , то mgh = ½ mv² .
Вы можете определить скорость, с которой он будет двигаться после падения с высоты ч , решив уравнение для v :
½ мв² = мг/ч
v² = 2 мг/м
v² = 2 гх
v = SQRT(2gh) = √(2gh)
Примечание: SQRT(2gh) и √(2gh) означает квадратный корень из 2gh . Обратите внимание, что масса 90 643 m 90 644 исключается из уравнения, а это означает, что все объекты падают с одинаковой скоростью.
Таким образом, если ч = 1 фут, а поскольку г = 32 фут/с², то v² = 2 * 32 * 1 = 64 и
v = 8 фут/с.
Химическая потенциальная энергия
Некоторые нестабильные молекулы, такие как нитроглицерин, обладают потенциальной энергией, готовой к высвобождению при определенных условиях. Выброс может быть взрывом, выделяющим кинетическую энергию в виде света, тепла и движущихся частиц.
Определенные смеси химических веществ могут вступать в реакцию — хотя и не так бурно — с выделением тепла и других форм кинетической энергии.
Электрическая потенциальная энергия
Электрическая розетка в вашем доме имеет потенциальную энергию 110 В или 220 В, в зависимости от страны, в которой вы живете. Как только электрическая цепь установлена, эта потенциальная энергия становится кинетической энергией движения электронов, а также тепла и других эффектов.
Потенциальная энергия ядра
Некоторые атомы имеют нестабильное ядро, которое может расщепляться и высвобождать кинетическую энергию. Например, уран-235 нестабилен и может разделиться на две части, высвобождая субатомные частицы и излучение с высокой скоростью. Его потенциальная энергия превращается в кинетическую энергию.
Применение потенциальной энергии
Управление высвобождением потенциальной энергии может привести к выполнению полезной работы. Мы используем пружины, чтобы помочь закрыть двери в наших домах. Плотины и электрические генераторы используют потенциальную энергию воды для выработки электроэнергии. Мы сжигаем топливо, чтобы приводить в движение наши автомобили и обогревать наши дома. Мы высвобождаем потенциальную энергию электричества для работы наших приборов. Ядерная потенциальная энергия также используется для создания электричества.
Мы высвобождаем потенциальную энергию электричества для работы наших приборов. Ядерная потенциальная энергия также используется для создания электричества.
Резюме
Потенциальная энергия — это когда объект может создавать кинетическую энергию или родственные формы энергии. Объект находится в состоянии равновесия, когда есть сила, которая пытается сдвинуть материю, и равная другая сила, препятствующая этому движению. Распространенными типами потенциальной энергии являются упругая, гравитационная, химическая, электрическая и ядерная. Когда потенциальная энергия высвобождается, ее можно использовать для совершения работы.
У вас большой потенциал
Ресурсы и ссылки
Условия Рона Куртуса
Веб-сайты
Ресурсы по физике
Книги
(Уведомление: Школа для чемпионов Mays Mays earrisions Commissions Commissions Wroops Wroops
.
-й. по энергетической физике
Поделитесь этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www. school-for-champions.com/science/
school-for-champions.com/science/
Energy_potential.htm
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа чемпионов
Темы физики
Потенциальная энергия
4.3 Движение снаряда | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Использовать одномерное движение в перпендикулярных направлениях для анализа движения снаряда.
- Рассчитайте дальность, время полета и максимальную высоту снаряда, который запускается и поражает плоскую горизонтальную поверхность.
- Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
- Рассчитать траекторию снаряда.
Снарядное движение — это движение объекта, брошенного или отброшенного в воздух, с ускорением только под действием силы тяжести. Применения движения снаряда в физике и технике многочисленны. Некоторые примеры включают метеоры, когда они входят в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядами , а их путь называется траекторией . Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Применения движения снаряда в физике и технике многочисленны. Некоторые примеры включают метеоры, когда они входят в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядами , а их путь называется траекторией . Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Наиболее важный факт, который следует здесь помнить, состоит в том, что движений вдоль перпендикулярных осей являются независимыми и поэтому могут быть проанализированы отдельно. Мы обсуждали этот факт в разделе «Векторы смещения и скорости», где увидели, что вертикальное и горизонтальное движения независимы. Ключом к анализу двумерного движения снаряда является разбиение его на два движения: одно по горизонтальной оси, а другое по вертикальной. (Этот выбор осей является наиболее разумным, потому что ускорение, вызванное силой тяжести, является вертикальным; таким образом, нет никакого ускорения вдоль горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось x — ось и вертикальная ось y — ось. Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. (Рисунок) иллюстрирует обозначение смещения, где мы определяем [латекс] \overset{\to }{s} [/latex] как общее смещение, а [латекс] \overset{\to }{x} [/latex ] и [latex] \overset{\to }{y} [/latex] — его вектора-компоненты вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , x и y .
(Этот выбор осей является наиболее разумным, потому что ускорение, вызванное силой тяжести, является вертикальным; таким образом, нет никакого ускорения вдоль горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось x — ось и вертикальная ось y — ось. Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. (Рисунок) иллюстрирует обозначение смещения, где мы определяем [латекс] \overset{\to }{s} [/latex] как общее смещение, а [латекс] \overset{\to }{x} [/latex ] и [latex] \overset{\to }{y} [/latex] — его вектора-компоненты вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , x и y .
Рисунок 4.11 Полное перемещение s футбольного мяча в точке на его пути. Вектор [latex] \overset{\to }{s} [/latex] имеет компоненты [latex] \overset{\to }{x} [/latex] и [latex] \overset{\to }{y} [ /latex] по горизонтальной и вертикальной осям. Его величина равна s, и он составляет угол θ с горизонтом.
Его величина равна s, и он составляет угол θ с горизонтом.
Чтобы полностью описать движение снаряда , мы должны включить скорость и ускорение, а также перемещение. Мы должны найти их компоненты вдоль 9{2}). [/latex]
Поскольку гравитация вертикальна, [латекс] {a}_{x}=0. [/latex] Если [latex] {a}_{x}=0, [/latex] это означает, что начальная скорость в направлении x равна конечной скорости в направлении x , или [latex] {v}_{x}={v}_{0x}. [/latex] С этими условиями на ускорение и скорость мы можем записать кинематическое (уравнение) через (уравнение) для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из движения с постоянным ускорением. Кинематические уравнения для движения в однородном гравитационном поле становятся кинематическими уравнениями с [латекс] {а}_{у}=\текст{−}г,\енспейс{а}_{х}=0: [/латекс] 9{2}-2g(y-{y}_{0}) [/latex]
Используя этот набор уравнений, мы можем проанализировать движение снаряда, учитывая некоторые важные моменты.
Стратегия решения задач: Движение снаряда
- Разложите движение на горизонтальную и вертикальную составляющие вдоль осей x и y . Величины компонент смещения [латекс] \перемещения{с} [/латекс] по этим осям равны х и лет. Величины компонентов скорости [латекс] \overset{\to }{v} [/латекс] равны [латекс] {v}_{x}=v\text{cos}\,\theta \,\text {и}\,{v}_{y}=v\text{sin}\,\theta , [/latex], где v — величина скорости, а θ — ее направление относительно горизонтали, как показано на (рис.).
- Рассматривайте движение как два независимых одномерных движения: одно по горизонтали, а другое по вертикали. Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
- Найдите неизвестные в двух отдельных движениях: горизонтальном и вертикальном. Обратите внимание, что единственной общей переменной между движениями является время t 9{2}}, [/латекс]
, где θ — направление смещения [латекс] \overset{\to}{s}.
 [/латекс]
[/латекс]
Рис. 4.12 (a) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения вдоль вертикальной и горизонтальной осей. (b) Горизонтальное движение простое, потому что [латекс] {а}_{х}=0 [/латекс] и [латекс] {v}_{х} [/латекс] — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (d) Движения x и y рекомбинируются, чтобы получить общую скорость в любой заданной точке траектории.
Пример
Снаряд фейерверка взрывается высоко и далеко
Во время фейерверка в воздух выстреливается снаряд с начальной скоростью 70,0 м/с под углом [латекс] 75,0\text{°} [/ латекс] над горизонталью, как показано на (рис.). Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей высшей точки над землей. а) Вычислите высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? в) Чему равно горизонтальное перемещение снаряда при взрыве? г) Чему равно полное перемещение от точки запуска до высшей точки?
а) Вычислите высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? в) Чему равно горизонтальное перемещение снаряда при взрыве? г) Чему равно полное перемещение от точки запуска до высшей точки?
Рисунок 4.13 Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
Стратегия
Движение можно разбить на горизонтальное и вертикальное, в которых [латекс] {a}_{x}=0 [/латекс] и [латекс] {a}_{y}=\text{−} грамм. [/latex] Затем мы можем определить [latex] {x}_{0} [/latex] и [latex] {y}_{0} [/latex] равными нулю и найти нужные количества. 9{2}}{2g}. [/latex]
Теперь мы должны найти [latex] {v}_{0y}, [/latex] составляющую начальной скорости в направлении y . Он задается как [латекс] {v}_{0y}={v}_{0}\text{sin}{\theta }_{0}, [/latex], где [латекс] {v}_{0 } [/latex] — начальная скорость 70,0 м/с, а [latex] {\theta }_{0}=75\text{°} [/latex] — начальный угол. Таким образом,
Таким образом,
[латекс] {v}_{0y}={v}_{0}\text{sin}\,\theta =(70.0\,\text{m}\text{/}\text{s })\text{sin}\,75\text{°}=67,6\,\text{m}\text{/}\text{s} [/latex] 9{2})}. [/latex]
Таким образом, у нас есть
[латекс] y=233\,\text{m}\text{.} [/latex]
Обратите внимание, что поскольку значение up положительно, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение в результате силы тяжести отрицательно. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м/с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты. 9{2}}=6. 90\text{s}\text{.} [/latex]
90\text{s}\text{.} [/latex]
Это время подходит и для больших фейерверков. Если вы можете увидеть запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется. Другой способ найти время — использовать [латекс] y\,\text{=}\,{y}_{0}+\frac{1}{2}({v}_{0y}+{v} _{у})т. [/latex] Это остается вам в качестве упражнения.
(c) Поскольку сопротивлением воздуха можно пренебречь, [латекс] {а}_{х}=0 [/латекс], а горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение — это горизонтальная скорость, умноженная на время по формуле [латекс] x={x}_{0}+{v}_{x}t, [/latex], где [латекс] {x}_{0} [/latex] равно нулю. Таким образом,
[latex] x={v}_{x}t, [/latex]
, где [latex] {v}_{x} [/latex] — x -компонент скорости, т.е. задано
[латекс] {v}_{x}={v}_{0}\text{cos}\,\theta =(70.0\,\text{m}\text{/}\text{s })\text{cos}75\text{°}=18.1\,\text{m}\text{/}\text{s}. [/latex]
Time t для обоих движений одинаково, поэтому x равно
[latex] x=(18. {2}}{2g}. [/латекс]
{2}}{2g}. [/латекс]
Это уравнение определяет максимальную высоту снаряда над точкой старта и зависит только от вертикальной составляющей начальной скорости.
Проверьте свое понимание
Камень брошен горизонтально со скалы [латекс] высотой 100,0\,\text{м} [/латекс] со скоростью 15,0 м/с. (a) Определите начало системы координат. б) Какое уравнение описывает горизонтальное движение? в) Какие уравнения описывают вертикальное движение? г) Какова скорость камня в момент удара?
Показать решение
Пример
Расчет движения снаряда: теннисист
Теннисист выигрывает матч на стадионе имени Артура Эша и бьет мячом по трибунам со скоростью 30 м/с и под углом [латекс] 45\text{°} [/ латекс] над горизонталью ((Рисунок)). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?
Рисунок 4. 14 Траектория удара теннисного мяча о трибуны.
14 Траектория удара теннисного мяча о трибуны.
Стратегия
Опять же, разложение этого двумерного движения на два независимых одномерных движения позволяет нам найти нужные величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением. Таким образом, мы сначала решаем для t . Пока мяч поднимается и падает вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается конечная скорость. Таким образом, мы рекомбинируем вертикальные и горизонтальные результаты, чтобы получить [латекс] \overset{\to }{v} [/латекс] в конечное время 9{2}. [/latex]
Если принять начальную позицию [latex] {y}_{0} [/latex] равной нулю, то конечная позиция будет y = 10 м. Начальная вертикальная скорость представляет собой вертикальную составляющую начальной скорости:
[латекс] {v}_{0y}={v}_{0}\text{sin}\,{\theta}_{0}=( 30,0\,\text{m}\text{/}\text{s})\text{sin}\,45\text{°}=21,2\,\text{m}\text{/}\text{s }. [/latex]
[/latex]
Подстановка y в (Рисунок) дает нам
[латекс] 10,0\,\text{m}=(21,2\,\text{м/с})t-(4,9{2}-(21,2\,\текст{м/с})t+10,0\,\текст{м}=0. [/latex]
Использование квадратичной формулы дает t = 3,79 с и t = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории — один раз по пути вверх и один раз по пути вниз — мы принимаем более длинное решение для времени, которое требуется мячу, чтобы достичь зрителя:
[латекс ] t=3.79\,\text{s}\text{.} [/latex]
Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м ниже начальной высоты, тратит 3,79с в воздухе.
(b) Мы можем найти конечные горизонтальную и вертикальную скорости [latex] {v}_{x} [/latex] и [latex] {v}_{y} [/latex] с использованием результата из (а). Затем мы можем объединить их, чтобы найти величину вектора полной скорости [латекс] \overset{\to }{v} [/латекс] и угол [латекс] \тета [/латекс], который он образует с горизонтом. Поскольку [латекс] {v}_{x} [/латекс] является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем и начальную скорость, и начальный угол. Следовательно, 9{-1}(\frac{21.2}{-15.9})=-53.1\text{°}. [/latex]
Поскольку [латекс] {v}_{x} [/латекс] является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем и начальную скорость, и начальный угол. Следовательно, 9{-1}(\frac{21.2}{-15.9})=-53.1\text{°}. [/latex]
Значение
(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м ниже начальной высоты, находится в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость [latex] 53,1\text{°} [/latex] ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется в точку по другую сторону от вершины траектории и, следовательно, имеет отрицательное значение 9.0907 y составляющая скорости. Величина скорости меньше, чем величина начальной скорости, которую мы ожидаем, поскольку она воздействует на высоту 10,0 м над уровнем запуска.
Время полета, траектория и дальность полета
Интерес представляют время полета, траектория и дальность полета снаряда, запущенного на плоской горизонтальной поверхности и упавшего на ту же поверхность. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах. 9{2}=0. [/latex]
В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах. 9{2}=0. [/latex]
Факторинг, мы имеем
[латекс] t({v}_{0}\text{sin}{\theta }_{0}-\frac{gt}{2})=0. [/latex]
Решение для t дает нам
[латекс] {T} _ {\ text {tof}} = \ frac {2 ({v} _ {0} \ text {sin} {\ theta }_{0})}{г}. [/latex]
Это время полета для снаряда, запущенного и ударившегося о плоскую горизонтальную поверхность. (Рисунок) не применяется, когда снаряд приземляется на другой высоте, чем он был запущен, как мы видели на (Рисунок) теннисиста, ударяющего мячом по трибунам. Другое решение t = 0, соответствует моменту запуска. Время полета линейно пропорционально начальной скорости в направлении y и обратно пропорционально g . Таким образом, на Луне, где гравитация составляет одну шестую от земной, снаряд, запущенный с той же скоростью, что и на Земле, будет находиться в воздухе в шесть раз дольше.
Траектория
Траектория снаряда может быть найдена путем исключения временной переменной t из кинематических уравнений для произвольного 9{2}\text{sin}2{\theta}_{0}}{g}. [/latex]
Обратите внимание, что (Рисунок) действителен только для запуска и удара о горизонтальную поверхность. Мы видим, что диапазон прямо пропорционален квадрату начальной скорости [latex] {v}_{0} [/latex] и [latex] \text{sin}2{\theta}_{0} [/latex] , и оно обратно пропорционально ускорению свободного падения. Таким образом, на Луне дальность была бы в шесть раз больше, чем на Земле, при той же начальной скорости. Кроме того, из коэффициента [латекс] \text{sin}2{\theta}_{0} [/latex] мы видим, что диапазон максимален при [латексе] 45\текст{°}. [/latex] Эти результаты показаны на (Рисунок). В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. В (b) мы видим, что диапазон максимален при [latex] 45\text{°}. [/latex] Это справедливо только для условий, в которых сопротивление воздуха не учитывается. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют [латекс] 90\текст{°}. [/latex] Снаряд, выпущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют [латекс] 90\текст{°}. [/latex] Снаряд, выпущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
Рисунок 4.15 Траектории снарядов на ровной местности. (a) Чем больше начальная скорость [латекс] {v}_{0}, [/латекс], тем больше диапазон для данного начального угла. (b) Влияние начального угла [латекс] {\ тета }_{0} [/латекс] на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон одинаковый для начальных углов [латекс] 15\текст{°} [/латекс] и [латекс] 75\текст{°}, [/латекс], хотя максимальная высота этих путей различна.
Пример
Сравнение ударов в гольфе
Игрок в гольф оказывается в двух разных ситуациях на разных лунках. На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и дать ему вылететь на грин. Он направляет бросок низко к земле под углом [latex] 30\text{°} [/latex] к горизонтали, чтобы мяч мог катиться после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным количеством качения после удара. Здесь он направляет выстрел под углом [latex] 70\text{°} [/latex] к горизонтали, чтобы свести к минимуму скатывание после удара. Оба выстрела попали в ровную поверхность.
Он направляет бросок низко к земле под углом [latex] 30\text{°} [/latex] к горизонтали, чтобы мяч мог катиться после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным количеством качения после удара. Здесь он направляет выстрел под углом [latex] 70\text{°} [/latex] к горизонтали, чтобы свести к минимуму скатывание после удара. Оба выстрела попали в ровную поверхность.
а) Какова начальная скорость мяча у второй лунки?
(б) Какова начальная скорость мяча у четвертой лунки?
(c) Напишите уравнение траектории для обоих случаев.
(d) Нарисуйте траектории.
Стратегия
Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (a), так и для (b). Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории. 9{2}\hfill \end{array} [/latex]
(d) Используя графическую утилиту, мы можем сравнить две траектории, показанные на (рис. ).
).
Рисунок 4.16 Две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка запуска.
Значение
Начальная скорость выстрела в [латекс] 70\text{°} [/латекс] больше, чем начальная скорость выстрела в [латекс] 30\текст{°}. [/latex] Обратите внимание на (Рисунок), что два снаряда, запущенные с одинаковой скоростью, но под разными углами, имеют одинаковую дальность, если углы запуска складываются в [латекс] 90\текст{°}. [/latex] Углы запуска в этом примере складываются, чтобы получить число больше, чем [latex] 90\text{°}. [/latex] Таким образом, выстрел в [latex] 70\text{°} [/latex] должен иметь большую стартовую скорость, чтобы достичь 90 м, иначе он приземлился бы на более коротком расстоянии.
Проверьте свое понимание
Если бы два удара в гольф на (рис.) были произведены с одинаковой скоростью, какой удар имел бы наибольшую дальность?
Показать решение
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем R очень мал по сравнению с окружностью Земли. Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказано уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на (Рисунок), который основан на рисунке в «Началах » Ньютона. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту задана горизонтальная скорость [латекс] 8000\,\текст{м}\текст{/}\текст{с} [/латекс] (или [латекс] 18000\текст{ми}\текст{ /}\text{hr}) [/latex] возле поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».
Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказано уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на (Рисунок), который основан на рисунке в «Началах » Ньютона. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту задана горизонтальная скорость [латекс] 8000\,\текст{м}\текст{/}\текст{с} [/латекс] (или [латекс] 18000\текст{ми}\текст{ /}\text{hr}) [/latex] возле поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».
Рисунок 4.17 Снаряд в спутник. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости диапазон увеличивается и становится длиннее, чем он был бы на ровной поверхности, потому что Земля изгибается под его траекторией. При скорости 8000 м/с достигается орбита.
В PhET Explorations: Projectile Motion узнайте о движении снаряда с точки зрения угла запуска и начальной скорости.
Резюме
- Снарядное движение — это движение объекта, подверженное только ускорению свободного падения, где ускорение постоянно, как вблизи поверхности Земли.
- Для решения задач движения снаряда мы анализируем движение снаряда в горизонтальном и вертикальном направлениях, используя одномерные кинематические уравнения для x и y .
- Время полета снаряда, запущенного с начальной вертикальной скоростью [латекс] {v}_{0y} [/латекс] по ровной поверхности, определяется выражением
[латекс] {T}_{tof}=\frac{2({v}_{0}\text{sin}\,\theta)}{g}.
 [/латекс]
[/латекс]Это уравнение справедливо только в том случае, если снаряд приземляется на той же высоте, с которой он был запущен.
- Максимальное горизонтальное расстояние, пройденное снарядом, называется дальностью полета. Опять же, уравнение для дальности справедливо только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен.
Концептуальные вопросы
Ответьте на следующие вопросы о движении снаряда на ровной поверхности при пренебрежимо малом сопротивлении воздуха с начальным углом, не равным ни [латексу] 0\текст{°} [/латексу], ни [латексу] 90\text{°}: [/latex] (a) Всегда ли скорость равна нулю? б) Когда скорость минимальна? Максимум? в) Может ли скорость когда-либо быть такой же, как начальная скорость, в любой другой момент времени, кроме t = 0? г) Может ли скорость когда-либо быть такой же, как начальная скорость, в любой другой момент времени, кроме t = 0?
Показать решение
Ответьте на следующие вопросы о движении снаряда на ровной поверхности при пренебрежимо малом сопротивлении воздуха, когда начальный угол не равен ни [латексу] 0\text{°} [/латексу], ни [латексу] 90\text{°}: [/latex] (a) Всегда ли ускорение равно нулю? (b) Всегда ли ускорение направлено в том же направлении, что и составляющая скорости? в) Всегда ли ускорение противоположно направлению составляющей скорости?
Десятицентовая монета кладется на край стола так, что она немного свисает. Четвертак скользит горизонтально по поверхности стола перпендикулярно краю и ударяется о монетку. Какая монета первой упадет на землю?
Четвертак скользит горизонтально по поверхности стола перпендикулярно краю и ударяется о монетку. Какая монета первой упадет на землю?
Показать решение
Задачи
Пуля выпущена горизонтально с высоты плеча (1,5 м) с начальной скоростью 200 м/с. а) Через какое время пуля упадет на землю? б) Какое расстояние пролетит пуля по горизонтали?
Показать решение
Мрамор скатывается со столешницы высотой 1,0 м и падает на пол в точке на расстоянии 3,0 м от края стола в горизонтальном направлении. а) Сколько времени шарик находится в воздухе? б) Какова скорость шарика, когда он оторвется от края стола? в) Какова его скорость в момент удара об пол?
Дротик брошен горизонтально со скоростью 10 м/с в мишень мишени для дротиков на расстоянии 2,4 м, как показано на следующем рисунке. а) На сколько ниже намеченной цели дротик попадает? (b) Что ваш ответ говорит вам о том, как опытные игроки в дартс бросают свои дротики?
Показать решение
Самолет, летящий горизонтально со скоростью 500 км/ч на высоте 800 м, сбрасывает ящик с припасами (см. следующий рисунок). Если парашют не раскроется, как далеко перед точкой выпуска ящик упадет на землю?
следующий рисунок). Если парашют не раскроется, как далеко перед точкой выпуска ящик упадет на землю?
Предположим, что самолет в предыдущей задаче выпускает снаряд горизонтально по направлению своего движения со скоростью 300 м/с относительно самолета. а) На каком расстоянии от точки выброса пуля упадет на землю? б) Какова его скорость в момент удара о землю?
Показать решение
Питчер в фастболе может бросить бейсбольный мяч со скоростью 40 м/с (90 миль/ч). (a) Предполагая, что питчер может выпустить мяч на расстоянии 16,7 м от «домашней» пластины, так что мяч движется горизонтально, сколько времени потребуется мячу, чтобы достичь «домашней» пластины? (b) Как далеко мяч падает между рукой питчера и домашней пластиной?
Снаряд запущен под углом [латекс] 30\текст{°} [/латекс] и через 20 с приземляется на той же высоте, на которой был запущен. а) Чему равна начальная скорость снаряда? б) Какова максимальная высота? в) Каков диапазон? (d) Рассчитайте перемещение от точки запуска до положения на его траектории за 15 с.
Показать решение
Баскетболист бьет по корзине на расстоянии 6,1 м и на высоте 3,0 м над полом. Если мяч выпущен на высоте 1,8 м над полом под углом [latex] 60\text{°} [/latex] над горизонтом, какой должна быть начальная скорость, чтобы он прошел через корзину?
В определенный момент воздушный шар находится в воздухе на высоте 100 м и снижается с постоянной скоростью 2,0 м/с. Именно в этот момент девочка бросает мяч горизонтально относительно себя с начальной скоростью 20 м/с. Когда она приземлится, где она найдет мяч? Не учитывать сопротивление воздуха.
Показать решение
Человек на мотоцикле, движущийся с постоянной скоростью 10 м/с, бросает пустую банку прямо вверх относительно себя с начальной скоростью 3,0 м/с. Найдите уравнение траектории, как ее видит сотрудник полиции на обочине дороги. Предположим, что начальное положение банки — это точка, в которую она была брошена. Не учитывать сопротивление воздуха.
Спортсмен может прыгнуть в длину на 8,0 м. На какое максимальное расстояние может прыгнуть спортсмен на Луне, где ускорение свободного падения составляет одну шестую земного?
Показать решение
Максимальное горизонтальное расстояние, на которое мальчик может бросить мяч, составляет 50 м. Предположим, что он может бросать с одинаковой начальной скоростью под любым углом. На какую высоту он подбрасывает мяч, когда бросает его прямо вверх?
Камень брошен со скалы под углом [латекс] 53\текст{°} [/латекс] к горизонту. Скала высотой 100 м. Начальная скорость камня 30 м/с. а) На какую высоту над краем утеса возвышается скала? б) Какое расстояние он переместил по горизонтали, когда находился на максимальной высоте? в) Через какое время после выброса он упадет на землю? г) Каков радиус скалы? д) Каково горизонтальное и вертикальное положение скалы относительно края обрыва в точке 9?0907 t = 2,0 с, t = 4,0 с и t = 6,0 с?
Показать решение
Пытаясь уйти от преследователей, секретный агент съезжает на лыжах со склона, наклоненного на [latex] 30\text{°} [/latex] ниже горизонта со скоростью 60 км/ч. Чтобы выжить и приземлиться на снег на 100 м ниже, он должен расчистить ущелье шириной 60 м. Он это делает? Не учитывать сопротивление воздуха.
Чтобы выжить и приземлиться на снег на 100 м ниже, он должен расчистить ущелье шириной 60 м. Он это делает? Не учитывать сопротивление воздуха.
Игрок в гольф на фервее находится в 70 м от грина, который расположен ниже уровня фервея на 20 м. Если игрок в гольф ударит по мячу под углом [latex] 40\text{°} [/latex] с начальной скоростью 20 м/с, насколько близко он подлетит к грину?
Показать решение
Снаряд выпущен по холму, основание которого находится на расстоянии 300 м. Снаряд выпущен на [latex] 60\text{°} [/latex] над горизонтом с начальной скоростью 75 м/с. Холм может быть аппроксимирован плоскостью, наклоненной под углом [latex] 20\text{°} [/latex] к горизонтали. Относительно системы координат, показанной на следующем рисунке, уравнение этой прямой имеет вид [латекс] y=(\text{tan}20\text{°})x-109. [/latex] Где на холме приземляется снаряд?
Астронавт на Марсе пинает футбольный мяч под углом [латекс] 45\текст{°} [/латекс] с начальной скоростью 15 м/с. Если ускорение свободного падения на Марсе равно 3,7 м/с, а) какова дальность футбольного удара по плоской поверхности? (b) Какова будет дальность такого же толчка на Луне, где гравитация составляет одну шестую от земной?
Если ускорение свободного падения на Марсе равно 3,7 м/с, а) какова дальность футбольного удара по плоской поверхности? (b) Какова будет дальность такого же толчка на Луне, где гравитация составляет одну шестую от земной?
Показать решение
Майку Пауэллу принадлежит рекорд по прыжкам в длину 8,95 м, установленный в 1991 году. Если он оторвался от земли под углом [latex] 15\text{°}, [/latex] какой была его начальная скорость?
Робот-гепард Массачусетского технологического института может перепрыгивать препятствия высотой 46 см и развивать скорость 12,0 км/ч. (a) Если робот стартует под углом [латекс] 60\текст{°} [/латекс] на этой скорости, какова его максимальная высота? б) Каким должен быть угол запуска, чтобы достичь высоты 46 см?
Показать решение
Гора Асама, Япония, является действующим вулканом. В 2009 году извержение выбросило твердые вулканические породы, которые упали на 1 км по горизонтали от кратера. Если бы вулканические породы были запущены под углом [латекс] 40\текст{°} [/латекс] к горизонту и приземлились на 900 м ниже кратера, (а) какова будет их начальная скорость и (б) каково время их полета?
Если бы вулканические породы были запущены под углом [латекс] 40\текст{°} [/латекс] к горизонту и приземлились на 900 м ниже кратера, (а) какова будет их начальная скорость и (б) каково время их полета?
Дрю Брис из Нового Орлеана Сэйнтс может бросить футбольный мяч со скоростью 23,0 м/с (50 миль в час). Если он направит бросок под углом [latex] 10\text{°} [/latex] от горизонтали, на какое расстояние он пролетит, если его нужно поймать на той же высоте, на которой он был брошен?
Показать решение
Лунный вездеход, использовавшийся в последних миссиях НАСА «Аполлон-» , достиг неофициальной наземной лунной скорости 5,0 м/с благодаря астронавту Юджину Сернану. Если бы марсоход двигался с такой скоростью по плоской лунной поверхности и наткнулся на небольшой выступ, который отбросил его от поверхности под углом [latex] 20\text{°}, [/latex], как долго он находился бы «в воздухе» на Луне?
Футбольные ворота высотой 2,44 метра.



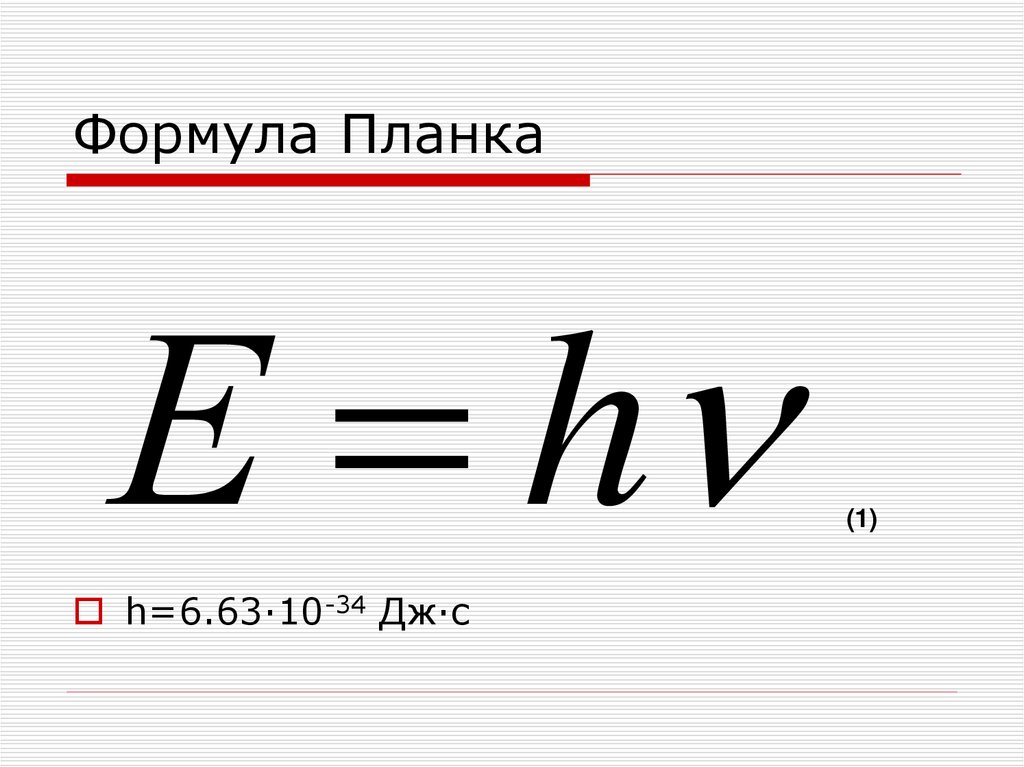 Процедуры решения задач здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.
Процедуры решения задач здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.