Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением. Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t \rightarrow 0$ материальная точка проходит путь ds, который называют элементарным. При этом:
$$d s=|d \bar{r}|=v d t$$
где $\bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=v\left(t_{2}-t_{1}\right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
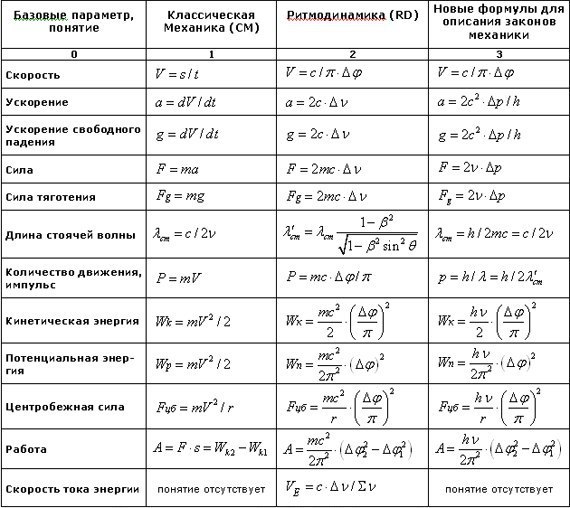
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой, чему равно перемещение, если точка двигалась 1-2-3-4.
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 — 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание.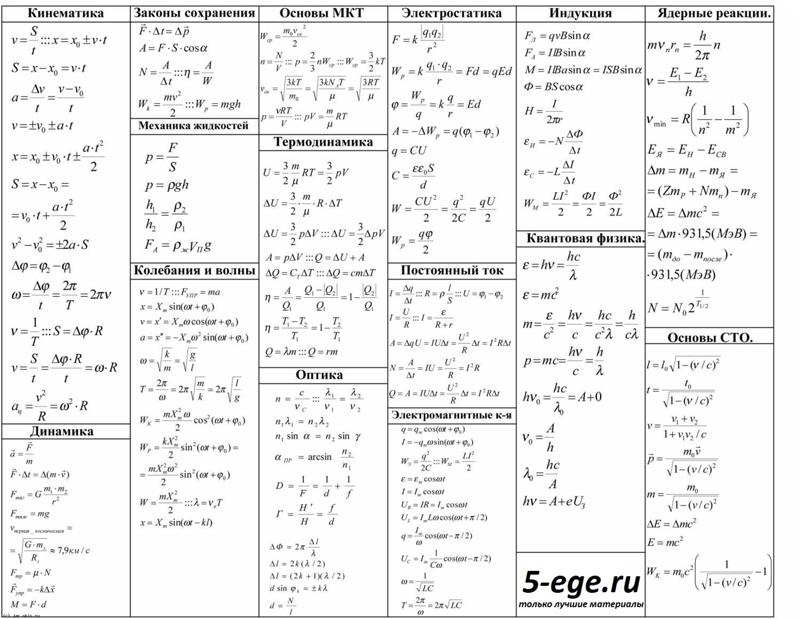
{2} \rho \frac{d l}{S}(1)$$называют сопротивлением участка цепи между сечениями 1 и 2. В выражении (1) имеем $\rho$ – удельное сопротивление проводника, S – площадь поперечного сечения проводника, dl — элемент длины проводника.
Если проводник является однородным ($\rho$=const) и имеет форму цилиндра (S=const), то формула (1) может быть представлена как:
$$R=\rho \frac{l}{S}(2)$$
где l – длина участка рассматриваемого проводника.
Надо отметить, что удельное сопротивление проводника ($\rho$) – это сопротивление проводника единичной длины с поперечным сечением равным единице. Или иначе говорят, что удельное сопротивление вещества – это сопротивление куба с ребром 1 м изготовленного из рассматриваемого вещества, которое выражено в Ом, при токе, который параллелен ребру куба. Величина обратная удельному сопротивлению:
$$\sigma=\frac{1}{\rho}(3)$$
называется удельной проводимостью.
{B}=\frac{\rho}{4 \pi} \cdot \frac{B-A}{B \cdot A}$$
Ответ. $R=\frac{\rho}{4 \pi} \cdot \frac{B-A}{B \cdot A}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какое количество витков проволоки (n) (удельное сопротивление ее равно $\rho$=100 мк Ом•м, диаметр d=1 см) требуется накрутить на фарфоровый цилиндр, имеющий радиус A=1 см, для того чтобы получить сопротивление R=8 Ом?
Решение. Основой для решения задачи будет формула для сопротивления вида:
$$R=\rho \frac{l}{S}(2.1)$$
Длину одного витка проволоки можно вычислить как:
$$l_{1}=2 \pi \cdot A(2.2)$$
Следовательно, длина всей проволоки (l) равна:
$$l=n \cdot 2 \pi \cdot A(2.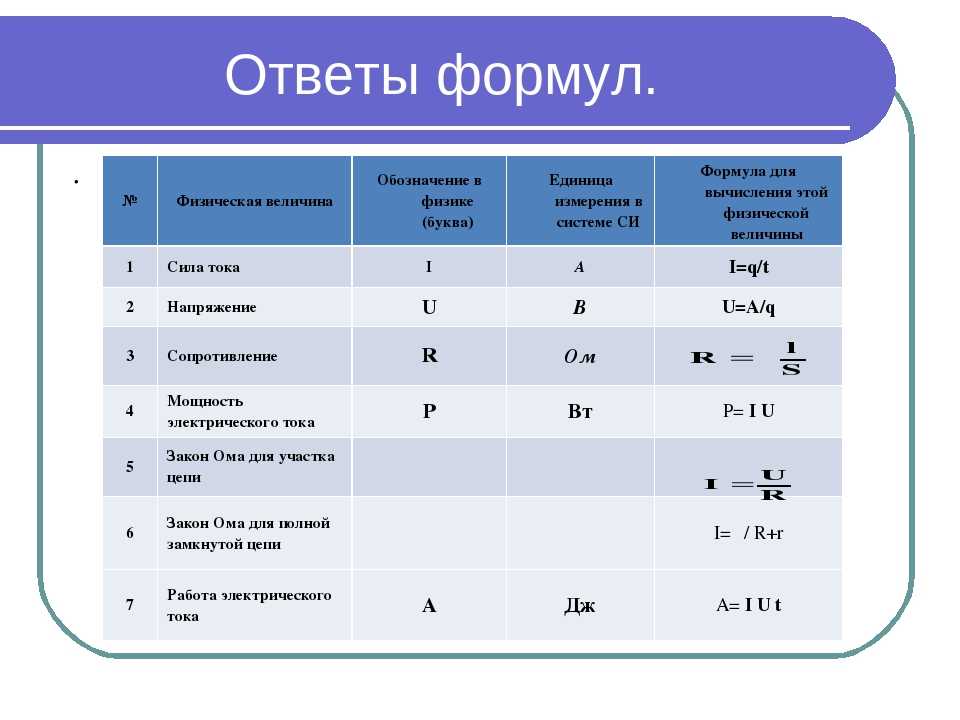
{-2}}=100$$
Ответ. n=100
Читать дальше: Формула внутренней энергии.
часто используемых уравнений – Гиперучебник по физике
[закрыть]
Механика
| Уравнения движения |
|---|
| V = V 0 + AT S = S 0 + v = S 0 + v v v v v v v v v v v v v v v v v v v v v v v . в 2 v 2 = v 0 2 + 2 a ( с 0014 — S 0 ) V = ½ ( V + V 0 ) |
| Работа |
|---|
| Работа |
|---|
| 9007 |
|---|
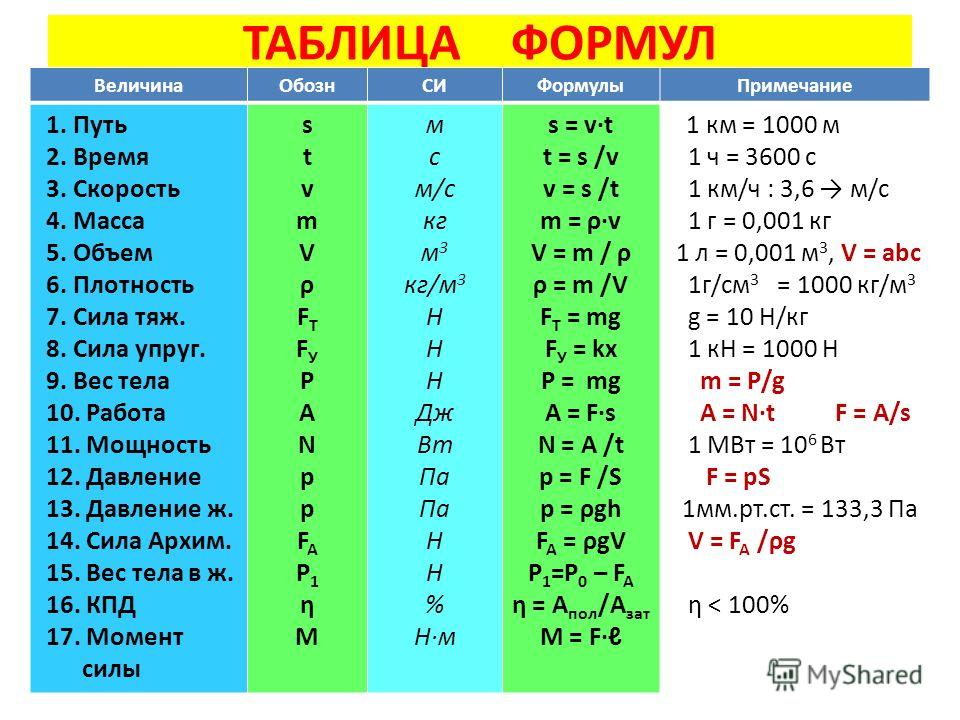θ| W = | ⌠ ⌡ | F · d s |
| power | |||
|---|---|---|---|
| |||
|
| equations of rotation |
|---|
| ω = ω 0 + α t θ = θ 0 + ω 0 t + ½α t 2 ω 2 = ω 0 2 + 2α(θ − θ 0 ) ω = ½(ω + ω 0 ) |
| torque |
|---|
| τ = rF sin θ |
| τ = r × F |
Thermal Physics
| efficiency | |||
|---|---|---|---|
| |||
|
c. o.p. | |||
|---|---|---|---|
| |||
|
Waves & Optics
Электричество и магнитизм
| Апеданс |
|---|
| Z = ±0013 R 2 + ( X L − X C ) 2 ] |
| Z = R + j ( X L − X C ) |
| no one’s law | ||||
|---|---|---|---|---|
| ||||
|
| ampere’s law | ||||
|---|---|---|---|---|
| ||||
|
Modern Physics
| Шродингер | Уравнение | |||
|---|---|---|---|---|
| ||||
