Что такое среднее пропорциональное в геометрии: Среднее пропорциональное | это… Что такое Среднее пропорциональное?

Среднее пропорциональное / Построения циркулем и линейкой / Треугольники / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Треугольники
5. Построения циркулем и линейкой
6. Среднее пропорциональное

Среднее пропорциональное положительных чисел и — это такое число , которое равно квадратному корню из произведения этих чисел, т.е. .

Среднее пропорциональное носит такое название, потому что число является средним членом пропорции .

Средним пропорциональным (или средним геометрическим) двух отрезков и , называется такой отрезок , что: .

Чтобы построить среднее пропорциональное двух отрезков используют циркуль и линейку.

Ход построения:

Пусть нам даны два отрезка и , строим их.

Затем строим с помощью линейки прямую , отмечаем на ней точку А и строим отрезок АЕ, равный отрезку .

Для этого строим с помощью циркуля окружность радиуса с центром А (полностью окружность строить необязательно, смотри выделенное красным цветом). Затем, аналогично строим отрезок ЕВ, равный отрезку .

Далее найдем середину отрезка АВ. Для этого строим две окружности с центрами А и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая пересечет отрезок АВ в его середине О.

Теперь строим окружность с центром О радиуса ОА.

Затем построим перпендикуляр к прямой так, чтобы он проходил через точку Е, которая делит отрезок АВ в отношении .  Для этого строим окружность произвольного радиуса с центром Е (полностью окружность строить необязательно, смотри выделенное фиолетовым цветом), данная окружность пересечет прямую в двух точках

М и В (точку В мы берем как точку пересечения данной окружности и данной прямой для того, чтобы не добавлять на рисунке лишние элементы, но важно помнить, что точки пересечения окружности с центром Е и прямой  могут быть и другие, все зависит от того, каким мы возьмем радиус окружности с центром Е).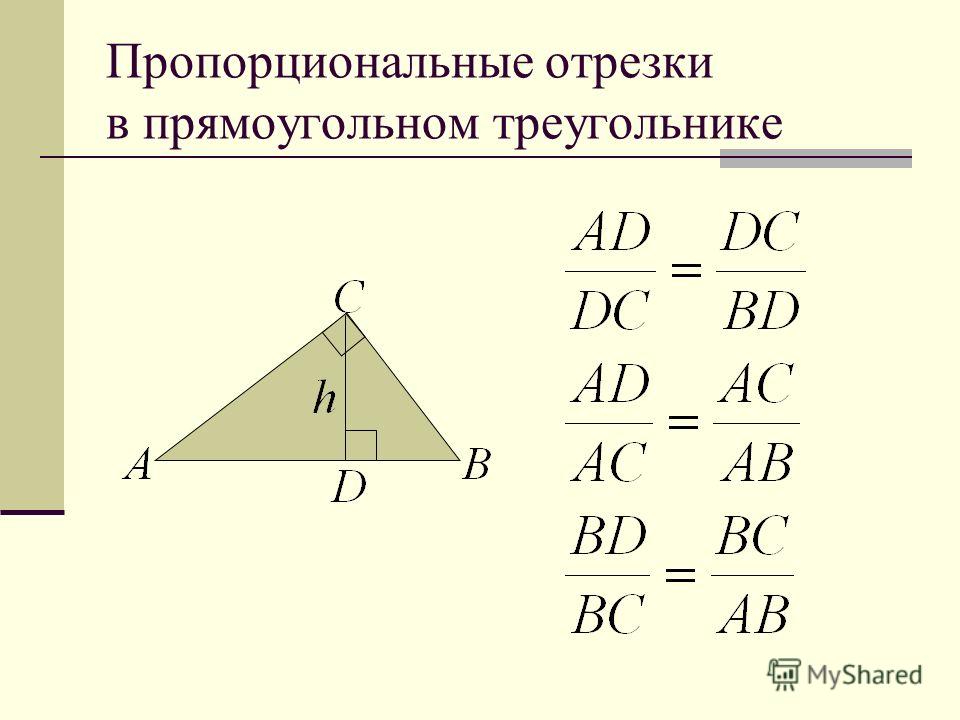 Далее строим две окружности с центрами М и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая будет перпендикулярна к прямой и пересечет окружность с центром О в точке К.

Длина отрезка ЕК и есть искомый отрезок , равный среднему пропорциональному отрезков и , т.е. или .

Советуем посмотреть:

Построение угла, равного данному

Построение биссектрисы угла

Построение перпендикулярных прямых

Построение середины отрезка

Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Биссектрисы треугольника

Высоты треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 1270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

Пропорциональные отрезки в прямоугольном треугольнике

Урок 22.

Геометрия 8 класс ФГОС

На этом уроке мы познакомимся со средним пропорциональным (средним геометрическим) и изучим пропорциональные отрезки в прямоугольном треугольнике. В ходе решения задач научимся находить те или иные элементы прямоугольного треугольника.

Конспект урока «Пропорциональные отрезки в прямоугольном треугольнике»

Начнём с повторения уже известных нам сведений о прямоугольном треугольнике.

Прямоугольным называется треугольник, у которого один из углов прямой.

Сторону, лежащую против прямого угла, называют гипотенузой, а две другие — катетами.

Вы уже знакомы с очень важной теоремой, теоремой Пифагора. Она гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

А также вам известны признаки равенства прямоугольных треугольников. Они могут быть равны: по двум катетам, по катету и прилежащему к нему углу, по гипотенузе и острому углу, по катету и гипотенузе.

Сегодня поговорим о пропорциональных отрезках в прямоугольном треугольнике. И начнём с задачи.

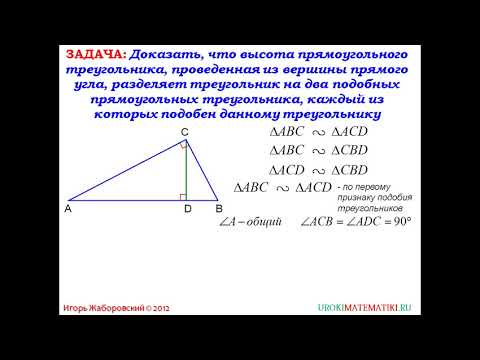
Задача. Докажите, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Доказательство.

 

1.

 

2.

 

3.

 

Так мы доказали, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых, в свою очередь, подобен данному треугольнику.

Определение. Отрезок  называется средним пропорциональным

(или средним геометрическим) для отрезков  и , если .

 Опираясь на данное определение и задачу, решённую нами, докажем следующие утверждения:

высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

В предыдущей задаче нами уже было доказано, что треугольники

 

 

катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.

Докажем второе утверждение.

Для этого воспользуемся подобием треугольников ABC и ACD. Запишем отношение соответствующих сторон.

 

 

 

Отсюда получаем, что АЦ равно корню квадратному из произведения АБ и АД.

Выполним задание.

Задача. Найдите элементы прямоугольного треугольника по известным данным.

 а)

б)

в)

г)

Решение.

а)

б)

 

 

в)

 

г)

 

 

Задача. По данным рисунка нужно найти площадь .

Решение.

а)  

1.

2.

3.

б)

1.

 

2.

3.

4.

Ответ: а) , б) .

Задача.  — ромб,  равно 12, . Найдите площадь ромба.

 Решение.

1.

2. Пусть  

 

 

 

 

3.

4.

 

Ответ: .

Подведём итоги урока.

Сегодня вы познакомились с определением среднего геометрического и узнали, как это понятие связано с прямоугольным треугольником.

А именно:

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.

 

Предыдущий урок 21 Средняя линия треугольника

Следующий урок 23 Практические приложения подобия треугольников

Получите полный комплект видеоуроков, тестов и презентаций Геометрия 8 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Среднее пропорциональное — объяснение, пример, формула и часто задаваемые вопросы

Термин «средняя пропорция» также упоминается как среднее геометрическое. Термин «среднее» при использовании отдельно или в контексте со средним, медианой или модой относится к среднему арифметическому или нахождению среднего. Среднее геометрическое или среднее пропорциональное не похоже на среднее арифметическое. В математике средние арифметические имеют дело со сложением, тогда как средние геометрические имеют дело с умножением. Давайте разберемся, что такое средняя пропорция с точки зрения соотношения и пропорции.

В математике Средняя пропорция между двумя членами отношения рассчитывается путем извлечения квадратного корня из произведения двух величин в отношении. Например, в пропорции p:q::r:s мы можем вычислить среднюю пропорцию для отношения p:q, вычислив квадратный корень из произведения величин p и q. Математически средняя пропорция выражается следующим образом:

Средняя пропорция — \[\sqrt{pq}\]

Определить среднюю пропорцию

Средняя пропорция или среднее геометрическое двух положительных чисел p и q есть положительное число x , например что \[\frac{p}{x} = \frac{x}{q}\].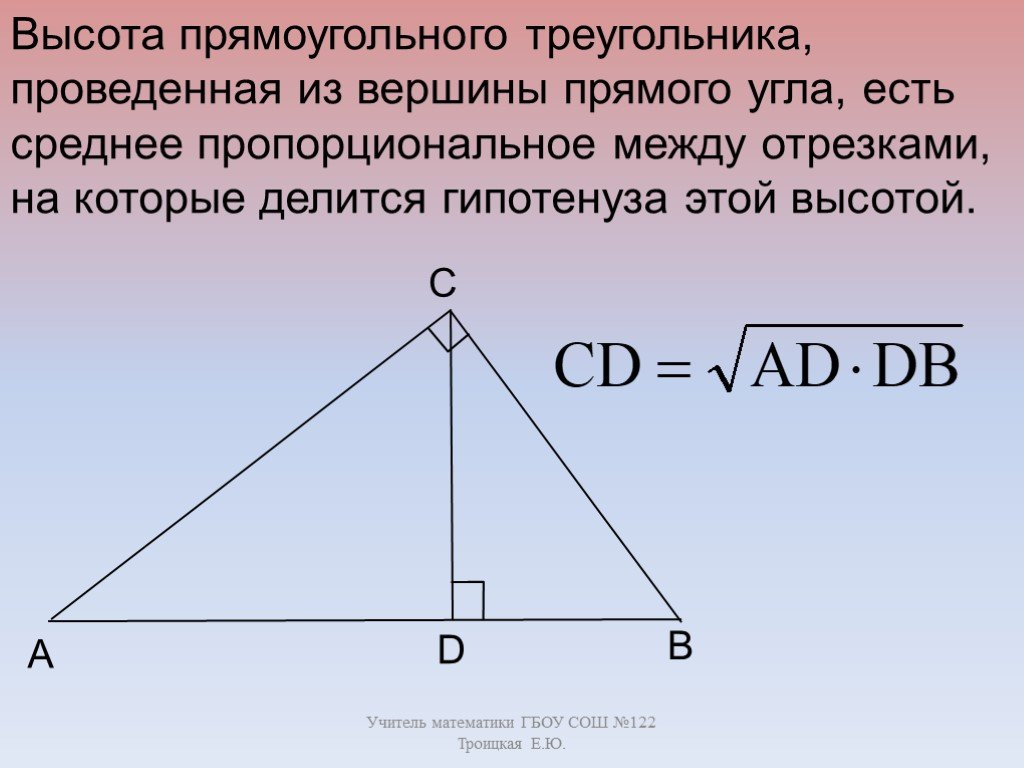 При решении переменной x = \[\sqrt{pq}\] 92= ​​\sqrt{100}\]

x = 10

Следовательно, средняя пропорция между 4 и 25 равна 10.

Средняя пропорция прямых углов

Среднее геометрическое или среднее пропорциональное прямоугольному треугольнику появляется с две популярные теоремы. Давайте разберемся в теореме о средней пропорциональности с точки зрения прямоугольных треугольников.

Теорема 1: Высота, проведенная к гипотенузе прямоугольного треугольника, создает два треугольника, которые подобны исходному треугольнику и друг другу.

Пример:

Согласно теореме, в правом ABC на высоте CD могут быть установлены следующие соотношения.

△ADC 〜 △CDB

△ACB 〜 △ADC и

△ACB 〜 △CDB

Поскольку треугольники подобны, мы можем установить пропорциональную связь между ними. Две ценные теоремы можно найти, используя 3 пропорции, приведенные ниже:

\[\frac{AB}{AC} = \frac{AC}{AD}, \frac{AB}{CB} = \frac{CB} {DB}, \frac{AD}{CD} = \frac{CD}{DB}\]

Правило высоты

Высота до гипотенузы прямоугольного треугольника равна средней, пропорциональной между левой и правой частями гипотенузы прямоугольного треугольника.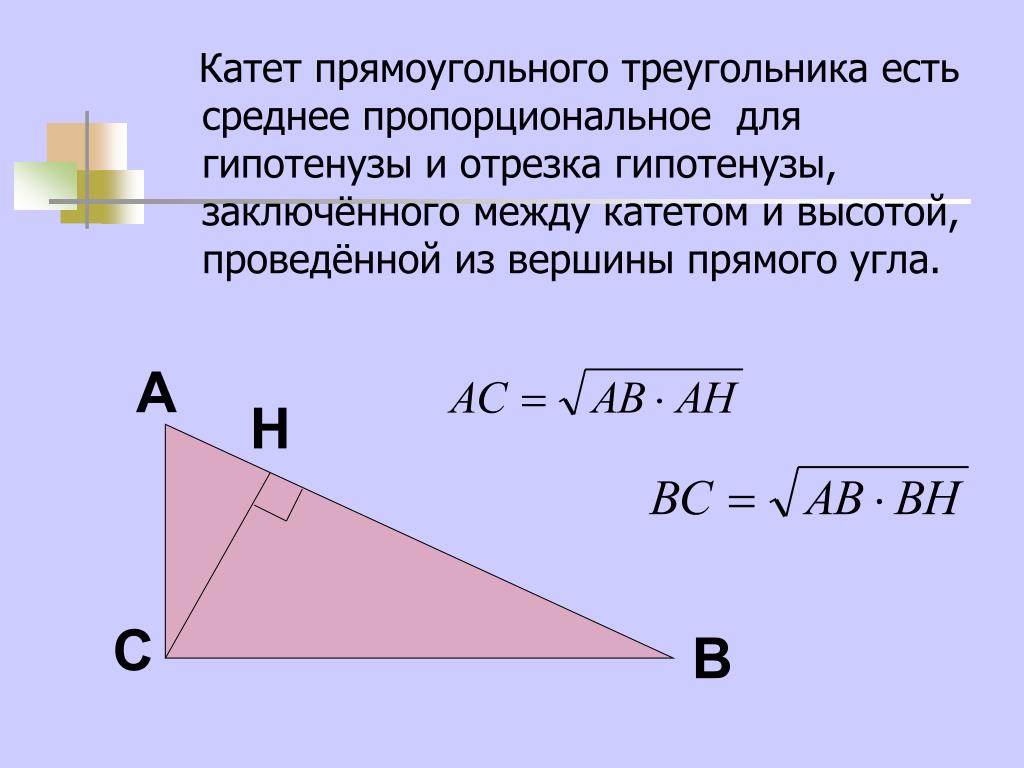

Математически правило высоты гласит:

\[\frac{\text{Одна часть гипотенузы (слева)}}{Высота} = \frac{Высота}{\text{Другая часть гипотенузы (справа)}} \]

Соответственно,

\[\frac{AD}{CD} = \frac{CD}{DB}\]

Правило катетов

Катеты прямоугольного треугольника являются средней долей гипотенузы и часть ноги непосредственно под гипотенузой.

Математически правило катетов гласит:

\[\frac{\text{Гипотенуза прямоугольного треугольника}}{\text{Контакты прямоугольного треугольника}} = \frac{\text{Контакты прямоугольного треугольника}}{Часть} \]

Соответственно,

\[\frac{AB}{AC} = \frac{AC}{AD} или \frac{AB}{CB} = \frac{CB}{DB}\]

Среднее Формула пропорции

Средняя пропорциональная Примеры с решениями

1. Найдите среднюю пропорциональную между 4 и 9.

Решение:

Пусть средняя пропорция между 4 и 92= ​​\sqrt{144} \]

k = 12

Следовательно, среднее соотношение между 9 и 16 равно 12.

3. Найдите значение x (длина AB)?

Решение:

Сначала найдем длину стороны гипотенузы BC.

BC = BD + DC = 16

Теперь, используя правило сторон:

\[\frac{\text{(Гипотенуза прямоугольного треугольника)}}{\text{(Каташки прямоугольного треугольника)}} =  \ frac{\text{(Контуры прямоугольного треугольника)}}{\text{(Часть)}}\]

Подставляя значение в приведенную выше формулу правила катетов, мы получаем 92 = \sqrt{49}\]

x = 7

Важность средней пропорциональности

Средняя пропорция — одна из самых важных тем математики. Он включает в себя различные теоремы, чтобы найти связь между двумя или более числами. Среднее пропорциональное значение важно для вас по следующим причинам. Основы важности пропорции среднего пригодятся в последующих темах, которые вы будете изучать на уроках математики. С помощью Mean Proportional вы можете изучить различные методы нахождения высоты, гипотенузы и основания прямоугольного треугольника.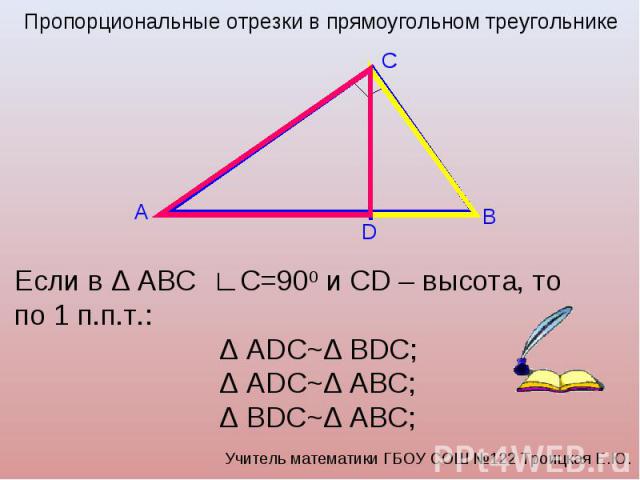 Примеры дадут вам представление о том, как решать различные типы вопросов на основе концепции средней пропорции.

Используя формулы средней пропорции, вы также можете узнать, является ли набор заданных чисел прямо пропорциональным или обратно пропорциональным. Среднее пропорциональное предоставляет вам множество примеров, которые помогут вам ясно понять концепции.

The Mean Proportional станет полезным учебным материалом во время повторения и подготовки к экзаменам. Это даст вам краткий обзор различных концепций, которые относятся к средней пропорции. Вы можете использовать Mean Proportional, чтобы пересмотреть всю тему и решить вопросы, связанные с ней. После того, как вы тщательно изучите Среднее пропорциональное, решение практических вопросов станет намного проще.

Решение вопросов, связанных со средним пропорциональным

Решение вопросов, связанных со средним пропорциональным, будет довольно простым, если вы знаете все формулы и теоремы из этой главы.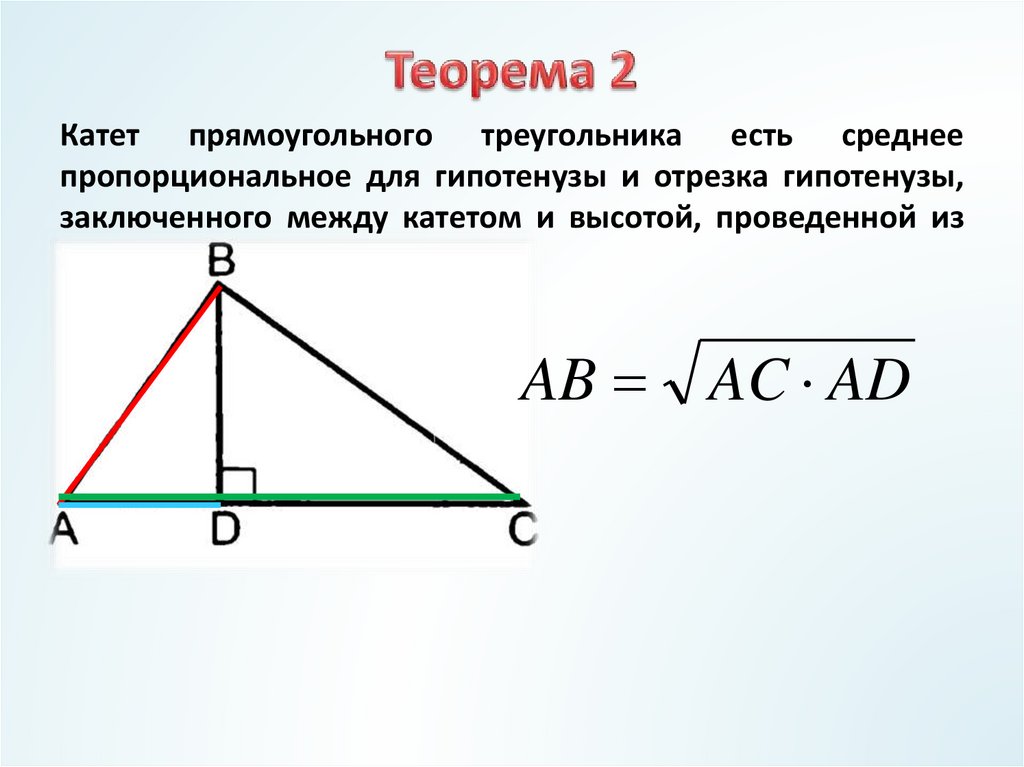 Вы можете пройти Mean Proportional на сайте Vedantu абсолютно бесплатно. Как только вы выучите все формулы и их применение, вы будете готовы решать вопросы, основанные на средней пропорции. Используйте следующие советы и приемы при решении таких вопросов, чтобы стать более эффективным: 

• Прежде чем вы начнете задавать вопросы, убедитесь, что у вас есть четкое представление обо всех темах, относящихся к средней пропорции.

• Внимательно прочитайте вопросы, чтобы понять, какие формулы или теоремы будут использоваться в них для получения правильных ответов.

• Обратитесь к примерам средней пропорции, чтобы понять правильную последовательность шагов, которую необходимо выполнить для решения конкретной проблемы.

• Убедитесь, что вы знаете вывод формулы или теоремы, поскольку они пригодятся при решении сложных вопросов, основанных на средней пропорции.

• Не используйте ярлыки для решения вопроса. Поскольку на вашем экзамене по математике есть пошаговая оценка, вы должны правильно решить вопрос, упомянув каждый шаг.

• Обращайтесь к среднему пропорциональному всякий раз, когда вы застряли на вопросе.

• Тщательно изучите все формулы, чтобы не забыть их при ответах на вопросы, связанные со средним пропорциональным.

• Помимо производных и формул, вы также должны знать определения каждого понятия, чтобы понять его значение.

Факты, чтобы запомнить

Средние пропорциональные и правила высоты и ног

… и высота и LEG Правила

Средняя доля

Средние пропорциональные из A и Arm20504204 Arm204504205 и 5 и и 5 4 10205 и 4 и .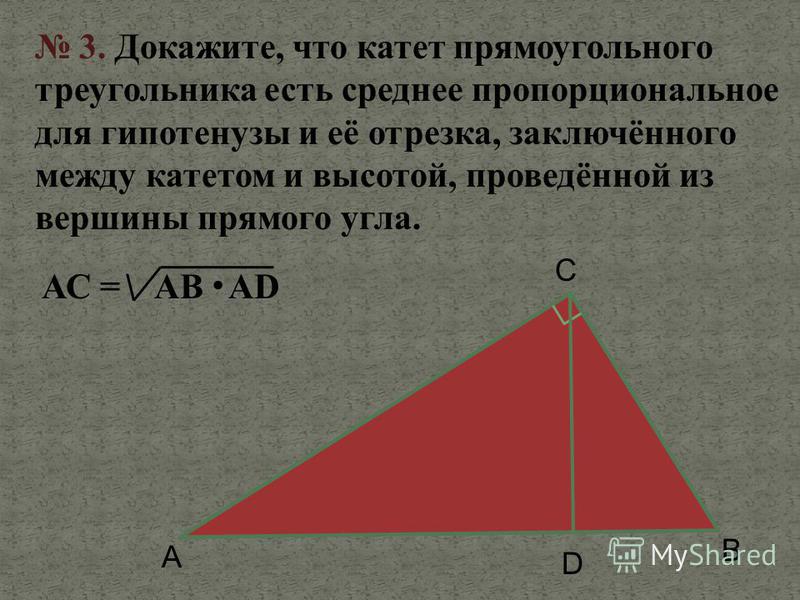

это значение x здесь:

a x   =   x b

это?

, но когда мы переходим, умножим (умножьте обе стороны на B , а также на x ) мы получаем:

A x = x 22323333239 29333393333333333333339339333933939339393933393339393339333 33933393933939393939393339333 33393333933933933393339333933393339393939393939393939393939н.

аб x   =  x

аб = х 2

Теперь мы можем найти x:

x = √(ab)

Пример: Чему равно среднее пропорциональное между 2 и 18?

Нас спрашивают «Каково здесь значение x?»

2 x   =   x 18

«2 равно x, как x равно 18» (36) = 6

, и это то, что мы заканчиваем:

2 6 = 6 18

. В основном говорится, что 6 — «Множество

020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202 2 умножить на 3 будет 6 , 6 умножить на 3 равно 18 )

(Это также среднее геометрическое двух чисел.)

Еще один пример, чтобы вы поняли, что такое Пример: 63 . среднее пропорциональное 5 и 500?

x = √ (5 × 500)

x = √ (2500) = 50

, так что это похоже на это:

Правые угловые треуговые прямоугольные треугольники.

Во-первых, интересная вещь:

• Возьмем прямоугольный треугольник , стоящий на гипотенузе (длинная сторона)
• Поставить линию высоты
• Он делит треугольник на два других треугольника, да?

Эти два новых треугольника похожи друг на друга и на исходный треугольник!

Это потому, что все они имеют одинаковые три угла.

Попробуйте сами: вырежьте из листа бумаги прямоугольный треугольник, затем разрежьте его по высоте и посмотрите, действительно ли кусочки похожи.

Мы можем использовать эти знания для решения некоторых проблем.

На самом деле мы получаем два правила:

Правило высоты

Высота есть среднее пропорциональное между левой и правой частями гиптонуса, например:

Пример: Найдите высоту

h высоты ( AD)

Используйте правило высоты:

слева высота   =   высота справа

Что для нас:

4.9 H = H 10

и решайте для H:

H ² = 4,9 × 10 = 49903

H ² = 4,9 × 10 = 49903

H ^{. треугольника является средним пропорциональным между гипотенузой и}

частью гипотенузы непосредственно под катетом :

и

Пример: Сколько будет

х (длина стороны АВ) ?

Сначала Найдите гипотенузу: BC = BD + DC = 9 + 7 = 16

Теперь Используйте правило ноги:

Гипотеновая

16 x = x 9

и решить для x:

x ² = 16 × 9 = 144

x = захваты.