Площадь (математика, 5 класс) – что такое, правило обозначения и понятие
4.6
Средняя оценка: 4.6
Всего получено оценок: 173.
4.6
Средняя оценка: 4.6
Всего получено оценок: 173.
В школьном курсе математики 4-5 класса рассматривается понятие площади. Это значение часто встречается как в реальной жизни, где мы постоянно интересуемся площадью квартиры, так и при решении задач.
Определение понятия
Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.
Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь.
2$.
Что мы узнали?
Мы познакомились с понятием площади. Узнали, что для каждой фигуры есть свой метод определения площади. Важно, чтобы основные параметры фигуры были выражены в одних и тех же единицах.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Галина Изотова
9/10
Данил Байков
9/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 173.
А какая ваша оценка?
§ Площадь фигур. Площадь квадрата. Площадь прямоугольника. Площадь сложной фигуры
Определение площади Формулы площадей фигур
Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная определение степени, можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD.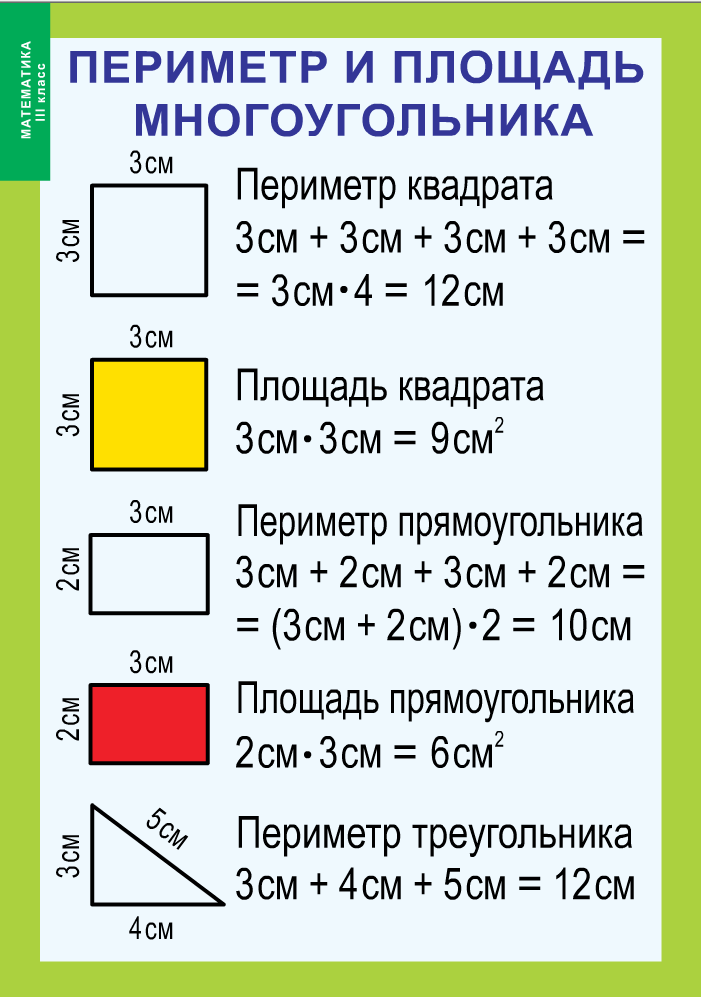
Найдём площадь треугольников
ABC и
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S ABC = SABCD : 2
S ABC = 20 : 2 = 10 см2
S ABC =
S ACD = 10 см2
Определение площади Формулы площадей фигур
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
Что такое площадь в математике? Определение, формулы, формы, примеры
Определение площади
Площадь определяется как общее пространство, занимаемое плоской (двухмерной) поверхностью или формой объекта.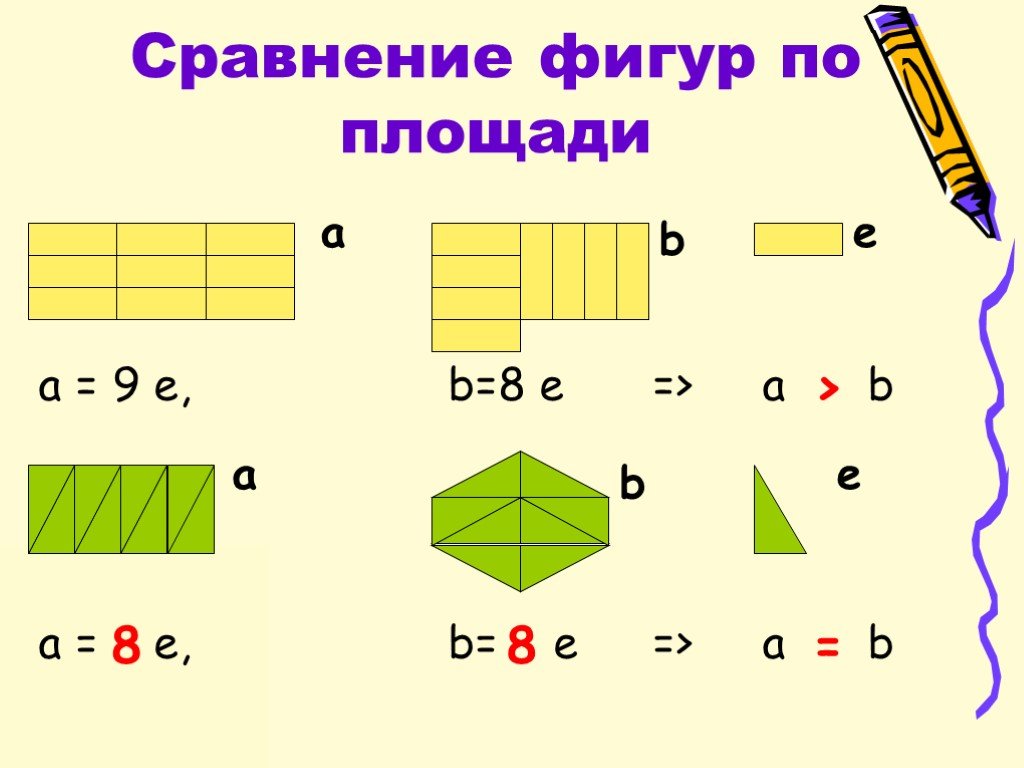
Пространство, ограниченное границей плоской фигуры, называется ее площадью . Площадь фигуры – это количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Площадь измеряется в квадратных единицах, таких как см² и м². Площадь фигуры – двумерная величина.
Термин «область» относится к пространству внутри границы или периметра замкнутой формы. Геометрия такой формы содержит как минимум три стороны, соединенные вместе, образуя границу. Символическое представление такого пространства в математике относится к формуле «площади». Для представления и рисования реальных объектов дизайнеры и архитекторы используют различные формы, такие как круг, треугольник, четырехугольник и многоугольник.
Изобретение колеса стало первым шагом к преобразованию объектов в геометрические формы. В первые дни интерпретация «площади» с использованием формулы для геометрических фигур развилась из экспериментов, проведенных Архимедом.
Родственные игры
Что такое формула вычисления площади?
Мы можем вычислить площадь фигуры, используя сетку.
Площадь любой фигуры — это количество квадратных единиц, которые могут в нее поместиться. Сетка состоит из множества квадратов, и каждый квадрат имеет стороны 1 на 1 единицу, т. е. площадь каждого квадрата равна 1 квадратной единице. Каждый квадрат известен как единичный квадрат.
Возьмите карандаш и нарисуйте квадрат на листе бумаги. Это двумерная фигура. Пространство, которое фигура занимает на бумаге, называется ее 9.0005 Зона .
Теперь представьте, что ваш квадрат состоит из меньших квадратов. Площадь фигуры рассчитывается как количество единичных квадратов, необходимых для покрытия общей площади поверхности этой конкретной двумерной формы. Квадратные сантиметры, квадратные футы, квадратные дюймы, квадратные метры и т. д. являются одними из распространенных единиц измерения площади.
Самый простой способ интерпретировать площадь геометрических фигур — использовать «единичные квадраты». Единичный квадрат — это квадрат, длина каждой стороны которого равна 1 единице.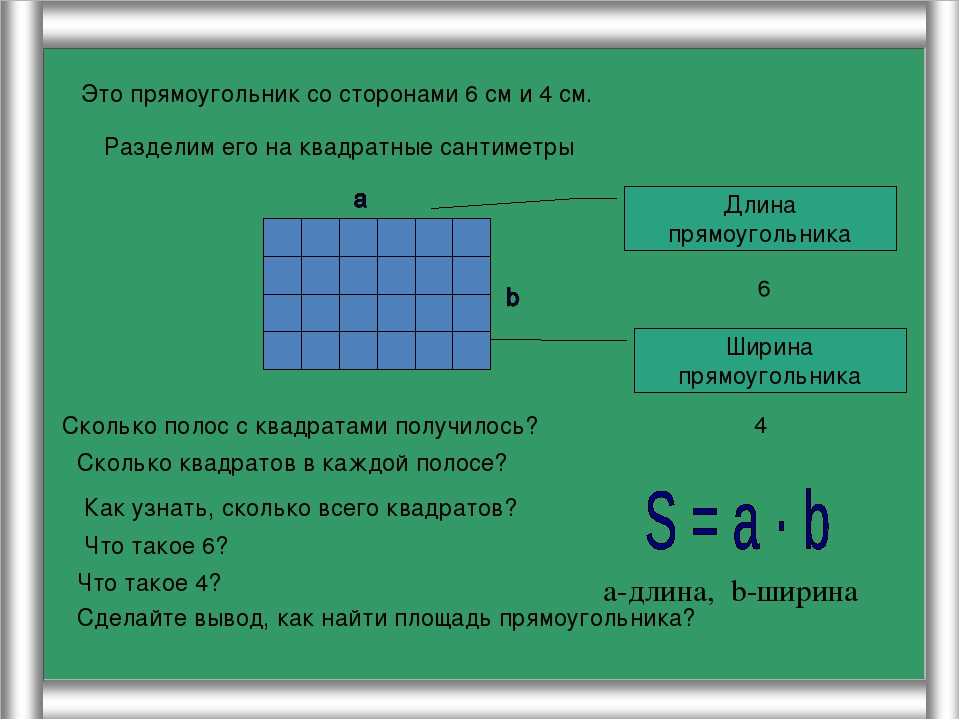
9{2})$.
Площадь фигуры — это количество заштрихованных единичных квадратов. На рисунке ниже количество заштрихованных единичных квадратов $= 24$. Следовательно, площадь фигуры $= 24$ квадратных единиц.
Как вычислить площадь, если в сетке есть еще и полединичные квадраты?
Чтобы понять это, давайте возьмем еще один пример:
Шаг 1 : Подсчитайте полные квадраты.
Есть 18 полных квадратов.
Шаг 2: Сосчитайте половинки квадратов.
Подсчитав, мы видим, что полуквадратов 6.
Шаг 3: 1 полный квадрат $= 1$ квадратная единица
Итак, 18 полных квадратов $= 18$ квадратных единиц
1 половина квадрата $= \frac{1}{2}$ квадратная единица
6 половина квадрата $= 3$ квадратных единиц
Общая площадь $= 18 + 3 = 21$ квадратных единиц.
Связанные рабочие листы
Происхождение термина: Площадь
Термин «площадь» происходит от латинского языка и означает «простой кусок пустой земли».
Это также означает «определенное количество пространства, содержащееся в наборе границ».
Подробнее о Зоне
Посмотрите на ковер в вашем доме. Чтобы купить ковер, подходящий к полу, нам нужно знать его площадь. Или ковер будет больше или меньше, чем пространство! Некоторые другие случаи, когда нам нужно знать площадь, — это при укладке плитки на пол, покраске стены или наклеивании на нее обоев или определении общего количества плиток, необходимых для строительства бассейна.
Формулы для вычисления площади
Нас окружает множество двумерных фигур: круг, треугольник, квадрат, прямоугольник, параллелограмм и трапеция. Вы можете нарисовать все эти фигуры на бумаге. Каждая фигура уникальна и уникальна, поэтому ее площадь также рассчитывается по-разному. Чтобы найти площадь, сначала определите форму. Затем используйте соответствующую формулу из списка, приведенного ниже, чтобы найти его площадь.
- Площадь объекта можно объяснить как количество материала, необходимого (например, бумаги, ткани, плитки) для покрытия поверхности в двухмерной плоскости.
- Для трехмерных плоскостей, таких как прямоугольный параллелепипед, куб, сфера и т. д., это называется площадью поверхности.
Площади составных фигур
Каждая плоская фигура не может быть классифицирована как простой прямоугольник, квадрат, треугольник или типичная форма в реальной жизни. Некоторые фигуры состоят из нескольких простых двумерных фигур. Соединим прямоугольник и полукруг.
Эти фигуры, образованные комбинацией двух или более простых фигур, называются « составные фигуры » или «составные фигуры ».
Чтобы найти площадь составной фигуры, мы должны найти сумму площадей всех фигур в ней. Итак, площадь только что нарисованной фигуры будет равна площади прямоугольника, l b плюс половина площади круга, ½ x πr² , где l и b — длина и ширина прямоугольника, r — радиус полукруга. 9{2})$
, где r — радиус полукруга, а b и h — основание и высота треугольника соответственно.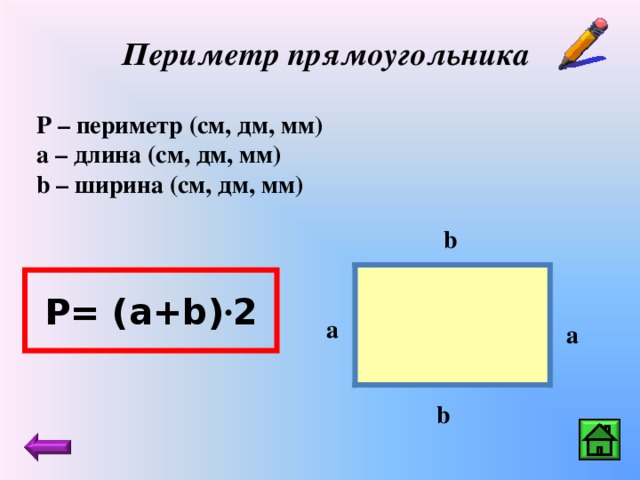
Площадь двумерных фигур
В таблице ниже перечислены фигуры и их формулы для расчета площади:
В таблице ниже приведены некоторые распространенные двумерные фигуры и формулы площади:
| 9012 30 | |
| Площадь $= 12 \times \text{base} \times \text{heightArea} = 12 \times b \times h$ 9{2} (\pi = 3,14)$ |
Площадь по периметру
| Площадь | Периметр980 Пространство, занимаемое замкнутой плоскостью в двумерной форме, называется область. | Периметр является мерой длины внешней границы замкнутой формы. | Площадь измеряется в квадратных единицах. | Периметр измеряется в единицах. | Пример: Площадь облицовки пола | Пример: Периметр ограждения сада | |
Площадь v. Объем
| Площадь | 12 7 3 3 6 Объем 6 0129 Площадь определяется для 2-мерного пространства. | Объем определяется для трехмерного пространства. |
| Пространство, занимаемое замкнутой плоскостью в двумерной форме, называется площадью. | Пространство, занимаемое трехмерной фигурой, называется объемом. | |
| Пример: Площадь пола | Пример: Объем комнаты |
Реальные приложения
Вот несколько способов, которыми вы можете применить знание площади цифр в своей повседневной жизни. жизнь.- Мы можем найти площадь подарочной бумаги, чтобы проверить, сможет ли она покрыть коробку или нет.
- Мы можем найти площадь квадрата или круга, чтобы найти площадь сигнального щита.
- Понятие площади было основой геометрии с первых дней. Ученые и астрономы воспользовались помощью узоров и геометрических форм, чтобы понять и установить передовые концепции в науке и математике.
- В современном аспекте при математическом моделировании таких объектов, как машины, инструменты, колеса, а также при проектировании одежды используются понятия площади и периметра. Он также служит основой для интегрального исчисления для понимания сложных объектов, таких как сферы и эллипсы.
Он также служит основой для интегрального исчисления для понимания сложных объектов, таких как сферы и эллипсы.Интересные факты
1. Площадь диска была рассчитана в V веке до н. э. Гиппократом Хиосским
2. Площадь треугольника также вычислена по формуле Герона
Вывод
Итак, мы узнали, что площадь — это двумерное пространство, которое занимает любой объект. Изучение форм, их площади и периметра становится намного интереснее, когда мы понимаем их в реальных приложениях. Использование площади в практической жизни – при покупке нового дома, земельного участка или даже небольшой картины.
Решенные примеры на площади
- Круг имеет диаметр 20 см. Найдите площадь этого круга.
Ответ: Для круга $d = 20$ $см$. 9{2}$.
Пример 4: Какова площадь следующей фигуры?
Решение: Полный квадрат $= 1$ квадратная единица
Итак, 14 полных квадратов $= 14$ квадратных единиц
1 половина квадрата $= \frac{1}{2}$ квадратных единиц
5 половин квадратов $ = 2,5$ квадратных единиц
Общая площадь $= 14 + 2,5 = 16,5$ квадратных единиц.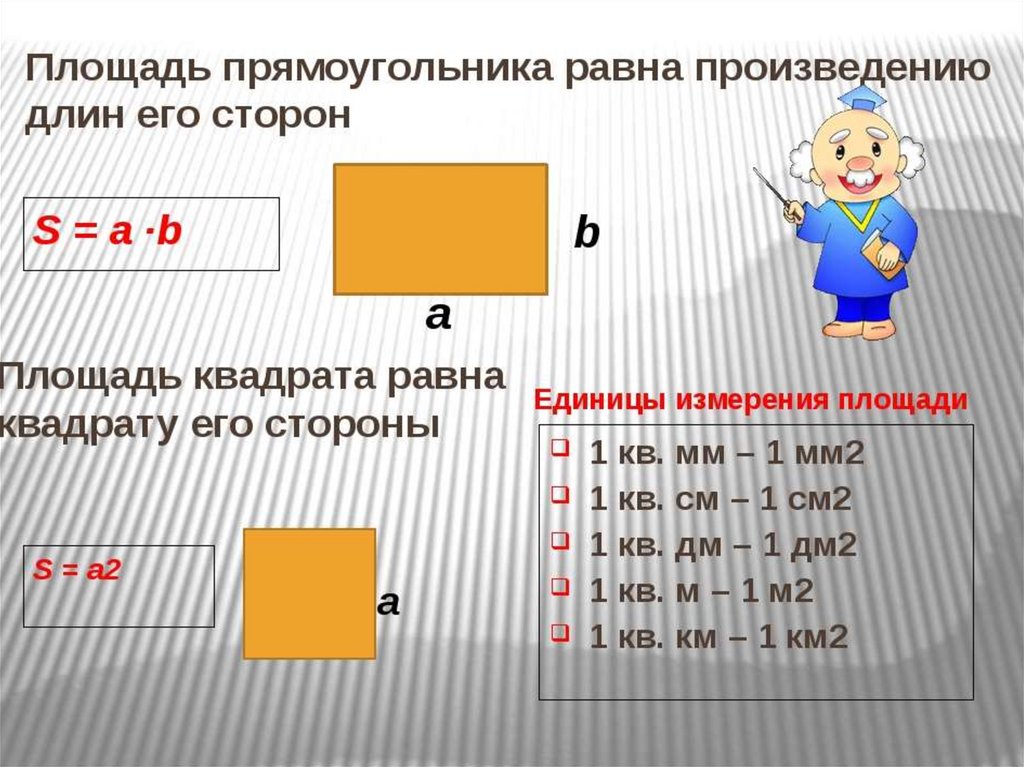
Пример 5: Какова площадь прямоугольного парка, длина и ширина которого равны 30 м и 50 м соответственно?
Решение: Данные Данные: 9{2}$
7
Площадь прямоугольного бассейна составляет 500 кв. футов. Если ширина бассейна составляет 20 футов, какова его длина?
25 футов
30 футов
50 футов
100 футов
Правильный ответ: 25 футов
Площадь прямоугольника $= \text{Length} \times \text=frac{Breadth} $
Длина Area}{Length} = \frac{500}{20} = 25$ ft
8
Какова площадь прямоугольного парка, длина и ширина которого равны 80 м и 100 м соответственно? 9{2}$
Часто задаваемые вопросы о площади
Чем отличаются периметр и площадь фигуры?
Периметр и площадь связаны с двумерной геометрией форм. Периметр — это общая длина контура вокруг фигуры, а площадь — это общее пространство внутри фигуры.
Почему площадь измеряется в квадратных единицах, а периметр — нет?
Площадь — это мера количества единичных квадратов, вписывающихся в двумерную фигуру, поэтому она выражается в квадратных единицах. Периметр является мерой длины контура фигуры и выражается в линейных единицах.
В чем важность концепции области обучения?
Знание площади формы дает учащимся четкое представление об общем пространстве, охватываемом границами этой формы. Эта концепция имеет множество практических применений, например определение площади ковра в комнате, определение общего размера стены, которую нужно покрасить, и т. д.
Как измеряется площадь неправильной формы?
Разделите неправильную форму на единичные квадраты и рассчитайте общее количество единичных квадратов. Если несколько единичных квадратов не заняты полностью, приблизьте их к 0 или 1 для каждого.
В чем разница между площадью и объемом?
Площадь относится к области, ограниченной замкнутой геометрической фигурой на двумерной плоскости. Она всегда измеряется в квадратных единицах.
Объем относится к области, ограниченной замкнутой геометрической фигурой в трехмерной плоскости. Он всегда измеряется в кубических единицах.
Кто изобрел понятие площади?
В пятом веке до нашей эры Гиппократ Хиосский показал, что площадь диска, т. е. области, заключенной в круг, пропорциональна квадрату его диаметра — как часть его квадратуры гиппократовской луны, но они не смогли определить константу пропорциональности.
Как мы используем понятие площади в повседневной жизни?
Мы используем понятие площади, когда выясняем, сколько материала потребуется для покрытия деревянного стола, сколько плитки потребуется для облицовки пола, сколько места потребуется для парковки, сколько краски потребуется для стены и т.
д.
Что такое площадь? Определение, площадь фигур Формула
Площадь – это площадь, занимаемая двухмерной фигурой. Другими словами, это величина, измеряющая количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Стандартной единицей площади являются квадратные единицы, которые обычно представляются как квадратные дюймы, квадратные футы и т. д. Давайте научимся вычислять площадь различных геометрических фигур с помощью примеров и практических вопросов.
| 1. | Что такое площадь? |
| 2. | Как рассчитать площадь? |
| 3. | Площадь геометрических фигур — Формула |
| 4. | Часто задаваемые вопросы по Зоне |
Что такое площадь?
Слово «площадь» означает свободную поверхность. Площадь фигуры вычисляется с помощью ее длины и ширины. Длина одномерна и измеряется в таких единицах, как футы (футы), ярды (ярды), дюймы (дюймы) и т.
д. Однако площадь формы является двумерной величиной. Следовательно, он измеряется в квадратных единицах, таких как квадратные дюймы или (в
Как рассчитать площадь?
Давайте посмотрим, как вычислить площадь фигуры с помощью сетки. Площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Сетка состоит из множества квадратов со сторонами 1 на 1 единицу. Площадь каждого из этих квадратов равна 1 квадратной единице. Следовательно, каждый квадрат известен как единичный квадрат. Посмотрите на рисунок, показанный ниже. Найдем площадь фигуры, начерченной на сетке.
Площадь этой фигуры равна количеству заштрихованных единичных квадратов.
Таким образом, площадь фигуры = 9 квадратных единиц.
Здесь площадь, занимаемая фигурой, равна 4 полным квадратам и 8 полуквадратам. Вместе это образует площадь 8 квадратных единиц. Если заштрихованная область меньше 1/2, мы можем опустить эти части. Для правильных фигур у нас есть определенные формулы для вычисления их площади. Обратите внимание, что это только приблизительное значение.
Площадь прямоугольника
Площадь прямоугольника — это площадь, занимаемая им. Рассмотрим желтый прямоугольник в сетке. Он занял 6 единиц.
В приведенном выше примере длина прямоугольника составляет 3 единицы, а ширина — 2 единицы. Площадь прямоугольника получается путем умножения его длины и ширины, что равносильно подсчету единиц квадратов.
Таким образом, формула площади прямоугольника: : площадь прямоугольника = длина × ширина. В данном случае это будет 2 × 3 = 6 квадратных единиц.
Площадь квадрата
Площадь квадрата – это занимаемая им площадь. Посмотрите на цветной квадрат, показанный в сетке ниже. Он занимает 25 квадратов.
Из рисунка видно, что длина каждой стороны цветного квадрата равна 5 единицам. Следовательно, площадь квадрата – это произведение его сторон, которое можно представить по формуле: Площадь квадрата = сторона × сторона. Итак, площадь этого квадрата = 5 × 5 = 25 квадратных единиц.
Площадь круга
Круг представляет собой изогнутую форму. Площадь круга – это количество пространства, заключенного в границах круга. Узнайте больше о π и радиусе, прежде чем мы перейдем к формуле площади круга.
Площадь круга рассчитывается по формуле: π r 
Площадь геометрических фигур — Формула
Каждая форма имеет разные размеры и формулы. В следующей таблице показан список формул для площади различных фигур.
| Форма | Площадь фигур — Формула |
|---|---|
Квадрат | Площадь квадрата = x 2 квадратных единиц |
Прямоугольник | Площадь прямоугольника = длина × ширина = l × w квадратных единиц |
Круг | Площадь круга = π r 2 квадратных единиц |
Треугольник | Площадь треугольника = \(\dfrac{1}{2}\times b \times h\) квадратных единиц |
Параллелограмм | Площадь параллелограмма = основание × высота = b × h квадратных единиц |
Равнобедренная трапеция | Площадь равнобедренной трапеции = \(\dfrac{1}{2}(a+b) h\) квадратных единиц |
Ромб | Площадь ромба = \(\dfrac{1}{2}\times (d1) \times (d2)\) квадратных единиц |
Воздушный змей | Площадь воздушного змея = \(\dfrac{1}{2}\times (d1) \times (d2)\) квадратных единиц |
☛ Связанные темы по площади
Ознакомьтесь со следующими темами, касающимися областей различной формы, и узнайте больше о формулах площади.
- Формула геометрической площади
- Площадь треугольника
Советы и подсказки
- Мы часто запоминаем формулы для вычисления площади фигур. Более простым методом было бы использование линий сетки, чтобы понять, как была получена формула.
- Мы часто путаем площадь и периметр фигуры. Полное понимание может быть построено путем отслеживания поверхности любой формы и наблюдения за тем, что область — это, по сути, пространство или область, покрытая формой.
Примеры на участке
Пример 1: Найдите площадь квадрата со стороной 7 см.
Решение :
Площадь квадрата = сторона × сторона. Здесь сторона = 7 см
Подставляя значения, 7 × 7 = 49.
Следовательно, площадь квадрата = 49 квадратных см.
Пример 2: Размеры прямоугольника 15 см и 8 см.
Найдите его площадь. Решение :
Площадь прямоугольника равна произведению его длины на ширину, что можно представить по формуле: Площадь = l × w.
Подставляя данные значения, получаем площадь прямоугольника = 15 × 8 = 120 см 2Пример 3: Можете ли вы найти площадь круга с радиусом 14 см?
Раствор :
Радиус круга = 14 см
Площадь круга рассчитывается по формуле π r 2
Подставляя значения в формулу, площадь = \(\dfrac{22}{7}\) × 14 × 14 = 616 квадратных см.
Пример 4. Вычислите площадь заданной формы путем подсчета квадратов.
Решение: Давайте посчитаем полные квадраты и половинки квадратов.
Есть 24 единичных квадрата и 5 полуквадратов.
Следовательно, площадь фигуры = 24 + (5 × ½) = 24 + 2,5 26,5 квадратных единиц
Найдите его площадь. перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что».
Почувствуйте разницу Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по области
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Зоне
Что такое площадь?
Площадь фигуры представляет собой двумерную величину, которая измеряется в квадратных единицах, таких как квадратные дюймы или (в 2 ), квадратные футы или (футы 2 ), квадратные ярды или (ярды 2 ), и т.д.
Как найти площадь неправильной формы?
Площадь неправильной формы можно найти, разделив фигуру на единичные квадраты. Когда фигура не занимает весь единичный квадрат, мы можем аппроксимировать и найти ее значение.
Как доказать площадь круга?
Если окружность сложить в треугольник, радиус станет высотой треугольника, а периметр станет его основанием, равным 2 × π × r. Мы знаем, что площадь треугольника находится путем умножения его основания и высоты, а затем деления на 2, что составляет: ½ × 2 × π × r × r.