5 класс правила по математике дробей – Действия с дробями

Как решать дроби 5 класса 🚩 Основные задачи на дроби 🚩 Математика

9 июня 2011

Автор КакПросто!

В 5 классе средней школы вводится понятие дроби. Дробь – это число, состоящее из целого количества долей единиц. Обыкновенные дроби записываются в виде ±m/n, число m называют числителем дроби, число n – его знаменателем.
Если модуль знаменателя больше модуля числителя, например 3/4, то дробь называется правильной, в противном случае – неправильной. Дробь может содержать целую часть, например 5 * (2/3).
К дробям можно применять различные арифметические операции.

Статьи по теме:

Инструкция

Приведение к общему знаменателю.

Пусть даны дроби a/b и c/d.

— В первую очередь находится число НОК(наименьшее общее кратное) для знаменателей дробей.

— Числитель и знаменатель первой дроби умножается на НОК/b

— Числитель и знаменатель второй дроби умножается на НОК/d

Пример приведён на рисунке.

Для сравнения дробей их необходимо привести к общему знаменателю, затем сравнить числители. Например, 3/4 < 4/5, см. рисунок.

Сложение и вычитание дробей.

Для нахождения суммы двух обыкновенных дробей их необходимо привести к общему знаменателю, после чего сложить числители, оставив знаменатель без изменений. Пример сложения дробей 1/2 и 1/3 приведён на рисунке.

Разность дробей находится аналогичным образом, после нахождения общего знаменателя, числители дробей вычитаются, см. пример на рисунке.

Умножение и деление дробей.

При умножении обыкновенных дробей, числители и знаменатели перемножаются между собой.

Для того, чтобы разделить две дроби, необходимо получить дробь обратную второй дроби, т.е. поменять его числитель и знаменатель местами, после чего произвести умножение полученных дробей.

Чтобы решить задачу с дробями, нужно научиться делать с ними арифметические действия. Они могут быть десятичные, но чаще всего используются натуральные дроби с числителем и знаменателем. Только после этого можно переходить на решения математических задач с дробными величинами.

Вам понадобится

• — калькулятор;
• — знания свойств дробей;
• — умение производить действия с дробями.

Инструкция

Дробью называют запись деления одного числа на другое. Зачастую это сделать нацело нельзя, поэтому и оставляют это действие «неоконченным . Число, которое является делимым (оно стоит над или перед знаком дроби), называются числителем, а второе число (под знаком дроби или после него) – знаменателем. Если числитель больше знаменателя, дробь называется неправильной, и из нее можно выделить целую часть. Если числитель меньше знаменателя, то такая дробь называется правильной, и ее целая часть равна 0.

Задачи с дробями делятся на несколько видов. Определите, к какому из них относится задача. Простейший вариант – нахождение доли числа, выраженной дробью. Для решения этой задачи достаточно умножить это число на дробь. Например, на склад завезли 8 т картошки. В первую неделю было продано 3/4 от ее общего количества. Сколько картошки осталось? Чтобы решить эту задачу, число 8 умножьте на 3/4. Получится 8∙3/4=6 т. Если нужно найти число по его части, умножьте известную часть числа на дробь, обратную той, которая показывает какова доля данной части в числе. Например, 8 человек из класса составляют 1/3 от общего количества учеников. Сколько детей учится в классе? Поскольку 8 человек это часть, которая представляет 1/3 от всего количества, то найдите обратную дробь, которая равна 3/1 или просто 3. Затем для получения количества учеников в классе 8∙3=24 ученика.

Когда нужно найти какую часть числа составляет одно число от другого, поделите число, которое представляет часть на то, которое является целым. К примеру, если расстояние между городами 300 км, а автомобиль проехал 200 км, какую часть этот составит от всего пути? Поделите часть пути 200 на полный путь 300, после сокращения дроби получите результат. 200/300=2/3.

Чтобы найти часть неизвестную долю от числа, когда есть известная, возьмите целое число за условную единицу, и отнимите от нее известную долю. Например, если уже прошло 4/7 части урока, сколько еще осталось? Возьмите весь урок как условную единицу и отнимите от нее 4/7. Получите 1-4/7=7/7-4/7=3/7.

Источники:

• решение задачи с дробями

Дробь представляет собой число, состоящее из одной или нескольких равных долей единицы. С дробями можно выполнять те же арифметические действия, что и с целыми числами: сложение, вычитание, умножение и деление.

Инструкция

Посмотрите, какие дроби имеются в решаемом вами примере: правильные, неправильные, десятичные. Для удобства расчетов с разными дробями, целесообразно перевести десятичные в правильные или неправильные, записав значение после запятой в числитель, а в знаменатель поставив 10.

Дроби с выделяемой целой частью приведите к неправильному виду, умножив число на знаменатель и полученное произведение прибавив к числителю. И, наоборот, чтобы выделить целое число из изначальной неправильной дроби, поделите числитель на знаменатель. Остаток от деления станет новым числителем. Кроме того, для таких дробей возможно выполнения арифметических действий сначала с целой частью, а потом – с дробной.

Чтобы выполнить арифметические действия сложения и вычитания с дробями, приведите их к общему знаменателю. Для этого нужно умножить знаменатель первой дроби на знаменатель второй. В числителе той дроби, чей знаменатель был изначально меньше, укажите значение знаменателя второй дроби и наоборот. Вычислите сумму двух дробей, просто сложив их новые числители. Например: 1/3 + 1/5 = 8/15 (общий знаменатель равен 15, 1/3 = 5/15; 1/5 = 3/15; 5 + 3 = 8). Точно так же выполняется и вычитание.

Чтобы рассчитать произведение дробей, умножьте сначала числитель одной дроби на числитель другой. Запишите результат в числитель новой дроби. После этого перемножьте и знаменатели. Итоговое значение укажите в знаменателе новой дроби. Например, 1/3 ? 1/5 = 1/15 (1 ? 1 = 1; 3 ? 5 = 15).

Чтобы поделить одну дробь на другую, умножьте сначала числитель первой на знаменатель второй. То же действие произведите и со второй дробью (делителем). Или перед выполнением всех действий сначала «переверните» делитель, если вам так удобнее: на месте числителя должен оказаться знаменатель. После этого умножьте знаменатель делимого на новый знаменатель делителя и перемножьте числители. Например, 1/3 : 1/5 = 5/3 = 1 2/3 (1 ? 5 = 5; 3 ? 1 = 3).

Источники:

• Основные задачи на дроби

Решение дробных задач в курсе школьной математике – это начальная подготовка учеников к изучению математического моделирования, являющегося более сложным, но имеющим широкое приложение понятием.

Инструкция

Дробными являются задачи, которые решаются с помощью рациональных уравнений обычно с одной неизвестной величиной, которая и будет итоговым или промежуточным ответом. Такие задачи удобнее решать табличным методом. Составляется таблица, строки в которой – объекты задачи, а столбцы – характеризующие величины. Решите задачу: от вокзала в аэропорт, расстояние между которыми 120 км, отправился поезд-экспресс. Пассажир, опоздавший на поезд на 10 минут, поехал на такси со скоростью, большей скорости экспресса на 10 км/ч. Найдите скорость поезда, если он прибыл по назначению одновременно с такси.

Составьте таблицу из двух строк (поезд, такси – объекты задачи) и трех столбцов (скорость, время и проделанный путь – физические характеристики объектов).

Заполните первую строку для поезда. Его скорость – неизвестная величина, которую требуется определить, поэтому она равна x. Время, которое экспресс был в пути, по формуле равно отношению всего пути к скорости. Это дробь с 120 в числителе и x в знаменателе – 120/х. Впишите характеристики такси. Скорость по условию задачи превышает скорость поезда на 10, значит, она равна x+10. Время в пути, соответственно, 120/(х+10). Путь объекты проделали одинаковый, 120 км.

Вспомните еще одну часть условия: вам известно, что пассажир опоздал на вокзал на 10 минут, а это 1/6 часа. Значит, разница между двумя значениями второго столбца равна 1/6.

Составьте уравнение: 120/х – 120/(х + 10) = 1/6. У этого равенства должно быть ограничение, а именно x>0, но поскольку скорость – это заведомо положительная величина, то в данном случае эта оговорка несущественна.

Решите уравнение относительно х. Дроби приведите к общему знаменателю х·(х+10), тогда получится квадратное уравнение:x² + 10·x – 7200 = 0D = 100 + 4·7200 = 28900×1 = (-10+170)/2 = 80; x2 = (-10-170)/2 = -90.

Для решения задачи подходит только первый корень уравнения x = 80.Ответ: скорость поезда равна 80 км/ч.

Видео по теме

Источники:

• Дробные рациональные уравнения

www.kakprosto.ru

Материал по алгебре (5 класс) на тему: Правила по теме «Обыкновенные дроби»

По теме: методические разработки, презентации и конспекты

Урок-игра по математике: Решение задач на нахождение дроби от числа и числа по его дроби.

Урок посвящен  году  российской истории.Методическая разработка занятия содержит план-конспект и презентацию к уроку….

Презентация к открытому уроку по теме «Дроби.Сравнение дробей. Правильные и неправильные дроби»

Презентация к открытому уроку в 5 классе….

Урок математики в 5 классе по теме «Правило сравнения десятичных дробей» (авторы учебника И.И.Зубарева, А.Г.Мордкович)

Данный урок  по типу является уроком изучения новой темы. Урок соответствует требованиям ФГОС, использованы информационно-коммуникативные технологии. Этапы урока были тесно взаимо…

Правила по теме «Десятичные дроби»

Материал для проверки знаний правил действий с десятичными дробями….

Методическая разработка контрольной работы по математике 6 класса по теме: «Деление обыкновенных дробей. Нахождение числа по его дроби.»

Тема: «Деление обыкновенных дробей. Нахождение числа по его дроби.».Форма: Контрольная  работаЦель: проверить знания учащихся по теме: «Деление обыкновенных дробей. Нахождение числа по его дроби….

Методическая разработка, план конспект урока по теме:»Понятие об обыкновенной дроби.Нахождение дроби от числа и числа по его дроби».

Методическая разработка, план конспект урока по теме:»Понятие об обыкновенной дроби.Нахождение дроби от числа и числа по его дроби»….

Конспект урока по математике в 6 классе по теме «Решение задач на нахождение дроби от числа и числа по его дроби»

На данном уроке по математике ученики тренируются в решении задач и развивают умение относить задачу к тому или иному типу….

nsportal.ru

Памятка (формулы по математике 5 класс)

Просмотр содержимого документа
«Памятка (формулы по математике 5 класс)»

1. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое

Х+45=90 45+(Х+12)=90

Х= 90-45 Х+12= 90-45

Х=45 Х+12=45

Х=33

1. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое

Х-45=90 (70-Х)-20=40

Х= 90+45 70-Х=40-20

Х=135 70-Х=20

Х=70-20

Х=50

1. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность

70-Х=30 40-(Х+12)=90

Х= 70-30 Х+12= 90+40

Х=40 Х+12=130

Х=130-12

Х=118

1. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.

x·25=50

x=50:25

x=2

1. Чтобы найти неизвестное делимое, нужно частное умножить на делитель

X:2=14

X=14·2

X=28

1. Чтобы найти неизвестный делитель, нужно делимое разделить на частное

28:x=14

X=28:14

X=2

Свойства сложения и вычитания

1. а+b=b+a

2. (a+b)+c=a+b+c=a+c+b=a+(b+c)

3. a-b+c=a+c-b (переставляем вместе со знаками)

4. a+b-c=a-c+b (переставляем вместе со знаками)

5. a-(b+c)= a-b-c (минус перед скобкой меняет знаки на противоположные)

6. a-(b-c)= a-b+c (минус перед скобкой меняет знаки на противоположные)

7. a-b-c=a-(b+c)

8. а-0=а

9. а+0=а

10. а-а=0

11. (a+b)c=ac+bc

12. (a-b)c=ac-bc

Свойства умножения

1.

2.

3.

4.

Площадь прямоугольника S=ab Периметр прямоугольника P=2(a+b)	Объем прямоугольного параллелепипеда V=abc Площадь поверхности прямоугольного параллелепипеда Sпов= 2(ab+bc+ac) Сумма длин всех ребер прямоугольного параллелепипеда l = 4(a+b+c)
Площадь квадрата S=a2 Периметр квадрата P=4a	Объем куба V=a3 Площадь поверхности куба Sпов= 6a2 Сумма длин всех ребер куба l=12a
Единицы измерения площадей 1га=10 000 1а=100

Формула деления с остатком

Формула деления с остатком: n = mk + r, где n — делимое, m — делитель, k — частное, r – остаток.

Формула степени числа

– квадрат числа а

– куб числа а

Формула пути

S=v·t

v=S:t

t=S:v

где S – расстояние, v – скорость, t – время

Формула радиуса

r = 2d, где r – радиус, d – диаметр

Сложение и вычитание обыкновенных дробей

Чтобы из неправильной дроби выделить целую часть, надо:

1. Разделить с остатком числитель на знаменатель;

2. Неполное частное будет целой частью;

3. Остаток от деления (если он есть) дает числитель, а делитель — знаменатель

Чтобы представить смешанное число в виде неправильной дроби, нужно

1. Умножить его целую часть на знаменатель дробной части

2. К полученному произведению прибавить числитель дробной части

3. Записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения

Пример:

Формула среднего арифметического

Среднее арифметическое = (сумма чисел) : (количество слагаемых)

Средняя скорость = (весь пройденный путь) : (все время движения)

Сумма чисел = (среднее арифметическое) * (количество чисел)

Прямой угол – равен 90°

Острый угол – меньше 90°

Тупой угол – больше 90°

Разряды числа

Целая часть

Дробная часть

Классы

Миллиарды

Миллионы

Тысячи

единицы

разряды

Сотни

Десятки

единицы

Сотни

Десятки

единицы

Сотни

Десятки

единицы

Сотни

Десятки

единицы

Десятые

Сотые

Тысячные

десятитысячные

стотысячные

миллионные

число

8

7

0

0

5

9

1

3

1

4

,

1

5

9

6

7

6

multiurok.ru

десятичные дроби в 5 классе

I.  Чтобы разделить число на десятичную дробь, нужно перенести запятые в делимом и делителе на столько цифр вправо, сколько их стоит после запятой в делителе, а затем выполнить деление на натуральное число.

Примеры.

Выполнить деление: 1) 16,38:0,7;   2) 15,6:0,15;    3) 3,114:4,5;   4) 53,84:0,1.

Решение. 

Пример 1)  16,38:0,7.

В делителе 0,7 после запятой стоит одна цифра, поэтому, перенесем запятые в делимом и делителе на одну цифру вправо.

Тогда нам нужно будет разделить

163,8 на 7.

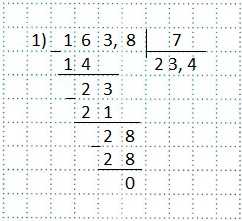Выполним деление по правилу деления десятичной дроби на натуральное  число.

Делим так, как делят натуральные числа. Как снесем цифру 8 — первую цифру после запятой (т.е. цифру в разряде десятых), так сразу поставим в частном запятую и продолжим деление.

Ответ: 23,4.

 

Пример 2) 15,6:0,15.

Переносим запятые в делимом (15,6) и делителе (0,15) на две цифры вправо, так как в делителе 0,15 после запятой стоят две цифры.

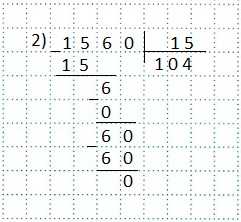Помним, что справа к десятичной дроби можно приписать сколько угодно нулей, и от этого десятичная дробь не изменится.

Тогда:

15,6:0,15=1560:15.

Выполняем деление натуральных чисел.

Ответ: 104.

 

Пример 3) 3,114:4,5.

Перенесем запятые в делимом и делителе на одну цифру вправо и разделим 31,14 на 45 по правилу деления десятичной дроби на натуральное число.

Итак:

3,114:4,5=31,14:45.

В частном поставим запятую сразу, как сносим цифру 1 в разряде десятых. Затем продолжаем деление.

Чтобы закончить деление нам пришлось приписать нуль к числу 9 — разности чисел 414 и 405. (мы знаем, что справа к десятичной дроби можно приписывать нули)

 

Ответ: 0,692.

Пример 4)  53,84:0,1.

Переносим запятые в делимом и делителе на

1 цифру вправо.

Получаем: 538,4:1=538,4. 

Проанализируем равенство: 53,84:0,1=538,4. Обращаем внимание на запятую в делимом в данном примере и на запятую в полученном частном. Замечаем, что запятая в делимом перенесена на 1 цифру вправо, как если бы мы умножали 53,84 на 10. (Смотрите видео «Умножение десятичной дроби на 10, 100, 1000 и т.д.») Отсюда правило деления десятичной дроби на 0,1; 0,01; 0,001 и т.д.

II. Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001 и т. д., нужно перенести запятую вправо на 1, 2, 3 и т. д. цифр. (Деление десятичной дроби на 0,1; 0,01; 0,001 и т. д. равносильно умножению этой десятичной дроби на 10, 100, 1000 и т.д.)

Примеры.

Выполнить деление: 1) 617,35:0,1;  2) 0,235:0,01;  

3) 2,7845:0,001;  4) 26,397:0,0001.

Решение.

Пример 1) 617,35:0,1.

Согласно правилу II деление на 0,1 равносильно умножению на 10, и запятую в делимом перенесем на 1 цифру вправо:

1) 617,35:0,1=6173,5.

Пример 2) 0,235:0,01.

Деление на 0,01 равносильно умножению на 100, значит, запятую в делимом перенесем на 2 цифры вправо:

2) 0,235:0,01=23,5.

Пример 3) 2,7845:0,001.

Так как деление на 0,001 равносильно умножению на 1000, то перенесем запятую на 3 цифры вправо:

3) 2,7845:0,001=2784,5.

Пример 4) 26,397:0,0001.

Разделить  десятичную дробь на 0,0001 — это все равно, что умножить ее на 10000 (переносим запятую на 4 цифры вправо). Получаем:

4) 26,397:0,0001=263970.

Смотрите видео «Деление на десятичную дробь»

 I.  Чтобы разделить десятичную дробь на натуральное число, нужно делить дробь на это число, как делят натуральные числа и поставить в частном запятую тогда, когда закончится деление целой части.

Примеры. 

Выполнить деление: 1) 96,25:5;  2) 4,78:4;  3) 183,06:45.

Решение.

Пример 1) 96,25:5.

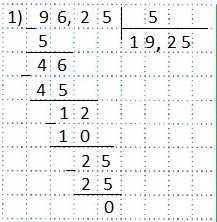Делим «уголком» так, как делят натуральные числа. После того, как сносим цифру 2 (число десятых — первая цифра после запятой в записи делимого 96,25), в частном ставим запятую и продолжаем деление.

Ответ: 19,25.

 

 

Пример 2) 4,78:4.

Делим так, как делят натуральные числа. В частном поставим запятую сразу, как снесем 7 — первую цифру после запятой в делимом 4,78. Продолжаем деление дальше. При вычитании 38-36 получаем 2, но деление не окончено. Как поступаем? Мы знаем, что в конце десятичной дроби можно приписывать нули — от этого значение дроби не изменится. Приписываем нуль и делим 20 на 4. Получаем 5 — деление окончено.

Ответ: 1,195.

 

Пример 3) 183,06:45.

Делим как 18306 на 45. В частном поставим запятую как только снесем цифру 0 — первую цифру после запятой в делимом 183,06. Так же, как в примере 2) нам пришлось приписать нуль к числу 36 — разности чисел 306 и 270.

Ответ: 4,068.

Вывод: при делении десятичной дроби на натуральное число в частном ставим запятую сразу после того, как сносим цифру в разряде десятых делимого. Обратите внимание: все выделенные красным цветом цифры в этих трех примерах относятся к разряду десятых долей делимого.

Смотрите видео: «Как разделить десятичную дробь на натуральное число».

II. Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.

Примеры.

Выполнить деление: 1) 41,56:10;  2) 123,45:100;  3) 0,47:100;  4) 8,5:1000;  5) 631,2:10000.

Решение.

Перенос запятой влево зависит от того, сколько в делителе нулей после единицы. Так, при делении десятичной дроби на 10 мы будем переносить в делимом запятую влево на одну цифру; при делении на 100 — перенесем запятую влево на две цифры; при делении на 1000 перенесем  в данной десятичной дроби запятую на три цифры влево. 

В примерах 3) и 4) пришлось приписать нули перед десятичной дробью, чтобы удобнее было переносить запятую. Однако, приписывать нули можно мысленно, и вы будете это делать, когда хорошо научитесь применять правило II для деления десятичной дроби на 10, 100, 1000 и т. д.

Смотрите видео: «Как разделить десятичную дробь на 10, 100, 1000 и т.д.»

 

www.mathematics-repetition.com

5 класс. Математика — Part 2

Рубрика «5 класс. Математика»

I.  Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

Примеры.

II.  Если нужно сложить дроби с разными знаменателями, то сначала дроби приводят к наименьшему общему знаменателю, а затем складывают дроби с одинаковыми знаменателями.

Примеры.

III.  Чтобы выполнить вычитание дробей с одинаковыми знаменателями, из числителя первой дроби вычитают числитель второй дроби, а знаменатель оставляют тот же.

Примеры.

IV.  Если нужно выполнить вычитание дробей с разными знаменателями, то их сначала приводят к общему знаменателю, а затем выполняют вычитание дробей с одинаковыми знаменателями.

Примеры.

V.  При выполнении действий сложения или вычитания смешанных чисел эти действия выполняют отдельно для целых частей и для дробных частей, а затем результат записывают в виде смешанного числа.

Примеры.

Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.

Нет, не нужно расписывать целые и дробные части смешанных чисел по отдельности.

Важно: не начинайте выполнять сложение, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ).

Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.

Важно: не начинайте выполнять вычитание, пока не приведете  дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ) и не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби. А если нельзя вычесть?

Тогда «занимаете» у целой части уменьшаемого одну целую единицу, представляете ее в виде неправильной дроби с таким же знаменателем (НОЗ),  и добавляете эту неправильную дробь (раздробленную единицу) к дробной части уменьшаемого.

• Простым называют число, которое имеет только два делителя: единицу и само это число.
•  Составным называют число, которое имеет более двух делителей.
•  Число 1 не относится ни к простым числам, ни к составным числам.
• Запись составного числа в виде произведения только простых чисел называется разложением составного числа на простые множители. Любое составное число можно единственным образом представить в виде произведения простых множителей.

Примеры. Разложить составное число столбиком на простые множители:

1) 48; 2) 75; 3) 80; 4) 120.
Запишем число 48, справа от него проведем вертикальную линию. Начинаем перебирать простые делители числа 48, начиная с самого меньшего — числа 2. Записываем 2 справа от линии. Под числом 48 запишем частное от деления числа 48 на 2. Это число 24, которое тоже делится на 2. Справа от числа 24 записываем 2, а под числом 24 — результат деления 24 на 2. Это число 12, которое опять делим на 2. Число 2 пишем справа, а под числом 12 ставим 6. Число 6 опять делим на 2, получаем число 3, которое пишем под числом 6. Число 3 делим на 3 и, наконец, под числом 3 пишем 1. Таким образом, получаем разложение числа 48 на простые множители: 48=2·2·2·2·3 или 48=2⁴∙3.

Наименьший простой делитель числа 75 — это число 3, его ставим справа от вертикальной линии. В результате деления числа 75 на 3 получаем 25. Число 25 запишем под числом 75. Число 25 делится на 5, поэтому, число 5 пишем справа от числа 25, а под числом 25 запишем число 5 — результат от деления 25 на 5. Число 5 делится на 5, под ним ставим  число 1. Результат: 75=3·5·5 или 75=3∙5².

Число 80 оканчивается нулем, значит, делится на 10. Число 10 — составное, он равно произведению простых чисел 2 и 5, поэтому, удобно записать справа от вертикальной черты произведение 2·5. тогда под числом 80 запишем число 8. Число 8 делим на 2 (пишем справа 2), под числом 8 записываем число 4. Снова делим на 2, получаем 2, делим на 2, остается 1. Результат: 80=2⁴∙5.

 

 

Число 120 разделим сразу на 10. Так как 10=2·5, то справа от вертикальной черты запишем 2·5. Под числом 120 записываем 12. Число 12 делим на 2, записываем под числом 12 число 6, которое делим на 2, а затем полученное число 3 делим на 3, получив в результате число 1. Результат: 120=2³∙3∙5.

 

 

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

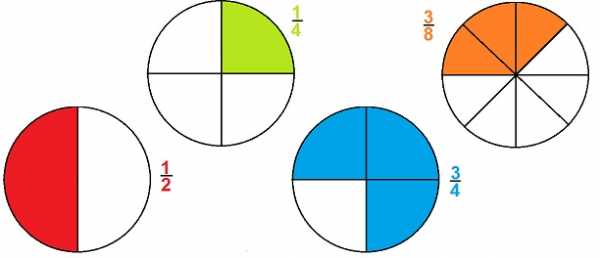
Закрашенные области всех трех кругов равны между собой, но над кругами записаны различные обыкновенные дроби. Почему? И все ли верно? Да, все верно, ведь можно разделить круг на:

• 4 части и закрасить 3 такие части;
• 8 частей и закрасить 6 таких частей;
• 12 частей и закрасить 9 таких частей.

Следовательно,

Мы убедились в правильности высказывания: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Примеры. Используя основное свойство дроби, замените звездочку таким числом, чтобы равенство было верным.

Рассуждаем так: числитель нужно увеличить во столько же раз, во сколько увеличили знаменатель дроби, т. е. в 4 раза (16:4=4). Вместо звездочки запишем значение 3·4=12.

Еще такие примеры.

Рассуждаем так: знаменатель нужно уменьшить во столько же раз, во сколько уменьшили числитель дроби, т. е. в 7 раз (21:3=7). Вместо звездочки запишем значение 28:7=4.

Еще такие примеры.

b-знаменатель дроби, показывает, на сколько равных частей разделили;

a-числитель дроби, показывает, сколько таких частей взяли. Дробная черта означает знак деления.

Иногда вместо горизонтальной дробной черты ставят наклонную, и обыкновенная дробь записывается так: a/b. В наших примерах обыкновенные дроби можно было бы записать так:

• У правильной дроби числитель меньше знаменателя.

Примеры правильных дробей.

• У неправильной дроби числитель больше знаменателя или равен знаменателю.

Примеры неправильных дробей.

Задача. В классе 24 учащихся,  5/8 из них составляют мальчики. Сколько мальчиков в классе?

 Решение.

Решить задачу можно, составив выражение:  (24:8)·5=15.

Ответ: 15 мальчиков в классе.

Задача.  Олово составляет 5/6 частей сплава. Найти массу сплава, если олова в нем содержится 250 г.

Решение.

Решить задачу можно, составив выражение: (250:5)·6=300.

Ответ: масса сплава 300 г.

•  Число, состоящее из целой части и дробной части, называется смешанным числом.
•  Чтобы неправильную дробь представить в виде смешанного числа, надо разделить числитель дроби на знаменатель, тогда неполное частное будет целой частью смешанного числа, остаток – числителем дробной части, а знаменатель останется тот же.
•  Чтобы представить смешанное число в виде неправильной дроби, нужно умножить целую часть смешанного числа на знаменатель, к полученному результату прибавить числитель дробной части и записать в числителе неправильной дроби, а знаменатель оставить тот же.

Примеры.

Представить неправильную дробь в виде смешанного числа:

Дробная часть означает знак деления. В столбик разделим числитель 9 на знаменатель 2. Частное 4 будет целой частью смешанного числа, остаток 1 станет числителем дробной части, а знаменатель 2 останется тот же.

 

Еще такие примеры.

Записать смешанное число в виде неправильной дроби:

Число 2 — целую часть смешанного числа умножают на знаменатель 4 дробной части, к полученному произведению прибавляют число 3 — числитель дробной части смешанного числа; результат 11 станет числителем неправильной дроби, а знаменатель 4 останется тот же.

Еще такие примеры.

 

Деление и числителя и знаменателя дроби на их общий делитель, отличный от единицы, называют сокращением дроби.

Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число.

Это число является наибольшим общим делителем числителя и знаменателя данной дроби.

Возможны следующие формы записи решения примеров на сокращение обыкновенных дробей.

Учащийся вправе выбрать любую форму записи.

 

Примеры. Упростить дроби.

Сократим дробь на 3 (делим числитель на 3;

делим знаменатель на 3).

 

 

Сокращаем дробь на 7.

 

 

 

Выполняем указанные действия в числителе и знаменателе дроби.

Полученную дробь сокращаем на 5.

 

 

Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем.

 

 

Разложим числитель и знаменатель этой дроби на простые множители.

 

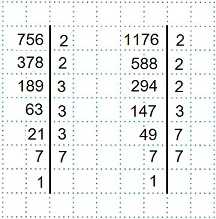Получаем: 756=2²·3³·7 и 1176=2³·3·7².

Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5).

Это произведение общих множителей, взятых с наименьшими показателями.

НОД(756; 1176)=2²·3·7.

 

 

Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7 получаем несократимую дробь 9/14.

А можно было записать разложения числителя и знаменателя  в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь 9/14.

И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2. Сокращаем дробь на 2. Числитель и знаменатель новой дроби — числа 378 и 588 также делятся на 2. Сокращаем дробь на 2. Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел 189 и 294 на 3.

(1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и 294 делятся на 3. Сокращаем дробь на 3.  Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7. Сокращаем дробь на 7 и получаем несократимую дробь 9/14.

• Луч Ох с началом отсчета в точке О,  на котором указаны единичный отрезок и направление, называют координатным лучом.
• Число, соответствующее точке координатного луча, называется координатой этой точки. Например, А(3). Читают: точка А с координатой 3.

Примеры.

1) Отметить на координатном луче точки А(4), В(8), С(12).

Выбираем единичный отрезок — одну клетку.

• Тогда 1 клетка будет соответствовать числу 1;
• 4 клетки от начала отсчета будут соответствовать числу 4;
• 8 клеток — числу 8, а 12 клеток — числу 12.

Читают: точка А с координатой 4. Точка В с координатой 8. Точка С с координатой 12.

 

 

2) Изобразить на координатном луче все правильные дроби со знаменателем, равным 12.

Выбираем единичный отрезок — 12 клеток. Тогда одна клетка будет равна одной двенадцатой доли единичного отрезка, равного 12 клеткам.

Любому числу координатного луча соответствует единственная точка. И если под и над  точкой стоят два числа, то это означает, что эти два числа равны между собой (смотрите тему: «Сокращение обыкновенных дробей»).

 

3) Начертить координатный луч, выбрать единичный отрезок, равный 6 клеткам и отметить точки: А( 1/6), В(2/3), С(1½), D (2¹/₃).

За единичный отрезок мы взяли 6 клеток.

• 1 клетка — это одна шестая часть единичного отрезка, т. е дробь 1/6.
• 2 клетки — две шестые части единичного отрезка или дробь 1/3 (2/6=1/3).
• 3 клетки — три шестые части единичного отрезка или дробь ½ (3/6=½).
• 4 клетки — четыре шестые части единичного отрезка или дробь 2/3 (4/6=2/3).
• 5 клеток — пять шестых частей единичного отрезка или несократимая дробь 5/6.
• 6 клеток — шесть шестых или один единичный отрезок (6/6=1).

Число 1½ означает, что ½ единичного отрезка (3 клетки) следует откладывать не от нуля, а от 1 целой.

Число 2¹/₃ изображаем так: отсчитываем 2 целые единицы (2·6=12 клеток) и еще 2 клетки.

 

4) На координатном луче отметить точки: А(5/8), В(1¾), С(2½).

Смотреть видео в хорошем разрешении на моём канале.

Чтобы выполнить вычитание десятичных дробей, нужно: 1) уравнять количество десятичных знаков в уменьшаемом и вычитаемом; 2) подписать вычитаемое под уменьшаемым так, чтобы запятая оказалась под запятой; 3) выполнить вычитание, не обращая внимания на запятую, и в полученном результате поставить запятую под запятыми уменьшаемого и вычитаемого.

Примеры. Выполнить вычитание десятичных дробей.

1) 24,538-18,292.

Решение. Записали вычитаемое под уменьшаемым так, что запятая оказалась под запятой. Выполнили вычитание, не обращая внимания на запятые и в полученном результате поставили запятую под запятыми в данных дробях.

24,538-18,292=6,246.

 

2) 145,723-98,943.

Решаем аналогично. Получили разность 46,780. Если убрать нуль на конце десятичной дроби, то значение дроби не изменится.

145,723-98,943=46,78.

 

 

3) 18-7,61.

Решение. Уравняем количество знаков после запятых в уменьшаемом и вычитаемом. Подписываем вычитаемое под уменьшаемым так, чтобы запятая оказалась под запятой. Выполняем вычитание, не обращая внимания на запятые, и в полученной разности ставим запятую под запятыми в данных дробях.

18-7,61=10,39.

Чтобы сложить десятичные дроби, нужно: 1) уравнять в этих дробях количество десятичных знаков; 2) записать их друг под другом так, чтобы запятая была записана под запятой; 3) выполнить сложение, не обращая внимания на запятую, и поставить в сумме запятую под запятыми в слагаемых дробях.

Примеры. Сложить десятичные дроби.

1) 0,07+13,23.

Решение. Применим переместительный закон сложения: 0,07+13,23=13,23+0,07 и запишем дроби друг под другом так, чтобы запятая оказалась под запятой. Складываем, не обращая внимания на запятую. В полученной сумме поставим запятую под запятыми в слагаемых. Нуль на конце полученного результата 13,30 можно отбросить.

13,23+0,07=13,3.

 

2) 11,21+9,3.

Решение. Записываем данные дроби друг под другом так, чтобы запятая оказалась под запятой. Уравниваем количество знаков после запятых в слагаемых. Для этого припишем справа нуль к дроби 9,3. Складываем, не обращая внимания на запятые и ставим в сумме запятую под запятыми в слагаемых.

11,23+9,3=20,51.

 

3) Вычислить рациональным способом. 1,245+(0,755+3,02).

Решение. Используем переместительный и сочетательный законы сложения.

1,245+(0,755+3,02)=(1,245+0,755)+3,02=2+3,02=5,02.

Пояснение: у слагаемых 1,245 и 0,755 одинаковое количество знаков после запятых (по три цифры), поэтому, удобно сложить их устно, как складывают целые числа, а затем отделить справа запятой три цифры, как было в слагаемых. Получилось 2,000. Три нуля после запятой отбрасываем, получается число 2. Прибавили 3,02 и получили 5,02.

1,245+(0,755+3,02)=5,02.

 

•  Десятичной дробью называют число, записанное в десятичной системе и имеющее разряды меньше единицы. (3,25; 0,1457 и т. д.)
•  Знаки, стоящие в десятичной дроби после запятой, называют десятичными знаками.
•  Десятичная дробь не изменится, если в конце десятичной дроби приписать или отбросить нули.

Обыкновенную дробь со знаменателем, записанным в виде единицы с последующими нулями, можно записать в виде десятичной дроби.

123,4567 — десятичная дробь. Читают: сто двадцать три целых, четыре тысячи пятьсот шестьдесят семь десятитысячных.

Разряды:

• 1 — сотни;
• 2 — десятки;
• 3 — единицы;
• 4 — десятые;
• 5 — сотые;
• 6 — тысячные;
• 7 — десятитысячные.

4,017 — десятичная дробь. Читают: четыре целые, семнадцать тысячных.

Разряды:

• 4 — единицы;
• 0 — десятые;
• 1 — сотые;
• 7 — тысячные.

Пример 1. Сравнить десятичные дроби 0,893 и 0,9.

Решение.

Уравняем число знаков после запятых, приписав к дроби 0,9 справа два нуля. Сравниваем поразрядно  десятичные дроби 0,893 и 0,900.

0,893<0,900.     Ответ: 0,893<0,9.

Пример 2. Сравнить числа 2/5 и 0,39.

Запишем обыкновенную дробь 2/5 в виде десятичной дроби. Сравниваем 0,4 и 0,39. Припишем к дроби 0,4 справа один нуль и сравним 0,40 и 0,39.

0,40>0,39.     Ответ: 2/5>0,39.

Пример 3. Изобразить на координатном луче десятичные дроби 0,5; 0, 3; 0,9.

Меньшее число будет располагаться на координатном луче левее, а большее — правее.

Так как 0,3<0,5<0,9, то крайним слева будет число 0,3, а крайним справа число 0,9.

Выберем единичный отрезок, равный 10 клеткам.

Одна клетка — это 1/10 единичного отрезка.

Тогда числу 0,3 будут соответствовать три клетки,

числу 0,5 — пять клеток, а числу 0,9 — девять клеток.

 

Страница 2 из 3«123»

www.mathematics-repetition.com

Правила в стихах по курсу математики 5-6 класс

Противоположные числа

1)        Жили на свете близнецы-братья,

Были похожи собой.

Из-за нелепого проклятья

Разделены судьбой.

Братья имели разные знаки,

  С ними по жизни шли,

Если ж случалось им повстречаться

В ноль превращались они.

***

           Два числа лишь знаками

Друг от друга отличные

Называются издавна

Противоположными числами

                

Раскрытие скобок

Много скобок в примерах,

Много скобок в задачах.

Как же нам поступить?

А, раскрыть!

Если увидишь перед скобками плюс,

То скобки опустишь просто.

Если же минус — насторожись

Знаки менять там нужно.

                Подобные слагаемые

      Приведу подобные, переводя буквы на предметы.

Посчитаю, получу верные ответы

(5m+1m=6m)

Пять морковок да одна будет шесть морковок.

(7s-2s=5s)

Семь свеколок минус две будет пять свеколок.

Модуль числа

     -Что такое модуль?- спросите меня.

Я отвечу вам:

-Модуль- расстояние от точки О до точки А.

Помните  друзья!

                 

Умножение и деление обыкновенных дробей

    1.  Кто умножать собрался

Дроби обыкновенные?

Подходи! Расскажу!

Ты числители бери- умножай,

Знаменатели бери-умножай.

Результат получай.

2.   Ведь дробь делить – пустяк,

Делители перевернет ведь всяк,

А дальше действуй, как при умножении,

И результат готов в одно мгновенье.

                 Умножение и деление рациональных чисел

 Умножение, деление — операции трудны.

Нужно и считать, и думать

Где поставить знак какой?

Плюс на минус будет минус,

Минус на минус будет плюс.

Правилом этим воспользуйся ты,  примени.

                 Квадрат и прямоугольник 

1.  Я — квадрат!

Ведь у меня четыре стороны

И все они равны.

Найду периметр свой я быстро,

Вот только сторону умножу на четыре.

2. Я – квадрат!

У меня равны диагонали,

Углы они мне делят пополам

На части равные разбившись.

   2. Я – прямоугольник!

      Ведь у меня четыре стороны,

      Противоположные равны.

      Сложу длину и ширину,

      Умножу сумму на два.

      Периметр свой я получу.

      А если вдруг умножу длину на ширину,

      То площадь я свою найду.

Формула пути

        Как нам вычислить пройденный путь?

Знаем факт и по этой теме!

Ты, дружочек, его не забудь:

Надо скорость умножить на время!

Объем куба

       -Кубик, кубик, где ты был?

-Я объем свой находил!

-И нашел? Сумел? Ура!

-Перемножил три ребра!

Пропорция

1.   Кто с задачами постарается,

Тот не упустит решений.

А пропорцией называется

Равенство отношений.

2.  Возьмём и приведём в пример пропорцию:

Произведение  крайних членов.

Чтоб не обидеть средних членов

Возьмём в пропорции и их.

Когда решим заданье с ними,

Увидим, что они равны.

3.  Крайний член пропорции

Я хочу найти.

Что мне делать? Как мне быть?

Как мне поступить?

Основное свойство применю:

Перемножу средние,

Разделю на крайний,

Крайний член найду.

Обыкновенная дробь

  Каждый может за версту.

Видеть дробную черту.

Над чертой — числитель, знайте,

Под чертой – знаменатель.

Дробь такую, непременно,

Надо звать обыкновенной.

Неизвестный делитель

       Чтобы найти неизвестный делитель,

Вы на делимое сразу взгляните:

Пусть оно фыркает, быстро за дело!

Делим его на частное смело!

Неизвестное делимое

       Пусть неизвестно делимое, дети,

Как же его получить нам в ответе?

Частное быстро за чубчик берите

И умножайте его на делитель.

Основное свойство частного

       И делимое, и делитель

На одно число разделите,

Тогда можете вы надеяться,

Ваше частное не изменится.

Коль делимое и делитель

На одно число вдруг умножатся.

Не волнуйтесь, и в этом случае

Ваше частное не потревожится.

Задачи на дроби

        Дробь от числа хотим найти,

Не надо мам тревожить.

Нам надо данное число

На эту дробь умножить.

Коль число по части вдруг

Отыскать решите,

То на данную вам дробь

Часть ту разделите.    

Сокращение дробей

        Дробь поменьше — и считать полегче.

Если знаменатель,

А за ним числитель

Разделить на общий их делитель,

Дробь мы сократили,

Счёт мы упростили.

НОД

   1.   Делитель есть простой

И наибольший общий,

Который получить

Совсем не сложно, в общем;

Числа натуральные

На простые множители

Разложите старательно,

Подумав, по возможности.

Сравните разложения

И выберите множители

Для чисел одинаковые,

Потом их перемножьте.

А произведение оставшихся сомножителей

И будет искомым

Делителем общим наибольшим.

2.    Умножая дробь на дробь.

Перемножь числители-

Запиши в числителе,

А потом так же точно и со знаменателем.

Десятичные дроби

1.    Чтобы дроби десятичные сравнить,

Вам много и не надобно учится.

Число знаков десятичных уравнять,

К одной из них справа нули приписать,

И, отбросив запятую потом,

Правое с левым сравнить числом.

2.    Чтобы нас вычесть, или сложить,

Вам не следует спешить.

Тут совет мы можем дать:

Друг под другом нас записать.

Запятая чтоб была под запятой,

А складывать надо так,

Как будто нет их ни одной.

А потом обратите внимание,

Что в самом конце, в ответе, её

Просто поставить на место свое.

3.    А вот ещё правило, оно не сложней:

Если в конце десятичных дробей

Нули отбросить или приписать,

Да хоть всю тетрадь нулями исписать!

Дробь, равная данной получится;

Так зачем же тогда мучиться?

4.    Как делить на десятичную дробь? Что вы смотрите кисло?

Мы сейчас это правило вместе поймем.

Вправо сдвинь запятую в двух числах настолько,

Сколько цифр у делителя за запятой.

А теперь и деленье возможно, поскольку

Это нацело делать есть способ простой.

5.   Милейшие дроби, к тому ж десятичные,

Взобрались на крышу по шаткой трубе.

— Мы здесь посидим, ведь погода отличная,

И кое о чём расскажу я тебе.

Ты знаешь, как нас перемножить, дражайшая?

Умножь, как натуральные числа, а дальше я,

Чтоб лучше запомнилось, песню спою:

Где же будет запятая?

Вот задача непростая!

Мы решим её, однако,

Показав высокий класс.

Отсчитаем столько знаков,

Сколько вместе есть у нас!

Сложение рациональных чисел

1.    Если уж захочется очень вам сложить

Числа отрицательные, нечего тужить:

Надо сумму модулей быстренько узнать

К ней потом знак «минус» взять да приписать.

2.   Если числа с разными знаками дадут,

Чтоб найти их сумму, все мы тут как тут,

Больший модуль быстро очень выбираем

Из него мы меньший модуль вычитаем,

Самое главное – знак не позабыть!

Вот какой поставить? – мы хотим спросить.

Вам секрет откроем, проще дела нет

Знак, где модуль больше, запиши в ответ.

3.   Хочу сложить я отрицательные числа,

Но не уверен, что верный получу ответ.

Пусть эти числа – долг,

Сложив долги, я больший получу должок,

А значит, минус получу в ответе.

Всё сходится, ура! Нашёл я верный путь решения.

4.   Правило сложения чисел отрицательных

И чисел положительных очень трудно.

Но запомнить его можно легко:

Ты должен мне — число отрицательное,

Деньги твои —  число положительное.

Сложить ты можешь и узнать, с деньгами ты,

Или они мои.

Решение уравнений

1.  При решении уравнения

Если в части одной,

Безразлично в какой

Встретится член отрицательный,

Мы к обеим частям

Равный член придадим,

Только  со знаком другим,

И найдем результат положительный.

2.  При решении уравнений

Правило такое применю:

Части обе на число разделю,

На любое, но не равное нулю.

3.  Стали числа танцевать:

2 плюс 3, конечно – 5!

3 плюс 2 – тоже 5

Получается опять…

3 плюс 5 равно восьми.

Получилось 5 плюс 3 –

8, что не говори!

Водят числа круглый год

Вокруг плюса хоровод:

Кружатся, стараются –

А сумма не меняется!

4.  Легко запомнить, друзья,

Признак делимости на 2.

Делю без остатка на 2

Лишь натуральные чётные числа.

Объём параллелепипеда

       Жил да был Параллелепипед

Парень не простой, прямоугольный, деловой.

С высотой, длиной и шириной.

Захотел найти объём он свой.

Перемножил измеренья, больше ничего.

Получил объём свой, вот и всё.

Перпендикуляр

       Однажды отрезок гулял по кривой,

От точки хотел он дойти до прямой.

А выбрать путь не знал какой,

Но хотел короткий и простой.

Чертёжный угольник ему помог.

Он встал на прямую и точку завлёк.

Отрезок увидел короткий свой путь.

– Перпендикуляром ты будь!

Среднее арифметическое

        Коля, Оля, Света и Макар

Делили общий гонорар.

Каждый сумму иметь хотел свою.

Коля предложил среднее арифметическое определить:

Все суммы сложить

И на четыре поделить.

Порядок выполнения действий

        При решении примеров

Расставь порядок действий.

Умножь или раздели – на первом месте –

Сильные действия.

Займись сложением потом или вычитанием –

Слабые действия.

Ответ получишь –

Запиши на своём месте.

Окружность и круг

1.    Меня зовут окружность,

Горожусь я нужностью.

Все до единой точки мои

От центра равноудалены.

Про радиус запомни скорей-

Это отрезок от центра до точки моей.

Всегда диаметр со мной,

Знай, это радиус двойной.

2.   Но что всего важней: диаметр мой (окружности)

Почти в 3 раза с одной седьмой

Меня короче.  Это отношение

Окружности к диаметру за двести лет

До нашей эры вывел Архимед

Что справедливо это заключение,

Ни в ком не может вызвать сомнения.

3.    Это я знаю и помню прекрасно:

Пи многие знаки мне лишни, напрасны

(3,14159265358…)

4.   У круга есть одна подруга,

Знакома всем её наружность.

Она идет по краю круга

И называется – окружность.

5.   Вы мне (кругу) должны на слово верить:

Площадь круга можно мерить.

Скажу собравшимся гостям:

Дели окружность пополам,

И множь на радиус. Тогда, как говорится,

Ты площадь выразишь в квадратных единицах.

6.   Чтоб  площадь круга нам найти

Не надо мучится часами.

Ты r в квадратик возведи

И умножь  его на  π,

А  π  знает каждый

Равно приближенно три.

7.     Гордый Рим трубил победу

Над твердыней Сиракуз;

Но трудами Архимеда

Много больше я горжусь.

Надо нынче нам собраться,

Оказать старинке честь.

Чтобы нам не ошибаться,

Чтоб  окружность верно счесть.

Надо только постараться

И запомнить всё как есть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть!

Треугольник

1.    Зовусь я треугольник,

Со мной хлопот не оберётся школьник…

По-разному  всегда я называюсь,

Когда углы иль стороны даны:

С одним тупым углом — тупоугольный

Коль острых два, а третий — прям – прямоугольный.

Бывало я равносторонний,

Когда мои все стороны равны.

Когда все разные даны,

То я зовусь разносторонним.

И если, наконец, равны две стороны,

То равнобедренным я называюсь.

2.   Медиана — отрезок не простой,

А в треугольнике вершину,

Соединившей с серединой,

Той, что напротив, стороны.

3.    Медиана — это обезьяна,

Которая бегает по сторонам

И делит

Сторону пополам.

4.    Биссектриса — это крыса,

Она шныряет по углам

И делит их пополам.

Углы

1.    Лишь только мы точку возьмём на прямой,

Тотчас два луча от неё побежали.

Развёрнутый угол ужель не узнали?

Напомним: его половина — прямой.

А градус? Нам выучить проще простого:

Одна девяностая часть от прямого.

2.    Углы запомнить очень просто:

Угол меньше девяносто зовется острым.

Тот, что равен девяносто, называется прямым.

А развернутый, среди прочих,

Самым выглядит большим,

Ста восьмидесяти равна у него величина.

Свойство 0

  1.   Ах, я толь, ах, я ноль,

Очень этим горжусь,

И злодействовать очень люблю.

Кто забыл мою власть,

А потом ещё и разделю,

И опять себя получу.

2.    Коль нуль к числу ты прибавляешь,

Иль отнимаешь от него,

В ответе тотчас получаешь

Опять — то самое число.

Попав как множитель средь чисел,

Он сводит мигом всех на нет.

И потому в произведенье

Один за всех несёт ответ.

А относительно деления

Во-первых, нужно помнить то,

Что уж давно  в научном мире

Делить на нуль запрещено.

Проценты

       Мой дружок меня спросил про проценты,

Как проценты записать в виде дроби.

Я ответил: «Очень просто,

Раздели число на 100, получи что нужно»

Сравнение дробей с одинаковыми числителями

1.   При сравнении дробей с одинаковыми числителями

Ошибиться не сумей.

Больше та подруга дробь,

У которой меньший знаменатель.

2.    Два числа-близнеца

Отличаются на 2

Да ещё они простые,

А не составные.

Прямопропорциональная зависимость

      У Макса  было две величины.

Одну решил он увеличить.

И увеличил так отлично,

Что стали равными они.

Решил Максим одну величину

Уменьшить раза в два.

Другая, вдруг, не стала думать-

Уменьшилась сама.

Вот и ходят друг за дружкой

Прямопропорциональные подружки.

Прямая

       Отвечайте сей же час:

Пересечься сколько раз

Две различные прямые

Могут в плоскости у нас?

Если речь о двух прямых,

Точка общая у них

Может лишь одна существовать.

Или вовсе нет. Вот и правильный ответ.

И ещё вопрос вам всем:

Ну, а если нет совсем

Общей точки у прямых?

Как же назовём мы их?

Если прямые не пересекаются,

Они параллельными называют.

 

obrazbase.ru