Графики важнейших функций и их преобразования — Математика — Теория, тесты, формулы и задачи
На этой странице представлены графики важнейших функций, изучаемых в школьном курсе математики. Также представлены примеры преобразования этих графиков в различных типичных ситуациях (рассмотрены случаи когда графики смешаются вдоль осей, симметрично отражаются относительно различных осей). Представлен также вид некоторых графиков функций с модулями. Знание того, как выглядят графики основных математических функций, а также того, как они преобразовываются в различных ситуациях, может очень помочь при решении различных сложных задач на экзаменах.
Изучать графики основных функций и их преобразования онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (адрес электронной почты и ссылки в социальных сетях здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
educon.by
ФУНКЦИИ И ГРАФИКИ – Репетитор по математике
Решим задачу: Первичная информация разделяется по серверам и №1 и №2 и обрабатывается на них. С сервера №1 при объеме Гб входящей в него информации выходит , а с сервера №2 при объеме Гб входящей в него информации выходит Гб обработанной информации; . Каков наибольший объем выходящей информации при общем объеме входящей информации 3364 Гб?
Итак, мы имеем два преобразователя, в которых подаем на вход некоторый объем данных, и получаем на выходе некоторый объем данных. Другими словами, мы имеем дело с числовой функцией:
То, что мы подаем на вход преобразователя — аргумент функции, или независимая переменная, а то, что получается на выходе — значение функции. Выразим значение функции через значение аргумента. Пусть , тогда . Получаем:
По условию задачи информация разделяется по серверам и №1 и №2, причем общий объеме входящей информации 3364 Гб. Пусть на первый сервер попадает Гб информации, тогда на второй попадает Гб:
Тогда весь объем информации, выходящей с обоих серверов равен
По условию задачи нужно найти наибольший объем выходящей информации. Введем функцию .
По условию задачи , следовательно . Отсюда
Найдем наибольшее значение функции на отрезке [].
Будем следовать стандартному алгоритму.
1. Найдем производную функции
2. Найдем нули производной.
Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен.
. Легко проверить, что это значение принадлежит отрезку [].
3. Определим знаки производной на отрезке []. Для этого найдем ее значение в правом конце отрезка:
Получаем, что справа от точки производная меньше нуля. Получили, что в точке производная функции меняет знак с «+» на «-«, следовательно это точка максимума функции, и функция принимает в этой точке наибольшее значение на отрезке [].
Найдем значение функции в точке .
Ответ: 1682
ege-ok.ru
Проект по математике «Графики улыбаются»
Введение:
Данная исследовательская работа позволит углубить мои знания по построению графиков линейной, квадратичной функции, а также раскроет новые знания о геометрических преобразованиях графиков, выходящие за рамки школьной программы.
Задачи:
Раскрыть возможности простейших преобразований для построения довольно сложных графиков;
Формировать умения по построению графиков с модулем;
Закрепить умение строить графики кусочно-элементарных функций;
Освоить метод линейного сплайна для построения графиков, содержащих модуль, научиться применять его в простых ситуациях.
Оглавление:
Титульный лист
Оглавление
Основная часть
Заключение
Литература
Приложения
На практике мы часто встречаемся с зависимостями между различными величинами не только в математике, но и в других сферах деятельности. С помощью графиков наиболее естественно отражаются функциональные зависимости одних величин от других.
Графический способ — один из самых удобных и наглядных способов представления и анализа информации.
Например, метеорологическая служба фиксирует изменения температуры, строя с помощью термографа (специального прибора, отмечающего температуру на движущейся ленте или на экране дисплея) график температуры.
Используя показания сейсмографов (приборов, непрерывно фиксирующих колебания почвы и строящих специальные графики-сейсмограммы) геологи могут предсказывать приближение землетрясения или цунами.
Врачи выявляют болезни сердца, изучая графики, полученные с помощью кардиографа, их называют кардиограммами.
Широко применяются графики в экономике, в частности кривая спроса и предложения, линия производственных возможностей.
Я поставила перед собой следующую проблему: как, используя графики некоторых функций, с помощью простейших преобразований (осевой и центральной симметрии, параллельного переноса и т.п.) научиться строить графики более сложных функций. Так как квадратичная функция дает больше возможностей для «накручивания» нескольких преобразований, поэтому в моих проектах в большей мере присутствуют графики именно квадратичной функции, но вместе с тем я брала также преобразования линейной функции.
Я повторила известные мне правила геометрических преобразований функций, построила несколько более сложных графиков.(см. приложение лист). Начальными графиками являлись прямая у =х и парабола у =х².
Правило1. График функции у=f(х)+к получается параллельным переносом графика f(х) в положительном направлении оси Ох на к единиц при к>0 и в отрицательном направлении этой оси на |к | при к<0
Правило2. График функции аf(х) получается растяжением графика f(х) вдоль оси Оу в а раз при а >1 и сжатием вдоль этой оси в 1/а раз при
0 < а <1.
Правило3. График функции у = -f(х)получается симметричным отображением графика f(х) относительно оси Ох.
Правило4. График функции у = f(-х)получается симметричным отображением графика f(х) относительно оси Оу.
Правило5. График функции у=f(х+с) получается параллельным переносом графика f(х) в положительном направлении оси Ох на |с| единиц при с<0 и в отрицательном направлении этой оси на |с| при с > 0.
Затем, закрепив свои знания о геометрических преобразованиях, я познакомилась с правилами построения графиков, содержащих модуль и научилась применять их к построению графиков с модулем.
Правило6. График функции у= | f(х) | получается из графика функции
у= f(х) так: часть графика у= f(х), лежащая над осью Ох сохраняется, часть его , лежащая под осью Ох, отображается симметрично относительно оси Ох.
Правило7. График функции у= f(| х | ) получается из графика функции
у= f(х) так: при х ≥0 график у= f(х) сохраняется, и эта же часть графика симметрично отображается относительно оси Оу.
Правило 8. График зависимости | у | = f(х ) получается из графика
у= f(х) , если все точки , для которых f(х) ≥0 сохраняются и они же переносятся симметрично относительно оси абцисс.
Правда, то, что в итоге получается, нельзя назвать графиком некоторой функции. Так как для того, чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси Оу, пересекалась с указанным графиком не более чем в одной точке. Но поскольку мой проект называется «Графики улыбаются», в результате получаются оригинальные картинки .(см приложение лист)
Одно из основных назначений функций- описание реальных процессов, происходящих в природе. Но издавна ученые- философы и естествоиспытатели выделяли два типа протекания этих процессов: постепенное(непрерывное) и скачкообразное. Так, при падении тела на землю сначала происходит непрерывное нарастание скорости движения, а в момент столкновения с поверхностью земли скорость изменяется скачкообразно, становясь равной нулю или меняя направление(знак) при «отскоке» тела от земли.
Переход от одной формулы к другой при описании реальных явлений обычно связан с нарушениями, возмущениями течения процесса в отдельные моменты. Со скачкообразным изменением тех или иных его характеристик. Такой переход иногда может сохранить непрерывность изменения величины,но вызвать излом ее графика. В последнем случае скачком меняется не величина. А скорость ее изменения.
Но раз есть разрывные процессы, то необходимы и средства для их описаний. С этой целью вводятся в действие функции, имеющие разрывы. Таковой является кусочно-заданная функция.
Используя полученные знания, я научилась с помощью простейших геометрических преобразований строить графики кусочно- заданных функций. (см приложение лист)
Подобная сложная конфигурация приводит к мысли, что графиками можно рисовать. Правда, фигуру в координатной плоскости уже нельзя будет называть графиком функции, но зато отдельные ее части этому определению соответствуют.
Итогом моей работы явились презентации следующих проектов : Лицо», «Человечек», «Цыпленок». (см. приложение лист)
При построении графиков можно пофантазировать и достроить рисунок. Можно придумать свои формулы, чтобы картинка получилась оригинальной. Так я . рисуя цыпленка, дорисовала некоторые детали. В результате получился симпатичный цыпленок. Эта картинка построена с помощью 3 графиков, каждый из которых получен из графика у =х² и с помощью простейших геометрических преобразований.
Проект «Лицо» представляет собой изображение лица человека, которое построено с помощью 12 сложных графиков. Для всех их исходным также является графики у =х² и у=х. Ход построения изложен ниже.
Проект «Человечек»построен из 11 графиков. (см приложение лист)В основном рисунок построен с помощью графиков, которые содержат сразу несколько модулей. Начальными графиками я брала у=х, у =х², х² +у² =r².
Заключение:
Итогом моей исследовательской работы явились проекты «Графики улыбаются»: картинки «Лицо», «Человечек», «Цыпленок». Я научилась применять метод геометрических преобразований на примере линейной функции и обратной пропорциональности, строить графики, содержащие модуль, строить графики кусочно — заданных формул.. Я сделала вывод, что графиками можно рисовать. И мои проекты это иллюстрируют..
Геометрические преобразования графиков, построение кусочно-заданной функции, графики, содержащие переменную под знаком модуля, позволили мне передать всю красоту математики.
Литература:
Факультативный курс по математике 7-9 класс. Учебное пособие для средней школы М. Просвещение, 1991.
Математика 8-9 классы Сборник элективных курсов М.Е.Козина .Волгоград.
Построение картинки «Лицо»
У=1/4 х ² -5 -6≤ х ≤ 6
Сжатие вдоль оси Оу
Параллельный перенос графика вдоль оси Оу на 5 единиц в отрицательном направлении
У=1/4 х ² -3 -2≤ х ≤ 2
Сжатие вдоль оси Оу в ¼ раза
Параллельный перенос вдоль оси Оу на 3 ед. в отрицательном направлении
У=-х ² +2 -1≤ х ≤ 1
У=1/3(х+3) ² +2 -5≤ х ≤ 1
Сжатие вдоль оси Ох в 1/3 раза
Сдвиг влево на 3 единицы
Сдвиг вверх на 2 единицы
У=1/5(х-3) ² +2 1≤ х ≤ 5
Сжатие вдоль оси Оу в 1/3 раза
Сдвиг влево на 3 единицы
Сдвиг вверх на 2 единицы
У=1/5(х+3) ² +4 -5≤ х ≤ -1
Сдвиг влево на 3 единицы
Сжатие вдоль оси Оу в 1/5 раза
Сдвиг вверх на 4 единицы
У=-1/5(х-3) ² +4
Симметрия относительно оси абцисс 1≤ х ≤ 5
Сдвиг вправо на 3 единицы
Сжатие вдоль оси Оу в 1/5 раза
Сдвиг вверх на 4 единицы
(х+3) ² +(у-3) ² =1
(х-3) ² +(у-3) ² =1
Окружность(3,3) радиус=1
У=-1/5(х+3) ² +5
Симметрия относительно оси абцисс -5≤ х ≤ -1
Сдвиг влево на 3 единицы
Сжатие вдоль оси Оу в 1/5 раза
Сдвиг вверх на 5 единиц
У=-1/5(х-3) ² +5
Симметрия относительно оси абцисс -1≤ х ≤ 5
Сдвиг вправо на 3 единицы
Сжатие вдоль оси Оу в 1/5 раза
Сдвиг вверх на 5 единиц
У=-15х ² +10 -6≤ х ≤ 6
Симметрия относительно оси абцисс
Растяжение вдоль оси Оу в 15 раз
Сдвиг вверх на 10 единиц.
Построение картинки «Человечек»
У²+х ² =36 окружность (0,0) радиус=6
оси 0х
сдвиг вниз на 4 единицы
прямая || оси 0х
симметрия точек, для
которых у≥0
относительно оси Ох
прямая || оси Оу
симметрия относительно
Оу
сдвиг вверх на 14 ед.
симметрия точек, для
которых у ≥0 относительно оси Ох
сдвиг вверх на 14 единиц
симметрия точек , для которых у≥0
относительно оси Ох
симметрия точек , для которых
у≥0
относительно оси Ох
симметрия
относительно оси абцисс
сдвиг вверх на 10 единиц
прямая || оси Ох
Построение картинки «Цыпленок»
У=1/5х²-6 -5≤ х ≤ 5
У=3-(х+3)² -1≤ х ≤ -5
Сдвиг влево на 3 единицы
Симметрия относительно оси Ох
Сдвиг вверх на 3 единицы
У=1/2(х-1) ² — 5 — 3/2 ≤ х ≤ 7/2
Сжатие вдоль оси Ох в ½ раза
Сдвиг вправо на 1 единицу
Сдвиг вниз на 5 единиц
infourok.ru
Урок по математике «Функции. Графики. Свойства»
«ФУНКЦИИ. ГРАФИКИ. СВОЙСТВА»
Цели урока:
систематизировать знания учащихся по теме «Функции. Графики. Свойства»;
закрепить умения определять функции по заданным формулам;
закрепить умения находить соответствия данных графиков функций с формулами;
закрепить умения учащихся выполнять построение графиков различных функций.
развивать логическое мышление.
Оборудование:
экран;
компьютер;
мультимедийный проектор;
приложение к уроку: ( Презентация) – на электронном носителе;
Ход урока:
Оргмомент. Сообщение темы и целей урока. Начало показа слайдов.
Актуализация знаний.
Ответить на вопросы:
Какие из данных графиков являются графиками каких – либо функций? (Слайд)
Дайте определение функции.
Каковы способы задания функции?
Функции заданы формулами. Назовите формулы, задающие линейную функцию (Слайд); функцию прямой пропорциональности (Слайд); функцию обратной пропорциональности (Слайд); квадратичную функцию (Слайд).
Что называется графиком функции?
Выберите описание каждой математической модели (Слайд).
Найдите соответствия графиков линейных функций заданным формулам (Слайд). Какой график является графиком прямой пропорциональности?
9) Найдите соответствия графиков функций обратной пропорциональности
заданным формулам (Слайд).
10) Найдите соответствия графиков квадратичной функций заданным
формулам (Слайд).
Повторение.
На доске изображены графики функций:
В процессе повторения свойств функций ученики отмечают их на доске для
данных графиков.
1) Область определения и область значения функции (Слайд).
2) Монотонность функции (Слайд).
3) Ограниченность функции. Наибольшее и наименьшее значение функции
(Слайд).
4) Непрерывность функции (Слайд).
5) Выпуклость функции (Слайд).
4. Прочитать график кусочной функции:
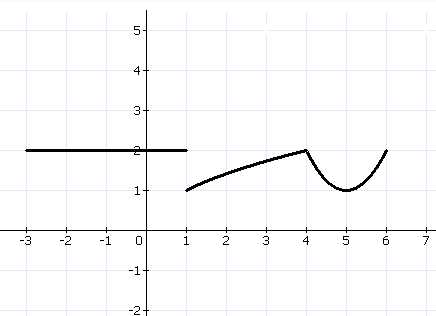
Самостоятельно с взаимопроверкой.
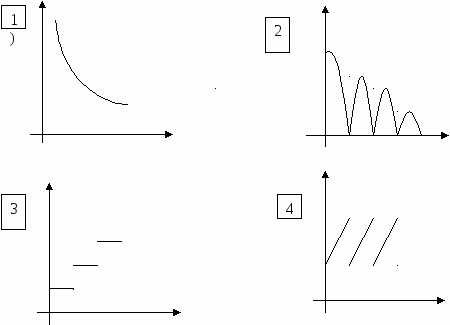
5. Сопоставить жизненную ситуацию с графиком функции:
а) Человек периодически стрижёт волосы, которые растут на голове.
б) Через каждый час на склад сдают новые детали.
в) Поднятый мяч выпускают из рук.
г) Процесс сушки яблок.
6. Построить и прочитать график кусочной функции: (Слайды)
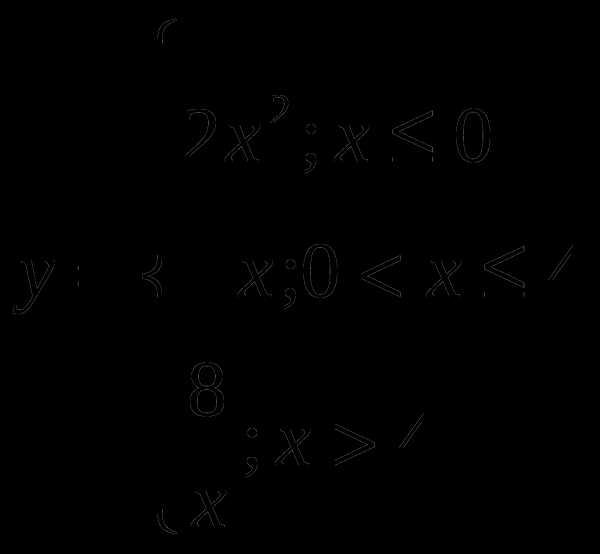
Самостоятельно с проверкой.
6. Домашнее задание.
1. Подобрать пословицы, которые можно изобразить в виде графика функции
2. Построить и прочитать график функции:
7. Итоги урока.
(раздаточный материал)
Тема: «ФУНКЦИИ. ГРАФИКИ. СВОЙСТВА»
1. Заполнить таблицу:
Д(у)
Е(у)
Монотонность
Ограни чен ность
Наиб. и наим. значе ние функ ции
Непре рыв ность
Выпуклость
2. Прочитать график:

3. Сопоставить жизненную ситуацию с графиком функции:
а) Человек периодически стрижёт волосы, которые растут на голове.
б) Через каждый час на склад сдают новые детали.
в) Поднятый мяч выпускают из рук.
г) Процесс сушки яблок.
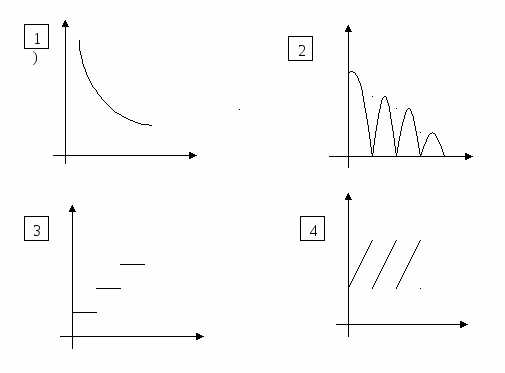
4. Построить и прочитать график кусочной функции:
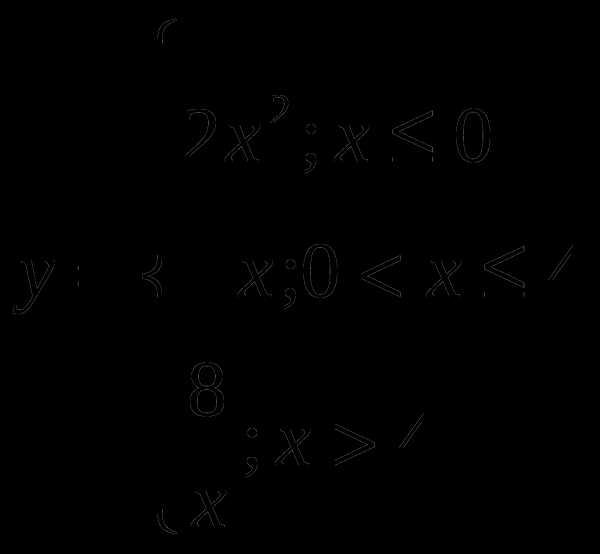
5. Подобрать пословицы, которые можно изобразить в виде графика функции
infourok.ru
