| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Деление дробей — как делить дроби 🤔
Поможем понять и полюбить математику
Начать учиться
197.
5K
Дроби — тема в математике, которую точно нельзя пропустить. Ведь мы сталкиваемся с ними почти в каждой сфере жизни: музыка, медицина, строительство. В этой статье обсудим деление.
Понятие дроби
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b.
Существует два формата записи:
обыкновенный вид — 1/2 или a/b,
десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — .
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Основные свойства дроби
1. Дробь не имеет значения, при условии, если знаменатель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Две дроби a/b и c/d называются равными, если a * d = b * c.
4.
Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление дробных чисел
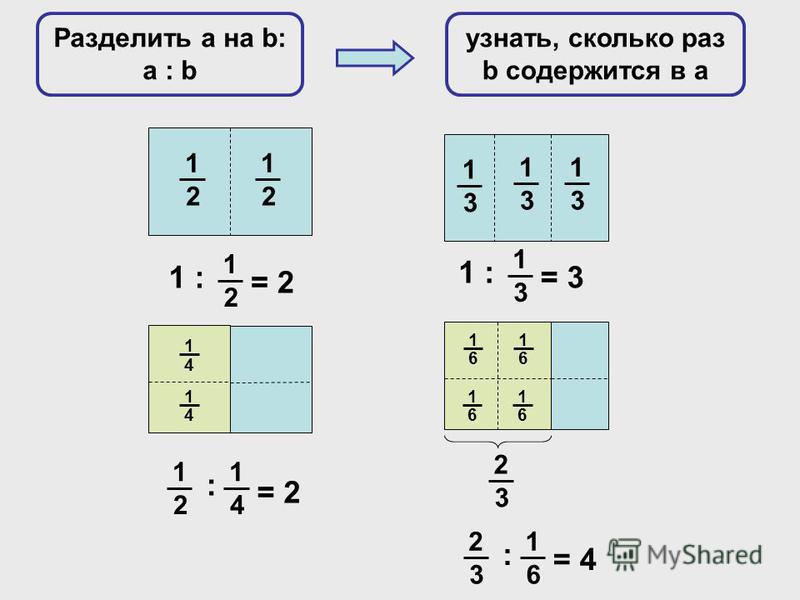
Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.
Свойства деления:
При делении на единицу получится такое же число: a : 1 = a.
На ноль делить нельзя.
При делении нуля на что-либо получится ноль: 0 : a = 0.
При делении числа на само себя получится единица: a : a = 1.
При деления суммы на какое-либо число, можно разделить на него каждое слагаемое и сложить полученные результаты: (a + b) : c = a : c + b : c.
При делении разности на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе: (a — b) : c = a : c — b : c.
При делении произведения двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель: (a * b) : c = (a : c) · b = a * (b : c).
Деление обыкновенных дробей
Как делить дробь на дробь? Выполняем следующую последовательность действий:
числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам не важно, одинаковые знаменатели или нет.
Деление дроби на натуральное число
Для деления дроби на натуральное число нужно:
представить данный делитель в виде неправильной дроби, где числитель равен этому числу, а знаменатель единица;
произвести деление по предыдущему правилу.
Деление натурального числа на дробь
Чтобы поделить натуральное число на обыкновенную дробь нужно:
делимое записать в виде дроби;
умножить полученную дробь на дробь, обратную делителю, воспользовавшись алгоритмом, который мы уже разобрали выше.
Деление на смешанное число
Для деления смешанных чисел необходимо:
представить числа в виде неправильных дробей
выполнить деление с полученными дробями.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
187.5K
Сложение дробей: теория и практика
К следующей статье
159.1K
Вычитание дробей
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.
е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс | 0046 | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | звездочка | умножение | 2/3 * 3/4 9 | знак умножения | умножение | 2 /3 × 5/6 |
| : | знак деления | деление | 1/2 : 3 |
| 4 деления 4 деления 6 | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
больше задач по математике 8 Сколько 1/3 разделить на 2 (Вычислить 1/3 ÷ 2?)Итак, вы хотите разделить дробь 1/3 на целое число 2, правильно ? Вы находитесь в правильном месте. В этом простом пошаговом руководстве мы покажем вам, что именно вам нужно сделать, чтобы разделить любую дробь на целое число (это очень просто). Продолжайте читать, чтобы узнать! Если вы уже знакомились с пошаговыми руководствами наших фракций, то знаете, что мы всегда начинаем шоу с краткого обзора для детей. Число над разделительной чертой является числителем, а число под чертой — знаменателем. Простые вещи, но иногда мы все можем стать немного забывчивыми! Чтобы визуализировать вопрос, который мы пытаемся решить, давайте поставим 1/3 и 2 рядом, чтобы было легче видеть: 1 / 3 ÷ 2 Вот невероятно простой способ вычислить, чему равно 1/3, деленное на 2. 1 / 3 х 2 «=» 1 / 6 Разве можно просто разделить дробь на целое число? Ага. Не хочу вас разочаровывать, но это может быть самая простая проблема, которую вам приходилось решать за весь день! В некоторых случаях новую дробь, которую мы получаем после выполнения расчета, можно еще упростить до меньших членов, но в этом случае дробь уже находится в самой низкой форме. Готово! Теперь вы точно знаете, как вычислить деление 1/3 на 2. Надеюсь, вы поняли этот процесс и можете использовать те же методы для деления других дробей на целые числа. Хотите быстро научиться или освежить в памяти, как делить дроби на целые числа, посмотрите это быстрое и информативное видео прямо сейчас! Преобразование 1/3, деленной на 2, в десятичное число Вот небольшой бонусный расчет, который поможет вам легко определить десятичный формат дроби, которую мы рассчитали. 1 / 6 «=» 0.1667 Процитируйте, дайте ссылку или ссылку на эту страницуЕсли вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
|
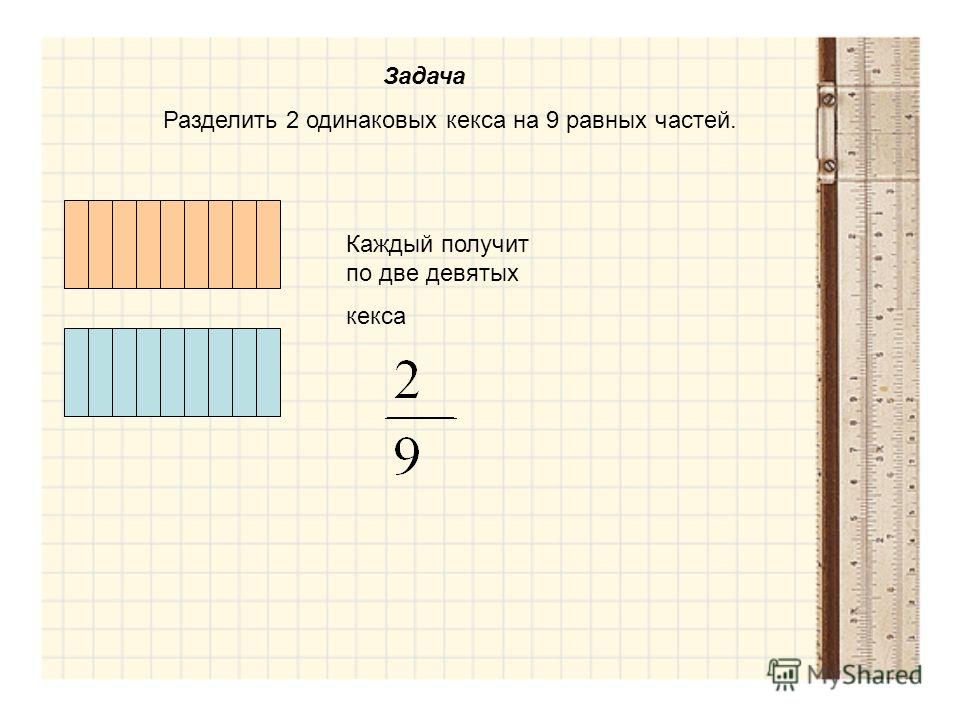
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
Шесть учеников приносят обед в школу. Остальные обедают в столовой. Проще говоря, какая часть студентов обедает в столовой?
1/6 рядов — морковь. Остальное петрушка. Сколько рядов засажено петрушкой?
Все, что нам нужно сделать здесь, это оставить числитель точно таким же (1) и умножить знаменатель на целое число:
Получив окончательную дробь, просто разделите числитель на знаменатель, чтобы получить ответ в десятичной форме: