Степень с целым показателем
Степень с целым показателем — это степень, показателем которой является любое целое число.
В прошлом уроке мы изучили степень с натуральным показателем. Этот вид степени тоже является степенью с целым показателем, поскольку натуральные числа относятся к целым числам.
Также, мы рассмотрели степень, показателем которой является 0. Этот вид степени тоже является степенью с целым показателем, поскольку 0 относится к целым числам.
Рассмотрим ещё один вид степени с целым показателем, а именно показателем которой является целое отрицательное число. Выглядят эти степени так:
2−2, 10−7, a−8
В дальнейшем любую степень с натуральным, нулевым или целым отрицательным показателем, мы будем называть степенью с целым показателем.
Правило вычисления
Рассмотрим следующую последовательность степеней:
20, 21, 22, 23, 24, 25
Первая степень в этой последовательности это степень 20.
Предыдущая степень с целым показателем будет уже с отрицательным показателем и выглядеть как 2−1.
2−1, 20, 21, 22, 23, 24, 25
А предыдущая степень с целым показателем, которая располагается до 2−1, будет степень 2−2
2−2, 2−1, 20, 21, 22, 23, 24, 25
Продолжим эту последовательность в сторону степеней с целыми отрицательными показателями:
2−5, 2−4, 2−3, 2−2, 2−1, 20, 21, 22, 23, 24, 25
Теперь попробуем вычислить эти степени. Степени с натуральными показателями и степень, показателем которой является 0, вычисляются легко:
А как вычислить степени с отрицательными показателями? Для начала немного отойдём от темы и затронем несколько закономерностей.
В отрицательную степень число возводится немного иначе. Следует понимать, что если при возведении в положительную степень число увеличивается, то при возведении в отрицательную степень это число наоборот уменьшается.
Если мы возьмём какое-нибудь число n, и начнём последовательно увеличивать его степень, то получим последовательность чисел, в которой каждое число меньше следующего в n раз.
Например, возьмём число 2. Начиная с нуля будем последовательно увеличивать его показатель:
20, 21, 22, 23, 24, 25
Вычислим эти степени:
1, 2, 4, 8, 16, 32
Получили последовательность чисел, в которой каждое число меньше следующего числа в 2 раза. Тогда логично предположить, что число, располагающееся до единицы, будет в два раза меньше единицы. Его можно получить, если 1 разделить на 2
Вернёмся к нашей исходной последовательности, где мы вычисляли степени. Получается, что степень 2−1 мы вычислили.
Она равна рациональному числу
Предыдущее за числом должно быть в два раза меньше, чем . Чтобы его получить разделим на 2
Получили . Это значение степени 2−2
Продолжая деление на 2 можно получить значения остальных степеней с целыми отрицательными показателями:
Заметим, что в данной последовательности значения степеней с отрицательными показателями являются обратными числами к значениям степеней с натуральными показателями:
К примеру, значение степени в 22 есть число 4. А значение степени 2−2 есть число . Числа 4 и являются обратными друг другу. А степени 22 и 2−2 отличаются только тем, что у них противоположные показатели.
Можно сделать вывод, что для вычисления степени с отрицательным показателем, нужно записать дробь, в числителе которой единица, а в знаменателе та же самая степень, но с противоположным показателем. Покажем это на примере степени 2−2
Вычислим степень, находящуюся в знаменателе:
Таким образом, чтобы вычислить степень вида a−n можно воспользоваться следующим правилом:
Данное правило можно доказать, используя правило деления степеней с одинаковыми основаниями.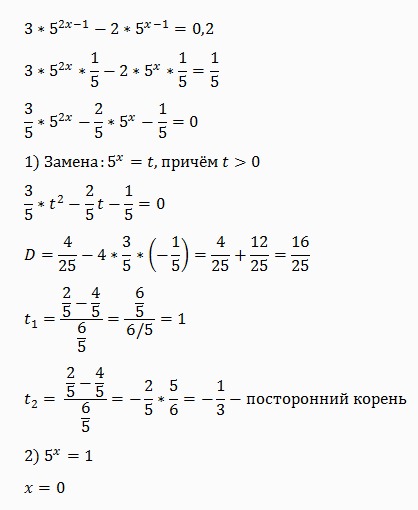
Допустим, потребовалось вычислить выражение 23 : 25. Запишем это деление в виде дроби
Воспользуемся правилом деления степеней с одинаковыми основаниями:
Получили степень с отрицательным показателем 2−2. Ранее мы выяснили, что её значение равно . Чтобы убедиться в этом, попробуем вычислить выражение как обычно, не используя правило деления степеней:
Получили рациональное число . Сократим его на 8. Тогда получим
Пример 2. Найти значение выражения 9−2
Воспользуемся правилом вычисления степени с целым отрицательным показателем:
Пример 3. Найти значение выражения 3−3
Следует упомянуть, что правило работает только тогда, когда a ≠ 0.
Действительно, если a будет равным нулю, то в знаменателе получим 0, а на нуль делить нельзя.
Пример 4. Найти значение выражения
Пример 5.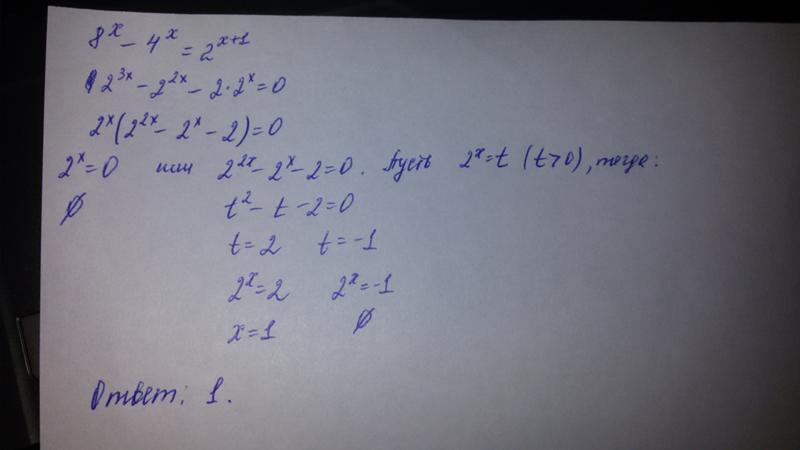
Найти значение выражения
При возведении обыкновенных дробей в отрицательную степень, можно пользоваться формулой . Решим предыдущие два примера с помощью этой формулы:
Желательно уметь возводить обыкновенную дробь в отрицательную степень как с помощью формулы, так и без неё.
Тождественные преобразования
Все тождественные преобразования, которые мы рассматривали при изучении степени с натуральным показателем, сохраняются и для степеней с целыми отрицательными показателями.
Например, чтобы представить выражение 2−1 × 2−3 в виде степени, можно воспользоваться основным свойством степени:
2−1 × 2−3 = 2−1 + (−3) = 2−4
Пример 2. Найти значение выражения 5−15 × 516
Воспользуемся основным свойством степени:
5−15 × 516 = 5−15 + 16 = 51 = 5
или:
Видим, что первый вариант решения намного проще и удобнее.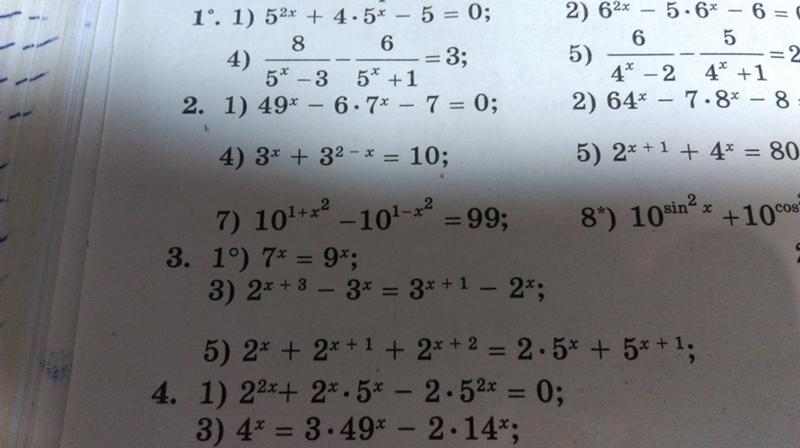
Пример 3. Найти значение выражения (10−4)−1
Воспользуемся правилом возведения степени в степень:
(10−4)−1 = 10−4 × (−1) = 104 = 10000
Пример 4. Найти значение выражения
Представим число основание 10 в виде произведения 2 × 5. Тогда числитель примет вид (2 × 5)−6
В числителе применим правило возведения в степень произведения:
Сократим получившуюся дробь на 5−6
Вычислим степень 2−6
Поднятие степени из знаменателя в числитель и наоборот
Если знаменатель дробного выражения содержит степень, то данную степень можно поднять в числитель, изменив знак показателя этой степени на противоположный. Значение выражения при этом не меняется. Данное преобразование иногда используется при упрощении выражений.
Рассмотрим следующее равенство:
Данное равенство является верным, поскольку выражение равно 20, а любое число в нулевой степени есть единица.
Попробуем поднять степень 22 из знаменателя в числитель, изменив знак показателя этой степени на противоположный. При этом, поднятую степень и ту степень, которая располагалась в числителе, соединим знаком умножения:
Получили выражение 22 × 2−2. Чтобы его вычислить, воспользуемся основным свойством степени:
22 × 2−2 = 22 + (−2) = 20 = 1
Получился тот же результат, что и раньше. Значит значение выражения не изменилось. Как это работает?
Если в равенстве поменять местами левую и правую часть, то получим равенство . Это позволяет заменять в выражениях дробь вида на тождественно равное ей выражение a−n.
Теперь представим выражение в виде произведения . То есть заменим деление умножением. Напомним, что при замене деления умножением, делимое умножают на число, обратное делителю. А обратное делителю число в данном случае это дробь
Теперь воспользуемся правилом .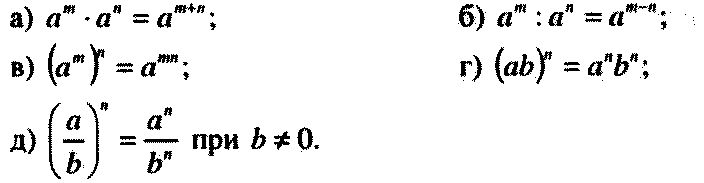
В произведении заменим дробь на тождественно равное ей выражение 2−2
Далее, как и раньше применяем основное свойство степени:
Получился тот же результат 1.
Таким же образом можно опустить степень из числителя в знаменатель, изменив знак показателя этой степени на противоположный.
Рассмотрим выражение . Чтобы найти его значение, воспользуемся правилом деления степеней с одинаковыми основаниями. В результате получим
Теперь попробуем решить этот пример, опустив степень 2−2 из числителя в знаменатель, изменив знак показателя этой степени на противоположный. При этом, опущенную степень 2−2 и ту степень, которая располагалась в знаменателе, соединим знаком умножения. А в числителе останется единица:
Дальнейшее вычисление не составит особого труда:
Как и в прошлом примере выражение представимо в виде произведения
Этим и объясняется появление единицы в числителе, после того как степень 2−2 была опущена в знаменатель.
Переносимых в знаменатель либо в числитель степеней может быть несколько. Например, знаменатель дроби содержит степени 32, a3, b4. Перенесём эти степени в числитель, изменив знаки их показателей на противоположные. В результате получим выражение 3−2a−3b−4.
Пример 2. Поднять степени из знаменателя дроби в числитель
Пример 3. Поднять степени из знаменателя дроби в числитель
Пример 4. Поднять степень из знаменателя дроби в числитель
Пример 5. Опустить степень из числителя дроби в знаменатель
Пример 6. Степень из числителя дроби опустить в знаменатель, а степень из знаменателя поднять в числитель
Представлять дробь в виде произведения вовсе не обязательно. Если пропустить эту запись, то данный пример можно решить короче:
Пример 7.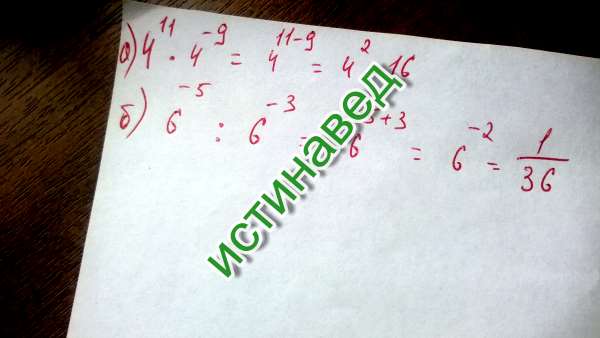
В дроби перенести из знаменателя в числитель только те степени, которые имеют отрицательные показатели:
Пример 8. Представить произведение 3x−5 в виде дроби, не содержащей степени с отрицательным показателем.
Перепишем произведение 3x−5 с помощью знака умножения:
3 × x−5
Сомножитель 3 оставим без изменений, а сомножитель x−5 заменим на тождественно равную ему дробь
Теперь согласно правилу умножения целого числа на дробь, умножим множитель 3 на числитель дроби . В результате образуется дробь
Пример 9. Представить произведение 3(x + y)−4 в виде дроби, не содержащей степени с отрицательным показателем.
Выражение состоит из сомножителей 3 и (x + y)−4. Сомножитель 3 оставим без изменений, а сомножитель (x + y)−4 заменим на тождественно равную ему дробь
Теперь умножим множитель 3 на числитель дроби .
В результате образуется дробь
Пример 10. Представить дробь в виде произведения.
Чтобы решить этот пример, достаточно поднять степень x2 в числитель, изменив знак показателя этой степени на противоположный:
Как и в прошлых примерах дробь можно было представить в виде произведения . Затем воспользовавшись правилом , заменить сомножитель на тождественно равный ему сомножитель x−2.
Пример 11. Представить дробь в виде произведения.
Пример 12. Найти значение выражения
Поднимем степень 2−3 из знаменателя в числитель, а степень 10−2 из числителя опустим в знаменатель:
Вычислим значения степеней, содержащихся в числителе и в знаменателе:
Сократим полученную дробь на 25. Тогда останется дробь , значение которой равно 2.
А если бы мы не подняли степень 2−3 в числитель, и степень 10−2 не опустили в знаменатель, а стали вычислять каждую степень по отдельности, то получили бы не очень компактное решение:
Возведение числа 10 в целую отрицательную степень
Число 10 в отрицательную степень возводится таким же образом, как и другие числа.
Например:
Замечаем, что количество нулей, которые получаются в ответе равны модулю показателя исходной степени. Например, в степени 10−2 модуль показателя равен 2. Это значит, что в ответе будет содержаться два нуля. Так оно и есть:
Чтобы возвести число 10 в отрицательную степень, нужно перед единицей записать количество нулей, равное модулю показателя исходной степени.
При этом после первого нуля следует поставить запятую. Примеры:
Представление чисел 0,1, 0,01, 0,001 в виде степени с основанием 10
Чтобы представить числа 0,1, 0,01, 0,001 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать отрицательный показатель, модуль которого равен количеству нулей исходного числа.
Представим число 0,1 в виде степени с основанием 10. Видим, что в числе 0,1 один нуль. Значит, число 0,1 в виде степени с основанием 10 будет представлено как 10−1. Показатель степени 10−1 равен −1.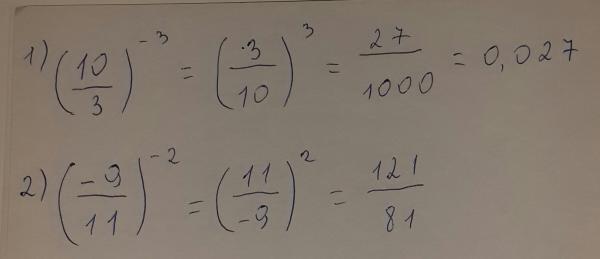
Модуль этого показателя равен количеству нулей в числе 0,1
0,1 = 10−1
Число 0,1 это результат деления , а эта дробь есть значение степени 10−1.
Пример 2. Представить число 0,01 в виде степени с основанием 10.
В числе 0,01 два нуля. Значит, число 0,01 в виде степени с основанием 10 будет представлено как 10−2. Показатель степени 10−2 равен −2. Модуль этого показателя равен количеству нулей в числе 0,01
0,01 = 10−2
Число 0,01 это результат деления , то есть , а эта дробь есть значение степени 10−2.
Пример 3. Представить число 0,001 в виде степени с основанием 10.
0,001 = 10−3
Пример 4. Представить число 0,0001 в виде степени с основанием 10.
0,0001 = 10−4
Пример 5. Представить число 0,00001 в виде степени с основанием 10.
0,00001 = 10−5
Стандартный вид числа
Запишем число 2 000 000 в виде произведения числа 2 и 1 000 000
2 × 1 000 000
Сомножитель 1 000 000 можно заменить на степень 106
2 × 106
Такой вид записи называют стандартным видом числа.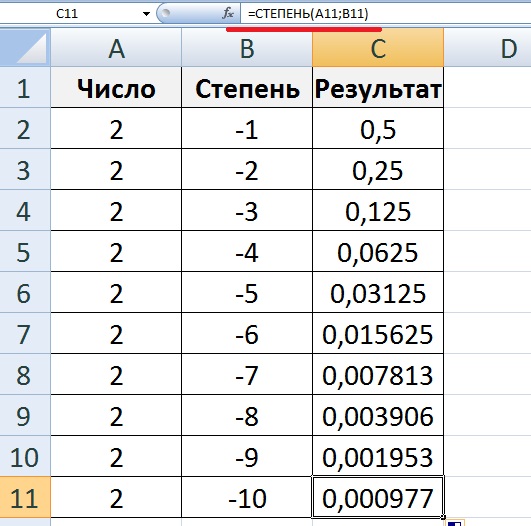
Стандартный вид числа позволяет записывать в компактном виде как большие, так и маленькие числа.
Например, маленькое число 0,005 можно записать в виде произведения числа 5 и десятичной дроби 0,001.
5 × 0,001
Десятичную дробь 0,001 можно заменить на степень с 10−3
5 × 10−3
Значит, число 0,005 в стандартном виде будет выглядеть как 5 × 10−3
0,005 = 5 × 10−3
По стандартному виду числа можно вычислить изначальное число. Так, при записи числа 2 000 000 в стандартном виде, мы получили произведение 2 × 106. Если вычислить это произведение, то снова получим 2 000 000
2 × 106 = 2 × 1 000 000 = 2 000 000
А при записи числа 0,005 в стандартном виде мы получили произведение 5 × 10−3. Если вычислить это произведение, то получим 0,005
То есть записывая число в стандартном виде нужно записывать его так, чтобы сохранить его изначальное значение.
Стандартным видом числа называют запись вида a × 10n, где 1 ≤ a < 10 и n — целое число.
Число а это исходное число, которое надо записать в стандартном виде. Оно должно удовлетворять неравенству 1 ≤ a < 10. Чаще всего исходное число надо приводить к виду, при котором неравенство 1 ≤ a < 10 становится верным.
Например, представим число 12 в стандартном виде. Для начала проверим становится ли верным неравенство 1 ≤ a < 10 при подстановке числа 12 вместо а
1 ≤ 12 < 10
Неравенство верным не становится. Чтобы сделать неравенство верным, приведём число 12 к виду, при котором оно удовлетворяло бы данному неравенству. Для этого передвинем в числе 12 запятую влево на одну цифру:
1,2
Число 12 обратилось в число 1,2. Это число будет удовлетворять неравенству 1 ≤ a < 10
1 ≤ 1,2 < 10
Теперь наша задача состоит в том, чтобы записать произведение a × 10n. С числом а мы разобрались — этим числом у нас будет 1,2. А как подобрать степень с основанием 10?
После переноса запятой на одну цифру влево, число 12 утратило своё изначальное значение.
Запятая на одну цифру влево двигается тогда, когда число делят на 10. А чтобы восстановить изначальное значение числа запятую нужно передвинуть обратно в правую сторону на одну цифру, то есть умножить число 1,2 на 10.
Значит, чтобы записать число 12 в стандартном виде, нужно представить его в виде произведения 1,2 × 10¹
12 = 1,2 × 10¹
Пример 2. Записать число 0,5 в стандартном виде.
Число 0,5 не удовлетворяет неравенству 1 ≤ a< 10, поэтому передвинем запятую в этом числе на одну цифру вправо. В результате получим число 5, которое удовлетворяет неравенству 1 ≤ a< 10.
Теперь запишем произведение вида a × 10n. Число a в данном случае это 5. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10n стало равным числу 0,5. Число 0,5 получится если умножить число 5 на множитель 0,1, который представим в виде степени 10−1. В результате получим следующую запись:
0,5 = 5 × 10−1
Пример 3.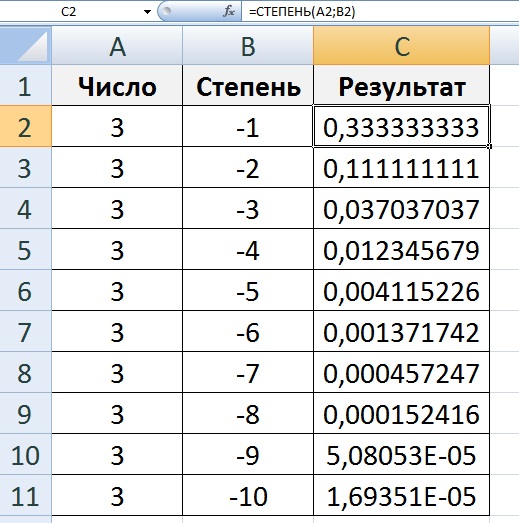
Записать число 652 000 в стандартном виде.
Число 652 000 не удовлетворяет неравенству 1 ≤ a< 10, поэтому передвинем запятую в этом числе на пять цифр влево. В результате получим число 6,52000 которое удовлетворяет неравенству 1 ≤ a< 10.
Теперь запишем произведение вида a × 10n. Число a в данном случае это 6,52000. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10n стало равным числу 652 000. Число 652 000 получится если число 6,52000 умножить на 100 000, а это есть степень 105. В результате получим следующую запись:
652 000 = 6,52000 × 105
Нули в конце десятичной дроби 6,52000 можно отбросить. Тогда получим более компактную запись:
652 000 = 6,52 × 105
Пример 5. Записать число 1 024 000 в стандартном виде.
Число 1 024 000 не удовлетворяет неравенству 1 ≤ a< 10, поэтому передвинем запятую в этом числе на шесть цифр влево.
В результате получим число 1,024000 которое удовлетворяет неравенству 1 ≤ a< 10.
Теперь запишем произведение вида a × 10n. Число a в данном случае это 1,024000 . А степень с основанием 10 надо выбрать так, чтобы произведение a × 10n было равно изначальному числу 1 024 000. Число 1 024 000 получится если число 1,024000 умножить на 1 000 000, а это есть степень 106. В результате получим следующую запись:
1 024 000 = 1,024000 × 106
Нули в конце десятичной дроби 1,024000 можно отбросить:
1 024 000 = 1,024 × 106
Отбрасывать можно только те нули, которые располагаются в конце, и после которых нет других цифр, бóльших нуля. В приведённом примере были отброшены только три нуля, а нуль располагавшийся между запятой и цифрой 2 был сохранен, несмотря на то, что он тоже располагался после запятой.
Пример 6. Записать число 0,000325 в стандартном виде.
Передвинем в данном числе запятую так, чтобы оно удовлетворяло неравенству 1 ≤ a< 10. В результате получим число 3,25
Теперь запишем произведение вида a × 10n. Число a в данном случае это 3,25. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10n было равно изначальному числу 0,000325. Число 0,000325 получится если число 3,25 умножить на множитель 0,0001 который представим в виде степени 10−4. В результате получим следующую запись:
0,000325 = 3,25 × 10−4
Задания для самостоятельного решения
Задание 1. Вычислите степень 3−2
Решение:
Показать решение
Задание 2. Вычислите степень (−3)−2
Решение:
Показать решение
Задание 3. Вычислите степень −3−2
Решение:
Показать решение
Задание 4. Вычислите степень (−1)−9
Решение:
Показать решение
Задание 5.
Вычислите степень
Решение:
Показать решение
Задание 6. Вычислите степень
Решение:
Показать решение
Задание 7. Вычислите степень −(−2)−3
Решение:
Показать решение
Задание 8. Вычислите степень
Решение:
Показать решение
Задание 9. Найдите значение выражения 8 × 4
Решение:
Показать решение
Задание 10. Найдите значение выражения 18 × (−9)−1
Решение:
Показать решение
Задание 11. Найдите значение выражения 2−3 − (−2)−4
Решение:
Показать решение
Задание 12. Найдите значение выражения
Решение:
Показать решение
Задание 13. Представить произведение a−4b в виде дроби, не содержащей степени с отрицательным показателем.
Решение:
Показать решение
Задание 14.
Представить произведение 7xy−3 в виде дроби, не содержащей степени с отрицательным показателем.
Решение:
Показать решение
Задание 15. Представить произведение 6(xy)−6 в виде дроби, не содержащей степени с отрицательным показателем.
Решение:
Показать решение
Задание 16. Представить произведение x−1y−2 в виде дроби, не содержащей степени с отрицательным показателем.
Решение:
Показать решение
Задание 17. Представить произведение 9a−1(a − b)−2 в виде дроби, не содержащей степени с отрицательным показателем.
Решение:
Показать решение
Задание 18. Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 19. Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 20.
Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 21. Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 22. Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 23. Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 24. Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 25. Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 26. Представьте дробь в виде произведения.
Решение:
Показать решение
Задание 27. Представьте число 3 000 000 в стандартном виде.
Решение:
3 000 000 = 3 × 106
Показать решение
Задание 28. Представьте число 0,35 в стандартном виде.
Решение:
0,35 = 3,5 × 10−1
Показать решение
Задание 29. Представьте число 21,56 в стандартном виде.
Решение:
21,56 = 2,156 × 101
Показать решение
Задание 30. Представьте число 0,000008 в стандартном виде.
Решение:
0,000008 = 8 × 10−6
Показать решение
Задание 31. Представьте число 0,000335 в стандартном виде.
Решение:
0,000335 = 3,35 × 10−4
Показать решение
Задание 32. Найдите значение выражения .
Решение:
Показать решение
Задание 33. Найдите значение выражения .
Решение:
Показать решение
Задание 34. Найдите значение выражения .
Решение:
Показать решение
Задание 35. Представьте в виде степени выражение .
Решение:
Показать решение
Задание 36.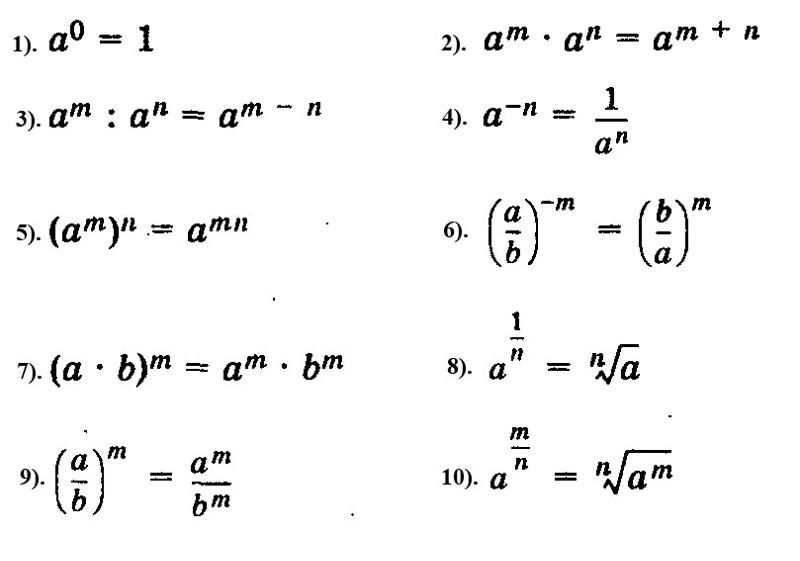
Решение:
Показать решение
Задание 37. Представьте в виде степени выражение .
Решение:
Показать решение
Задание 38. Представьте в виде степени выражение .
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями.
Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс | 0046 | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | звездочка | умножение | 2/3 * 3/4 9 | знак умножения | умножение | 2 /3 × 5/6 |
| : | знак деления | деление | 1/2 : 3 |
| 4 деления 4 деления 6 | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций . PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — Символы группировки — скобки (){}, возведения в степень, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будьте осторожны; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
другие математические задачи »
|
Какая часть от общей суммы была использована?