Уравнение касательной к графику функции f(X) в точке х0
Таблица производных
Функция f (х) | Производная f ‘ (х) |
С, где С — любое число | 0 |
хп, где п – любое число | пхп-1 |
ех | ех |
aх | ахlnа |
lnх | |
lоg a x | |
sin х | cosх |
cos х | -sinх |
tg х | |
ctgх |
y = f(x0) + f ‘(x0)(x – x0)
21
Обратные тригонометрические функции
Функция | Область определения | Область значений |
y = arcsinx | [-1;1] | [-/2; /2] |
y = arccosx | [-1;1] | [0; ] |
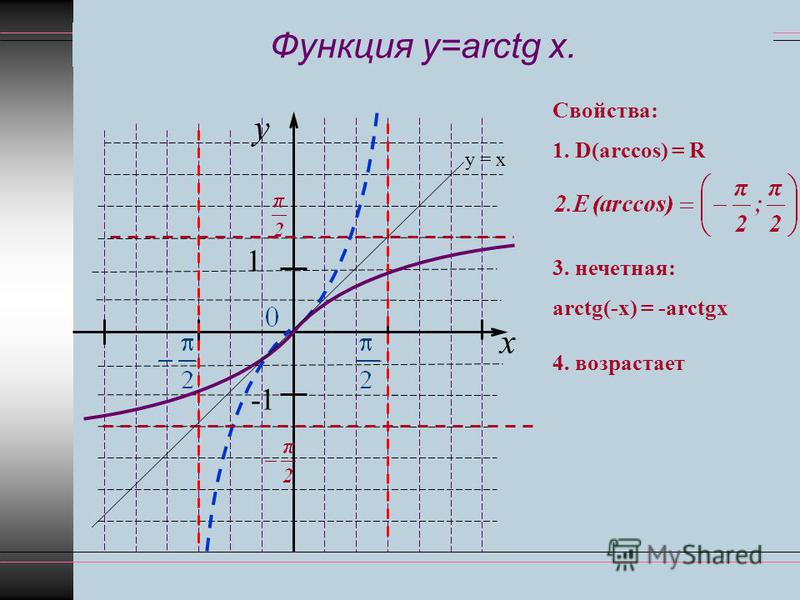
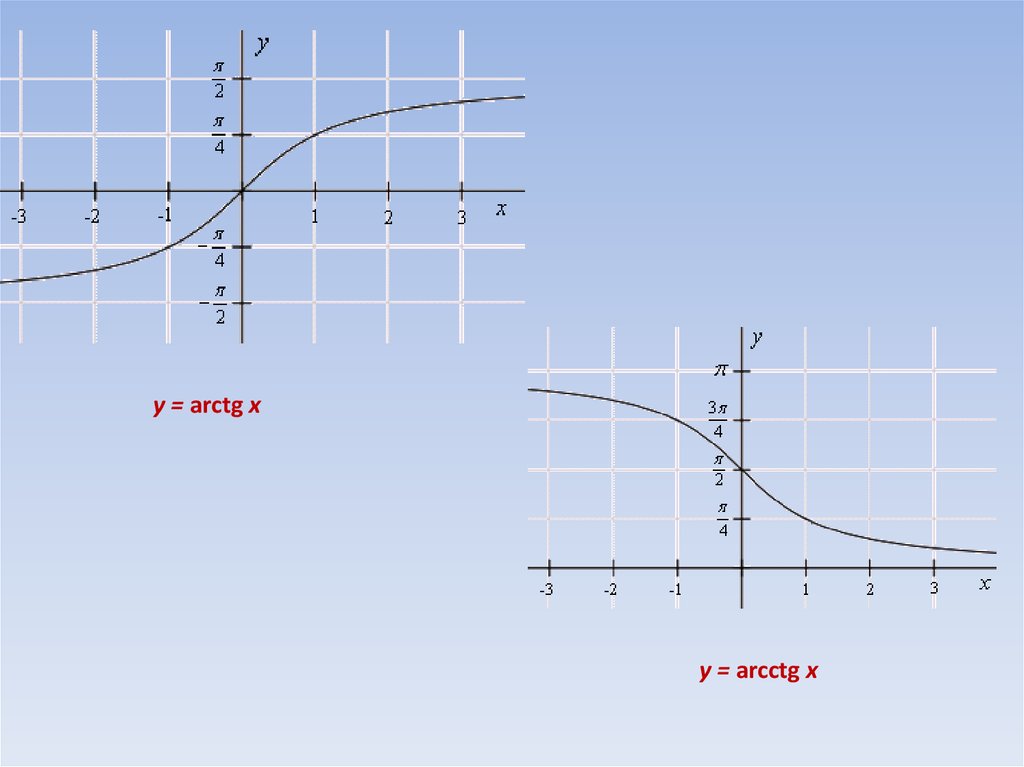
y = arctgx | x – любое | (-/2; /2) |
y = arcctgx | x – любое | (0; ) |
sin(arcsin x) = x
cos(arccos x) = x
tg(arctg x) = x
ctg(arcctg x) = x arcsin(-x) = — arcsinx
sin(arсcos x)= arccos(-x)=-arccos x
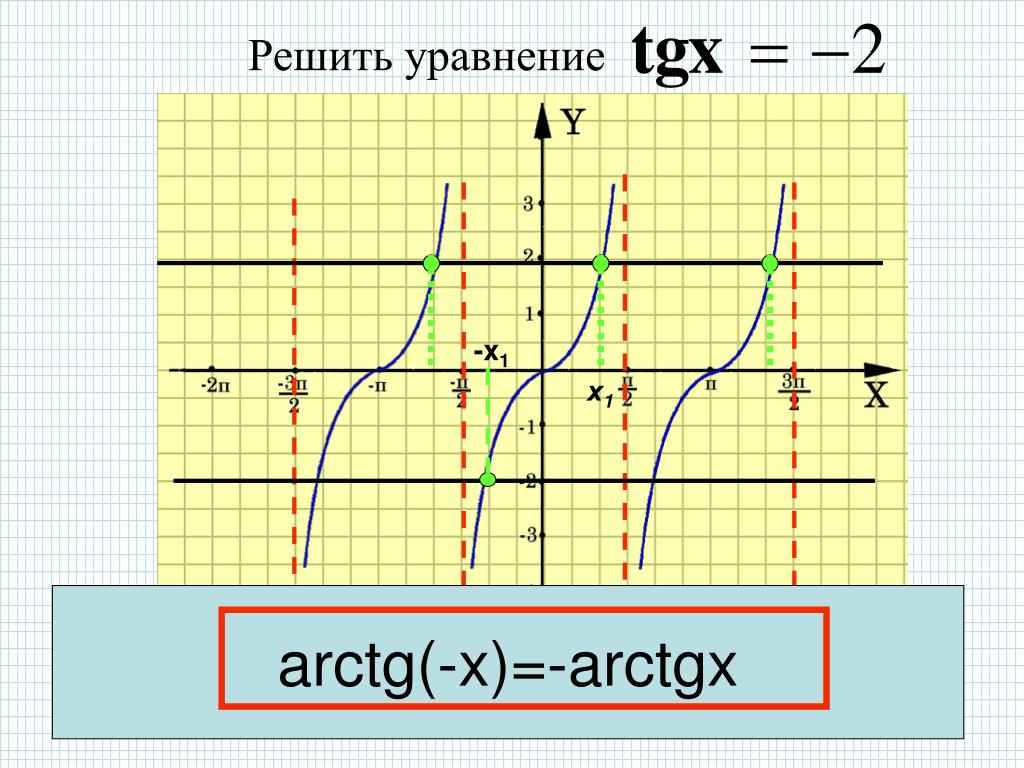
cos(arcsin x) = arctg(-x) = — arctg x
tg (arcctg x) = arcctg(-x) =-arcctgx
ctg (arctg x) =
14
Значения тригонометрических функций
a | 0o | 30o | 45o | 60o | 90o | 120o | 135o |
a | 0 | /6 | /4 | /3 | /2 | 2/3 | 3/4 |
sin | 0 | 1 | |||||
cos | 1 | 0 | |||||
tg | 0 | 1 | — | — 1 | |||
ctg | — | 1 | 0 | — 1 |
Формулы
90o- | 90o+ | 270o- | 270o+ | |
/2 — | /2 + | 3/2- | 3/2+ | |
sin | cos | cos | -cos | -cos |
cos | sin | -sin | -sin | sin |
tg | ctg | -ctg | ctg | -ctg |
ctg | tg | -tg | tg | -tg |
sin(-x) = -sinx cos(-x) = cos x
sin(x-y) = — sin(y-x) cos(x-y) = cos(y-x)
16
для некоторых углов
150o | 180o | 210o | 225o | 270o | 300o | 330o | 360o |
5/6 | | 7/6 | 5/4 | 3/2 | 5/3 | 11/6 | 2 |
0 | — 1 | 0 | |||||
-1 | 0 | 1 | |||||
0 | 1 | — | 0 | ||||
— | 1 | 0 | — |
приведения
180o- | 180o+ | 360o- | 360o+ | |
— | + | 2 — | 2 + | |
sin | sin | -sin | -sin | sin |
cos | -cos | -cos | cos | cos |
tg | -tg | tg | -tg | tg |
ctg | -ctg | ctg | -ctg | ctg |
tg(-x) = — tgx ctg(-x) = — ctg x
tg(x-y) = — tg(y-x) ctg(x-y) = — ctg(y-x)
17
Исчисление— Доказательство $\operatorname{arccot}(x)= \arctan(\frac{1}{x})$
спросил
Изменено 1 год, 11 месяцев назад
Просмотрено 392 раза
$\begingroup$
$\newcommand{\ac}{\operatorname{arccot}}$ Вот мое доказательство:
$ \theta = \ac(x)$
$ \cot \theta = x $
$ \displaystyle \tan \theta = \frac{1}{\cot \theta} = \frac{1}{ x}$
$ \displaystyle \theta = \arctan \frac{1}{x}$
Но на основе графика $\ac(x) = \arctan(\frac{1}{x})$ выполняется только при $ x > 0$. Что не так с моим доказательством? Какая ошибка произошла внутри доказательства?
Что не так с моим доказательством? Какая ошибка произошла внутри доказательства?
- исчисление
- функции
- проверка решения
- обратная функция
- поддельные пруфы
$\endgroup$
11
$\begingroup$
ПОДСКАЗКА. Используя фигуру прямоугольного треугольника, очевидно, что для $0\lt \theta\lt \dfrac{\pi}{2}$ выполняется предлагаемое равенство.
откуда равенство верно для всех $x\gt 0$.
Однако для $x\lt0$ равенство неверно, так как, например,
$$\operatorname{arccot}(-2)\приблизительно2.6779\\\arctan(-\dfrac 12)\приблизительно-1.1071$$
$\endgroup$
1
$\begingroup$
Существует два соглашения по главному значению:
- $\operatorname{arccot} x \in (-\pi/2, \pi/2]$ с разрывом в нуле.

- $\operatorname{arccot} x \in (0, \pi)$
См. https://mathworld.wolfram.com/InverseCotangent.html
Получается, что $\operatorname{arccot} x = \arctan(1/x)$ для всех $x\ne 0$ при одном соглашении главное значение. 9\circ$ и определите свой диапазон в любом случае до кратного $\pi.$
$\endgroup$
4
$\begingroup$
Длинный комментарий:
Первая проблема с $$\arctan\left(\frac1x\right)=\operatorname{arccot}(x)$$ заключается в том, что $\arctan$ — нечетная функция, а $\operatorname{ arccot}$ нет.
В самом деле, $\forall x\in\Bbb R$ выполняется следующее:
$$\arctan(x)+\operatorname{arccot}(x)=\frac\pi2\implies\operatorname{arccot}( х)=\frac\pi2-\arctan(x)$$
Следовательно, если $x>0$, то
$$\arctan\left(\frac1{-x}\right)=-\arctan\left(\frac1x\right)=-\operatorname{arccot}(x)=-\operatorname{arccot}(-(-x) ))$$
и мы не можем просто поставить знак под аргументом. Поэтому,
$$\arctan\left(\frac1x\right)=\begin{cases}-\operatorname{arccot}(-x), &x<0\\\operatorname{arccot}(x),&x>0\end{cases }$$
Поэтому,
$$\arctan\left(\frac1x\right)=\begin{cases}-\operatorname{arccot}(-x), &x<0\\\operatorname{arccot}(x),&x>0\end{cases }$$
$\endgroup$
арктангенс(х+1)+арктангенс(х – 1)=арктангенс(12)
Предыдущая статья Следующая статья
(Последнее обновление: 28 января 2023 г.)
Постановка задачи: EE Board, март 1998 г.
Найдите x в уравнении: arctan(x + 1) + arctan(x – 1) = arctan(12).
- А. 1,5
- Б. 1,34
- С. 1.20
- Д. 1,25
Ответ на задачу:
Эквивалентное значение x равно 1.33
Просмотр Решение:
Этот контент предназначен для премиум-пользователей. Устали от рекламы?
Подпишитесь, чтобы разблокировать контент! и Удалить рекламу.
Последнее решение задач плоской тригонометрии
- Решение: Сколько квадратных единиц будет иметь площадь нового треугольника?
- Решение: Даны три стороны.
 Какова площадь треугольника?
Какова площадь треугольника? - Решение: Найдите длину линии, разделяющей пополам самую длинную сторону треугольного участка 9.0026
- Решение: Чему равна третья сторона треугольника?
- Решение: Определить сторону равностороннего треугольника
- Решение: найти высоту памятника на горизонтальной плоскости
- Решение: Какова высота башни?
- Решение: Определить скорость корабля
- Решение: На каком расстоянии в метрах от здания находится точка А?
- Решение: если высота башни B равна 120 м, найдите высоту башни A .
- Решение: Определить длину провода и угол, который он образует
- Решение: Определить длину стержня
- Решение: Какова высота башни?
- Решение: Какова будет путевая скорость самолета, если он будет лететь по этому курсу?
- Решение: сколько часов второй корабль будет точно к северу от корабля А?
- Решение: Найдите высоты, если площади треугольников отличаются на 21
- Решение: Определите кратчайшее расстояние от башни C до шоссе .
- Решение: Найдите высоту соседнего здания в метрах 92 θ)
- Решение: Найдите значение (sinθ + cosθtanθ)/cosθ
- Решение: Найдите значение y в данном: y=(1+cos2θ)tanθ
- Решение: Если тангенс x=1/2, тангенс y=1/3, каково значение тангенса (x+y)?
- Решение: если sec 2A=1/sin13A , определите угол A в градусах
- Решение: Вычислить котангенс угла
- Решение: Найдите значение sin(arc cos 15/17)
- Решение: если cos65° + cos55° = cosθ, найдите θ в радианах 92А – sinA=1
- Решение: Найдите G, если csc (11G – 16 градусов) = sec (5G + 26 градусов)
- Решение: Если sinxcosx + sin2x = 1, каковы значения x?
- Решение: Найдите x, если tan3x=5tanx
- Решение: если sin 3A = cos 6B, то
- Решение: Найдите θ в следующем уравнении: sin 2θ = cosθ
- Решение: CSC 520° равно
- Решение: Каковы значения sinB и cosB в 4-м квадранте?
- Решение. В каком квадранте находится A, если sec A положителен, а csc A отрицателен? 92А эквивалентно
- Решение: чему равен Sin(B–A), если B=270 градусов и A — острый угол
- Решение: Найдите расстояние «d» между центрами двух последовательных отверстий
- Решение: Каков вертикальный подъем поезда на этом расстоянии?
- Решение: Найдите кратчайшее расстояние от одной дороги до заправочной станции
- Решение: Найдите расстояние от точки пересечения биссектрис угла
- Решение: На каком расстоянии от основания дома
- Решение: Найдите высоту здания
- Решение: Найдите расстояние между двумя башнями
- Решение: Какой высоты столб?
- Решение: Как далеко друг от друга два города?
- Решение: Найдите длину самой короткой лестницы .
- Решение: Если длина лестницы 50 футов, то какой ширины будет улица?
- Решение: Найдите высоту холма, если высота башни 116 футов
- Решение: Какова ширина реки?
- Решение: На каком расстоянии друг от друга две башни?
- Решение: Найдите радиус 60-й параллели широты.
- Решение: Насколько высока более высокая башня?
- Решение: Найдите высоту маяка .
- Решение: Если дополнение к углу тета составляет 2/5 его дополнения
- Решение: Найдите высоту фонарного столба, если угол возвышения меняется
- Решение: Как долго спутник находится над горизонтом?
- Решение: Найдите высоту башни
- Решение: Какое расстояние должен пройти автомобиль по трассе?
- Решение: Найдите длину хорды окружности радиусом 20 см
- Решение: Какова площадь фронтона?
- Решение: Найдите наибольший угол треугольника, образованного соединением центров
- Решение: вычислить скорость лодки
- Решение: Определите отношение b:a, если стороны прямоугольного треугольника равны a, a+b, a+2b
- Решение: Найдите наименьший угол в милах 92 θ
- Решение: Каково максимальное значение 3-2cos θ?
- Решение: если 2log3 (по основанию x)+log2 (по основанию x)=2+log6 (по основанию x), то x равно .
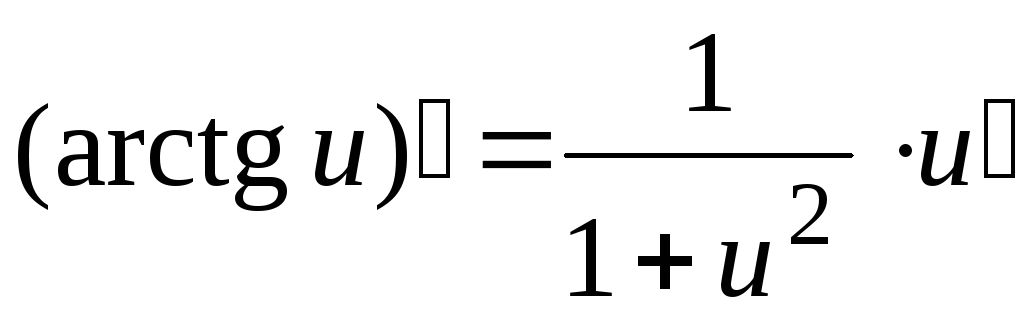

 Какова площадь треугольника?
Какова площадь треугольника?