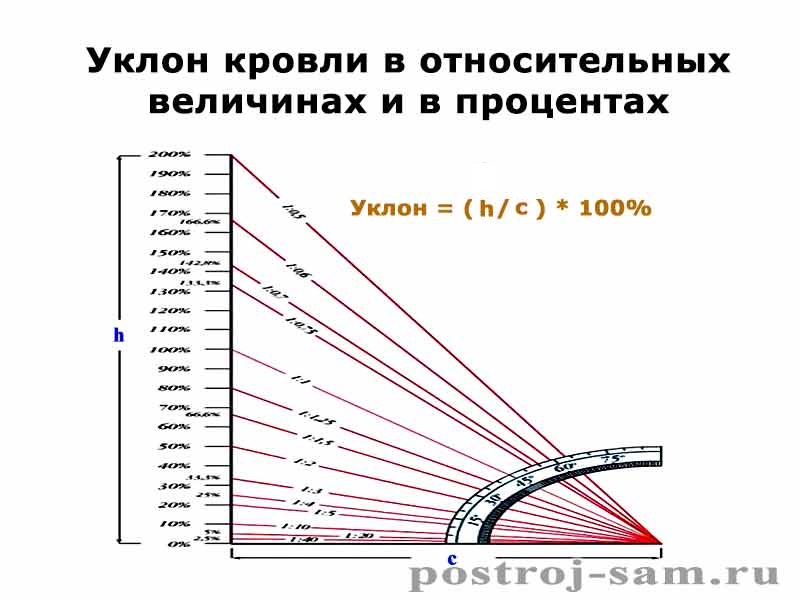
1 градус на 1 метр: Перевод уклона из см/м в градусы онлайн калькулятор

1 градус на 1 метр

Вы искали 1 градус на 1 метр? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 5 градусов угол, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 градус на 1 метр».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 градус на 1 метр,5 градусов угол,градусы в проценты,градусы в проценты калькулятор,градусы в проценты онлайн,градусы в проценты онлайн калькулятор,градусы перевести в уклон,как градусы перевести в проценты уклона,как градусы перевести в сантиметры,как перевести градусы в сантиметры,как перевести проценты уклона в градусы,как проценты уклона перевести в градусы,калькулятор градусы в проценты,калькулятор перевод процентов в градусы,онлайн перевод градусов в проценты,перевести градусы в проценты онлайн,перевести градусы в уклон,перевести проценты в градусы,перевести проценты в градусы онлайн,перевести уклон в градусы,перевести уклон в процентах в градусы,перевод градусов в проценты,перевод градусов в проценты онлайн,перевод из градусов в проценты,перевод процентов в градусы,перевод уклона в градусы,перевод уклона из процентов в градусы,проценты в градусы калькулятор,проценты в градусы онлайн,проценты в градусы таблица,проценты перевести в градусы онлайн,сколько в одном градусе сантиметров,сколько сантиметров в одном градусе,таблица проценты в градусы,угол 10 градусов,угол 12 градусов,угол 5 градусов,угол в 10 в градусах,угол в процентах перевести в градусы,уклон 10 процентов в градусы,уклон в перевести в градусы,уклон в перевод в градусы,уклон в процентах перевести в градусы,уклон перевести в градусы.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 1 градус на 1 метр. Просто введите задачу в окошко и нажмите «решить» здесь (например, градусы в проценты).

Решить задачу 1 градус на 1 метр вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Уклон плоских крыш — База знаний ТЕХНОНИКОЛЬ

Уклон крыши необходим для эффективного отвода воды с поверхности ската.

При нарушении уклона крыши образуются застойные зоны, которые способствуют сокращению срока службы водоизоляционного ковра.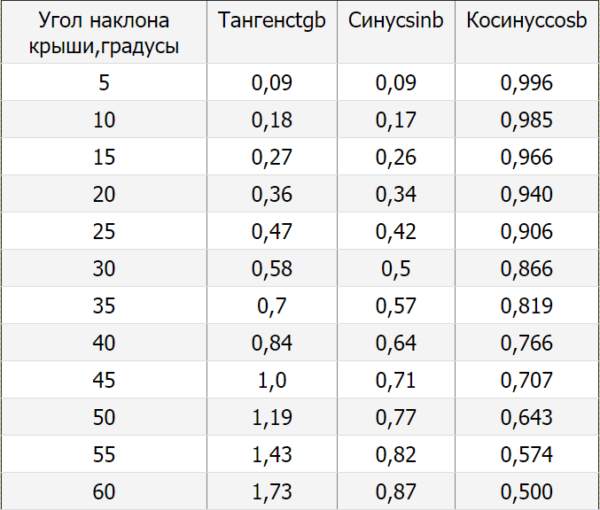

Крыша с большим уклоном «прощает» мелкие ошибки при монтаже и увеличивает срок службы конструкции.

В чем измеряется уклон крыши

Уклоном называют величину крутизны ската крыши.

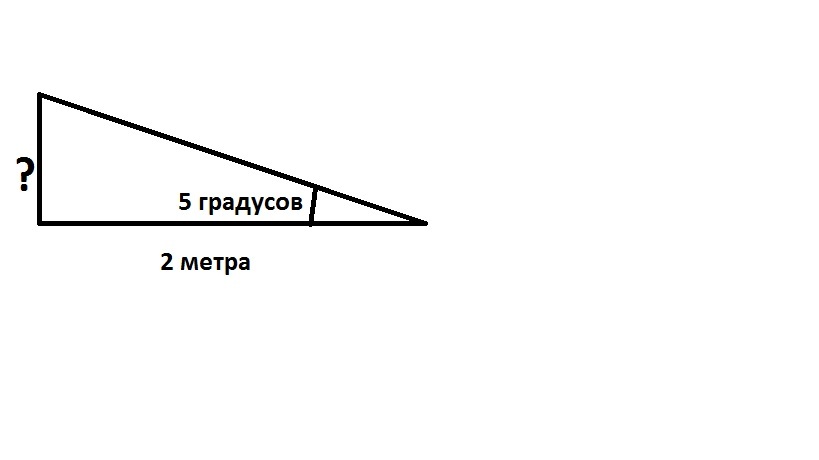
Если представить крышу в разрезе, то получится прямоугольный треугольник. Уклоном будет считаться тангенс угла α, который равен отношению противолежащего катета к прилежащему.

Уклон может измеряться в градусах – °, процентах – %, а также может быть выражен коэффициентом уклона i.

Крыши с уклоном до 12° принято считать плоскими, а с уклоном 12° и более — скатными.

Перевод уклона из градусов в проценты

Для перевода уклона из градусов в проценты следует тангенс угла в градусах умножить на 100:

Для перевода уклона из процентов в градусы следует вычислить функцию арктангенса угла в процентах, умноженного на 0,01:

Сводная таблица с уклонами в различных величинах

Коэффициент уклона, i	Угол наклона, °	Наклон, %
0,008	0,5	0,8
0,01	0,6	1,0
0,015	0,9	1,5
0,02	1,1	2,0
0,03	1,7	3,0
0,05	2,9	5,0
0,10	5,7	10,0
0,12	6,8	12,0
0,15	8,5	15,0
0,20	11,3	20,0
0,25	14	25,0
0,30	16,7	30,0
0,45	24,2	45,0
0,60	31	60,0
1,00	45	100,0

Минимальный уклон крыши

В соответствии с действующими нормативными документами в строительстве, устройство скатов крыши необходимо выполнять с уклоном не менее 1,5% (i=0,015, 0,9°), т.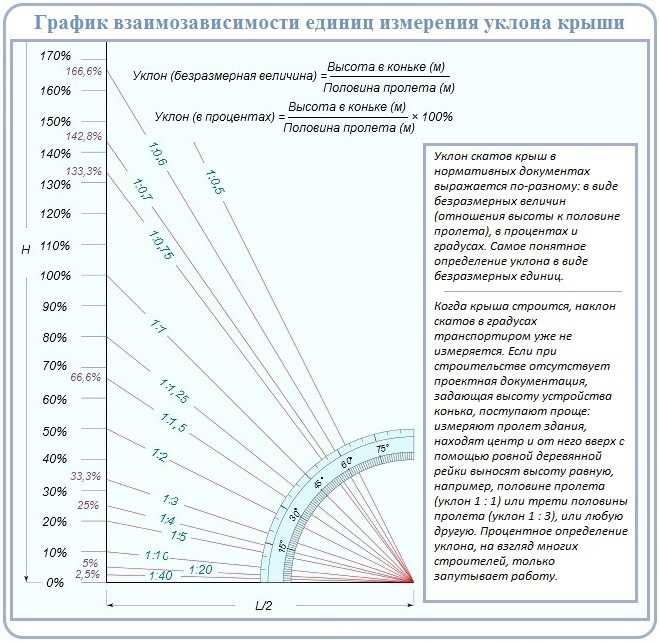 е. 1,5 см подъема ската крыши на 100 см длины.

 

#плоская #крыша #кровля #Кровля плоская #ПГС #КМС #Поддержка #Проектирование #Консультация #Выбор решения #Помощь в подборе решения #техническая #конструкция #состав

Оцените эту статью

4.5 (119)

Система координат

— Преобразование 1 метра в градусы в определенном месте с помощью PostGIS

Учитывая точку в EPSG:4326 Мне нужно знать, сколько градусов (приблизительно) составляет 1 метр в этом месте с помощью PostGIS. Похоже, http://postgis.net/docs/manual-2.1/ST_Line_Interpolate_Point. html здесь полезен, но я не могу понять.

Другой способ сформулировать этот вопрос: какая здесь одна точка (X), которая вернет меня на 1 метр назад при выполнении следующего запроса?

 ST_Расстояние(
   'SRID=4326;POINT(точка ввода)'::география,
   'SRID=4326;POINT(X)'::geography) AS geography_distance
   ;
 

Я бы с радостью принял точку в любом направлении.

Вот тот же вопрос, но с использованием «FME’s Tester» Преобразование 1 метра в десятичные градусы с использованием FME

• postgis
• система координат

5

Вы можете выполнить следующий запрос, вы можете изменить координаты в CTE start_coords :

 WITH start_coords AS (ВЫБЕРИТЕ 5 AS в длину, 40 AS в ширину),
start_point AS (SELECT *, ST_MakePoint(long, lat)::geography AS geog FROM start_coords)
ВЫБРАТЬ
    шп.лат,
    сп.долг,
    ST_Расстояние(
        сп.геог,
        ST_MakePoint(sp. long, sp.lat + 1)::geography
    ) AS one_deg_lat_north, -- в метрах
    1/ST_Расстояние(
        сп.геог,
        ST_MakePoint(sp.long, sp.lat + 1)::geography
    ) AS one_meter_lat_north, -- в градусах
    ST_Расстояние(
        сп.геог,
        ST_MakePoint(sp.long, sp.lat - 1)::geography
    ) AS one_deg_lat_south, -- в метрах
    1/ST_Расстояние(
        сп.геог,
        ST_MakePoint(sp.long, sp.lat - 1)::geography
    ) AS one_meter_lat_south, -- в градусах
    ST_Расстояние(
        сп.геог,
        ST_MakePoint(sp.long + 1, sp.lat)::география
    ) AS one_deg_long_east, -- в метрах
    1/ST_Расстояние(
        сп.геог,
        ST_MakePoint(sp.long + 1, sp.lat)::география
    ) AS one_meter_long_east, -- в градусах
    ST_Расстояние(
        сп.геог,
        ST_MakePoint(sp.long - 1, sp.lat)::geography
    ) AS one_deg_long_west, -- в метрах
    1/ST_Расстояние(
        сп.геог,
        ST_MakePoint(sp.long - 1, sp.lat)::geography
    ) AS one_meter_long_west -- в градусах
ОТ start_point sp
;
 

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. 9Система координат 0000 — Алгоритм смещения широты/долготы на некоторое количество метров

Я ищу алгоритм, который при заданной паре широты и долготы и переводе вектора в метрах в декартовых координатах (x,y) дал бы мне новая координата. Что-то вроде обратного гаверсина. Я также мог бы работать с расстоянием и преобразованием направления, но это, вероятно, было бы медленнее и не так точно. В идеале алгоритм должен быть быстрым, так как я работаю над встроенной системой. Точность не критична, в пределах 10 метров было бы хорошо.

• система координат
• алгоритм
• сферическая геометрия

2

Если ваши смещения не слишком велики (менее нескольких километров) и вы находитесь не прямо на полюсах, используйте быструю и грубую оценку, что 111 111 метров (111,111 км) в направлении y составляет 1 градус (широты). ) и 111 111 * cos(широта) метров в направлении x составляет 1 градус (долготы).

12

Как говорит Лидман в своем ответе, авиационные формулы Уильямса являются бесценным источником, и чтобы сохранить точность в пределах 10 метров для перемещений до 1 км, вам, вероятно, придется использовать более сложные из них.

Но если вы готовы принять ошибки более 10 м для точек, смещенных более чем на 200 м, вы можете использовать упрощенный расчет плоской земли. Думаю ошибки все равно будут меньше 50м при выносах до 1км.

 //Позиция, десятичные градусы
 широта = 51,0
 долгота = 0,0
 //Радиус Земли, сфера
 Р=6378137
 //смещения в метрах
 дн = 100
 де = 100
 //Смещение координат в радианах
 dLat = dn/R
 dLon = de/(R*Cos(Pi*lat/180))
 //OffsetPosition, десятичные градусы
 latO = широта + dLat * 180/Pi
 lonO = lon + dLon * 180/Pi
 

Это должно вернуть:

 latO = 51,00089832
 lonO = 0,001427437
 

8

Я считаю, что Авиационный формуляр отлично подходит для таких типов формул и алгоритмов. Для вашей проблемы проверьте «широта/долгота с заданным радиусом и расстоянием»: здесь

Обратите внимание, что этот алгоритм может быть слишком сложным для вашего использования, если вы хотите, чтобы функции тригонометрии использовались на низком уровне и т. д.

1

Я создал простую пользовательскую карту на Картах Google, которая иллюстрирует алгоритм оценки, упомянутый в принятом ответе (1/111111 == один метр). Не стесняйтесь посмотреть и поиграть с ним здесь:

https://drive.google.com/open?id=1XWlZ8BM00PIZ4qk43DieoJjcXjK4z7xe&usp=sharing

Чтобы дать больше контекста — на этой карте показаны координаты 0,0 , а затем показывает еще две булавки, которые находятся в 1 метре к северу и в 1 метре к востоку от

0,0 .

Возможно, имеет смысл сначала спроецировать точку. Вы можете сделать что-то вроде этого псевдокода:

 falt_coordinate = latlon_to_utm (исходная_координата)
новая_плоская_координата = плоская_координата + (х, у)
result_coordinate = utm_to_latlon (new_flat_coordinate)
 

, где (x,y) — желаемое смещение.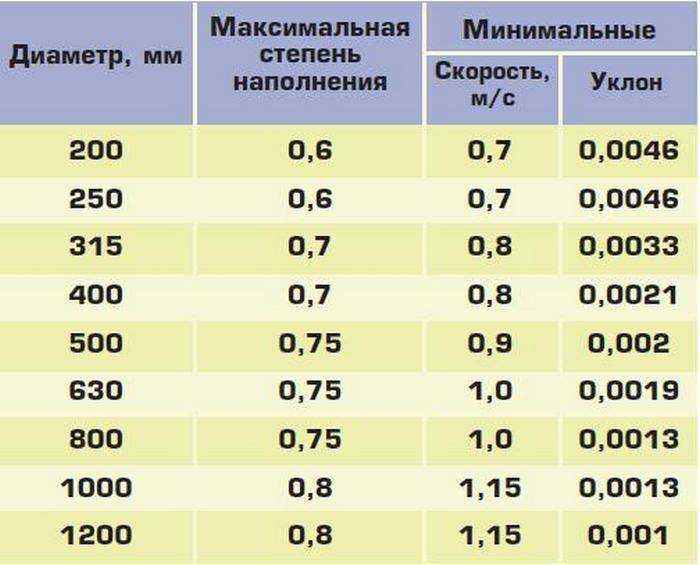

Вам не нужно использовать utm, подойдет любая плоская система координат, которая имеет смысл в вашем регионе.

С каким программным обеспечением вы работаете?

2

Вот код Python для ответа whuber

 из математического импорта, радианы
defmeters_to_lat_lon_displacement(m, origin_latitude):
    широта = м/111111
    lon = m/(111111 * cos(радианы(исходная_широта)))
    вернуться лат, долгота
 

Вот код R

 deg2rad = function(deg) {(deg * pi) / (180)}
м_к_широте_лон_смещение = функция (м, исходная_широта){
  широта = м/111111
  lon = m/(111111 * cos((deg2rad(origin_latitude))))
  возврат (список (широта = широта, долгота = долгота))
}
 

1

Вот версия Swift , используемая на кодише , ответ на SO:

 extension CLLocationCoordinate2D {
  
  func earthRadius() -> CLLocationDistance {
    пусть earthRadiusInMetersAtSeaLevel = 6378137. 0
    пусть earthRadiusInMetersAtPole = 6356752,314
    
    пусть r1 = EarthRadiusInMetersAtSeaLevel
    пусть r2 = earthRadiusInMetersAtPole
    пусть бета = широта
    
    пусть earthRadiuseAtGivenLatitude = (
      ( pow(pow(r1, 2) * cos(beta), 2) + pow(pow(r2, 2) * sin(beta), 2)) /
        ( pow (r1 * cos (бета), 2) + pow (r2 * sin (бета), 2))
    )
    .квадратный корень()
    
    вернуть землюRadiuseAtGivenLatitude
  }
  
  функция locationByAdding(
    расстояние: CLLocationDistance,
    подшипник: CLLocationDegrees
  ) -> CLLocationCoordinate2D {
    пусть широта = self.latitude
    пусть долгота = self.longitude
    
    пусть earthRadiusInMeters = self.earthRadius()
    пусть brng = подшипник.степениToRadians
    var lat = широта.степениToRadians
    var lon = долгота.градусы в радианах
    
    лат = асин (
      sin(lat) * cos(distance / earthRadiusInMeters) +
        cos(lat) * sin(distance / earthRadiusInMeters) * cos(brng)
    )
    лон += атан2(
      sin(brng) * sin(distance / earthRadiusInMeters) * cos(lat),
      cos(расстояние/земнойрадиусвметрах) - sin(lat) * sin(lat)
    )
    
    пусть newCoordinate = CLLocationCoordinate2D (
      широта: лат. radiansToDegrees,
      долгота: lon.radiansToDegrees
    )
    
    вернуть новые координаты
  }
}
расширение с плавающей запятой {
  var степенейToRadians: Self { self * .pi / 180 }
  var radiansToDegrees: Self { self * 180 / .pi }
}
 

1

Все вышеперечисленные ответы хороши, но вы можете сделать это и в ArcMap стандартными инструментами — https://desktop.arcgis.com/en/arcmap/10.3/manage-data/editing-fundamentals/moving-a- функция-относительно-его-текущего-местоположения-дельта-x-y-.htm

Хотите улучшить этот пост? Предоставьте подробные ответы на этот вопрос, включая цитаты и объяснение того, почему ваш ответ правильный. Ответы без достаточной детализации могут быть отредактированы или удалены.

Прямая формула Винсенти должна работать.

1

Спасибо за ответ на Stack Exchange географических информационных систем!

• Пожалуйста, ответьте на вопрос .

  No related posts.