00:02:16
Валерий Волков 11 05.02.2015
Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!
Новости образования
ЕГЭ по математике
Профильный уровень
Задание 1 Задание 2
Задание 3 Задание 4
Задание 5 Задание 6
Задание 7 Задание 8
Задание 9 Задание 10
Задание 11 Задание 12
Задание 13 Задание 14
Задание 15 Задание 16
Задание 17 Задание 18
Задание 19 Задание 20
Задание 21
ГИА по математике
Задача 1 Задача 2
Задача 3 Задача 4
Задача 5 Задача 6
Задача 7 Задача 8
Задача 9 Задача 10
Задача 11 Задача 12
Задача 13 Задача 14
Задача 15 Задача 16
Задача 19 Задача 20
Задача 21 Задача 22
Задача 23 Задача 24
Задача 25 Задача 26
Демонстрационные варианты ОГЭ по математике
Математика.
5 класс.
Натуральные числа
Обыкновенные дроби
Десятичные дроби
Проценты
Математика. 6 класс.
Делимость чисел
Сложение и вычитание дробей с разными знаменателями
Умножение и деление обыкновенных дробей
Отношения и пропорции
Положительные и отрицательные числа
Измерение величин
Математика. 7 класс.
Преобразование выражений
Многочлены
Формулы сокращенного умножения
Математика. 8 класс.
Модуль числа. Уравнения и неравенства.
Квадратные уравнения
Квадратные неравенства
Уравнения с параметром
Задачи с параметром
Математика. 9 класс.
Функции и их свойства
Прогрессии
Векторы
Комбинаторика, статистика и теория вероятностей
Математика.
10 — 11 класс.
Числовые функции
Тригонометрические функции
Тригонометрические уравнения
Преобразование тригонометрических выражений
Производная
Степенные функции
Показательная функция
Логарифмические функции
Первообразная и интеграл
Уравнения и неравенства
Комбинаторика
Создаёте видеоуроки?
Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.
Физкультминутки для школьников и дошкольников
Подготовка к ЕГЭ Подготовка к ОГЭ© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
функций — Как решать многочлены 5-й степени?
спросил
Изменено 1 год, 2 месяца назад
Просмотрено 29 тысяч раз
$\begingroup$
Я искал в Википедии формулу для корней многочлена 5-й степени, но там сказано, что по теореме Абеля это невозможно.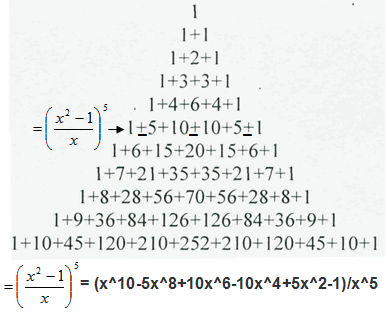
В принципе, как точных значений корней таких функций могут быть выражены иначе, чем радикалом (поскольку мы знаем, что для некоторых функций это не радикал)?
Если нет, то является ли численное решение/построение графика единственным способом решения таких многочленов?
Редактировать: Я нашел здесь ссылку, которая объясняет все способы решения вышеупомянутых функций.
- функции
- многочлены
- корни
- радикалы
$\endgroup$
11
$\begingroup$
$\endgroup$0
$\begingroup$
Как упоминалось выше, не существует общей формулы для нахождения всех корней любого уравнения 5-й степени, но существуют различные специальные методы решения.
Мой собственный фаворит:
— Проверив, посмотрите, есть ли у полинома какие-либо простые действительные решения, такие как x = 0 или x = 1 или -1, или 2, или -2. Если это так, разделите многоугольник на (x-a), где a — найденный корень, а затем решите полученное уравнение 4-й степени по правилу Феррари.
— Если очевидного реального корня не существует, его необходимо найти. Это можно сделать, заметив, что если f(p) и f(-p) имеют разные знаки, то корень должен лежать между x=p и x=-p. Теперь мы пробуем среднюю точку между p и -p, скажем, q. Затем мы повторяем описанную выше процедуру, постоянно уменьшая интервал, в котором можно найти корень. Когда интервал достаточно мал, мы нашли корень.
— это метод деления пополам; когда такой корень был выделен, мы делим многочлен на этот корень, получая уравнение 4-й степени, которое снова может быть решено Феррари или любым другим методом.
$\endgroup$
$\begingroup$
Явные элементарные числа генерируются из рациональных чисел путем применения конечных чисел $\exp$, $\ln$ и/или радикалов.
Ясно, что элементарные числа содержат все алгебраические числа, а явные элементарные числа содержат все явные алгебраические числа (числа, представляемые радикалами).
Чоу доказывает в [Chow 1999] свое
Следствие 1:
«Если гипотеза Шенуэля верна, то алгебраические числа в «явных элементарных числах» являются в точности корнями полиномиальных уравнений с целыми коэффициентами, которые разрешимы в радикалах».
Значит, квинтики, не разрешимые в радикалах, не могут быть решены элементарными числами (т.е. применением элементарных функций).
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
факторинг — Как факторизовать многочлены до 5-й степени?
спросил
Изменено 3 года, 8 месяцев назад
Просмотрено 14 тысяч раз
$\begingroup$
92+4)$$
Но как бы вы сделали это шаг за шагом? Я видел пару видео и блогов об этом, но они в основном используют примеры, где их является общим фактором между выражениями, но в данном случае их нет.
- полиномы
- факторинг
$\endgroup$
7
$\begingroup$
Время от времени вы находите многочлен более высокой степени, который можно разложить на множители путем проверки. В этом случае есть способ просто «увидеть» один шаг факторизации: 92+1)$$
Так вот, в большинстве случаев таких красивых паттернов не бывает. Тогда у вас останется теорема о рациональных корнях. Из того факта, что наш опережающий коэффициент равен $2$, а наш постоянный член равен $4$, заключаем, что любой линейный множитель будет соответствовать нулю вида $\pm\frac{p}{q}$, где $p$ равно множитель $4$, а $q$ — множитель $2$. Это дает нам несколько вариантов: $\pm 4, \pm 2, \pm 1, \pm \frac12$. Попробовав несколько из них, мы видим, что вставка $x=\frac12$ на самом деле дает значение $0$. Это говорит нам о том, что $(x-\frac12)$ является множителем, или очищающим знаменателем, $(2x-1)$.
$\endgroup$
$\begingroup$
Работая в предположении, что такой многочлен не является неприводимым и можно разложить на множители (что в данном случае ясно, поскольку у вас уже есть факторизация), мы обычно начинаем с поиска рациональных корней.
Теорема о рациональном корне утверждает, что если $z = \frac{a}{b}$ является рациональным корнем многочлена (в младших терминах), то $b$ должно делить старший коэффициент, а $a$ должно делить постоянный срок. Это дает нам несколько потенциальных рациональных корней:
$$ \left\{ \pm 1, \pm 2, \pm 4, \pm \frac{1}{2} \right\}. $$
Методом проб и ошибок можно определить, что единственным из них, который является корнем, является $\frac{1}{2}$. Отсюда мы знаем, что
$$ 2x^5 — x^4 + 10x^3 — 5x^2 + 8x — 4 = \left( x — \frac{1}{2} \right) q(x), $$
где $q$ — полином степени 4.