| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Корень слова, что это такое?
Корень слова — это его главная значимая часть, в которой заключено общее значение всех однокоренных слов.
Узнаем, что такое корень слова, если подберем слова и вычленим в их составе общую значимую часть, которая объединяет их в одну семью.
Корень — главная морфемаКак главная морфема, корень объединяет слова по общности их значения, например:
водный — подводный — водяной — водник — подводник — водянистый.
Все эти слова обозначают предметы или признаки, имеющие отношения к водной стихии, так как в их морфемном составе прослеживается один и тот же корень вод-.
Слова с одним и тем же корнем называются однокоренными.
В слове может быть один или два корня
водный — водолаз — водосброс— водохранилище.
Следует различать слова с совпадающими по звучанию и написанию корнями, но разными по значению:
- гора — гористый — горный — горняк- горняцкий;
- угореть — загорать — перегореть — нагорать — пригореть.
В морфемном составе этих слов вычленим корень гор-, но это не один и тот же корень, а разные морфемы, не совпадающие по своему лексическому значению.
Корень в составе различных слов
Слов, состоящих из одного корня и окончания, в русском языке насчитывается немного, например:
вода, село, поле, земля, небо, юный, белый, зелёный, первый, пятый, веду, несу, иду.
Корни этих слов способны выступать без приставок и словообразовательных суффиксов, поэтому их называют свободными.
Большинство слов русского языка состоят из сочетания разных морфем:
1. корня, суффикса, окончания
- сельский
- домик
- юность
- голосок
2. приставки, корня , окончания
- предобрый
- соавтор
- побежим
3. приставки, корня, суффикса, окончания
- заплывать
- пришкольный
- украшение
4. приставки, корня, суффикса, суффикса
- по—дружески
- набросив
- уплотнив
и т. д.
Некоторые корни в свободном виде не встречаются. Они являются связанными с приставками, суффиксами или с другими корнями:
- -сяг- присяга, досягнуть, посягать;
- -у- разуть, обуть, обувь;
Как определить корень в слове?
Чтобы определить корень в слове, подбираем родственные слова и вычленяем в них общую значимую часть, в которой содержится их основное лексическое значение, например:
лес — лесной — лесник — лесничий — лесничество;
Общей частью, имеющей значение «множество деревьев в природе», этого ряда однокоренных слов является морфема лес-, которую назовем корнем.
Рассмотрим другой ряд слов:
трава — травка, травинка, травушка, травяной, затравенеть.
Главной морфемой этого ряда родственных слов является часть трав-, которую выделим в качестве корня.
Видео «Корень слова. Однокоренные слова. Написание корня в однокоренных словах»
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Является ли квадратный корень из 2 рациональным числом?
Действительные числа, которые не могут быть представлены простой дробью, называются иррациональными числами.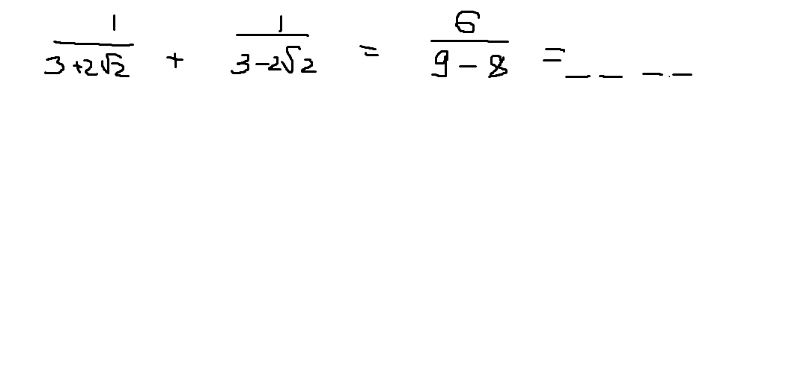
Его нельзя представить в виде отношения типа p/q, где p и q — целые числа, q≠0. Это несоответствие рациональных чисел. Иррациональные числа обычно записываются как R \ Q, где знак обратной косой черты означает «установить минус». Его также можно записать как R-Q, что представляет собой разницу между набором действительных и рациональных чисел.
Расчеты на основе этих цифр несколько сложнее. К иррациональным числам относятся √5, √11, √21 и так далее. Если такие числа используются в арифметических операциях, сначала должны быть оценены значения под корнем.
Что такое рациональные числа? Рациональные числа имеют вид p/q, где p и q — целые числа, а q ≠ 0. Из-за лежащей в основе структуры чисел, формы p/q, большинству людей трудно отличить дроби от рациональных чисел. Когда рациональное число делится, вывод находится в десятичной форме, которая может быть как оканчивающейся, так и повторяющейся. 3, 4, 5 и т. д. — некоторые примеры рациональных чисел, поскольку они могут быть выражены дробью как 3/1, 4/1 и 5/1.
Иррациональные числа — это любые числа, не являющиеся рациональными числами. Иррациональные числа могут быть представлены десятичными знаками, но не дробями, что означает, что они не могут быть представлены как отношение двух целых чисел. После запятой иррациональные числа имеют бесконечное количество неповторяющихся цифр.
Вещественное число, которое не может быть представлено как отношение целых чисел, называется иррациональным числом. Например, √3 — иррациональное число.
Десятичное расширение иррационального числа не заканчивается и не повторяется. Определение иррационального — это число, которое не имеет отношения или для которого нельзя установить отношение, то есть число, которое не может быть представлено никаким другим способом, кроме как с использованием корней. Иными словами, иррациональные числа нельзя представить в виде отношения двух целых чисел.
Примеры иррациональных чисел
√3, √5 и т.
д. — некоторые примеры иррациональных чисел, поскольку они не могут быть выражены в форме p/q. Число Эйлера, золотое сечение, π и т. д. также являются примерами иррациональных чисел. 1/0, 2/0, 3/0 и т. д. иррациональны, потому что дают нам неограниченные значения.
Решение:
Похожие вопросыИррациональные числа — это действительные числа, которые нельзя записать в виде p/q, где p и q — целые числа, а q≠0. Например, √3 и √5 и так далее иррациональны. Рациональное число — это любое число, которое можно записать в виде p/q, где p и q — целые числа, а q≠0.
Рациональное число — это своего рода действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √2 не может быть выражено в виде p/q. В качестве альтернативы 2 является простым числом или рациональным числом.
Здесь заданное число √2 равно 1,4121, что дает результат бесконечной и неповторяющейся десятичной дроби и не может быть выражено в виде дроби .., поэтому √2 — это иррациональное число.
Вопрос 1: Является ли √7 рациональным или иррациональным числом?
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √7 не может быть выражено в виде p/q. Альтернативно, 7 является простым числом. Это означает, что число 7 не имеет пары и не делится на 2. Следовательно, √7 — иррациональное число.
Вопрос 2: Определите, является ли 5.152152…. является рациональным числом.
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0.
