Phosphoryl Podands Ph3P(O)Ch3O(Ch3Ch3O)nCh3P(O)Ph3 (Ln, n = 0–5): Complexation and Extraction of Rare Earth Elements. Crystal Structures of [Ln2L03(NO3)6]xh3O (Ln = Nd, x = 1.99 Ln = Eu, x = 1 Ln = Er, x = 6.5 Ln = Lu, x = 6) and [LnL2(NO3)3(h3O)] — статья
Phosphoryl Podands Ph3P(O)Ch3O(Ch3Ch3O)nCh3P(O)Ph3 (Ln, n = 0–5): Complexation and Extraction of Rare Earth Elements. Crystal Structures of [Ln2L03(NO3)6]xh3O (Ln = Nd, x = 1.99 Ln = Eu, x = 1 Ln = Er, x = 6.5 Ln = Lu, x = 6) and [LnL2(NO3)3(h3O)]статья
Информация о цитировании статьи получена из
Scopus,
Web of Science
Статья опубликована в журнале из списка Web of Science и/или Scopus
Дата последнего поиска статьи во внешних источниках: 25 января 2019 г.
- Авторы: Polyakova I.N., Krivorot’ko E.S., Ivanova I.S., Pyatova E.N., Demin S.V., Zhilov V.I., Baulin V.E., Ilyukhin A.B., Tsivadze A.Yu
- Журнал: Russian Journal of Inorganic Chemistry
- Том: 63
- Номер: 10
- Год издания: 2018
- Издательство: Maik Nauka/Interperiodica Publishing
- Местоположение издательства: Russian Federation
- Первая страница: 1372
- Последняя страница: 1380
- Оригинальные версии: Фосфорилподанды Ph3P(O)Ch3O(Ch3Ch3O)nCh3P(O)Ph3 (Ln, n = 0–5): комплексообразование и экстракция редкоземельных элементов
- DOI:
10.
1134/s0036023618100169 - Добавил в систему: Жилов Валерий Иванович
1134/s0036023618100169Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
10.17Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Здравствуйте! Помогите решить задачу»На трёх полках расставили 36 чашек так,что на верхней полке чашек вдвое больше,чем на нижней,а на средней полке.
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Решено
Туристы проплыли на лодке по озеру 18 км за такое же время, что и 15 км против течения реки. Найдите скорость лодки по озеру, если скорость течения реки 2 км/ч
Начертите квадрат, сторона которого равна 8 см. Постройте : а) прямоугольник, площадь которого составляет 25 % площади квадрата ; б) прямоугольник, 80 % площади которого равны площади квадрата.
Пользуйтесь нашим приложением
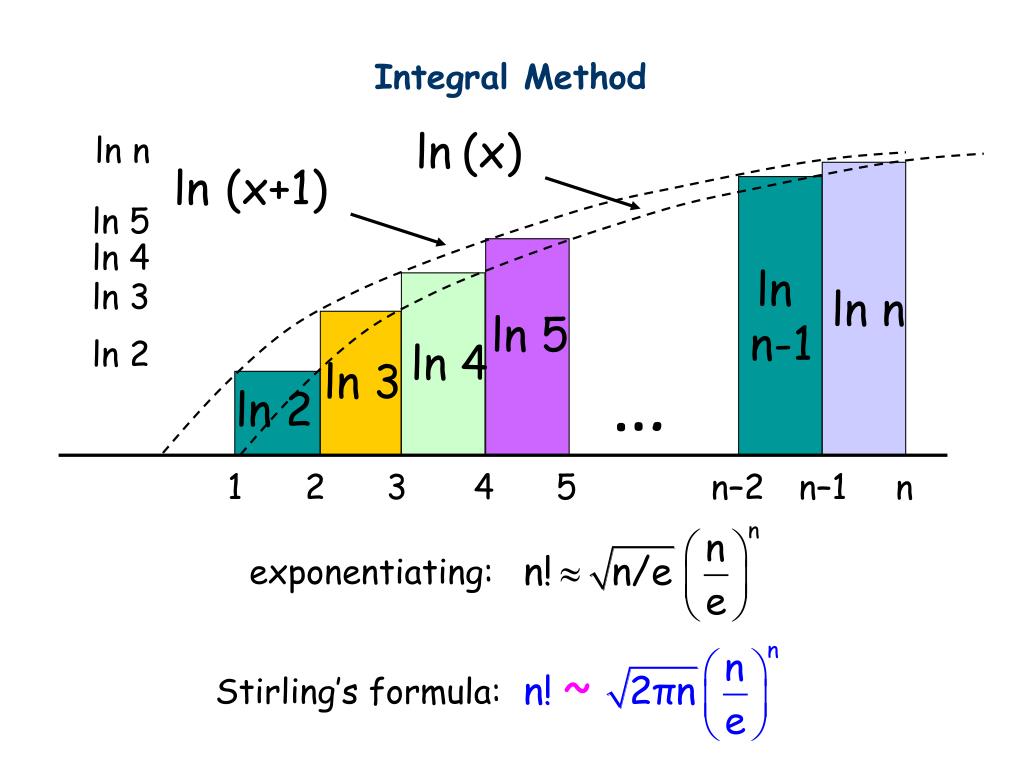
реальный анализ — Что такое $\log(n+1)-\log(n)$?
спросил
Изменено 4 года, 4 месяца назад
Просмотрено 6к раз
$\begingroup$
Что такое разрыв $\log(n+1)-\log(n)$ между log последовательных целых чисел? То есть какая точность логарифмов правильно определяет целые числа? 93}-\cdots\приблизительно\frac1n.
$$
$\endgroup$
$\begingroup$
Особенно ответ Лайма абсолютно правильный и очень хороший подход. Позвольте мне показать концептуально несколько более простой вариант, в котором используется только производная, а именно $(\log x)’=1/x$. Это строго убывающая функция, поэтому $\log x$ вогнута. В частности, его график находится ниже касательной в любой точке графика.
Получаем $\log (n+1)< \log n + 1/n$ и $\log n< \log (n+1) - 1/(n+1)$. Подводя итог:
$$\frac{1}{n+1} < \log (n+1)-\log n < \frac{1}{n}$$
$\endgroup$
$\begingroup$
Это довольно похоже на предыдущие ответы, но я думаю, что на это все же стоит обратить внимание. Вы спрашиваете о наклоне хорды графика $\log x$, хорды, соединяющей $(n,\log n)$ с $(n+1,\log(n+1))$. По теореме о среднем значении это равно наклону касательной $1/x$ при некотором $x$ между $n$ и $n+1$.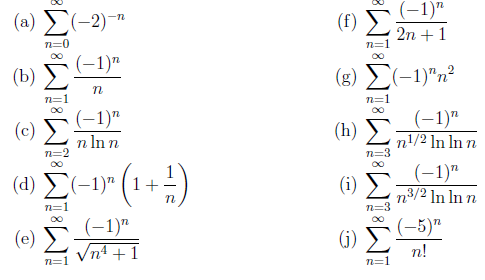
$\endgroup$ 9х \frac1t dt$. (Для $x>0$.)
Тогда $\ln(n+1)-\ln(n)$ — это площадь под кривой $f(x)=\frac1x$ от $n$ до $n+ 1$.
Ищем площадь на интервале длины $1$. Таким образом, численно площадь должна быть равна «средней» высоте. Поскольку функция $\frac1x$ строго убывает, мы получаем хорошее приближение к этой «средней» высоте, оценивая функцию $\frac1x$ в средней точке интервала (а именно в $n+\frac12$).
Итак, $\ln(n+1)-\ln(n)\приблизительно \frac{1}{n+\frac12}$, причем приближение становится все лучше и лучше по мере увеличения $n$.
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
92}$в логе тест и условия успехаЗадавать вопрос
спросил
Изменено 6 лет, 9 месяцев назад
Просмотрено 3к раз
$\begingroup$
92}.$$Я думаю, что есть тест соотношения, и когда я попробовал, он застрял
****Важно, хотя на этот вопрос был дан очень хороший ответ, просто у меня возникла проблема с одним из ответов, поэтому я ПРОСТО оставил комментарий и был бы признателен если кто-то сможет обратиться к нему
Спасибо!***
- исчисление
- реальный анализ
- последовательности-и-серии
$\endgroup$
2
92}$ расходится по тесту сравнения.