Сколько будет 5 в 3 степени?
Сколько будет 5 в 3 степени?
5 в 3 степени Возведение в степень это операция перемножения числа на само себя заданное количество раз. Пять в третьей степени равно 125.
Сколько будет 100 в 3 степени?
3 в степени 100 = 5.× 10 в степени 47 eddibear3a и 2 других пользователей посчитали ответ полезным!
Сколько будет 3 в 9 степени?
9 в 3 степени Решение: Возведение в степень это операция перемножения числа на само себя заданное количество раз. Девять в третьей степени равно 729.
Как правильно считать степени?
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры. Условие: возведите – 2 в степень 4 .
Как складывать числа в одинаковой степени?
Как складывать числа с одинаковыми степенями Сначала возводим каждое число в степень и затем выполняем сложение. В уравнениях это будет происходить немного иначе. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать.
В уравнениях это будет происходить немного иначе. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать.
Как можно узнать какой степени уравнение?
Степень уравнения — это максимальный или наибольший показатель степени переменной, присутствующей в уравнении. Чтобы ее определить, достаточно обратить внимание на значение степеней имеющихся переменных. Максимальная величина и определяет степень уравнения.
Как определить степень уравнения с двумя неизвестными?
Степенью уравнения с несколькими неизвестными называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая. 3x2y + xy + 25 = 0. Для наглядности расставим показатели первой степени (которые обычно не ставят): 3x2y1 + x1y1 + 251 = 0.
Какое уравнение называется дробным рациональным?
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.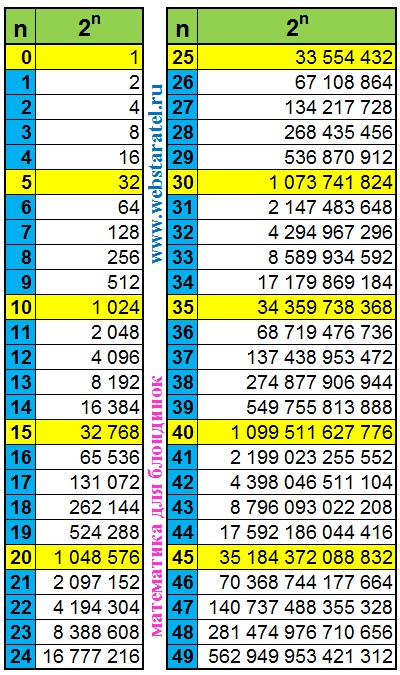 Чтобы решить дробное уравнение, необходимо: … умножить обе части уравнения на общий знаменатель; 3.
Чтобы решить дробное уравнение, необходимо: … умножить обе части уравнения на общий знаменатель; 3.
Что такое уравнение первой степени?
Уравнением первой степени с двумя неизвестными называется уравнение вида ax + bx = c, где x, y – неизвестные, a, b (коэффициенты при неизвестных), не равные оба нулю, c – любое число. … Каждая пара значений x и y, подстановка которых в уравнение с двумя неизвестными x и y, обращает его в верное равенство.
Что такое уравнение второй степени?
Определение: Квадратным уравнением называется уравнение вида: ax2 + bx + c = 0, где a, b, c — действительные числа, где а ≠ 0. Выражение D = b2 — 4ac называется дискриминантом квадратного уравнения. …
Что значит найти решение системы уравнений?
Решить систему уравнений — это значит найти все её решения или установить, что решений нет. a) Пара чисел (1; 1) является решением системы уравнений, т. … обращает каждое уравнение системы в верное числовое равенство.
… обращает каждое уравнение системы в верное числовое равенство.
Как решать через дискриминант?
Как решать квадратные уравнения через дискриминант
- как найти дискрининант: D = b2 − 4ac;
- если дискриминант отрицательный — зафиксировать, что действительных корней нет;
- если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b2/2a;
Сколько корней у Биквадратного уравнения?
где a, b и c — числа, причём a≠0. Следовательно, биквадратное уравнение может иметь 4, 3, 2 корня, 1 корень либо не иметь корней.
Сколько корней имеет Биквадратное уравнение?
Дискриминант положительный, один корень положительный, а другой отрицательный, значит, биквадратное уравнение имеет 2 корня.
Какое уравнение является дробным рациональным уравнением?
Дробно—рациональные уравнения – уравнения, которые можно свести к виду P(x)Q(x) P ( x ) Q ( x ) =0 , где P(x) и Q(x) — выражения с иксом (или другой переменной). Проще говоря, это уравнения, в которых есть хотя бы одна дробь с переменной в знаменателе.
Проще говоря, это уравнения, в которых есть хотя бы одна дробь с переменной в знаменателе.
Что такое рациональное выражение?
Рациональное выражение – это любое выражение, составленное из чисел, буквенных переменных, арифметических операций и возведения в степень.
Как определить целое выражение?
Целое выражение – это математическое выражение, составленное из чисел и буквенных переменных с помощью действий сложения, вычитания и умножения. Также к целым относятся выражения, которые имеют в своем составе деление на какое либо число, отличное от нуля.
Что называется целым рациональным выражением?
Целым рациональным выражением называется выражение, которое может быть составлено из чисел и переменных с помощью знаков сложения, вычитания, умножения и возведения в степень с натуральным показателем с возможным использованием скобок.
Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников
Числа в Python 3: целые, вещественные, комплексные.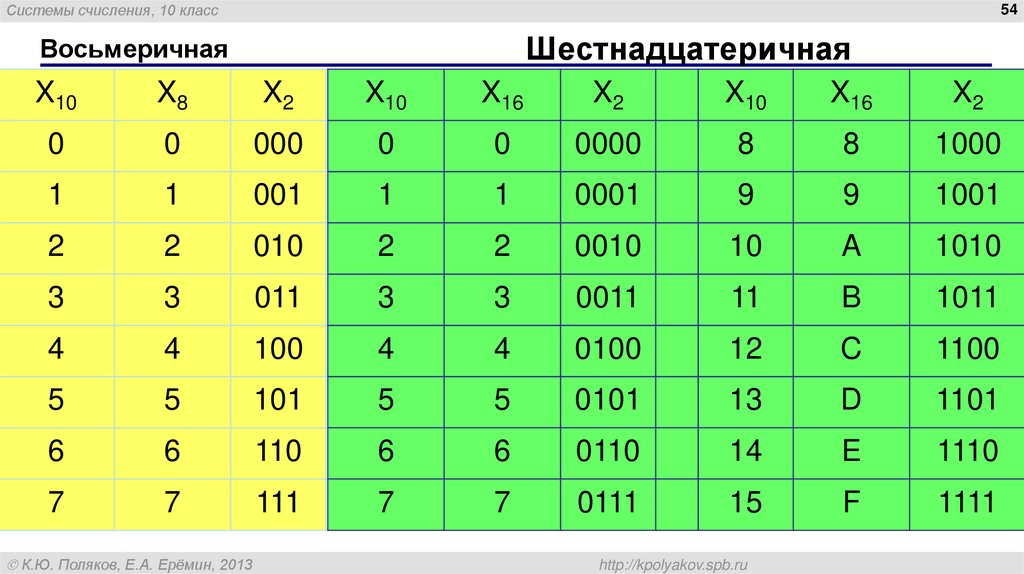 Работа с числами и операции над ними.
Работа с числами и операции над ними.
Целые числа (int)
Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:
| x + y | Сложение |
| x — y | Вычитание |
| x * y | Умножение |
| x / y | Деление |
| x // y | Получение целой части от деления |
| x % y | Остаток от деления |
| -x | Смена знака числа |
| abs(x) | Модуль числа |
| divmod(x, y) | Пара (x // y, x % y) |
| x ** y | Возведение в степень |
| pow(x, y[, z]) | xy по модулю (если модуль задан) |
Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти).
>>> 255 + 34 289 >>> 5 * 2 10 >>> 20 / 3 6.y Побитовое исключающее или x & y Побитовое и x << n Битовый сдвиг влево x >> y Битовый сдвиг вправо ~x Инверсия битов Дополнительные методы
int.bit_length() - количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.
>>> n = -37 >>> bin(n) '-0b100101' >>> n.bit_length() 6int.to_bytes(length, byteorder, *, signed=False) - возвращает строку байтов, представляющих это число.
>>> (1024).to_bytes(2, byteorder='big') b'\x04\x00' >>> (1024).to_bytes(10, byteorder='big') b'\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00' >>> (-1024).to_bytes(10, byteorder='big', signed=True) b'\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00' >>> x = 1000 >>> x.to_bytes((x.bit_length() // 8) + 1, byteorder='little') b'\xe8\x03'classmethod int.
from_bytes(bytes, byteorder, *, signed=False) - возвращает число из данной строки байтов.
>>> int.from_bytes(b'\x00\x10', byteorder='big') 16 >>> int.from_bytes(b'\x00\x10', byteorder='little') 4096 >>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True) -1024 >>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False) 64512 >>> int.from_bytes([255, 0, 0], byteorder='big') 16711680Системы счисления
Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:
- int([object], [основание системы счисления]) - преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.

- bin(x) - преобразование целого числа в двоичную строку.
- hex(х) - преобразование целого числа в шестнадцатеричную строку.
- oct(х) - преобразование целого числа в восьмеричную строку.
Примеры:
>>> a = int('19') # Переводим строку в число
>>> b = int('19.5') # Строка не является целым числом
Traceback (most recent call last):
File "", line 1, in
ValueError: invalid literal for int() with base 10: '19.5'
>>> c = int(19.5) # Применённая к числу с плавающей точкой, отсекает дробную часть
>>> print(a, c)
19 19
>>> bin(19)
'0b10011'
>>> oct(19)
'0o23'
>>> hex(19)
'0x13'
>>> 0b10011 # Так тоже можно записывать числовые константы
19
>>> int('10011', 2)
19
>>> int('0b10011', 2)
19 Вещественные числа (float)
Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 0.9999999999999999
Для высокой точности используют другие объекты (например Decimal и Fraction)).
Также вещественные числа не поддерживают длинную арифметику:
>>> a = 3 ** 1000 >>> a + 0.1 Traceback (most recent call last): File "", line 1, in OverflowError: int too large to convert to float
Простенькие примеры работы с числами:
>>> c = 150 >>> d = 12.9 >>> c + d 162.9 >>> p = abs(d - c) # Модуль числа >>> print(p) 137.1 >>> round(p) # Округление 137
Дополнительные методы
float.as_integer_ratio() - пара целых чисел, чьё отношение равно этому числу.
float.is_integer() - является ли значение целым числом.
float.hex() - переводит float в hex (шестнадцатеричную систему счисления).
classmethod float.fromhex(s) - float из шестнадцатеричной строки.
>>> (10.5).hex() '0x1.5000000000000p+3' >>> float.fromhex('0x1.5000000000000p+3') 10.5
Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.
Модуль math предоставляет более сложные математические функции.
>>> import math >>> math.pi 3.141592653589793 >>> math.sqrt(85) 9.219544457292887
Модуль random реализует генератор случайных чисел и функции случайного выбора.
>>> import random >>> random.random() 0.15651968855132303
Комплексные числа (complex)
В Python встроены также и комплексные числа:
>>> x = complex(1, 2) >>> print(x) (1+2j) >>> y = complex(3, 4) >>> print(y) (3+4j) >>> z = x + y >>> print(x) (1+2j) >>> print(z) (4+6j) >>> z = x * y >>> print(z) (-5+10j) >>> z = x / y >>> print(z) (0.44+0.08j) >>> print(x.conjugate()) # Сопряжённое число (1-2j) >>> print(x.imag) # Мнимая часть 2.0 >>> print(x.real) # Действительная часть 1.0 >>> print(x > y) # Комплексные числа нельзя сравнить Traceback (most recent call last): File "", line 1, in TypeError: unorderable types: complex() > complex() >>> print(x == y) # Но можно проверить на равенство False >>> abs(3 + 4j) # Модуль комплексного числа 5.0 >>> pow(3 + 4j, 2) # Возведение в степень (-7+24j)
Для работы с комплексными числами используется также модуль cmath.
Для вставки кода на Python в комментарий заключайте его в теги <pre><code>Ваш код</code></pre>
Свежее
- Модуль csv - чтение и запись CSV файлов
- Создаём сайт на Django, используя хорошие практики. Часть 1: создаём проект
- Онлайн-обучение Python: сравнение популярных программ
Категории
- Книги о Python
- GUI (графический интерфейс пользователя)
- Курсы Python
- Модули
- Новости мира Python
- NumPy
- Обработка данных
- Основы программирования
- Примеры программ
- Типы данных в Python
- Видео
- Python для Web
- Работа для Python-программистов
Полезные материалы
- Сделай свой вклад в развитие сайта!
- Самоучитель Python
- Карта сайта
- Отзывы на книги по Python
- Реклама на сайте
Мы в соцсетях
Как решить число 3 в третьей степени? – Обзоры Вики
Когда число находится в «третьей степени», это означает, что вы будете умножение числа на само себя в три раза.
Отсюда, чему равно 8 в степени 3? Ответ: 8 в степени 3 можно представить как 8.3 = 8 × 8 × 8 = 512.
Каково значение 3 степени 3? Следовательно, 27 является 3rd мощность 3.
Дополнительно Какова третья степень числа 3? Экспонентные таблицы и шаблоны
| Полномочия 3 | Полномочия 9 |
|---|---|
| 33 = 27 | 93 = 729 |
| 34 = 81 | 94 = 6561 |
| 35 = 243 | 95 = 59,049 |
| 36 = 729 | 96 = 531,441 |
Как умножать дроби? Есть 3 простых шага для умножения дробей
- Умножьте верхние числа (числители).
- Умножьте нижние числа (знаменатели).
- При необходимости упростите дробь.
Какова третья степень числа 3?
Пояснение: 53 = 5 × 5 × 5 = 125. 53 также можно понимать как 5 куб. Всякий раз, когда число (х) умножается само на себя трижды, полученный ответ называется кубом этого числа.
Всякий раз, когда число (х) умножается само на себя трижды, полученный ответ называется кубом этого числа.
Что такое показатель числа 5? Полномочия и показатели
| базовый номер | 2-я степень | 5-я степень |
|---|---|---|
| 3 | 9 | 243 |
| 4 | 16 | 1,024 |
| 5 | 25 | 3,125 |
| 6 | 36 | 7,776 |
Какое число равно 10 в третьей степени? Ответ: Значение 10 увеличено до 3.rd мощность т.е. 103 is 1000.
Как написать 2 в степени 3?
2 в третьей степени можно записать как 23 = 2×2×2, поскольку 2 умножается на себя в 3 раза. Здесь 2 называется «основанием», а 3 - «показателем» или «степенью».
Также каков ответ 10 степени 3? Ответ: Значение 10 увеличено до 3.rd мощность т.е. 103 is 1000.
Как написать 7 в степени 3?
Ответ: 7 в степени 3 можно выразить как 73 = 7×7×7 = 343.
Чему равна третья степень числа 3? Ответ: 1 в степени 3 равно 3.
3 в степени 1 можно записать как 31. Где число 3 называется основанием, тогда как 1 является степенью выражения, и мы знаем, что любое число, возведенное в степень единицы, равно самому числу.
Как написать 6 в степени 3?
Ответ: 6 в степени 3 можно выразить как 63 = 6×6×6= 216. Объяснение: два важных термина, часто используемые в экспонентах, — это основание и степени. Чтобы найти 6 в степени 3, мы можем записать это в экспоненциальной форме как 63 где 6 - основание, а 3 - мощность.
Как решить дроби?
Что такое дробная математика? дробь, В арифметике, число, выраженное как частное, в котором числитель делится на знаменатель. В простой дроби оба являются целыми числами. У сложной дроби в числителе или знаменателе есть дробь. В правильной дроби числитель меньше знаменателя.
В простой дроби оба являются целыми числами. У сложной дроби в числителе или знаменателе есть дробь. В правильной дроби числитель меньше знаменателя.
Как написать 4 в кубе?
Изучение чисел куба
- куб. = 1 3 = 1 × 1 × 1. = …
- куб. = 2 3 = 2 × 2 × 2. = …
- куб. = 3 3 = 3 × 3 × 3. = …
- куб. = 4 3 = 4 × 4 × 4. = …
- куб. = 5 3 = 5 × 5 × 5. = 125.
- куб. = 6 3 = 6 × 6 × 6. = 216.
- куб. = 7 3 = 7 × 7 × 7. = 343.
- куб. = 8 3 = 8 × 8 × 8. = 512.
Что такое куб числа 8? Поскольку кубический корень из 8 — целое число, 8 — совершенный куб.
. ..
..
Кубический корень из 8 в радикальной форме: ∛8.
| 1. | Что такое кубический корень из 8? |
|---|---|
| 3. | Является ли кубический корень из 8 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 8 |
Что такое 3 в степени 3?
Таблицы экспонент и паттерны
| Полномочия 3 | Полномочия 9 |
|---|---|
| 33 = 27 | 93 = 729 |
| 34 = 81 | 94 = 6561 |
| 35 = 243 | 95 = 59,049 |
| 36 = 729 | 96 = 531,441 |
Чему равен показатель 2? Показатель 2 стоит количество раз, когда значение 4 умножается. То, на что умножается число 4, называется «основой». Другой способ понять это, показатель степени - это число, умноженное на «4», которое появляется в уравнении умножения.
Каков показатель степени 2 3?
Ответ: 27 в степени 2/3 равно 9.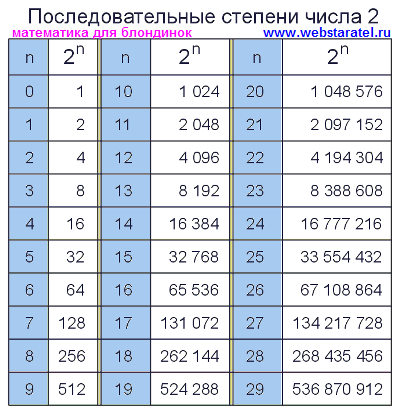
Как получить 6 в 3-й степени? Ответ: 6 в 3-й степени 63 = 216.
Сколько 7 в показателе 3?
Ответ: 7 в степени 3 можно выразить как 73 = 7×7×7 = 343.
Чему равно 9 в степени 3? Ответ: 9 в степени 3 можно представить как 9.3 = 9 × 9 × 9 = 729.
Степени поражения легких: КТ1, КТ2, КТ3, КТ4
Компьютерная томография (КТ) легких считается «золотым стандартом» диагностики воспаления легких, в частности пневмонии, ассоциированной с COVID-19. На томограммах — множественных сканах дыхательного органа в трех плоскостях — визуализируются нефункциональные участки уплотнения или инфильтрации легочной ткани.
Когда говорят о поражении легких при пневмонии, то имеют в виду, что альвеолы — маленькие пузырькообразные полости легких, которые отвечают за хранение воздуха и газообмен, заполняются жидкостью, слизью, фиброзной тканью и «выходят из строя».
На ранних стадиях пневмония может протекать практически бессимптомно или вызывать незначительный дискомфорт: кашель, затрудненное дыхание, повышение температуры. Однако она быстро переходит в более тяжелую форму и человек начинает ощущать нехватку воздуха, спазм в груди, вызванный отеком легких, или острый респираторный дистресс-синдром — обширный воспалительный процесс, который дает осложнение на сердце и в некоторых случаях приводит к летальному исходу.
Однако она быстро переходит в более тяжелую форму и человек начинает ощущать нехватку воздуха, спазм в груди, вызванный отеком легких, или острый респираторный дистресс-синдром — обширный воспалительный процесс, который дает осложнение на сердце и в некоторых случаях приводит к летальному исходу.
В этой связи очень важно вовремя распознать пневмонию и начать лечение. КТ легких — единственный метод диагностики, который позволяет выявить очаги инфильтрации и оценить степень их выраженности, даже если поражено менее 5% легких.
После компьютерной томографии легких, особенно при наличии подозрений на вирусную пневмонию, пациентов в первую очередь интересуют результаты и расшифровка обследований. В этой статье мы расскажем о том, что означает КТ1, КТ2, КТ3, КТ4 в заключении, и на что следует обратить внимание, если пневмония все-таки была обнаружена.
Что означает КТ1, КТ2, КТ3, КТ4 при вирусной пневмонии COVID-19?
Чтобы врачи могли объективно оценивать объем поражения легких, взвешивать риски и реагировать на вызовы, был принят единый стандарт классификации вирусных пневмоний по степени тяжести, где:
КТ-0 — отсутствие признаков вирусной пневмонии;
КТ-1 — легкая форма пневмонии с участками «матового стекла», выраженность патологических изменений менее 25%;
КТ-2 — умеренная пневмония, поражено 25-50% легких;
КТ-3 — среднетяжелая пневмония, поражено 50-75% легких;
КТ-4 — тяжелая форма пневмонии, поражено >75% легких.
Процент деструкции легочной ткани определяется по томограммам. Врач-рентгенолог оценивает по пятибалльной шкале каждую из пяти долей легких.* Если признаки пневмонии не выявлены, то значение соответствует 0; 1 балл свидетельствует о поражении легких 5%, и так далее.
* Согласно «Временным методическим рекомендациям» Министерства Здравоохранения РФ от октября 2020 г., принятая и описанная выше балльная система оценки легочных сегментов и долей упразднена. Объективность оценки поддерживается программным обеспечением и медицинской экспертизой.
Иными словами, сокращение КТ1, КТ2, КТ3 или КТ4, которое врач-рентгенолог пишет в заключении, указывает на объемы нефункциональной легочной ткани в совокупности с другими признаками, характерными для той или иной стадии. Это эмпирическая визуальная шкала, принятая рентгенологами.
Данную шкалу визуальной оценки легких по результатам компьютерной томографии (или МСКТ) разработали только во время пандемии новой коронавирусной инфекции. Ее ввели специалисты из Центра диагностики и телемедицины США, изучив КТ-исследования 13 003 человек, которые составили основную выборку.
Ее ввели специалисты из Центра диагностики и телемедицины США, изучив КТ-исследования 13 003 человек, которые составили основную выборку.
Примечательно, что скорость перехода пневмонии к следующей, более осложненной степени зависит не только от возраста пациента (чем старше, тем быстрее), но и от текущей стадии заболевания. А именно, если вирусная пневмония SARS-CoV-2 у пациента была выявлена еще на первой стадии (КТ1), то предотвратить переход к следующей (КТ2) будет легче как минимум потому, что сравнительно малому числу вирионов требуется больше времени, чтобы распространиться по легким и спровоцировать более обширный воспалительный процесс. В то время как переход от КТ3 к КТ4 происходит очень быстро, и тогда жизнь пациента находится под угрозой. Анализируя уже упомянутую группу пациентов, ученые из США пришли к выводу, что при переходе в следующую группу, риск летального исхода при коронавирусе увеличивался примерно на 38%.
Процент вовлечения паренхимы (собственно поражения) легких в заключениях обычно указан приблизительно, поэтому диапазон значений может быть довольно широким, однако это не главный показатель. При определении степени тяжести воспаления легких учитываются и другие признаки воспаления легких:
При определении степени тяжести воспаления легких учитываются и другие признаки воспаления легких:
1) Наличие «матовых стекол» на сканах КТ, их локализация, консолидация. «Матовые стекла» — это светлые участки легких на томограммах, которые свидетельствуют об очагах инфильтрации. Плотная ткань не пропускает рентгеновские лучи. «Матовые стекла» — основной признак поражения легких на КТ. Их распространенность и консолидация соответствует тяжелым стадиям пневмонии КТ3 и КТ4.
2) Утолщение междолькового пространства легких или «симптом булыжной мостовой» — ткань легких на сканах КТ имеет внешнее визуальное сходство с брусчаткой. Соответствует тяжелой стадии пневмонии КТ4.
3) Симптом «обратного гало» или «ободка́» — на томограммах выглядит как светлые кольца. Это участки уплотнения вокруг очага инфекции. Считается признаком организующейся пневмонии.
4) Ретикулярные изменения — тонкие линии патологически измененного легочного интерстиция, формирующие сеть.
Если в заключении указана «полисегментарная пневмония», это значит, что признаки воспалительного процесса обнаружены в обоих легких, в нескольких сегментах.
Поражение легких КТ1
На сканах КТ легких обнаружены «матовые стекла» — менее трех. Диаметр очага инфильтрации не превышает 3 см, иные патологические изменения легких не обнаружены. У пациента может быть высокая температура, затрудненное дыхание, кашель, иногда явные симптомы отсутствуют. Лечиться от внебольничной пневмонии КТ1 можно в амбулаторных условиях и дома после консультации врача.
Поражение легких КТ2
КТ2 означает, что обнаружено более трех участков воспаления легких по типу «матового стекла» диаметром не более 5 см. Также как и в случае с КТ1, это внебольничная пневмония, при которой не нужна госпитализация. Пациент лечится дома, соблюдая рекомендации врача. КТ легких поможет ответить на вопрос — имеется ли активный воспалительный процесс и тенденция к консолидации «матовых стекол». Если лечение не помогает, и становится хуже, рекомендовано сделать повторное КТ легких, чтобы оценить динамику и скорректировать лечение. Поскольку у пациента с умеренной пневмонией КТ2 может быть поражено до 50% легких, после основного лечения необходима реабилитация.
Если лечение не помогает, и становится хуже, рекомендовано сделать повторное КТ легких, чтобы оценить динамику и скорректировать лечение. Поскольку у пациента с умеренной пневмонией КТ2 может быть поражено до 50% легких, после основного лечения необходима реабилитация.
Поражение легких КТ3
Обнаружены множественные участки «матового стекла» с тенденцией к консолидации. Это основной признак, но возможны и другие: ретикулярные изменения, «дерево в почках» или центрилобулярные очаги. При пневмонии КТ3 поражено более 50% легких, нужна срочная госпитализация и интенсивная терапия. Множественные инфекционные очаги и подавленные защитные силы организма способствуют тому, что переход от КТ3 к КТ4 происходит быстрее и легче, чем от КТ1 к КТ2.
Поражение легких КТ4
Критическая стадия поражения легких, когда более 75% легких не участвует в газообмене. На томограммах визуализируется как диффузное поражение лёгочной ткани с ретикулярными изменениями и симптомом «булыжной мостовой», гидроторакс. Пациент может нуждаться в реанимации с искусственной вентиляцией легких (ИВЛ).
Пациент может нуждаться в реанимации с искусственной вентиляцией легких (ИВЛ).
Human Papillomavirus высокого канцерогенного риска (16, 18, 31, 33, 35, 39, 45, 51, 52, 56, 58, 59, 66, 68 типы), ДНК количественно, скрининг с определением возможности интеграции вируса в геном [реал-тайм ПЦР]
Исследование используется для диагностики папиллома-вирусной инфекции, с одновременным определением количества вирусной ДНК в исследуемом материале. Анализ позволяет сделать вывод о степени поражения слизистой, оценить эффективность терапии в процессе лечения. Определяется суммарное количество ДНК 14 типов ВПЧ высокого канцерогенного риска (ВКР) с отдельным определением ДНК ВПЧ 16-го, 18-го и 45-го генотипов. Тест также позволяет оценить вероятность интеграции ВПЧ 16-го, 18-го и 45-го типа в геном человека (что является опасным и прогностически неблагоприятным фактором).
Синонимы русские
Папиллома-вирусы высокого канцерогенного риска, вирусы папилломы высокого канцерогенного риска, ВПЧ высокого канцерогенного риска.
Синонимы английские
Human Papillomavirus, DNA; HPV, Viral Load.
Метод исследования
Полимеразная цепная реакция в режиме реального времени.
Какой биоматериал можно использовать для исследования?
Соскоб урогенитальный.
Как правильно подготовиться к исследованию?
- Женщинам исследование рекомендуется производить до менструации или через 2-3 дня после её окончания.
- Мужчинам не мочиться в течение 3 часов до взятия урогенитального мазка.
Общая информация об исследовании
Вирусы папилломы человека (ВПЧ) представляют собой широко распространённую и вариабельную группу вирусов, поражающих эпителий кожи и слизистых оболочек и обладающих онкогенным потенциалом. ВПЧ передаётся при тесном контакте с инфицированным эпителием, поэтому основные пути заражения – половой и контактно-бытовой. Возможна передача ВПЧ от инфицированной матери к плоду.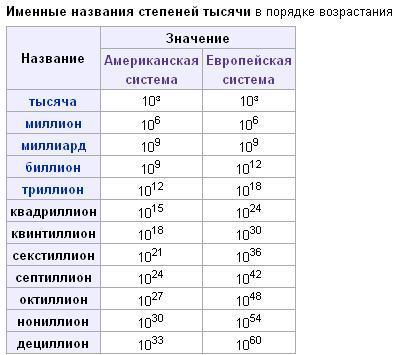
К факторам, провоцирующим развитие ВПЧ-инфекции, относятся ранее начало половой жизни, большое количество половых партнеров, сниженный иммунитет, применение оральных контрацептивов, авитаминозы, инфекции, передаваемые половым путём, курение и проживание в крупных городах.
Инкубационный период может длиться от 2 месяцев до 2-10 лет. Характерно скрытое течение заболевания, при котором отсутствуют клинические проявления, а при кольпоскопическом, цитологическом и гистологическом обследовании выявляется норма. В 30 % случаев в течение 6-12 месяцев может произойти избавление от вируса. Диагностика скрытой ВПЧ-инфекции осуществляется только методом ПЦР.
ВПЧ может по-разному воздействовать на эпителий: способствовать возникновению доброкачественных образований (папиллом, кондилом) или объединению ДНК папиллома-вируса с геном клетки, что приводит к дисплазии (неоплазии) и в дальнейшем к раку (чаще всего в переходной зоне шейки матки).
К папиллома-вирусам высокого онкогенного риска относятся ВПЧ типов 16, 18, 31, 33, 35, 39, 45, 51, 52, 56, 58, 59, 66, 68.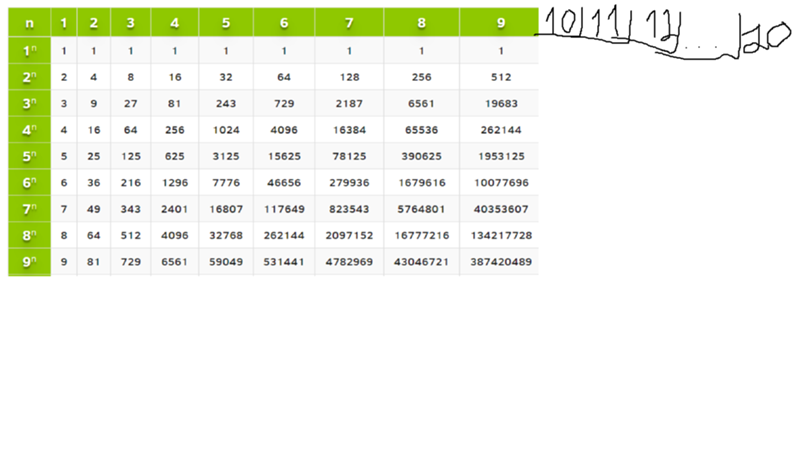
Для выявления возбудителя используется метод полимеразной цепной реакции, которая позволяет обнаружить ДНК вируса. Принцип метода основан на многократном увеличении числа копий специфичного для данного возбудителя участка ДНК.
Полимеразная цепная реакция (ПЦР) – это метод молекулярной диагностики, позволяющий выявлять генетический материал возбудителя на ранних этапах заболевания. Он характеризуется высокими показателями диагностической чувствительности и специфичности, быстротой получения конечного результата и доступностью. Особенностью метода является возможность выявлять ДНК вируса даже при малом содержании её в исследуемом биологическом материале. Метод основан на многократном увеличении числа копий специфичного для данного возбудителя участка ДНК. Для диагностики может использоваться разнообразный биологический материал, взятый у детей, взрослых лиц, людей с патологией иммунной системы, беременных женщин. Метод позволяет определять количество молекул ДНК исследуемого вируса, что является важным в диагностике острой формы инфекции, реактивации персистентной инфекции, носительстве вируса, а также при контроле эффективности проводимой противовирусной терапии.
По данным исследований, количественное содержание вируса в материале коррелирует со степенью неоплазии: чем выше вирусная нагрузка, тем выраженнее цитологические изменения в эпителии. При обследовании необходимо учитывать генотип вируса, наличие и степень цитологических и гистологических изменений в тканях, увеличение или снижение вирусной нагрузки через несколько месяцев (6 месяцев и более) после предыдущего обследования.
В исследовании проводится определение суммарного количества ДНК 14 типов ВПЧ высокого канцерогенного риска (ВКР) с отдельным определением ДНК ВПЧ 16, 18 и 45 генотипов. ВПЧ ВКР являются главной этиологической причиной развития РШМ и предшествующей ему тяжелой дисплазии. ВПЧ обнаруживается в 95 % случаев РШМ, из них 16, 18, 45 генотипы в совокупности являются причиной 75 % плоскоклеточных раков и 94 % аденокарцином шейки матки.
Известно, что развитие РШМ часто ассоциировано с интеграцией ДНК вируса в геном клетки-хозяина. Наиболее часто интегрируют ВПЧ 16 и 18 генотипов, при этом происходит разрыв участка Е1/Е2 при сохранении онкогена Е6/Е7. В тест-системе, на которой выполняется данное исследование, по разным каналам прибора детектируются разные участки генома ВПЧ 16, 18 и 45 типов. Выявление области Е6 при отсутствии области Е1/Е2 позволяет косвенно судить о возможности интеграции вируса в геном человека. В случае обнаружения возможности интеграции вируса в геном в бланк ответа выводится соответствующая информация.
В тест-системе, на которой выполняется данное исследование, по разным каналам прибора детектируются разные участки генома ВПЧ 16, 18 и 45 типов. Выявление области Е6 при отсутствии области Е1/Е2 позволяет косвенно судить о возможности интеграции вируса в геном человека. В случае обнаружения возможности интеграции вируса в геном в бланк ответа выводится соответствующая информация.
Для чего используется исследование?
- Чтобы оценить риск развития новообразований, ассоциированных с ВПЧ (рак шейки матки, рак прямой кишки, рак аногенитальной области и других локализаций).
- Для контроля за эффективностью лечения предраковых заболеваний, ассоциированных с ВПЧ.
- Для мониторинга папиллома-вирусной инфекции и прогнозирования ее течения.
Когда назначается исследование?
- При выявлении цитологических изменений в мазке на атипию, в мазке по Папаниколау, в гистологическом препарате.
- При кондиломах и других морфологических изменениях половых путей.

- При скрининге рака шейки матки у женщин старше 25-30 лет (в качестве дополнительного исследования).
- При наблюдении за инфицированными ВПЧ.
- При лечении рака и предраковых состояний, ассоциированных с ВПЧ.
Что означают результаты?
Уровень вирусной нагрузки интерпретируется с учетом результатов цитологического исследования мазков, гистологических изменений в биоптате и генотипа вируса, изменении его количества с течением времени.
- Количество ДНК ВПЧ не определяется при отсутствии вируса в исследуемом образце или его минимальном количестве (ниже детектируемого уровня) – риск развития патологического процесса, связанного с ВПЧ, минимальный.
- Клинически малозначимая концентрация вируса (менее 103 копий ДНК ВПЧ на 105 клеток) – минимальный риск развития дисплазии, транзиторное течение вирусного процесса.
- Клинически значимая концентрация вируса (более 103 копий ДНК ВПЧ на 105 клеток) – хроническая инфекция с высоким риском развития дисплазии и РШМ.

- Более 105 копий ДНК ВПЧ на 105 клеток при установленном факте персистентного течения инфекции (ВПЧ выявляется более 1 года) – усиленная вирусная нагрузка, ассоциированная с повышенным риском тяжелой дисплазии, часто встречается при РШМ.
- Снижение вирусной нагрузки в 10 раз за 6 месяцев – транзиторная инфекция.
- Рост вирусной нагрузки через 6 и более месяцев после лечения указывает на возможность рецидива.
Важные замечания
- Инфицирование ВПЧ не всегда приводит к раку шейки матки.
- Возможно одновременное заражение несколькими генотипами ВПЧ.
- Результат анализа должен интерпретироваться с учетом заключений цитологического и гистологического исследований.
Также рекомендуется
- Human Papillomavirus 16/18 (HPV 16/18), ДНК [реал-тайм ПЦР]
- Human Papillomavirus 6/11 (HPV 6/11), ДНК [реал-тайм ПЦР]
- Human Papillomavirus высокого канцерогенного риска (16, 18, 31, 33, 35, 39, 45, 51, 52, 56, 58, 59 типы), ДНК генотипирование [реал-тайм ПЦР]
- Цитологическое исследование мазков (соскобов) с поверхности шейки матки (наружного маточного зева) и цервикального канала - окрашивание по Папаниколау (Рар-тест)
- Цитологическое исследование мазков (соскобов) с поверхности шейки матки (наружного маточного зева) и цервикального канала на атипию
- Антиген плоскоклеточной карциномы (SCCA)
Кто назначает исследование?
Акушер-гинеколог, дерматовенеролог, уролог, инфекционист, проктолог, педиатр, ЛОР.
Литература
- Arbyn M. et al. (2010). "European Guidelines for Quality Assurance in Cervical Cancer Screening. Second Edition–Summary Document". Annals of Oncology 21 (3): 448–458.
- Hsiu-Ting Tsai, Ching-Hu Wu, Hsiao-Ling Lai, et al. Association between Quantitative High-Risk Human Papillomavirus DNA Load and Cervical Intraepithelial Neoplasm Risk Cancer Epidemiol Biomarkers Prev 2005;14:2544-2549.
- Saslow D, Solomon D, Lawson HW, et al. American Cancer Society, American Society for Colposcopy and Cervical Pathology, and American Society for Clinical Pathology Screening Guidelines for the Prevention and Early Detection of Cervical Cancer. Am J Clin Pathol. 2012;137:516-542.
- "Genital HPV Infection – CDC Fact Sheet". Centers for Disease Control and Prevention (CDC). April 10, 2008. Retrieved 13 November 2009.
- Материалы и рекомендации Противоракового Общества России. Режим доступа: http://www.pror.ru/
Мерзляк 5 класс — § 20.
 Степень числа
Степень числа
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Как называют выражение 85 ? Как при этом называют число 8? Число 5?
85 — степень
8 — основание степени
5 — показатель степени
2. Как читают запись 85?
Запись можно прочитать двумя способами:
- Восемь в пятой степени
- Пятая степень числа восемь
3. Как называют вторую степень числа? Третью степень числа?
- Вторую степень числа называют квадратом числа.
- Третью степень числа называют кубом числа.
4. Как читают запись а2? а3?
- а² — читают «а в квадрате».
- а³ — читают «а в кубе».
5. Чему равна первая степень числа?
Число в степени 1 равно самому числу.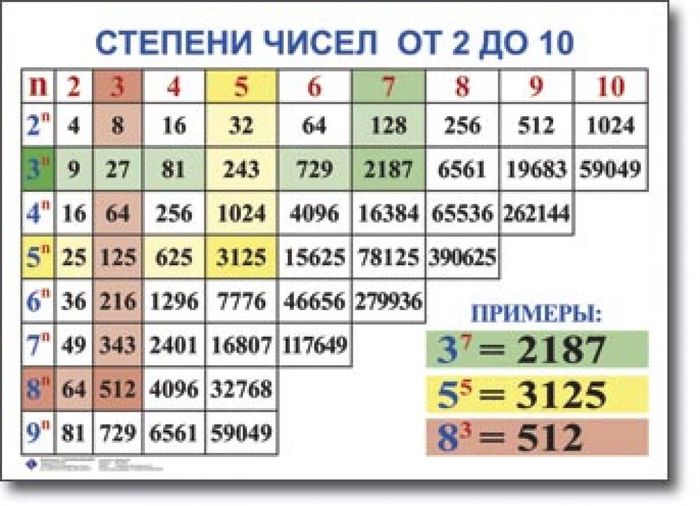 Например: 6¹ = 6, 23¹ = 23 и т.д.
Например: 6¹ = 6, 23¹ = 23 и т.д.
6. В каком порядке выполняют вычисления, если в числовое выражение входит степень?
Сначала выполняют возведение числа в степень, а потом все остальные действия в привычном порядке.
Решаем устно
1. Решите уравнение:
2. Верно ли равенство 90 = 14 • 5 + 20? Да, равенство верно.
Можно ли утверждать, что при делении 90 на 14 получим неполное частное 5 и остаток 20? Да, это верное утверждение.
3. Вася разложил 60 яблок на кучки по 8 яблок, и ещё 4 яблока у него осталось. На сколько кучек Вася разложил яблоки?
60 = 8 • 7 + 4
У Васи получилось 7 кучек по 8 яблок и ещё одна кучка с 4 яблоками, то есть всего 8 кучек.
Ответ: 8 кучек.
4. Турист должен преодолеть маршрут длиной 25 км. После того как он шёл 4 ч с одной и той же скоростью, ему осталось пройти 1 км. С какой скоростью шёл турист?
1) 25 — 1 = 24 (км) — турист прошёл за 4 часа.
2) 24 : 4 = 6 (км/ч) — скорость туриста.
Ответ: 6 км/ч.
5. На двух участках росло 20 кустов роз. После того как с первого участка пересадили 2 куста роз на второй, на обоих участках стало по 10 кустов роз. Сколько кустов роз росло на каждом участке?
1) 10 + 2 = 12 (кустов) — роз росло на первом участке сначала.
2) 10 — 2 = 8 (кустов) — роз росло на втором участке сначала.
Ответ: на первом участке росло 12 кустов роз, а на втором — 8 кустов роз.
Упражнения
548. Назовите основание и показатель степени:
- 48 — основание 4, показатель 8
- 1310 — основание 13, показатель 10
- а9 — основание а, показатель 9
- 6m — основание 6, показатель m
- 239 — основание 2, показатель 39
- 93¹— основание 93, показатель 1
549. Упростите выражение, заменив произведение одинаковых множителей степенью:
550. Найдите значение выражения:
Найдите значение выражения:
- 33 = 3 • 3 • 3 = 9 • 3 = 27
- 72 = 7 • 7 = 49
- 54 = 5 • 5 • 5 • 5= 25 • 5 • 5 = 125 • 5 = 625
- 25 = 2 • 2 • 2 • 2 • 2= 4 • 4 • 2 = 16 • 2 = 32
- 06 = 0 • 0 • 0 • 0 • 0 • 0= 0
- 112 = 1 • 1 • 1 • 1 • 1 • 1 • 1 • 1 • 1 • 1 • 1 • 1 = 1
551. Найдите значение выражения:
- 93 = 9 • 9 • 9 = 81 • 9 = 729
- 122 = 12 •12 = 144
- 24 = 2 • 2 • 2 • 2= 4 • 2 • 2 = 8 • 2 = 16
- 1100 = 2 • 2 • 2 • 2 • 2= 4 • 4 • 2 = 16 • 2 = 32
- 1001 = 100
- 103 = 10 • 10 • 10 = 100 • 10 = 1 000
552. Вычислите:
553. Вычислите:
554. Найдите значение выражения:
1) 16 — с3, если с = 2
16 — 23 = 16 — 8 = 8
2) х3 — х2, если х = 10
103 — 102 = 1000 — 100 = 900
3) 15а2, если а = 4
15 • 42 = 15 • 16 = 240
4) a2b3, если а = 6, b = 10
62 • 103 = 36 • 1 000 = 36 000
5) (x2 — y2) : (х — у), если х = 4, у = 2
(42 — 22) : (4 — 2) = (16 — 4) : 2 = 12 : 2 = 6
6) (x2 — y2) : х — у, если x = 4, y = 2
(42 — 22) : 4 — 2 = (16 — 4) : 4 — 2 = 12 : 4 — 2 = 3 — 2 = 1
7) x2 — y2 : (х — у), если х = 4, у = 2
42 — 22 : (4 — 2) = 16 — 4 : 2 = 16 — 2 = 14
8) x2 — y2 : х — y, если x = 4, у = 2
42 — 22 : 4 — 2 = 16 — 4 : 4 — 2 = 16 — 1 — 2 = 13
555. Найдите значение выражения:
Найдите значение выражения:
1) x2 — 14, если х = 5; 7; 18
- если х = 5, то x2 — 14 = 52 — 14 = 25 — 14 = 11
- если х = 7, то x2 — 14 = 72 — 14 = 49 — 14 = 35
- если х = 18, то x2 — 14 = 182 — 14 = 324 — 14 = 310
2) 2y2 + 13, если у = 6; 8; 9; 100
- если у = 6, то 2y2 + 13 = 2 • 62 + 13 = 2 • 36 + 13 = 72 + 13 = 85
- если у = 8, то 2y2 + 13 = 2 • 82 + 13 = 2 • 64 + 13 = 128 + 13 = 141
- если у = 9, то 2y2 + 13 = 2 • 92 + 13 = 2 • 81 + 13 = 162 + 13 = 175
- если у = 100, то 2y2 + 13 = 2 • 1002 + 13 = 2 • 10 000 + 13 = 20 000 + 13 = 20 013
556. Запишите в виде степени с основанием 3 число:
- 9 = 32
- 27 = 33
- 243 = 35
- 81 = 34
557. Запишите в виде степени с основанием 2 число:
Запишите в виде степени с основанием 2 число:
- 4 = 22
- 16 = 24
- 32 = 25
- 256 = 28
558. Составьте числовое выражение и найдите его значение:
1) сумма куба числа 5 и квадрата числа 8
53 + 82 = 125 + 64 = 189
2) разность квадратов чисел 6 и 2
62 — 22 = 36 — 4 = 32
3) квадрат разности чисел 6 и 2
(6 + 2)2 = 42 = 16
4) разность куба числа 3 и квадрата числа 5
33 — 52 = 27 — 25 = 2
559. Составьте числовое выражение и найдите его значение:
1) куб разности чисел 9 и 8
(9 — 8)3 = 13 = 1
2) квадрат суммы чисел 8 и 7
(8 + 7)2 = 152 = 225
3) сумма квадратов чисел 8 и 7
82 + 72 = 64 + 49 = 113
4) разность кубов чисел 4 и 1
43 — 13 = 64 — 1 = 63
Упражнения для повторения
560. Решите уравнение:
Решите уравнение:
561. Для приготовления десяти порций мороженого используют 200 г сахара. На сколько порций мороженого хватит 500 г сахара?
1) 200 : 10 = 20 (гр) — сахара потребуется на изготовление 1 порции мороженого.
2) 500 : 20 = 25 (порций) — мороженого можно изготовить.
Ответ: 25 порций.
562. Вася задумал трёхзначное число, у которого с каждым из чисел 652, 153 и 673 совпадает один из разрядов, а два других не совпадают. Какое число задумал Вася?
Выбранные цифры должны использоваться только один единственный раз во всех трёх числах. Этому условию удовлетворяют следующие цифры:
- в числе 652 — цифра 2, обозначающая единицы
- в числе 153 — цифра 1, обозначающая сотни
- в числе 673 — цифра 7, обозначающая десятки
Значит Вася задумал число 172.
Ответ: 172.
Задача от мудрой совы
563. В очереди за билетами в цирк стояли Миша, Наташа, Петя, Дима и Маша.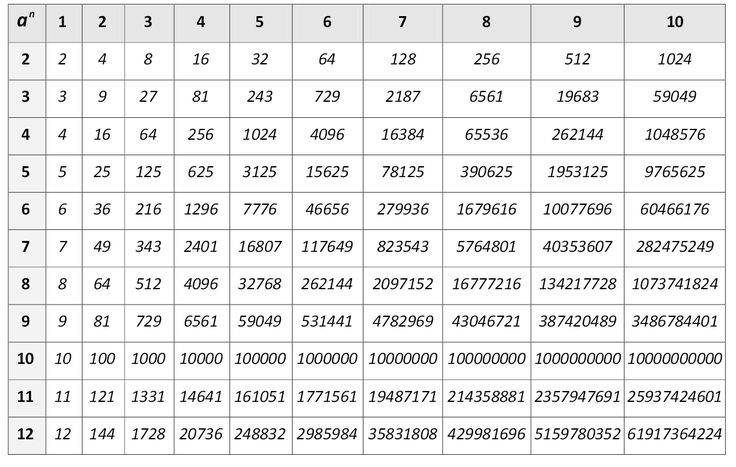 Маша купила билет раньше, чем Миша, но позже, чем Наташа. Петя и Наташа не стояли рядом, а Дима не был рядом ни с Наташей, ни с Машей, ни с Петей. Кто за кем стоял в очереди?
Маша купила билет раньше, чем Миша, но позже, чем Наташа. Петя и Наташа не стояли рядом, а Дима не был рядом ни с Наташей, ни с Машей, ни с Петей. Кто за кем стоял в очереди?
Расположим ребят в таком порядке, чтобы условия задачи были выполнены:
Наташа ⇒ Маша ⇒ Петя ⇒ Миша ⇒ Дима
Ответ: Наташа стояла первой, Маша — второй, Петя — третьим, Миша — четвёртым, а Дима — пятым.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
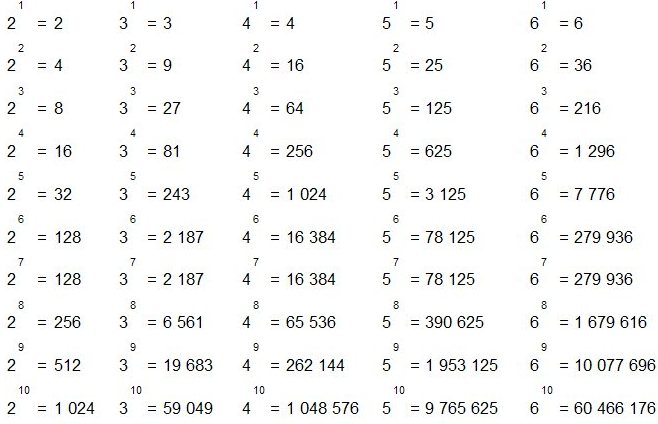
3 силовой стол
Вы ищете больше числовых диаграмм, используйте этот калькулятор
- Power Table Generator
- Калькулятор мощности
Установите флажок, чтобы преобразовать экспоненциальный результат в число. Число Поднятый силой Равно
- 3 1 = 3
- 3 2 = 9
- 3 3 = 27
- 3 4 = 81
- 3 5 = 243
- 3 6 = 729
- 3 7 = 2187
- 3 8 = 6561
- 3 9 = 19683
- 3 10 = 59049
от 1 до 10
- 3 11 = 177147
- 3 12 = 531441
- 3 13 = 1594323
- 3 14 = 4782969
- 3 15 = 14348907
- 3 16 = 43046721
- 3 17 = 1263
- 3 18 = 387420489
- 3 19 = 1162261467
- 3 20 = 3486784401
11 to 20
- 3 21 = 10460353203
- 3 22 = 3138118969999007
- 3 22 = 3131896967
- 3 22 = 313815969999797798
- 22 = 3131896967
- 3 22 = 3138110967 9007
- 3 22 .
 0026 24 = 282429536481
0026 24 = 282429536481 - 3 25 = 847288609443
- 3 26 = 2541865828329
- 3 27 = 7625597484987
- 3 28 = 22876792454961
- 3 29 = 68630377364883
- 3 30 = 2058
094649
21–30
- 3 31 = 617673396283947
- 3 32 = 1853020188851841
- 3 33 = 555
66555523 - 3 34 = 16677181699666568
- 3 35 = 50031545098999704
- 3 36 = 150094635296999100
- 3 37 = 4502830997300
- 3 38 = 1350851717672992000
- 3 39 = 4052555153018976000
- 3 40 = 1215766545
29000 - 3 41 = 364729963771707
- 3 42 = 1094189812370000
- 3 43 = 328256967394537100000
- 3 44 = 9847703611300000
- 3 45 = 2.
 954312706550834e+21
954312706550834e+21 - 3 46 = 8.862938119652502e+21
- 3 47 = 2.6588814358957506e +22
- 3 48 = 7,9766444307687251E+22
- 3 49 = 2,3929932923061753E+23
- 3 50 = 7,178997776779269269269269269269269186918691869186918ERISHINGINGINGINSION+692691876918769187691869186918691869187692ERSHIT0022 51 to 60
- 3 51 = 2.1536939630755577e+24
- 3 52 = 6.461081889226673e+24
- 3 53 = 1.938324566768002e+25
- 3 54 = 5.8149737003040055e+25
- 3 55 = 1.74449211007e+26
- 3 56 = 5.233476330273605e+26
- 3 57 = 1.57004289816e+27
- 3 58 = 4.710128697246245e+27
- 3 59 = 1.4130386091738735e+28
- 3 60 = 4.23
2752162e+28 - 3 61 = 1.
 2717347482564862e+29
2717347482564862e+29 - 3 62 = 3.8152042447694586e+29
- 3 63 = 1.1445612734308376e+30
- 3 64 = 3.433683820292513e+30
- 3 65 = 1.030105146087754e+31
- 3 66 = 3.0438263262e+31
- 3 67 = 9.270946314789785e+31
- 3 68 = 2.7812838944369356e+32
- 3 69 = 8.343851683310806e+32
- 3 70 = 2.503155504993242e+33
61 to 70
- 3 71 = 7.509466514979726 e+33
- 3 72 = 2.2528399544939177e+34
- 3 73 = 6.7585198634817535e+34
- 3 74 = 2.0275559526e+35
- 3 75 = 6.082667877133578e+35
- 3 76 = 1.8248003631400735e+36
- 3 77 = 5.47440108942022e+36
- 3 78 = 1.6423203268260662e+37
- 3 79 = 4.
 926960980478198e+37
926960980478198e+37 - 3 80 = 1.4780882941434595e +38
71 to 80
- 3 81 = 4.434264882430379e+38
- 3 82 = 1.33027946472 e+39
- 3 83 = 3.9
- 394187341e+39
- 3 84 = 1.1972515182562023e+40
- 3 85 = 3.5917545547686066e+40
- 3 86 = 1.077526366430582e+41
- 3 87 = 3.23257
- 917462e+41
- 3 88 = 9.697737297875238e+41
- 3 89 = 2.1189362571e+42
- 3 90 = 8.727963568087713e+42
81 to 90
- 3 91 = 2.61838
263137e+43 - 3 92 = 7.855167211278941e+43
- 3 93 = 2.3565501633836824e+44
- 3 94 = 7.0696504047e+44
- 3 95 = 2.1208951470453142e+45
- 3 96 = 6.
 362685441135942e+45
362685441135942e+45- 3 97 = 1.
- 56323407826e+46
- 3 98 = 5.726416897022348e+46
- 3 99 = 1.71792506045e+47
- 3 100 = 5.153775207320113e+47
Browse by Numbers
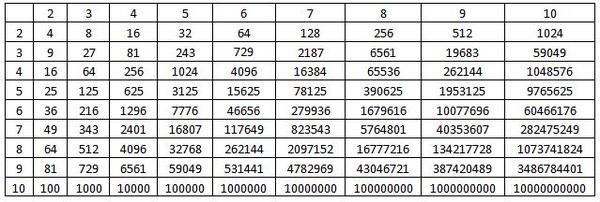
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Основная идея и правила для логарифмов 9к=с$$ для любого заданного числа $c$.
 Другими словами, логарифм дает показатель степени в качестве вывода, если вы даете ему результат возведения в степень в качестве ввода. Чтобы получить все ответы на приведенные выше задачи, нам просто нужно логарифмировать результат возведения в степень $c$, и это даст правильный показатель степени $k$ от $2$. Решением вышеперечисленных проблем являются:
\начать{выравнивать*}
\log_2 8 &= 3\\
\log_2 4 &=2\\
\log_2 16 &= 4\\
\log_2 1 &=0
\конец{выравнивание*}
9к = с
\label{натуральный логб}
\конец{собрать}
для любого числа $c$.
Поскольку использование базы $e$ так естественно для математиков, они иногда просто используют обозначение $\log x$ вместо $\ln x$. Однако другие могут использовать обозначение $\log x$ для логарифма по основанию 10, т. е. в качестве сокращенного обозначения для $\log_{10} x$. Из-за этой двусмысленности, если кто-то использует $\log x$ без указания основания логарифма, вы можете не знать, какое основание он подразумевает. В таком случае хорошо спросить.
Другими словами, логарифм дает показатель степени в качестве вывода, если вы даете ему результат возведения в степень в качестве ввода. Чтобы получить все ответы на приведенные выше задачи, нам просто нужно логарифмировать результат возведения в степень $c$, и это даст правильный показатель степени $k$ от $2$. Решением вышеперечисленных проблем являются:
\начать{выравнивать*}
\log_2 8 &= 3\\
\log_2 4 &=2\\
\log_2 16 &= 4\\
\log_2 1 &=0
\конец{выравнивание*}
9к = с
\label{натуральный логб}
\конец{собрать}
для любого числа $c$.
Поскольку использование базы $e$ так естественно для математиков, они иногда просто используют обозначение $\log x$ вместо $\ln x$. Однако другие могут использовать обозначение $\log x$ для логарифма по основанию 10, т. е. в качестве сокращенного обозначения для $\log_{10} x$. Из-за этой двусмысленности, если кто-то использует $\log x$ без указания основания логарифма, вы можете не знать, какое основание он подразумевает. В таком случае хорошо спросить. x$ и $\ln x$ являются обратными функциями. Мы будем использовать уравнения \eqref{lnexpinversesa} и \eqref{lnexpinversesb}, чтобы вывести следующие правила логарифмирования. 9{-1}=\frac{1}{x}$$
и приведенное выше правило для журнала мощности. Просто подставьте $y=-1$ в правило журнала мощности, и вы получите это
$$\ln(1/x) = - \ln (x).$$
x$ и $\ln x$ являются обратными функциями. Мы будем использовать уравнения \eqref{lnexpinversesa} и \eqref{lnexpinversesb}, чтобы вывести следующие правила логарифмирования. 9{-1}=\frac{1}{x}$$
и приведенное выше правило для журнала мощности. Просто подставьте $y=-1$ в правило журнала мощности, и вы получите это
$$\ln(1/x) = - \ln (x).$$Примеры научной записи: Сокращение уравнений и чисел
Научная запись похожа на стенографию для записи очень больших или очень маленьких чисел. Вместо того, чтобы записывать число в десятичной форме, число сокращается до числа, умноженного на степень десяти.
Примеры научных обозначений
Реклама
Математическая стенография
В научной записи:
- Первое число в математическом уравнении называется «коэффициентом». Коэффициент должен быть больше или равен единице и меньше 10. Например, чтобы создать научное представление числа 256, коэффициент будет равен 2,56.

- Второе число в уравнении представляет собой степень числа 10, записанную как 10 с показателем степени, например 10 2 , что означает 10 x 10.
Объединив эти два числа, можно получить уравнение научной записи для 256 - 2,56 x 10 2 .
Отрицательная экспонента показывает, что десятичная дробь сдвинута на столько же знаков влево, а положительная экспонента показывает, что десятичная дробь сдвинута на столько же разрядов вправо.
Примеры научной записи
Вот примеры научной записи:
- 1 = 10 0
- 10 = 1 x 10¹
0
0
00025 100 = 1 x 10²
- 1000 = 1 x 10³
- 10000 = 1 x 10 4
- 100000 = 1 x 10 5
- 42,000,000 = 4.2 x 10 7
- 676,000,000,000 = 6.76 x 10 11
- 0.1 = 1 x 10 -1
- 0.
 01 = 1 x 10 -2
01 = 1 x 10 -2
- 0.001 = 1 x 10 - 3
- 0.0001 = 1 x 10 -4
- 0.00001 = 1 x 10 -5
- 0.00000078 = 7.8 x 10 -7
- 0.000000000000000 = 3.56 x 10 -13
Реальные примеры научных обозначений
Узнайте, как научные обозначения используются для выражения больших чисел.
- 7 x 10 9 = Население мира составляет около 7 миллиардов, записанное как 7 000 000 000
- 1,08 x 10 9 = приблизительная скорость света 1080 миллионов км в час или 1 080 000 000 км в час
- 9,3 x 10 7 = Расстояние от Земли до Солнца 93 миллиона миль или 93 000 000 миль
- 3,99 x 10 13 = Расстояние от Солнца, 900 000 000 000 км
- 9,4605284 × 10 15 = расстояние в горе составляет менее 9,5 трлн.
 140 миллионов квадратных миль или 140 000 000 квадратных миль
140 миллионов квадратных миль или 140 000 000 квадратных миль
- 1,0 x 10 14 = Приблизительное количество клеток в организме человека составляет 100 триллионов или 100 000 000 000 000 30010 1002370026 -3 = Плотность кислорода 1332 миллионных г/см3 или 0,001332 г/см3
- 2,4 x 10 -3 = Диаметр песчинки 24 десятитысячных дюйма или 0,0024 дюйма
- 7.53 x 10 -10 = Mass of a dust particle is 0.000000000753 kg
- 9.1093822 × 10 -31 = Mass of an electron is 0.000000000000000000000000000000822 kg
- 4.0 x 10 -7 = Length of самая короткая длина волны видимого света (фиолетового цвета) составляет 0,0000004 метра
Реклама
Вычисления в экспоненциальном представлении
Экспоненциальное представление упрощает выполнение математических функций с большими числами.
Вот пять примеров:
- Умножить (4 x 10 4 ) и (7 x 10 5 )
- Первые 4 x 7 = 28
- Далее добавить 7 009 Результат 5 09 степеней, 4 +
- 28 x 10 9
- Переписать в стандартной форме, 2,8 x 10 10
- Разделить (6 x 10 5 ) на (4 x 10 4 )
- 6/4 = 1,5
- Экспоненты вычтения 5 - 4 = 1
- Ответ 1,5 x 10 1 или 15
- Умножение (4 x 10 -7 ) и (3,25 x 10 )
- 4 x 3,25 = 13
- Сложение показателей = -7 + 9 = 2
- Ответ: 13 x 10 2 или 1300
нужно:
- (2,456 x 10 5 ) + (6.
 0034 × 10 8 )
0034 × 10 8 )- Изменение 2,456 x 10 5 до 0,002456 x 10 8
- 0,002456 + 6.00344434 = 6,00566689566. 6,0056666666666666666668. 7,0056. 7005679566. 8
- Вычесть (7 × 10 5 ) - (5,2 × 10 4 )
- Изменить на 7 × 10 5 на 0,52 × 10 4
- 7 - 0,52 = 6,48
- Ответ = 6,48 x 10 4
50007
Теперь вы видите множество примеров научной записи.
Статьи по теме
Десятичные разряды: простые примеры для их понимания и использования
Возможно, вы уже знаете, что десятичные дроби — это маленькие точки между числами, которые выглядят как точки. Но почему они важны и что они делают? Продолжайте читать, чтобы узнать все о десятичных дробях и десятичных разрядах в малых и больших числах.
Примеры квадратного уравнения
Что такое квадратное уравнение? Квадратное уравнение — это уравнение второй степени, то есть оно содержит хотя бы один член, возведенный в квадрат.
 Стандартная форма: ax² + bx + c = 0, где a, b и c — константы или числовые коэффициенты, а x — неизвестная переменная. Продолжайте читать примеры квадратных уравнений в стандартных и нестандартных формах, а также список членов квадратных уравнений.
Стандартная форма: ax² + bx + c = 0, где a, b и c — константы или числовые коэффициенты, а x — неизвестная переменная. Продолжайте читать примеры квадратных уравнений в стандартных и нестандартных формах, а также список членов квадратных уравнений.
Научное обозначение
Научное обозначениеНаучное обозначение
Обзор экспонента Преобразование в научный формат Химики часто работают с очень большими или очень маленькими числами. За Например, в алмазе весом 1 карат содержится 10 300 000 000 000 000 000 000 атомов углерода каждый. из которых имеет массу 0,000,000,000,000,000,000,000,020 грамм. это невозможно умножьте эти числа на большинстве калькуляторов, потому что они не могут принять ни одно из этих чисел. здесь написано. Чтобы сделать такой расчет, необходимо выразить эти числа в научное обозначение , как число от 1 до 10, умноженное на 10, возведенное в какой-то показатель.

Обзор экспонента
Ниже приведены некоторые основы экспоненциальной математики.
Любое число, возведенное в нулевую степень, равно 1. 1= 1 10= 1 Любое число, возведенное в первую степень, равно самому себе. 1 1 = 1 10 1 = 10 Любое число, возведенное в n -ю степень, равно произведение этого числа, умноженное на себя n -1 раз. 
2 2 = 2 х 2 = 4 10 5 = 10 х 10 х 10 х 10 х 10 = 100 000 Деление на число, возведенное в степень, равносильно умножению на это число возведено в степень противоположного знака. Преобразование в научный формат
Для преобразования чисел в экспоненциальное представление можно использовать следующее правило: показатель степени в экспоненциальном представлении равен тому, сколько раз десятичная точка должна быть перешел к получению числа от 1 до 10. В 1990 году население Чикаго составляло 6 070 000 1000.
 Чтобы преобразовать это число в научное представление, мы перемещаем десятичную точку
налево шесть раз.
Чтобы преобразовать это число в научное представление, мы перемещаем десятичную точку
налево шесть раз.6 070 000 = 6,070 x 10 6 Чтобы перевести 10 300 000 000 000 000 000 000 атомов углерода в научные обозначения, мы переместите запятую влево 22 раза.
10 300 000 000 000 000 000 000 = 1,03 x 10 22
Чтобы преобразовать числа меньше 1 в экспоненциальное представление, мы должны переместить десятичную дробь указать вправо. Например, десятичная точка в 0,000985 должна быть перемещена вправо. четыре раза.
0,000985 = 9,85 х 10 -4
Преобразование 0,000,000,000,000,000,000,000,020 граммов на атом углерода в научные нотация включает перемещение десятичной точки вправо 23 раза.
0,000,000,000,000,000,000,000,020 = 2,0 х 10 -23
Основная причина преобразования чисел в экспоненциальное представление состоит в том, чтобы сделать расчеты с необычно большими или малыми числами менее громоздки.
 Потому что нулей нет
больше используется для установки десятичной точки, все цифры в числе в экспоненциальном представлении
существенны, как показывают следующие примеры.
Потому что нулей нет
больше используется для установки десятичной точки, все цифры в числе в экспоненциальном представлении
существенны, как показывают следующие примеры.2,4 х 10 22 2 значащие цифры 9,80 x 10 -4 3 значащие цифры 1,055 x 10 -22 4 значащие цифры Практическая задача 8 Преобразуйте следующие числа в научная нотация.
(а) 0,004694
(б) 1,98
(в) 4 679 000
Нажмите здесь, чтобы проверьте свои ответы на практическое задание 8
единиц | Ошибки | Значимые цифры | Научное обозначение
Вернуться к теме «Общая химия» Отзыв
3.
 3: Научная нотация — Химия LibreTexts
3: Научная нотация — Химия LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 52555
Рисунок \(\PageIndex{1}\) (Источник: предоставлено НАСА; источник: http://commons.wikimedia.org/wiki/File:The_Sun_by_the_Atmospheric_Imaging_Assembly_of_NASA%2527s_Solar_Dynamics_Observatory_-_20100819.jpg(откроется в новом окне); Лицензия: общественное достояние)- Научное представление позволяет нам выражать очень большие или очень маленькие числа удобным способом.
- В научной записи используется коэффициент (число от 1 до 10) и степень десяти, достаточная для фактического числа.
- Что такое научная запись?
- Для чего мы используем научные обозначения?
- Что такое начальный нуль?
- Выразите 150 000 000 в экспоненциальном представлении.
- Экспресс 0,000043 в экспоненциальном представлении.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Фундамент СК-12
- Лицензия
- СК-12
- Программа ООР или издатель
- СК-12
- Показать страницу Оглавление
- нет на странице
- Теги
- научная нотация
- источник@https://flexbooks.
 ck12.org/cbook/ck-12-chemistry-flexbook-2.0/
ck12.org/cbook/ck-12-chemistry-flexbook-2.0/
Как далеко Солнце от Земли?
Астрономы привыкли к очень большим числам. В то время как Луна находится всего в \(406 697 \: \text{км}\) от Земли на максимальном расстоянии, Солнце находится намного дальше \(\left( 150 \: \text{миллионов км} \right)\). Проксима Центавра, ближайшая к Земле звезда, находится на расстоянии \(39 900 000 000 000 \: \text{км}\) — и это только начало больших расстояний.
 На другом конце шкалы некоторые биологи имеют дело с очень маленькими числами: типичный гриб может быть всего 30 микрометров \(\left( 0,000030 \: \text{метров} \right)\) в длину, а вирус может быть всего 0,03 микрометра \(\left( 0,00000003 \: \text{meters} \right)\). 9{11}\), чтобы получить правильный номер. Научную нотацию иногда называют экспоненциальной нотацией. Сводная информация о единицах СИ приведена в таблице ниже.
На другом конце шкалы некоторые биологи имеют дело с очень маленькими числами: типичный гриб может быть всего 30 микрометров \(\left( 0,000030 \: \text{метров} \right)\) в длину, а вирус может быть всего 0,03 микрометра \(\left( 0,00000003 \: \text{meters} \right)\). 9{11}\), чтобы получить правильный номер. Научную нотацию иногда называют экспоненциальной нотацией. Сводная информация о единицах СИ приведена в таблице ниже.Таблица \(\PageIndex{1}\): префиксы SI Префикс Сокращение блока Экспоненциальный коэффициент Значение Пример  Эта цифра поможет вам лучше видеть десятичную точку. Число 0,01 с меньшей вероятностью будет неправильно понято, чем число 0,01, где вы можете не увидеть десятичную дробь.
Эта цифра поможет вам лучше видеть десятичную точку. Число 0,01 с меньшей вероятностью будет неправильно понято, чем число 0,01, где вы можете не увидеть десятичную дробь.Резюме
Обзор
Эта страница под названием 3.3: Научная нотация распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

ПОД ЛИЦЕНЗИЕЙ
Видео с вопросами: Выражение степеней десяти с помощью префикса
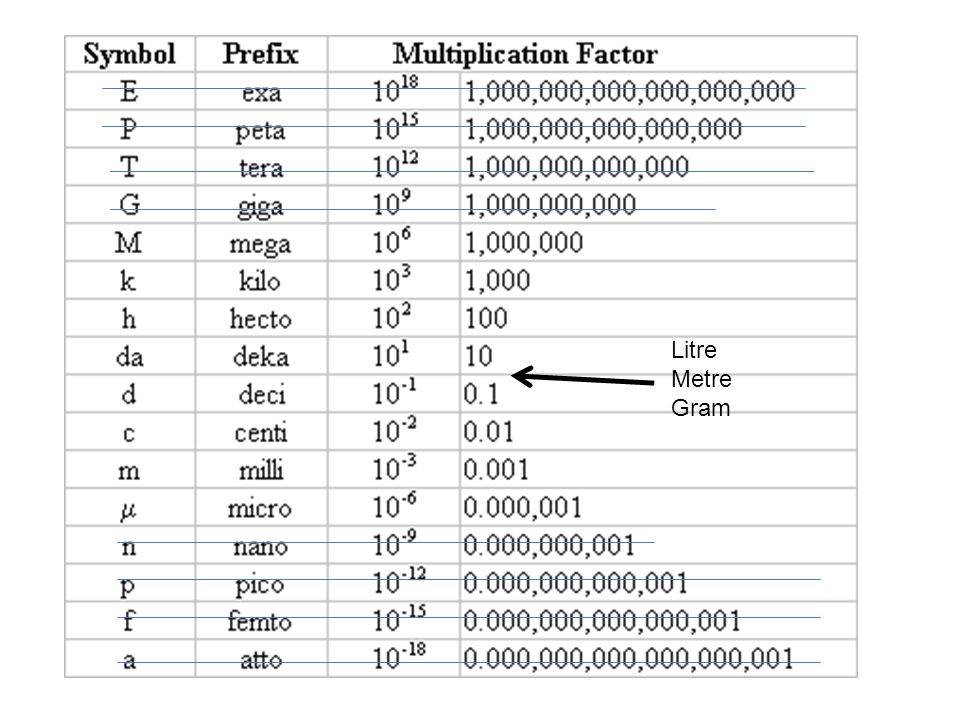
Стенограмма видео
Что из следующего является числом герц в гигагерце, сокращенно ГГц? (A) 10 в степени шесть герц, (B) 10 в степени восемь герц, (C) 10 в степени девять герц, (D) 10 в степени 10 герц, (E) 10 в степени мощность 12 герц.
Итак, в этом вопросе нас спрашивают о префиксе гига-, в данном случае относящемся к единице герц. Напомним, что герц является единицей частоты и определяется как количество циклов волны в секунду. Цикл волны — это один повторяющийся участок волны. На графике это будет представлено пиком и впадиной. Итак, для этой волны, если ось 𝑥 представляет собой время в секундах, а эта точка здесь равна одной секунде, то мы бы сказали, что эта волна имеет частоту один герц, потому что через одну секунду мы можем видеть, что волна имеет один цикл. Однако в этом вопросе нас спрашивают о преобразовании герц в гигагерц.

Giga — один из ряда распространенных префиксов, которые используются в научной записи для описания больших чисел. Один из способов ответить на этот вопрос — вспомнить список префиксов и чисел, которые они представляют. А потом мы можем найти гига- в этом списке и прочитать ответ. Однако давайте помнить, что эти префиксы нужно использовать вместе с единицей измерения, в данном случае герцами. Например, нет смысла говорить просто о гига-, а вот гигагерц — это вполне определенная величина. Начнем наш список с приставки кило-. А при использовании с герцами у нас есть один килогерц, сокращенно один кГц. Это равно 1000 герц, потому что мы знаем, что приставка кило- означает 1000.
Мы также знаем, что в экспоненциальном представлении 1000 можно записать как 10 в степени три. Таким образом, один килогерц равен 10 в степени трех герц. Теперь 10 в степени трех на самом деле не является одним из наших возможных ответов на этот вопрос. Итак, давайте продолжим наш список префиксов.

Следующий префикс в нашем списке — мега-, который при использовании с герцами дает нам мегагерц, сокращенно один МГц. Приставка мега- означает один миллион. А в научной записи мы можем записать один миллион как 10 в шестой степени. Итак, мегагерц равен 10 в степени шесть герц. Итак, 10 в степени шесть герц на самом деле является одним из возможных ответов на этот вопрос. И мы знаем, что это неправильный ответ, потому что мы только что видели, что 10 в степени шесть герц равно мегагерцу. Так что она тоже не может быть равна гигагерцу.
Итак, давайте продолжим наш список префиксов. А следующий у нас гига- и вместе с герцем дает нам один гигагерц, сокращенно один ГГц. Приставка гига- означает один миллиард, что мы можем записать в научной записи как 10 в степени девять. Таким образом, гигагерц равен 10 в степени девять герц. Помните, что гигагерц — это именно та величина, которая нас интересует в этом вопросе. И 10 в степени девять герц — возможный ответ на наш вопрос. И теперь мы знаем, что на самом деле это правильный ответ на вопрос, поскольку мы только что видели, что один гигагерц действительно равен 10 в степени 9 герц.

Прежде чем мы закончим, давайте отметим несколько интересных вещей об оставшихся вариантах ответа на этот вопрос. Например, вариант (В) был равен 10 в степени восемь герц. Но наш список префиксов пошел прямо от 10 в степени шесть герц до 10 в степени девять герц и пропустил любой возможный префикс для 10 в степени восемь герц.
Это потому, что для перехода вниз по нашему списку префиксов мы умножаем на 1000 или 10 в степени три. Это означает, что мы в основном добавляем три, чтобы перейти к следующей строке. Итак, мы идем от 10 в степени три к 10 в степени шесть в 10 в степени девятки, и так далее. Таким образом, только степени 10, кратные трем, имеют общий префикс, используемый для их описания. Это означает, что наш вариант (В), 10 в степени восемь герц, здесь не является правильным ответом. Но у него также нет общего префикса для его описания.
Используя эти знания о том, как работает наш список, мы также можем предположить, что 10 в степени 10, вариант (D), также не имеет общего имени префикса, поскольку 10 в степени не кратно трем.

91 to 100
41 to 50


 from_bytes(bytes, byteorder, *, signed=False) - возвращает число из данной строки байтов.
from_bytes(bytes, byteorder, *, signed=False) - возвращает число из данной строки байтов.
 1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999
1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999 5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5
5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5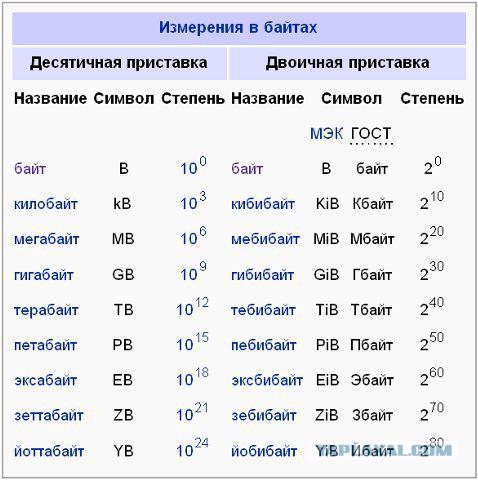 conjugate()) # Сопряжённое число
(1-2j)
>>> print(x.imag) # Мнимая часть
2.0
>>> print(x.real) # Действительная часть
1.0
>>> print(x > y) # Комплексные числа нельзя сравнить
Traceback (most recent call last):
File "", line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y) # Но можно проверить на равенство
False
>>> abs(3 + 4j) # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2) # Возведение в степень
(-7+24j)
conjugate()) # Сопряжённое число
(1-2j)
>>> print(x.imag) # Мнимая часть
2.0
>>> print(x.real) # Действительная часть
1.0
>>> print(x > y) # Комплексные числа нельзя сравнить
Traceback (most recent call last):
File "", line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y) # Но можно проверить на равенство
False
>>> abs(3 + 4j) # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2) # Возведение в степень
(-7+24j)
 0026 24 = 282429536481
0026 24 = 282429536481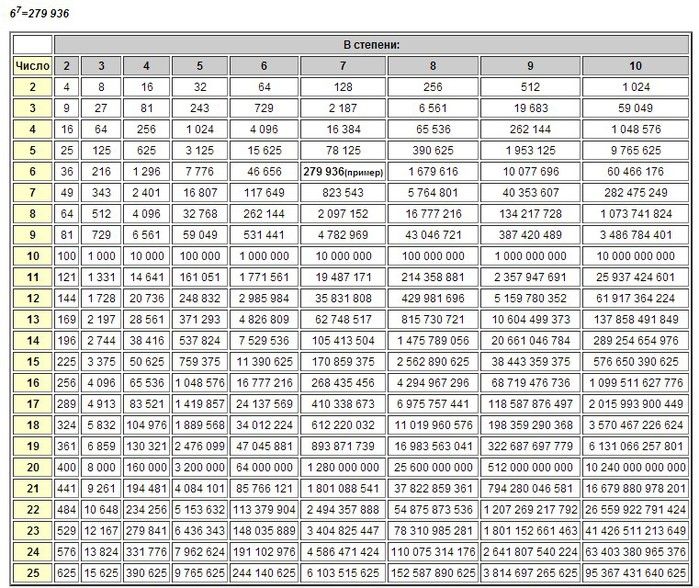 954312706550834e+21
954312706550834e+21