11 класс задачи на совместную работу егэ с решением: Задачи на работу на ЕГЭ по математике

Задачи на работу на ЕГЭ по математике

Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.

Задачи на работу также решаются с помощью одной-единственной формулы: . Здесь — работа, — время, а величина , которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, продавец в супермаркете надувает воздушные шарики. Количество шариков, которые он надует за час — это и есть его производительность.

Правила решения задач на работу очень просты.

1. , то есть работа производительность время. Из этой формулы легко найти или .
2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один). Написана книга (одна). А вот если речь идет о количестве кирпичей, страниц или построенных домов — работа как раз и равна этому количеству.
3. Если трудятся двое рабочих (два экскаватора, два завода. ..) — их производительности складываются. Очень логичное правило.
4. В качестве переменной удобно взять именно производительность.

Покажем, как все это применяется на практике.

---

1. Заказ на деталей первый рабочий выполняет на час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на деталь больше?

Так же, как и в задачах на движение, заполним таблицу.

В колонке «работа» и для первого, и для второго рабочего запишем: . В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем ее за . Тогда производительность первого рабочего равна (он делает на одну деталь в час больше). , время работы первого рабочего равно , время работы второго равно .

первый рабочий
второй рабочий

Первый рабочий выполнил заказ на час быстрее. Следовательно, на меньше, чем , то есть

Мы уже решали такие уравнения. Оно легко сводится к квадратному:

Дискриминант равен . Корни уравнения: , . Очевидно, производительность рабочего не может быть отрицательной — ведь он производит детали, а не уничтожает их 🙂 Значит, отрицательный корень не подходит.

Ответ: .

---

2. Двое рабочих, работая вместе, могут выполнить работу за дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?

В этой задаче (в отличие от предыдущей) ничего не сказано о том, какая это работа, чему равен ее объем. Значит, работу можем принять за единицу.

А что же обозначить за переменные? Мы уже говорили, что за переменную удобно обозначить производительность. Пусть — производительность первого рабочего. Но тогда производительность второго нам тоже понадобится, и ее мы обозначим за .

По условию, первый рабочий за два дня делает такую же часть работы, какую второй — за три дня. Значит, . Отсюда .

Работая вместе, эти двое сделали всю работу за дней. При совместной работе производительности складываются, значит,

.

Итак, первый рабочий за день выполняет всей работы. Значит, на всю работу ему понадобится дней.

Ответ: .

---

3. Первая труба пропускает на литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом литров она заполняет на минуты дольше, чем вторая труба заполняет резервуар объемом литров?

Всевозможные задачи про две трубы, которые наполняют какой-либо резервуар для воды — это тоже задачи на работу. В них также фигурируют известные вам величины — производительность, время и работа.

Примем производительность первой трубы за . Именно эту величину и требуется найти в задаче. Тогда производительность второй трубы равна , поскольку она пропускает на один литр в минуту больше, чем первая. Заполним таблицу

первая труба
вторая труба

Первая труба заполняет резервуар на две минуты дольше, чем вторая. Значит, . Составим уравнение:

и решим его.

Ответ: .

. Андрей и Паша красят забор за часов. Паша и Володя красят этот же забор за часов, а Володя и Андрей — за часов. За сколько часов мальчики покрасят забор, работая втроем?

Мы уже решали задачи на движение. Правила те же. Отличие лишь в том, что здесь работают трое, и переменных будет тоже три. Пусть — производительность Андрея, — производительность Паши, а — производительность Володи. Забор, то есть величину работы, примем за — ведь мы ничего не можем сказать о его размере.

	производительность	работа
Андрей
Паша
Володя
Вместе

Андрей и Паша покрасили забор за часов.

Мы помним, что при совместной работе производительности складываются. Запишем уравнение:

Аналогично,


Тогда


.
Можно искать , и по отдельности, но лучше просто сложить все три уравнения. Получим, что

Значит, работая втроем, Андрей, Паша и Володя красят за час одну восьмую часть забора. Весь забор они покрасят за часов.
Ответ: .

---

Читаем дальше: Задачи на проценты

Задачи на совместную работу. ЕГЭ по математике

Лучшие репетиторы для сдачи ЕГЭ

Математика

Русский язык

История

Открытый банк заданий по теме задачи на совместную работу. Задания B11 из ЕГЭ по математике (профильный уровень)

Тип задания: 11
Тема: Задачи на совместную работу

Условие

Обе трубы наполняют бассейн за 6 часов, а первая труба — за 10 часов. За сколько часов наполнит бассейн вторая труба?

Показать решение

Решение

Объём бассейна примем за 1. Тогда за 1 час две трубы заполнят \frac16часть бассейна, первая труба за 1 час заполнит \frac{1}{10}часть бассейна. Значит, вторая труба за 1 час заполнит \frac16-\frac{1}{10}=\frac{1}{15}часть бассейна. Весь бассейн вторая труба заполнит за 1 : \frac{1}{15}=\frac{15}{1}=15часов.

Ответ

15

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема: Задачи на совместную работу

Условие

Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если ёмкость объёмом 420 литров она заполняет на 15 минут дольше, чем вторая труба заполняет ёмкость объёмом 280 литров?

Показать решение

Решение

Пусть первая труба пропускает x литров воды в минуту. Тогда вторая труба пропускает за одну минуту x + 2 литра. Первая труба заполняет ёмкость объёмом 420 литров за время \frac{420}{x} мин, а вторая труба заполняет ёмкость объёмом 280 литров за \frac{280}{x+2} мин, что различается на 15 минут. 2-22x-168=0,

x_1=12, x_2=-\frac{14}{3}.

Отрицательное значение не удовлетворяет условию. Первая труба пропускает 12 литров воды в минуту.

Ответ

12

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема: Задачи на совместную работу

Условие

Один рабочий может выполнить заказ за 9 часов, другой — за 6 часов. За сколько часов выполнят весь заказ оба рабочих вместе?

Показать решение

Решение

Весь заказ примем за 1, тогда \frac19 — часть работы, выполненная первым рабочим за 1 час, \frac16 — часть работы, выполненная вторым рабочим за 1 час. Тогда часть работы, выполненная двумя рабочими за 1 час равна \frac19+\frac16=\frac{5}{18}. Всю работу оба рабочих выполняют за 1:\frac{5}{18}=\frac{18}{5}=3,6 часа.

Ответ

3,6

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». 2+2x-120=0

x_1=-12,\,x_2=10.

Отрицательное значение не удовлетворяет условию. Второй рабочий делает 10 деталей в час.

Ответ

10

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема: Задачи на совместную работу

Условие

Ремонт одной и той же квартиры Виктор и Алексей делают за 8 дней. Андрей, работая с Виктором, затрачивают на работу столько же времени. Однако, Андрею с Алексеем на ремонт требуется 12 дней. Сколько дней займет ремонт квартиры при одновременной работе всех трех мастеров?

Показать решение

Решение

Примем объем работы за единицу. Пусть x — количество дней, за которое необходимо выполнить всю работу Виктору; за y дней работу выполнит Алексей, Андрей выполнит всю работу за z дней; тогда \frac{1}{x} — производительность Виктора, \frac{1}{y} — производительность Алексея, \frac{1}{z} — производительность Андрея.

По первому условию Виктор и Алексей сделают всю работу за 8 дней, значит, их общая производительность \frac18. Составим уравнение \frac{1}{x}+\frac{1}{y}=\frac18.

По второму условию Виктор и Андрей сделают всю работу за 8 дней. Значит, их общая производительность \frac18. Составим уравнение \frac{1}{x}+\frac{1}{z}=\frac18.

По третьему условию Андрей и Алексей выполнят всю работу за 12 дней. Значит, их общая производительность \frac{1}{12}. Составим уравнение \frac{1}{y}+\frac{1}{z}=\frac{1}{12}.

Получим систему уравнений:

\begin{cases} \frac{1}{x}+\frac{1}{y}=\frac18,\\ \frac{1}{x}+\frac{1}{z}=\frac18,\\ \frac{1}{y}+\frac{1}{z}=\frac{1}{12}; \end{cases}

2\left( \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \right )=\frac18+\frac18+\frac{1}{12},

2\left( \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \right )=\frac13,

\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac16,

1:\frac16=6 (дней).

Итак, всю работу Виктор, Алексей и Андрей сделают за 6 дней.

Ответ

6

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема: Задачи на совместную работу

Условие

Два маляра могут выполнить работу по покраске стен помещения за 15 дней, а первый из них в одиночку — за 20 дней. Сколько дней необходимо второму маляру, чтобы выполнить работу самостоятельно?

Показать решение

Решение

Пусть x — производительность труда первого маляра, y — производительность труда второго маляра. Тогда x+y — производительность труда обоих маляров при совместной работе. Обозначив всю проделанную работу по покраске стен за 1, получим, что первый маляр проделает эту работу в одиночку за \frac{1}{x} дней, второй маляр — за \frac{1}{y} дней, а два маляра, работая вместе, — за \frac{1}{x+y} дней. Составим и решим систему уравнений

\begin{cases} \frac{1}{x+y}=15 \\ \frac{1}{x}=20; \end{cases} \begin{cases} y=\frac{1}{15}-\frac{1}{20}, \\ x=\frac{1}{20}; \end{cases}

откуда y=\frac{1}{60}, \frac{1}{y}=60 дней. Таким образом, второй маляр, работая самостоятельно, выполнит всю работу за 60 дней.

Ответ

60

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 11
Тема: Задачи на совместную работу

Условие

Первый рабочий обтачивает на токарном станке на 1 заготовку в день меньше, чем второй. При этом известно, что на обработку 420 деталей ему потребуется на 9 дней больше, чем второму на обтачивание 252 деталей. Определите, сколько деталей в день способен обточить второй рабочий.

Показать решение

Решение

Допустим, что второй рабочий за день способен обработать x деталей. В это время первый сделает x – 1 деталь. Время, которое нужно первому рабочему на то, чтобы выточить 420 деталей, равно \frac{420}{x-1} дней, второй же выточит 252 детали за \frac{252}{x} дней.

С учетом того, что на выполнение указанной работы первому рабочему нужно на 9 дней больше, чем второму, получаем уравнение:

\frac{420}{x-1} — \frac{252}{x}=9

Решаем его относительно x:

\frac{420}{x-1} — \frac{252}{x}=9 \cdot x(x-1)

420 \cdot x-252 \cdot (x-1)=9x \cdot (x-1)

9 \cdot x^2-9 \cdot x-420 \cdot x+252 \cdot x-252=0

9 \cdot x^2-177 \cdot x-252=0|:3

3 \cdot x^2-59 \cdot x-84=0

D = b^2 — 4ac = (-59)^2 -4\cdot 3\cdot (-84)=3481+1008=4489

x_1=\frac{-b-\sqrt{D}}{2 \cdot a}=\frac{59-67}{6}=-\frac{8}{6}

x_2=\frac{-b+\sqrt{D}}{2 \cdot a}=\frac{59+67}{6}=\frac{126}{6}=21

Количество деталей в час может быть только положительным числом, поэтому единственный ответ: x₂ = 21 деталь делает второй рабочий за рабочий день.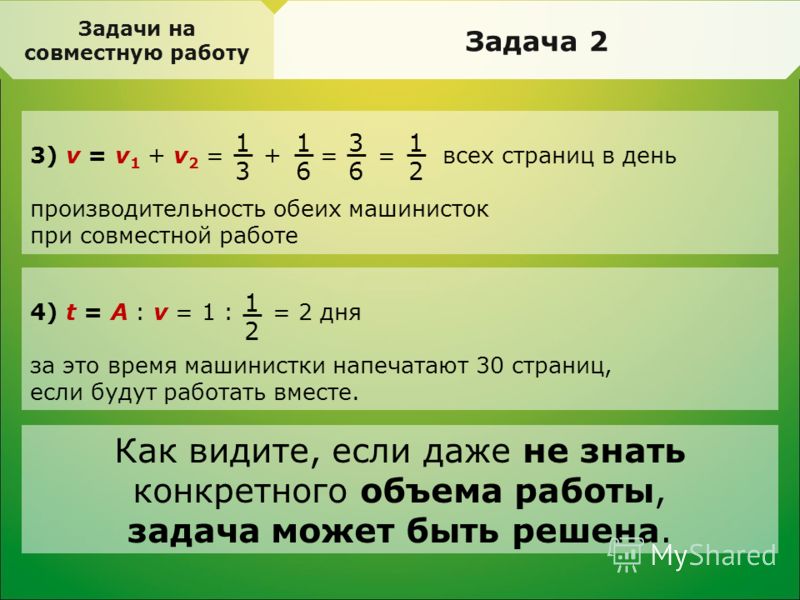

Ответ

21

Тип задания: 11

Тема: Задачи на совместную работу

Условие

Оля и Витя начали одновременно решать одинаковый тест. За один час Оля успевает решать 12 вопросов, а Витя 21 вопрос. Оля закончила решать тест на 105 минут позже Вити. Определите количество вопросов в тесте.

Показать решение

Решение

Обозначим за x – количество вопросов в тесте. Тогда:

\frac{x}{12} – общее время решения всего теста Оли;

\frac{x}{21} – общее время решения всего теста Вити;

Мы знаем, что Оля решила тест на 105 (т.е. \frac74 часа) минут позже Вити, значит верно уравнение:

\frac{x}{12}-\frac{x}{21}=\frac{7}{4}

\frac{x}{28}=\frac{7}{4}

x=\frac{7 \cdot 28}{4}=49

Значит тест содержит 49 вопросов.

Ответ

49

Тип задания: 11
Тема: Задачи на совместную работу

Условие

Через первую трубу в бассейн попадает на 8 литров воды в минуту меньше, чем через вторую. 2-4ac=64-4\cdot1\cdot(-180)=784

x=\frac{-b\pm \sqrt{D}}{2a} = \frac{-8\pm 28}{2}

x_1=10;\enspace x_2=-18

Так как пропускная способность воды не может быть отрицательной, то правильным ответом будет 10 литров

Ответ

10

Лучшие репетиторы для сдачи ЕГЭ

Математика

Русский язык

История

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Примеры совместного обучения или групповой работы

Вовлечение студентов

Озадачьте вашего партнера

• Студенты в течение минуты создают сложный вопрос на основе содержания лекции до этого момента.
• Студенты задают вопрос человеку, сидящему рядом с ними.
• Чтобы продвинуть это задание еще дальше, попросите учащихся записать свои вопросы и сдать их. Эти вопросы можно использовать для создания тестов или экзаменов. Их также можно просмотреть, чтобы оценить понимание учащимися.

Think-Pair-Share/Write-Pair-Share

• Преподаватель задает вопрос, требующий анализа, оценки или обобщения.
• Ученикам требуется несколько минут, чтобы обдумать подходящий ответ.
• Учащиеся поворачиваются к партнеру (или небольшим группам) и делятся своими ответами. Сделайте еще один шаг вперед, попросив студентов найти кого-то, кто пришел к ответу, отличному от их собственного, и убедить своего партнера передумать.
• Ответы учащихся передаются в больших группах или всему классу во время последующего обсуждения.

Наверстать упущенное

• Остановиться на переходном этапе лекции.
• Предложите учащимся обратиться к партнеру или поработать в малых группах, чтобы сравнить записи и задать уточняющие вопросы.
• Через несколько минут задайте несколько вопросов.

Дебаты в аквариуме

• Попросите учащихся сесть группами по три человека.
• Назначение ролей. Например, человек слева занимает одну позицию по теме для обсуждения, человек справа занимает противоположную позицию, а человек в середине делает заметки и решает, какая сторона является наиболее убедительной, и аргументирует свой выбор. .
• Подведите итоги, попросив несколько групп подвести итоги их обсуждений.

Тематическое исследование

• Создайте от четырех до пяти тематических исследований одинаковой сложности.
• Предложите учащимся работать в группах по четыре или пять человек, чтобы они проработали и проанализировали свой пример из практики.
• Предоставьте 10-15 минут (или достаточное время) для работы с делами.
• Прогуляйтесь и ответьте на любые вопросы.
• Случайным образом созовите группы и попросите учащихся поделиться своим анализом. Продолжайте до тех пор, пока не будет рассмотрено каждое тематическое исследование.

Групповое обучение

• Начните курс, дав учащимся несколько заданий, таких как чтение или выполнение лабораторных работ. Подумайте о том, чтобы поручить их выполнить перед уроком.
• Проверьте понимание учащимися материала с помощью быстрой викторины с несколькими вариантами ответов. Предложите учащимся представить свои ответы.
• Распределите учащихся по группам и попросите их обсудить свои ответы с членами группы, чтобы достичь консенсуса. Пусть каждая группа представит по одному ответу на викторину.
• Запишите как индивидуальные оценочные баллы учащегося, так и окончательный групповой оценочный балл (оба используются для оценки каждого учащегося по курсу).
• Прочитайте лекцию, специально нацеленную на любые неверные представления или пробелы в знаниях, выявленные в ходе оценок.
• Дайте группам сложное задание, например, решить проблему или применить теорию к реальной ситуации.
• Дополнительную информацию об этой стратегии можно найти на совместном групповом обучении.

Групповое решение проблем

Существует множество стратегий обучения, в которых учащиеся работают вместе над решением проблемы, включая обучение на основе запросов, аутентичное обучение и исследовательское обучение. Хотя каждый из них имеет свои уникальные характеристики, в основном они включают:

• Постановку задачи перед учащимися.
• Предоставление некоторой структуры или руководства по решению проблемы. Однако обратите внимание, что все они ориентированы на учащихся, в которых преподаватель может играть минимальную роль.
• Достижение окончательного результата или решения.

Групповая работа: Эффективное использование совместных учебных групп | Центр обучения

Синтия Дж. Брэйм и Рэйчел Бил

Версия для печати

Процитируйте это руководство: Brame, C.J. & Biel, R. (2015). Организация и содействие групповой работе: Эффективное использование совместных учебных групп. Учебный центр Университета Вандербильта. Получено [сегодняшняя дата] с http://cft.vanderbilt.edu/guides-sub-pages/setting-up-and-facilitating-group-work-using-cooperative-learning-groups-efficiently/.

---

Многие преподаватели университетских дисциплин используют групповую работу для улучшения обучения своих студентов. Независимо от того, является ли целью улучшение понимания учащимися содержания, формирование конкретных передаваемых навыков или сочетание этих двух факторов, преподаватели часто обращаются к работе в малых группах, чтобы извлечь выгоду из преимуществ обучения по принципу «равный-равному». Этот тип групповой работы формально называется совместным обучением и определяется как использование в обучении небольших групп для поощрения совместной работы учащихся с целью максимизации их собственного обучения и обучения друг друга (Johnson, et al., 2008).

Совместное обучение характеризуется положительной взаимозависимостью, когда учащиеся понимают, что более высокая производительность отдельных лиц приводит к более высокой успеваемости всей группы (Johnson, et al., 2014). Это может быть формальным или неформальным, но часто включает специальное вмешательство инструктора, чтобы максимизировать взаимодействие и обучение студентов. Он бесконечно адаптируется, работает в малых и больших классах и в разных дисциплинах и может быть одним из самых эффективных подходов к обучению, доступных преподавателям колледжей.

• Как это может выглядеть?
• Какова теоретическая основа?
• Есть доказательства того, что это работает?
• Какие подходы могут помочь сделать его эффективным?
• Ссылки

Как это может выглядеть?

Группы неформального совместного обучения
При неформальном совместном обучении небольшие, временные, специальные группы из двух-четырех учащихся работают вместе в течение коротких периодов времени в классе, обычно до одного урока, чтобы отвечать на вопросы или отвечать на подсказки, заданные инструктором.

Дополнительные примеры организации неформальной групповой работы

Подумай-пару-поделись

Преподаватель задает вопрос для обсуждения. Студентам предлагается подумать или написать об ответе на вопрос, прежде чем обратиться к сверстнику, чтобы обсудить свои ответы. Затем группы делятся своими ответами с классом.

Одноранговая инструкция

Эта модификация алгоритма «думай-пары-распространяй» включает персональные устройства для ответов (например, кликеры). Публикуемый вопрос, как правило, представляет собой концептуальный вопрос с множественным выбором. Учащиеся обдумывают свой ответ и голосуют за ответ, прежде чем обратиться к соседу для обсуждения. Студенты могут изменить свои ответы после обсуждения, а «обмен» осуществляется инструктором, который показывает график ответов студентов и использует его в качестве стимула для обсуждения в большом классе. Этот подход особенно хорошо подходит для больших классов.

Лобзик

При таком подходе учащиеся работают в группах по четыре человека, чтобы стать экспертами в одном сегменте нового материала, в то время как другие «команды экспертов» в классе работают над другими сегментами нового материала. Затем класс перестраивается, образуя новые группы, в которых есть по одному члену от каждой экспертной группы. Затем члены новой команды по очереди обучают друг друга тому материалу, в котором они являются экспертами.

 

Формальные совместные учебные группы

При формальном совместном обучении учащиеся работают вместе в течение одного или нескольких уроков, чтобы выполнить совместное задание или задание (Johnson et al., 2014). Есть несколько функций, которые могут помочь этим группам работать хорошо:

• Преподаватель определяет цели обучения для занятия и распределяет учащихся по группам.

• Группы, как правило, неоднородны, и особое внимание уделяется навыкам, необходимым для успешного выполнения задания.

• В группах учащимся могут быть назначены определенные роли, при этом инструктор сообщает критерии успеха и типы необходимых социальных навыков.

• Важно отметить, что инструктор продолжает играть активную роль во время работы в группах, наблюдая за работой и оценивая групповую и индивидуальную работу.

• Инструкторы также призывают группы размышлять над своим взаимодействием, чтобы определить потенциальные улучшения для будущей групповой работы.

В этом видео показан пример формальных групп совместного обучения в классе Дэвида Маттеса в Университете Миннесоты:

Существует много более конкретных типов групповой работы, которые подпадают под общие описания, данные здесь, включая групповое обучение, проблемно-ориентированное обучение и ориентированное на процесс управляемое исследовательское обучение.

 

Какова теоретическая основа?

Использование совместных учебных групп в обучении основано на принципе конструктивизма с особым вниманием к вкладу, который может внести социальное взаимодействие. По сути, конструктивизм основывается на идее о том, что люди учатся, накапливая свои собственные знания, соединяя новые идеи и опыт с существующими знаниями и опытом для формирования нового или расширенного понимания (Брэнсфорд и др., 19).99). Рассмотрение роли, которую группы могут играть в этом процессе, основано на теории социальной взаимозависимости, которая выросла из идентификации Куртом Коффкой и Куртом Левином групп как динамических образований, которые могут демонстрировать различную взаимозависимость между членами, при этом члены группы мотивированы на достижение общих целей. . Мортон Дойч концептуализировал различные типы взаимозависимости с положительной корреляцией между достижением целей членами группы, способствующими сотрудничеству.

Лев Выготский расширил эту работу, изучив взаимосвязь между познавательными процессами и социальной деятельностью, разработав социокультурную теорию развития. Социокультурная теория развития предполагает, что обучение происходит, когда учащиеся решают проблемы, выходящие за рамки их текущего уровня развития, при поддержке своего преподавателя или своих сверстников. Таким образом, идея зоны ближайшего развития, поддерживаемая позитивной групповой взаимозависимостью, является основой совместного обучения (Davidson and Major, 2014; Johnson, et al., 2014).

Совместное обучение следует этой идее, поскольку группы работают вместе, чтобы изучить или решить проблему, при этом каждый человек несет ответственность за понимание всех аспектов. Небольшие группы важны для этого процесса, потому что учащиеся могут быть услышаны и слышать своих сверстников, в то время как в традиционной обстановке класса учащиеся могут проводить больше времени, слушая то, что говорит преподаватель.

Совместное обучение использует как взаимозависимость целей, так и взаимозависимость ресурсов для обеспечения взаимодействия и общения между членами группы. Изменение роли инструктора с чтения лекций на помощь группам помогает создать социальную среду, в которой студенты могут учиться посредством взаимодействия.

Есть доказательства того, что это работает?

Дэвид Джонсон, Роджер Джонсон и Карл Смит провели метаанализ 168 исследований, сравнивающих совместное обучение с конкурентным обучением и индивидуальным обучением у студентов колледжей (Johnson et al. , 2006). Они обнаружили, что совместное обучение приводит к более высоким академическим достижениям, чем конкурентное обучение и индивидуальное обучение во всех исследованиях, демонстрируя средний взвешенный размер эффекта 0,54 при сравнении сотрудничества и конкуренции и 0,51 при сравнении сотрудничества и индивидуального обучения. По сути, эти результаты показывают, что совместное обучение повышает академическую успеваемость учащихся примерно на половину стандартного отклонения по сравнению с некооперативными моделями обучения, и этот эффект считается умеренным. Важно отметить, что показатели академической успеваемости определялись в каждом исследовании и варьировались от когнитивных задач более низкого уровня (например, приобретение и сохранение знаний) до когнитивной деятельности более высокого уровня (например, творческое решение проблем) и от вербальных задач до математических задач и процедурных задач. задачи. Метаанализ также показал существенное влияние на другие показатели, включая самооценку и позитивное отношение к обучению. Джордж Кух и его коллеги также пришли к выводу, что совместное групповое обучение способствует вовлечению учащихся и академической успеваемости (Kuh et al., 2007).

Springer, Stanne и Donovan (1999) подтвердили эти результаты в своем мета-анализе 39 исследований в университетских классах STEM. Они обнаружили, что учащиеся, которые участвовали в различных типах обучения в малых группах, от расширенных формальных взаимодействий до кратких неформальных взаимодействий, имели более высокие академические успехи, демонстрировали более благоприятное отношение к учебе и проявляли большую настойчивость на курсах STEM, чем учащиеся, которые не участвовали. в обучении STEM в малых группах.

В приведенной ниже рамке представлены результаты трех отдельных исследований, в которых изучалось влияние групп совместного обучения.

 

Какие подходы могут помочь сделать групповую работу эффективной?

Подготовка

Сформулируйте свои цели для групповой работы, включая как академические цели, которых вы хотите достичь от учащихся, так и социальные навыки, которые вы хотите, чтобы они развили.

Определите форму группы, которая поможет достичь ваших целей.

• При неформальном групповом обучении группы часто формируются ad hoc из ближайших соседей по классу.

• При формальном групповом обучении инструктору полезно формировать группы, неоднородные в отношении определенных навыков или способностей, относящихся к групповым заданиям. Например, группы могут быть неоднородными в отношении академических навыков в дисциплине или в отношении других навыков, связанных с групповым заданием (например, способности проектирования, навыки программирования, навыки письма, организационные навыки) (Johnson et al, 2006).

• Обычно рекомендуются группы от 2 до 6 человек, при этом группы, состоящие из трех человек, демонстрируют наилучшие результаты в решении некоторых задач (Johnson et al., 2006; Heller and Hollabaugh, 1992).

• Чтобы избежать распространенных проблем в групповой работе, таких как доминирование одного учащегося или избегание конфликтов, может быть полезно распределить роли между членами группы (например, менеджер, скептик, педагог, посредник) и регулярно менять их. основе (Хеллер и Холлабо, 1992). Распределение этих ролей не обязательно в хорошо функционирующих группах, но может быть полезно для учащихся, которые не знакомы с групповой работой или не имеют навыков ее выполнения.

Выберите метод оценки, который будет способствовать позитивной групповой взаимозависимости, а также индивидуальной ответственности.

• В командном обучении два подхода способствуют положительной взаимозависимости и индивидуальной ответственности. Сначала учащиеся проходят индивидуальный тест по оценке готовности, а затем сразу же снова проходят тот же тест всей группой. Их оценка представляет собой совокупность двух баллов. Во-вторых, учащиеся вместе выполняют групповой проект и получают групповой балл за проект. Однако они также распределяют баллы между своими партнерами по группе, позволяя учащимся оценивать вклад участников, чтобы внести свой вклад в окончательную оценку.

• Хеллер и Холлабо (1992) описывают подход, в котором они включили групповое решение проблем в класс. Студенты регулярно решали задачи в малых группах, сдавая одно решение. Кроме того, тесты были построены таким образом, что 25% баллов были получены за групповую задачу, при этом только те люди, которые посещали сеансы группового решения задач, могли участвовать в групповой тестовой задаче. Такой подход может помочь предотвратить проблему «безбилетника», которая может мешать групповой работе.

• Университет Нового Южного Уэльса описывает различные способы оценки групповой работы, начиная от общих групповых оценок и заканчивая оценками, являющимися средними значениями индивидуальных оценок, строго индивидуальными оценками и их комбинацией. Они также предлагают способы оценки не только продукта групповой работы, но и самого процесса. Опять же, наличие части оценки, основанной на индивидуальном вкладе, помогает бороться с проблемой безбилетника.

Группы помощи в начале работы

Объясните задачу группы, в том числе ваши цели в отношении их успеваемости и социального взаимодействия.

Объясните, как задача включает в себя как позитивную взаимозависимость, так и индивидуальную ответственность, и как вы будете оценивать каждую из них.

Назначайте групповые роли или давайте группам подсказки, чтобы помочь им сформулировать эффективные способы взаимодействия. Университет Нового Южного Уэльса предоставляет ценный набор инструментов, помогающих группам внедрять передовые методы при первой встрече. На сайте также есть несколько упражнений для построения групповой динамики; они могут быть особенно полезны для групп, которые будут работать над более крупными проектами.

Мониторинг групповой работы

Регулярно наблюдайте за групповыми взаимодействиями и прогрессом , распространяя их во время групповой работы, собирая документы в процессе работы, или и то, и другое. Когда вы наблюдаете проблемы, вмешивайтесь, чтобы помочь учащимся продвигаться вперед по заданию и эффективно работать вместе. Университет Нового Южного Уэльса предоставляет раздаточные материалы, которые преподаватели могут использовать для содействия эффективному групповому взаимодействию, например, раздаточный материал, помогающий студентам слушать вдумчиво или давать конструктивную обратную связь, или помогать группам определять конкретные проблемы, с которыми они могут столкнуться.

Оценка и отражение

В дополнение к предоставлению отзывов о групповой и индивидуальной работе (ссылка на раздел подготовки выше) также полезно предоставить группе структуру для размышлений о том, что хорошо сработало в их группе, а что можно было бы улучшить. Грэм Гиббс (1994) предлагает использовать контрольные списки, показанные ниже.

Университет Нового Южного Уэльса предлагает другие виды рефлексивной деятельности, которые могут помочь учащимся определить эффективную групповую практику и избежать неэффективной практики в будущем совместном обучении.

 

Ссылки

Брансфорд, Дж. Д., Браун, А. Л., и Кокинг, Р. Р. (редакторы) (1999). Как люди учатся: мозг, разум, опыт и школа . Вашингтон, округ Колумбия: Издательство Национальной академии.

Bruffee, KA (1993). Совместное обучение: высшее образование, взаимозависимость и авторитет знаний. Балтимор, Мэриленд: Издательство Университета Джона Хопкинса.

Кабрера, А.Ф., Криссман, Дж.Л., Бернал, Э.М., Нора, А., Теренцини, П.Т., и Паскарелла, Э.Т. (2002). Совместное обучение: его влияние на развитие и разнообразие студентов колледжа. Журнал развития студентов колледжей, 43 (1), 20–34.

Дэвидсон, Н., и Мейджор, С. Х. (2014). Пересечение границ: совместное обучение, совместное обучение и проблемно-ориентированное обучение. Журнал передового опыта в преподавании в колледжах, 25 (3 и 4), 7–55.

Диз, Р.Л. (1991). Роль кооперативного подхода в повышении способности решать проблемы в коррекционном курсе колледжа. Журнал исследований в области математического образования, 22 (5), 409-21.

Гокхале, А.А. (1995). Совместное обучение улучшает критическое мышление. Журнал технологического образования, 7 (1).

Хеллер, П., и Холлабо, М. (1992) Обучение решению проблем посредством совместной группировки. Часть 2: Разработка задач и структурирование групп. Американский журнал физики 60, 637-644.

Джонсон Д.В., Джонсон Р.Т. и Смит К.А. (2006). Активное обучение: Сотрудничество в университетском классе (издание 3 ^rd ). Эдина, Миннесота: Взаимодействие.

Джонсон, Д.В., Джонсон, Р.Т., и Холубек, Э.Дж. (2008). Сотрудничество в классе (8 ^-й выпуск). Эдина, Миннесота: Взаимодействие.

Джонсон Д.В., Джонсон Р.Т. и Смит К.А. (2014). Совместное обучение: улучшение преподавания в университете за счет практического применения проверенной теории. Журнал передового опыта в преподавании в колледже 25, 85-118.

Джонс, Д. Дж., и Брикнер, Д. (1996). Внедрение совместного обучения в массовом курсе базовой механики. Материалы ежегодной конференции Американского общества инженерного образования.

Кух, Г. Д., Кинзи, Дж., Бакли, Дж., Бриджес, Б., и Хайек, Дж. К. (2007). Собираем воедино головоломку успеха учащихся: исследования, предложения и рекомендации (Отчет ASHE о высшем образовании, № 32). Сан-Франциско, Калифорния: Джосси-Басс.

Лав, А. Г., Дитрих, А., Фицджеральд, Дж., и Гордон, Д. (2014). Интеграция совместного обучения в классе и за его пределами. Журнал передового опыта в преподавании в колледже, 25 (3 и 4), 177-196.

Smith, ME, Hinckley, CC, & Volk, G.L. (1991). Совместное обучение в студенческой лаборатории. Журнал химического образования 68 (5), 413-415.

Спрингер, Л., Станн, М.Е., и Донован, С.С. (1999). Влияние обучения в малых группах на студентов естественных наук, математики, техники и технологий: метаанализ. Review of Educational Research, 96 (1), 21–51.

Урибе, Д., Кляйн, Дж. Д., и Салливан, Х.