gto_norm_03_eng
%PDF-1.5 % 1 0 obj >/OCGs[7 0 R 873 0 R]>>/Pages 3 0 R/Type/Catalog>> endobj 2 0 obj >stream 2018-02-07T10:10:37+03:00Adobe Illustrator CC (Macintosh)2018-02-07T10:11:25+03:002018-02-07T10:11:25+03:00
01application/pdf
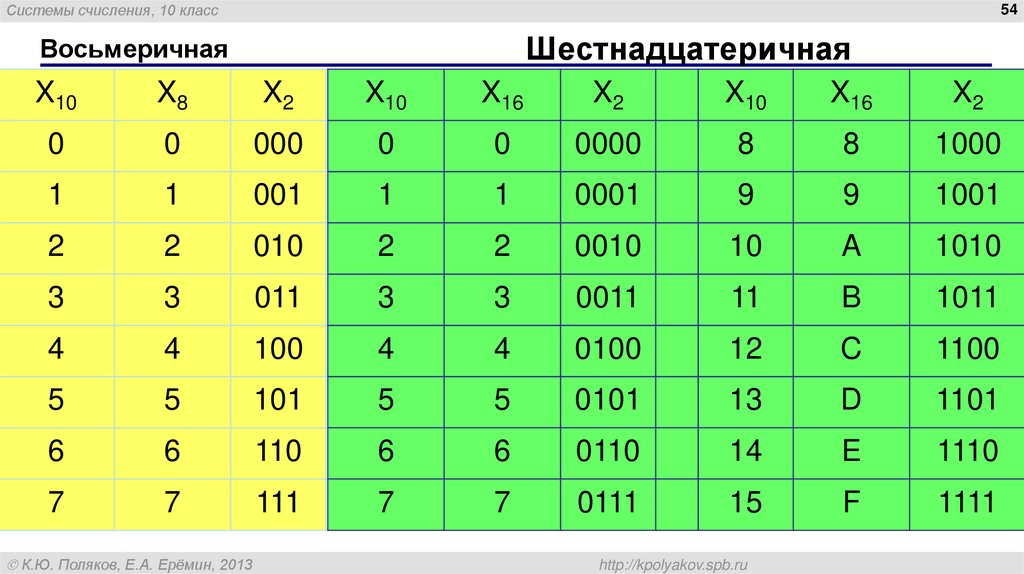did:ad5746e4-40f4-4df2-a0dd-8ce148479f81uuid:a4c33fb4-763b-c24a-a533-768ad29596d9xmp.did:ea23c21a-bbe9-4f71-ab33-f61c022c02e0proof:pdfuuid:442adba5-f05b-0d48-a507-3ffa9c4db14fxmp.did:d2a3e9b2-404a-4db7-af14-51bdfc7a0cdexmp.did:ea23c21a-bbe9-4f71-ab33-f61c022c02e0proof:pdf
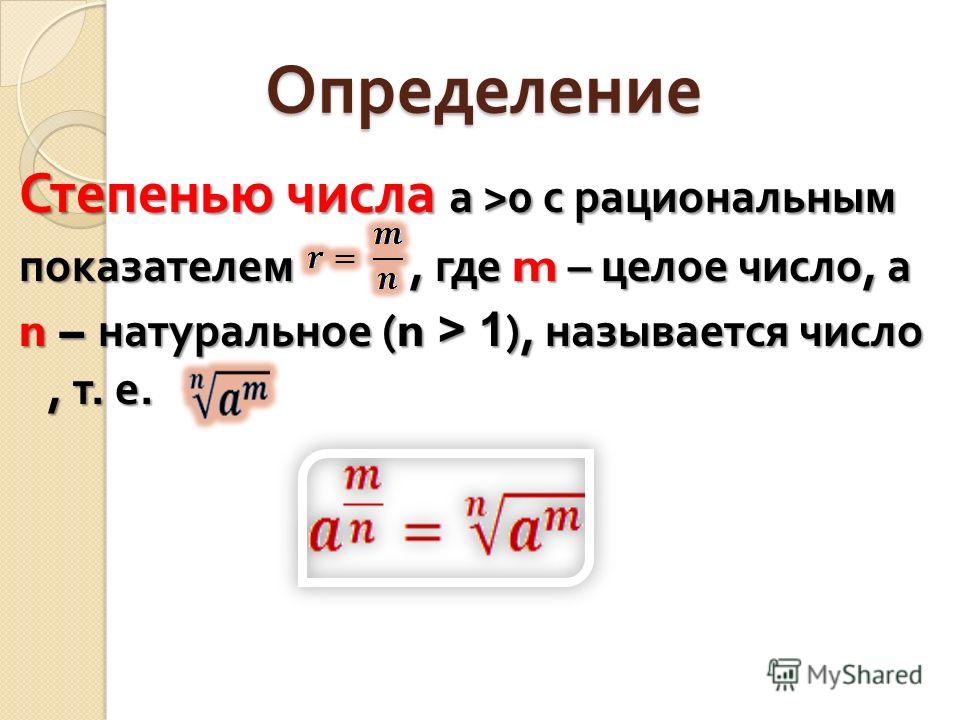66928 5.66928 303.307 425.197]/Type/Page>>
endobj
10 0 obj
>/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 900 0 R/TrimBox[5.66928 5.66928 303.307 425.197]/Type/Page>>
endobj
892 0 obj
>stream
H|n$
z:zd«xKV`2$A_=t5Q:o?~e-3y{q2[:sG-̃OXCТаблица степеней 2 (двойки)
Приведенная таблица кроме степени двойки показывает максимальные числа, которые может хранить компьютер для заданного числа бит. Причем как для целых так и чисел со знаком.
Исторически сложилось, что компьютеры используют двоичную систему счисления, а, соответственно, и хранения данных. Таким образом, любое число можно представить как последовательность нулей и единиц (бит информации). Существует несколько способов представления чисел в виде двоичной последовательности.
Рассмотрим наиболее простой из них — это целое положительное число. Тогда чем больше число нам нужно записать, тем более длинная последовательность бит нам необходима.
Ниже представлена таблица степеней числа 2. Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.
См. также: Таблица степеней других натуральных чисел.
Как пользоваться
таблицей степеней числа два?Первый столбец — это степень двойки, который одновременно, обозначает число бит, которое представляет число.
Второй столбец — значение двойки в соответствующей степени (n).
Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (27) — это 128
Третий столбец — максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце).
Пример определения максимального целого числа без знака.
Если использовать данные из предыдущего примера, мы знаем, что 27 = 128. Это верно, если мы хотим понять, какое количество чисел, можно представить с помощью семи бит. Но, поскольку первое число — это ноль, то максимальное число, которое можно представить с помощью семи бит 128 — 1 = 127 . Это и есть значение третьего столбца.
| Степень двойки (n) |
Значение степени двойки 2n |
Максимальное число без знака, записанное с помощью n бит |
Максимальное число со знаком, записанное с помощью n бит |
| 0 | 1 | - | - |
| 1 | 2 | 1 | - |
| 2 | 4 | 3 | 1 |
| 3 | 8 | 7 | 3 |
| 4 | 16 | 15 | 7 |
| 5 | 32 | 31 | 15 |
| 6 | 64 | 63 | 31 |
| 7 | 128 | 127 | 63 |
| 8 | 256 | 255 | 127 |
| 9 | 512 | 511 | 255 |
| 10 | 1 024 | 1 023 | 511 |
| 11 | 2 048 | 2 047 | 1023 |
| 12 | 40 96 | 4 095 | 2047 |
| 13 | 8 192 | 8 191 | 4095 |
| 14 | 16 384 | 16 383 | 8191 |
| 15 | 32 768 | 32 767 | 16383 |
| 16 | 65 536 | 65 535 | 32767 |
| 17 | 131 072 | 131 071 | 65 535 |
| 18 | 262 144 | 262 143 | 131 071 |
| 19 | 524 288 | 524 287 | 262 143 |
| 20 | 1 048 576 | 1 048 575 | 524 287 |
| 21 | 2 097 152 | 2 097 151 | 1 048 575 |
| 22 | 4 194 304 | 4 194 303 | 2 097 151 |
| 23 | 8 388 608 | 8 388 607 | 4 194 303 |
| 24 | 16 777 216 | 16 777 215 | 8 388 607 |
| 25 | 33 554 432 | 33 554 431 | 16 777 215 |
| 26 | 67 108 864 | 67 108 863 | 33 554 431 |
| 27 | 134 217 728 | 134 217 727 | 67 108 863 |
| 28 | 268 435 456 | 268 435 455 | 134 217 727 |
| 29 | 536 870 912 | 536 870 911 | 268 435 455 |
| 30 | 1 073 741 824 | 1 073 741 823 | 536 870 911 |
| 31 | 2 147 483 648 | 2 147 483 647 | 1 073 741 823 |
| 32 | 4 294 967 296 | 4 294 967 295 | 2 147 483 647 |
Необходимо принять во внимание, что не все числа в компьютере представлены таким образом.
Существуют и другие способы представления данных. Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения «плюс/минус». Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.
Для этого же самого примера ( 27 ) семью битами можно записать максимум число +63, поскольку один бит занят знаком «плюс». Но мы можем хранить и число «-63», что было бы невозможно, если бы все биты были бы зарезервированы под хранение числа.
Примеры использования таблицы степеней числа два
Например, нам необходимо узнать, в какую степень нужно возвести число 2, чтобы получить 256. Во втором столбце находим число 256 и считываем, что 256 это два в степени восемь.
Аналогично, 2 в 11 степени равно 2048.
2 в 13 степени равно 8,192.
2 в 15 степени равно 32,768
2 в 17 степени равно 131,072
См. также: Таблица степеней других натуральных чисел.
0
Хранение и кодирование информации | Описание курса | Использование электронных таблиц Excel
Названия больших чисел и количество нулей в них
Существует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Числа состоят из цифр. Число 52 состоит из двух цифр: 5 и 2. Числа с 1 впереди и последующими нулями имеют названия. Всем известны: 10 — десять, 100 — сто, 1000 — тысяча, 1 000 000 — миллион. Так как большие числа с большим числом нулей записывать неудобно, используют сокращения в виде степеней: запись 1011 означает число с 11-ю нулями, запись 1052 означает число с 52-мя нулями и т.д. Приведем названия чисел с десятками и сотнями нулей.
Названия «круглых» чисел, которые можно встретить в школьной программе:
1 000 000 — миллион (6 нулей)
1 000 000 000 — миллиард или биллион (9 нулей)
1 000 000 000 000 — триллион (12 нулей)
1 000 000 000 000 000 — квадриллион (15 нулей)
1 000 000 000 000 000 000 — квинтиллион (18 нулей)
1 000 000 000 000 000 000 000 — секстиллион (21 нуль)
1 000 000 000 000 000 000 000 000 — септиллион (24 нуля)
1 000 000 000 000 000 000 000 000 000 — октиллион (27 нулей)
1 000 000 000 000 000 000 000 000 000 000 — нониллион (30 нулей)
1 000 000 000 000 000 000 000 000 000 000 000 — дециллион (33 нуля)
Еще некоторые примеры интересных названий:
10100 — гугол, googol (100 нулей)
1010100 — гуголплекс, googolplex (десять в степени гугол)
10140 — асанкхейя, asankhyeya или сто квинквадрагинтиллионов
10303 — центиллион, centillion
103003 — миллиллион, millillion
103000003 — милли-миллиллион, milli-millillion
Самого большого числа в мире не существует, так как любое большое число всегда можно увеличить, умножить, возвести в степень, и получится другое большее число.
Бесконечность не является числом.
Из известных самых больших чисел, имеющих название (математическое доказательство) можно выделить: число TREE(3), число SCG(13), число Лоудера, число Мозера, число Скьюза, число Райо, число Грэма, инфитеиплеон.
Таблица больших чисел с указанием количества нулей и названиями на русском и английском.
| Число нулей | Краткая запись | Название | Название на английском |
|---|---|---|---|
| 3 | 103 | тысяча | thousand |
| 6 | 106 | миллион | million |
| 9 | 109 | миллиард (биллион) | billion |
| 12 | 1012 | триллион | trillion |
| 15 | 1015 | квадриллион | quadrillion |
| 18 | 1018 | квинтиллион | quintillion |
| 21 | 1021 | секстиллион | sextillion |
| 24 | 1024 | септиллион | septillion |
| 27 | 1027 | октиллион | octillion |
| 30 | 1030 | нониллион | nonillion |
| 33 | 1033 | дециллион | decillion |
| 36 | 1036 | ундециллион | undecillion |
| 39 | 1039 | дуодециллион | duodecillion |
| 42 | 1042 | тредециллион | tredecillion |
| 45 | 1045 | кватуордециллион | quattuordecillion |
| 48 | 1048 | квиндециллион | quindecillion |
| 51 | 1051 | сексдециллион | sexdecillion |
| 54 | 1054 | септендециллион | septendecillion |
| 57 | 1057 | октодециллион | octodecillion |
| 60 | 1060 | новемдециллион | novemdecillion |
| 63 | 1063 | вигинтиллион | vigintillion |
| 66 | 1066 | унвигинтиллион | unvigintillion |
| 69 | 1069 | дуовигинтиллион | duovigintillion |
| 72 | 1072 | тревигинтиллион | trevigintillion |
| 75 | 1075 | кватуорвигинтиллион | quattuorvigintillion |
| 78 | 1078 | квинвигинтиллион | quinvigintillion |
| 81 | 1081 | сексвигинтиллион | sexvigintillion |
| 84 | 1084 | септенвигинтиллион | septenvigintillion |
| 87 | 1087 | октовигинтиллион | octovigintillion |
| 90 | 1090 | новемвигинтиллион | novemvigintillion |
| 93 | 1093 | тригинтиллион | trigintillion |
| 96 | 1096 | унтригинтиллион | untrigintillion |
| 99 | 1099 | дуотригинтиллион | duotrigintillion |
| 102 | 10102 | третригинтиллион | trestrigintillion |
| 105 | 10105 | кватортригинтиллион | quattuortrigintillion |
| 108 | 10108 | квинтригинтиллион | quintrigintillion |
| 111 | 10111 | секстригинтиллион | sextrigintillion |
| 114 | 10114 | септентригинтиллион | septentrigintillion |
| 117 | 10117 | октотригинтиллион | octotrigintillion |
| 120 | 10120 | новемтригинтиллион | novemtrigintillion |
| 123 | 10123 | квадрагинтиллион | quadragintillion |
| 126 | 10126 | унквадрагинтиллион | unquadragintillion |
| 129 | 10129 | дуоквадрагинтиллион | duoquadragintillion |
| 132 | 10132 | треквадрагинтиллион | trequadragintillion |
| 135 | 10135 | кваторквадрагинтиллион | quattuorquadragintillion |
| 138 | 10138 | квинквадрагинтиллион | quinquadragintillion |
| 141 | 10141 | сексквадрагинтиллион | sexquadragintillion |
| 144 | 10144 | септенквадрагинтиллион | septenquadragintillion |
| 147 | 10147 | октоквадрагинтиллион | octoquadragintillion |
| 150 | 10150 | новемквадрагинтиллион | novemquadragintillion |
| 153 | 10153 | квинквагинтиллион | quinquagintillion |
| 156 | 10156 | унквинкагинтиллион | unquinquagintillion |
| 159 | 10159 | дуоквинкагинтиллион | duoquinquagintillion |
| 162 | 10162 | треквинкагинтиллион | trequinquagintillion |
| 165 | 10165 | кваторквинкагинтиллион | quattuorquinquagintillion |
| 168 | 10168 | квинквинкагинтиллион | quinquinquagintillion |
| 171 | 10171 | сексквинкагинтиллион | sexquinquagintillion |
| 174 | 10174 | септенквинкагинтиллион | septenquinquagintillion |
| 177 | 10177 | октоквинкагинтиллион | octoquinquagintillion |
| 180 | 10180 | новемквинкагинтиллион | novemquinquagintillion |
| 183 | 10183 | сексагинтиллион | sexagintillion |
| 186 | 10186 | унсексагинтиллион | unsexagintillion |
| 189 | 10189 | дуосексагинтиллион | duosexagintillion |
| 192 | 10192 | тресексагинтиллион | tresexagintillion |
| 195 | 10195 | кваторсексагинтиллион | quattuorsexagintillion |
| 198 | 10198 | квинсексагинтиллион | quinsexagintillion |
| 201 | 10201 | секссексагинтиллион | sexsexagintillion |
| 204 | 10204 | септенсексагинтиллион | septensexagintillion |
| 207 | 10207 | октосексагинтиллион | octosexagintillion |
| 210 | 10210 | новемсексагинтиллион | novemsexagintillion |
| 213 | 10213 | септагинтиллион | septuagintillion |
| 216 | 10216 | унсептагинтиллион | unseptuagintillion |
| 219 | 10219 | дуосептагинтиллион | duoseptuagintillion |
| 222 | 10222 | тресептагинтиллион | treseptuagintillion |
| 225 | 10225 | кваторсептагинтиллион | quattuorseptuagintillion |
| 228 | 10228 | квинсептагинтиллион | quinseptuagintillion |
| 231 | 10231 | секссептагинтиллион | sexseptuagintillion |
| 234 | 10234 | септенсептагинтиллион | septenseptuagintillion |
| 237 | 10237 | октосептагинтиллион | octoseptuagintillion |
| 240 | 10240 | новемсептагинтиллион | novemseptuagintillion |
| 243 | 10243 | октогинтиллион | octogintillion |
| 246 | 10246 | уноктогинтиллион | unoctogintillion |
| 249 | 10249 | дуооктогинтиллион | duooctogintillion |
| 252 | 10252 | треоктогинтиллион | treoctogintillion |
| 255 | 10255 | кватороктогинтиллион | quattuoroctogintillion |
| 258 | 10258 | квиноктогинтиллион | quinoctogintillion |
| 261 | 10261 | сексоктогинтиллион | sexoctogintillion |
| 264 | 10264 | септоктогинтиллион | septoctogintillion |
| 267 | 10267 | октооктогинтиллион | octooctogintillion |
| 270 | 10270 | новемоктогинтиллион | novemoctogintillion |
| 273 | 10273 | нонагинтиллион | nonagintillion |
| 276 | 10276 | уннонагинтиллион | unnonagintillion |
| 279 | 10279 | дуононагинтиллион | duononagintillion |
| 282 | 10282 | тренонагинтиллион | trenonagintillion |
| 285 | 10285 | кваторнонагинтиллион | quattuornonagintillion |
| 288 | 10288 | квиннонагинтиллион | quinnonagintillion |
| 291 | 10291 | секснонагинтиллион | sexnonagintillion |
| 294 | 10294 | септеннонагинтиллион | septennonagintillion |
| 297 | 10297 | октононагинтиллион | octononagintillion |
| 300 | 10300 | новемнонагинтиллион | novemnonagintillion |
| 303 | 10303 | центиллион | centillion |
Возведение в степень в Python – способы, типы степеней, отбратные операции
Содержание:развернуть
Когда я был студентом, мой преподаватель по методам программирования любил повторять: «В математике все идеи простые».
Чаще всего, фраза звучала в момент объяснения новой сложной темы, а потому вызывала определённые внутренние противоречия.
С возведением в степень всё не так — это действительно простая операция.
История
Возведение в степень — частный случай умножения, поэтому данную операцию изначально не рассматривали, как самостоятельную. Но уже в работах Диофанта Александрийского степени отведено особое место. В частности «Отец Алгебры» применял понятия кубов и квадратов числа.
Возведение в степень определяется как результат n-кратного умножения числа самого на себя.
Эта операция была известна ещё в древнем Вавилоне, однако современный её вид устоялся лишь в XVII веке.
Как умножение позволяет сократить количество символов сложения:
6 + 6 + 6 + 6 + 6 + 6 = 6 * 6
Так и степень сокращает запись умножения:
- 6 — это основание;
- 2 — показатель степени (это число говорит о том, сколько раз число в основании должно быть умножено само на себя).
или «галочка». Этот символ популярен и вне программирования.Определение
В Python возведение в степень записывается при помощи двойной «звёздочки» — «**»
a = 2 ** 4 print(a) > 16Вторая форма записи — встроенная функция pow():
# первый аргумент — основание, а второй — показатель b = pow(2, 4) print(b) > 16Обратные операции
Извлечение корня
У возведения в степень две обратные операции. Первая — извлечение корня. Подробнее о корнях в Python вы можете почитать в нашей статье. Отметим лишь, что корень в питоне вычисляется с помощью той же функции pow():
# корень четвёртой степени из 16 root = pow(16, (1/4)) print(root) > 2.0Либо с применением оператора «**»:
# корень кубический из 27 cub_root = 27 ** (1/3) print(cub_root) > 3.0Для извлечения квадратного корня справедливы оба вышеуказанных способа, но существует и третий, специализированный.
Для его применения требуется импортировать модуль math:import math # квадратный корень из 100 sqr_root = math.sqrt(100) print(sqr_root) > 10.0Логарифмирование
Логарифмирование — вторая обратная операция.
Логарифмом числа «b» по основанию «a» зовётся такой показатель степени, в который следует возвести «a», чтобы получить «b».
Здесь
x— логарифм. Пример из математики — найдем значение выражения:Легче всего эта запись читается в формате вопроса: «В какую степень нужно возвести 2, чтобы получить 16?». Очевидно, в 4-ю. Следовательно,
В питоне операция нахождения логарифма также заложена в функционал модуля math:
import math # отыщем логарифм 100 по основанию 10 # 100 — основание логарифма, а 10 — аргумент log = math.log(100, 10) print(log) > 2.0Степень
Целочисленная
В целочисленную степень можно возводить положительные и отрицательные
intиfloatчисла:# int print(3 ** 9) > 19683 print(pow(-2, 10)) > 1024 # float print(3. 14 ** 9)
> 29673.367320587102
print(pow(-1.1, 1001))
> -2.7169262098066285e+41И функция
pow()и оператор «**» умеют возводить комплексные числа:# complex a = complex(2, 1) print(pow(a, 2)) > (3+4j) print(a ** 2) > (3+4j)Показатель степени может быть положительным, отрицательным и нулевым:
# + print(12 ** 4) > 20736 # - print(100 ** -2) > 0.0001 # 0 print(1231 ** 0) > 1Результат не определён, когда 0 возводят в отрицательную степень:
print(0 ** -4) > ZeroDivisionError: 0.0 cannot be raised to a negative powerОшибка деления на ноль возникает из-за следующего свойства степени:
Рациональная
Возведение числа в рациональную степень напрямую связано с извлечением корня из этого числа отношением:
Если рациональный показатель отрицательный, а основание равно нулю, то Питон все ещё будет выдавать ошибку:
print(0 ** -(5/4)) > ZeroDivisionError: 0. 0 cannot be raised to a negative powerВ случае, когда основание меньше нуля, числитель показателя нечётный, а знаменатель, напротив, чётный, результат получается комплексным. Но это свойство рациональных степеней учитывается только в функции
pow():print(pow(-5, (5/4))) > (-5.286856317202822-5.286856317202821j) print(type(pow(-5, (5/4)))) > <class 'complex'>В остальном возведение в рациональную степень работает, как и для целочисленной:
print(0 ** (3/2)) > 0.0 print(pow(1, (23/24))) > 1.0 print(10 ** (6/7)) > 7.196856730011519Вещественная
В начале автор объявил, что возведение в степень — штука несложная. Так вот, для вещественных степеней это уже не совсем так. Идеи, заложенные в эту операцию, хоть и просты, но их много, и каждая из них достойна собственной статьи. Описать вкратце разложение в ряд Тейлора и численное интегрирование не получится.
Это будет не справедливо, как по отношению к вам, так и к математике. Поэтому, выделим главное:Python умеет возводить в вещественную степень даже вещественные числа (пусть и псевдо)
Сделать такое инструментами математики ой как непросто:
# возведём число Пи в степень e print(pow(math.pi, math.e)) > 22.45915771836104Ноль в степени ноль
Дискуссии по поводу значения 0 в степени 0 продолжаются уже больше двух веков. Обычно значение нуля в нулевой степени принято считать неопределённым, но символическое соглашение о том, что «0 в степени 0 равно 1» помогает в записи формул и алгоритмов. Ровно поэтому так сделано и в Python:
print(pow(0, 0)) > 1 print(0 ** 0) > 1Статья 12. Размер ежемесячной страховой выплаты \ КонсультантПлюс
- Главная
- Документы
- Статья 12. Размер ежемесячной страховой выплаты
Подготовлена редакция документа с изменениями, не вступившими в силу
Федеральный закон от 24.
07.1998 N 125-ФЗ
(ред. от 25.02.2022)
«Об обязательном социальном страховании от несчастных случаев на производстве и профессиональных заболеваний»Статья 12. Размер ежемесячной страховой выплаты
1. Размер ежемесячной страховой выплаты определяется как доля среднего месячного заработка застрахованного, исчисленная в соответствии со степенью утраты им профессиональной трудоспособности.
(в ред. Федерального закона от 07.07.2003 N 118-ФЗ)
(см. текст в предыдущей редакции)
2. При расчете размера утраченного застрахованным в результате наступления страхового случая заработка учитываются выплаты и иные вознаграждения, начисленные в пользу физических лиц по гражданско-правовому договору, предметом которого являются выполнение работ и (или) оказание услуг, договору авторского заказа, в соответствии с которыми заказчик обязан уплачивать страховщику страховые взносы.
(в ред. Федерального закона от 29.12.2015 N 394-ФЗ)
(см. текст в предыдущей редакции)
Все виды заработка учитываются в суммах, начисленных до удержания налогов, уплаты сборов и других обязательных платежей.
В местностях, где установлены районные коэффициенты, процентные надбавки к заработной плате, размер ежемесячной страховой выплаты определяется с учетом этих коэффициентов и надбавок.
При исчислении среднемесячного заработка застрахованного, направленного страхователем для работы за пределы территории Российской Федерации, учитываются как суммы заработка по основному месту работы, так и суммы заработка, начисленные в иностранной валюте (если на них начислялись страховые взносы), которые пересчитываются в рубли по курсу Центрального банка Российской Федерации, установленному на день назначения ежемесячной страховой выплаты.
(в ред. Федерального закона от 08.12.2010 N 348-ФЗ)
(см. текст в предыдущей редакции)
3. Среднемесячный заработок застрахованного исчисляется путем деления общей суммы его заработка (с учетом премий, начисленных в расчетном периоде) за 12 месяцев повлекшей повреждение здоровья работы, предшествовавших месяцу, в котором с ним произошел несчастный случай на производстве, установлен диагноз профессионального заболевания или (по выбору застрахованного) установлена утрата (снижение) его профессиональной трудоспособности, на 12.
При расчете среднемесячного заработка застрахованного месяцы, не полностью им проработанные, а также месяцы, за которые отсутствуют сведения о заработке застрахованного, заменяются предшествующими месяцами, полностью проработанными на работе, повлекшей повреждение здоровья, и за которые имеются сведения о заработке, либо исключаются в случае невозможности их замены. Замена не полностью проработанных застрахованным месяцев не производится в случае, если в этот период за ним сохранялся в соответствии с законодательством Российской Федерации средний заработок, на который начисляются страховые взносы в соответствии со статьей 20.1 настоящего Федерального закона.(в ред. Федеральных законов от 07.07.2003 N 118-ФЗ, от 29.12.2015 N 394-ФЗ)
(см. текст в предыдущей редакции)
Если повлекшая повреждение здоровья работа продолжалась менее 12 месяцев или 12 месяцев, но сведения о заработке за один или несколько месяцев отсутствуют, среднемесячный заработок застрахованного исчисляется путем деления общей суммы его заработка за фактически проработанное им число месяцев, за которые имеются сведения о заработке и которые предшествовали месяцу, в котором с ним произошел несчастный случай на производстве, установлен диагноз профессионального заболевания или (по выбору застрахованного) установлена утрата (снижение) его профессиональной трудоспособности, на число фактически проработанных месяцев.
В случае, если период работы, повлекшей повреждение здоровья, составил менее одного полного календарного месяца, ежемесячная страховая выплата исчисляется исходя из условного месячного заработка, определяемого путем деления суммы заработка за проработанное время на количество проработанных дней и умножения полученного результата на количество рабочих дней в месяце, исчисленное в среднем за год.(в ред. Федерального закона от 29.12.2015 N 394-ФЗ)
(см. текст в предыдущей редакции)
По желанию застрахованного при наступлении страхового случая по причине получения им профессионального заболевания средний месячный заработок может быть подсчитан за последние 12 месяцев работы, предшествовавших прекращению работы, повлекшей такое заболевание.
4. Ежемесячные страховые выплаты застрахованному, не достигшему на момент назначения обеспечения по страхованию возраста 18 лет, исчисляются из его среднего заработка, но не менее установленной в соответствии с законом величины прожиточного минимума трудоспособного населения в целом по Российской Федерации.
(п. 4 в ред. Федерального закона от 07.07.2003 N 118-ФЗ)
(см. текст в предыдущей редакции)
5. Если страховой случай наступил после окончания срока действия трудового договора, а также гражданско-правового договора, предметом которого являлись выполнение работ и (или) оказание услуг, договора авторского заказа и в соответствии с указанными договорами предусматривалась уплата страховых взносов страховщику, ежемесячная страховая выплата исчисляется из заработка застрахованного до окончания срока действия указанного договора.
(п. 5 в ред. Федерального закона от 29.12.2015 N 394-ФЗ)
(см. текст в предыдущей редакции)
6. Если в заработке застрахованного до наступления страхового случая произошли устойчивые изменения, улучшающие его имущественное положение (повышена заработная плата по занимаемой должности, он переведен на более высокооплачиваемую работу, поступил на работу после окончания учебного учреждения по очной форме обучения и в других случаях, когда доказана устойчивость изменения или возможности изменения оплаты труда застрахованного), при подсчете его среднего месячного заработка учитывается только заработок, который он получил или должен был получить после соответствующего изменения.
7. Если застрахованный (страхователь) не имеет возможности представить справку (справки) о заработке, из которого должна быть исчислена ежемесячная страховая выплата, ежемесячная страховая выплата рассчитывается из тарифной ставки (должностного оклада), установленной в отрасли (подотрасли) для данной профессии и сходных условий труда ко времени обращения за страховыми выплатами, или (по выбору застрахованного) величины прожиточного минимума трудоспособного населения в целом по Российской Федерации, установленной в соответствии с федеральным законом на день обращения за назначением обеспечения по страхованию. При этом, если застрахованный на момент наступления страхового случая работал на условиях неполного рабочего времени (неполного рабочего дня (смены) или неполной рабочей недели), размер ежемесячной страховой выплаты подлежит уменьшению пропорционально продолжительности рабочего времени застрахованного.
КонсультантПлюс: примечание.
С 01.01.2023 абз. 2 п. 7 ст. 12 излагается в новой редакции (ФЗ от 14.
07.2022 N 237-ФЗ). См. будущую редакцию.В указанном случае территориальный орган страховщика по заявлению застрахованного направляет запрос в территориальный орган Пенсионного фонда Российской Федерации о представлении сведений о заработной плате, иных выплатах и вознаграждениях застрахованного у соответствующего страхователя за календарный год, предшествующий году, в котором с ним произошел несчастный случай на производстве, установлен диагноз профессионального заболевания или (по выбору застрахованного) установлена утрата (снижение) его профессиональной трудоспособности, или по желанию застрахованного при наступлении страхового случая по причине получения им профессионального заболевания — за последний календарный год работы, повлекшей такое заболевание. Форма заявления застрахованного, форма и порядок направления запроса, форма, порядок и сроки представления территориальным органом Пенсионного фонда Российской Федерации запрашиваемых сведений устанавливаются федеральным органом исполнительной власти, осуществляющим функции по выработке государственной политики и нормативно-правовому регулированию в сфере социального страхования.
При наличии указанных сведений ежемесячная страховая выплата исчисляется исходя из этих сведений.В случае, если после назначения ежемесячной страховой выплаты, исчисленной в порядке, предусмотренном абзацами первым и вторым настоящего пункта, застрахованный (страхователь) представит в территориальный орган страховщика справку (справки) о заработке застрахованного, из которого должна была первоначально исчисляться ежемесячная страховая выплата, назначенная ежемесячная страховая выплата подлежит перерасчету с месяца, следующего за месяцем, в котором была представлена соответствующая справка (справки). При этом размер пересчитанной ежемесячной страховой выплаты не может быть меньше ранее установленного размера.
(п. 7 в ред. Федерального закона от 29.12.2015 N 394-ФЗ)
(см. текст в предыдущей редакции)
8. Лицам, имеющим право на получение страховых выплат в случае смерти застрахованного, размер ежемесячной страховой выплаты исчисляется исходя из его среднего месячного заработка за вычетом долей, приходящихся на него самого и трудоспособных лиц, состоявших на его иждивении, но не имеющих право на получение страховых выплат.
Для определения размера ежемесячных страховых выплат каждому лицу, имеющему право на их получение, общий размер указанных выплат делится на число лиц, имеющих право на получение страховых выплат в случае смерти застрахованного.(в ред. Федеральных законов от 25.10.2001 N 141-ФЗ, от 07.07.2003 N 118-ФЗ)
(см. текст в предыдущей редакции)
9. Ежемесячная страховая выплата в дальнейшем перерасчету не подлежит, за исключением следующих случаев:
изменение степени утраты профессиональной трудоспособности;
изменение круга лиц, имеющих право на получение страховых выплат в случае смерти застрахованного;
уточнение данных о размере фактического заработка застрахованного;
индексация ежемесячной страховой выплаты.
(п. 9 в ред. Федерального закона от 29.12.2015 N 394-ФЗ)
(см. текст в предыдущей редакции)
10. При назначении ежемесячной страховой выплаты суммы заработка, из которого исчисляется размер ежемесячной страховой выплаты, полученные за период до дня проведения индексации размеров ежемесячных страховых выплат в соответствии с пунктом 11 настоящей статьи, увеличиваются с учетом соответствующих коэффициентов, установленных для индексации размера ежемесячной страховой выплаты.
При этом коэффициенты, примененные к суммам заработка, к назначенному размеру ежемесячной страховой выплаты не применяются.(в ред. Федерального закона от 09.12.2010 N 350-ФЗ)
(см. текст в предыдущей редакции)
КонсультантПлюс: примечание.
Ежемесячные страховые выплаты, назначенные начиная с 06.10.2006, подлежат перерасчету с даты их назначения с учетом коэффициентов, установленных абз. 2 — 5 п. 10 ст. 12 данного документа (ФЗ от 19.05.2010 N 90-ФЗ).
В связи с повышением стоимости жизни и изменениями в уровне оплаты труда суммы заработка, из которого исчисляется размер ежемесячной страховой выплаты, увеличиваются с учетом следующих коэффициентов:
(абзац введен Федеральным законом от 19.05.2010 N 90-ФЗ)
за 1971 год и предшествующие периоды — 11,2; за 1972 год — 10,9; за 1973 год — 10,6; за 1974 год — 10,3; за 1975 год — 10,0; за 1976 год — 9,7; за 1977 год — 9,4; за 1978 год — 9,1; за 1979 год — 8,8; за 1980 год — 8,5; за 1981 год — 8,2; за 1982 год — 7,9; за 1983 год — 7,6; за 1984 год — 7,3; за 1985 год — 7,0; за 1986 год — 6,7; за 1987 год — 6,4; за 1988 год — 6,1; за 1989 год — 5,8; за 1990 год — 5,5; за 1991 год — 4,3.
(абзац введен Федеральным законом от 19.05.2010 N 90-ФЗ)
Суммы заработка, из которого исчисляется размер ежемесячной страховой выплаты, дополнительно увеличиваются за период до 1 января 1991 года с учетом коэффициента 6, с 1 января 1991 года по 31 декабря 1991 года — с учетом коэффициента 3.
(абзац введен Федеральным законом от 19.05.2010 N 90-ФЗ)
В связи с повышением стоимости жизни и изменениями в уровне оплаты труда при исчислении размера ежемесячной страховой выплаты суммы заработка, полученные за период с 1 января 1992 года по 31 января 1993 года, увеличиваются с учетом коэффициента 3.
(абзац введен Федеральным законом от 19.05.2010 N 90-ФЗ)
Суммы заработка, из которого исчисляется размер ежемесячной страховой выплаты, полученные за период до 1 мая 2002 года, увеличиваются пропорционально повышению в централизованном порядке в период по 1 мая 2002 года включительно минимального размера оплаты труда.
(абзац введен Федеральным законом от 09.
12.2010 N 350-ФЗ)11. Размер ежемесячной страховой выплаты подлежит индексации один раз в год с 1 февраля текущего года исходя из индекса роста потребительских цен за предыдущий год. Коэффициент индексации определяется Правительством Российской Федерации.
(п. 11 в ред. Федерального закона от 19.12.2016 N 444-ФЗ)
(см. текст в предыдущей редакции)
КонсультантПлюс: примечание.
Размеры выплат, установленные до 01.01.2018 и превышающие максимальный размер, установленный в соответствии с п. 12 и 13 ст. 12 (в ред. ФЗ от 19.12.2016 N 444-ФЗ), не изменяются.
12. Максимальный размер ежемесячной страховой выплаты не может превышать 72 290,4 рубля.
(в ред. Федерального закона от 19.12.2016 N 444-ФЗ)
(см. текст в предыдущей редакции)
При назначении страховых выплат застрахованному по нескольким страховым случаям ограничение максимальным размером применяется к общей сумме страховой выплаты.
При назначении страховых выплат лицам, имеющим право на их получение в связи со смертью застрахованного, ограничение максимальным размером применяется к общей сумме страховых выплат, назначенных в связи со смертью застрахованного.
(п. 12 введен Федеральным законом от 07.07.2003 N 118-ФЗ)
13. Установленный пунктом 12 настоящей статьи максимальный размер ежемесячной страховой выплаты подлежит индексации один раз в год с 1 февраля текущего года исходя из индекса роста потребительских цен за предыдущий год. Коэффициент индексации определяется Правительством Российской Федерации.
(п. 13 введен Федеральным законом от 19.12.2016 N 444-ФЗ)
Статья 11. Размер единовременной страховой выплаты Статья 13. Освидетельствование, переосвидетельствование застрахованного учреждением медико-социальной экспертизы
Всего лишь степени двойки
И. Акулич
«Квант» №2, 2012Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Используя показатели степени, ее можно записать в эквивалентном виде: 20, 21, 22, 23, 24, .
.. Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами.Несомненно, многие читатели встречали ее в классической истории об изобретателе шахмат, который попросил у правителя в награду за первую клетку шахматной доски одно пшеничное зерно, за вторую — два, за третью — четыре, и так далее, всё время удваивая число зерен. Понятно, что суммарное их количество равно
S = 20 + 21 + 22 + 23 + 24 + … + 263. (1)
Но так как эта сумма неимоверно велика и во много раз превосходит годовой урожай зерновых по всему миру, вышло, что мудрец ободрал правителя как липку.1
Однако зададимся сейчас другим вопросом: как с наименьшими затратами труда подсчитать величину S? Обладатели калькулятора (или, паче того, компьютера) вполне могут за обозримое время выполнить перемножения, а затем сложить полученные 64 числа, получив ответ: 18 446 744 073 709 551 615.
А поскольку объем вычислений немалый, то и вероятность ошибки весьма велика.Кто похитрей, могут углядеть в этой последовательности геометрическую прогрессию. Не знакомые же с этим понятием (или те, кто попросту забыл стандартную формулу суммы геометрической прогрессии) могут использовать следующие рассуждения. Давайте-ка умножим обе части равенства (1) на 2. Так как при удвоении степени двойки ее показатель увеличивается на 1, то получим
2S = 21 + 22 + 23 + 24 + … + 264. (2)
Теперь из (2) вычтем (1). В левой части, понятное дело, получится 2S – S = S. В правой же части произойдет массовое взаимное уничтожение почти всех степеней двойки — от 21 до 263 включительно, и останется лишь 264 – 20 = 264 – 1. Итак:
S = 264 – 1.
Что ж, выражение заметно упростилось, и теперь, имея калькулятор, позволяющий возводить в степень, можно найти значение этой величины без малейших проблем.
А если и калькулятора нет — как быть? Перемножать в столбик 64 двойки? Еще чего не хватало! Опытный инженер или математик-прикладник, для которого главный фактор — время, сумел бы быстро оценить ответ, т.е. найти его приближенно с приемлемой точностью. Как правило, в быту (да и в большинстве естественных наук) вполне допустима погрешность в 2–3%, а если она не превосходит 1% — то это просто великолепно! Оказывается, подсчитать наши зерна с такой погрешностью можно вообще без калькулятора, и всего за несколько минут. Как? Сейчас увидите.
Итак, надо возможно точней найти произведение 64 двоек (единицу в силу ее ничтожности отбросим сразу). Разобьем их на отдельную группу из 4 двоек и еще на 6 групп по 10 двоек. Произведение двоек в отдельной группе равно 24 = 16. А произведение 10 двоек в каждой из остальных групп равно 210 = 1024 (убедитесь, кто сомневается!). Но 1024 — это около 1000, т.е. 103. Поэтому S должно быть близко к произведению числа 16 на 6 чисел, каждое из которых равно 103, т.
е. S ≈ 16·1018 (ибо 18 = 3·6). Правда, погрешность здесь все же великовата: ведь 6 раз при замене 1024 на 1000 мы ошибались в 1,024 раза, а всего мы ошиблись, как легко видеть, в 1,0246 раз. Так что теперь — дополнительно перемножать 1,024 шесть раз само на себя? Нет уж, обойдемся! Известно, что для числа х, которое во много раз меньше 1, с высокой точностью справедлива следующая приближенная формула: (1 + x)n ≈ 1 + xn.Поэтому 1,0246 = (1 + 0,24)6 ≈ 1 + 0,24·6 = 1,144. Посему надо найденное нами число 16·1018 умножить на число 1,144, в результате чего получится 18 304 000 000 000 000 000, а это отличается от правильного ответа менее чем на 1%. Чего мы и добивались!
В данном случае нам крупно повезло: одна из степеней двойки (а именно — десятая) оказалась весьма близка к одной из степеней десятки (а именно — третьей). Это позволяет нам быстро оценивать значение любой степени двойки, не обязательно 64-й.
Среди степеней других чисел подобное встречается нечасто. Например, 510 отличается от 107 также в 1,024 раза, но… в меньшую сторону.2 Впрочем, это того же поля ягода: поскольку 210·510 = 1010, то во сколько раз 210превосходит 103, во столько же раз 510меньше, чем 107.Другая интересная особенность рассматриваемой последовательности заключается в том, что любое натуральное число можно построить из различных степеней двойки, причем единственным способом. Например, для номера текущего года имеем
2012 = 22 + 23 + 24 + 26 + 27 + 28 + 29 + 210.
Доказать эти возможность и единственность не составляет особого труда. Начнем с возможности. Пусть нам надо представить в виде суммы различных степеней двойки некоторое натуральное число N.
Сначала запишем его в виде суммы N единиц. Так как единица — это 20, то первоначально N есть сумма одинаковых степеней двойки. Затем начнем объединять их по парам. Сумма двух чисел, равных 20, — это 21, так что в результате получится заведомо меньшее количество слагаемых, равных 21, и, возможно, одно число 20, если ему не нашлось пары. Далее попарно объединяем одинаковые слагаемые 21, получая еще меньшее количество чисел 22 (здесь тоже возможно появление непарной степени двойки 21). Затем снова объединяем равные слагаемые попарно, и так далее. Рано или поздно процесс завершится, ибо количество одинаковых степеней двойки после каждого объединения уменьшается. Когда оно станет равным 1 — дело кончено. Осталось сложить все получившиеся непарные степени двойки — и представление готово.Что касается доказательства единственности представления, то здесь хорошо подходит метод «от противного».
Пусть одно и то же число N удалось представить в виде двух наборов различных степеней двойки, которые не полностью совпадают (т. е. имеются степени двойки, входящие в один набор, но не входящие в другой, и наоборот). Для начала отбросим все совпадающие степени двойки из обоих наборов (если таковые имеются). Получатся два представления одного и того же числа (меньшего или равного N) в виде суммы различных степеней двойки, причем все степени в представлениях различны. В каждом из представлений выделим наибольшую степень. В силу изложенного выше, для двух представлений эти степени различны. То представление, для которого эта степень больше, назовем первым, другое — вторым. Итак, пусть в первом представлении наибольшая степень равна 2m, тогда во втором она, очевидно, не превышает 2m–1. Но поскольку (и мы с этим уже сталкивались выше, подсчитывая зерна на шахматной доске) справедливо равенство2m = (2m–1 + 2m–2 + .
.. + 20) + 1,то 2m строго больше суммы всех степеней двойки, не превосходящих 2m–1. По этой причине уже наибольшая степень двойки, входящая в первое представление, наверняка больше суммы всех степеней двойки, входящих во второе представление. Противоречие!
Фактически мы только что обосновали возможность записи чисел в двоичной системе счисления. Как известно, в ней используются лишь две цифры — ноль и единица, и каждое натуральное число записывается в двоичной системе единственным способом (например, упомянутое выше 2012 — как 11 111 011 100). Если пронумеровать разряды (двоичные цифры) справа налево, начиная с нуля, то номера тех разрядов, в которых стоят единицы, как раз и будут показателями степеней двоек, входящих в представление.3
Менее известно следующее свойство множества целых неотрицательных степеней двойки. Давайте некоторым из них произвольным образом присвоим знак «минус», т.
е. из положительных сделаем отрицательными. Единственное требование — чтобы в результате и положительных, и отрицательных чисел оказалось бесконечное количество. Например, можно присвоить знак «минус» каждой пятой степени двойки или, допустим, оставить положительными только числа 210, 2100, 21000, и так далее — вариантов здесь сколько угодно.Как ни удивительно, но любое целое число можно (и притом единственным способом) представить в виде суммы различных слагаемых нашей «положительно-отрицательной» последовательности.4 И доказать это не очень-то сложно (например, индукцией по показателям степеней двоек). Главная идея доказательства — наличие сколь угодно больших по абсолютной величине как положительных, так и отрицательных слагаемых. Попробуйте выполнить доказательство сами.
Интересно понаблюдать за последними цифрами членов последовательности степеней двойки. Так как каждое последующее число последовательности получается удвоением предыдущего, то последняя цифра каждого из них полностью определяется последней цифрой предыдущего числа.
А так как различных цифр ограниченное количество, последовательность последних цифр степеней двойки просто обязана быть периодической! Длина периода, естественно, не превышает 10 (поскольку именно столько цифр мы используем), но это сильно завышенное значение. Попробуем оценить его, не выписывая пока саму последовательность. Ясно, что последние цифры всех степеней двойки, начиная с 21, четные. Кроме того, среди них не может быть нуля — потому что число, оканчивающееся нулем, делится на 5, в чем заподозрить степени двойки никак нельзя. А так как четных цифр без нуля имеется всего четыре, то и длина периода не превосходит 4.Проверка показывает, что так оно и есть, причем периодичность проявляется почти сразу: 1, 2, 4, 8, 6, 2, 4, 8, 6, … — в полном соответствии с теорией!
Не менее успешно можно оценить и длину периода последней пары цифр последовательности степеней двойки. Так как все степени двойки, начиная с 22, делятся на 4, то и числа, образованные их последними двумя цифрами, делятся на 4.
Не более чем двузначных чисел, делящихся на 4, имеется всего 25 (для однозначных чисел предпоследней цифрой считаем ноль), но из них надо выбросить пять чисел, оканчивающихся нулем: 00, 20, 40, 60 и 80. Так что период может содержать не более 25 – 5 = 20 чисел. Проверка показывает, что так и есть, начинается период с числа 22 и содержит пары цифр: 04, 08, 16, 32, 64, 28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, 44, 88, 76, 52, а затем опять 04 и так далее.Аналогично можно доказать, что длина периода последних m цифр последовательности степеней двойки не превышает 4·5m–1 (более того — на самом деле она равна 4·5m–1, но доказать это значительно сложнее).
Итак, на последние цифры степеней двойки наложены довольно жесткие ограничения. А как насчет первых цифр? Здесь ситуация практически противоположная. Оказывается, для любого набора цифр (первая из которых — не ноль) найдется степень двойки, начинающаяся с этого набора цифр.
И таких степеней двойки бесконечно много! Например, существует бесконечное количество степеней двойки, начинающихся с цифр 2012 или, скажем, 3 333 333 333 333 333 333 333.А если рассмотреть только одну самую первую цифру различных степеней двойки — какие значения она может принимать? Нетрудно убедиться, что любые — от 1 до 9 включительно (нуля среди них, естественно, нет). Но какие из них встречаются чаще, а какие реже? Как-то сразу не видно причин, по которым одна цифра должна встречаться чаще другой. Однако более глубокие размышления показывают, что как раз равной встречаемости цифр ожидать не приходится. Действительно, если первая цифра какой-либо степени двойки есть 5, 6, 7, 8 или 9, то первая цифра следующей за ней степени двойки будет обязательно единицей! Поэтому должен иметь место «перекос», по крайней мере, в сторону единицы. Следовательно, вряд ли и остальные цифры будут «равнопредставленными».
Практика (а именно — прямой компьютерный расчет для первых нескольких десятков тысяч степеней двойки) подтверждает наши подозрения.
Вот какова относительная доля первых цифр степеней двойки с округлением до 4 знаков после запятой:1 — 0,3010
2 — 0,1761
3 — 0,1249
4 — 0,0969
5 — 0,0792
6 — 0,0669
7 — 0,0580
8 — 0,0512
9 — 0,0458Как видим, с ростом цифр эта величина убывает (и потому та же единица примерно в 6,5 раз чаще бывает первой цифрой степеней двойки, чем девятка). Как ни покажется странным, но практически такое же соотношение количеств первых цифр будет иметь место почти для любой последовательности степеней — не только двойки, но, скажем, и тройки, пятерки, восьмерки и вообще почти любого числа, в том числе и нецелого (исключение составляют лишь некоторые «особые» числа). Причины этого весьма глубоки и непросты, и для их уяснения надо знать логарифмы. Для тех, кто с ними знаком, приоткроем завесу: оказывается, относительная доля степеней двойки 5, десятичная запись которых начинается с цифры F (для F = 1, 2, …, 9), составляет lg (F + 1) – lg (F), где lg — так называемый десятичный логарифм, равный показателю степени, в которую надо возвести число 10, чтобы получить число, стоящее под знаком логарифма.
6Используя упомянутую выше связь между степенями двойки и пятерки, А. Канель обнаружил интересное явление. Давайте из последовательности первых цифр степеней двойки (1, 2, 4, 8, 1, 3, 6, 1, 2, 5, …) выберем несколько цифр подряд и запишем их в обратном порядке. Оказывается, эти цифры непременно встретятся тоже подряд, начиная с некоторого места, в последовательности первых цифр степеней пятерки.7
Степени двойки также являются своеобразным «генератором» для производства широко известных совершенных чисел, которые равны сумме всех своих делителей, за исключением себя самого. Например, у числа 6 четыре делителя: 1, 2, 3 и 6. Отбросим тот, который равен самому числу 6. Осталось три делителя, сумма которых как раз равна 1 + 2 + 3 = 6. Поэтому 6 — совершенное число.
Для получения совершенного числа возьмем две последовательные степени двойки: 2n–1 и 2n. Уменьшим большую из них на 1, получим 2n – 1.
Оказывается, если это — простое число, то, домножив его на предыдущую степень двойки, мы образуем совершенное число 2n–1 (2n – 1). Например, при п = 3 получаем исходные числа 4 и 8. Так как 8 – 1 = 7 — простое число, то 4·7 = 28 — совершенное число.8 Более того — в свое время Леонард Эйлер доказал, что все четные совершенные числа имеют именно такой вид. Нечетные совершенные числа пока не обнаружены (и мало кто верит в их существование).Тесную связь имеют степени двойки с так называемыми числами Каталана, последовательность которых имеет вид 1, 1, 2, 5, 14, 42, 132, 429… Они часто возникают при решении различных комбинаторных задач. Например, сколькими способами можно разбить выпуклый n-угольник на треугольники непересекающимися диагоналями? Всё тот же Эйлер выяснил, что это значение равно (n – 1)-му числу Каталана (обозначим его Kn–1), и он же выяснил, что Kn = Kn–1·(4n – 6)/n.
Последовательность чисел Каталана имеет множество любопытных свойств, и одно из них (как раз связанное с темой этой статьи) заключается в том, что порядковые номера всех нечетных чисел Каталана являются степенями двойки!Степени двойки нередко встречаются в различных задачах, причем не только в условиях, но и в ответах. Возьмем, например, популярную когда-то (да и поныне не забытую) Ханойскую башню. Так называлась игра-головоломка, придуманная в XIX веке французским математиком Э. Люка. Она содержит три стержня, на один из которых надето n дисков с отверстием в середине каждого. Диаметры всех дисков различны, и они расположены в порядке убывания снизу вверх, т. е. самый большой диск — внизу (см. рисунок). Получилась как бы башня из дисков.
Требуется перенести эту башню на другой стержень, соблюдая такие правила: перекладывать диски строго по одному (снимая верхний диск с любого стержня) и всегда класть только меньший диск на больший, но не наоборот. Спрашивается: какое наименьшее число ходов для этого потребуется? (Ходом мы называем снятие диска с одного стержня и надевание его на другой.
) Ответ: оно равно 2n – 1, что легко доказывается по индукции.Пусть для n дисков потребное наименьшее число ходов равно Xn. Найдем Xn+1. В процессе работы рано или поздно придется снимать самый большой диск со стержня, на который первоначально были надеты все диски. Так как этот диск можно надевать только на пустой стержень (иначе он «придавит» меньший диск, что запрещено), то все верхние n дисков придется предварительно перенести на третий стержень. Для этого потребуется не меньше Xn ходов. Далее переносим наибольший диск на пустой стержень — вот еще один ход. Наконец, чтобы сверху его «притиснуть» меньшими n дисками, опять потребуется не меньше Xn ходов. Итак, Xn+1 ≥ Xn + 1 + Xn = 2Xn + 1. С другой стороны, описанные выше действия показывают, как можно справиться с задачей именно 2Xn + 1 ходами.
Поэтому окончательно Xn+1 =2Xn + 1. Получено рекуррентное соотношение, но для того чтобы его привести к «нормальному» виду, надо еще найти X1. Ну, это проще простого: X1 = 1 (меньше просто не бывает!). Не составляет труда, основываясь на этих данных, выяснить, что Xn = 2n – 1.Вот еще одна интересная задача:
Найдите все натуральные числа, которые нельзя представить в виде суммы нескольких (не менее двух) последовательных натуральных чисел.
Давайте проверим сначала наименьшие числа. Ясно, что число 1 в указанном виде непредставимо. Зато все нечетные, которые больше 1, представить, конечно, можно. В самом деле, любое нечетное число, большее 1, можно записать как 2k + 1 (k — натуральное), что есть сумма двух последовательных натуральных чисел: 2k + 1 = k + (k + 1).
А как обстоят дела с четными числами? Легко убедиться, что числа 2 и 4 нельзя представить в требуемом виде.
Может, и для всех четных чисел так? Увы, следующее же четное число опровергает наше предположение: 6 = 1 + 2 + 3. Зато число 8 опять не поддается. Правда, следующие числа вновь уступают натиску: 10 = 1 + 2 + 3 + 4, 12 = 3 + 4 + 5, 14 = 2 + 3 + 4 + 5, а вот 16 — вновь непредставимо.Что ж, накопленная информация позволяет сделать предварительные выводы. Обратите внимание: не удалось представить в указанном виде только степени двойки. Верно ли это для остальных чисел? Оказывается, да! В самом деле, рассмотрим сумму всех натуральных чисел от m до n включительно. Так как всего их, по условию, не меньше двух, то n > m. Как известно, сумма последовательных членов арифметической прогрессии (а ведь именно с ней мы имеем дело!) равна произведению полусуммы первого и последнего членов на их количество. Полусумма равна (n + m)/2, а количество чисел равно n – m + 1. Поэтому сумма равна (n + m)(n – m + 1)/2.
Заметим, что в числителе находятся два сомножителя, каждый из которых строго больше 1, и при этом четность их — различна. Выходит, что сумма всех натуральных чисел от m до n включительно делится на нечетное число, большее 1, и потому не может быть степенью двойки. Так что теперь понятно, почему не удалось представить степени двойки в нужном виде.Осталось убедиться, что не степени двойки представить можно. Что касается нечетных чисел, то с ними мы уже разобрались выше. Возьмем какое-либо четное число, не являющееся степенью двойки. Пусть наибольшая степень двойки, на которую оно делится, это 2a (a — натуральное). Тогда если число поделить на 2a, получится уже нечетное число, большее 1, которое мы запишем в знакомом виде — как 2k + 1 (k — тоже натуральное). Значит, в целом наше четное число, не являющееся степенью двойки, равно 2a (2k + 1). А теперь рассмотрим два варианта:
- 2a+1 > 2k + 1. Возьмем сумму 2k + 1 последовательных натуральных чисел, среднее из которых равно 2a. Легко видеть, что тогда наименьшее из них равно 2a – k, а наибольшее равно 2a + k, причем наименьшее (и, значит, все остальные) — положительное, т. е. действительно натуральное. Ну, а сумма, очевидно, составляет как раз 2a(2k + 1).
- 2a+1 < 2k + 1. Возьмем сумму 2a+1 последовательных натуральных чисел. Здесь нельзя указать среднее число, ибо количество чисел четное, но указать пару средних чисел можно: пусть это числа k и k + 1. Тогда наименьшее из всех чисел равно k + 1 – 2a (и тоже положительное!), а наибольшее равно k + 2a. Сумма их тоже равна 2a(2k + 1).
Вот и всё. Итак, ответ: непредставимые числа — это степени двойки, и только они.
А вот еще одна задача (впервые ее предложил В. Произволов, но в несколько иной формулировке):
Садовый участок окружен сплошным забором из N досок. Согласно приказу тети Полли Том Сойер белит забор, но по собственной системе: продвигаясь всё время по часовой стрелке, сначала белит произвольную доску, затем пропускает одну доску и белит следующую, затем пропускает две доски и белит следующую, затем пропускает три доски и белит следующую, и так далее, каждый раз пропуская на одну доску больше (при этом некоторые доски могут быть побелены несколько раз — Тома это не смущает).
Том считает, что при такой схеме рано или поздно все доски будут побелены, а тетя Полли уверена, что хотя бы одна доска останется непобеленной, сколько бы Том ни работал. При каких N прав Том, а при каких — тетя Полли?
Описанная система побелки представляется довольно хаотичной, поэтому первоначально может показаться, что для любого (или почти любого) N каждой доске когда-нибудь достанется своя доля известки, т.
е., в основном, прав Том. Но первое впечатление обманчиво, потому что на самом деле Том прав только для значений N, являющихся степенями двойки. Для остальных N найдется доска, которая так и останется навеки непобеленной. Доказательство этого факта довольно громоздко (хотя, в принципе, несложно). Предлагаем читателю выполнить его самому.Вот каковы они — степени двойки. С виду — проще простого, а как копнешь… И затронули мы здесь далеко не все удивительные и загадочные свойства этой последовательности, а лишь те, что бросились в глаза. Ну, а читателю предоставляется право самостоятельно продолжить исследования в этой области. Несомненно, они окажутся плодотворными.
1 Впрочем, действительно ли правитель согласился выплатить требуемое, история умалчивает. Более вероятно, что для мудреца все закончилось длительным тюремным заключением по статье «за наглость».
2 Для любопытных вот еще одно хорошее совпадение: 69 = 10 077 696, в котором относительное расхождение с ближайшей степенью десятки всего около 0,8%, что примерно втрое меньше, чем для 210.
3 Повсеместно используемая десятичная система устроена по такому же принципу. Только вместо степеней двойки используются степени десятки (потому она так и называется), а цифры в записи показывают, в каком количестве очередную степень десятки надо прибавлять.
4 При этом число 0 (ноль) представляется как полное отсутствие слагаемых (т.е., формально говоря, нулевое их количество).
5 И не только двойки, как было отмечено ранее!
6 Жаждущие подробностей могут прочесть статью В. Болтянского «Часто ли степени двойки начинаются с единицы?» («Квант» №5 за 1978 г.), а также статью В. Арнольда «Статистика первых цифр степеней двойки и передел мира» («Квант» №1 за 1998 г.).
7 См. задачу М1599 из «Задачника «Кванта» («Квант» №6 за 1997 г.).
8 В настоящее время известны 43 совершенных числа, наибольшее из которых равно 230402456(230402457 – 1). Оно содержит свыше 18 миллионов цифр.Доказательство того, что число в нулевой степени равно единице
You are here: Главная → Статьи → Доказательство нулевой степени Почему (-3) 0 = 1? Как это доказано?
Как в уроке про минус и ноль экспоненты, вы можете посмотреть на следующую последовательность и спросите, что по логике будет дальше:
(-3) 4 = 81
(-3) 3 = -27
(-3) 2 = 9
(-3) 1 = -3
(-3) 0 = ????Вы можете использовать тот же шаблон и для других чисел. Как только ваш ребенок обнаружит, что правило для этой последовательности состоит в том, что на каждом шаге вы делите на -3, тогда следующим логическим шагом будет то, что (-3) 0 = 1.
В видео ниже показана та же идея: обучение нулевому показателю степени, начиная с шаблона. Это обосновывает правило и делает его логичным, а не просто «объявленной» математикой без доказательств.
В видео также показана идея доказательства, поясняемая ниже: мы можем умножать степени одного и того же основания и делать из этого вывод, каким должно быть число в нулевой степени.Другая идея для доказательства состоит в том, чтобы сначала обратить внимание на следующее правило умножения ( n любое целое число):
n 3 · n 4 = ( n · n · n ) · (н · н · н · н) = N 7
N 6 · N 2 = ( N · N · N · N · n · n) · ( n · n) = n 8
Вы заметили ярлык? Для любых целых чисел x и y вы можете просто добавить показатели:
n x · n y = ( n · n · n ·…· т · т · т) · (н ·.
..· н)
= п х + у Математика логична, и ее правила работают во всех случаях (утверждается, что теоремы применимы «для любого целого числа n » или «для всех целых чисел»). Итак, предположим, что мы не знаем, что такое (-3) 0 . Чем бы ни был (-3) 0 , если он подчиняется приведенному выше правилу, то
(-3) 7 · (-3) 0 = (-3) 7 + 0 Другими словами,
(-3) 7 · (-3) 0 = (-3) 7
(-3) 3 · (-3) 0 = (-3) 3 + 0 Другими словами,
(-3) 3 · (-3) 0 = (-3) 3
(-3) 15 · (-3) 0 = (-3) 15 + 0 Другими словами,
(-3) 15 · (-3) 0 = (-3) 15
…и так далее для всех возможных показателей.
На самом деле мы можем написать, что (-3) x · (-3) 0 = (-3) x , где x — любое целое число.Поскольку мы предполагаем, что еще не знаем, что такое (-3) 0 , давайте заменим его буквой P. Теперь посмотрите на уравнения, которые мы нашли выше. Зная то, что вы знаете о свойствах умножения, каким числом может быть P?
(-3) 7 · P = (-3) 7 (-3) 3 · P = (-3) 3 (-3) 15 · Р = (-3) 15 Другими словами… какое единственное число, при умножении на которое ничего не меняется? 🙂
Вопрос. В чем разница между -1 в нулевой степени и (-1) в нулевая мощность? Будет ли ответ 1 для обоих?
Пример 1: -1 0 = ____
Пример 2: (-1) 0 = ___Ответ: Как уже объяснялось, ответ на (-1) 0 равно 1, так как мы возводим число -1 (минус 1) в нулевую степень.
Однако в случае -1 0 отрицательный знак не означает отрицательное число, а вместо этого означает , противоположное числу следующего. Итак, мы сначала вычисляем 1 0 , а затем берем обратное значение, что дает -1. Другой пример: в выражении -(-3) 2 первый отрицательный знак означает, что вы берете противоположное остальной части выражения. Так как (-3) 2 = 9, затем -(-3) 2 = -9.
Вопрос. Почему ноль с нулевым показателем степени выдает ошибку?? Объясните, пожалуйста, почему его нет. Другими словами, что такое 0 0 ?
Ответ: Степень от нуля до нуля часто называют «неопределенной формой», поскольку она может иметь несколько различных значений.
Поскольку x 0 равно 1 для всех чисел x, отличных от 0, было бы логично определить, что 0 0 = 1.
Но мы могли бы также думать о том, что 0 0 имеет значение 0, потому что ноль в любой степени (кроме нулевой степени) равен нулю.
Кроме того, логарифм 0 0 будет равен 0 · бесконечности, что само по себе является неопределенной формой. Так что законы логарифмов с ним не работают.
Из-за этих проблем степень от нуля до нуля обычно считается неопределенной.
Однако, если необходимо определить степень от нуля до нуля, чтобы иметь какое-то значение, 1 является наиболее логичным определением для его значения. Это может быть «удобно», если вам нужен какой-то результат, работающий во всех случаях (например, биномиальная теорема).
См. также Что такое 0 в 0 степени? от доктора математики.
В чем разница между степенью и показателем степени?
ВартанПоказатель степени — это маленькое возвышенное число. «Степень» — это все: базовое число, возведенное в некоторый показатель, или значение (ответ), которое вы получите, если вычислите число, возведенное в некоторый показатель. Например, 8 — это степень (от 2), поскольку 2 3 = 8.
В этом случае 3 — показатель степени, а 2 3 (все выражение) — степень. Меню уроков математики
Преобразователь экспоненциальной записи
Базовый калькулятор
Преобразователь научной записи
введите число или экспоненциальное представление
Операнд 1
Ответ:
= 3,456 × 10 11
научная запись= 3,456e11
научная запись= 345,6 × 10 9
инженерная запись 9 миллиардов; префикс гига-(Г)= 3,456 × 10 11
стандартная форма11
Порядок величины
для научных и стандартных форм= 345600000000
(действительное число)= триста сорок пять миллиардов шестьсот миллионов
словоформа
Чем этот калькулятор может быть лучше?Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.
Получить виджет для этого калькулятора© Calculator Soup
Поделись этим калькулятором и Страница 9б где a — число или десятичное число, такое что абсолютное значение a больше или равно единице и меньше десяти или 1 ≤ | и | < 10. b – степень числа 10, необходимая для того, чтобы научная запись была математически эквивалентна исходному числу.
- Перемещайте десятичную точку в вашем номере, пока слева от десятичной точки не останется только одна ненулевая цифра. Полученное десятичное число равно и .
- Подсчитайте, на сколько знаков вы передвинули десятичную точку. Это число b .
- Если вы переместите десятичную запятую влево b будет положительным.
Если вы переместите десятичную дробь вправо b будет отрицательным.
Если не нужно было перемещать десятичную дробь b = 0 . - Напишите свой номер научной записи как 9b и читать как « a умножить на 10 в степени b «.
- Удалять нули в конце, только если они изначально стояли слева от десятичной точки.
Пример: преобразование 357 096 в экспоненциальную запись
- Переместите десятичную дробь на 5 знаков влево, чтобы получить 3,57096
- а = 3,57096
- Мы переместили десятичную дробь влево, чтобы b было положительным 9-4 = 3,456 x 0,0001 = 0,0003456
- Как печатать отрицательные степени в Word
- Лучший способ печатать степени в Word.
- Поместите указатель вставки туда, где вам нужен текст To the Power of Symbol .
- Нажмите и удерживайте одну из клавиш Alt на клавиатуре.
- Удерживая нажатой клавишу Alt, нажмите В силу Альтернативный код символа ( 0178 для ² ). Вы должны использовать цифровую клавиатуру для ввода альтернативного кода. Если вы используете ноутбук без цифровой клавиатуры, этот метод может вам не подойти. На некоторых ноутбуках есть скрытая цифровая клавиатура, которую можно включить, нажав Fn+NmLk на клавиатуре.
- Отпустите клавишу Alt после ввода кода Alt, чтобы вставить символ в документ.
- Прежде всего, поместите указатель вставки туда, где вам нужно ввести символ.
- Теперь одновременно нажмите Option + 00B2 на клавиатуре, чтобы вставить символ.
- Поместите указатель вставки в нужное место.
- Нажмите и удерживайте клавишу Alt
- Удерживая нажатой клавишу Alt, введите 0178 с помощью цифровой клавиатуры, чтобы вставить символ.
- Нажмите кнопку Start и найдите карту символов. Приложение «Карта символов» появится в результатах поиска, нажмите, чтобы открыть.
- Появится диалоговое окно Карта символов. Нажмите, чтобы проверить Расширенный вид Установите флажок, чтобы развернуть диалоговое окно для дополнительных параметров.
- В расширенном представлении введите Верхний индекс в поле поиска.
- Теперь вы должны увидеть Власть символов в диалоговом окне карты персонажей. Теперь дважды щелкните его, чтобы выбрать. Либо нажмите кнопку Select .
- После выбора символа двойным щелчком он должен появиться в поле Символ для копирования: , затем нажмите Копировать , чтобы скопировать символ.
- Переключитесь на документ Microsoft Word или Excel, поместите указатель вставки в нужное место и нажмите Ctrl+V для вставки.
- Откройте документ Word.
- Щелкните, чтобы поместить указатель вставки туда, куда вы хотите вставить символ.
- Перейдите на вкладку «Вставка».
- В категории «Символы» щелкните раскрывающийся список «Символ» и выберите кнопку «Дополнительные символы».
- Чтобы легко найти В силу символа, введите 00B2 в поле кода символа в нижней части окна. После ввода этого кода символа появится выбранное значение В силу символа.
- Теперь нажмите кнопку «Вставить», чтобы вставить символ в документ.
- Закройте диалоговое окно.
- Пылезащитный колпачок из анодированного алюминия
- Бумажный конус, армированный кевларовым волокном
- Высокотемпературная звуковая катушка с армирующей манжетой Nomex® из фильерной шнуровки
- Каркас звуковой катушки из анодированного алюминия
- Оптимизированная и согласованная магнитная геометрия и геометрия податливости
- Оптимизированный полюсный наконечник и вентиляция крестовины
- Свинцовая проволока из износостойкой мишуры с периодической прошивкой
- Жесткая корзина из литого под давлением алюминия
- Запатентованное изолированное цельнометаллическое входное пружинное клеммное соединение 8 AWG
- 1 год гарантии
- 2016 2016
- 2011 Сабвуферы Power T0 DVC — инструкция по эксплуатации
Напишите нам по электронной почте
- Просмотр процесса
- Подача претензии по гарантии
- Имя и фамилия с полным адресом доставки
- Название продукта (T0D415)
- Серийный номер (12 или 13 цифр)
- Диагностика отказа (нет выхода, нет индикатора питания и т. д.)
- Отсканированная копия оригинальной квитанции, отправленная по электронной почте на адрес [email protected]ckfordcorp. com (имя дилера, дата покупки и приобретенный товар должны быть разборчивы)
- Кредитная/дебетовая карта (при оплате негарантийных претензий)
- Никаких денежных переводов или чеков.
- Номер RA Печатается вне коробки (как можно больше)
- Копия оригинальной квитанции
Дополнительные ресурсы
См. Калькулятор научной нотации для сложения, вычитания, умножения и деления чисел в научной нотации или E-нотации.
Для округления значащих цифр используйте Калькулятор значимых цифр.
Чтобы увидеть, насколько стандартная форма похожа на экспоненциальную запись, посетите Калькулятор стандартной формы.
90 (ноль в нулевой степени) равно? Почему математики и школьные учителя расходятся во мнениях?Умница:
Я знаю!
= = = = .
Теперь просто подставляем x=0, и мы видим, что ноль к нулю равен единице!
Умный ученик:
Нет, ты не прав! Вам не разрешено делить на ноль, что вы и сделали на последнем шаге. Вот как это сделать:
= = = =
, что верно, поскольку любое произведение, умноженное на 0, равно 0. Это означает, что
= .
Самый умный ученик :
Это тоже не работает, потому что если тогда
будет
, то ваш третий шаг также включает в себя деление на ноль, что недопустимо! Вместо этого мы можем подумать о функции и посмотреть, что произойдет, когда x>0 станет меньше.
Имеем:=
=
=
=
=
=
=
=
=
Таким образом, поскольку = 1, это означает, что = 1. не доказывает этого. Переменная x, имеющая значение, близкое к нулю, отличается от переменной x, имеющей значение точно равное нулю. Получается, что не определено. не имеет значения.
Учитель исчисления:
Для всех у нас есть
.
Следовательно,
То есть, когда x становится сколь угодно близким к (но остается положительным), остается равным .
С другой стороны, для действительных чисел y, таких что , мы имеем
.
Следовательно,
То есть, когда y становится произвольно близким к , остается на .
Таким образом, мы видим, что функция имеет разрыв в точке . В частности, когда мы приближаемся к (0,0) по линии с x=0, мы получаем
, но когда мы приближаемся к (0,0) по линии с y=0 и x>0, мы получаем
.
Таким образом, значение будет зависеть от направления, в котором мы берем предел. Это означает, что нет никакого способа определить, что сделает функцию непрерывной в точке .
Математик: Ноль в нулевой степени равен единице. Почему? Потому что так сказали математики. Нет, это правда.
Рассмотрим задачу определения функции для натуральных чисел y и x. Существует ряд определений, которые все дают одинаковые результаты. Например, одна идея состоит в том, чтобы использовать для нашего определения:
:=
, где y повторяется x раз. В этом случае, когда x равен единице, y повторяется только один раз, поэтому мы получаем
= .
Однако это определение естественным образом распространяется от целых положительных чисел до целых неотрицательных, так что, когда x равно нулю, y повторяется ноль раз, что дает
=
, что верно для любого y. Следовательно, когда y равно нулю, у нас есть
.
Смотрите, мы только что это доказали! Но это только для одного возможного определения .
Что, если мы воспользуемся другим определением? Например, предположим, что мы решили определить как:= .
На словах это означает, что значение равно тому, что приближается по мере того, как действительное число z становится все меньше и меньше, приближаясь к значению x произвольно близко.
[Пояснение: читатель спросил, как это возможно, что мы можем использовать в нашем определении , которое кажется рекурсивным. Причина, по которой это нормально, заключается в том, что мы работаем здесь только с , и все согласны с тем, что в этом случае равно. По сути, мы используем известные случаи для построения функции, имеющей значение для более сложного случая x=0 и y=0.]
Интересно, что, используя это определение, мы получим
= = =
Следовательно, мы найдем это, а не . Конечно, это определение, которое мы только что использовали, кажется довольно неестественным, но оно согласуется с представлением здравого смысла о том, что означает для всех положительных действительных чисел x и y, и сохраняет непрерывность функции при приближении к x = 0 и y.
=0 по определенной линии.Итак, какое из этих двух определений (если любое из них) верное? Что такое на самом деле ? Что ж, для x>0 и y>0 мы знаем, что мы подразумеваем под . Но когда x=0 и y=0, формула не имеет очевидного смысла. Значение будет зависеть от нашего предпочтительного выбора определения того, что мы подразумеваем под этим утверждением, и нашей интуиции о том, что означает для положительных значений, недостаточно, чтобы сделать вывод, что это означает для нулевых значений.
Но если это так, то как математики могут это утверждать? Ну, просто потому, что это полезно. Некоторые очень важные формулы становятся менее элегантными для записи, если вместо этого мы используем или говорим, что это не определено. Например, рассмотрим биномиальную теорему, которая утверждает, что:
=
где означает биномиальные коэффициенты.
Теперь, установив a=0 с обеих сторон и предположив, что мы получаем
= =
=
=
=
, где я использовал это для k>0, а это .
Так получилось, что правая часть имеет магический фактор. Следовательно, если мы не используем, то биномиальная теорема (как написано) не выполняется, когда a = 0, потому что тогда не равно .Если бы математики использовали или сказали, что это не определено, тогда биномиальная теорема продолжала бы выполняться (в той или иной форме), хотя и не так, как написано выше. Однако в этом случае теорема была бы более сложной, потому что ей пришлось бы обрабатывать частный случай терма, соответствующего k = 0. Мы получаем элегантность и простоту, используя .
Есть еще несколько причин, по которым использование предпочтительнее, но они сводятся к тому, что этот выбор более полезен, чем альтернативные варианты, приводит к более простым теоремам или кажется более «естественным» для математиков. Выбор не «правильный», он просто приятный.
Эта запись была размещена в — Математик, Математика, Философский. Добавьте постоянную ссылку в закладки.
Как набирать символ «В силу» на клавиатуре
В сегодняшней статье вы узнаете, как использовать некоторые сочетания клавиш для ввода любых В силу символа где угодно, например, в Word/Excel/Google Docs, используя Windows или Mac.
Приведенные ниже практические шаги покажут вам все, что вам нужно знать.
Примечание. В этом руководстве я покажу вам, как вводить символ степени двойки (²). Идея та же, что и для остальных экспонентов.
Связанный:
Содержание
Краткий справочник по силе символовЧтобы ввести символ степени двойки на Mac, нажмите Option + сочетание клавиш 00B2 на клавиатуре. Для пользователей Windows просто нажмите клавишу Alt и введите 0178 с помощью цифровой клавиатуры, затем отпустите клавишу Alt.
В основном это идея набирать эти надстрочные символы. Таким образом, если вы хотите легко ввести любой из этих символов на клавиатуре, сначала определите альтернативный код этого конкретного символа и, удерживая клавишу Alt, введите альтернативный код с помощью цифровой клавиатуры.
Однако не все альтернативные коды символов можно использовать, нажав клавишу Alt. Я покажу вам в ближайшее время. Просто продолжайте читать.В таблице ниже показаны все альтернативные коды для в степени от 0 до 10 . Используйте приведенные ниже сочетания клавиш Alt Code, чтобы ввести любую экспоненту на клавиатуре.
Description Symbol Alt Code Shortcut To the Power of 0 ⁰ 2070, Alt+X To the Power of 1 ¹ Alt+ 0185 В степени 2 ² Alt+0178 к мощности 3 ³ ALT+0179 до мощности 4 ⁴ 2074, ALT+x 98⁴ 2074, ALT+x 98⁴ . 2075, Alt+x к мощности 6 ⁶ 2076, ALT+x . из 8 ⁸ 2078, Alt+X к мощности 9 ⁹ 2079, ALT+x до мощности N ⁿ 207F, ALT+X ⁿ 207F, ALT+x ⁿ 207F, alt+x ⁿ . Ярлыки кода работают только в Microsoft Word. И чтобы использовать эти сочетания клавиш, сначала введите код в Microsoft Word, выберите его и нажмите Alt+X на клавиатуре. Код будет преобразован в Силу символа.В приведенном выше кратком руководстве приведены некоторые полезные сочетания клавиш и альтернативные коды для ввода любого надстрочного символа как в Windows, так и в Mac.
Для получения более подробной информации ниже приведены некоторые другие методы, которые вы также можете использовать для вставки этого символа в свою работу, например в документ Word или Excel.
Примечание. В следующих методах я покажу вам, как ввести степень двойки в качестве примера. Однако те же методы можно использовать для ввода или вставки других символов надстрочного индекса.
Как ввести «В силу символа» [текст] на клавиатуреMicrosoft Office предоставляет несколько способов ввода В силу символа или вставка символов, не имеющих специальных клавиш на клавиатуре.
В этом разделе я предоставлю вам различные методы, которые вы можете использовать для ввода или вставки этого и любого другого символа на вашем ПК, например, в MS Office (например, Word, Excel или PowerPoint) для пользователей Mac и Windows. .
Без лишних слов, приступим.
Использование альтернативного кода символа в степени 2 (только для Windows)В степени 2 (²) Альтернативный код символа равен 0178 .
Несмотря на то, что эти символы не имеют специальных клавиш на клавиатуре, вы все равно можете набирать их на клавиатуре с помощью метода альтернативного кода. Для этого нажмите и удерживайте клавишу Alt, одновременно нажимая альтернативный код «степень двойки» (например, 0178 для ²) с помощью цифровой клавиатуры.
Используйте приведенную выше таблицу комбинаций To the Power of, чтобы ввести любой To the Power of на клавиатуре.
Этот метод работает только в Windows.
И ваша клавиатура также должна иметь цифровую клавиатуру.Ниже приводится разбивка шагов, которые вы можете предпринять, чтобы ввести To the Power of Sign на вашем ПК с Windows:
Вот как вы можете ввести этот символ в Word, используя метод Alt Code.
Использование сочетания клавиш «В силу силы символа» (Mac и Windows)Для пользователей Mac сочетание клавиш для символа степени двойки : Option + 00B2 .
Для пользователей Windows используйте метод альтернативного кода, нажав клавишу [Alt] при вводе альтернативного кода символа, указанного в таблице выше.Для ввода альтернативного кода необходимо использовать цифровую клавиатуру. Также убедитесь, что клавиша Num Lock включена.
Ниже приведена разбивка ярлыка To the Power of Symbol для Mac:
Ниже приведена разбивка ярлыка To the Power of Symbol для Windows:
Это шаги, которые вы можете использовать для ввода этого знака в Word или Excel.
Копировать и вставить В силу символовЕще один простой способ добраться до Силы символов на любом ПК — использовать мой любимый метод: скопируйте и вставьте .
Все, что вам нужно сделать, это скопировать символ откуда-нибудь, например, с веб-страницы или карты символов для пользователей Windows, и перейти туда, где вам нужен символ (скажем, в Word или Excel), а затем нажать Ctrl+V, чтобы вставить.
Ниже приведен символ, который можно скопировать и вставить в документ Word. Просто выделите его и нажмите Ctrl+C, чтобы скопировать, переключитесь в Microsoft Word, поместите указатель вставки в нужное место и нажмите Ctrl+V, чтобы вставить.
X ⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹
В качестве альтернативы просто нажмите кнопку копирования в начале этого поста.
Для пользователей Windows: выполните следующие инструкции, чтобы скопировать и вставить мощность символа с помощью диалогового окна карты символов.
Вот как вы можете использовать диалоговое окно «Карта символов» для копирования и вставки любого символа на ПК с Windows.
Использование диалогового окна «Вставка символа»Диалоговое окно «Вставка символа» представляет собой библиотеку символов, из которой вы можете вставить любой символ в документ Word всего несколькими щелчками мыши.
Выполните следующие действия, чтобы вставить этот символ (²) в Word или Excel с помощью диалогового окна вставки символа.
Появится диалоговое окно Символ.
Символ будет вставлен точно туда, куда вы поместили указатель вставки.
Это шаги, которые вы можете использовать, чтобы вставить этот символ в Word.
ВыводКак видите, существует несколько различных методов, которые вы можете использовать для ввода To the Power of Sign в Microsoft Word.
Использование ярлыков для Windows и Mac является самым быстрым вариантом для этой задачи. Ярлыки всегда быстрые.
Большое спасибо за чтение этого блога.
Если у вас есть что сказать или задать вопросы относительно Силы Символ , пишите в комментариях.
Power 12″ T0 Сабвуфер DVC 4 Ом
Сабвуфер T0D412 имитирует характеристики и дизайн наших старших братьев серии Power. Наш 12-дюймовый T0 оснащен двумя звуковыми катушками с сопротивлением 4 Ом, среднеквадратичной мощностью 700 Вт и имеет решетку со встроенным декоративным кольцом.
Подробнее
1 Обзор
Найти дилера
ОбзорТехнологииТехнические характеристикиПоддержкаПроводка WizardBox Advisor Технология, которая увеличивает площадь поверхности конуса до 25%, поэтому он работает как сабвуфер гораздо большего размера. Корзина FlexFit не только выглядит соответствующе, но и обеспечивает чрезвычайную гибкость для экстремальных установок. значок Power Series, проверенный пытками!0010
КРАТКИЙ ОБЗОР ХАРАКТЕРИСТИК
Technologies
Klippel Verified
«> Klippel — это программа сертификации колонок, позволяющая нам поставлять самые лучшие сабвуферы.Узнать больше
x
Klippel Verified
Klippel — это программа сертификации акустических систем, позволяющая нам поставлять самые лучшие сабвуферы.
CEA-2031
«> Мощность динамиков Rockford Fosgate соответствует отраслевым стандартам CEA-2031.Узнать больше
x
CEA-2031
Мощность динамиков Rockford Fosgate соответствует отраслевым стандартам CEA-2031.
Прошитые провода из мишуры
Повышенная надежность и производительность за счет снижения усталости и возможного короткого замыкания.
Узнать больше
x
Прошитые провода из мишуры
Повышенная надежность и производительность за счет снижения усталости и возможного короткого замыкания.
Основа звуковой катушки из анодированного алюминия
</li>
</ol>
Solution… Rockford Fosgate subwoofers use aluminum formers or voice coils for their excellent heat dissipation and SPL capabilities unlike many other plastic substitutes.»> В сабвуферах Rockford Fosgate используются каркасы звуковых катушек из анодированного алюминия, обеспечивающие превосходное рассеивание тепла (до …Узнать больше
x
Формирователи звуковых катушек из анодированного алюминия
«> В сабвуферах Rockford Fosgate используются каркасы звуковых катушек из анодированного алюминия, обеспечивающие превосходное рассеивание тепла (до 100° при полной мощности). В отличие от традиционных пластиковых заменителей, алюминий действует как радиатор, быстро рассеивая накопление тепла на звуковой катушке. Это позволяет сабвуферам оставаться прохладными в условиях высокого звукового давления.VAST Surround — сабвуферы
Техника вертикального крепления объемного звучания значительно увеличивает эффективную площадь излучающего конуса сабвуфера до 25%.
Узнать больше
x
Объемный звук VAST — сабвуферы
Техника вертикального крепления объемного звучания значительно увеличивает эффективную площадь излучающего конуса сабвуфера до 25%.
Корзина FlexFit для сабвуфера
<div><br></div>»> Рама с прорезью позволяет точно настроить монтажное положение сабвуфера.Узнать больше
x
Корзина FlexFit для сабвуфера
Рама с прорезью позволяет точно настроить положение установки сабвуфера.
Терминалы SWIFT™
Позволяет быстро конфигурировать звуковые катушки для последовательного или параллельного подключения.
Узнать больше
x
Терминалы SWIFT™
This removable impedance selection jumper also provides fused protection in severe overload conditions.»> Позволяет быстро настроить звуковые катушки для последовательного или параллельного подключения.Specifications
Nominal Impedance
Dual 4-Ohm
Speaker Connector
Compression Terminal
Mounting Depth
6.875 in. (174.6 mm)
SPL (dB @ 1w/1m)
84.1
Fs (Гц)
26
QTS
0,53
QES
0,58
RE (OHMS)
6.20
LE (MH)
8.47
LE (MH)
8.47777777777777777777777777777777777777777777777777777777777777
(MH)
8.2010
(MH)
8.2010
.0010
6,00
Размер
12 дюймов
Диаметр звуковой катушки
3 дюйма (75,5 мм)
Вес в упаковке
31,16 фунта.
(14,13 кг)VAS (литры)
55,1
Xmax (MM)
14,8
Диаметр выреза
11,25 дюйма. футов (3,0 литра)
Допустимая мощность (Вт RMS)
700 Вт RMS
1400 Вт Макс.Вес магнита (унции)
106 унций. (3,00 кг.)
CEA -2031 Соответствует
SD (CM 2 )
548
Совместимость
Поддержка
Статьи о базе знаний
Показать все темы базы знаний
Спросите наших экспертов
Разрешение на возврат
Обратитесь к авторизованному дилеру Rockford Fosgate, у которого вы приобрели этот продукт. Если вам нужна дополнительная помощь, позвоните по номеру 1-800-669-9899 в службу поддержки клиентов Rockford.
Вы должны получить RA# (номер разрешения на возврат), чтобы вернуть любой продукт в Rockford Fosgate. Вы несете ответственность за доставку продукта в Rockford.Процесс авторизации возврата
Сначала выполните диагностику
Прежде чем запрашивать RA, попытайтесь диагностировать сбой. Многие продукты, которые мы получаем, отправляются обратно без проблем, обычно из-за неправильной установки. Воспользуйтесь нашей базой знаний RFTECH:Knowledge Base для устранения неполадок.
Связаться со службой поддержки
Пожалуйста, позвоните нам в рабочее время по номеру 1-800-669-9899 (вариант № 1) и подготовьте следующую информацию:
Инструкции по отправке
При отправке продукта на упаковке ДОЛЖНА быть указана следующая информация:
Адрес доставки
Отправьте товар (предпочтительно UPS или FedEx) по следующему адресу:
Rockford/AJR International
300 Regency DR
Glendale Heights, IL 60139
RA#:____________________________Мастер подключения
Обратитесь к руководству пользователя вашего усилителя, чтобы узнать минимальное рекомендуемое сопротивление.
Схема подключения №1
Wiring Diagram #2
Wiring Diagram #3
Wiring Diagram #4
Wiring Diagram #5
Wiring Diagram #6
Wiring Diagram #7
Wiring Diagram #8
Wiring Diagram #9
Box Advisor.
Моргантаун, Западная Виргиния, США; Квотербек «Канзас Джейхокс» Джалон Дэниелс (6) празднует победу над «Канзас Джейхокс» на стадионе «Маунтинир Филд» на миланском стадионе «Пушкар». Обязательный кредит: Бен Куин-USA TODAY Sports Добро пожаловать на 2-ю неделю моего поста о силовом рейтинге Большой 12 – это была богатая событиями неделя в Большой 12, и я погрузился во все девять из них здесь:
1. Оклахома (2-0) 33, Кент Стэйт (0 -2) 3
На прошлой неделе: 2
Оклахома вторую неделю подряд справилась с задачей против более слабого соперника. Трансфер UCF Диллон Габриэль снова выглядел крепким, финишировав со счетом 21-28 на 296 ярдов и трех тачдаунов. Марвин Мимс набрал 163 ярда на приеме в игре, и Сунерс прокатились. Будет интересно посмотреть на эту команду, когда она столкнется с настоящим испытанием, которое должно скоро состояться. Их следующая игра выходит на гастроли *проверил заметки*, о. Небраска.2. Штат Оклахома (2-0) 34, Штат Аризона (1-1) 17
На прошлой неделе: 3
Штат Оклахома следует за своими соперниками в штате после очередной победы над школой на меньшей конференции. Спенсер Сандерс управлял мячом 14 раз за день и выглядел комфортно. Это был легкий старт для «Ковбоев».3. Штат Айова (2-0) 10, Айова (1-1) 7
На прошлой неделе: 5
Штат Айова наконец преодолел горб в соперничестве с Айовой, начав со счетом 2-0 в первом раз с 2012 года и выиграл свою первую игру против «Соколиных глаз» под руководством тренера Мэтта Кэмпбелла. Поскольку Огайо посетит Эймса в следующую субботу, импульс постепенно начнет катиться к первому матчу «Большой 12» дома против Бэйлора.4. Штат Канзас (2-0) 40, Миссури 12
На прошлой неделе: 4
Штат Канзас одержал вторую победу подряд, открыв сезон, присоединившись к другим шести командам, чтобы сделать это на конференции. Если бы штат Канзас разгромил респектабельную программу, они бы удержали их впереди штата Айова. Тем не менее, «Уайлдкэтс» играли с одним из четырех бывших отказов Большой 12 (наряду с «Техас А&М», «Небраска» и «Колорадо»), группой, которая в тот день проиграла со счетом 0–4, проиграв «ВВС», «Аппалачи Стэйт» и «Южная Джорджия».5. Бейлор (1-1) 20, BYU (2-0) 26 (F/2OT)
На прошлой неделе: 5
Бейлор был сбит в конце игры группой спортсменов из Бригама Янга. «Медведи» упустили возможности, PAT, который мог бы иметь значение, и уступили очки Cougars, что абсолютно снизило их шансы на победу. Каждый раз, когда вы позволяете бойцам из УБЯ набирать столько очков, вы понимаете, что вам нужно переоценить свои активы.6. Техас (1-1) 19, Алабама (2-0) 20
Предыдущая неделя: 6
Техас проиграл свою первую игру в сезоне, уступив победный драйв сопернику за последние 90 секунд. Его фанаты, которые обливали себя напитками на протяжении всей четвертой четверти, наблюдали, как выездная команда реализовала победный удар в части стадиона в форме матки, чтобы закрепить победу. После двух игр «Лонгхорны» приближаются к своему рекорду 5-7 по сравнению с прошлым годом, но это означает всего лишь шесть побед.7. TCU (2-0) 59, штат Тарлтон (1-1) 17
На прошлой неделе: 7
Я мог бы понизить рейтинг TCU за игру в Тарлтоне, но я этого не сделал. Макс Дагган бросил на 390 ярдов, и каким-то образом ни один бросок не достиг 100 ярдов. Распространение мяча вокруг или ярдов после проблемы с ловлей в Форт-Уэрте? Я позволю тебе решить.8. Канзас (2-0) 55, Западная Вирджиния (0-2) 42 (ОТ)
На прошлой неделе: 8
Канзас СНОВА поднялся в рейтинге силы на этой неделе, начав 1-0 на втором месте Кампания Большой 12 под руководством главного тренера Лэнса Лейпольда. Это лучший старт, о котором «Джейхокс» могли мечтать в этом году, и у них еще впереди пара грозных матчей с «Хьюстоном» на выезде на следующей неделе, а через неделю — с командой «Дьюк» со счетом 2:0. Если Канзас продолжит побеждать, у меня не будет другого выбора, кроме как поставить их впереди Техаса, поскольку они были последней командой, которая обыграла Лонгхорнов на их собственной территории, пока другая программа не выиграла в Остине в субботу.
или «галочка». Этот символ популярен и вне программирования.
Для его применения требуется импортировать модуль 
14 ** 9)
> 29673.367320587102
print(pow(-1.1, 1001))
> -2.7169262098066285e+41
0 cannot be raised to a negative power
Это будет не справедливо, как по отношению к вам, так и к математике. Поэтому, выделим главное: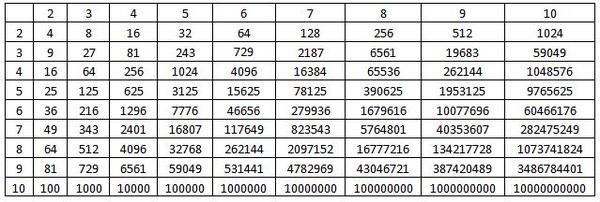
07.1998 N 125-ФЗ
(ред. от 25.02.2022)
«Об обязательном социальном страховании от несчастных случаев на производстве и профессиональных заболеваний»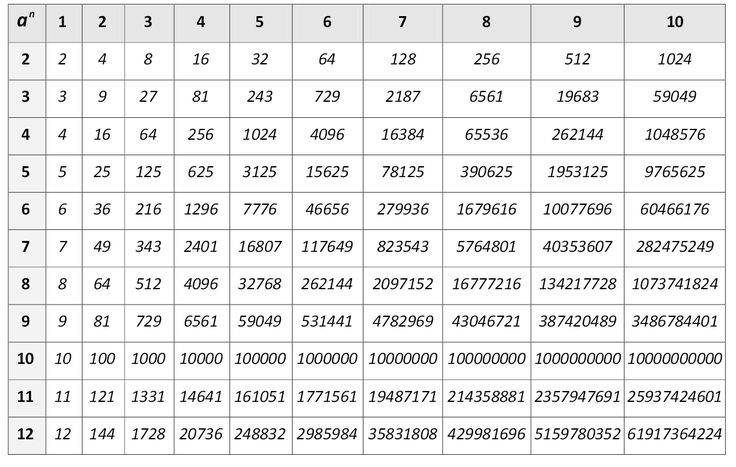
При расчете среднемесячного заработка застрахованного месяцы, не полностью им проработанные, а также месяцы, за которые отсутствуют сведения о заработке застрахованного, заменяются предшествующими месяцами, полностью проработанными на работе, повлекшей повреждение здоровья, и за которые имеются сведения о заработке, либо исключаются в случае невозможности их замены. Замена не полностью проработанных застрахованным месяцев не производится в случае, если в этот период за ним сохранялся в соответствии с законодательством Российской Федерации средний заработок, на который начисляются страховые взносы в соответствии со статьей 20.1 настоящего Федерального закона.
В случае, если период работы, повлекшей повреждение здоровья, составил менее одного полного календарного месяца, ежемесячная страховая выплата исчисляется исходя из условного месячного заработка, определяемого путем деления суммы заработка за проработанное время на количество проработанных дней и умножения полученного результата на количество рабочих дней в месяце, исчисленное в среднем за год.
07.2022 N 237-ФЗ). См. будущую редакцию.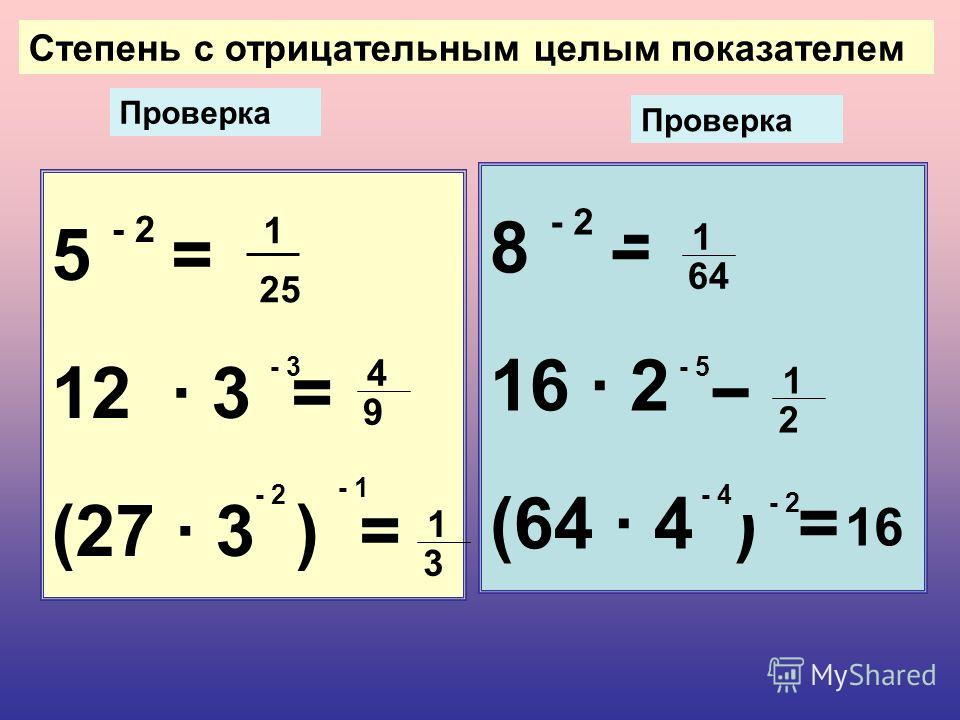
При наличии указанных сведений ежемесячная страховая выплата исчисляется исходя из этих сведений.
Для определения размера ежемесячных страховых выплат каждому лицу, имеющему право на их получение, общий размер указанных выплат делится на число лиц, имеющих право на получение страховых выплат в случае смерти застрахованного.
При этом коэффициенты, примененные к суммам заработка, к назначенному размеру ежемесячной страховой выплаты не применяются.
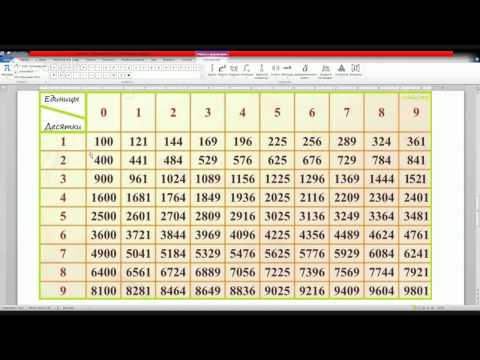12.2010 N 350-ФЗ)
.. Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами.
А поскольку объем вычислений немалый, то и вероятность ошибки весьма велика.
е. S ≈ 16·1018 (ибо 18 = 3·6). Правда, погрешность здесь все же великовата: ведь 6 раз при замене 1024 на 1000 мы ошибались в 1,024 раза, а всего мы ошиблись, как легко видеть, в 1,0246 раз. Так что теперь — дополнительно перемножать 1,024 шесть раз само на себя? Нет уж, обойдемся! Известно, что для числа х, которое во много раз меньше 1, с высокой точностью справедлива следующая приближенная формула: (1 + x)n ≈ 1 + xn.
Среди степеней других чисел подобное встречается нечасто. Например, 510 отличается от 107 также в 1,024 раза, но… в меньшую сторону.2 Впрочем, это того же поля ягода: поскольку 210·510 = 1010, то во сколько раз 210превосходит 103, во столько же раз 510меньше, чем 107.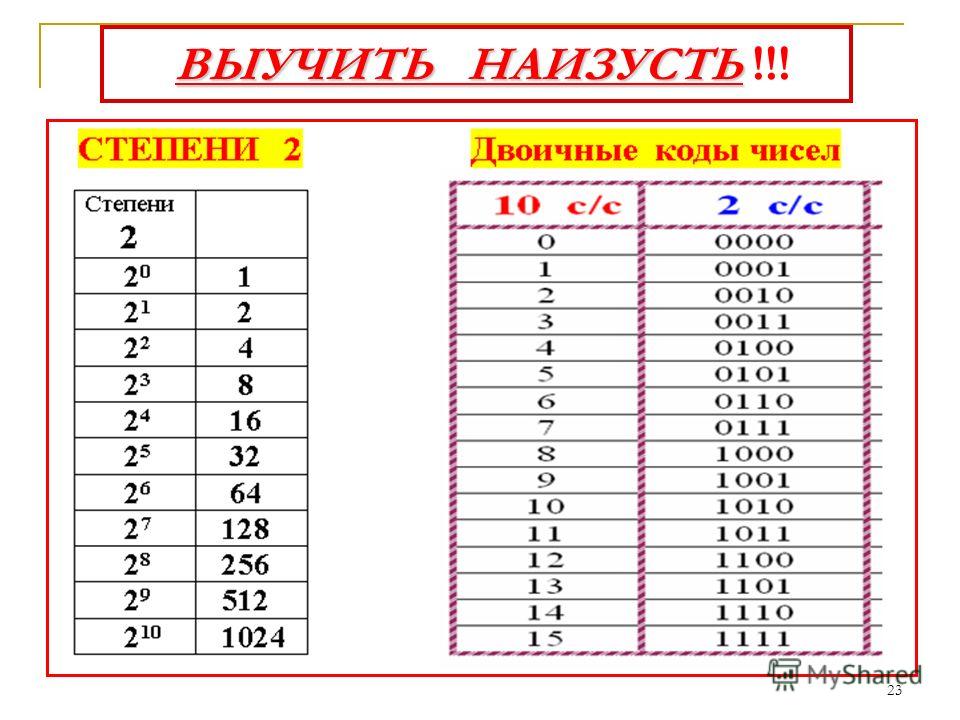
Сначала запишем его в виде суммы N единиц. Так как единица — это 20, то первоначально N есть сумма одинаковых степеней двойки. Затем начнем объединять их по парам. Сумма двух чисел, равных 20, — это 21, так что в результате получится заведомо меньшее количество слагаемых, равных 21, и, возможно, одно число 20, если ему не нашлось пары. Далее попарно объединяем одинаковые слагаемые 21, получая еще меньшее количество чисел 22 (здесь тоже возможно появление непарной степени двойки 21). Затем снова объединяем равные слагаемые попарно, и так далее. Рано или поздно процесс завершится, ибо количество одинаковых степеней двойки после каждого объединения уменьшается. Когда оно станет равным 1 — дело кончено. Осталось сложить все получившиеся непарные степени двойки — и представление готово.
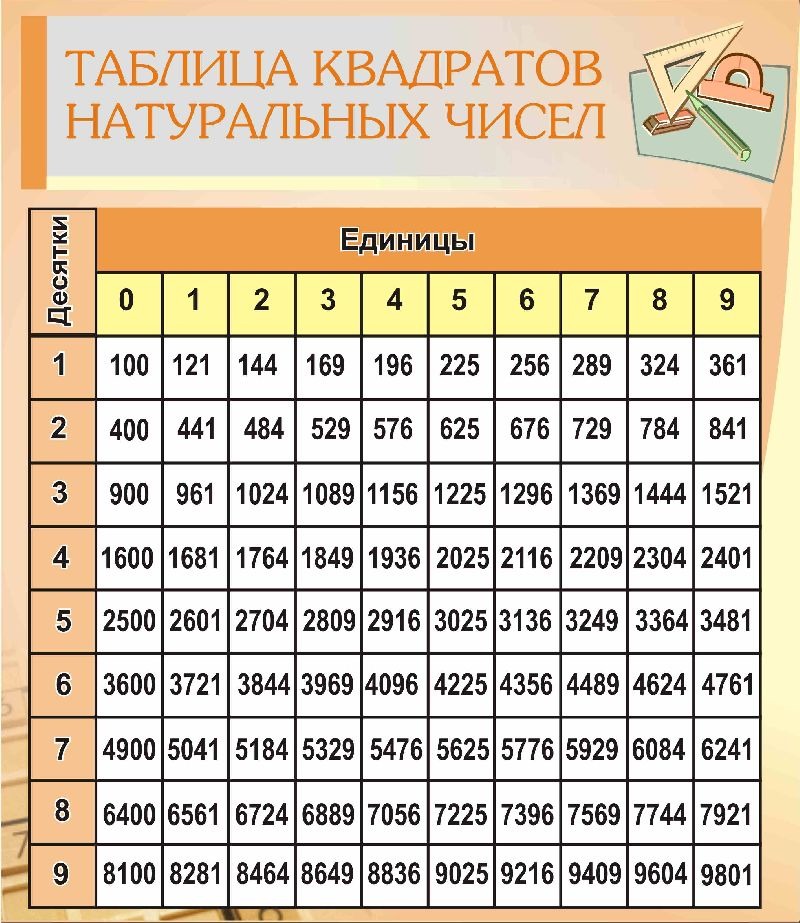Пусть одно и то же число N удалось представить в виде двух наборов различных степеней двойки, которые не полностью совпадают (т. е. имеются степени двойки, входящие в один набор, но не входящие в другой, и наоборот). Для начала отбросим все совпадающие степени двойки из обоих наборов (если таковые имеются). Получатся два представления одного и того же числа (меньшего или равного N) в виде суммы различных степеней двойки, причем все степени в представлениях различны. В каждом из представлений выделим наибольшую степень. В силу изложенного выше, для двух представлений эти степени различны. То представление, для которого эта степень больше, назовем первым, другое — вторым. Итак, пусть в первом представлении наибольшая степень равна 2m, тогда во втором она, очевидно, не превышает 2m–1. Но поскольку (и мы с этим уже сталкивались выше, подсчитывая зерна на шахматной доске) справедливо равенство
.. + 20) + 1,
е. из положительных сделаем отрицательными. Единственное требование — чтобы в результате и положительных, и отрицательных чисел оказалось бесконечное количество. Например, можно присвоить знак «минус» каждой пятой степени двойки или, допустим, оставить положительными только числа 210, 2100, 21000, и так далее — вариантов здесь сколько угодно.
А так как различных цифр ограниченное количество, последовательность последних цифр степеней двойки просто обязана быть периодической! Длина периода, естественно, не превышает 10 (поскольку именно столько цифр мы используем), но это сильно завышенное значение. Попробуем оценить его, не выписывая пока саму последовательность. Ясно, что последние цифры всех степеней двойки, начиная с 21, четные. Кроме того, среди них не может быть нуля — потому что число, оканчивающееся нулем, делится на 5, в чем заподозрить степени двойки никак нельзя. А так как четных цифр без нуля имеется всего четыре, то и длина периода не превосходит 4.
Не более чем двузначных чисел, делящихся на 4, имеется всего 25 (для однозначных чисел предпоследней цифрой считаем ноль), но из них надо выбросить пять чисел, оканчивающихся нулем: 00, 20, 40, 60 и 80. Так что период может содержать не более 25 – 5 = 20 чисел. Проверка показывает, что так и есть, начинается период с числа 22 и содержит пары цифр: 04, 08, 16, 32, 64, 28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, 44, 88, 76, 52, а затем опять 04 и так далее.
И таких степеней двойки бесконечно много! Например, существует бесконечное количество степеней двойки, начинающихся с цифр 2012 или, скажем, 3 333 333 333 333 333 333 333.
Вот какова относительная доля первых цифр степеней двойки с округлением до 4 знаков после запятой:
6
Оказывается, если это — простое число, то, домножив его на предыдущую степень двойки, мы образуем совершенное число 2n–1 (2n – 1). Например, при п = 3 получаем исходные числа 4 и 8. Так как 8 – 1 = 7 — простое число, то 4·7 = 28 — совершенное число.8 Более того — в свое время Леонард Эйлер доказал, что все четные совершенные числа имеют именно такой вид. Нечетные совершенные числа пока не обнаружены (и мало кто верит в их существование).
Последовательность чисел Каталана имеет множество любопытных свойств, и одно из них (как раз связанное с темой этой статьи) заключается в том, что порядковые номера всех нечетных чисел Каталана являются степенями двойки!
) Ответ: оно равно 2n – 1, что легко доказывается по индукции.
Поэтому окончательно Xn+1 =2Xn + 1. Получено рекуррентное соотношение, но для того чтобы его привести к «нормальному» виду, надо еще найти X1. Ну, это проще простого: X1 = 1 (меньше просто не бывает!). Не составляет труда, основываясь на этих данных, выяснить, что Xn = 2n – 1.
Может, и для всех четных чисел так? Увы, следующее же четное число опровергает наше предположение: 6 = 1 + 2 + 3. Зато число 8 опять не поддается. Правда, следующие числа вновь уступают натиску: 10 = 1 + 2 + 3 + 4, 12 = 3 + 4 + 5, 14 = 2 + 3 + 4 + 5, а вот 16 — вновь непредставимо.
Заметим, что в числителе находятся два сомножителя, каждый из которых строго больше 1, и при этом четность их — различна. Выходит, что сумма всех натуральных чисел от m до n включительно делится на нечетное число, большее 1, и потому не может быть степенью двойки. Так что теперь понятно, почему не удалось представить степени двойки в нужном виде.
Возьмем сумму 2k + 1 последовательных натуральных чисел, среднее из которых равно 2a. Легко видеть, что тогда наименьшее из них равно 2a – k, а наибольшее равно 2a + k, причем наименьшее (и, значит, все остальные) — положительное, т. е. действительно натуральное. Ну, а сумма, очевидно, составляет как раз 2a(2k + 1).
е., в основном, прав Том. Но первое впечатление обманчиво, потому что на самом деле Том прав только для значений N, являющихся степенями двойки. Для остальных N найдется доска, которая так и останется навеки непобеленной. Доказательство этого факта довольно громоздко (хотя, в принципе, несложно). Предлагаем читателю выполнить его самому.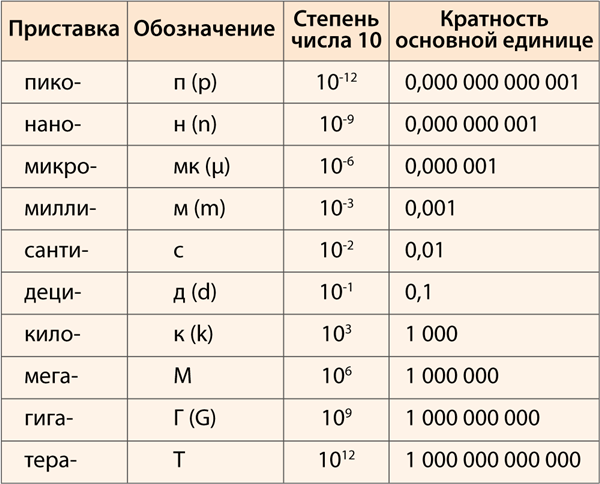
В видео также показана идея доказательства, поясняемая ниже: мы можем умножать степени одного и того же основания и делать из этого вывод, каким должно быть число в нулевой степени.
..· н)
= п х + у 
На самом деле мы можем написать, что (-3) x · (-3) 0 = (-3) x , где x — любое целое число.
Однако в случае -1 0 отрицательный знак не означает отрицательное число, а вместо этого означает , противоположное числу следующего. Итак, мы сначала вычисляем 1 0 , а затем берем обратное значение, что дает -1.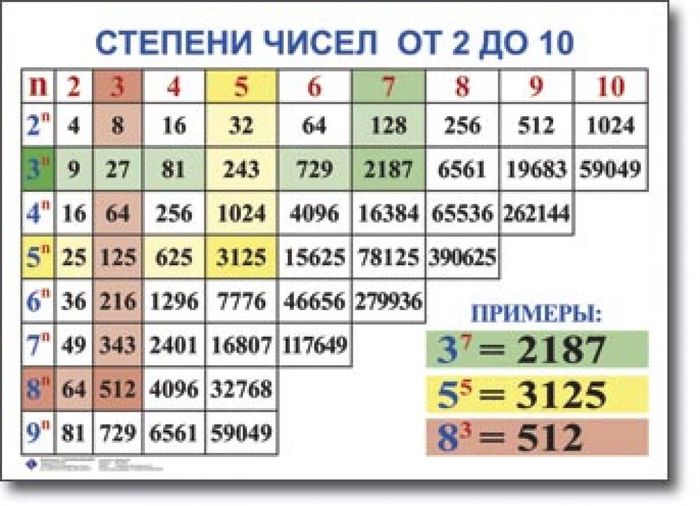 
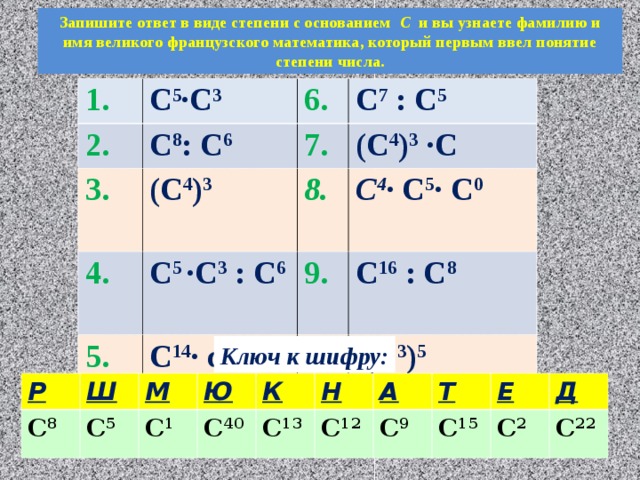В этом случае 3 — показатель степени, а 2 3 (все выражение) — степень. 
Имеем: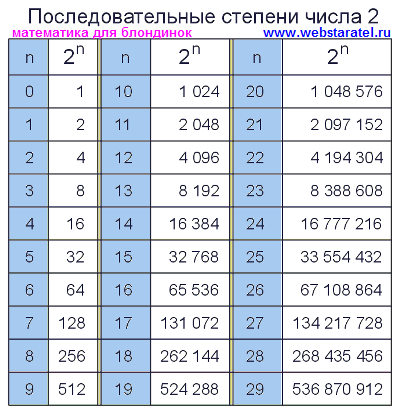
Что, если мы воспользуемся другим определением? Например, предположим, что мы решили определить как
=0 по определенной линии.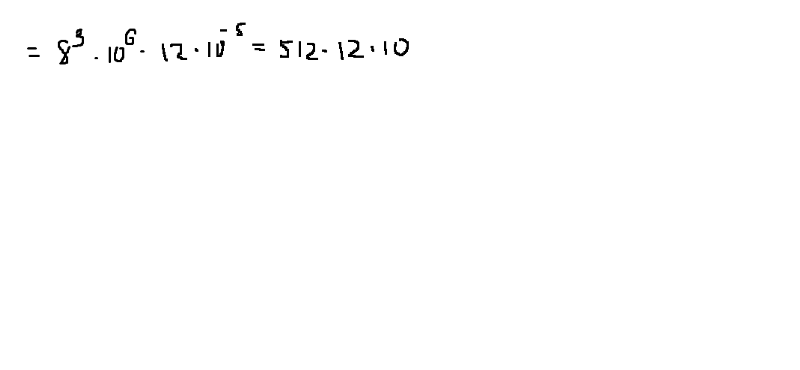
Так получилось, что правая часть имеет магический фактор. Следовательно, если мы не используем, то биномиальная теорема (как написано) не выполняется, когда a = 0, потому что тогда не равно .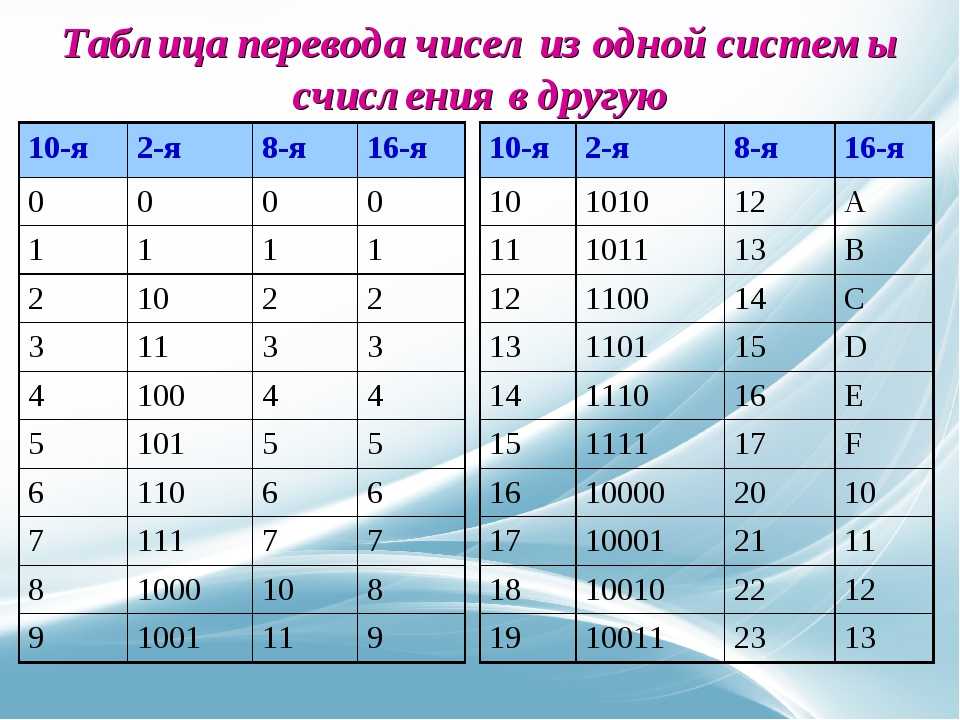
Однако не все альтернативные коды символов можно использовать, нажав клавишу Alt. Я покажу вам в ближайшее время. Просто продолжайте читать.
Ярлыки кода работают только в Microsoft Word. И чтобы использовать эти сочетания клавиш, сначала введите код в Microsoft Word, выберите его и нажмите Alt+X на клавиатуре. Код будет преобразован в Силу символа.
И ваша клавиатура также должна иметь цифровую клавиатуру.
Для пользователей Windows используйте метод альтернативного кода, нажав клавишу [Alt] при вводе альтернативного кода символа, указанного в таблице выше.
(14,13 кг)
Вы должны получить RA# (номер разрешения на возврат), чтобы вернуть любой продукт в Rockford Fosgate. Вы несете ответственность за доставку продукта в Rockford.
com (имя дилера, дата покупки и приобретенный товар должны быть разборчивы)
Моргантаун, Западная Виргиния, США; Квотербек «Канзас Джейхокс» Джалон Дэниелс (6) празднует победу над «Канзас Джейхокс» на стадионе «Маунтинир Филд» на миланском стадионе «Пушкар». Обязательный кредит: Бен Куин-USA TODAY Sports 
Небраска.
Если бы штат Канзас разгромил респектабельную программу, они бы удержали их впереди штата Айова. Тем не менее, «Уайлдкэтс» играли с одним из четырех бывших отказов Большой 12 (наряду с «Техас А&М», «Небраска» и «Колорадо»), группой, которая в тот день проиграла со счетом 0–4, проиграв «ВВС», «Аппалачи Стэйт» и «Южная Джорджия».
После двух игр «Лонгхорны» приближаются к своему рекорду 5-7 по сравнению с прошлым годом, но это означает всего лишь шесть побед.