Умножение в столбик — как умножать в столбик в 3 и 4 класс
Поможем понять и полюбить математику
Начать учиться
226.7K
Вычислять результат действий с многозначными числами в строку бывает непросто. Чтобы не удерживать промежуточные результаты в голове, можно использовать метод столбика. В этой статье рассмотрим такой способ умножения.
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
- Однозначное — состоит из одного знака.
- Двузначное — из двух.
- Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи.
Их принято отсчитывать с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
- Например, в числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.
Умножение — арифметическое действие, в котором участвуют два аргумента — множители. Результат их умножения называется произведением.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства умножения
От перестановки множителей местами произведение не меняется.
- a × b = b × a
Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
- a × b × c = (a × b) × c = a × (b × c)
Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.
Важно помнить правило: умножение в столбик с нулями дает в результате ноль:
- а × 0 = 0, где а — любое натуральное число.
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
Записываем произведение в виде столбика.
Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.
Возьмем пример 234 × 2:
Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
Ответ запишем под чертой:
Производить действия необходимо в следующей последовательности:
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 × 8063:
Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:
Последовательно перемножаем значения разрядов. Результатом является неполное произведение.
Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т. д. Результат запишем под чертой.
По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:
Далее складываем два произведения в столбик.
Получившееся семизначное число — результат умножения исходных натуральных чисел.
Ответ: 8 063 × 207 = 1 669 041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Не важно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
157.5K
Вычитание дробей
К следующей статье
590.9K
Деление в столбик
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Эффективный счёт в уме или разминка для мозга / Хабр
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.
А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:
31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 x 1 = 900 - 1 = 899.
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400; 3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68.
Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,
600 : 25 = (600 : 100) x 4 = 6 x 4 = 24; 24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600.
Теперь не кажется невозможным умножить в уме 625 на 53:
625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = = (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125.
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:
Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю.
2 = 17000 + 19000 + 2000 + 25 = 38025.
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
M = 10m + n, K = 10a + 10 - n.
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77.
Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001.
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
48 x 42 = 2016.
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09.
2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 =
= 10000 + 19000 + 1000 + 8000 + 25 = 38025.
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».
Калькулятор времени | Сложение, вычитание, умножение, деление Время
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Используйте
Калькулятор времени для сложения, вычитания, умножения и деления времени в днях, часах, минутах и секундах.
Калькулятор может складывать и вычитать отрезки времени или умножать и делить время на число или десятичную дробь. Ответы включают эквивалентное время в днях, часах, минутах или секундах.
Как рассчитать время
Ниже объясняется, как выполнять математические операции со временем. См. примеры сложения, вычитания, умножения и деления отрезков времени.
Как складывать время
Складывать дни, часы, минуты и секунды от наименьшей единицы времени к наибольшей.
- Добавить секунды
- Если общее количество секунд больше 59, вычтите 60 из секунд и перенесите 1 в минуты
- Добавьте минуты, включая все перенесенные из расчета секунд
- Если общее количество минут больше 59, вычтите 60 из минут и перенесите 1 в часы
- Добавьте часы, включая перенесенные из расчета минут
- Если общее количество часов больше 24, вычтите 24 из часов и перенесите 1 в дни
- Добавьте дни, включая любые перенесенные из расчета часов
Добавление Пример времени.
ПроблемаДобавить 2 дня 21 часа 45 минут 39 секунд до 5 дней 10 часов 45 минут 22 секунды
2 дня
21 часа
45 минут
39 секунд
и плюс;
5 дней
10 часов
45 минут
22 секунды
- 39секунды + 22 секунды = 61 секунда
2 дня
21 час
45 минут
39 секунд
+плюс;
5 дней
10 часов
45 минут
22 секунды
=
61 секунда
- 61 секунда — 60 = 1 секунда, перенести 1 в минуты
- 1 минута + 45 минут + 45 минут = 91 минута
перенос
1 минута
2 дня
21 час
45 минут
39 секунд
+ плюс;
5 дней
10 часов
45 минут
22 секунды
=
91 минута
1 секунда
- 91 минута — 60 = 31 минута, перевести 1 в часы
- 1 час + 21 час + 10 часов = 32 часа
перенос
1 час
1 минута
2 дня
21 час
45 минут
39 секунд
3 9
5 дней
10 часов
45 минут
22 секунды
=
32 часа
31 минута
1 секунда
- 32 часа — 24 = 8 часов, перенос 1 на дни
- 1 день + 2 дня + 5 дней = 8 дней
Перенос
1 день
1 час
1 минута
2 Дни
21 часа
45 минут
39 секунд
& Plus;
5 дней
10 часов
45 минут
22 секунды
=
8 дней
8 часов
31 минута
1 секунда
- Завершено Добавление времени Математическая задача
2 дня
21 час
45 минут
39 секунд
+плюс;
5 дней
10 часов
45 минут
22 секунды
=
8 дней
8 часов
31 минута
1 секунда
Как вычесть время
Вычитание дней, часов, минут и секунд от наименьшей единицы времени к наибольшей.
- Вычесть секунды
- Если секунды, которые вы вычитаете, больше верхнего числа, заимствуйте 1 минуту из первых минут и добавьте 60 к первым секундам. Затем вычтите.
- Вычесть минуты
- Если количество минут, которые вы вычитаете, превышает максимальное число, заимствуйте 1 час от максимального количества часов и добавьте 60 к максимальному количеству минут. Затем вычтите.
- Вычесть часы
- Если часы, которые вы вычитаете, больше, чем верхнее число, заимствуйте 1 день из верхних дней и добавьте 24 к верхним часам. Затем вычтите.
- Вычесть дни
Обратите внимание, что в любом случае, когда вам необходимо заимствовать, если следующая по величине единица равна 0, то заимствование производится из 2-й по величине единицы. Так же, как и при длинном вычитании, берите взаймы со следующего по величине разряда.
Время вычитания Пример задачи
Вычесть 2 дня 21 час 56 минут 18 секунд из 5 дней 0 часов 10 минут 13 секунд
5 дней
0 часов
10 минут
13 секунд
−
2 дня
21 час
56 минут
18 секунд
- Вычесть секунды
- 13 секунд меньше 18 секунд, поэтому заимствуйте 1 из первых минут
- 1 минута = 60 секунд, поэтому добавьте 60 секунд к 13, чтобы получить 73
- 73 секунды — 18 секунд = 55 секунд
одолжить
1 минута
5 дней
0 часов
9 минут
73 секунд
—
2 дня
21 часа
56 минут
18 секунд
& Equals;
55 секунд
- Вычесть минуты
- 9 минут меньше 56 минут, поэтому заимствуйте 1 из часов
- Есть 0 часов, поэтому займите 1 из дней
- 1 день = 24 часа и 1 час = 60 минут, поэтому добавьте 24 к часам, затем заимствуйте 1 из часов, чтобы получить 23
- Добавьте 60 минут к 9, чтобы получить 69
- 69 минут — 56 минут = 13 минут
borrow
1 day
1 hour
1 minute
4 days
23 hours
69 minutes
73 seconds
−
2 days
21 hours
56 minutes
18 секунд
=
13 минут
55 секунд
- Вычесть часы
- 23 часа — 21 час = 2 часа
borrow
1 day
1 hour
1 minute
4 days
23 hours
69 minutes
73 seconds
−
2 days
21 hours
56 minutes
18 секунд
=
2 часа
13 минут
55 секунд
- Вычесть дни
- 4 дня — 2 дня = 2 дня
borrow
1 day
1 hour
1 minute
4 days
23 hours
69 minutes
73 seconds
−
2 days
21 hours
56 minutes
18 секунд
=
2 дня
2 часа
13 минут
55 секунд
- Математическая задача на вычитание времени
5 дней
0 часов
10 минут
13 секунд
—
2 дня
21 часа
56 минут
18 Seconds
& Equals;
2 дня
2 часа
13 минут
55 секунд
Как умножить время
Умножить дни, часы, минуты и секунды на кратное число, работая от наименьшей единицы времени к наибольшей.
- Умножить каждую единицу времени на кратное
- Работая от наименьшей единицы времени к наибольшей, преобразовать лишние единицы времени в следующую более высокую единицу
- Если секунды больше 59, разделите на 60, чтобы получить целое число и остаток
- Сохраните остаток как общее количество секунд и добавьте целое число к минутам
- Если минуты больше 59, разделите на 60, чтобы получить целое число и остаток
- Сохраните остаток как общее количество минут и добавьте целое число к часам
- Если часов больше 23, разделите на 24, чтобы получить целое число и остаток
- Сохраните остаток как общее количество часов и добавьте целое число к дням
Умножение времени Пример задачи
Умножение 2 дня 10 часов 32 минуты 16 секунд на 5
2 дня
10 часов
32 минуты
16 секунд
- Умножение каждую единицу времени на 5
2 дня
10 часов
32 минуты
16 секунд
=
10 дней
50 часов
160 минут
80 секунд
- 80 секунд больше 59поэтому конвертируйте лишнее в минуты
- 80 разделить на 60 равно 1 с остатком 20
- Сохранить 20 секунд и перенести 1 на минуты
- 160 + 1 = 161 минута
перенос
1 минута
=
10 дней
50 часов
161 минута
20 секунд
- 161 минута больше 59, поэтому переведите лишнее в часы
- 161 разделить на 60 равно 2 с остатком 41
- Держите 41 секунду и переносите 2 на часы
- 50 + 2 = 52 часа
перенос
2 часа
1 минута
=
10 дней
52 часа
41 минута
20 секунд
- 52 часа больше 24, поэтому преобразуйте лишнее в дни
- 52 разделить на 24 равно 2 с остатком 4
- Хранить 4 часа и носить с собой 2 дня
- 10 + 2 = 12 дней
перенос
2 дня
2 часа
1 минута
=
12 дней
4 часа
41 минута
20 секунд
- Завершенная математическая задача на умножение времени
2 дня
10 часов
32 минуты
16 секунд
=
12 дней
4 часа
41 минута
20 секунд
Как разделить время
Разделите дни, часы, минуты и секунды на делитель, работая от наименьшей единицы времени к наибольшей.
- Разделить каждую единицу времени на делитель
- Затем, работая от наибольшей единицы времени к наименьшей, преобразуйте любые десятичные значения в целые числа, сдвигая десятичную сумму к меньшей единице времени
- Если в днях есть десятичная дробь, сохраните целое число как общее количество дней и преобразуйте десятичную дробь в часы
- Поскольку 1 день = 24 часа, умножьте десятичную дробь на 24 и прибавьте результат к часам .
- Если в часах есть десятичная дробь, сохраните целое число как общее количество часов и преобразуйте десятичную дробь в минуты
- Поскольку 1 час = 60 минут, умножьте десятичную дробь на 60 и прибавьте результат к минутам
- Если минуты имеют десятичную дробь, сохраните целое число как общее количество минут и преобразуйте десятичную дробь в секунды
- Поскольку 1 минута = 60 секунд, умножьте десятичную дробь на 60 и прибавьте результат к секундам
- Если в секундах есть десятичная дробь, вы обычно можете оставить это как окончательный ответ в зависимости от вашего приложения
Разделение времени Пример задачи
Разделить 4 дня 10 часов 13 минут 16 секунд на 4
4 дня
10 часов
13 минут
16 секунд
- Разделите каждую единицу времени на 4
4 дня
10 часов
13 минут
16 секунд
=
1 день
2,5 часа
3,25 минуты
4 секунды
- Работа от наименьшей единицы времени к наименьшей Преобразование любых десятичных значений в целые числа
- Часы — это не целое число, поэтому преобразуйте десятичную дробь в минуты
- 2,5 часа — это 2 часа плюс 0,5 часа
- Так как 1 час = 60 минут, 0,5 от 1 часа равняется 0,5 от 60 минут = 30 минут
- Хранить 2 часа и носить с собой 30 минут
- 30 + 3,25 = 33,25 минуты
перенос
30 минут
=
1 день
2 часа
33,25 минуты
4 секунды
- Минуты не являются целым числом, поэтому преобразуйте десятичную дробь в секунды
- 33,25 минуты равно 33 минутам плюс 0,25 минуты
- Так как 1 минута = 60 секунд, 0,25 от 1 минуты равняется 0,25 от 60 секунд = 15 секунд
- Сохранить 33 минуты и перенести 15 на секунды
- 15 + 4 = 19секунд
перенос
30 минут
15 секунд
=
1 день
2 часа
33 минуты
19 секунд
- Завершенная математическая задача на деление времени
4 дня
10 часов
13 минут
16 секунд
=
1 дней
2 часа
33 минуты
19 seconds
Time Conversion Units
1 day
24 hours
1,440 minutes
86,400 seconds
1 hour
60 minutes
3,600 seconds
1 minute
60 seconds
1 second
Цитируйте этот контент, страницу или калькулятор как:
Фьюри, Эдвард «Калькулятор времени | Сложение, вычитание, умножение, деление времени» на https://www.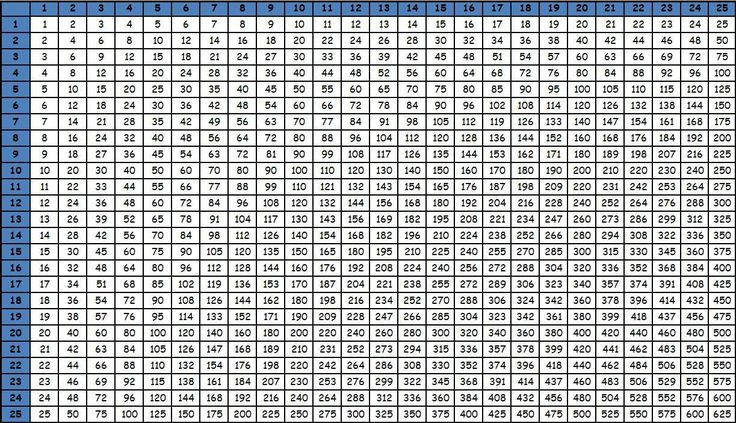
calculatorsoup.com/calculators/time/time-calculator.php из КалькуляторСуп, https://www.calculatorsoup.com — Онлайн калькуляторы
Подписаться на CalculatorSoup:
Таблица умножения на 14 – Выучить таблицу умножения на 14
Запоминание таблицы умножения на 14 может стать отличным упражнением для тренировки мозга для младших школьников. Знание таблицы 14 является основным при изучении математики. Если вы не освоите таблицу умножения на 14 на кончике языка, вам будет трудно выполнять быстрые математические вычисления в уме. В этом уроке мы узнаем о таблице 14 с числами от 1 до 10, а также о некоторых хитростях, позволяющих легко запомнить эти таблицы умножения.
Таблица умножения на 14 умножений:
| 1. | Таблица умножения 14 |
2. | Советы по 14-кратному столу |
| 3. | Часто задаваемые вопросы о таблице умножения на 14 |
Таблица умножения 14
Изучение таблицы умножения из 14 необходимо, так как она используется для длинного умножения и деления. У него есть и другие преимущества, такие как:
- Таблица умножения на 14 помогает легко решать математические задачи.
- Учащиеся могут использовать свои знания для быстрого решения любых задач на умножение.
- Таблица 14 помогает понять закономерности кратных чисел.
Просмотрите таблицу 14 раз для чисел от 1 до 10, показанных ниже.
Таблица умножения на 14
| Таблица умножения на 14 до 10 | |
|---|---|
| 14 × 1 = 14 | 14 × 6 = 84 |
| 14 × 2 = 28 | 14 × 7 = 98 |
| 14 × 3 = 42 | 14 × 8 = 112 |
| 14 × 4 = 56 | 14 × 9 = 126 |
| 14 × 5 = 70 | 14 × 10 = 140 |
Вы можете распечатать или сохранить таблицу 14 в формате PDF, нажав на ссылку ниже.
☛ Таблица умножения на 14
Советы для 14-кратного стола
1. Чтобы запомнить таблицу умножения на 14, сначала нам нужно запомнить таблицу умножения на 4. Число, кратное 4, равно 4, 8, 12, 16, 20, 24, 28, 32, 36, 40. . .
2. Чтобы получить числа, кратные 14, прибавьте натуральные числа к разряду десятков кратных 4. Таким образом, таблица умножения на 14 получается следующим образом: (1+0)4, (2+0)8 , (3+1)2, (4+1)6, (5+2)0, (6+2)4, (7+2)8, (8+3)2, (9+3)6, (10+4)0 = 14, 28, 42, 56, 70, 84, 98, 112, 126, 140
3. 14 не имеет правил, которые делают таблицу умножения 14 легко запомнить, но есть закономерность для каждых пяти кратных четырнадцати, то есть 14, 28, 42, 56, 70, 84, 98, 112, 126, 140. Последняя цифра этих кратных всегда повторяется, что означает, что учащиеся могут запомнить эти цифры, чтобы помочь им с таблицей умножения на 14.
Таблица от 14 до 20
| 14 × 11 = 154 | 14 × 16 = 224 |
| 14 × 12 = 168 | 14 × 17 = 238 |
| 14 × 13 = 182 | 14 × 18 = 252 |
| 14 × 14 = 196 | 14 × 19 = 266 |
| 14 × 15 = 210 | 14 × 20 = 280 |
Часто задаваемые вопросы о таблице умножения на 14
Что такое Таблица умножения на 14?
| 14 × 1 = 14 | 14 × 6 = 84 |
| 14 × 2 = 28 | 14 × 7 = 98 |
| 14 × 3 = 42 | 14 × 8 = 112 |
| 14 × 4 = 56 | 14 × 9 = 126 |
| 14 × 5 = 70 | 14 × 10 = 140 |
В чем хитрость 14 Table?
Один из самых важных приемов для запоминания таблицы умножения на 14 — это запоминание таблицы 4 и ее кратных чисел.