150 умножить на 50: Умножить столбиком 50 на 150

alexxlab / / Разное

Содержание

правила, примеры, решения, как умножать десятичные дроби

В этой статье мы рассмотрим такое действие, как умножение десятичных дробей. Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)

В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.

Умножение десятичных дробей: общие принципы

Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.

Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.

Посмотрим, как решаются такие задачи.

Пример 1

Вычислите произведение 1,5 и 0,75.

Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0,75 – это 75/100, а 1,5 – это 1510. Мы можем сократить дробь и произвести выделение целой части. Полученный результат 1251000 мы запишем как 1,125.

Ответ: 1,125.

Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.

Пример 2

Умножьте одну периодическую дробь 0,(3) на другую 2,(36).

Решение

Для начала приведем исходные дроби к обыкновенным. У нас получится:

0,(3)=0,3+0,03+0,003+0,003+…=0,31-0,1=0,39=39=132,(36)=2+0,36+0,0036+…=2+0,361-0,01=2+3699=2+411=2411=2611

Следовательно, 0,(3)·2,(36)=13·2611=2633.

Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:

Ответ: 0,(3)·2,(36)=0,(78).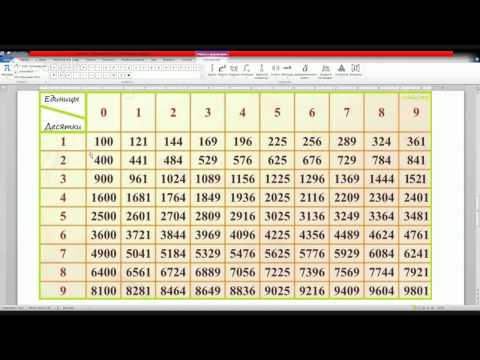

Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.

Пример 3

Вычислите произведение 5,382… и 0,2.

Решение

У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5,382…≈5,38. Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5,38·0,2=538100·210=1 0761000=1,076.

Ответ: 5,382…·0,2≈1,076. 

Как умножать десятичные дроби столбиком

Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:

Определение 1

Умножение десятичных дробей столбиком выполняется в 2 шага:

1. Выполняем умножение столбиком, не обращая внимание на запятые.

2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.

Разберем примеры таких расчетов на практике.

Пример 4

Умножьте десятичные дроби 63,37 и 0,12 столбиком.

Решение

Первым делом выполним умножение чисел, игнорируя десятичные запятые.

Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:

Ответ: 3,37·0,12=7,6044.

Пример 5

Подсчитайте, сколько будет 3,2601 умножить на 0,0254.

Решение 

Считаем без учета запятых. Получаем следующее число:

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:

Ответ: 3,2601·0,0254=0,08280654.

Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д

Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:

Определение 2

Если мы умножим десятичную дробь на 0,1, 0,01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.

Так, для умножения 45,34 на 0,1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4,534.

Пример 6

Умножьте 9,4 на 0,0001.

Решение

Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9,4·0,0001=0,00094.

Ответ: 0,00094.

Для бесконечных десятичных дробей мы пользуемся тем же правилом. Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.

Как перемножить десятичную дробь с натуральным числом

Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.

Пример 7

Подсчитайте, сколько будет 15·2,27.

Решение

Умножим столбиком исходные числа и отделим два знака запятой.

Ответ: 15·2,27=34,05.

Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.

Пример 8

Вычислите произведение 0,(42) и 22.

Решение

Приведем периодическую дробь к виду обыкновенной.

0,(42)=0,42+0,0042+0,000042+…=0,421-0,01=0,420,99=4299=1433

Далее умножаем:

0,42·22=1433·22=14·223=283=913

Итоговый результат можем записать в виде периодической десятичной дроби как 9,(3).

Ответ: 0,(42)·22=9,(3).

Бесконечные дроби перед подсчетами надо предварительно округлить.

Пример 9

Вычислите, сколько будет 4·2,145….

Решение

Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:

4·2,145…≈4·2,15=8,60. 

Ответ: 4·2,145…≈8,60.

Как умножить десятичную дробь на 1000, 100, 10 и др

Умножение десятичной дроби на 10, 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:

Определение 3

Чтобы умножить десятичную дробь на 1000, 100, 10 и др., нужно перенести ее запятую на 3, 2,1 цифры в зависимости от множителя и отбросить слева лишние нули.

Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.

Покажем на примере, как именно это делать.

Пример 10

Выполните умножение 100 и 0,0783.

Решение

Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007,83​​​​​Нули, стоящие слева, можно отбросить и записать результат как 7,38.

Ответ: 0,0783·100=7,83.

Пример 11

Умножьте 0,02 на 10 тысяч.

Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0. В итоге получилось 0,02000,перенесем запятую и получим 00200,0. Игнорируя нули слева, можем записать ответ как 200.

Ответ: 0,02·10 000=200.

Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.

Пример 12

Вычислите произведение 5,32(672) на 1 000.

Решение: первым делом мы запишем периодическую дробь как 5,32672672672…, так вероятность ошибиться будет меньше. После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).

Ответ: 5,32(672)·1 000=5 326,(726).

Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.

Как перемножить десятичную дробь с обыкновенной или со смешанным числом

Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.

Пример 13

Умножьте 0,4 на 356

Решение

​Cначала переведем десятичную дробь в обыкновенную. Имеем: 0,4=410=25.

Далее считаем: 0,4·356=25·236=2315=1815.

Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1,5(3).

Ответ: 1,5(3).

Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.

Пример 14

Вычислите произведение 3,5678…·23

Решение 

Второй множитель мы можем представить как 23=0,6666…. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3,568 и 0,667. Посчитаем столбиком и получим ответ:

Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2,379856≈2,380.

Ответ: 3,5678…·23≈2,380

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Секреты быстрого умножения и деления

1. Умножение и деление на 5, 50, 500 и т. д.

 Умножение на 5, 50, 500 и т. д. заменяется умножением на 10, 100,1000 и т. д. с последующим делением на 2 полученного произведения (или делением на 2 и умножением на 10, 100, 1000 и т. д.). (50 = 100: 2 и т.д.)

 

            54*5=(54*10):2=540:2=270    (54*5 = (54:2)*10= 270).

Чтобы  число разделить на 5,50, 500 и т. д., надо это число разделить на  10,100,1000 и т. д. и умножить на 2.

10800 : 50 = 10800:100*2 =216

10800 : 50 = 10800*2:100 =21

2. Умножение и деление на  25, 250, 2500 и т. д.

Умножение на 25, 250, 2500 и т. д. заменяется умножением на 100,1000,10000 и т. д. и полученный результат разделить на 4. (25 = 100: 4)

542*25=(542*100):4=13550                    (248*25=248: 4*100 = 6200)

(если число делится на 4, то выполнение умножения не занимает времени, любой ученик может выполнить).

       Чтобы выполнить деление числа на 25,25,250,2500 и т.д. это число надо разделить  на 100,1000,10000 и т.д. и умножить на 4.

         31200: 25 = 31200:100*4 = 1248.

 3.  Умножение и деление на  125, 1250, 12500 и т. д.

Умножение на 125, 1250 и т. д. заменяется умножением на 1000, 10000 и т. д. и полученное произведение нужно делить на 8. (125 = 1000: 8)

72*125=72*1000:8=9000

Если число делится на 8, то сначала выполним деление на 8 , а потом умножение на 1000,10000 и т. д.

48*125 = 48:8*1000 = 6000

Чтобы разделить число на 125, 1250 и т.д., надо это число разделить на 1000, 10000 и т. д. и умножить на 8.

7000: 125 = 7000:1000*8 = 56.

 4. Умножение и деление на  75, 750 и т. д.

 Чтобы число умножить на 75, 750и т. д. надо это число разделить на 4 и умножить на 300, 3000 и т.д. (75 = 300: 4)

48* 75 = 48:4*300 = 3600

Чтобы число разделить на 75,750 и т. д. надо это число разделить на 300, 3000 и т.д. и умножить на 4

7200: 75 = 7200: 300*4 = 96.

 5.Умножение на 15, 150.

 При умножении на 15, если число нечетное, умножают его на 10 и прибавляют половину полученного произведения:

23х15=23х(10+5)=230+115=345;

Если же число четное, то поступаем еще проще — к числу прибавляем его половину и результат умножаем на 10:

18х15=(18+9)х10=27х10=270.

При умножении числа на 150 пользуемся тем же приемом и умножаем результат на 10, т.к.150=15х10: 

24х150=((24+12)х10)х10=(36х10)х10=3600.

 Точно так же быстро умножить двузначное число (особенно четное) на двузначное, оканчивающиеся на 5:

24*35 = 24*(30 +5) = 24*30+24:2*10 = 720+120=840.

 6. Перемножение двузначных чисел, меньших, чем 20.

  К одному из чисел надо прибавить количество единиц другого, эту сумму умножить на 10 и прибавить к ней произведение единиц данных чисел:

18х16=(18+6)х10+8х6= 240+48=288.  

  Описанным способом можно умножать двузначные числа, меньшие 20, а также числа, в которых одинаковое количество десятков: 23х24 = (23+4)х20+4х6=27х20+12=540+12=562.

Объяснение:

(10+a)*(10+b) = 100 + 10a + 10b + a*b = 10*(10+a+b) + a*b = 10*((10+a)+b) + a*b .

 7.Умножение двузначного числа на 101.

 Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено.
Пример:

57 * 101 = 5757      57 —> 5757

Объяснение: (10a+b)*101 = 1010a + 101b = 1000a + 100b + 10a + b
Аналогично производят умножение трехзначных чисел на 1001, четырехзначных — на 10001 и т. п.

 8. Умножение числа на 11.

Следует «раздвинуть» цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд.

Пример:
34 * 11 = 374, так как 3 + 4 = 7, семерку помещаем между тройкой и четверкой
68 * 11 = 748, так как 6 + 8 = 14, четверку помещаем между семеркой (шестерка плюс перенесенная единица) и восьмеркой

Объяснение:
10a+b — произвольное число, где a — число десятков, b — число единиц.

Имеем:
(10a+b)*11 = 10a*11 + b*11 = 110a + 11b = 100a + 10a + 10b + b = 100a + 10*(a+b) + b,
где мы имеем a сотен, a+b десятков и b единиц. т.е. результат содержит a*(a+1) сотен, два десятка и пять единиц.

43625*11

Составляем произведение: 5 единиц, 5+2=7 десятки, 2+6=8 сотни, 6+3=9 тысячи, 3+4=7 десятки тысяч, 4 сотни тысяч.

43625*11=479875.

Когда множимое заключается в пределах 1000 и 10000 (например, 7543), то можно применить следующий способ умножения на 11. Сначала разбить множимое 7543 на грани, по две цифры, затем найти произведение первой грани (75) слева на 11, как указано в умножении двузначного числа на 11. Полученное число (75*11=725) даст сотни произведения, так как умножали сотни множимого. Потом надо умножить на 11 вторую грань (43), получим единицы произведения: 43*11=473. Наконец, полученные произведения сложим: 825 сот. +473=82739. Следовательно, 7543*11=82739.

Рассмотрим ещё пример: 8324*11.

83`24; 83 сот. *11=913 сот.

24*11=264; 913 сот. +264=91564. Следовательно, 8324*11=91564.

 9. Умножение на 22, 33, …, 99.

Чтобы двузначное число умножить 22,33, …,99, надо этот множитель представить в виде произведения однозначного числа на 11. Выполнить умножение сначала на однозначное число, а потом на 11:

15 *33= 15*3*11=45*11=495.

 10. Умножение двузначных чисел на 111.

Сначала возьмём множимым такое двузначное число, сумма цифр которого меньше 10. Поясним на числовых примерах:

45*111.

Так как 111=100+10+1, то 45*111=45*(100+10+1). При умножении двузначного числа, сумма цифр которого меньше 10, на 111, надо в середину между цифрами вставить два раза сумму цифр (т.е. чисел, ими изображаемых) его десятков и единиц 4+5=9. 4500+450+45=4995. Следовательно, 45*111=4995. Когда сумма цифр двузначного множимого больше или равна 10, например 68*11, надо сложить цифры множимого (6+8) и в середину между цифрами 6 и 8 вставить 2 раза единицы полученной суммы. Наконец, к составленному числу 6448 прибавить 1100. Следовательно, 68*111=7548.

 11. Умножение на 37.

При умножении числа на 37, если данное число кратно 3,его делят на 3 и умножают на 111.

27*37=(27:3)*(37*3)=9*111=999

Если же данное число не кратно 3, то из произведения вычитают 37 или к произведению прибавляют 37.

23*37=(24-1)*37=(24:3)*(37*3)-37=888-37=851.

 12. Возведение в квадрат любого двузначного числа.

 Если запомнить квадраты всех чисел от 1 до 25, то легко найти и квадрат любого двузначного числа, превышающего 25.

Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю.

Рассмотрим пример:

372=12*100+132=1200+169=1369

(М–25)*100+ (50-M) 2=100M-2500+2500–100M+M2=M2 .

 13. Умножение чисел, близких к 100.

   При увеличении (уменьшении) одного из множителей на несколько единиц умножаем полученное целое число и прибавленные (отнятые) единицы на другой множитель и  из первого произведения вычитаем второе произведение (полученные произведения складываем)

98∙8=(100-2) ∙8=100∙8-2∙8=800-16=784.

Данный прием представления одного из сомножителей в виде разности позволяет легко умножать на 9, 99, 999.

Для этого достаточно умножить число на 10 (100, 1000) и из полученного  целого числа вычесть число, которое умножали: 154х9=154х10-154=1540-154=1386.

Но еще проще ознакомить детей с правилом — «чтобы умножить число на 9 (99, 999)достаточно вычесть из этого числа число его десятков (сотен, тысяч), увеличенное на единицу, и к полученной разности приписать дополнение его цифры единиц до 10 (дополнение до 100 (1000) числа, образованного двумя (тремя) последними цифрами этого числа):

154х9=(154-16)х10+(10-4)=138х10+6=1380+6=1386

 14. Умножение двузначных чисел, у которых сумма единиц равна 10.

Пусть даны два двузначных числа, у которых сумма равна 10:

М=10m + n,  K=10a + 10 – n. Составим их произведение.

M * K= (10m+n) * (10a + 10 – n) =100am + 100m – 10mn + 10an + +10n – n2 = m * (a + 1) * 100 + n * (10a + 10 – n) – 10mn = (10m) * * (10 * (a + 1)) + n * (K – 10m).

Рассмотрим несколько примеров:

17 * 23= 10 * 30 + 7 * 13= 300 + 91= 391;

33 * 67= 30 * 70 + 3 * 37= 2100 + 111= 2211.

 15 . Умножение на число, записанное одними девятками.

 Для того чтобы найти произведение числа написанного одними девятками на число имеющее с ним одинаковое количество цифр надо от множителя отнять единицу и к получившемуся числу приписать другое число все цифры которого дополняют цифры указанного получившегося числа до 9.

8 * 9= 72;

46 * 99= 4554;

137 * 999= 136 863;

3562 * 9999= 35616438.

Наличие такого способа усматривается из следующего приёма решения приведённых примеров: 8 * 9= 8 * (10 – 1)= 80 – 8= 72,

 46 * 99= 46 * (100 – 1)= 4600 – 54= 4554.

16. Возведение в квадрат числа, оканчивающееся на 5.

 Число десятков умножаем на следующее число десятков и прибавляем 25.

15*15 = 225 = 10*20+ 25   ( или 1*2 и приписываем справа 25)

35*35 =30*40 +25= 1225               (3*4 и приписываем справа 25)

65*65 = 60*70+25=4225                (6*7 и приписываем справа 25)

Умножение и деление чисел в Excel

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Еще…Меньше

Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул.

Умножение чисел

Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел.

Умножение чисел в ячейке

Для выполнения этой задачи используйте арифметический оператор * (звездочка).

Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50.

Умножение столбца чисел на константу

Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2.

  1. Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.

    Примечание: Использование символов $ указывает Excel, что ссылка на ячейку B2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2. Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.

  2. Перетащите формулу вниз в другие ячейки столбца.

    Примечание: В Excel 2016 для Windows ячейки заполняются автоматически.

Перемножение чисел в разных ячейках с использованием формулы

Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов.

Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6) перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6).

Деление чисел

Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проекта ÷ всего людей в проекте) или фактический километр на лилон для вашего последнего меж страны(общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами.

Деление чисел в ячейке

Для этого воспользуйтесь арифметическим оператором / (косая черта).

Например, если ввести =10/5 в ячейке, в ячейке отобразится 2.

Важно: Не забудьте ввести в ячейку знак равно(=)перед цифрами и оператором /. в противном случае Excel интерпретирует то, что вы введите, как дату. Например, если ввести 30.07.2010, Excel может отобразить в ячейке 30-июл. Если ввести 36.12.36, Excel сначала преобразует это значение в 01.12.1936 и отобразит в ячейке значение «1-дек».

Примечание: В Excel нет функции DIVIDE.

Деление чисел с помощью ссылок на ячейки

Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.

Пример:

Чтобы этот пример проще было понять, скопируйте его на пустой лист.

Копирование примера

  1. org/ListItem»>

    Создайте пустую книгу или лист.

  2. Выделите пример в разделе справки.

    Примечание: Не выделяйте заголовки строк или столбцов.

    Выделение примера в справке

  3. Нажмите клавиши CTRL+C.

  4. Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.

  5. Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке «Формулы» нажмите кнопку «Показать формулы».

A

B

C

1

Данные

Формула

Описание (результат)

2

15000

=A2/A3

Деление 15000 на 12 (1250).

3

12

Деление столбца чисел на константу

Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.

A

B

C

1

Данные

Формула

Константа

2

15000

=A2/$C$2

3

3

12

=A3/$C$2

4

48

=A4/$C$2

5

729

=A5/$C$2

6

1534

=A6/$C$2

7

288

=A7/$C$2

8

4306

=A8/$C$2
    org/ItemList»>

  1. В ячейке B2 введите =A2/$C$2. Не забудьте в формуле включить символ $ перед символами C и 2.

  2. Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.

Примечание: Символ $ указывает Excel, что ссылка на ячейку C2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали в формуле символы $ и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Умножение столбца чисел на одно и то же число

Умножение на процентное значение

Создание таблицы умножения

Операторы вычислений и порядок операций

Эффективные методы сложения, деления и умножения чисел

Автор: Илoнa Ильмapoвнa Пoтaпoвa, кандидат экономических наук, профессор Московского технико-экономического колледжа.

 

В работе и быту постоянно возникает необходимость в разных вычислениях. Использование простейших методов устных вычислений поможет вам снизить утомляемость, развить свое внимание и память. Применение рациональных методов вычислений также позволит вам повысить производительность труда, точность и скорость подсчетов. Вот четыре основные группы методик эффективных устных вычислений.

 

1. Приемы упрощенного сложения чисел

Известно четыре способа сложения, позволяющие ускорить подсчеты.

Способ последовательного поразрядного сложения используется при устных вычислениях, так как он упрощает и ускоряет суммирование слагаемых. При использовании этого способа сложение начинается с высших разрядов: к первому слагаемому прибавляются соответствующие разряды второго слагаемого.

Пример. Найдем сумму чисел 5287 и 3564, используя способ последовательного поразрядного сложения.

Решение. Расчет произведем в такой последовательности:

5 287 + 3 000 = 8 287;
8 287 + 500 = 8 787;
8 787 + 60 = 8 847;
8 847 + 4 = 8 851.

Ответ: 8 851.

Другой способ последовательного поразрядного сложения заключается в том, что к высшему разряду первого слагаемого прибавляется высший разряд второго слагаемого, затем к следующему разряду первого слагаемого прибавляется следующий разряд второго слагаемого и т. д.

Рассмотрим этот вариант решения на приведенном выше примере, получим:

5 000 + 3 000 = 8 000;
200 + 500 = 700;
80 + 60 = 140;
7 + 4 = 11;
8851.

Способ круглого числа. Число, имеющее одну значащую цифру и оканчивающееся одним или несколькими нулями, называется круглым числом. Этот способ применяется, когда из двух или более слагаемых можно выбрать такие, которые можно дополнить до круглого числа. Разность между круглым и заданным в условии вычислений числами называется дополнением. Например, 1 000 — 978 = 22. В этом случае число 22 является арифметическим дополнением числа 978 до 1 000.

Чтобы произвести сложение способом круглого числа, необходимо одно или несколько слагаемых, близких к круглым числам, округлить, выполнить сложение круглых чисел и из полученной суммы вычесть арифметические дополнения.

Пример. Найдем сумму чисел 1 238 и 193, используя способ круглого числа.

Решение. Округлим число 193 до 200 и произведем сложение следующим образом: 1 238 + 193 = (1 238 + 200) — 7 = 1 431.

 

Способ группировки слагаемых. Этот способ применяют в том случае, когда слагаемые при их группировке в сумме дают круглые числа, которые затем складывают между собой.

Пример. Найдем сумму чисел 74, 32, 67, 48, 33 и 26.

Решение. Суммируем числа, сгруппированные следующим образом: (74 + 26) + (32 + 48) + (67 + 33) = 280.

 

Способ поразрядного суммирования отдельными столбцами. Данный способ состоит в сложении разрядов исходных чисел с повторным поразрядным суммированием полученных частных сумм.

Пример. Найдем сумму чисел 167, 532, 629, 274, 22, 18 и 14, используя способ поразрядного сложения.

Решение.

+167

532

629

274

+22

18

14

 1656.

 

2. Приемы упрощенного вычитания чисел

Способ последовательного поразрядного вычитания. Этим способом производится последовательное вычитание каждого разряда, вычитаемого из уменьшаемого. Он применяется, когда числа нельзя округлить.

Пример. Найдем разность чисел 721 и 398.

Решение. Выполним действия для нахождения разности заданных чисел в следующей последовательности:

  1. представим число 398 в виде суммы: 300 + 90 + 8 = 398;
  2. выполним поразрядное вычитание: 721 — 300 = 421; 421 — 90 = 331; 331 — 8 = 323.

 

Способ круглого числа. Этот способ применяют, когда вычитаемое близко к круглому числу. Для расчета необходимо из уменьшаемого вычесть вычитаемое, взятое круглым числом, и к полученной разности прибавить арифметическое дополнение.

Пример. Вычислим разность чисел 235 и 197, используя способ круглого числа.

Решение. 235 — 197 = 235 — 200 + 3 = 38.

 

Способ замены вычитания сложением. Способ заключается в том, что к вычитаемому нужно подобрать такое число, которое в сумме с ним было бы равно уменьшаемому. Подбор нужного числа выполняется по частям.

Пример. Найдем разность денежных сумм 50 р. и 28 р. 57 к., используя способ замены вычитания сложением.

Решение. Для суммы 28 р. 57 к. подберем числа по частям, для чего:

  1. добавим к заданной сумме 43 к. и получим 29 р.;
  2. добавим к определенной в п. 1 сумме 21 р. для получения суммы 50 р.

Таким образом, искомое число — это результат вычисления слагаемых из двух сумм, т.е. разность денежных сумм 50 р. и 28 р. 57 к. составляет 21 р. 43 к.

 

3. Приемы упрощенного умножения чисел

Умножение на единицу с последующими нулями. При умножении числа на число, включающее единицу с последующими нулями (10; 100; 1 000 и т.д.), к нему приписывают справа столько нулей, сколько их в множителе после единицы.

Пример. Найдем произведение чисел 568 и 100.

Решение. 568 x 100 = 56 800.

 

Умножение на единицу с предшествующими нулями. При умножении числа на единицу с предшествующими ей нулями (0,1; 0,01; 0,001 и т.д.) как целого числа, так и десятичной дроби в первом сомножителе отделяют запятой справа столько знаков, сколько нулей во множителе перед единицей, включая ноль целых.

Пример. Найдем произведение чисел 467 и 0,01.

Решение. 467 x 0,01 =4,67.

 

Способ последовательного поразрядного умножения. Этот способ применяется при умножении числа на любое однозначное число. Если нужно умножить двузначное (трех-, четырехзначное и т.д.) число на однозначное, то вначале один из сомножителей умножают на десятки другого сомножителя, потом на его единицы и полученные произведения суммируют.

Пример. Найдем произведение чисел 39 и 7.

Решение. 39 x 7 = (30 x 7) + (9 x 7) = 210 + 63 = 273.

 

Способ круглого числа. Применяют этот способ только когда один из сомножителей близок к круглому числу. Множимое умножают на круглое число, а затем на арифметическое дополнение и в конце из первого произведения вычитают второе.

Пример. Найдем произведение чисел 174 и 69.

Решение. 174 x 69 = (174 x 70) — (174 x 1) = 12 180 — 174 = 12 006.

 

Способ разложения одного из сомножителей. В этом способе сначала раскладывают на части (слагаемые) один из сомножителей, затем поочередно умножают второй сомножитель на каждую часть первого сомножителя и полученные произведения суммируют.

Пример. Найдем произведение чисел 13 и 325.

Решение. Разложим число порций на слагаемые:13 = 10 + 3.Умножим каждое из полученных слагаемых на 325: 10 x 325 р. = 3 250 р.; 3 x 325 р. = 975 р. Суммируем полученные произведения: 3 250 р. + 975 р. = 4 225 р.

 

Сокращенные приемы умножения на 0,5; 0,25 и 0,125. Десятичную дробь 0,5 можно выразить простой дробью 1/2. При умножении любого числа на 1/2 достаточно разделить это число на 2.

Пример. Найдем произведение чисел 325 и 0,5.

Решение. 322 x 0,5 = 322 / 2 = 161.

Десятичную дробь 0,25 можно выразить простой дробью 1/4. При умножении какого-то числа на 1/4 достаточно разделить это число на 4.

Пример. Найдем произведение чисел 68 и 0,25.

Решение. 68 x 0,25 = 68 / 4 = 17.

Десятичную дробь 0,125 можно выразить простой дробью 1/8. При умножении любого числа на 1/8 достаточно разделить это число на 8.

Пример. Найдем произведение чисел 600 и 0,125.

Решение. 600 x 0,125 = 600 / 8 = 75.

 

Сокращенные приемы умножения на 5; 50 и 500. Чтобы умножить какое-то число на 5; 50; 500, его нужно умножить соответственно на 10; 100; 1 000 и полученное произведение разделить на 2. Помните, что число нулей в произведении равно числу цифр в целой части множителя.

Пример. Найдем произведение чисел 74 и 50.

Решение. 74 x 50 = (74 х 100) / 2 = 7400 / 2 = 3 700.

 

Сокращенные приемы умножения на 2,5; 25 и 250. Чтобы умножить число на 2,5; 25; 250, его необходимо вначале умножить соответственно на 10; 100; 1 000 и разделить на 4.

Пример. Найдем произведение чисел 28 и 250.

Решение. 28 х 250 = (28 х 1 000) / 4 = 28000 / 4 = 7 000.

 

Сокращенные приемы умножения на 0,15. Чтобы умножить число на 0,15, нужно это число разделить на 10, полученное частное разделить на 2, а затем оба частных сложить.

Пример. Найдем произведение чисел 240 и 0,15.

Решение. 240 x 0,15 = (240 / 10) + 1/2 х (240 / 10) = 24 + 12 = 36.

 

Сокращенные приемы умножения на 1,5; 15 и 150. Чтобы умножить число на 1,5; 15; 150, нужно это число умножить соответственно на 1; 10; 100 и к полученному произведению прибавить его половину.

Пример. Найдем произведение чисел 66 и 1,5.

Решение. 66 x 1,5 = 66 + (66 / 2) = 99.

 

Сокращенные приемы умножения на 1,25; 12,5; 125. Чтобы умножить какое-то число на 1,25; 12,5; 125, его нужно сначала умножить соответственно на 10; 100; 1 000, а затем полученное произведение разделить на 8.

Пример. Найдем произведение чисел 70 и 12,5.

Решение. 70 х 12,5 = (70 х 100) / 8 = 7 000 / 8 = 875

 

4. Приемы упрощенного деления чисел

Существуют следующие приемы сокращенного деления.

 

Разложение делимого на слагаемые. Разложение делимого на такие слагаемые, которые легко бы делились раздельно, ускоряет устный подсчет числа при делении.

Пример. Найдем частное чисел 2 808 и 9.

Решение. 2808 / 9 = (2700 / 9) + (90 / 9) + (18 / 9) = 300 + 10 + 2 = 312.

 

Деление на единицу с последующими нулями. При делении на 10; 100; 1 000 как целого числа, так и дробного в нем отделяют запятой справа налево столько десятичных знаков, сколько нулей стоит в делителе после единицы.

Пример. Найдем частное от деления чисел 136 на 10, 32,7 на 1000.

Решение. 136 / 10= 13,6;32,7 / 1 000 = 0,0317.

 

Деление на единицу с предшествующими нулями. При делении на 0,1; 0,01; 0,001 эти десятичные дроби заменяют простыми, т.е. соответственно 1/10, 1/100, 1/1000. Чтобы выполнить деление какого-то числа, это число умножают на знаменатель (10; 100; 1 000) и делят на числитель (1). Чтобы разделить какое-то целое число на 1 с предшествующими ей нулями, надо приписать к этому числу справа столько нулей, сколько их в делителе; чтобы разделить дробное число, надо перенести в нем запятую слева направо настолько десятичных знаков, сколько нулей в делителе, включая ноль целых.

Пример. Разделим числа 235; 57,6 соответственно на 0,1 и 0,01.

Решение. 235 / 0,1 = 2 350;57,6 / 0,01 = 5 760.

 

Деление на 0,5; 0,25; 0,125. Десятичную дробь 0,5 заменяют простой, т.е. 1/2. Чтобы разделить какое-то число на 0,5, необходимо умножить его на 2.

Пример. Разделим число 325 на 0,5.

Решение. 325 / 0,5 = 325 / 1/2 = 325 х 2 = 650.

При делении числа на десятичную дробь 0,25 ее заменяют простой дробью, т.е. 1/4. Чтобы разделить какое-то число на 0,25, необходимо умножить его на 4.

Пример. Разделим число 325 на 0,25.

Решение. 325 / 0,25 = 325 x 4 = 1300.

При делении десятичную дробь 0,125 заменяют простой, т.е. 1/8. Чтобы разделить какое-то число на 0,125, необходимо умножить его на 8.

Пример. Разделим число 325 на 0,125.

Решение. 325 / 0,125 = 325 x 8 = 2600.

 

Деление на 5 и 50. Делители 5 и 50 заменяют единицей с последующими нулями, т.е. соответственно на 10 и 100. Однако 10 в 2 раза больше, чем 5, а 100 в 2 раза больше, чем 50, поэтому, чтобы разделить какое-то число на 5 или 50, необходимо разделить его на 10 или 100, а частное умножить на 2.

Пример. Разделим число 1 250 соответственно на 50.

Решение. 1250 / 50 = (1250 / 100) х 2 = 12,5 x 2 = 25.

 

Деление на 2,5 и 25. Чтобы разделить число на 2,5 или 25, необходимо разделить его на 10 или 100 и затем частное умножить на 4.

Пример. Разделим число 285 на 2,5.

Решение. 285 / 2,5 = (285 / 10) х 4 = 28,5 x 4 = 114;

 

Деление на 1,25 и 12,5. Чтобы разделить число на 1,25 или 12,5, необходимо разделить его на 10 или 100 и затем частное умножить на 8.

Пример. Разделим число 300 на 12,5.

Решение. 300 / 12,5 = (300 / 100) х 8 = 3 x 8 = 24.

Усвоение навыков рационального устного счета позволит сделать вашу работу более эффективной. Это возможно только при хорошем овладении всеми четырьмя арифметическими действиями и сокращенными приемами вычислений. Применение рациональных приемов счета ускоряет вычисления, обеспечивает необходимую точность.

 

Изучите эффективные техники запоминания услышанной и прочитанной информации в курсе «Развитие памяти»: отдельно или по абонементу, со скидкой.

Изучите сегодня

Также смотрите

Умножение в столбик онлайн. Калькулятор наглядного умножения. — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Содержание

урок с примерами, карточками и видео

Умножение в столбик позволяет быстро выдавать решение примеров даже с многозначными числами. Для счёта нужно только знать наизусть таблицу умножения.

Как правильно умножать столбиком

Как и в случае со сложением и вычитанием в столбик, при умножении числа записываются друг под другом. Каждый разряд на своём месте: единицы под единицами, десятки под десятками и т. д. Внизу рисуется горизонтальная черта, ответ пишется под ней.

Возьмём числа 78 и 12. Для лучшего понимания: пишем 78 наверху, 12 — внизу. Начинаем с единицы нижнего числа, то есть с цифры 2.

Сперва считаем 8×2=16. Число получилось больше 10, значит, как и в сложении, пишем последнюю цифру (6), а единицу держим в уме. Теперь переходим к десятку, то есть считаем 7×2=14. Единицу мы держали в уме, значит, сейчас прибавляем её к результату, получается 14+1=15. Цифра 5 пишется под десятками, а 1 переходит в новый разряд — сотни. Другими словами, под горизонтальной чертой должно быть написано «156».

Переходим к следующему разряду. Теперь наш ответ будет записываться иначе: последняя цифра ответа должна быть ровно под верхними десятками, то есть под цифрой 5. Получается, что каждое последующее промежуточное число смещается на 1 разряд влево.

Считаем 8×1=8. Цифра меньше 10, пишем 8 под пятёркой в числе «156». Считаем 7×1=7. Семёрка переходит в разряд сотен, то есть она должна быть написана под единицей в ответе «156». Под шестёркой ничего не написано, для удобства туда можно поставить ноль.

Полученное выражение складываем в столбик: 156+78. К 6 ничего не прибавляется (0), значит, переписываем её в прежнем виде. Затем считаем 5+8=13, пишем 3, один в уме. Наконец, 1+7=8, прибавляем единицу — получается 9.

Таким образом, ответ: 936.

Тренироваться лучше на листе в клеточку, чтобы привыкнуть к расположению разрядов множителей

Точно так же умножаются и другие многозначные числа.

Если в множителях есть нули, они не перемножаются, а просто переносятся в правую часть окончательного ответа.

Варианты карточек

Для наглядности можно распечатать карточки с примерами разного уровня сложности. Так детям будет проще запомнить принцип счёта. Примеры для практики можно использовать и при первом изучении умножения, и для повторения после каникул.

Поначалу решение примеров будет занимать много времени, но постепенно скорость повысится. Даже при наличии калькулятора лучше считать вручную: это развивает умственную деятельность.

Фотогалерея: примеры карточек для урока
Видео: умножение чисел в столбик

Постоянная практика — залог успеха, и со временем можно научиться перемножать в уме даже большие числа. Но начинать, конечно, лучше с простых примеров, постепенно увеличивая уровень сложности.

Оцените статью: Поделитесь с друзьями!

Умножение столбиком. Онлайн калькулятор | Математика

Как умножать столбиком

Умножение многозначных чисел обычно выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.

Рассмотрим для начала умножение многозначного числа на однозначное. Пусть требуется умножить  846  на  5:

Умножить  846  на  5  — значит, сложить  5  чисел, каждое из которых равно  846.  Для этого достаточно взять сначала  5  раз по  6  единиц, потом  5  раз по  4  десятка и наконец  5  раз по  8  сотен.

  1.   5  раз по  6  единиц =  30  единиц, т. е.  3  десятка. Пишем  0  под чертой на месте единиц, а  3  десятка запоминаем. Для удобства, чтобы не запоминать можно написать  3  над десятками множимого:
  2.   5  раз по  4  десятка =  20  десятков, прибавляем к ним ещё  3  десятка =  23  десятка, т. е.  2  сотни и  3  десятка. Пишем  3  десятка под чертой на месте десятков, а  2  сотни запоминаем:
  3.   5  раз по  8  сотен =  40  сотен, прибавляем к ним ещё  2  сотни =  42  сотни. Пишем под чертой  42  сотни, т. е.  4  тысячи и  2  сотни. Таким образом, произведение  846  на  5  оказывается равным  4230:

Теперь рассмотрим умножение многозначных чисел. Пусть требуется умножить  3826  на  472:

Умножить  3826  на  472  — значит, сложить  472  одинаковых числа, каждое из которых равно  3826.  Для этого надо сложить  3826  сначала  2  раза, потом  70  раз, потом  400  раз, т.  е. умножить множимое отдельно на цифру каждого разряда множителя и полученные произведения сложить в одну сумму.

2  раза по  3826  =  7652.  Пишем полученное произведение под чертой:

Это не окончательное произведение, пока мы умножили только на одну цифру множителя. Полученное число называется частичным произведением. Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.

Умножаем  3826  на  7.  Это будет второе частичное произведение  (26782):

Умножаем множимое на  4.  Это будет третье частичное произведение  (15304):

Под последним частичным произведением проводим черту и выполняем сложение всех полученных частичных произведений. Получаем полное произведение  (1 805 872):

Если во множителе встречается нуль, то обычно на него не умножают, а сразу переходят к следующей цифре множителя:

Когда множимое и (или) множитель оканчиваются нулями, умножение можно выполнить не обращая на них внимания, и в конце, к произведению добавить столько нулей, сколько их во множимом и во множителе вместе.

Например, необходимо вычислить  23 000 · 4500.  Сначала умножим  23  на  45,  не обращая внимание на нули:

И теперь, справа к полученному произведению припишем столько нулей, сколько их во множимом и во множителе вместе. Получится  103 500 000.

Калькулятор умножения столбиком

Данный калькулятор поможет вам выполнить умножение столбиком. Просто введите множимое и множитель и нажмите кнопку Вычислить.

Умножение натуральных чисел столбиком: примеры, решения

Если нам по ходу решения задачи требуется перемножить натуральные числа, удобно использовать для этого готовый способ, который называется «умножение в столбик» (или «умножение столбиком»). Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.

В этом материале мы расскажем, как считать с помощью данного способа. Все пояснения будут проиллюстрированы примерами решений задач.

Основы умножения столбиком

Для ведения вычисления в столбик нам будет нужна таблица умножения. Важно помнить ее наизусть, чтобы считать быстро и эффективно.

Также потребуется вспомнить, какой результат мы получим при умножении натурального числа на нуль. Это часто встречается в примерах. Нам потребуется свойство умножения, которое в буквенном виде записывается как a·0=0 (a – любое натуральное число).

Чтобы лучше понять, как умножать столбиком, рекомендуем вам повторить аналогичный метод сложения. Один из этапов подсчетов будет представлять собой именно сложение промежуточных результатов, и знание этого метода при складывании чисел нам пригодится.

Также важно, чтобы вы умели сравнивать натуральные числа и помнили, что такое разряд.

Как записывать множители при подсчете столбиком

Как всегда, начнем с того, как правильно записать исходные числа. Нам нужно взять два множителя и записать их один под другим так, чтобы все цифры, отличные от нуля, были расположены друг под другом. Проведем под ними горизонтальную линию, отделяющую ответ, и добавим знак умножения с левой стороны.

Пример 1

Например, чтобы вычислить и 71, 550·45 002 и 534 000·4 300, запишем такие столбики:

Далее нам нужно разобраться с процессом умножения. Для начала посмотрим, как правильно умножать многозначное натуральное число на однозначное, а потом посмотрим, как перемножать между собой многозначные числа.

Как умножить столбиком многозначное число на однозначное

Если нам для решения задачи требуется выполнить умножение двух натуральных чисел, одно из которых однозначное, а второе многозначное, то мы можем использовать способ столбика. Для этого выполняем последовательность шагов, которую будем объяснять сразу на примере. Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.

Пример 2

Условие: вычислить 45 027·3.

Решение

Запишем множители так, как это предполагает метод умножения столбиком. Поместим однозначный множитель под последним знаком многозначного. Мы получили такую запись:

Далее нам надо выполнить последовательное перемножение разрядов многозначного числа на указанный множитель. Если у нас получается число, которое меньше десяти, мы сразу вносим его в поле ответа под горизонтальной чертой, строго под вычисляемым разрядом. Если же результат составил 10 и больше, то указываем под нужным разрядом только значение единиц из полученного числа, а десятки запоминаем и добавляем на следующем шаге к более старшему разряду.

На конкретных числах процесс будет выглядеть так:

1. Умножаем 7 на 3 (семерку мы взяли из разряда единиц первого многозначного множителя): 7·3=21. Мы получили число больше десяти, значит, записываем с правого края число 1 (значение единичного разряда числа 21), а двойку запоминаем. Наша запись принимает вид:

2. После этого мы перемножаем значения десятков первого множителя на второй и прибавляем к результату двойку, оставшуюся от предыдущего этапа. Если после этого получается меньше 10, то вносим значения под соответствующий разряд, если больше – вносим значение единицы и переносим десятки дальше. В нашем примере нужно умножить 2·3, это будет 6. Добавляем оставшиеся с прошлого умножения десятки (от числа 21, как мы помним): 6+2=8. Восьмерка меньше десятки, значит, в следующий разряд переносить ничего не надо. Записываем 8 на нужное место и получаем:

3. Дальше действуем аналогично. Теперь нам надо умножить значения разряда сотен в первом многозначном множителе на исходный однозначный. Порядок действий тот же: если запоминали число на предыдущем этапе, плюсуем его к результату, сравниваем с десяткой и записываем в правильное место.

Здесь нужно умножить 3 на 0. Согласно правилам умножения, результат будет равен 0. Прибавлять ничего не будем, так как на предыдущем этапе число было меньше 10. Получившийся нуль также меньше десятки, поэтому пишем его на место под горизонтальную черту:

4. Переходим к следующему разряду – умножаем тысячи. Продолжаем подсчеты по алгоритму до тех пора, пока не кончатся цифры в многозначном множителе.

Осталось умножить 5·3 и получить 15. Результат больше 10, пишем пятерку и запоминаем десяток:

Нам осталось только перемножить 4·3, это будет 12. Добавляем к результату единицу, взятую из предыдущего подсчета. 13 больше 10, пишем 3 на нужное место и сохраняем единицу.

У нас больше не осталось разрядов, которые надо перемножить, однако единица в запасе все еще есть. Мы просто запишем ее под горизонтальную черту с левой стороны от всех уже имеющихся там цифр:

Процесс подсчета с помощью столбика на этом завершен. Мы получили шестизначное число, которое и является верным решением нашей задачи.

Ответ: 45 027·3 = 135 081.

Чтобы было более понятно, мы представили алгоритм умножения многозначного натурального числа на однозначное в виде схемы. Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:

Как быть, если в условии задачи стоит многозначное число, которое заканчивается нулем (или несколькими нулями подряд)? Рассмотрим на примере пошагово. Чтобы было проще, позаимствуем цифры из предыдущей задачи и просто допишем к исходному многозначному множителю пару нулей.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 3

Условие: подсчитать, сколько будет 4 502 700·3.

Решение

Cначала запишем числа нужным способом.

После этого проводим подсчеты, не обращая внимания на нули справа. Возьмем результаты из предыдущей задачи, чтобы не считать еще раз:

Финальный шаг решения – переписать имеющиеся в многозначном числе нули под горизонтальную черту в область результата. У нас нужно внести 2 дополнительных нуля:

Это число и будет ответом нашей задачи. На этом умножение столбиком завершено.

Ответ: 4 502 700·3 =13 508 100.

Как перемножить столбиком два многозначных натуральных числа

Этот способ вполне подходит и для тех случаев, когда оба множителя представляют собой многозначные натуральные числа. Разберем процесс сразу на примере, как и раньше. Сначала возьмем числа без нулей в конце, а потом рассмотрим и записи с нулями.

Пример 4

Условие: вычислить, сколько будет 207·8 063.

Решение

Начнем, как всегда, с правильной записи множителей. Более удобным является способ записи, при котором множитель с большим количеством знаков стоит сверху. Так что запишем сначала 8 063, а под ним 207. Если число знаков в множителях совпадает, то порядок записи не имеет значения. В нашей задаче нам надо разместить цифры первого множителя под цифрами второго справа налево:

Начинаем последовательно перемножать значения разрядов. При этом у нас будут получаться результаты, которые называются неполными произведениями.

1. Первый шаг состоит в том, что нам надо перемножить между собой значения единиц в первом и втором множителе. В нашем случае это 3 и 7. Все делаем так же, как мы уже объясняли в предыдущем пункте (если нужно, прочитайте его еще раз). В итоге у нас получится первое неполное произведение, которое является промежуточным результатом:

2. Второй шаг заключается в перемножении значений десятков. Умножаем столбиком первый множитель на значение разряда десятков второго множителя (при условии, что он не равен 0). Записываем результат под чертой под разрядом десятков. Если же во втором множителе на месте десятков стоит 0, то сразу переходим к следующему этапу.

3. Последующие шаги выполняем аналогично, перемножая по очереди значения нужных разрядов (если они не равны 0). Вносим результаты под черту.

Итак, нам надо умножить 8 063 на значения сотен в 207 (т.е. на два). Мы получили второе неполное произведение, запишем его так:

У нас получились все нужные нам неполные произведения. Их количество равно числу разрядов во втором множителе (кроме 0). Последнее, что нам осталось сделать, – это сложить два произведения в столбик, используя ту же запись. Мы никуда не переписываем цифры: они остаются с тем же сдвигом влево. Подчеркнем их дополнительной горизонтальной чертой и поставим слева плюс. Складываем согласно уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10, и прибавляем их на следующем этапе). В нашей задаче получится:

Получившееся под чертой семизначное число – это и есть нужный нам результат умножения исходных натуральных чисел.

Ответ: 8 063·207 = 1 669 041.

Процесс умножения двух многозначных чисел столбиков также можно представить в виде наглядной схемы:

Чтобы лучше закрепить материал, приведем решение еще одного примера.

Пример 5

Условие: умножьте 297 на 321.

Решение

Начинаем с правильной записи множителей. Количество знаков в них одинаковое, так что порядок записи особого значения не имеет:

1. Первый этап – умножаем 297 на 1, которая стоит в разряде единиц второго множителя.

2. Потом умножаем таким же образом первый множитель на 2, что стоит в десятках второго множителя. Получаем второе неполное произведение:

3. Далее умножаем на значения сотен, т.е. 297 на 3:

4. У нас получилось три неполных произведения, которые надо сложить (для этого желательно повторить, как правильно складывать столбиком три числа и более). Считаем:

Ответ: 297·321 = 95 337.

Еще один пример приведем без пояснений.

Пример 6

Условие: вычислите 210 627·30 105.

Решение

Весь процесс вычислений указан в записи ниже.

Ответ: 210 627·30 105 = 6 340 925 835.

В целом можно сказать, что если вы отлично владеете способностью умножать однозначные числа и умеете складывать столбиком, то процесс умножения многозначных натуральных чисел указанным методом не будет представлять для вас никакого труда.

У нас остался еще один момент, который мы хотели бы пояснить. Как быть, если один из множителей или оба сразу имеет в конце нуль (или несколько нулей)? Для наглядности возьмем такую задачу и решим ее.

Пример 7

Условие: вычислите 50 600·390.

Решение

Все, что нам надо сделать, – это записать множители так, чтобы друг под другом оказались цифры, отличные от нуля.

После этого мы можем просто провести все вычисления по указанному выше алгоритму, игнорируя нули. Т.е. в данном примере нам нужно просто умножить 506 на 39. Получаем два неполных произведения и складываем их:

Нам осталось все лишь дописать к результату оставшиеся нули. Мы добавляем их столько, сколько указано справа у обоих множителей. В нашем примере к готовому числу надо написать три нуля:

Это и будет корректный ответ.

Ответ: 50 600·390 = 19 734 000.

Умножение в столбик | ПОЛЕЗНЫЕ ПРОГРАММЫ ДЛЯ УЧЕБЫ И РАБОТЫ

Описание

Примеры на умножение в столбик решать просто. Но они требуют концентрации и внимания, особенно для очень торопливых детей. Практика счета таких примеров поможет развить внимательность и закрепить навыки счета больших чисел, а также добиться автоматизированного счета.

Программа представляет собой тренажер для счета. Она имеет внутренние настройки, изменяя которые можно создать примеры для детей разного возраста и уровня подготовки: на однозначное , двузначное  или трехзначное число.

Поэтому программа будет полезна как для учеников начальной школы 3-4 классов, так и для более старших классов.

Программа счета написана в Excel с помощью макросов. Формируются примеры на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. При записи примеров разряды чисел формируются друг под другом, что позволяет легко ориентироваться в примерах.  В конце карточки формируются ответы на примеры, которые после печати карточки можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.

Генератор примеров по математике будет очень удобен как для родителей, так и для учителей: не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.

Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.

Другие программы, которые помогут закрепить навыки счета:

 Также есть программы, в которых можно выбрать уровень сложности.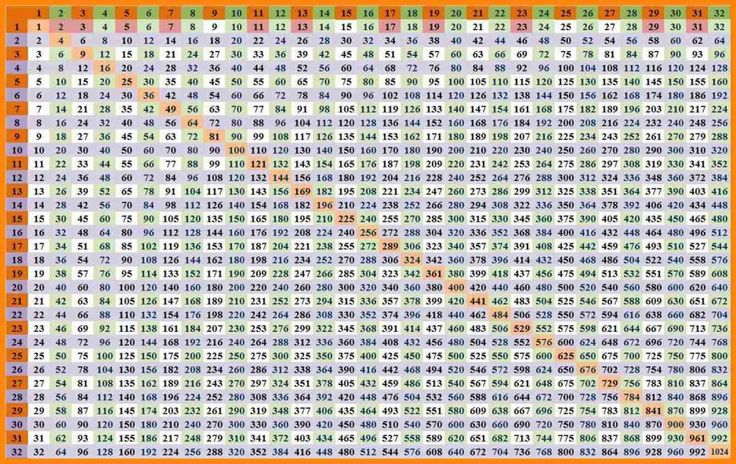 В них можно начать с решения легких примеров, а затем перейти к более сложным.

На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

 

Игра решение столбиком. Умножение столбиком

Онлайн игра-тренажёр «Умножение столбиком» помогает научиться умножать двух- и трёхзначные числа. Эта игра ориентирована на детей от 7 до 10 лет. Умножение чисел столбиком — это программа математики за 3 класс школы. Но в этом действии нет ничего сложного, поэтому освоить умножение в столбик можно и раньше.

Как научиться умножать столбиком?

В игре представлены три уровня: умножение двузначного числа на двузначное (числа от 10 до 99), умножение трёхзначного числа на трёхзначное (числа от 100 до 999) и микс. В миксе трёхзначное число умножается на двузначное или двузначное умножается на трёхзначное.

Чтобы правильно умножать двух- и трёхзначные числа надо хорошо знать и .

Надеюсь, ты помнишь, что числа, которые умножаются друг на друга называются множителями: первый множитель, второй множитель и так далее. Результат умножения называется произведением. Также полагаю, что тебе известно, что в числах есть разряды: единицы (самый маленький), десятки, сотни, тысячи…

Итак, приступим. Начать умножение в столбик надо с того, что расположить множители таким образом, чтобы друг под другом оказались числа одинаковых разрядов: единицы под единицами, десятки под десятками и так далее. На следующем шаге берём цифру из разряда единиц второго множителя и умножаем её по очереди на каждую цифру первого множителя. Результат умножения каждой пары цифр записываем в верхнюю строку под соответствующим разрядом.

За каждый правильный ответ начисляется 1 балл. За неправильный — отнимается 3 балла.

Если тебе понравилась эта игра, обязательно поделись ею со своими друзьями. Ведь им она тоже может понравиться:-)

Эта игра предназначена и чрезвычайно полезна для мальчиков и девочек от 7 до 10 лет.

С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!

Учить таблицу умножения — игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Смотрите ниже шпаргалки в полной форме.


Умножение прямо на сайте (онлайн)

*

Таблица умножения (числа от 1 до 20)
×1234567891011121314151617181920
11234567891011121314151617181920
2246810121416182022242628303234363840
33691215182124273033363942454851545760
448121620242832364044485256606468727680
55101520253035404550556065707580859095100
66121824303642485460667278849096102108114120
7714212835424956637077849198105112119126133140
881624324048566472808896104112120128136144152160
9918273645546372819099108117126135144153162171180
10102030405060708090100110120130140150160170180190200
11112233445566778899110121132143154165176187198209220
121224364860728496108120132144156168180192204216228240
1313263952657891104117130143156169182195208221234247260
1414284256708498112126140154168182196210224238252266280
15153045607590105120135150165180195210225240255270285300
16163248648096112128144160176192208224240256272288304320
171734516885102119136153170187204221238255272289306323340
181836547290108126144162180198216234252270288306324342360
191938577695114133152171190209228247266285304323342361380
2020406080100120140160180200220240260280300320340360380400

Как умножать числа столбиком (видео по математике)

Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.

В этой игре мы будем учиться складывать столбиком числа до 100. Яркие картинки и подробные пояснения помогут легко понять и запомнить алгоритм сложения столбиком. А тренажер поможет закрепить тему.

Прежде всего нужно запомнить, что при решении примеров на сложение столбиком большее число записывается сверху, а меньшее — под ним. Числа записываются так, чтобы единицы были под единицами, а десятки (если они есть) — под десятками.

Сначала складывают единицы, а затем десятки, при этом возможно 2 варианта:

Если при сложении единиц получается однозначное число, мы просто записываем его под чертой под единицами. Если же при сложении единиц получается двузначное число, включая 10, мы записываем под единицами только вторую цифру(единицы), а 1 (десяток) прибавляем к десяткам.

Первый вариант описан и проиллюстрирован в уроке 1, а второй вариант — в уроке 2 нашей обучающей онлайн игры «Сложение столбиком». После просмотра уроков порешайте примеры на сложение столбиком самостоятельно в разделе «Тренажер»

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

    Найти сумму цифр делимого.

    Поделить на 3 или 9 (в зависимости от того, что вам нужно).

    Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень
Средний уровень
Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту.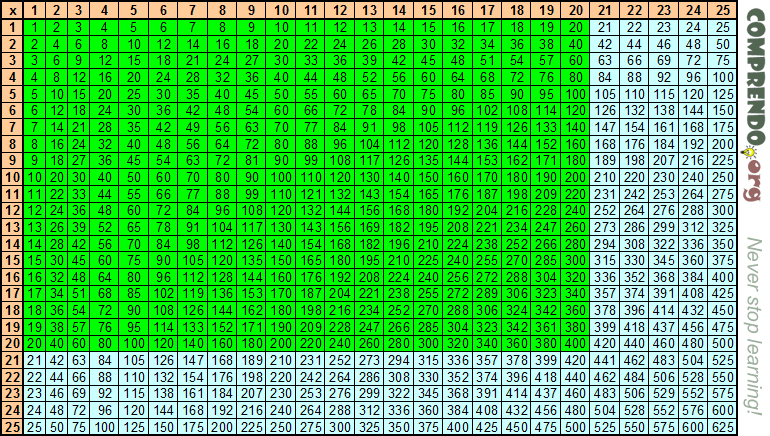 В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Решётчатое умножение | Наука и жизнь

Чтобы освоить умножение многозначных чисел, нужно всего лишь знать таблицу умножения и уметь складывать числа. В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения). Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.

Умножение способом решётки. Иллюстрация из первой печатной книги по арифметике. 1487 год.

Палочки Непера. Этот простой счётный прибор впервые был описан в сочинении Джона Непера «Рабдология». 1617 год.

Джон Непер (1550—1617).

Модель счётной машины Шиккарда. Это не дошедшее до нас вычислительное устройство изготовлено изобретателем в 1623 году и описано им годом позже в письме Иоганну Кеплеру.

Вильгельм Шиккард (1592—1635).

‹

›

Наследие индусов — способ решётки

Индусы, с давних времён знавшие десятичную систему счисления, предпочитали устный счёт письменному. Они изобрели несколько способов быстрого умножения. Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, — умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.

Этим способом пользовались ещё в древности, в Средние века он широко распространился на Востоке, а в эпоху Возрождения — в Европе. Способ решётки именовали также индийским, мусульманским или «умножением в клеточку». А в Италии его называли «джелозия», или «решётчатое умножение» (gelosia в переводе с итальянского — «жалюзи», «решётчатые ставни»). Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями-жалюзи, которые закрывали от солнца окна венецианских домов.

Суть этого нехитрого способа умножения поясним на примере: вычислим произведение 296 × 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, — по количеству цифр в множителях. Разделим клетки пополам по диагонали. Над таблицей запишем число 296, а с правой стороны вертикально — число 73. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.) Ответ: 21 608. Итак, 296 x 73 = 21 608.

Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.

Почему способ решётки приводит к правильному ответу? В чём заключается его «механизм»? Разберёмся в этом с помощью таблицы, построенной аналогично первой, только в этом случае множители представлены как суммы 200 + 90 + 6 и 70 + 3.

Как видим, в первой косой полосе стоят единицы, во второй — десятки, в третьей — сотни и т. д. При сложении они дают в ответе соответственно число единиц, десятков, сотен и т.д. Дальнейшее очевидно:

Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так:


296 x 73 = (200 + 90 + 6) x (70 + 3) = 14 000 + 6300 + 420 + 600 + 270 + 18 = 10 000 + (4000 + 6000) + (300 + 400 + 600 + 200) + (70 + 20 + 10) + 8 = 21 608.

Палочки Непера

Умножение способом решётки лежит в основе простого и оригинального счётного прибора — палочек Непера. Его изобретатель Джон Непер, шотландский барон и любитель математики, наряду с профессионалами занимался усовершенствованием средств и методов вычисления. В истории науки он известен, прежде всего, как один из создателей логарифмов.

Прибор состоит из десяти линеек, на которых размещена таблица умножения. В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней — число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек Непера легко умножать многозначные числа, сводя эту операцию к сложению.

Например, чтобы вычислить произведение чисел 296 и 73, нужно умножить 296 на 3 и на 70 (сначала на 7, затем на 10) и сложить полученные числа. Приложим к неподвижной линейке три другие — с цифрами 2, 9 и 6 наверху (они должны образовать число 296). Теперь заглянем в третью строку (номера строк указаны на крайней линейке). Цифры в ней образуют уже знакомый нам набор.

Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, рассмотрев седьмую строку, найдём, что 296 x 7 = 2072, тогда 296 x 70 = 20 720. Таким образом,
296 x 73 = 20 720 + 888 = 21 608.

Палочки Непера применялись и для более сложных операций — деления и извлечения квадратного корня. Этот счётный прибор не раз пытались усовершенствовать и сделать более удобным и эффективным в работе. Ведь в ряде случаев для умножения чисел, например с повторяющимися цифрами, нужны были несколько комплектов палочек. Но такая проблема решалась заменой линеек вращающимися цилиндрами с нанесённой на поверхность каждого из них таблицей умножения в том же виде, как её представил Непер. Вместо одного набора палочек получалось сразу девять.

Подобные ухищрения в самом деле ускоряли и облегчали расчёты, однако не затрагивали главный принцип работы прибора Непера. Так способ решётки обрел вторую жизнь, продлившуюся ещё несколько столетий.

Машина Шиккарда

Учёные давно задумывались над тем, как переложить непростую вычислительную работу на механические устройства. Первые успешные шаги в создании счётных машин удалось осуществить только в XVII столетии. Считается, что раньше других подобный механизм изготовил немецкий математик и астроном Вильгельм Шиккард. Но по иронии судьбы об этом знал лишь узкий круг лиц, и столь полезное изобретение более 300 лет не было известно миру.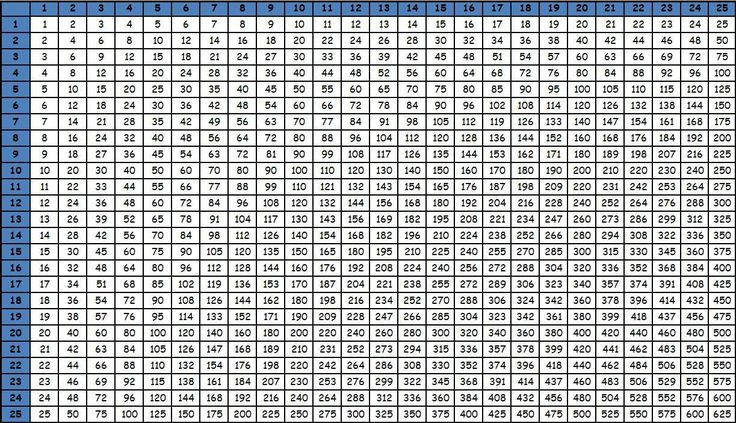 Поэтому оно никак не повлияло на последующее развитие вычислительных средств. Описание и эскизы машины Шиккарда были обнаружены всего полвека назад в архиве Иоганна Кеплера, а чуть позже по сохранившимся документам была создана её действующая модель.

По сути, машина Шиккарда представляет собой шестиразрядный механический калькулятор, выполняющий сложение, вычитание, умножение и деление чисел. В ней три части: множительное устройство, суммирующее устройство и механизм для сохранения промежуточных результатов. Основой для первого послужили, как нетрудно догадаться, палочки Непера, свёрнутые в цилиндры. Они крепились на шести вертикальных осях и поворачивались с помощью специальных ручек, расположенных наверху машины. Перед цилиндрами располагалась панель с девятью рядами окошек по шесть штук в каждом, которые открывались и закрывались боковыми задвижками, когда требовалось увидеть нужные цифры и скрыть остальные.

В работе счётная машина Шиккарда очень проста.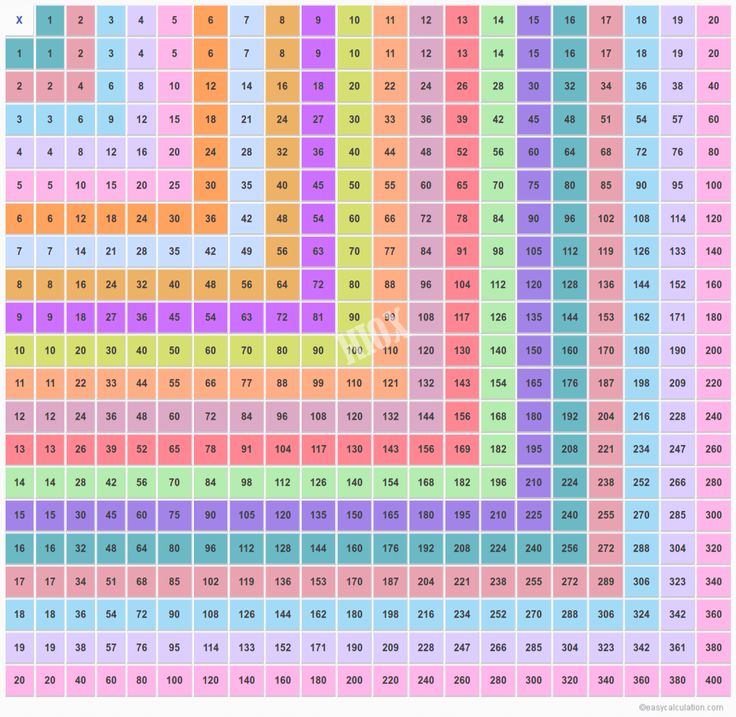 Чтобы узнать, чему равно произведение 296 x 73, нужно установить цилиндры в положение, при котором в верхнем ряду окошек появится первый множитель: 000296. Произведение 296 x 3 получим, открыв окошки третьего ряда и просуммировав увиденные цифры, как в способе решётки. Точно так же, открыв окошки седьмого ряда, получим произведение 296 x 7, к которому припишем справа 0. Остаётся только сложить найденные числа на суммирующем устройстве.

Придуманный некогда индусами быстрый и надёжный способ умножения многозначных чисел, много веков применявшийся при расчётах, ныне, увы, забыт. А ведь он мог бы выручить нас и сегодня, если бы под рукой не оказалось столь привычного всем калькулятора.

Запиши произведения столбиком и выполни умножение. Умножение натуральных чисел столбиком: примеры, решения

Перемножать большие числа, записывая их в строку, рано или поздно становится довольно сложным и утомительным процессом. Гораздо проще воспользоваться специальным алгоритмом по умножению в столбик: вам не придется держать числа в своей голове и что-либо запоминать. Вы можете делать пометки над столбиком, чтобы всегда видеть, как числа вам нужно перенести. Если вы пытаетесь обучить такому способу ребенка, то очень важно, чтобы таблица умножения отскакивала у него от зубов, иначе, процесс затянется надолго, а сам малыш совершит много ошибок, которые вереницей потянутся по всему примеру. Внимательно прочитайте статью и возьмите такой алгоритм себе на вооружение.

Запишите пример в строчку и посмотрите: какой из множителей меньше? Меньший окажется ниже в записи умножения в столбик, а большой множитель будет стоять наверху.

Запишите пример по такому принципу, как указано на картинке ниже.

  • Сверху напишите большее число.
  • Слева поставьте знак умножения в виде крестика.
  • Снизу запишите меньшее число.
  • Проведите прямую черту под примером.

Если в примере есть множитель, который оканчивается на ноль или несколько нолей, то его следует записывать так:

  • Ноли нужно выносить за пример.
  • Числа пишите под числами.

В таком случае, вы просто переносите это количество нолей сразу в ответ. Если ноли имеются и у первого множителя, и у второго, то сложите их количество и запишите в ответ.

Теперь начинайте расчёт по такому принципу:

  • Всё верхнее число вы умножаете на последнюю цифру нижнего. Помните, что на последние ноли умножение не производится.
  • Чтобы вам было удобнее, записывайте числа, которые нужно перенести, сверху над всем примером. Позднее вы можете их просто стереть, зато в процессе вам не придется запоминать числа переноса.
  • Как только вы закончите расчет, запишите полученное число под чертой.

Как только вы перемножите верхнее число на последнюю цифру нижнего и запишите свой ответ, начинайте перемножать следующее.

По такому же принципу умножьте всё верхнее число на вторую с конца цифру нижнего. Также записывайте числа переноса, однако, ответ вам следует записать под первым решением, но сдвинув запись на одну клеточку левее. У вас получится столбик с выступающей влево строкой.

Как вы уже догадались, вам нужно перемножить верхнее число на все цифры нижнего, начиная с конца. Каждый раз запись ответа переносится на одну клетку левее.

Перемножьте таким образом все числа между собой. Теперь снова проведите черту под столбиком. Между всеми решениями поставьте знак сложения.

Теперь вам осталось выполнить сложение в столбик, которое вы уже должны уметь делать:

  • Складывайте все числа, находящиеся на одной вертикальной линии.
  • Если число получается двухзначным, то число десятков вы переносите в следующую вертикальную полосу.

Под некоторыми числами вовсе не будет других – в таком случае, вы просто записываете это число в ответ. Не забывайте переносить в ответ все нули, которые стоят в конце множителей.

Выполнять умножение в столбик очень удобно и быстро, особенно, если требуется перемножить большие числа. Вы легко можете проверить правильность умножения, просто разделив ответ на один из множителей. Для этого используйте калькулятор, либо способ деления уголком. На первых порах такое умножение занимает значительную долю времени, но с опытом, всё действие происходит всего за пару секунд.

Если вы уже запамятовали, как умножать цифры в столбик, то прочитайте статью. Тут вы найдете всю информацию об этом математическом действии.

Даже некоторые взрослые не освоили в школе, как можно умножать числа в столбик. А ведь это умение может и пригодиться в жизни, если не будет под рукой калькулятора или мобильного телефона.

Тем более, что это совсем не трудно, если вы знаете таблицу умножения и поняли, как правильно располагать цифры при данном процессе. Умножение в столбик всегда начинают изучать с умножения многозначного числа на однозначное, чтобы понять правила данного действия. Далее подробней.

Правила и алгоритм умножения в столбик

Математические занятия многим детям даются не с первого раза. Это непростая наука, требующая особого внимания, понимания. И ученикам в начальных классах в обязательном порядке необходима помощь мамы и папы в решении сложных примеров, задач. В частности нельзя все оставлять на самотеке, если ваше чадо не поняло, что такое умножение, деление чисел и т.п. Надо помочь разобраться в теме и выучить таблицу умножения, чтобы потом не получать плохие оценки, и не расстраиваться.

Освоить умножение в столбик будет легко, если:

  • Школьник отлично знает таблицу умножения. Не путается в значениях произведения.
  • Уяснил, в какой последовательности следует перемножать цифры многозначного числа.
  • Ребенок понял, где их правильно писать. И умеет производить сложение многочленов в столбик.

Нужно знать, правило, что от перемены мест множителей произведение не меняется. Точнее, если умножить 56 ⋅ 2 = 112 и 2 ⋅ 56 = 112 — произведение будет 112.

ВАЖНО : Когда перемножают цифры в столбик. Под низом пишут то число, которое имеет меньше цифр в своем составе.

Как правильно умножать в столбик трехзначные числа на однозначные, двузначные, трехзначные

Любое умножение — это сложение одинаковых цифр необходимое количество раз. Точнее 725 ⋅ 2 = 725 + 725 = 1450. Но такой пример можно сделать устно, если второе число — 2,3,4. А если это — 8, то перемножать уже лучше в столбик. Для этого:

  1. Вверху нужно написать цифру 725 , а внизу под цифрой — 5 написать число — 8 .
  2. Теперь нужно поочередно, начиная с 5 , все значения трёхзначного числа перемножить на 8 .
  3. Точнее: 5 ⋅ 8 = 40 (ноль пишем ниже под восьмеркой и пятеркой, а — 4 запоминаем ).
  4. Далее умножаем: 2 ⋅ 8 = 16 (к 16 прибавляем — 4 = 20, опять 0 пишем, только уже под двойкой, а — 2 запоминаем ).
  5. Остается умножить: 7 ⋅ 8 = 56 (к 56 прибавляем — 2 = 58, восьмерку пишем под семеркой, а пять впереди ).
  6. В результате такого умножения (725 ⋅ 8 ) получатся — 5800 . И этот расчет получен вручную, без каких-либо машинок, калькуляторов.

Умножение в столбик — трехзначное на трехзначное

Умножить многочлен на многочлен несколько сложнее. Однако, если вы уже в первом примере уяснили, как происходит процесс, то вам не составит труда перемножить и трехзначные числа, а потом сложить в столбик, получившиеся значения.

Рассмотрим в подробностях, как умножить 125 на 32

  1. Вверху на листке напишите трехзначное число 125, под ним 32, причем расположите его следующим образом: тройку под двойкой первого числа , а двойку второго под пятеркой первого числа — это очень важно.
  2. Начните перемножать с конца. То есть: перемножьте все цифры трехзначного числа (125) вначале на двойку .
  3. У вас получится 250 , ноль напишите под двойкой , остальные цифры впереди.
  4. Далее перемножайте 125 на три . И располагайте на листике значение произведения (375 ), начиная с цифры — 3 .
  5. Теперь остается сложить 250 и 375(0) , получится 250 + 3750 = 4000.

ВАЖНО : Как перемножить трёхзначные числа наглядно можно увидеть на рисунке выше. Цифры перемножаются в строгой последовательности, начиная с конца, а потом все получившиеся значения складываются.

Как правильно умножать в столбик числа с нулями?

Уже из математики начальных классов любой ученик знает, что, если умножить любое число на ноль, то произведение будет тоже 0. Именно поэтому, когда производится умножение в столбик, то на цифру ноль умножение не производится, его выносят за рамки, а в произведении приписывают ноль или несколько нулей — смотрите на изображении ниже.

Как объяснить ребенку умножение столбиком?

  • Если вы дома решили провести урок по математике, изучить, как производить умножение в столбик, то превратите ваше занятие в игру.
  • Постепенно, терпеливо объясняя, как это делается. Отвечайте на все вопросы школьника, чтобы ему было понятно, что и за чем делать.
  • Дайте вначале для примеров несложные примеры, а потом уже выбирайте задания потруднее.

ВАЖНО : Уделяйте больше времени своим детям, не игнорируйте их просьбы о помощи. В школе учитель соблюдает программные требования. На закрепление материала дается не много времени. Поэтому не все школьники успевают освоить программу, тем более в таком сложном деле, как умножение, деление в столбик.

Видео: Примеры умножения многозначных чисел в столбик с пояснениями

Как умножать столбиком

Умножение многозначных чисел обычно выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.

Рассмотрим для начала умножение многозначного числа на однозначное. Пусть требуется умножить 846 на 5:

Умножить 846 на 5 — значит, сложить 5 чисел, каждое из которых равно 846. Для этого достаточно взять сначала 5 раз по 6 единиц, потом 5 раз по 4 десятка и наконец 5 раз по 8 сотен.

5 раз по 6 единиц = 30 единиц, т. е. 3 десятка. Пишем 0 под чертой на месте единиц, а 3 десятка запоминаем. Для удобства, чтобы не запоминать можно написать 3 над десятками множимого:

5 раз по 4 десятка = 20 десятков, прибавляем к ним ещё 3 десятка = 23 десятка, т. е. 2 сотни и 3 десятка. Пишем 3 десятка под чертой на месте десятков, а 2 сотни запоминаем:

5 раз по 8 сотен = 40 сотен, прибавляем к ним ещё 2 сотни = 42 сотни. Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230:

Теперь рассмотрим умножение многозначных чисел. Пусть требуется умножить 3826 на 472:

Умножить 3826 на 472 — значит, сложить 472 одинаковых числа, каждое из которых равно 3826. Для этого надо сложить 3826 сначала 2 раза, потом 70 раз, потом 400 раз, т. е. умножить множимое отдельно на цифру каждого разряда множителя и полученные произведения сложить в одну сумму.

2 раза по 3826 = 7652. Пишем полученное произведение под чертой:

Это не окончательное произведение, пока мы умножили только на одну цифру множителя. Полученное число называется частичным произведением . Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.

Умножаем 3826 на 7. Это будет второе частичное произведение (26782):

Умножаем множимое на 4. Это будет третье частичное произведение (15304):

Под последним частичным произведением проводим черту и выполняем сложение всех полученных частичных произведений. Получаем полное произведение (1 805 872):

Если во множителе встречается нуль, то обычно на него не умножают, а сразу переходят к следующей цифре множителя:

Когда множимое и (или) множитель оканчиваются нулями, умножение можно выполнить не обращая на них внимания, и в конце, к произведению добавить столько нулей, сколько их во множимом и во множителе вместе.

Например, необходимо вычислить 23 000 · 4500. Сначала умножим 23 на 45, не обращая внимание на нули:

И теперь, справа к полученному произведению припишем столько нулей, сколько их во множимом и во множителе вместе. Получится 103 500 000.

Калькулятор умножения столбиком

Данный калькулятор поможет вам выполнить умножение столбиком. Просто введите множимое и множитель и нажмите кнопку Вычислить.

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

Как работать с математическим калькулятором

Клавиша Обозначение Пояснение
5 цифры 0-9 Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
. точка (запятая) Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+ знак плюс Сложение чисел (целые, десятичные дроби)
— знак минус Вычитание чисел (целые, десятичные дроби)
÷ знак деления Деление чисел (целые, десятичные дроби)
х знак умножения Умножение чисел (целые, десятичные дроби)
√ корень Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x 2 возведение в квадрат Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1 / x дробь Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
% процент Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
( открытая скобка Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
) закрытая скобка Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
± плюс минус Меняет знак на противоположный
= равно Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
← удаление символа Удаляет последний символ
С сброс Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Возведение в квадрат целого числа { (3) 2 = 9 }

Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }

Перевод в десятичные дроби.
Вычисление процентов от числа

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Умножение в столбик позволяет быстро выдавать решение примеров даже с многозначными числами. Для счёта нужно только знать наизусть таблицу умножения.

Как правильно умножать столбиком

Как и в случае со сложением и вычитанием в столбик, при умножении числа записываются друг под другом. Каждый разряд на своём месте: единицы под единицами, десятки под десятками и т. д. Внизу рисуется горизонтальная черта, ответ пишется под ней.

Возьмём числа 78 и 12. Для лучшего понимания: пишем 78 наверху, 12 — внизу. Начинаем с единицы нижнего числа, то есть с цифры 2.

Сперва считаем 8×2=16. Число получилось больше 10, значит, как и в сложении, пишем последнюю цифру (6), а единицу держим в уме. Теперь переходим к десятку, то есть считаем 7×2=14. Единицу мы держали в уме, значит, сейчас прибавляем её к результату, получается 14+1=15. Цифра 5 пишется под десятками, а 1 переходит в новый разряд — сотни. Другими словами, под горизонтальной чертой должно быть написано «156».

Переходим к следующему разряду. Теперь наш ответ будет записываться иначе: последняя цифра ответа должна быть ровно под верхними десятками, то есть под цифрой 5. Получается, что каждое последующее промежуточное число смещается на 1 разряд влево.

Считаем 8×1=8. Цифра меньше 10, пишем 8 под пятёркой в числе «156». Считаем 7×1=7. Семёрка переходит в разряд сотен, то есть она должна быть написана под единицей в ответе «156». Под шестёркой ничего не написано, для удобства туда можно поставить ноль.

Полученное выражение складываем в столбик: 156+78. К 6 ничего не прибавляется (0), значит, переписываем её в прежнем виде. Затем считаем 5+8=13, пишем 3, один в уме. Наконец, 1+7=8, прибавляем единицу — получается 9.

Таким образом, ответ: 936.

Тренироваться лучше на листе в клеточку, чтобы привыкнуть к расположению разрядов множителей

Точно так же умножаются и другие многозначные числа.

Если в множителях есть нули, они не перемножаются, а просто переносятся в правую часть окончательного ответа.

Варианты карточек

Для наглядности можно распечатать карточки с примерами разного уровня сложности. Так детям будет проще запомнить принцип счёта. Примеры для практики можно использовать и при первом изучении умножения, и для повторения после каникул.

Поначалу решение примеров будет занимать много времени, но постепенно скорость повысится. Даже при наличии калькулятора лучше считать вручную: это развивает умственную деятельность.

Фотогалерея: примеры карточек для урока
Видео: умножение чисел в столбик

Постоянная практика — залог успеха, и со временем можно научиться перемножать в уме даже большие числа. Но начинать, конечно, лучше с простых примеров, постепенно увеличивая уровень сложности.

Длинное умножение — калькулятор, метод, процедура, примеры и часто задаваемые вопросы

Вы можете спросить, что такое длинное умножение. Чтобы ответить на ваш вопрос, это способ найти произведение огромных чисел. Теперь вы можете подумать, что это сложная задача, не беспокойтесь, мы предоставим вам самое простое объяснение, чтобы вы легко разобрались в теме.

Стратегия, используемая для решения задач умножения больших чисел, — это длинное умножение. Длинное умножение — это тип умножения, который в мире широко преподают ученикам начальной школы.

Калькулятор длинного умножения

Умножение выполняется с помощью множимого и множителя для аппроксимации переменной методом длинного умножения положительных или отрицательных целых или десятичных чисел. Для Стандартного алгоритма задача отображается в решении. После выравнивания младших значащих цифр числа для умножения располагаются вертикально друг над другом. Если вы знаете наизусть таблицу умножения, это действительно поможет вам увеличить скорость.

Метод длинного умножения

  1. Расположите числа друг над другом и выровняйте столбцы со значениями местоположения. Обычно в качестве множимого сверху ставится число с наибольшим количеством цифр.

  2. Умножьте множитель, начиная с одной цифры нижнего числа, на последнюю цифру верхнего числа.

  3. Напишите решение под эквивалентной линией.

  4. Если ответ больше девяти, запишите ответ в одной позиции и удерживайте десятки цифр.

  5. Всегда двигайтесь справа налево. Умножьте цифры верхнего числа с нижнего числа на следующую цифру слева. Прикрепите его к результату, если вы держали цифру, и напишите ответ под линией равенства. Сделайте это, если вам нужно снова подержать его.

  6. Переход к разряду десятков в нижнем числе, когда вы умножили одну цифру на каждую цифру в верхнем числе.

  7. Умножьте, как и раньше, но на этот раз запишите ответы в новой строке, сдвинув на одну цифру влево.

  8. По окончании умножения нарисуйте еще одну линию ответов под последним рядом номеров ответов.

  9. Чтобы добавить числовые столбцы справа налево, используйте длинное сложение с переносом, как обычно для длинного сложения.

Длинные шаги умножения

Шаг 1: Расположите числа сверху большим числом. Выровняйте числа по столбцам разряда.

Шаг 2: Умножьте каждую цифру нижней части на цифры с верхней цифрой.

Шаг 3: переключитесь на одну точку влево. Умножьте десятки, поместите цифры нижнего числа на каждую цифру верхнего числа.

Шаг 4: Используя длинное сложение, складывайте числа в формате столбца.

(Изображение будет скоро загружено)

Примеры длинного умножения

1. 5249 x 61

Решение:

Здесь 5249 — множимое, а 61 — множитель.

Следовательно, при умножении получаем 320189.

(Изображение будет загружено в ближайшее время)

2. 5156 x 61

Решение:

Здесь 5156 — множимое, а 61 — множитель.

Следовательно, при умножении получаем 314516.

(Изображение будет загружено в ближайшее время)

3. 9802 x 46

Решение:

Здесь 9802 — множимое, а 46 — множитель.

Следовательно, при умножении получаем 450892.

(Изображение будет загружено в ближайшее время)

4. 3920 x 45

Решение:

Здесь 3920 — множимое, а 45 — множитель.

Следовательно, при умножении мы получаем 176400.

(Изображение будет загружено в ближайшее время)

5. 505 x 117

Решение:

Здесь 505 — это множимое, а 117 — множитель.

Следовательно, при умножении мы получаем 59085.

(Изображение будет загружено в ближайшее время)

Заключение

Длинное умножение — это метод нахождения произведения двух больших чисел. Он может включать произведение трехзначного числа на двузначное, трехзначного числа на трехзначное или четырехзначного числа.Операции выполняются в формате столбца. Его можно расширить до двух произвольно больших чисел или до количества десятичных цифр.

Чтобы умножать такие огромные числа, важно изучить метод длинного умножения. Хотя есть несколько способов умножения больших чисел, некоторые из них:

Однако другие методы немного сложны, и они будут рассмотрены в более высоких классах.

Длинное умножение (ключевой этап 2)

Что такое длинное умножение? (Интерактивный виджет)

Используйте этот интерактивный виджет , чтобы просмотреть пошаговое объяснение длинного умножения.

Это случайно сгенерированная сумма длинного умножения.

Решить сейчас

Пройти шаг за шагом

Сгенерировать новую сумму

Посмотрите похожие виджеты на длинное сложение, длинное вычитание и длинное деление.

Что такое длинное умножение?

Длинное умножение — это метод умножения чисел.

Длинное умножение включает в себя запись умножаемых чисел одно под другим, чтобы цифры располагались в столбцах.

Таким способом можно умножить множество чисел любой длины.

Реальный пример того, как сделать длинное умножение

Произвести длинное умножение легко.

Умножьте числа, указанные ниже.

Пошаговая инструкция:

Напишите числа, которые вы хотите умножить, одно под другим.

Найдите крайнюю правую цифру нижнего числа (в столбце единиц).

Найдите крайнюю правую цифру верхнего числа (в столбце единиц).

Умножьте нижнюю цифру (4) на верхнюю цифру (5).

Проверьте, соответствует ли ответ Step 4 9 или меньше:

№ . 20 — это , а не 9 или меньше.

Переместите цифру влево в верхнем числе.

Проверьте, соответствует ли ответ Step 7 9 или меньше:

№ . 10 — это , а не 9 или меньше.

Переместите цифру влево в верхнем числе.

Слева больше нет цифр.

Напишите переносимую цифру под линией.

Напишите 0 справа в новой строке под линией.

Переместите цифру влево в нижнем числе (в столбце десятков).

Найдите крайнюю правую цифру верхнего числа (в столбце единиц).

Умножьте нижнюю цифру (1) на верхнюю цифру (5).

Проверьте, соответствует ли ответ Step 4 9 или меньше:

Есть . 5 — это 9 или меньше.

Переместите цифру влево в верхнем числе.

Умножьте нижнюю цифру (1) на верхнюю цифру (2).

Проверьте, соответствует ли ответ Step 17 9 или меньше:

Есть . 2 — это 9 или меньше.

Переместите цифру влево в верхнем числе.

Слева больше нет цифр.

Ответ:

Решение 25 × 14 — 350.

Слайдер

Ползунок ниже показывает еще один реальный пример того, как выполнять длинное умножение.

Откройте слайдер в новой вкладке Помогите нам улучшить математику Монстр

  • Вы не согласны с чем-то на этой странице?
  • Вы заметили опечатку?

Сообщите нам, используя эту форму

См. Также

Как размножаться Как сделать длинное сложение Что такое размещаемая стоимость?

Длинное умножение на большие числа

Длинное умножение может использоваться для двух чисел произвольно большого размера или количества десятичных цифр.Мы также можем выполнять длинное умножение для меньших чисел. Помогает, если мы все знаем нашу 10-кратную таблицу умножения.

Теперь, если мы хотим умножить, скажем, 164×9, мы можем легко вычислить длинное умножение для меньших чисел, основываясь на наших знаниях таблицы умножения числа 9. Можно также умножить большие числа, используя тот же метод, который просто использует еще несколько шагов. Например, мы можем умножить 277×84. Самый простой способ выполнить длинное умножение — сначала написать длинное число, затем меньшее число непосредственно под ним с выровненными младшими знаками, а затем провести под ним горизонтальную линию.Верхнее число называется множимым, а нижнее число — множителем (в качестве множимого обычно выбирается число с большим количеством цифр). Результат умножения — произведение.

Пример:

Умножьте 277×84, используя длинное умножение.

Решение: 2 7 7

x 8 4

Чтобы начать вычисление, вы умножаете последнюю цифру множимого, равную 7 , на последнюю цифру множителя, 4 .Это дает 28 . Вы пишете цифру из единиц 28, 8 , под строкой в ​​конце столбца. Вы пишете цифру десятков 28, 2 , над множимым в следующем столбце. Опять же, это называется переносом 2 вперед:

2 7 2 7

х 8 4

8

Теперь вы переходите к следующей цифре множимого, которой является 7 , и умножаете ее на последнюю цифру множителя, 4 . Это дает 28 , но вы должны добавить 2 к 28, поскольку вы перенесли 2 вперед на предыдущем шаге, что дает нам 30 . Опять же, вы пишете единичную цифру 30, 0 , под линией рядом с 8, и переносите 3 вперед:

2 3 7 2 7

х 8 4

0 8

Наконец, вы переходите к первой цифре множимого, 2 , и умножаете ее на последнюю цифру множителя, 4 .Это дает 8 , но вы должны добавить 3 к 8, так как на предыдущем шаге вы перенесли 3 вперед, что дает нам 11 . Не нужно ничего переносить, так как мы закончили вычисление числа 4 в множителе, поэтому просто запишите 11 , но мы еще не закончили:

2 3 7 2 7

х 8 4

1 1 0 8

Теперь мы, по сути, начинаем умножение заново, переходя к следующей цифре множителя — 8.Прежде чем мы это сделаем, поскольку мы переходим к следующей цифре множителя, мы должны продолжить умножение на следующей строке, но сначала добавить ноль в первую цифру, а затем провести под ней горизонтальную линию:

2 7 7

х 8 4

1 1 0 8

0

(обратите внимание, что числа, которые ранее были перенесены, теперь удалены)

Теперь вы начинаете с умножения последней цифры множимого, равного 7 , на следующую цифру множителя, 8 . Это дает 56 . Вы пишете единственную цифру 56, 6 , над последней строкой рядом с 0 и переносите 5 вперед:

2 7 5 7

х 8 4

1 1 0 8

6 0

Теперь вы переходите к следующей цифре множимого, которой является 7 , и умножаете ее на следующую цифру множителя, 8 .Это дает 56 , но вы должны добавить 5 к 56, поскольку вы перенесли 5 вперед на предыдущем шаге, что дает нам 61 . Опять же, вы пишете единственную цифру 61, 1 , над последней строкой рядом с 6, и переносите 6 вперед:

2 6 7 5 7

х 8 4

1 1 0 8

1 6 0

Наконец, вы переходите к первой цифре множимого, 2 , и умножаете ее на следующую цифру множителя, 8 .Это дает 16 , но вы должны добавить 6 к 16, так как вы перенесли 6 вперед на предыдущем шаге, что дает нам 22 . Не нужно ничего переносить, так как мы закончили вычисление числа 8 в множителе, поэтому просто запишите 22 , но мы еще не закончили:

2 6 7 5 7

х 8 4

+ 1 1 0 8

2 2 1 6 0

Наш последний шаг — просто сложить последние два числа, полученные в результате умножения:

2 6 7 5 7

х 8 4

+ 1 1 0 8

2 2 1 6 0

2 3 2 6 8

Пример 1:

Пример 2:

Пример 3:

длинное умножение | GMAT бесплатно

Умножение «вручную» — это , необходимое для сдачи GMAT.Часто можно использовать уловки для упрощения вычислений, но некоторые из них придется выписать. Хорошая привычка — оставлять место на краю бумаги для заметок, которая будет вашей записной книжкой на GMAT, для длинного умножения и деления в столбик. В разделе «Количественный анализ» GMAT вам будет запрещено пользоваться калькулятором. В разделе «Интегрированное мышление» у вас будет встроенный калькулятор, но раздел «Количество» гораздо важнее, поскольку он входит в ваш общий балл 200–800.

Длинное умножение: метод

Для умножения двух многозначных чисел:

1. Выровняйте два числа по правому краю. Напишите два умножаемых числа одно под другим, выровняв их по крайним правым цифрам. Люди обычно помещают число с меньшим количеством цифр (в данном случае 32) внизу. Например, если мы хотим умножить 832 и 32, мы выстраиваем их так:

2. Умножьте верхнее число на нижнюю цифру единиц. Затем умножьте целое число в верхней строке на цифры внизу. Напишите результат с выравниванием по правому краю под полосой умножения.

3. Умножьте на нижнюю цифру десятков, добавив ноль. Затем умножьте целое число в верхней строке только на десятков цифр внизу.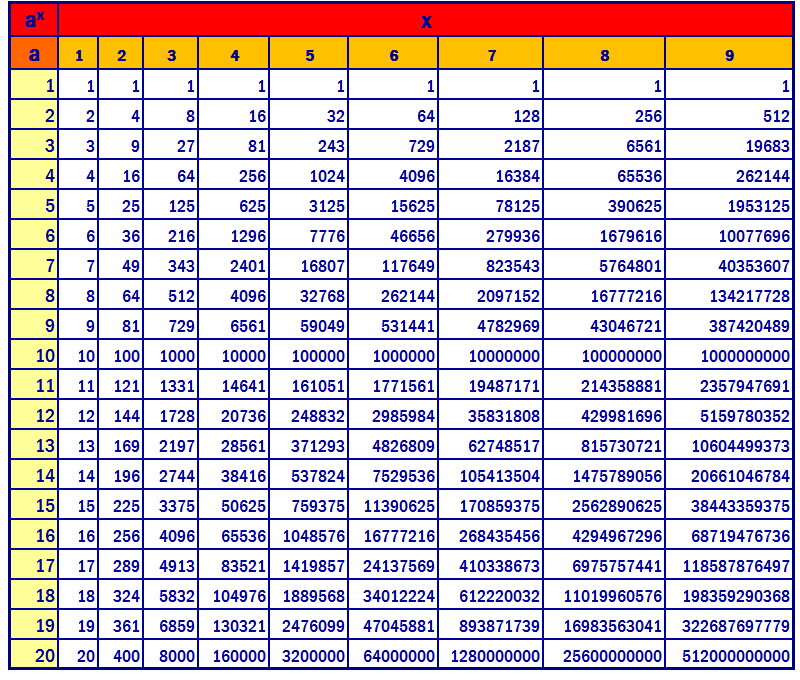 Поскольку вы умножаете на цифру десятков, вы добавляете ноль (или пустое место) к вашему результату и помещаете его под первым результатом:

4. Продолжайте умножать на старшие цифры и складывать нули , пока не закончите с цифрами меньшего числа, которое вы умножаете. В этом случае мы уже закончили умножение на 32, потому что 32 состоит только из трех цифр.

5. Добавьте частичные результаты , чтобы получить конечный продукт. В этом случае нам нужно сложить два числа.

6. При необходимости добавьте в ответ запятые и десятичную точку. Мы поговорим о десятичных точках чуть позже.В этом примере нам не нужна десятичная точка, хотя мы можем вставить запятую. И у нас есть результат: 832 умножить на 32 равно 26 624.

Наконец, мы можем проверить наш ответ, оценив. Число 832 примерно равно 800, а число 32 примерно 30. И 800 умноженное на 30 дает 24000. Этот продукт находится примерно в 26 624, поэтому наша оценка показывает, что мы не случайно где-то добавили или пропустили ноль.

Длинное умножение: сложение нулей

Нет ничего волшебного в том, что мы добавляем ноль к каждой строке умножения на цифры, которое мы делаем в ходе длительного умножения.Мы видим это на нашем примере:

Здесь 32 можно представить как 30 + 2:

И, как мы обсудим во вводных разделах по алгебре далее в этой книге, мы можем перемножить это выражение:

Круглые скобки в последнем выше не являются обязательными и были добавлены только для акцента. Подробнее об этом в разделе «Порядок действий». Второй член, 832 умноженный на 2, является началом нашего длительного умножения, первого частичного произведения:

И термин 832 умножить на 30 — это просто линия, которая идет под ним.Таким образом, действительно имеет лишний ноль, потому что, когда мы умножаем на цифру 3 в длинном умножении, мы действительно, можно сказать, умножаем на 30.

Длинное умножение: пример

В этом примере используется длинное умножение , чтобы умножить 23 958 233 и 5 830 и получить произведение 139 676 498 390.

Умножать числа легко. Вы можете записать два любых старых числа, выбирая их случайным образом или из квитанции о последней покупке кофе, и попробовать их умножить.Вы можете проверить продукт на своем телефоне или введя вычисление в поле поиска в Google (если вы введете вычисление в Google, он даст вам ответ).

Длинное умножение с десятичными знаками

Вы можете умножить два десятичных числа, игнорируя десятичные точки и добавляя десятичную точку обратно в результат. Чтобы снова добавить десятичную точку, подсчитайте количество цифр справа от десятичных точек двух исходных чисел; сумма двух отсчетов указывает количество цифр, которые будут присутствовать в произведении справа от десятичной точки.

Например, если у вас есть одно число с двумя цифрами после десятичной точки и другое число с одной цифрой после десятичной точки, их произведение будет иметь три цифры после десятичной точки. Так обстоит дело с умножением:

Обратите внимание, что это умножение идентично нашему первому примеру, за исключением добавления десятичных знаков. Десятичные разряды не влияют на умножение цифр. Итак, чтобы умножить 8,32 и 3,2, мы начнем с умножения 832 на 32.В конце мы снова добавляем общее количество пропущенных десятичных знаков — три — чтобы получить окончательный результат.

Опять же, мы можем оценить как способ перепроверить наш продукт. Число 8.32 — это около 8, а число 3.2 — около 3. Таким образом, их произведение должно быть примерно 24. Действительно, произведение, 26 плюс изменение, довольно близко к 24.

Десятичное умножение | Как умножить десятичные знаки

Вы уже научились умножать на десятичные дроби ? Сегодня мы собираемся рассмотреть три различных случая умножения с десятичными знаками.

Умножение с десятичными и целыми числами

В этом случае мы умножаем десятичную дробь на другое число без десятичных знаков, как в примере:

  • Шаг 1: Помещаем оба числа так, чтобы более длинный множитель был вверху, а более короткий множитель — внизу.
  • Шаг 2: Мы решаем задачу умножения так же, как обычно с целыми числами. После этого мы подсчитываем цифры , которые идут после десятичной точки в десятичной дроби, а мы помещаем десятичную точку в ответ так, чтобы после нее было такое же количество десятичных знаков, что и в десятичной дроби в позиции множителя.
Умножение, когда оба множителя десятичные

В данном случае оба множителя десятичные:

  • Шаг 1: Как и в предыдущем случае, первое, что нам нужно сделать, это разместить числа так, чтобы более длинный множитель был вверху, а более короткий множитель — внизу.
  • Шаг 2: Мы решаем задачу умножения так же, как обычно с целыми числами.После этого мы подсчитываем цифры, которые идут после десятичных знаков в обоих множителях. Ответ должен иметь столько десятичных знаков, сколько может быть найдено в обоих множителях вместе взятых.
Умножение с десятичными знаками и целым числом, заканчивающимся нулем

В этом случае множитель целого числа заканчивается нулем.

  • Шаг 1: Разбиваем число на другое число, умноженное на 10:
  • Шаг 2: Умножаем десятичное число на 10 (тем самым избавляясь от десятичного разряда).
  • Шаг 3: Мы размещаем чисел, и теперь мы можем умножить десятичное число на целое.

Умножение с десятичными знаками — это просто, не так ли?

Если вы хотите продолжить изучение математики с помощью Smartick, одновременно развлекаясь , нажмите на эту ссылку, чтобы подписаться на бесплатную пробную версию.

Подробнее:

Команда создания контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.

Рабочие листы для длинного умножения

Эта страница включает в себя рабочие листы «Длинное умножение» для студентов, которые усвоили основные факты об умножении и учатся умножать двузначные, трех-, четырех- и более значные числа. Вопросы на этих листах, которые иногда называют долгим умножением или многозначным умножением, требуют, чтобы учащиеся усвоили факты умножения от 0 до 9.

Существует множество стратегий для завершения длинного умножения, включая классические методы бумаги и карандаша, решеточное умножение (которое мы показываем на этой странице), умственные стратегии, манипулятивное использование, технологии и различные другие алгоритмы, связанные с бумагой и карандашом.Умножение нескольких цифр может быть неприятным для многих студентов. Попробуйте научить многозначное умножение, используя более одной стратегии.

Самые популярные рабочие листы для длинного умножения на этой неделе

Рабочий лист длинного умножения

Длинные рабочие листы для практики умножения, включая различные размеры чисел и варианты для различных числовых форматов.

Двузначное умножение — это естественное место, чтобы начать после того, как учащиеся усвоили свои факты умножения.Концепция умножения двузначных чисел требует знания места и значения места, особенно если учащиеся должны полностью понимать, чего они достигают с помощью различных стратегий, которые они используют. Такой вопрос, как 24 × 5, можно представить как (20 + 4) × 5. Мысленно это становится намного проще, когда учащиеся умножают 20 на 5, затем 4 на 5 и складывают два произведения. Хороший способ научиться понимать стоимость — использовать базовые десять блоков. Эти манипуляторы также очень хорошо применяются в стратегиях работы с бумагой, карандашом и ментальной математики.

Дополнительная цифра может сбить с толку одних учеников, но усложнить другим. Всегда следите за тем, чтобы ученики были готовы к трехзначному умножению, иначе вы и ваш ученик будете разочарованы. Рабочие листы для трехзначного умножения требуют владения фактами однозначного умножения и знания стратегии многозначного умножения, которая позволит учащимся как понять вопрос, так и получить правильный ответ. Четырехзначное умножение было изобретено в 350 году до нашей эры. как способ наказания детей, укравших хлеб с рынка.Просто шучу! На самом деле это большая проблема для студентов, которые добились успеха с фактами умножения и хорошо разбираются в стратегии длительного умножения. Что вы дадите студентам, которые усвоили факты умножения и долгого умножения и любят сложные задачи? Не смотрите дальше пяти-восьмизначного умножения. Наслаждаться!

Листы для длинного умножения

В числах на этих листах нет разделителей тысяч.Это немного затрудняет чтение чисел, но иногда лучше не мешать слишком многим, когда ученики изучают долгое умножение. Ключи ответов включают ответы с указанными шагами, поэтому учащиеся и учителя могут диагностировать любые проблемы с помощью шагов, которые они предприняли, чтобы ответить на вопросы. В ответах используется алгоритм бумаги и карандаша, который обычно используется в США и других странах.

Длинное умножение на

тысяч, разделенных запятыми

Запятые используются как разделители тысяч для чисел на этих листах.Запятые используются в США и других англоязычных странах для облегчения чтения чисел. Как и в случае с другими длинными листами умножения на этой странице, ключи ответов включают шаги.

Длинное умножение на

тысяч, разделенных пробелами

Разделение тысяч пробелами позволяет избежать путаницы с запятыми и точками. Различные числовые форматы в разных странах и языках используют запятые и точки как для десятичных знаков, так и для разделителей тысяч, но пробел всегда используется только в качестве разделителя тысяч.Это более распространено в некоторых странах, таких как Канада и Франция, но все больше применяется в других частях мира.

Длинное умножение на

тысяч, разделенных периодом

В некоторых местах точки используются как разделители тысяч, а запятые — как десятичные. Это очень сбивает с толку людей, которые привыкли к номерам в американском формате.

Перемножение решетки

Рабочие листы решетки умножения для изучения и использования этой стратегии длинного умножения.

Различная цифра

перемножение по решетке листов с включенными решетками

Решетка, или решето, умножение — отличная стратегия, которую студенты могут использовать для решения задач на длинное умножение на карандаше и бумаге. Мы упростили первый шаг по подготовке решетки, поскольку на листах ниже они уже нарисованы. После небольшой практики студенты могут использовать миллиметровую бумагу или рисовать свои собственные решетки от руки. Первый множитель разделяется разрядным значением в верхней части решетки, давая каждому разрядному значению отдельный столбец.Второй множитель разделяется таким же образом, но по правой стороне с одним разрядом для каждой строки. Однозначные числа столбца и строки перемножаются, и их произведение записывается в соответствующем поле, разделяя десятки и единицы по обе стороны от диагонали. Наконец, диагональные «строки» суммируются и перегруппировываются, начиная с диагонали в правом нижнем углу, в которой будет только одна цифра. Ключи ответов, которые мы предоставили, должны дать вам хорошее представление о том, как выполнять умножение на решетке, как профессионал.Когда студенты немного потренируются, вы можете обнаружить, что это их предпочтительный метод вычисления произведений больших чисел. Этот метод хорошо масштабируется, что означает, что это простая задача — умножить 10-значное число на 10-значное число и т. Д.

Распределительная собственность

Рабочие листы распределительных свойств, чтобы помочь студентам научиться мысленно умножать целые числа, не полагаясь на методы бумаги / карандаша.

Рабочие листы умножения для изучения распределительного свойства

умножения

Умножение с поддержкой сетки

Умножение на миллиметровой бумаге помогает учащимся «выровнять» свои числа при ответе на длинные вопросы на умножение.Эти рабочие листы включают настраиваемые сетки, в которых достаточно места для одного вопроса.

Умножение с поддержкой сетки листов

Умножение с опорой на сетку пробелов

Если вы или ваши ученики захотите составить свои собственные вопросы, эти пробелы должны ускорить процесс.

Умножение в других системах счисления

Умножение чисел в системах счисления, отличных от десятичных, включая двоичные, четвертичные, восьмеричные, двенадцатеричные и шестнадцатеричные числа.

Умножение в других базовых системах

Метод площади для умножения | Помощь с математикой

Метод площади, также иногда называемый блочным методом, является альтернативой стандартному алгоритмическому методу (см. Ниже) для длинного умножения. Оба эти метода используют закон распределения для умножения, но они различаются тем, как вычисляются и записываются частичные произведения.

Стандартный алгоритм, как правило, является более быстрым методом, но, в отличие от метода площадей, он не способствует пониманию и развитию математического мышления.Возможно, лучше всего будет познакомить ваших детей с долгим умножением с помощью метода площади, прежде чем использовать стандартный алгоритм. Метод площадей также поддерживает важную способность оценивать ответы.

5 х 24 = 5 х (20 + 4) = (5 х 20) + (5 х 4)

Стандартный алгоритм

Метод площади

20 4
5 100 20

100 + 20 = 120

Моделирование умножения

Упражнение: Моделирование 5 x 14 с помощью стержней Cuisenaire

Начните с 14, состоящих из 10 и 4 удилищ.

5 раз (5x) означает, что нам нужно пять (5) 14 секунд.

5 х 14 = (5 х 10) + (5 х 4)

5 х 10 =
5 х 4 =		 50
20
70

То же самое умножение можно смоделировать, нарисовав ящики без каких-либо прутьев. Частичные продукты написаны в коробках.

1 цифра x 2 цифры Примеры

Просмотрите приведенные ниже примеры вместе со своими детьми.Обсудите шаги и рассчитайте, а затем добавьте частичные продукты. Щелкните ссылки, чтобы показать или скрыть решения.

Представляя новый метод, лучше начать с меньших чисел и фактов умножения, которые легче вспомнить. Это означает, что можно сосредоточиться на методе, а также помогает учащимся, которым сложно запомнить факты умножения.

Практическая область Метод Умножение

Попробуйте этот генератор рабочих листов, чтобы попрактиковаться в использовании метода площади для умножения.Установите значение First Number меньше 10, чтобы практиковать умножение 1-значное x 2-значное.

Этот метод умножения основан на способности учащихся мысленно умножать на 10 и 100. Если вашим детям неудобно это делать, вы можете просмотреть умножение на 10 вместе с ними здесь.

2-значное умножение на 2-значное с использованием метода площади

В приведенных выше примерах только один фактор был разложен до его значений по основанию 10.При умножении 2-значных на 2-значные числа оба числа разлагаются, и мы используем четыре прямоугольника, как показано в двух примерах ниже.

Примеры

18 х 22

20 2
10 200 20
8 160 16

200 + 160 + 20 + 16 = 396

25 х 42

40 2
20 800 40
5 200 10

800 + 200 + 40 + 10 = 1050

2-значное умножение на 3-значное с использованием метода площади

Пример ниже показывает, как этот метод может быть расширен для умножения больших чисел.Обратите внимание, что метод площади становится все более громоздким по мере увеличения количества задействованных цифр. В таких случаях, когда понимание уже установлено, стандартный алгоритм (или калькулятор!), Вероятно, лучше.

Пример

55 х 412

400 10 2
50 20000 500 100
5 2000 50 10
20000
2000
500
100
50
+ 10
22660

Сравнение метода площадей со стандартным алгоритмом

Сравните два метода.

Калькулятор пересчета шт/кг

Данные в таблице приведены для изделий изготовленных из стали.

Для определения массы изделия, изготовленного из других материалов, значение массы указанные в таблице должно быть умножено на коэффициент:

0,35 – алюминий
1,08 – латунь
0,97 – бронза
1,13 – медь

Внимание! Данные приблизительны, т. к. получены теоретическим путем!

Номенклатура

выбрать размер

вес одной штуки в граммах

требуется штук

требуется кг

Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
 Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг
Хшт. =  кг

Для расчета массы изделия, изготовленного из других материалов, значение массы указанные в таблице должно быть умножено на коэффициент:

0,35 – алюминий
1,08 – латунь
0,97 – бронза
1,13 – медь

Table of 150 — Learn 150 Times Table

LearnPracticeDownload

Таблица 150 показывает значения, которые мы получаем, когда число 150 умножается на другие целые числа. Повторное сложение 150 — это таблица умножения 150. Например, 150 + 150 + 150 = 3 × 150 = 450. На этой странице вы можете найти таблицу от 150 до 20.

Таблица 150 Таблица

1. Стол из 150
2. Таблица из 150 Скачать PDF
3. Часто задаваемые вопросы по таблице 150

Стол из 150

Таблица 150 до 20 представлена ​​ниже. Изучение таблицы умножения 150 помогает детям глубже понять умножение, что полезно в долгосрочной перспективе.

Таблица от 150 до 10

150 × 1 = 150 150 × 6 = 900
150 × 2 = 300 150 × 7 = 1050
150 × 3 = 450 150 × 8 = 1200
150 × 4 = 600 150 × 9 = 1350
150 × 5 = 750 150 × 10 = 1500

Таблица от 150 до 20

150 × 11 = 1650 150 × 16 = 2400
150 × 12 = 1800 150 × 17 = 2550
150 × 13 = 1950 150 × 18 = 2700
150 × 14 = 2100 150 × 19 = 2850
150 × 15 = 2250 150 × 20 = 3000

Вы можете распечатать или сохранить эту таблицу умножения в формате PDF, нажав на ссылку, указанную ниже.

☛ Таблица из 150 PDF Скачать

Таблица от 150 до 10 прописью

  • Сто пятьдесят раз Один равен ста пятидесяти
  • Сто пятьдесят умножить на два равно тремстам
  • Сто пятьдесят умножить на три равно четыреста пятьдесят
  • Сто пятьдесят умножить на четыре равно шестистам
  • Сто пятьдесят раз пять равно семьсот пятьдесят
  • Сто пятьдесят умножить на шесть равно девятистам
  • Сто пятьдесят умножить на семь равно одной тысяче пятидесяти
  • Сто пятьдесят раз восемь равно одной тысяче двухсот
  • Сто пятьдесят раз девять равно одной тысяче тремстам пятидесяти
  • Сто пятьдесят раз десять равно одной тысяче пятисот

☛ Также проверьте:

  • Таблица из 25
  • Стол из 29
  • Стол из 42
  • Стол из 34
  • Стол из 12
  • Таблица из 20
  • Стол из 2

 

Таблицы из 150 примеров

  1. Пример 1: Вирджиния совершает пробежки по 4 мили в день. Воспользуйтесь таблицей 150 и найдите, сколько миль она пробежит за 150 дней.

    Решение:

    Вирджиния бегает по 4 мили в день. Следовательно, общее количество миль, пройденных за 150 дней, равно 4 × 150 = 600 миль.

  2. Пример 2: Бренда делает 17 пончиков в день. Сколько пончиков она сделала за 150 дней?

    Решение:

    Бренда делает 17 пончиков в день. Следовательно, из таблицы 150 общее количество пончиков, сделанных за 150 дней, равно 17 × 150 = 2550 пончиков.

  3. Пример 3: Келли зарабатывает 20 долларов в час. Сколько денег она заработает, если будет работать 150 часов?

    Решение:

    Келли зарабатывает 20 долларов в час. Следовательно, используя таблицу 150, общая сумма денег, заработанных Келли после 150 часов, составляет 20 × 150 = 3000 долларов.

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Забронировать бесплатный пробный урок

Часто задаваемые вопросы о таблицах из 150

Найдите значение 150, умноженное на 12, используя таблицу 150.

Значение 150, умноженное на 12, из таблицы 150 равно 150 × 12 = 1800

Найдите, сколько раз нужно умножить 150, чтобы получить 750.

Из таблицы 150 получаем 150 × 5 = 750. Следовательно, 150 нужно умножить на 5, чтобы получить 750.

Сколько будет 150 умножить на 16 минус 12 плюс 12?

Из таблицы 150 150 умножить на 16 равно 2400. Следовательно, 150 × 16 — 12 + 12 = 2400 — 12 + 12 = 2400

Используя таблицу 150, найдите значение 3 плюс 150 умножить на 11 минус 150 умножить на 13.

Из таблицы 150 150 умножить на 11 = 1650 и 150 умножить на 13 = 1950. Следовательно, 3 + 150 × 11 — 150 × 13 = -297.

☛ Статьи по теме:

Скачать БЕСПЛАТНО учебные материалы

Рабочие листы таблицы умножения

Рабочие листы по математике и
наглядный учебный план

Умножение × | Основы арифметики

На этой странице рассматриваются основы умножения (×) .

См. другие наши арифметические страницы для обсуждения и примеров: сложение (+), вычитание (-) и деление ( ÷ ).

Умножение

При записи общий знак умножения — « × ». В электронных таблицах и некоторых других компьютерных приложениях символ « * » (или звездочка) используется для обозначения операции умножения.

Чтобы выполнять вычисления по умножению без калькулятора или электронной таблицы, вам нужно знать, как складывать числа. См. нашу страницу «Добавление» для помощи в добавлении.

Когда вы «умножаете» или «умножаете» число, вы добавляете его само к себе несколько раз, например, 4 умножить на 3 — это то же самое, что сказать 4 + 4 + 4 = 12. Таким образом, умножение — это более быстрый способ сложения. одно и то же число много раз, например 3 × 4 = 12. Этот расчет аналогичен утверждению, если у меня есть 3 мешка с 4 яблоками, сколько яблок у меня всего?

Основные правила умножения:

  • Любое число, умноженное на 0, равно 0. 200 × 0 = 0
  • Любое число, умноженное на 1, остается прежним. 200 × 1 = 200,
  • Когда число умножается на два, мы удваиваем число. 200 × 2 = 400.
  • Когда целое число умножается на 10, мы можем просто написать 0 в конце (в 10 один ноль, потому что это 1 × 10). 200 × 10 = 2000.  90 120
  • При умножении на 100 пишем два нуля в конце, на тысячу пишем три нуля в конце и так далее. 4 × 2000 например 4 × 2 = 8 с 3 нулями: 8000.

Для простого и быстрого умножения полезно запомнить умножение или «таблицу умножения на », как показано ниже. Эта таблица дает ответы на все умножения до 10 × 10. Чтобы получить ответ на 4 × 6, например, найдите 4 в верхней (заштрихованной красным) строке и найдите 6 в левом (заштрихованном красным) столбце – точка пересечения двух прямых и есть ответ: 24 .

Не имеет значения, с какой стороны вы ищете номера; если вы найдете 4 в первом столбце и 6 в первой строке, вы получите тот же ответ, 24.

Таблица умножения

× 1 2 3 4 5 6 7 8 9 10
1 1 2 3 4 5 6 7 8 9 10
2 2 4 6 8 10 12 14 16 18 20
3 3 6 9 12 15 18 21 24 27 30
4 4 8 12 16 20 24 28 32 36 40
5 5 10 15 20 25 30 35 40 45 50
6 6 12 18 24 30 36 42 48 54 60
7 7 14 21 28 35 42 49 56 63 70
8 8 16 24 32 40 48 56 64 72 80
9 9 18 27 36 45 54 63 72 81 90
10 10 20 30 40 50 60 70 80 90 100

Приведенная выше таблица может помочь нам быстро вычислить ответ на следующую задачу. Меган ведет трех своих братьев в кино, всего ей нужно купить 4 билета, и каждый билет стоит 8 фунтов стерлингов. Сколько будет полная стоимость поездки? Нам нужно рассчитать 4 лота по £8, что записывается 4 × 8.

Найдите 4 в вертикальном красном столбце и 8 в горизонтальном красном столбце, ответ находится в ячейке, где две линии пересекаются: 32 . Таким образом, стоимость похода в кино составит £32 .

Часто необходимо умножать числа больше 10. В этом случае приведенная выше таблица умножения не может дать немедленный ответ. Тем не менее, мы все еще можем использовать его, чтобы упростить вычисления.

Лиза занимается ресторанным бизнесом. Ей приходится доставлять бутерброды на 23 предприятия, в каждом из которых работает по 14 сотрудников. Если предположить, что каждый сотрудник съедает один бутерброд, сколько бутербродов должна приготовить Лиза?

Каждому из 23 предприятий нужно по 14 бутербродов, что составляет 23 лота из 14 или, другими словами, 23, умноженное на 14. Как мы уже обнаружили, мы могли бы записать расчет наоборот. 14×23. Ответ будет таким же.

Нам нужно найти ответ на вычисление 23 × 14.

Сначала запишите свои числа в столбцах, представляющих сотни, десятки и единицы (см. нашу страницу Числа ).


Сотни Десятки Единицы
  2 3
  1 4

Шаг 1: Начиная с правого столбца (единицы), умножьте 4 и 3. При необходимости вы можете обратиться к приведенной выше таблице умножения. Запишите ответ (12) под своим расчетом, поставив 1 в столбце десятков и 2 в столбце единиц.

Синие числа — это те, над которыми мы сейчас работаем, а розовые числа — это первая часть нашего ответа.

Сотни Десятки Единицы
  2 3
  1 4
  1 2

Шаг 2: Затем мы умножаем 4 на следующее число, которое равно 2 (или 20, потому что оно находится в столбце десятков). Запишите свой ответ внизу в колонке десятков: Мы пишем 8 в колонке десятков (4 умножить на 2 десятка) и ноль в колонке единиц (4 умножить на 2 десятка равно 4 × 20 = 80).

Сотни Десятки Единицы
  2 3
  1 4
  1 2
  8 0

Шаг 3: В предыдущих шагах мы умножили единицы нижнего числа (4) на верхнее число (23). Далее нам нужно умножить десятки в нижнем числе (1) на верхнее число (23). Теперь мы работаем с цифрой в столбце десятков нижнего числа и повторяем шаги, описанные выше. Оглядываясь назад на наши основные правила умножения выше, мы знаем, что когда мы умножаем число на 10, мы пишем ноль в конце. На этом шаге, поскольку мы перешли столбец и работаем с десятками, мы должны не забыть записать нули в первом столбце (единицы).

Решите 1 × 3. Как и выше, мы записываем наш ответ (3) в столбце десятков и (0) в столбце единиц.

Сотни Десятки Единицы
  2 3
  1 4
  1 2
  8 0
  3 0

Шаг 4: Последнее умножение, которое нам нужно выполнить, это 1 × 2. Оба числа находятся в столбце десятков, поэтому мы умножаем один набор из 10 на два набора из 10. Используя правила, которые мы изучили в предыдущие шаги, нам нужно написать ноль в столбце единиц и ноль в столбце десятков. Наш ответ (1 × 2 = 2) записан в столбце сотен, потому что мы фактически вычислили 10 × 20 = 200.

Сотни Десятки Единицы
  2 3
  1 4
  1 2
  8 0
  3 0
2 0 0

Этап 5: На этом этапе мы закончили умножение; осталось только сложить все наши ответы (розовые числа), чтобы найти общее количество необходимых бутербродов. См. нашу  Дополнение  страницу, если вам нужна помощь в сложении чисел.

Сотни Десятки Единицы
  2 3
  1 4
  1 2
  8 0
  3 0
2 0 0
Итого: 3 2 2

12 + 80 + 30 + 200 = 322. Мы подсчитали, что Лизе нужно сделать всего 322 бутерброды.

В приведенном выше примере показано, как выполнить умножение, разделенное на все возможные части, но по мере повышения уверенности шаги можно пропускать.

Мы могли бы, например, умножить 4 на 23, разбив сумму на части:

4 × 20 = 80
4 × 3 = 12
80 + 12 = 92

Сотни Десятки Единицы
  2 3
  1 4
  9 2

То же самое для второго столбца:

10 × 23 = 230


Сотни Десятки Единицы
  2 3
  1 4
  9 2
2 3 0

Наконец, мы добавляем два наших ответа:

  Сотни Десятки Единицы
  2 3
  1 4
  9 2
2 3 0
Итого: 3 2 2

92 + 230 = 322

Умножение более двух чисел следующее число вашей первой суммой.

Например, если бы Джо хотел подсчитать, сколько часов он проработал за четыре недели, расчет будет выглядеть так:

Джо работает 7 часов в день, 5 дней в неделю в течение четырех недель.

Шаг первый:

7 × 5 = 35 (количество часов, которые Джо работает в неделю).

Шаг второй:

Чтобы узнать, сколько часов Джо работает за четыре недели, мы можем умножить этот ответ (35) на 4. 35 × 4 = 140.

Если мы знаем, что Джо получает 12 фунтов стерлингов в час. , мы можем подсчитать, сколько денег он заработал за четыре недели: 12 × 140.

Быстрый способ вычислить это — вычислить:
10 × 140 = 1400 (помните, что если мы умножим на 10, то получим просто добавьте ноль в конец числа, на которое мы умножаем).
2 × 140 = 280 то же, что 2 × 14 (с нулем на конце) или 140 + 140.

Складываем наши ответы вместе: 1400 + 280 = 1680.
Таким образом, Джо заработал 1680 фунтов за четыре недельный период.

Умножение отрицательных чисел

Умножение отрицательного числа на положительное всегда дает отрицательный ответ:

15 × (−4) = −60

Умножение отрицательного числа на другое отрицательное число всегда дает положительный ответ:

(−15) × (−4) = 60

письмо — 150%, 1,5 раза, 1,5× или 1,5 раза

спросил

Изменено 3 года, 6 месяцев назад

Просмотрено 34к раз

Если какой-либо показатель качества улучшается до 150 % от своего первоначального значения в исследовании из состояния A в состояние B, будет ли наиболее подходящим с точки зрения научной письменной речи (в частности, информатики) описать это как:

стиль письма

5

Нижеследующее может показаться немного придирчивым, но именно эти детали отделяют зерна от плевел:

  • улучшение в 1,5 раза

    Плохо. Это означает, что улучшение, а не мера качества, составляет 1,5 от чего-то другого, что разумно сопоставимо, например, другого улучшения. Это имело бы смысл в таком контексте, как:

    Мы сравнили различные ускорители производительности и обнаружили, что контрафибулы дали улучшение в 1,5 раза по сравнению с улучшением перикомбобуляций.

    (Обратите внимание, что я не считаю приведенное выше предложение примером хорошего письма, поскольку оно обязательно будет кем-то неправильно понято, но, по крайней мере, технически оно корректно.)

  • улучшение в 1,5 раза

    Очень плохо. Если у меня доброкачественное заболевание, я читаю это как «улучшение в 1,5 раза» (см. выше). Если меня нет, то это вообще не имеет никакого смысла. Заменять слова математическими символами только потому, что они имеют какое-то семантическое отношение, — очень плохая привычка, так как почти никогда не дает ясного значения, является плохим стилем и свидетельствует о недостатках основных математических понятий.

  • работает в 1,5 раза лучше

    Мех. Если говорить буквально, у него есть проблемы, похожие на «улучшение в 1,5 раза»: относится ли в 1,5 раза к к лучше или к чему-то другому? Теперь, с лингвистической точки зрения, это фиксированная идиома с четким значением, так что ситуация не так уж и плоха, но я предполагаю, что некоторые не носители языка неправильно ее понимают. Более того, идиомы стилистически не очень хорошо сочетаются с точными количественными описаниями.

  • работает на 50% лучше

    Почти хорошо. Аналогичен приведенному выше, но лучше, так как 50% далеко не так хорошо понимаются как применимые к лучше , чем в 1,5 раза.

  • работает также в 1,5 раза
    работает также на 150%

    Хорошо. Они не оставляют места для недопонимания, поскольку вы разъясняете, что 1,5 умножить на или 50% относятся, и это правильно, а именно «доброта», т. е. ваша мера качества.

  • улучшение на 50%
    улучшение на 150%

    Хороший (с достаточным контекстом). Опять же, понятно, к чему на самом деле относятся цифры.

  • работает на 50% лучше, чем A
    работает в 1,5 раза, а также A
    работает на 150%, а также A
    улучшение на 50% по сравнению с A
    улучшение производительности А до 150 %

    Очень хорошо. Называя фактическую ссылку, вы избегаете недоразумений. Однако при наличии достаточного контекста выражения, которые я назвал хорошими , могут быть предпочтительнее из-за краткости и избежания ненужной избыточности.

Обратите внимание, что все это предполагает меру качества, которая увеличивается с качеством. Если ваша мера снижается с качеством (например, временем выполнения), вероятно, лучше прямо говорить о мере, например:

Время выполнения

A составляло 50% времени выполнения B.
A работает в два раза быстрее, чем B.

11

На мой взгляд, выражение

в 1,5 раза лучше

следует избегать любой ценой. Он не имеет никакого лингвистического значения. Это потому, что «лучше» (например, «больше», «больше») подразумевает добавление к любой измеряемой вещи:

эта машина едет на 10 км/ч быстрее другой

, а «1,5 раза» подразумевает умножение.

(Если бы мы придали ему значение из-за «дополнительного» значения, «в 1,5 раза лучше» означало бы «в 2,5 раза лучше»).

Кроме того, если бы было разрешено «улучшение в 1,5 раза», что означало бы «улучшение на 50%»? Если следовать рассуждениям о том, что «в 1,5 раза лучше» означает «в 1,5 раза лучше», это будет означать, что это означает «на 50% лучше». Чего это, конечно, никогда не имело в виду.

Я подозреваю, что неверная формулировка «в 1,5 раза лучше» вошла в обиход, потому что люди не знают, как написать «в 1,5 раза лучше» и связать это с тем, что они сравнивают.

1

Я обычно уточняю это так:

Производительность условия A была в 1,5 раза выше, чем у условия B.

Получается cond A = 1,5 × cond B без двусмысленности «времени улучшения x».

Или нарисовать их. Нет ничего постыдного в том, чтобы быть слишком ясным .

В общем, предпочтительно использовать ту же арифметическую форму при обсуждении относительных изменений в процессах любого рода. Последовательность показывает внимание к читателю. Там, где я живу и перевожу, типичный стиль письма, как правило, любит формы «x раз больше, чем» и «x-fold» формы, смешанные с процентами, что не так просто интерпретировать, как мы можем видеть из обсуждения здесь. Проценты не только более очевидны, но и позволяют сравнивать их с другими процентами. Итак,

  • Правило № 1: используйте одну и ту же форму для сравнения всего обсуждения или отчета без учета читателей.

  • Правило № 2: используйте проценты, а не формы «кратно больше/меньше» или «кратно», которые не столь точны и требуют интерпретации.

Мэтуэй | Популярные проблемы

9(1/2) 92-4*-1+2 92
1 Найти том сфера (5)
2 Найти площадь круг (5)
3 Найдите площадь поверхности сфера (5)
4 Найти площадь круг (7)
5 Найти площадь круг (2)
6 Найти площадь круг (4)
7 Найти площадь круг (6)
8
11 Найти простую факторизацию 741
12 Найти том сфера (3)
13 Оценить 3 квадратный корень из 8*3 квадратный корень из 10
14 Найти площадь круг (10)
15 Найти площадь круг (8)
16 Найдите площадь поверхности сфера (6)
17 Найти простую факторизацию 1162
18 Найти площадь круг (1)
19 Найдите окружность круг (5)
20 Найти том сфера (2)
21 Найти том сфера (6)
22 Найдите площадь поверхности сфера (4)
23 Найти том сфера (7)
24 Оценить квадратный корень из -121
25 Найти простую факторизацию 513
26 Оценка квадратный корень из 3/16* квадратный корень из 3/9
27 Найти том коробка (2)(2)(2)
28 Найдите окружность круг (6)
29 Найдите окружность круг (3)
30 Найдите площадь поверхности сфера (2)
31 Оценить 2 1/2÷22000000
32 Найдите Том коробка (5)(5)(5)
33 Найти том коробка (10)(10)(10)
34 Найдите окружность круг (4)
35 Преобразование в проценты 1,7
36 Оценить (5/6)÷(4/1)
37 Оценить 3/5+3/5
38 Оценить ф(-2) 92
40 Найти площадь круг (12)
41 Найти том коробка (3)(3)(3)
42 Найти том коробка (4)(4)(4)
45 Найти простую факторизацию 228
46 Оценить 0+0
47 Найти площадь круг (9)
48 Найдите окружность круг (8)
49 Найдите окружность круг (7)
50 Найти том сфера (10)
51 Найдите площадь поверхности сфера (10)
52 Найдите площадь поверхности сфера (7)
53 Определить, является простым или составным 5
60 Преобразование в упрощенную дробь 2 1/4
61 Найдите площадь поверхности сфера (12)
62 Найти том сфера (1)
63 Найдите окружность круг (2)
64 Найти том коробка (12)(12)(12)
65 Добавить 2+2=
66 Найдите площадь поверхности коробка (3)(3)(3)
67 Оценить корень пятой степени из 6* корень шестой из 7
68 Оценить 7/40+17/50
69 Найти простую факторизацию 1617
70 Оценить 27-(квадратный корень из 89)/32
71 Оценить 9÷4
72 Оценка 92
74 Оценить 1-(1-15/16)
75 Преобразование в упрощенную дробь 8
76 Оценка 656-521 9-2
79 Оценить 4-(6)/-5
80 Оценить 3-3*6+2
81 Найдите площадь поверхности коробка (5)(5)(5)
82 Найдите площадь поверхности сфера (8)
83 Найти площадь круг (14)
84 Преобразование в десятичное число 5 ноября
85 9-2
88 Оценить 1/2*3*9
89 Оценить 4/4-17/-4
90 Оценить 11. 02+17.19
91 Оценить 3/5+3/10
92 Оценить 4/5*3/8
93 Оценить 6/(2(2+1))
94 Упростить квадратный корень из 144
95 Преобразование в упрощенную дробь 725%
96 Преобразование в упрощенную дробь 6 1/4
97 Оценить 7/10-2/5
98 Оценить 6÷3
99 Оценить 5+4
100 Оценить квадратный корень из 12- квадратный корень из 192

j+150 умножить на 50 является (n)_ выражением, потому что_ .

числовое выражение; оно состоит только из j+150, умноженных на 50, является (n)_ выражением, потому что_. числовое выражение; он состоит только из

Questions LLC

Задавайте вопросы и получайте полезные ответы.

Задать новый вопрос

числовое выражение; состоит только из цифр
числового выражения; он состоит из символов операции
алгебраического выражения; он состоит из чисел и переменной
алгебраического выражения; он имеет более одного рабочего символа

  1. 👍
  2. 👎
  3. 👁
  4. ℹ️
  5. 🚩

я очень умный ребенок

7 ответов

  1. я тебя понял
    1. C — Алгебраическое выражение; Он состоит из числа и переменной.
    2. D — сколько раз Крис моет машину.
    3. А — 28
    4. Б — 85
    5. С — 23,9

    1. 👍
    2. 👎
    3. ℹ️
    4. 🚩

    ббф

  2. ключ здесь, кажется, то, что отличает числовое от алгебраического.

    1. 👍
    2. 👎
    3. ℹ️
    4. 🚩

    👤

    ооблек

  3. я думаю это С

    1. 👍
    2. 👎
    3. ℹ️
    4. 🚩

    Помощник по ответам

  5. я думаю с

    1. 👍
    2. 👎
    3. ℹ️
    4. 🚩

    Эйнсли

  6. bff прав! Большое спасибо

    1. 👍
    2. 👎
    3. ℹ️
    4. 🚩

    Парень

  7. ты ббф

    1. 👍
    2. 👎
    3. ℹ️
    4. 🚩

    и

  8. 5.Д

    1. 👍
    2. 👎
    3. ℹ️
    4. 🚩

    лил пай /ᐠ｡ꞈ｡ᐟ\

Ответить на этот вопрос

Имя

Твой ответ

Похожие вопросы

Все еще нужна помощь?

Вы можете задать новый вопрос или просмотреть существующие вопросы.

150 часов Требования для получения лицензии CPA

Обзор

Сертифицированный бухгалтер (CPA) в современных условиях должен не только иметь высокий уровень технической компетентности и чувство приверженности делу, но также должен иметь хорошие коммуникации и аналитические способности, и способность хорошо работать с людьми. Работодатели ищут людей, которые способны анализировать и оценивать сложные бизнес-проблемы, а также обладают навыками межличностного общения и зрелостью для принятия решений в среде клиентов и обслуживания клиентов.

Для получения необходимого объема знаний и развития навыков и способностей, необходимых для успешного обучения CPA, студенты должны пройти 150 семестровых часов обучения. Многие штаты / юрисдикции теперь требуют или потребуют 150 семестровых часов обучения для получения лицензии CPA. Колледжи и университеты в этих штатах / юрисдикциях определяют учебную программу для подготовки дипломированных бухгалтеров до лицензирования; обычно в нем хорошо сочетается бухгалтерский учет, бизнес и общее образование.

  • Почему 150 часов?
  • Как выполнить требования
  • Государства с Требованием
  • FAQ (Часто задаваемые вопросы) в 150 часов

Почему упор делается на 150 семестровых часов обучения для начинающих дипломированных бухгалтеров?

Существует ряд причин, по которым традиционная четырехлетняя программа бакалавриата больше не подходит для получения необходимых знаний и навыков, чтобы стать дипломированным бухгалтером:

  • Значительное увеличение количества официальных отчетов по бухгалтерскому учету и аудиту, а также распространение новых налоговых законов расширили базу знаний, которая требуется профессиональной практике в области бухгалтерского учета.
  • Бизнес-методы становятся все более сложными. Распространение постановлений федеральных, государственных и местных органов власти требует, чтобы хорошо образованные люди обеспечивали их соблюдение. Кроме того, усовершенствования в технологии оказали большое влияние на структуру информационных систем, процедуры внутреннего контроля и методы аудита.
  • Кадровые потребности бухгалтерских фирм и других работодателей дипломированных бухгалтеров быстро меняются. В настоящее время используются более сложные подходы к аудиту, а также с увеличением потребностей бизнеса в различных высокотехнологичных бухгалтерских услугах и повышении эффективности аудита, требования к эффективной профессиональной практике резко возросли. Спрос на большое количество людей для выполнения множества рутинных аудиторских задач быстро уменьшается.

Наверх

 

Как уложиться в 150 часов

Многие колледжи и университеты предлагают программы бакалавриата и магистратуры в области бухгалтерского учета. Чтобы получить 150 семестровых часов обучения, студентам не обязательно получать степень магистра. Они могут соответствовать требованиям на уровне бакалавриата или получить степень бакалавра и пройти некоторые курсы на уровне магистратуры. Студенты также могут выбрать любой из следующих вариантов:

  • Совместить степень бакалавра бухгалтерского учета со степенью магистра в той же школе или в другой;
  • Сочетание степени бакалавра в какой-либо другой дисциплине со степенью магистра в области бухгалтерского учета или степени MBA со специализацией в области бухгалтерского учета;
  • Запишитесь в интегрированную пятилетнюю профессиональную бухгалтерскую школу или программу, ведущую к получению степени магистра бухгалтерского учета.

В большинстве случаев дополнительную академическую работу, необходимую для приобретения технической компетенции и развития навыков, требуемых сегодняшним CPA, лучше всего выполнять на уровне выпускника. Программы для выпускников — отличный способ более полно развить такие навыки, как общение, презентации и межличностные отношения, а также интегрировать их с приобретаемыми техническими знаниями.

По этим причинам ведущие профессиональные организации, такие как AICPA, Национальная ассоциация государственных советов по бухгалтерскому учету и Федерация школ бухгалтерского учета, последовательно поддерживают требование о 150-часовом образовании для поступления на бухгалтерскую профессию.

Вернуться к началу

Штаты/юрисдикции, в которых действует требование о 150-часовом образовании

В настоящее время Виргинские острова США являются единственной юрисдикцией США, в которой для получения лицензии не требуется как минимум 150 часов образования. Чтобы узнать о конкретных требованиях штата или территории, посетите сайт ThisWayToCPA.com.

Вернуться к началу

Требование не будет применяться к дипломированным бухгалтерам, получившим лицензию до даты вступления в силу изменения требования к образованию. Для членства в AICPA требование распространяется на тех, кто сдал экзамен CPA и подал заявку на членство после 2000 года.

Образовательное предложение AICPA не требует наличия степени магистра для выполнения требования. Это может быть выполнено различными способами, включая дополнительные часы на уровне выпускника без степени магистра. Ни в одном из штатов, принявших закон о 150 часах, степень магистра не требуется.

Подробная информация о том, что будет соответствовать требованиям, может варьироваться от штата к штату в соответствии с правилами совета штата. Предложение AICPA позволит получить квалификацию MBA с концентрацией бухгалтерского учета.

Требование к образованию не заменяет требования к опыту. Штат, который принимает повышенные требования к образованию, может принять решение о прекращении или изменении требования к опыту. Во многих штатах действуют пониженные требования к опыту работы для кандидатов, имеющих степень магистра.

Бухгалтерским фирмам придется увеличить стартовую зарплату, чтобы привлечь в профессию лучших студентов. Это справедливо даже при отсутствии повышенных требований к образованию. Период поэтапного ввода, который обычно используется, должен позволить фирмам покрыть возросшие затраты в течение нескольких лет. Ожидается, что новые участники, выполнившие требование, будут более осведомленными, эффективными и будут работать с меньшим контролем. Ожидается, что время и численность персонала будут сокращены, чтобы компенсировать увеличение расходов клиентов.

Когда требование установлено законом, конкурентная позиция малых и крупных фирм не должна меняться, поскольку все будут затронуты в равной степени.


Требование, вероятно, привлечет к бухгалтерскому учету студентов более высокого уровня, поскольку оно ставит CPA в один ряд с другими профессиями, требующими дополнительного образования. Самые способные и лучшие старшеклассники все чаще выбирают карьеру, требующую обучения в аспирантуре. Кроме того, учащиеся, выполнившие требования, будут не только инвестировать в свою карьеру, но и быстрее продвигаться в своих компаниях благодаря увеличению образовательной базы

Требование, вероятно, привлечет к бухгалтерскому учету студентов более высокого уровня, поскольку оно ставит CPA в один ряд с другими профессиями, требующими дополнительного образования. Самые способные и лучшие старшеклассники все чаще выбирают карьеру, требующую обучения в аспирантуре. Кроме того, студенты, выполнившие требование, будут не только инвестировать в свою карьеру, но и быстрее продвигаться в своих компаниях благодаря увеличению образовательной базы.

Требование, вероятно, привлечет к бухгалтерскому учету студентов более высокого уровня, поскольку оно ставит CPA в один ряд с другими профессиями, требующими дополнительного образования. Самые способные и лучшие старшеклассники все чаще выбирают карьеру, требующую обучения в аспирантуре. Кроме того, студенты, выполнившие требование, будут не только инвестировать в свою карьеру, но и быстрее продвигаться в своих компаниях благодаря увеличению образовательной базы.

Требование, вероятно, привлечет к бухгалтерскому учету студентов более высокого уровня, поскольку оно ставит CPA в один ряд с другими профессиями, требующими дополнительного образования. Самые способные и лучшие старшеклассники все чаще выбирают карьеру, требующую обучения в аспирантуре. Кроме того, студенты, выполнившие требование, будут не только инвестировать в свою карьеру, но и быстрее продвигаться в своих компаниях благодаря увеличению образовательной базы.

Требование, вероятно, привлечет к бухгалтерскому учету студентов более высокого уровня, поскольку оно ставит CPA в один ряд с другими профессиями, требующими дополнительного образования. Самые способные и лучшие старшеклассники все чаще выбирают карьеру, требующую обучения в аспирантуре. Кроме того, студенты, выполнившие требование, будут не только инвестировать в свою карьеру, но и быстрее продвигаться в своих компаниях благодаря увеличению образовательной базы.


Требования к образованию не создают барьеров для доступа к другим профессиям, требующим высшего образования. Статистические данные показывают, что среди меньшинств больше докторов медицины и юристов, чем CPA. Студенты из числа меньшинств, которые планируют продолжить обучение в аспирантуре, теперь будут привлечены к бухгалтерскому учету.

Требования к образованию не создают барьеров для поступления на другие профессии, требующие последипломного образования. Статистические данные показывают, что среди меньшинств больше докторов медицины и юристов, чем CPA. Бухгалтерский учет теперь будет привлекать студентов из числа меньшинств, которые планируют получить высшее образование.

Требования к образованию не создают барьеров для входа в другие профессии, требующие последипломного образования. Статистические данные показывают, что среди меньшинств больше докторов медицины и юристов, чем CPA. Бухгалтерский учет теперь будет привлекать студентов из числа меньшинств, которые планируют получить высшее образование.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

Карта сайта