2 корня из 10 как посчитать. Формулы корней. Свойства корней. Как умножать корни? Примеры
2 корня из 10 как посчитать. Формулы корней. Свойства корней. Как умножать корни? Примеры
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Желательно инженерный – такой, в котором имеется кнопочка со знаком корня: «√». Обычно для извлечения корня достаточно набрать само число, а потом нажать на кнопку: «√».
В большинстве современных мобильных телефонов имеется приложение «калькулятор» с функцией извлечения корня. Порядок нахождения корня числа с помощью телефонного калькулятора аналогичен вышеизложенному.
Пример.
Найти из 2.
Включаем калькулятор (если он выключен) и последовательно нажимаем кнопки с изображением двойки и корня («2» «√»). Нажимать на клавишу «=», как правило, не нужно. В результате получаем число типа 1,4142 (количество знаков и «округленность» зависит от разрядности и настроек калькулятора).
Примечание: при попытке найти корень калькулятор обычно выдает об ошибке.
Если есть доступ к компьютеру, то найти корень числа очень просто.
1. Можно воспользоваться приложением «Калькулятор», имеющемся практически на любом компьютере. Для Windows ХР эту программу можно запустить следующим образом:
«Пуск» — «Все программы» — «Стандартные» — «Калькулятор».
Вид лучше установить «обычный». Кстати, в отличие от реального калькулятора кнопка для извлечения корня помечена как «sqrt», а не «√».
Если добраться до калькулятора указанным способом не , то можно запустить стандартный калькулятор «вручную»:
«Пуск» — «Выполнить» — «calc».
2. Для нахождения корня числа можно также воспользоваться некоторыми программами, установленными на компьютере. Кроме того, программы собственный встроенный калькулятор.
Например, для приложения MS Excel можно проделать следующую последовательность действий:
Запускаем MS Excel.
Записываем в любую клетку число, из которого нужно извлечь корень.
Помещаем указатель клетки на другое место
Нажимаем кнопочку выбора функции (fx)
Выбираем функцию «КОРЕНЬ»
В качестве аргумента функции указываем клетку с числом
Нажимаем «ОК» или «Еnter»
Преимуществом данного способа является то, что теперь достаточно ввести в клетку с числом любое значение, как в с функцией тут же появляется .
Примечание.
Имеется несколько других, более экзотических способа найти корень числа. Например, «уголком», с помощью логарифмической линейки или таблиц Брадиса. Однако, в этой статье эти методы не рассматриваются ввиду их сложности и практической бесполезности.
Видео по теме
Источники:
- как находить корень числа
Иногда возникают ситуации, когда приходится выполнять какие-либо математические вычисления, в том числе извлекать корни квадратные и корни большей степени из числа. Корень степени «n» из числа «a» представляет собой число, n-я степень которого и есть число «a».
Инструкция
Чтобы найти корень «n» из , сделайте следующее.
Нажмите на своем компьютере «Пуск» — «Все программы» — «Стандартные». Затем войдите в подраздел «Служебные» и выберите «Калькулятор». Можете сделать это вручную: нажмите «Пуск», введите «calk» в строку «выполнить» и нажмите «Enter». Откроется . Для извлечения корня квадратного из какого-либо числа, введите это в строку калькулятора и нажмите кнопку с надписью «sqrt». Калькулятор произведет извлечение из введенного числа корня второй степени, называемого квадратным.
Для того чтобы извлечь корень, степень которого выше второй, нужно воспользоваться другим видом калькулятора. Для этого в интерфейсе калькулятора нажмите кнопку «Вид» и в меню выберите строку «Инженерный» или «Научный». Этот вид калькулятора имеет необходимую для вычисления корня n-й степени функцию.
Для извлечения корня третьей степени (), на «инженерном» калькуляторе наберите нужное число и нажмите кнопку «3√». Для получения корня, степень которого выше 3-й, наберите нужное число, нажмите кнопку со значком «y√x» и затем введите число – показатель степени. После этого нажмите знак равенства (кнопка «=») и вы получите искомый корень.
После этого нажмите знак равенства (кнопка «=») и вы получите искомый корень.
Если на вашем калькуляторе отсутствует функция «y√x», следующее.
Для извлечения кубического корня введите подкоренное выражение, потом поставьте в чек боксе, который расположен рядом с надписью «Inv», отметку. Этим действием вы переведете функции кнопок калькулятора на обратные, т.е., щелкнув по кнопке для возведения в куб, вы произведете извлечение корня кубического. На кнопке, которая вам
Библиографическое описание: Прямостанов С. М., Лысогорова Л. В. Методы извлечения квадратного корня // Юный ученый. 2017. №2.2. С. 76-77..02.2019).
Ключевые слова : квадратный корень, извлечение квадратного корня.
На уроках математики я познакомился с понятием квадратного корня, и операцией извлечения квадратного корн. Мне стало интересно извлечение квадратного корня возможно только по таблице квадратов, с помощью калькулятора или есть способ извлечения вручную. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Рассмотрим следующие способы:
Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. Таким образом
- Канадский метод. Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность — не более двух — трёх знаков после запятой.
где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например:
=5,92
- Столбиком. Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр. Для ручного извлечения корня применяется запись, похожая на деление столбиком
Алгоритм извлечения квадратного корня
1. От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
2.Извлечение начинается слева направо, и подбираем число, квадрат которого не превосходит числа, стоящего в первой грани. Это число возводим в квадрат и записывает под числом, стоящим в первой грани.
3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа.
4.К получившейся разности сносим следующую грань, полученное число будет делимым . Образовываем делитель . Первую подобранную цифру ответа удваиваем (умножаем на 2), получаем число десятков делителя, а число единиц должно быть таким, чтобы его произведение на весь делитель не превосходило делимого. Подобранную цифру записываем в ответ.
5.К получившейся разности сносим следующую грань и выполняем действия по алгоритму. Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)
Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)
Данным способом можно извлекать числа с разной точностью, например с точностью до тысячных. (Рис.2)
Рассматривая различные способы извлечения квадратного корня, можно сделать вывод: в каждом конкретном случае нужно определиться с выбором наиболее эффективного для того, чтобы меньше затратить времени для решения
Литература:
- Киселев А. Элементы алгебры и анализа. Часть первая.-М.-1928 г
Ключевые слова: квадратный корень, извлечение квадратного корня .
Аннотация: В статье описываются способы извлечения квадратного корня, и приведены примеры извлечения корней.
Как извлечь корень из числа. В этой статье мы будем учиться извлекать квадратный корень из четырехзначных и пятизначных чисел.
Давайте, для примера, извлечем квадратный корень из числа 1936.
Следовательно, .
Последняя цифра в числе 1936 — цифра 6. На 6 заканчивается квадрат числа 4 и числа 6. Следовательно, 1936 может быть квадратом числа 44 или числа 46. Осталось проверить с помощью умножения.
Значит,
Извлечем квадратный корень из числа 15129.
Следовательно, .
Последняя цифра в числе 15129 — цифра 9. На 9 заканчивается квадрат числа 3 и числа 7. Следовательно, 15129 может быть квадратом числа 123 или числа 127. Проверим с помощью умножения.
Значит,
Как извлечь корень — видеоА теперь предлагаю вам посмотреть видео Анны Денисовой — «Как извлечь корень «, автора сайта » Простая физика «, в котором она рассказывает, как извлекать квадратные и кубические корни без калькулятора.
В видео рассматривается несколько способов извлечения корней:
1. Самый простой способ извлечения квадратного корня.
2. Подбором, используя квадрат суммы.
3. Вавилонский способ.
4. Способ извлечения квадратного корня в столбик.
5. Быстрый способ извлечения кубического корня.
6. Способ извлечения кубического корня в столбик.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.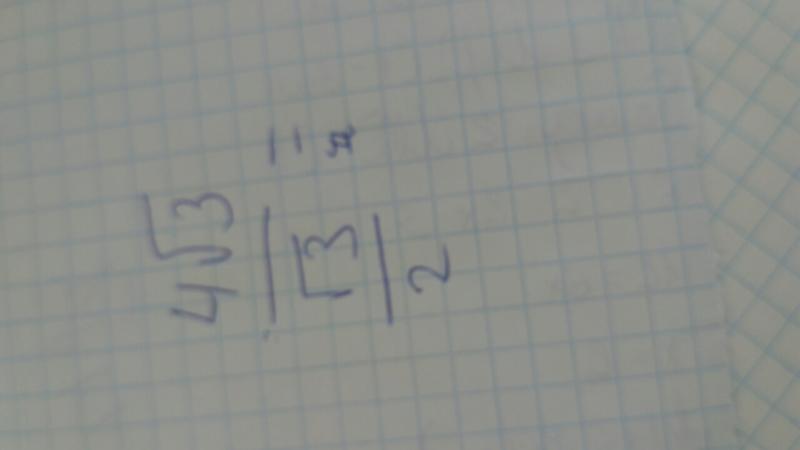 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Как умножать радикалы за 3 простых шага — Mashup Math
Узнайте, как умножать радикалы и как умножать квадратные корни за 3 простых шага (бесплатный рабочий лист включен) Прежде чем вы научитесь умножать радикалы и умножать квадратные корни, вам необходимо убедиться, что вы знакомы со следующими словарными терминами: подкоренное число и — это значение внутри радикального символа. Подкоренное число может включать числа, переменные или и то, и другое.
Подкоренное число может включать числа, переменные или и то, и другое.
Свойство умножения квадратных корней
Ключом к обучению умножению радикалов является понимание свойства умножения квадратных корней .
Свойство гласит, что всякий раз, когда вы перемножаете подкоренные, вы берете произведение подкоренных и подставляете их под один единственный радикал.
Например, радикал 5 умножить на радикал 3 равен радикалу 15 (поскольку 5 умножить на 3 равно 15).
Теперь давайте рассмотрим пример умножения радикалов и умножения квадратных корней за 3 простых шага.
Проблема:
Шаг первый: упростите квадратные корни (если возможно) В этом примере подкоренные числа 3 и подкоренные числа 15 не могут быть упрощены, поэтому мы можем пока оставить их такими, какие они есть.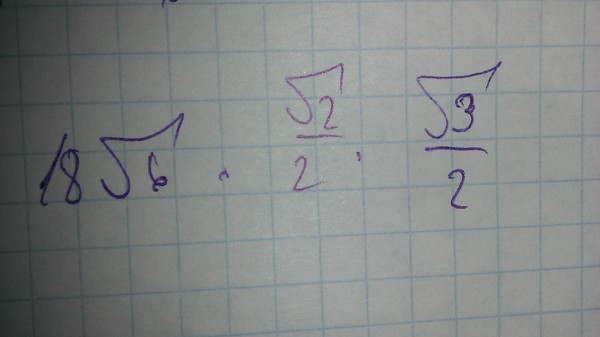
Теперь вы можете применить свойство умножения квадратных корней и умножить подкоренные вместе. В этом случае радикал, умноженный на 3 радикала 15, равен радикалу 45 (потому что 3 умножить на 15 равно 45).
Третий и последний шаг — упростить результат, если это возможно.
Можно ли упростить радикал 45?
Ответ: да.
Так как радикал 45 равен радикалу 9, умноженному на радикал 5, и поскольку радикал 9 равен 3 (поскольку 9 — полный квадрат), мы можем упростить радикал 45 до 3-кратного радикала 5 (см. диаграмму ниже для более подробной информации). посмотрите, как упростить квадратные корни).
Наконец, мы можем заключить, что окончательный ответ:
Ищете другие примеры задач? Посмотрите бесплатный видеоурок ниже, чтобы узнать больше о том, как умножать радикалы и как умножать квадратные корни: Как умножать радикалы и как умножать квадратные корни Рабочий лист (с ответами)Вы хотите попрактиковаться в умножении радикалов, умножении квадратных корней, упрощении радикалов и упрощении квадратных корней?
Щелкните ссылку ниже, чтобы получить доступ к бесплатному рабочему листу от Kuta Software:
Бесплатный рабочий лист по умножению радикалов
Поделитесь своими идеями, вопросами и комментариями ниже!
(Никогда не пропустите блог Mashup Math — нажмите здесь, чтобы получить наш еженедельный информационный бюллетень!)
Продолжайте учиться: Автор: Энтони Персико.
