2 степень числа: Степени 2. Степени числа 2. Таблица степеней 2. 2 в степени

7 класс. Алгебра. Степень с натуральным показателем и ее свойства. — Как легко запомнить степени числа 2.

Комментарии преподавателя

На этом уроке мы рассмотрим таблицу основных степеней.
Вначале вспомним определение степени. Затем составим таблицу основных степеней чисел от 1 до 10 и решим ряд задач с ее использованием.

 

 

Тема: Сте­пень с на­ту­раль­ным по­ка­за­те­лем и ее свой­ства

Урок: Таб­ли­ца ос­нов­ных сте­пе­ней

На­по­ми­на­ние опре­де­ле­ния:

Здесь a — ос­но­ва­ние сте­пе­ни,

n— по­ка­за­тель сте­пе­ни,

— n-ая сте­пень числа.

Из опре­де­ле­ния сте­пе­ни по­лу­ча­ем таб­ли­цу ос­нов­ных сте­пе­ней, где ос­но­ва­ние – про­стые числа в пре­де­лах 10.

Таб­ли­ца ос­нов­ных сте­пе­ней:

Пря­мая и об­рат­ная за­да­чи

1) Вы­чис­лить  Ре­ше­ние:

По опре­де­ле­нию сте­пе­ни: 

2) Число 729 за­пи­сать в виде сте­пе­ни.

Ре­ше­ние ос­но­ва­но на ос­нов­ной тео­ре­ме ариф­ме­ти­ки. Видим, что 

729 де­лит­ся на 3. Раз­ло­жим число 729 по сте­пе­ням 3.

729	3
243	3
81	3
27	3
9	3
3	3
1

По­лу­ча­ем, что.

3) Число 256 за­пи­сать в виде сте­пе­ни.

Раз­ла­га­ем дан­ное число по сте­пе­ням двой­ки по ос­нов­ной тео­ре­ме ариф­ме­ти­ки.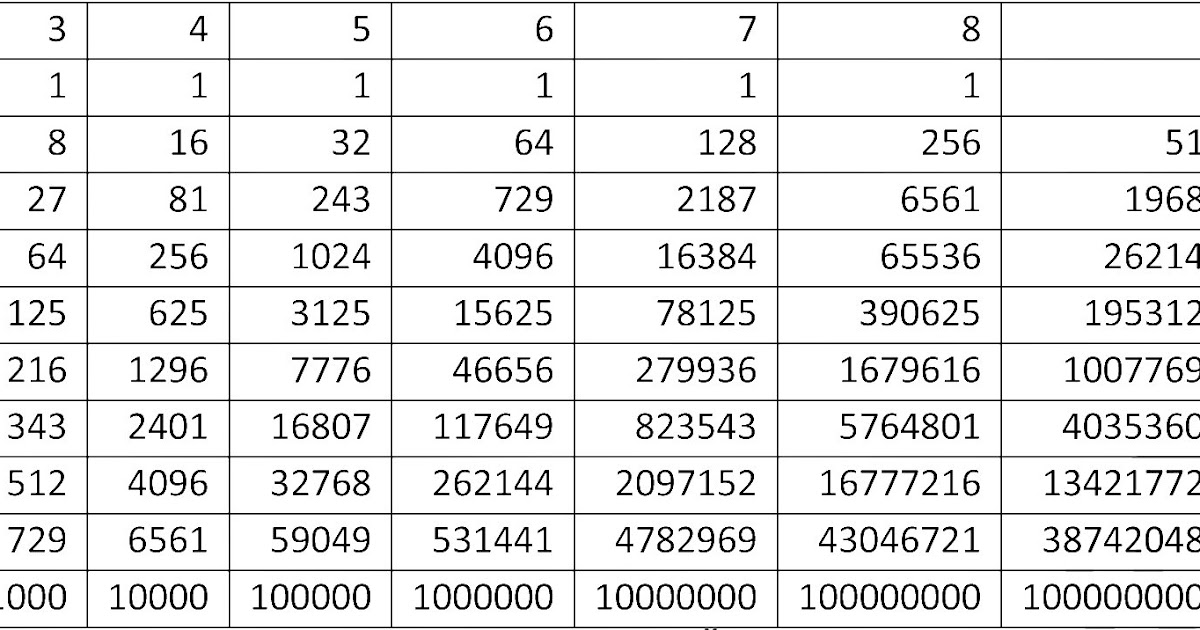

256	2
128	2
64	2
32	2
16	2
8	2
4	2
2	2
1

По­лу­ча­ем, что.

За­да­ча: дано . Срав­нить n и k.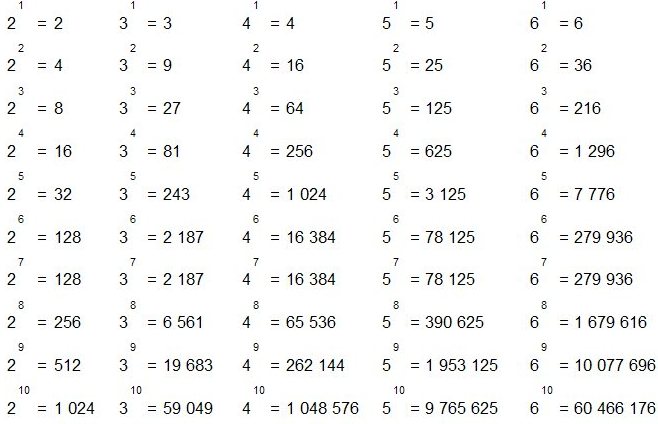

Ре­ше­ние:

По таб­ли­це или по ос­нов­ной тео­ре­ме ариф­ме­ти­ки на­хо­дим:

n = 7, k = 5

Ответ: 

Для прак­ти­че­ских вы­чис­ле­ний удоб­но про­дол­жить таб­ли­цу для чисел 1, 0, -1, 10.

Про­дол­же­ние таб­ли­цы для чисел 1; 0; — 1; 10

(свод­ка пра­вил)

n – на­ту­раль­ное число.

Решим за­да­чи на таб­ли­цу (или ос­нов­ную тео­ре­му ариф­ме­ти­ки).

За­да­ча: Найти k, если:

а) 

Раз­ла­га­ем 512 по ос­нов­ной тео­ре­ме ариф­ме­ти­ки либо ис­поль­зу­ем таб­ли­цу сте­пе­ней.

512	2
256	2
128	2
64	2
32	2
16	2
8	2
4	2
2	2
1

 

Ответ: .

б) 

Раз­ла­га­ем по ос­нов­ной тео­ре­ме ариф­ме­ти­ки либо ис­поль­зу­ем таб­ли­цу сте­пе­ней.

625	5
125	5
25	5
5	5
1

 

Ответ: .

в)

Раз­ла­га­ем по ос­нов­ной тео­ре­ме ариф­ме­ти­ки либо ис­поль­зу­ем таб­ли­цу сте­пе­ней.

343	7
49	7
7	7
1

 

Ответ: .

г)

Раз­ла­га­ем по ос­нов­ной тео­ре­ме ариф­ме­ти­ки либо ис­поль­зу­ем таб­ли­цу сте­пе­ней. Видим, что  де­лит­ся на 3, так как сумма цифр 18 де­лит­ся на 3.

	3
243	3
81	3
27	3
9	3
3	3
1

 

Ответ: .

За­да­ча: Вы­чис­лить.

а) 

б) 

За­да­ча: Пред­ста­вить в виде куба неко­то­ро­го числа.

а) 125.

. Зна­чит, .

Ответ: 

б)

. Зна­чит, .

Ответ: 

в) 

. Зна­чит, .

Ответ: .

Итак, мы рас­смот­ре­ли таб­ли­цу ос­нов­ных сте­пе­ней, пра­ви­ло ее фор­ми­ро­ва­ния и ис­поль­зо­ва­ние в раз­лич­ных ти­по­вых за­да­чах.

 

Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/tablitsa-osnovnyh-stepeney?konspekt&chapter_id=2

Источник видео: http://www.youtube.com/watch?v=mRYXKA9wqk4

1.1.2 Степень с натуральным показателем

Видеоурок 1: Свойства степени с натуральным показателем

Видеоурок 2: Степень с натуральным показателем и ее свойства

Лекция: Степень с натуральным показателем

Степень с натуральным показателем

Под степенью некоторого числа «а» с некоторым показателем «n» понимают произведение числа «а» само на себя «n» раз.

 

Когда говорят о степени с натуральным показателем, это означает, что число «n» должно быть целым и не отрицательным.

а — основание степени, которое показывает, какое число следует умножать само на себя, 

n — показатель степени — он говорит, сколько раз основание нужно умножить само на себя.

Например:

8⁴ = 8 * 8 * 8 * 8 = 4096.

В данном случае под основанием степени понимают число «8», показателем степени считается число «4», под значением степени понимается число «4096». 

Самой большой и распространенной ошибкой при подсчете степени является умножение показателя на основание — ЭТО НЕ ВЕРНО!

Когда речь идет о степени с натуральным показателем, имеется в виду, что только показатель степени (n) должен быть натуральным числом. 

В качестве основания можно брать любые числа с числовой прямой.

Например,

(-0,1)³ = (-0,1) * (-0,1) * (-0,1) = (-0,001).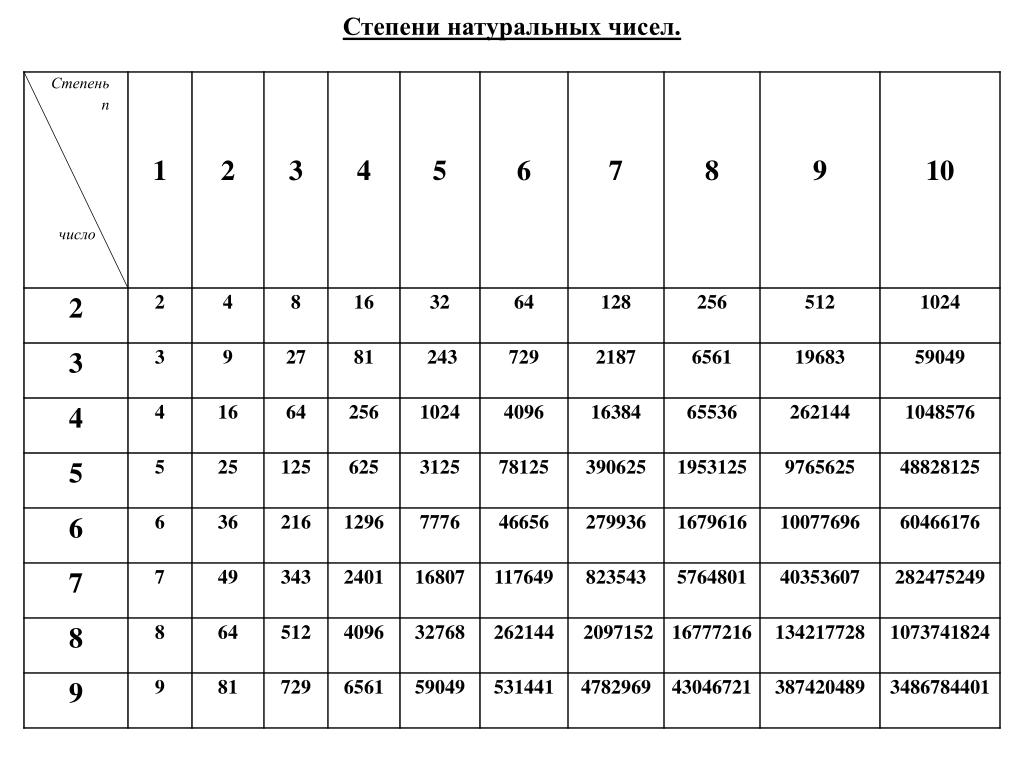

Математическое действие, которое совершается над основанием и показателем степени, называется возведение в степень. 

Сложение \ вычитание — математические действия первой ступени, умножение \ деление — действие второй ступени, возведение степени — это математическое действие третьей ступени, то есть одной из высших. 

Данная иерархия математических действий определяет порядок при расчете. Если данное действие встречается в задачах среди двух предыдущих, то оно делается в первую очередь.

Например:

15 + 6 *2²  = 39

В данном примере необходимо сначала возвести 2 в степень, то есть

2² = 4,

затем полученный результат умножить на 6, то есть

4 * 6 = 24,

затем

24 + 15 = 39.

Степень с натуральным показателем используется не только для конкретных вычислений, но и для удобства записи больших чисел. В данном случае еще используется понятие «стандартный вид числа». Данная запись подразумевает умножение некоторого числа от 1 до 9 на основание степени равное 10 с некоторым показателем степени.

Например, для записи радиуса Земли в стандартном виде используют следующую запись:

6400000 м = 6,4 * 10⁶ м,

а масса Земли, например, записывается следующим образом:

6 * 10²⁴ кг.

Свойства степени

Для удобства решений примеров со степенями необходимо знать основные их свойства:

1. Если Вам необходимо умножить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.

aⁿ * a^m = a^n+m

Например:

5² * 5⁴ = 5⁶.

2. Если необходимо разделить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть. Обратите внимани, для действий со степенями с натуральным показателем показатель степени делимого должен быть больше показателя степени делителя. В противном случае, частным данного действия будет число с отрицательным показателем степени.

aⁿ / a^m = a^n-m 

Например,

5⁴ * 5² = 5².

3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.

(aⁿ )^m = a^n*m

Например,

(5⁴ )² = 5⁸.

4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.

(a * b)^m = a^m * b^m

Например,

(5 * 8 )² = 5² * 8².

5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.

(a / b)^m = a^m / b^m

6. Любое число, которое возводится в показатель степени, равный единице, равно первоначальному числу.

а¹ = а

Например,

5¹ = 5.

7. При возведении любого числа в степень с показателем ноль, результатом данного вычисления всегда будет единица.

а⁰ = 1

Например,

7⁰ = 1.

2.2 Характерные химические свойства и получение простых веществ — металлов: щелочных, щелочноземельных, алюминия; переходных элементов (меди, цинка, хрома, железа)

1.2.4 Общая характеристика неметаллов IVA – VIIA групп в связи с их положением в Периодической системе химических элементов Д.И.Менделеева и особенностями строения их атомов

2.1.3 «Просвещенный абсолютизм». Законодательное оформление сословного строя

1.4.6 Смута. Социальные движения в России в начале XVII в. Борьба с Речью Посполитой и со Швецией

1.2.1 Возникновение государственности у восточных славян. Князья и дружина. Вечевые порядки. Принятие христианства

• Вконтакте
• Сайт

Самый быстрый словарь в мире | Vocabulary.com

ПЕРЕЙТИ К СОДЕРЖАНИЮ

0. вторая степень произведение двух равных слагаемых

1. Вторая империя имперское правительство Наполеона III во Франции в 1852-1870 гг.

2. второй сакер (бейсбол) человек, играющий на второй базе

3. 63″>

   свечная сила сила света, измеряемая в канделах

4. второсортный человек второсортных способностей или ценности

5. помощник Тот, кто поддерживает предложение или петицию в качестве необходимой предварительной подготовки к обсуждению или голосованию

6. тощий диппер голый пловец

7. вторая природа, приобретенное поведение, которое практикуется так долго, что кажется врожденным

8. вторая база База, которой бегун должен коснуться вторым в бейсболе

9. второй год используется для второго года обучения в средней школе или колледже США

10. 71″>

    вторая передача передача, имеющая второе по величине передаточное отношение в коробке передач автомобиля

11. второстепенное существо второго ранга или важности или ценности

12. второй период второй дивизион, на который делится ход игры

13. подержанный автомобиль автомобиль, бывший в собственности; не новая машина

14. второй прирост второй прирост деревьев, покрывающий территорию, где первоначальный древостой был уничтожен пожаром или вырубкой

15. Вторая мировая война война между союзниками и странами Оси с 1939 по 1945 год

16. 36″>

    Местоимения и глаголы второго лица, относящиеся к лицу, к которому обращаются

17. оправдывать, игнорировать или делать поправку на

18. транжира безрассудно расточительный потребитель

19. второе сословие дворянство во Франции и пэрство в Британии

Калькулятор степени двойки

Автор: Артуро Баррантес

Отзыв от Luis Hoyos

Последнее обновление: 11 октября 2022 г.

Содержание:

• Что такое показатель степени числа 2?
• Как вычислить степень числа 2 с любым показателем степени?
• Другие полезные инструменты, такие как калькулятор степени двойки
• Часто задаваемые вопросы

Калькулятор степени двойки — это удобный инструмент, который поможет вам определить результат двойки в степени любого числа, даже отрицательного. {30} = 2 \times 2 \times …\умножить на 2= 1 073 741 824 230=2×2×…×2=1 073 741 824.

Однако для отрицательного показателя степени мы используем обратную величину 2, а затем выполняем те же действия. Вот пример:

1. Напишите обратное число 2, которое равно 12\frac{1}{2}21​.
2. Узнать показатель степени. Представьте, что у нас есть −3-3−3.
3. Умножить новое основание столько раз, сколько указывает показатель степени
4. В нашем примере 2 в степени -3 равно: 12×12×12=18\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8} 21​×21​×21​=81​.

Другие полезные инструменты, такие как калькулятор степени двойки

Поскольку вы уже знаете, как вычислить 2 в степени любого числа, вы можете взглянуть на другие связанные инструменты:

• Калькулятор степени;
• Силовая функция; и
• Степень числа 10.

Часто задаваемые вопросы

Сколько будет 2 в степени -1?

Результат 1/2 или 0,5.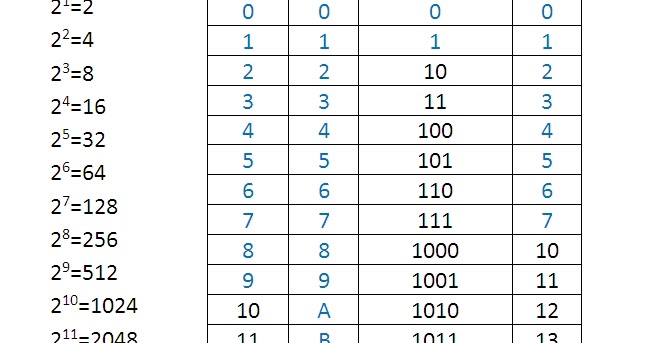

1. Определить степень, в которую он возведен. В данном случае это -1.
2. Учитывая, что у нас есть отрицательный показатель, сначала мы должны получить обратный показатель. Для 2 обратное число равно 1/2 .
3. Умножьте основание на один раз: результат равен 1/2.

Как вычислить 2 в степени 8?

Результат 256. Вы можете использовать инструмент Омникалькулятора: Калькулятор степени двойки или:

1. Определите степень, в которую она возведена. В данном случае это 8.
2. Умножить восемь раз на основание: 2 * … 8 раз … * 2. Результат 256.

Сколько будет 2 в степени 30?

Результат: 1 073 741 824. Вы можете использовать инструмент Омникалькулятора: Калькулятор степени 2 или:

1. Определите степень, в которую он возведен. В данном случае это 30.
2. Умножьте основание в тридцать раз: 2 * … 30 раз … * 2. Результат 1 073 741 824.

Сколько будет 2 в степени 3?

Результат равен 8.