2 умножить на 3 сколько будет: Сколько будет 5 плюс 5 умножить на 2 в квадрате

Математика. Умножение | Сайт Леонида Некина

На этот раз нам понадобятся несколько пятикопеечных монет и, конечно же, снова счеты. Допустим, мы хотим купить себе конфет. Каждая конфета стоит $5$ копеек. Значит, чтобы купить две конфеты, мы должны отдать продавщице две пятикопеечные монеты — кладем их перед собой на стол. Теперь посчитаем, сколько здесь копеек — откладываем на счетах:

$5 + 5 = 10$

Эту же запись можно сделать немножко покороче. Когда я беру $2$ раза по $5$, я записываю это в виде примера на умножение:

$2 \cdot 5 = 10$

Это читается: «Два раза по пять равно десяти». (Хотя это и не общепринятый способ чтения, я всё же настоятельно бы посоветовал пока читать эту запись именно так.) Теперь, допустим, мы хотим купить $3$ конфеты. Выкладываем перед собой три монеты, откладываем на счетах $3$ раза по $5$ и получаем:

$5 + 5 + 5 = 15$

Или в виде примера на умножение:

$3 \cdot 5 = 15$

Еще пара таких демонстраций — и ребенок уже способен справляться с подобными примерами самостоятельно. Монеты вскоре становятся не нужны — достаточно одних счет. Теперь снова дело за практикой. Постепенно ребенок научится (почти безошибочно) считать все примеры из таблицы умножения. При этом многие ответы он мимоходом выучит наизусть. Настает время обратить его внимание на некоторые хитрости.

(1) Числа в примерах на умножение можно менять местами. Так, к примеру, $5$ раз по $3$ это ровно столько же, сколько $3$ раза по $5$. В этом легко убедиться если посмотреть на такую картинку:

●  ●  ●  ●  ●
●  ●  ●  ●  ●
●  ●  ●  ●  ●

Здесь пять столбцов по три кружка в каждом столбце, а значит, общее число кружков ${5 \cdot 3}$. С другой стороны, здесь три ряда по пять кружков в каждом ряду, то есть всего кружков ${3 \cdot 5}$. Таким образом, $5 \cdot 3 = 3 \cdot 5$. Теперь, когда мы узнали эту хитрость, нам позволительно читать запись

$5 \cdot 3$

как «пять умножить на три». Именно так принято говорить по-русски, однако по сути это неправильно. «Пять умножить на три» означает буквально «берем пятерку три раза», в то время как запись «${5 \cdot 3}$» означает на самом-то деле «берем тройку пять раз». Большой беды в этой путанице нет, потому что «пять умножить на три» в точности равно «трем умножить на пять». Другое русское выражение — «пятью три» — является, безусловно, более правильным. Не берусь утверждать про все иностранные языки, но по крайней мере в английском, немецком и французском выражение «${5 \cdot 3}$» читается (в буквальном переводе) как «пять раз по три».

(2) Умножать на $10$, оказывается, очень легко. Чтобы в этом убедиться, снова достаем полный набор наших монет. Допустим у нас есть $23$ копейки (две дестюльника и три копейки):

●
●
○
○
○

Мы хотим, чтобы денег у нас стало в $10$ раз больше. Докладываем монетки таким образом:

●  ●  ●  ●  ●  ●  ●  ●  ●  ●
●  ●  ●  ●  ●  ●  ●  ●  ●  ●
○  ○  ○  ○  ○  ○  ○  ○  ○  ○
○  ○  ○  ○  ○  ○  ○  ○  ○  ○
○  ○  ○  ○  ○  ○  ○  ○  ○  ○

Затем каждый ряд дестюльников заменяем на рубль, а каждый ряд копеек заменяем на дестюльник. Получаем $2$ рубля и $3$ дестюльника, то есть $230$ копеек. Чтобы умножить число на $10$, надо к этому числу справа приписать ноль:

$10 \cdot 23 = 23 \cdot 10 = 230$

Пусть у нас на счетах отложено число $23$. Умножить на $10$ — это значит все отложенные бусинки «переселить» на один ряд выше. Впрочем, будет очень полезно один разок действительно десять раз «тупо» отложить на счетах число $23$ (или любое другое) и посмотреть, что получится.

(3) Допустим, мы хотим на счетах умножить на $30$ число $23$. Будем ли мы откладывать $23$ тридцать раз? Нет, конечно. Мы сразу отложим $23$ десять раз, то есть попросту отложим число $230$. Всего надо так сделать $3$ раза, потому что $30$ это не что иное как $3$ раза по $10$. Получаем:

$30 \cdot 23 = 3 \cdot 230 = 690$

Умножать на $100$ тоже очень просто, потому что $100$ — это $10$ раз по $10$. Умножим $23$ на $10$. Приписав ноль, получим $230$. Потом еще раз умножим на десять. Припишем еще один ноль: $2300$. В итоге выходит:

$100 \cdot 23 = 23 \cdot 100 = 2300$

При умножении на $100$ к числу надо приписать два нуля. А на счетах при умножении на $100$ все отложенные бусинки «переселяются» на два ряда выше.

А если мы захотим умножить $23$ на $300$? Сразу откладываем на счетах $2300$ и делаем так всего три раза. Получаем:

$300 \cdot 23 =3 \cdot 2300 = 6900$

А если надо умножить $230$ на $300$? Тут всё то же самое:

$300 \cdot 230 = 3 \cdot 23000 = 69000$

Мы замечаем одну полезную вещь: когда мы перемножаем «круглые» числа (то есть такие, которые оканчиваются на ноль), мы можем поначалу вовсе отбросить все конечные нули, выполнить умножение без них, а потом к результату приписать столько нулей, сколько мы отбросили. Например, в примере на умножение

$300 \cdot 230$

мы отбрасываем три конечных нуля и получаем

$3 \cdot 23 = 69$

Теперь сталось только приписать сюда те самые три нуля, которые мы отбросили:

$300 \cdot 230 = 69000$

(4) Если на $10$ умножать очень легко, то и на $11$ ненамного труднее. Допустим, мы хотим умножить на $11$ всё то же самое число $23$. Для этого надо число $23$ отложить на счетах $11$ раз. Но мы уже знаем, какое число мы получим после того, как сделаем это $10$ раз. Это $230$. Поэтому мы сразу откладываем $230$, после чего нам остается отложить $23$ только один раз. Мы получаем ответ всего в два «хода»:

$11 \cdot 23 = 253$

Однако, если так легко умножать на $11$, то и на $12$ — тоже нетрудно. Одни раз отложим $230$ и два раза по $23$. В результате получим (в три «хода»):

$12 \cdot 23 = 276$

Умножать на $20$ мы уже умеем. Для этого понадобится лишь два «хода»: два раза по $230$ — и готово!

А сколько «ходов» нужно чтобы умножить $23$ на $21$? — Только три: откладываем два раза по $230$ и один раз $23$.

Теперь нам нетрудно будет вычислить и такие примеры:

$101 \cdot 23$ (в два «хода),

$102 \cdot 23$ (в три «хода»).

Оказывается, мы уже умеем легко перемножать между собой довольно большие числа.

(5) Пусть нам теперь требуется вычислить $9 \cdot 23$. Значит ли это, что мы должны, по старинке, откладывать на счетах число $23$ целых девять раз? Нет, не значит. Допустим, мы просчитались, и вместо девяти раз отложили это число десять раз. Такую ситуацию легко исправить. Прокручиваем последний, лишний, «ход» в обратную сторону (то есть, вычитаем $23$) — и всё в порядке. Но ведь мы уже заранее знаем, что получится, если отложить число $23$ десять раз. Поэтому мы можем сознательно как бы просчитаться, а потом поправиться. Откладываем $230$, вычитаем $23$, и получаем ответ (в два «хода»):

$9 \cdot 23 = 207$

Подобным же образом, чтобы вычислить $8 \cdot 23$, надо «поправиться» два раза. Откладываем $230$ и два раза отнимаем $23$ (всего три «хода» вместо восьми):

$8 \cdot 23 = 184$

Используя данный прием, мы теперь сумеем легко вычислить:

$19 \cdot 23$ (в три «хода),

$99 \cdot 23$ (в два «хода»)

и тому подобное.

Разумеется, усложнение примеров не самоцель. Важно, чтобы ребенок разобрался во всех хитростях и научился ими пользоваться. Однако перемножать на счетах числа в пределах $24$ — это вполне посильная задача. В этом случае для решения одного примера понадобится не более шести «ходов».

(6) Самый легкий случай — это когда требуется умножить на число $0$ (ноль). Отложим ли мы число $23$ ноль раз или ноль бусинок отложим $23$ раза, результат всё равно один:

$0 \cdot 23 = 0$

$23 \cdot 0 = 0$

Замечание 1. В качестве знака умножения вместо точки часто используют косой крестик. Так, записи  ${3 \cdot 5}$  и  ${3 \times 5}$  означают одно и то же.

Замечание 2. В русскоязычных школьных учебниках по математике умножение определяется как ${2 \cdot 5 = 2 + 2 + 2 + 2 + 2}$. Хотя такое определение и не приводит к ошибкам в вычислениях, по сути оно неверно. Когда мы говорим две конфеты, мы имеем в виду конфета + конфета. Когда мы говорим две монеты по пять копеек, мы имеем в виду $5$ копеек + $5$ копеек. Здесь двойка отвечает на вопрос сколько и стоит на первом места, а пятерка отвечает на вопрос что и стоит на втором месте. И такой порядок принят всегда — что бы мы ни пересчитывали: будь то предметы, деньги, метры, минуты или что угодно. Отступать от этого порядка при переходе к «голым» числам было бы совершенно нелогично. Важно понимать, что слова «две монеты» задают точно такое же отношение между понятиями двойка и монета, какое существует между числами $2$ и $5$ в записи ${2 \cdot 5}$, тем более что за абстрактным числом $5$ вполне может стоять не что иное, как пятикопеечная монета. Знак умножения ($\cdot$) между «голым» числами ставится только для того, чтобы они не слились в одно число ($25$). Во всех остальных случаях этот знак не нужен и, как правило, опускается.

Конспект

1. Чтобы узнать, сколько стоят три конфеты по пять копеек, мы откладываем на счетах три раза по пять бусинок. На бумаге эта задача и ее ответ записывается в виде ${5 + 5 + 5 =15}$ или сокращенно $3 \cdot 5 = 15$ (три раза по пять равно пятнадцать). Это пример на умножение: следовало бы говорить, что мы пять умножили на три и получили пятнадцать.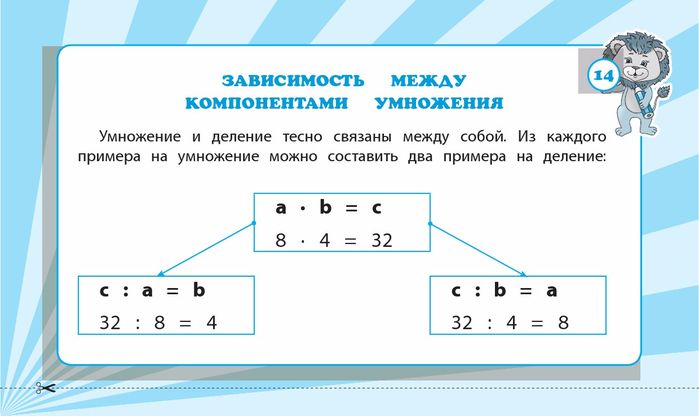 Однако на практике запись $3 \cdot 5$ в русском языке принято не совсем правильно читать «три умножить на пять». Эта путаница не приводит к недоразумениям, потому что если взять пять раз по три, то мы получим тот же самый результат — пятнадцать. Числа, входящие в пример на умножение можно менять местами. Пять умножить на три это то же самое, что и три умножить на пять: $3 \cdot 5 = 5 \cdot 3 = 15$.

2. Чтобы умножить число на $10$, надо приписать к нему справа ноль. При этом бусинки на счетах «переселяются» на один ряд выше. При умножении на сто мы приписываем к чилу два нуля, а бусинки на счетах «переселяем» на два ряда выше. Когда мы перемножаем «круглые» числа (оканчивающиеся на $0$), мы можем поначалу отбросить все конечные нули, выполнить умножение без них, а потом к результату приписать столько нулей, сколько мы отбросили.

3. Чтобы умножить $23$ на $30$, откладываем на счетах три раза число $230$. Умножая $23$ на $31$, откладываем на счетах три раза число $230$ и один раз число $23$. При умножении $23$ на $102$ откладываем на счетах один раз число $2300$ и два раза число $23$.

4. Чтобы умножить $23$ на $9$, откладываем на счетах число $230$ и отнимаем от него число $23$. Умножая $23$ на $98$, откладываем $2300$ и два раза отнимаем $23$.

5. При умножении любого числа на ноль получается ноль ($0$).

Задачи (в дополнение к обычным примерам на умножение)

1.5.1. Как удобнее вычислять:

$7$ раз по $8$ или $8$ раз по $7$?

$11$ раз по $19$ или $19$ раз по $11$?

и т. п.

1.5.2. За сколько «ходов» можно вычислить следующие примеры:

$15 \cdot 15$

$89 \cdot 9$

$16 \cdot 201$

$13 \cdot 0$

и т. п.

Примеры из «динамических» прописей

Примеры из таблицы умножения

Умножение в пределах таблицы 24 × 24

 

таблица умножения | интернет проект BeginnerSchool.ru

Мы все знаем, что учить таблицу умножения необходимо. А необходимо потому, что зная назубок таблицу умножения/деления от 1 до 10, ребенок без труда освоит внетабличное умножение и деление. Но как же легче всего выучить таблицу умножения. Ответ неоднозначен, для каждого ребенка нужен индивидуальный подход. Но все же можно дать общие для всех советы.
Для начала надо объяснить ребенку, что такое умножение. Умножение связано с действием сложения. Объясните ребенку, что перемножаемые числа называются множителями, а полученное число называется произведением.

Итак, начинаем с умножения на 2:
Что такое 2 × 2, это 2 + 2 и равно 4. Положим две конфеты на одну тарелочку и еще две конфеты на другую. Если конфеты сосчитать все вместе получится четыре, то есть 2 конфеты умножить на 2 тарелочки, получится 4 конфеты: 2 × 2 = 4.

Теперь, чтобы проверить результат, разделите 4 конфеты обратно на две тарелки: 4 ÷ 2 = 2.

А как еще можно поровну разделить конфеты? Конечно же, по четырем тарелкам. Если на каждую тарелку положить по конфете:

4 ÷ 4 = 1

4 ÷ 1 = 4

 проверим: 4 × 1 = 4.

Теперь добавим на каждую тарелочку еще по конфете. Считаем все конфеты, получаем 6, как получилось? Три конфеты умножили на две тарелочки: 3 × 2 = 3 + 3 = 2 + 2 + 2 = 6.

То есть три умножить на два это 2 раза по 3 или 3 раза по 2, и если взять три тарелочки по две конфеты, то все равно получится 6 конфет.

От перемены мест множителей произведение не меняется: 3 × 2 = 2 × 3 = 6.

Теперь деление: 6 ÷ 2 = 3, берем 6 конфет и раскладываем поровну на две тарелки, получаем на каждой по три конфеты. Также показываем деление шести конфет по трем тарелкам, получаем по две конфеты на каждой тарелке: 6 ÷ 3 = 2.

Таким образом, можно разобрать каждый пример умножения на 2, на 3 и так далее.
Когда ребенок уверенно будет решать такого рода примеры, приступайте к постепенному заучиванию таблицы умножения, сначала на 2, потом на 3 и так далее до 9.

Объясните особенности умножения на 1 и на 10:

При умножении любого числа на 1, в результате получите это же число:

1 × 1 = 1

 1 × 2 = 2

 1 × 3 = 3

 1 × 99 = 99

и так далее.

При умножении любого числа на 10, в результате получим то же число, но с добавленным справа нулем: 10 × 3 = 30, один ноль, потому что в цифре 10 один ноль, а если умножать не на 10, а на 100, то получим справа два нуля: 100 × 3 = 300. И так далее с 1000, 10000…

То есть для того, чтобы умножить число на 10, 100, 1000 и так далее (например 4 × 10), сначала вспоминаем правило умножения на 1, то есть пишем то же число (4) и дописываем к нему справа столько нулей, сколько во втором множителе (10), (4 × 10 = 40).

Таблица умножения:

Про особенности умножения на 9 мы писали в статье “Чудеса умножения“.

О том как выучить таблицу умножения, читайте в статье “Как выучить таблицу умножения“.

После того (или вместе с тем), как ребенок освоит таблицу умножения, знакомим его с таблицей Пифагора:

В таблице Пифагора по вертикали (в первом столбце) и горизонтали (в первой строке) расположены числа от 1 до 10. На пересечении строк и столбцов располагаются произведения этих чисел:

Проверить таблицу умножения можно следующим образом. Нарисуйте таблицу Пифагора, не заполняя произведения, заштрихуйте некоторые ячейки следующим образом:

Теперь пусть ребенок самостоятельно заполнит заштрихованные клетки, должно получиться следующее:

Теперь сами придумайте рисунок.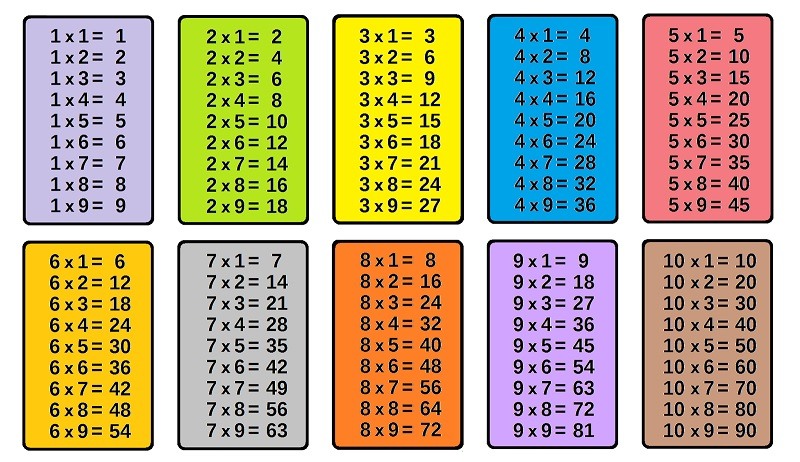

Если вы хотите получать анонсы наших статей, подпишитесь на рассылку “Новости сайта”.

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

выбор слова — два раза три

На это действительно можно ответить, если посмотреть, как мы используем и «умножить на два» («умножить на три», «умножить на четыре» и т. д.) как отдельную фразу для умножения чего угодно. предшествует и «два раза» («трижды», «четыре раза» и т. д.) как отдельная фраза для умножения всего, что идет после нее.

Вот несколько цитат из Корпуса современного американского английского:

*

Знаете ли вы, каково это иметь тройню? всего все умножить на три : три пары грязных ручонок, размазывающих еду по всей вашей новой одежде чихуахуа; три пары ног в странных мягких башмачках; три пары глаз, карие, как у моего мужа.

• Географически Иран намного больше страны, чем Ирак. Население в три раза больше населения

• Ей ни за что не придется платить 333 доллара в час, умножить на три , за секс с этим парнем.

• На кону 518 делегатов, что более в три раза превышает число , присужденное до сих пор в непредсказуемом соревновании

• Новая краска. Новая мебель. Все эти особые штрихи для новорожденного раза три.

• армия, в основном состоящая из афинян, разгромила персидскую армию ветеранов , в три раза превышающую ее численность

• — 88 ключей захватили семью.
  — Это верное утверждение. Я имею в виду буквально, потому что там не было 88 клавиш. Это было 88 раз два, три раза, четыре раза и, наконец, пять раз.
  — Пять роялей в доме?
  — Да.

• Светодиод может работать в два-три раза дороже, чем по сравнению с обычными источниками света

• В следующем месяце вы выписываете три чека на 100 долларов и вкладываете каждый в конверт, в котором просят только 50 долларов, и теперь вы чувствуете, что у вас есть настоящие деньги, сбережения, , как будто вы потратили 50 долларов и сэкономили 50 долларов, как будто у вас есть 50 долларов, которые нужно потратить, и это умножить на три.

• Меркурий, умноженный на три
  За три пролета MESSENGER снимает портреты частей Меркурия[.]

• А понесли почти в три раза больше раненых

• Нефертити Таймс Три

• Я видел нож, парень, который был, вероятно, в три раза больше моего папы

• После «Спи спокойно, милый» трижды , мы с Ионой редко переставали быть родителями.

• FUNAI патрулирует 54 000 квадратных миль отдаленной территории, площадь которой более в три раза превышает площадь Швейцарии

• Я мог ощущать чувства других людей в три раза глубже

  чем другие дети, и моя реакция будет раза три . [Глядь — оба варианта в одном предложении!]

Их гораздо больше, но суть вы поняли.

Если бы «A умножить на B» имело бы только одно возможное дерево синтаксического анализа, только один из двух вариантов был бы продуктивным, и, таким образом, половина приведенных выше кавычек была бы неграмматической и действительно не существовала бы. Но все они есть и все в порядке, что доказывает коммутативность умножения не только в математике, но и в английском языке.

TL;DR: Иногда в «А умножить на Б» часть «умножить на В» считается единой единицей, в других случаях это «умножить на А». Оба чтения возможны и продуктивны, и достаточно часто вы даже можете использовать их полностью взаимозаменяемо, ничего не реструктурируя. Вы можете патрулировать территорию, в три раза превышающую площадь Швейцарии, и вы можете патрулировать территорию, в три раза превышающую территорию Швейцарии.

Итак, 2×3 — это 2+2+2, это 3+3.

Редактировать: Важно отметить, что это верно не для всех языков. Например, в русском языке «трижды два» можно разобрать только как «[трижды] два»; разбор «три [умножить на два]» невозможен. Так что вопрос о том, как английский справляется с этим, действительно правильный вопрос, и действительно вопрос об английском языке, а не о том, как вообще работает человеческий мозг.

Умножение дробей с помощью стержней Кюизенера

Умножение — это операция, значение которой многие учащиеся не понимают. Когда он сочетается с дробными значениями, проблема понимания операции умножения с дробными значениями требует серьезного изучения с множеством различных возможностей.

Использование стержней Кюизенера может быть одним из них. Они могут обеспечить конкретные пропорциональные представления для числовых значений и операций. В этой статье рассматривается умножение с дробными значениями.

Обзор

• Знакомство со Жезлами
• Представление дробей с помощью стержней Кюизенера
• Дробные представления
• Введение в умножение дробей
• Дробные числа меньше, чем одно целое число
• Дробные числа, умноженные на дробные числа
• Смешанный раз смешанный

Знакомство со стержнями Кюизенера

Количество стержней – десять, длина – от 1 до 10 см.

Каждая длина определяется уникальным цветом:
Белый, красный, светло-зеленый, фиолетовый, желтый, темно-зеленый, черный, коричневый, синий и оранжевый

Заглавные буквы используются для обозначения различных стержней. Обратите внимание, что шаблон использует начальную букву до тех пор, пока не появятся три буквы «В», поэтому используются конечные буквы, а затем возвращаются к начальной букве для оранжевого цвета.

Представление дробей с помощью стержней Кюизенера

Для представления дробей или операций с дробями с помощью стержней Кюизенера необходимо выбрать стержень или комбинацию стержней для одного целого или единичного значения.

Ниже приведены некоторые из бесконечных возможностей, которые можно использовать целиком или по отдельности.

Задания, в которых используются конкретные модели, позволяют учащимся научиться создавать мысленные представления на основе визуальных аспектов конкретных моделей. Эти мысленные представления необходимы для понимания дробей и их операций.

Некоторые примеры дробных представлений

Пример с более короткими обозначениями.

Как бы вы завершили эти пять?

Ответы :

• W = 1/2
• Г = 1/3
• Р = 2
• R = 2/3 и D = 2

Образцы больше единицы

Когда учащиеся освоят дроби меньше единицы, им следует давать задачи с целыми числами и дробями больше единицы, смешанными числами.

Как бы вы их завершили?

Ответы :

• 2
• 3
• 4 1/2

 

Введение в умножение дробей

Умножение дробей можно разделить на четыре группы. Давайте кратко рассмотрим каждый тип, чтобы увидеть отношения между факторами и продуктами.

Позже мы рассмотрим каждый тип более подробно и некоторые учебные аспекты.

Первое: умножение дроби на дробь .

Когда дробь, меньшая единицы, умножается на другую дробь, меньшую единицы, результатом является произведение меньшего, чем любой из множителей.

Например , представьте себе такую ​​задачу:

У человека есть половинка шоколадного батончика и он делится ею с другом. Сколько получает каждый человек?

1/2 1/2 батончика = 1/4 батончика.

Три способа установки со стержнями Кюизенера:

При умножении целых чисел произведение всегда больше любого из множителей.

Здесь произведение меньше любого множителя. Это может быть проблемой для студентов, которые считают, что произведение умножения всегда больше, чем множители.

Второй тип: умножение целого числа на дробь

Второй тип — это умножение целого числа на дробь.

Например, после того, как дети закончили есть пиццу, осталось только три коробки с пиццей, и в каждой было около 1/4 пиццы. Сколько пиццы осталось?

3 коробки Х 1/4 пиццы = 3/4 пиццы фракция. Стоимость этого продукта находится между двумя факторами, если только один из факторов не равен единице; тогда он равен другому множителю. Задачи этого типа по-прежнему не соответствуют ложному предположению, что умножение производит больше произведений, чем множители.

Мама говорит, что я могу посмотреть половину фильма, потом заняться домашними делами, а когда домашние дела будут сделаны, я могу посмотреть остальное. Фильм идет два с половиной часа. Когда я должен заняться домашними делами, если я начну смотреть фильм сейчас?

1/2 от 2 1/2 часов = 1 1/4 часа

Четвертый: умножение смешанного числа на смешанное число

чем любой фактор. Например,
Хуан берет напрокат два фильма по два с половиной часа каждый. Он посмотрел полтора, прежде чем уйти на тренировку. Сколько часов фильмов он отсмотрел (просмотрел)?
1 1/2 от 2 1/2 =

Краткое изложение четырех способов умножения дробей

Четыре сравнения, рассмотренные выше:

1. Дробь, умноженная на дробь: 1/2 * 1/2,
2. Целое число, умноженное на дробь: 2 * 1/2 или дробь, умноженная на целое число 1/2 * 2,
3. Дробь, умноженная на дробь: 1/2 * 1 1/2 или смешанное число, умноженное на дробь: 1 1/2 * 1/2, и
4. Смешанное число, умноженное на смешанное число 1 1/2 * 1 1/2.

Частично они выводятся из физического вида цифр для каждого фактора.

Однако существует также связь между значениями продукта и факторами. Продукты не только наименьшие, когда факторы наименьшие, но и величины этих продуктов меньше, чем сами факторы. Это интересно и полезно знать.

Например:

Множители меньше единицы:

• 1/2 от 1/2 = 1/4
• 1/2 * 2/3 = 1/3
• 1/2 х 1/5 = 1/10
• 1/2 * 1/4 = 1/8

Один множитель меньше единицы, а другой больше единицы:

• 1/2 от 2 = 1
• 1 /2 х 3 = 1 1/2
• 1/2 * 1 1/2 = 3/4

Оба множителя больше единицы:

• 1 1/2 * 1 1/2 = 2 1/4
• 1 1/2 x 2 1/2 = 3 3/4
• 1 1/2 от 2 = 3

Один фактор равен одному:

• 1/2 от 1 = 1/2
• 1 * 2 1/2 = 2 1/2
• 2 1/4 х 1 = 2 1/4

Учебные рекомендации

При обучении умножению дробей большинство преподавателей начинают с умножения дробей меньше единицы и целых чисел. Обычно находят дробные части целых чисел, которые приводят к хорошим продуктам (1/2 x 4 = 2, хорошо, 1/2 от 5 не очень).

Затем перейдите к целым числам, умноженным на дроби: 4 * 1/2 = 2.

Затем обе дроби меньше одной 1/2 от 1/2 = 1/4. Как только учащиеся узнают, как решать такие типы задач, слишком многие учителя считают, что учащиеся могут обобщить процедуру, которая работает для умножения дробей всех типов. Эта практика, отсутствие понимания умножения дробей оставляет большинство людей в неведении о понимании умножения дробных чисел и различных отношениях факторов и продуктов.

Палочки Кюизенера помогают учащимся создавать и обобщать мысленные представления, расширяя их понимание дробей до операции умножения на дроби и возникающих взаимосвязей.

Постановка и решение задач на дробные числа, меньшие одного умножения на целые числа

Начнем с 1/3 от 3.

Первое, что нужно сделать, это решить, что использовать для представления единицы. Если белый выбран как один, то светло-зеленый будет иметь значение три, потому что три белых составляют светло-зеленый, следовательно, одна треть светло-зеленого стержня может быть представлена ​​​​белым, а мы уже знаем, что белый — это один, поэтому 1 /3 из 3 = 1,

Давайте посмотрим на другое произведение, которое больше единицы, 1/3 от 6 = 2.

Опять же, первое, что нужно сделать, это решить, что использовать для представления одного. Если мы выберем белый как один, то светло-зеленый будет иметь значение шесть. Три красных составляют зеленый, поэтому одна треть светло-зеленого — это красный, поскольку белый — это один, тогда красных будет два.

Давайте попробуем решить задачу с продуктом меньше единицы, 1/3 от 1.

У Чи есть упаковка мясного фарша весом один фунт, и она хочет приготовить три гамбургера.

Если белые представляют один, это означает, что у нас не будет стержней меньше белого цвета для представления трех гамбургеров. Чтобы решить эту проблему, выберите стержень большего размера, чтобы использовать его для упаковки мяса весом в один фунт, чтобы были стержни меньшего размера для представления гамбургеров.

Учащиеся, которые раньше использовали стержни, узнают, что если они считают светло-зеленый = 1, то белый цвет можно использовать для представления гамбургеров, потому что 3 белых стержня = 1 зеленому стержню. Следовательно, светло-зеленый в этом представлении равен единице, а белый меньше единицы, или 1/3.

Учащимся необходимо несколько раз попрактиковаться в задачах на умножение дробных значений меньше единицы и целых чисел с помощью стержней, а также с другими манипуляциями и представлениями.

Самая большая трудность для учащихся – умение связать дробные числа. значения и целые значения на один и тот же стержень и плавно переходя от задачи к задаче. это развитие веха, которую учащиеся изо всех сил пытаются получить для понимания дробей, разрядное значение, кратные числа и другие математические понятия.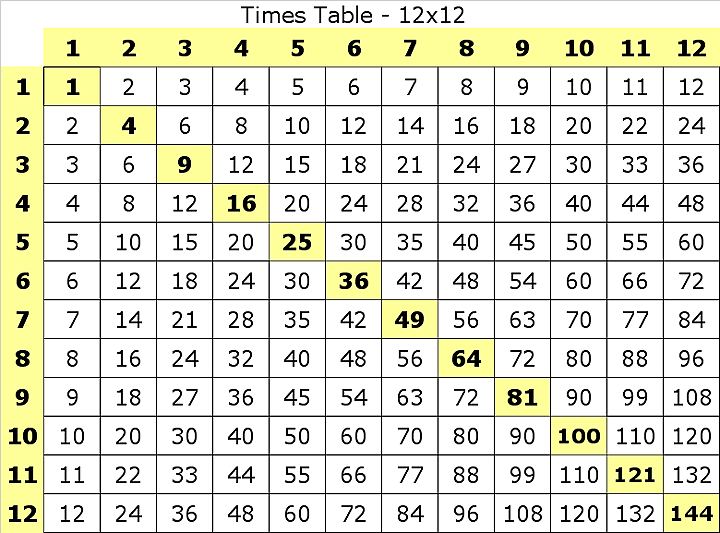

Постановка и решение задач на целые числа, умноженные на дробные числа меньше единицы

Предыдущие примеры включали дробную часть, умноженную на целое число меньше одного раза со значением единицы и больше: 1/3 X 3 = 1, 1/3 X 6 = 2 и 1/3 X 1 = 1/3

Однако примеры целых чисел, умноженных на дробные числа меньше единицы: 3 X 1/3 = 1, 6 X 1/3 = 2 и 1 X 1 /3 = 1/3 не были включены.

В то время как учащиеся, которые понимают свойства умножения, могут использовать свойство перестановочности и рационализировать три раза, когда одна треть равна одной трети от трех (3 * 1/3 = 1/3 * 3) и аналогично для других. Есть разница в том, как эти проблемы возникают в мире и представляются.

Способность понимать, представлять и решать задачи с дробными значениями и операцией умножения требует большего, чем знание 3 * 1/3 = 1/3 * 3 по свойству коммутативности.

Итак, давайте рассмотрим пример с целым числом и дробью со значением меньше единицы.

У Кейт есть три видео. Каждая длится треть часа (20 минут). Если она будет смотреть их всех подряд, сколько это займет времени?

Для этой задачи треть часа нужно представить три раза. Если светло-зеленый представляет один час, то белый может представлять одну треть часа.

Для решения задачи требуется три белых, по одному на каждое третьечасовое видео. Три трети часа или 1 час.

Больше дробных чисел меньше, чем одно целое число

Вы можете подумать, что примеры были подогнаны под размеры стержней, и задаетесь вопросом, что происходит, когда подгонка не так хороша.

Давайте посмотрим, как настроить такую ​​задачу, как одна треть из пяти.

• Что составляет треть пяти пальцев? (брутто?)
• Если у меня есть пять мешков с почвой и я хочу положить по одной трети в каждый из трех горшков, сколько мешков пойдет в каждый?

Поскольку светло-зеленый — это первая известная нам удочка, которая может быть сопоставлена ​​с тремя другими удочками (тремя белыми), мы можем использовать ее как одну. Если представить светло-зеленый цвет как один, то пять светло-зеленых палочек представляют пять. Пять светло-зеленых палочек или сочетание оранжевого и желтого также представляют собой пять светло-зеленых. В любом случае желтый стержень будет на 1/3 из пяти светло-зеленым или комбинацией оранжевого и желтого.

Еще …

Вы, наверное, заметили, что все примеры имеют только одну дробную часть или числитель один. Также возможно представлять дробные числа меньше единицы, с несколькими дробными частями (числитель больше единицы), умноженными на целое число.

Пример 1

У Майка было десять десятицентовиков, и он отдал три пятых Джозе. Сколько получил Хоза?

Три пятых десяти. Нужно представлять группу из десяти десятицентовиков. Если белый представляет собой одну центовую монету, то оранжевый представляет десять. Одна пятая — это красный цвет, поэтому три пятых — это три красных, один красный равен двум десятицентовым монетам, а три — шести десятицентовым монетам.

Пример 2

Группа из одиннадцати детей шла в кино, когда один из них заметил, что потерял деньги, чтобы попасть в шоу. Остальные десять решили, что если каждый даст три пятых доллара этому одиннадцатому человеку, этого будет достаточно для того, чтобы купить билет в кино. Сколько дали этому человеку? (10 х 3/5).

Давайте попробуем два способа: 3/5 х 10 и 10 х 3/5:

Если мы позволим белым представлять один доллар, то оранжевый будет десять долларов. Одна пятая часть оранжевого — красный, поэтому три пятых — это три красных. Стоимость в долларах была установлена ​​как белая, равная одному доллару. Следовательно, оранжевый цвет равен десяти долларам, красный — двум долларам, а три красных — шести долларам.

Второй способ представления этого числа состоит в том, чтобы изобразить три пятых доллара светло-зеленым цветом, взять десять из них и найти значение для всех десяти.

Пример 3

Папа всегда пытается заставить людей думать, поэтому он говорит такие вещи, как на столе три пакета, вам нужно взять две трети из них (2/3 X 3). Сколько мне нужно было взять?

Давайте попробуем это же двумя способами: 2/3 X 3 и 3 X 2/3:

Первые две трети из трех:

Второй трижды по две трети или три группы по две трети:

Для 3 x 2/3.
Зеленый был выбран для обозначения одного из них.
Если зеленый = 1, то красный = 2/3
Следовательно, три красных стержня представляют собой три группы по две трети.

Резюме

Учащимся труднее работать с дробными частями больше единицы/части (1/2, 1/3, 1/4, 1/5…). Им требуется время, чтобы обобщить свое понимание от одной трети до двух третей и других кратных дробных частей для других дробей.

Учащимся нужно дать время, чтобы соединить их прежнее понимание сложения и умножения целых и дробных чисел. Когда они это сделают, они поймут, что две трети можно представить себе как две трети, умноженные на одну треть, или одну треть, добавленную дважды.

Для понимания дробных значений, когда множитель имеет числитель больше единицы, мы должны знать, что он кратен единице дробной части. Например, три пятых кратны одной пятой. Следовательно, три пятых имеют множители 3 и 1/5.

Предыдущий опыт работы с кратными, пропуском счета, умножением в виде строк и столбцов, площадью, прямоугольниками, квадратами и повторным сложением необходим для понимания дробей и умножения.

Дробные числа меньше единицы, умноженные на дробное число меньше единицы

Правильная дробь умножается на правильную дробь, но я не люблю называть дроби правильными и неправильными. Это дроби, и иногда одна полезнее другой, но эта полезность может определяться только использованием, а не формой, в которой находится число.

Вы наверняка поняли, что знание того, что представлять как единицу, является ключом к получению точного решения. Любая реальная или мировая проблема требует, чтобы для каждой проблемы было выбрано единичное значение, представляющее значение единицы. Это действительно помогает отметить это как часть представления, чтобы все знали присвоенные значения.

Давайте рассмотрим несколько примеров того, как дробные числа меньше единицы умножаются на дробное число меньше единицы.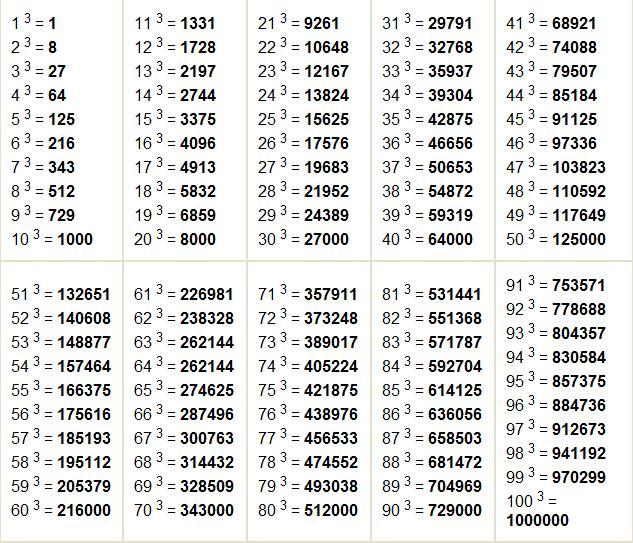

Пример 1:

Папа, брат и я косили соседский двор. Мы с братом скосили половину переднего двора, что, по словам отца, составляло две пятых всего двора. Какую часть всего двора я косил? 1/2 фасада, что составляет 2/5 всего двора.

Сначала решите, что использовать как единицу, чтобы можно было представить две пятых.

Затем спросите, что такое половина двух пятых, и представьте ее.

Затем определите значение Белого, если Желтое равно единице. Учащимся, возможно, потребуется напомнить, чтобы они спросили, какую часть целого (одного стержня или единицы) представляет верхний стержень. В этом случае белый — это и 1/2 от 2/5, и 1/5 от желтого или один. Это проблема многих маленьких детей. Объекты, имеющие одинаковые одновременные значения.

Вам может быть интересно, как учащиеся выбирают удочку для единицы (одной). Для задачи, которую мы только что решили, мы знали, что хотим сделать две пятых, поэтому имеет смысл выбрать стержень, который можно использовать для представления пятых. Есть только два стержня, из которых можно выбрать: Желтый и Оранжевый. Если вы раньше не использовали удилища Кюизенера, вам придется подумать об этом. Те, кто испытал их в течение нескольких часов, думая о том, какие стержни можно использовать для создания поездов, чтобы соответствовать другим стержням, будут знать, какие цветные стержни можно использовать, чтобы равномерно соответствовать другим. Может быть даже полезно предложить учащимся составить список или таблицу этих отношений.

Итак, для этой задачи мы использовали желтый цвет, но давайте посмотрим, как он был бы представлен, если бы он был оранжевым.

Во-первых, мы решили использовать Оранжевый как единицу, чтобы две пятых были представлены красным.

Затем спросите, что такое половина двух пятых, и изобразите это красным.

Затем определите значение 1/2 от 2/5. Так как Оранжевый — один, то Красный — 1/5 его. Опять же, многим учащимся нужно будет напомнить, чтобы они спросили, какая часть
целого (одного стержня или единицы) представляет верхний стержень.

При выборе чего-либо для представления единицы или единицы, думать о том, какие стержни соответствуют другим стержням, не работает, тогда это простое правило всегда будет работать:

Сначала попробуйте использовать знаменатель второго множителя. Если это не сработает, умножьте знаменатели и определите, какой стержень или комбинация стержней потребуется, чтобы получить длину (см) такого количества белых.

Например, если проблема была 2/3 X 4/5. Желтый был бы первым выбором, но 2/3 желтого цвета не могут быть представлены целыми стержнями. Таким образом, 3 * 5 = 15, и вместо одного можно использовать три желтых или оранжевый и желтый. Две трети могут быть представлены двумя желтыми).

Не говорите об этом ученикам. Скажите им, чтобы они подумали о размере частей, которые они хотят использовать. Если не поможет, то подскажите что поможет. Поиск единичного стержня может быть интересным и сложным, но если учащимся предложить умножать знаменатели, некоторые будут продолжать делать это, даже когда это нежелательно. Например, 1/5 х 5/9. Если знаменатели перемножить (45), то четыре оранжевых стержня и один желтый стержень будут представлять один. Эта комбинация будет работать, но использование blueE обеспечивает лучшее представление, чтобы облегчить концептуальное понимание, что облегчит решение задач учащимися и беглость математики. Изучение правил без концептуализации — это процедурное знание без знания того, когда и как его использовать.

Другой пример

Этот пример представляет собой наиболее сложный тип задачи на правильную дробь, умноженную на другую правильную дробь. Их следует избегать до тех пор, пока ученики не освоят остальные.

Мать дала Мэри пакет конфет и велела разделить его с братом и сестрой. Когда ее брат увидел ее с конфетами, он спросил, можно ли ему немного. Мэри сказала ему, что он может, но она должна разделить его между ними тремя. Итак, она и ее брат разделили его на три равные группы. Ее брат взял свою долю и оставил Мэри с двумя третями в мешке. Когда ее сестра обнаружила конфеты, она подошла к Мэри и попросила свою долю. Мэри снова сказала, что ей сказали разделить его на три части и поделиться. Итак, они разделили его на три равные группы, ее сестра ушла со своей, а Мэри положила две трети в мешок. Сколько конфет из первоначального мешка в итоге досталось Мэри?

Проблема :
Конфеты, оставшиеся после того, как ее брату и сестре дали долю, составляют 2/3 конфет, оставшихся после того, как она дала долю ее брату и оставила Мэри 2/3 первоначального мешка.

Сначала подумайте, что вы хотите оштрафовать две трети мешка, в котором две трети того, что было в исходном мешке (2/3 мешка из 2/3 мешка).

Затем решите Пусть bluE = один и найдите две трети синего цвета. Два светло-зеленых.

Затем найдите две трети светло-зеленого (2/3 от 2/3).

Это можно представить двумя способами.

1. светло-зеленый представляет 2/3 синего, а красный представляет 2/3 двух светло-зеленых, которые считаются одним темно-зеленым
2. светло-зеленый представляет 2/3 синего, а белый представляет 2/3 светло-зеленого

Сложность понимания умножения дробей связана с распознаванием частей и целых чисел, а также того, как они соотносятся и изменяются в зависимости от их значений и операции умножения.

Примером такой двойственности значений является ситуация, когда две светло-зеленые палочки используются как две части (2/3), а также вместе как единое целое (2/3), чтобы определить, что составляет две трети.

Чтобы понять эти взаимосвязи, учащимся требуется много времени, чтобы испытать, интерпретировать, построить понимание и связать это понимание. Один из способов выделить время для достаточного опыта состоит в том, чтобы либо отложить обучение умножению дробей процедурно, либо полностью прекратить обучение этому процедурно и позволить ученику изобретать свои собственные алгоритмические процедуры.

Чтобы понять, почему произведения дробей так разнообразны. Использование конкретных представлений помогает учащимся понять, почему, и начинает предлагать различные подходы к размышлению о проблемах.

Смешанная дробь, умноженная на смешанную дробь

Задачи на умножение смешанной дроби на смешанную дробь можно решить путем умножения четырех множителей и сложения произведений. Хотя эта идея важна для понимания умножения, она не так очевидна, когда для решения подобных задач используется стандартный алгоритм.

Давайте посмотрим, как можно объединить предыдущие идеи для умножения смешанных дробей:

Пример 1 1/2 X 2 1/2:

Сначала определите коэффициенты, которые необходимо умножить.

Затем решите, как его изобразить.

После того, как решено, как будет представлена ​​единица, можно решить задачу путем умножения четырех пар чисел: 1 x 2, 1 x 1/2, 1/2 x 2 и 1/2 x 1/. 2. Как показано выше.

Однако, когда человек поймет, как работает умножение дробей, он сможет найти всевозможные короткие пути. Например: в задаче 1 1/2 умножить на 2 1/2 ее можно решить мысленно, подумав:

1 х 2 1/2 = 2 1/2 и 1/2 х 2 1/2 = 1 1/4.
Затем объедините 2 1/2 + 1 1/4, чтобы получить 3 3/4

Другой пример: 12 1/4 X 12 1/4
12 х 12 = 144 900 62 12 х 1/4 = 3
1/4 х 12 = 3
1/4 х 1/4 = 1/16
144 + 3 + 3 + 1/16 = 150 1/16

Я считаю, что это проще, чем использование традиционного алгоритма, когда нужно умножить 49 x 49 и разделить этот продукт, 1401, на 16, и, что более важно, это приходит с пониманием.

Учащиеся, имеющие достаточный конкретный опыт, поймут все методы и будут иметь уверенность и способность выбирать стратегию, основанную на точных мысленных образах. Алгоритм не помогает учащимся концептуально понять умножение дробей. Поэтому, хотя это может быть быстрее, нужно понимать, почему пары чисел должны быть умножены и что это означает для каждого типа.

Резюме

Некоторые ученики всегда хотят запомнить правило, потому что они отказались от мысли, что они могут понять математику, или они не видят никаких преимуществ в решении задач, кроме как с помощью правил. Они обнаруживают, что все, что им обычно нужно сделать, это взять правило и использовать его, когда им представляют проблемы, уже поставленные на рабочих листах, но жизнь не представляет проблемы таким образом.

Предлагая задачи в реальных ситуациях и предлагая учащимся понять их мир, большинство учащихся будут тратить время и усилия, чтобы научиться использовать математику, чтобы понимать и объяснять мир.