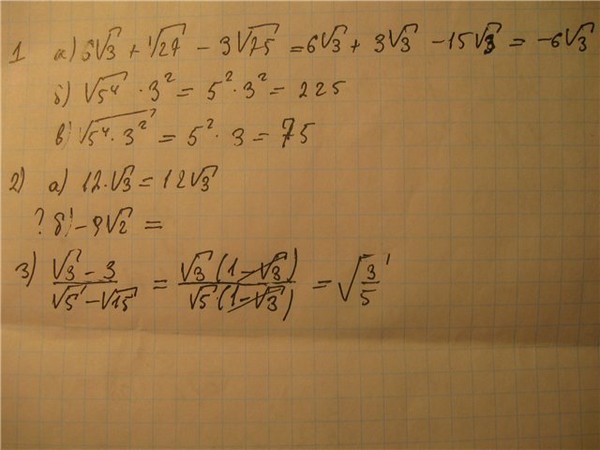Радикалы и абсолютные значения — Концепция
Поскольку любой четный корень должен быть положительным числом (в противном случае он будет мнимым), при упрощении корней с переменными необходимо использовать абсолютное значение, что гарантирует положительный ответ. При работе с подкоренными выражениями это требование не распространяется ни на один нечетный корень, потому что нечетные корни существуют для отрицательных чисел. Кроме того, абсолютное значение не нужно, если из корня выходит четное число переменной — ответ должен быть положительным.
При работе с подкоренными выражениями это требование не распространяется ни на один нечетный корень, потому что нечетные корни существуют для отрицательных чисел. Кроме того, абсолютное значение не нужно, если из корня выходит четное число переменной — ответ должен быть положительным.
абсолютное значение квадратные корни даже корень нечетная степень
Абсолютное значение и квадратные корни, поэтому сейчас мы поговорим об абсолютных значениях, и иногда случается так, что нам действительно нужно абсолютное значение, когда мы даем наш ответ, и что мы собираемся делать это посмотреть на ряд примеров и поговорить о том, когда они нам нужны, а когда нет.
 3 в квадрате равно 9, квадратный корень из девяти равен 3. Квадратный корень из минус 3 в квадрате. Когда мы возводим в квадрат отрицательное число, мы на самом деле получаем положительное, поэтому -3 умножить на -3 равно 9.квадратный корень из 9 снова равен 3. Хорошо, кубический корень из 8 имеет три двойки в восьми, поэтому получается 2, а кубический корень из минус 8 равен -2. Отрицательное 2, умноженное на 3, само по себе является отрицательным восемью, поэтому мы рассмотрели здесь, когда у нас есть нечетный корень, хорошо, кубический корень, здесь мы можем получить положительный ответ или отрицательный ответ.
3 в квадрате равно 9, квадратный корень из девяти равен 3. Квадратный корень из минус 3 в квадрате. Когда мы возводим в квадрат отрицательное число, мы на самом деле получаем положительное, поэтому -3 умножить на -3 равно 9.квадратный корень из 9 снова равен 3. Хорошо, кубический корень из 8 имеет три двойки в восьми, поэтому получается 2, а кубический корень из минус 8 равен -2. Отрицательное 2, умноженное на 3, само по себе является отрицательным восемью, поэтому мы рассмотрели здесь, когда у нас есть нечетный корень, хорошо, кубический корень, здесь мы можем получить положительный ответ или отрицательный ответ.  Что происходит, так это то, что мы возводим его в квадрат, чтобы он стал положительным, а затем извлекаем из него квадратный корень, чтобы он на самом деле оставался положительным, потому что мы не знаем, является ли x положительным или отрицательным, мы должны поставить знаки абсолютного значения снаружи чтобы сделать этот термин положительным, хорошо, поэтому квадратный корень из x в кубе. Мы можем убрать один х, и у нас все еще останется один х внутри, но мы знаем, что это должно быть положительным, потому что мы не можем извлечь отрицательное значение из квадратного корня, поэтому еще раз мы должны ввести абсолютное значение знаки в порядке, потому что все, что выходит из квадратного корня, должно быть положительным. Хорошо, а как насчет квадратного корня из x в четвертой степени. Хорошо, мы знаем, что это 4 х, поэтому мы можем убрать 2 из них, оставив нам х в квадрате. Нужны ли в этом случае абсолютные значения? Нет, потому что х в квадрате всегда будет положительным, хорошо? Итак, всякий раз, когда нам нужны абсолютные значения, в основном это одно из практических правил, которое я всегда использую, когда вы берете четный корень, так что здесь это квадратный корень, здесь на самом деле немного невидимая 2 и всякий раз, когда вы берете четный корень и у нас есть добавочная мощность для переменной, хорошо, так что здесь у нас есть один х, один х, х в квадрате.
Что происходит, так это то, что мы возводим его в квадрат, чтобы он стал положительным, а затем извлекаем из него квадратный корень, чтобы он на самом деле оставался положительным, потому что мы не знаем, является ли x положительным или отрицательным, мы должны поставить знаки абсолютного значения снаружи чтобы сделать этот термин положительным, хорошо, поэтому квадратный корень из x в кубе. Мы можем убрать один х, и у нас все еще останется один х внутри, но мы знаем, что это должно быть положительным, потому что мы не можем извлечь отрицательное значение из квадратного корня, поэтому еще раз мы должны ввести абсолютное значение знаки в порядке, потому что все, что выходит из квадратного корня, должно быть положительным. Хорошо, а как насчет квадратного корня из x в четвертой степени. Хорошо, мы знаем, что это 4 х, поэтому мы можем убрать 2 из них, оставив нам х в квадрате. Нужны ли в этом случае абсолютные значения? Нет, потому что х в квадрате всегда будет положительным, хорошо? Итак, всякий раз, когда нам нужны абсолютные значения, в основном это одно из практических правил, которое я всегда использую, когда вы берете четный корень, так что здесь это квадратный корень, здесь на самом деле немного невидимая 2 и всякий раз, когда вы берете четный корень и у нас есть добавочная мощность для переменной, хорошо, так что здесь у нас есть один х, один х, х в квадрате.