натуральные числа, двузначные числа, распечатать фото в хорошем качестве с крупными цифрами
Мы составили таблицу квадратов натуральных чисел до 10 и двузначных чисел, которой удобно пользоваться: благодаря ей не нужно в уме возводить число во вторую степень. Достаточно распечатать таблицу и найти в ней подходящее значение
Таблица квадратов от 1 до 100. Фото: shutterstock.comАлександр Мельников Преподаватель информатики и математики Анна Стрельцова Автор КП
Содержание
- Таблица квадратов натуральных чисел
- Таблица квадратов двузначных чисел
- Таблица квадратов до 100
- Вопросы и ответы
Квадратом числа называют произведение на самого себя один раз или возведение во вторую степень. В школе это действие проходят в 5 классе. Например, чтобы вычислить квадрат числа 5, нужно умножить его на 5: в итоге получится 25. С натуральными числами до 10 вычисления довольно просты, а посчитать квадрат двузначного числа в уме уже сложнее. Поэтому для удобства можно пользоваться таблицами: это облегчает вычисления.
В школе это действие проходят в 5 классе. Например, чтобы вычислить квадрат числа 5, нужно умножить его на 5: в итоге получится 25. С натуральными числами до 10 вычисления довольно просты, а посчитать квадрат двузначного числа в уме уже сложнее. Поэтому для удобства можно пользоваться таблицами: это облегчает вычисления.
Таблица квадратов натуральных чисел
Натуральные числа — те числа, которые мы используем при счете или при перечислении вещей, объектов. К натуральным относятся только полные и неотрицательные числа. В математике их много: поэтому мы сделали таблицу квадратов натуральных чисел от 1 до 10.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| n² | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
Таблица квадратов двузначных чисел
Чтобы вычислить квадрат двузначного числа, умножить число на самого себя. В результате получается уже четырехзначное число. Если при вычислении квадратов чисел до 10 достаточно вспомнить таблицу умножения, то посчитать квадрат двузначного числа в уме уже сложнее. Проще всего для таких вычислений использовать таблицу.
В результате получается уже четырехзначное число. Если при вычислении квадратов чисел до 10 достаточно вспомнить таблицу умножения, то посчитать квадрат двузначного числа в уме уже сложнее. Проще всего для таких вычислений использовать таблицу.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 362 |
| 2 | 200 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 300 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Скачать таблицу двузначных чисел
Таблица квадратов до 100
В таблице мы собрали квадраты чисел от 1 до 100: она пригодится как школьникам, так и студентам. Вы можете распечатать таблицу или пользоваться ей онлайн.
Вы можете распечатать таблицу или пользоваться ей онлайн.
| 1²=1 | 11²=121 | 21²=441 | 31²=961 | 41²=1681 |
| 2²=4 | 12²=144 | 22²=484 | 32²=1024 | 42²=1764 |
| 3²=9 | 13²=169 | 23²=529 | 33²=1089 | 43²=1849 |
| 4²=16 | 14²=196 | 24²=576 | 34²=1156 | 44²=1936 |
| 5²=25 | 15²=225 | 25²=625 | 35²=1225 | 45²=2025 |
| 6²=36 | 16²=256 | 26²=676 | 36²=1296 | 46²=2116 |
| 7²=49 | 17²=289 | 27²=729 | 37²=1369 | 47²=2209 |
| 8²=64 | 18²=324 | 28²=784 | 38²=1444 | 48²=2304 |
| 9²=81 | 19²=361 | 29²=841 | 39²=1521 | 49²=2401 |
| 10²=100 | 20²=400 | 30²=900 | 40²=1600 | 50²=2500 |
| 51²=2601 | 61²=3721 | 71²=5041 | 81²=6561 | 91²=8281 |
| 52²=2704 | 62²=3844 | 72²=5184 | 82²=6724 | 92²=8464 |
| 53²=2809 | 63²=3969 | 73²=5329 | 83²=6889 | 93²=8649 |
| 54²=2916 | 64²=4096 | 74²=5476 | 84²=7056 | 94²=8836 |
| 55²=3025 | 65²=4225 | 75²=5625 | 85²=7225 | 95²=9025 |
| 56²=3136 | 66²=4356 | 76²=5776 | 86²=7396 | 96²=9216 |
| 57²=3249 | 67²=4489 | 77²=5929 | 87²=7569 | 97²=9409 |
| 58²=3364 | 68²=4624 | 78²=6084 | 88²=7744 | 98²=9604 |
| 59²=3481 | 69²=4761 | 79²=6241 | 89²=7921 | 99²=9801 |
| 60²=3600 | 70²=4900 | 80²=6400 | 90²=8100 | 100²=10000 |
Скачать таблицу двузначных чисел
Популярные вопросы и ответы
Отвечает Александр Мельников, преподаватель информатики и математики онлайн-школы «Коалиция», эксперт ЕГЭ и ОГЭ, сертифицированный преподаватель проекта «Математическая вертикаль».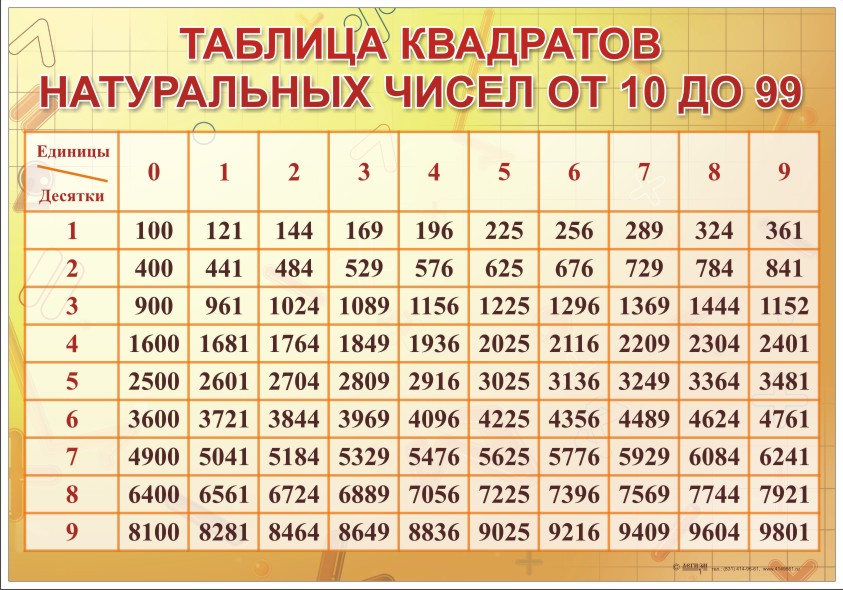
Как пользоваться таблицей квадратов?
Таблица квадратов — это таблица, содержащая квадраты чисел. Квадрат числа — это результат умножения какого-либо числа на самого себя, то есть число, возведенное во вторую степень.
В таблице пересечение цифр слева в столбце и сверху в строке дает квадрат искомого числа. Например, нужно найти квадрат числа 15. В столбце слева берем первую цифру данного числа «1». В самой верхней строке берем вторую цифру данного числа «5». На пересечении данных цифр получаем квадрат числа 15, то есть 225.
Таблицу квадратов также можно использовать для извлечения квадратного корня — обратной операции возведения в квадрат. Например, √225=15.
Как быстро выучить таблицу квадратов?
Если мы говорим о сдаче ОГЭ и ЕГЭ базового уровня по математике, то учить таблицу квадратов необязательно, так как она будет в справочном материале. А вот для ЕГЭ по профильной математике это делать нужно: справочные материалы не предоставляются.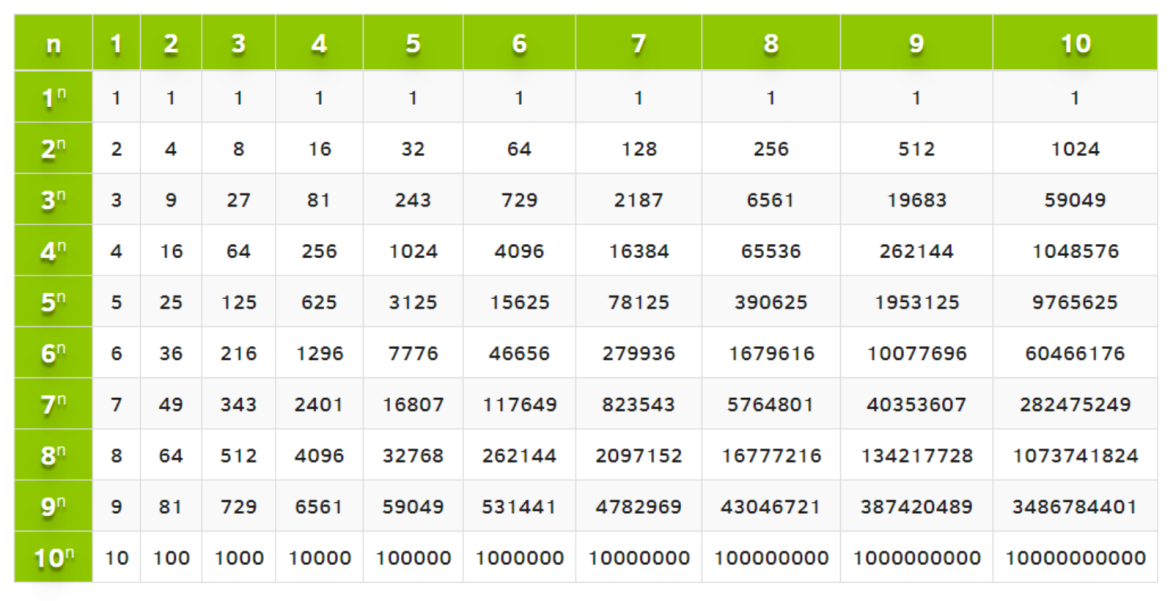 Пригодится таблица квадратов и позже, при обучении в вузе. Вот несколько советов, как это сделать.
Пригодится таблица квадратов и позже, при обучении в вузе. Вот несколько советов, как это сделать.
1. Если число заканчивается на 0, его легко возвести в квадрат — необходимо только дописать пару нулей: 60 х 60 = 3600.
2. Если число заканчивается на 5, то следует умножить первую цифру (x) на (x+1) и дописать к полученному числу «25». 65 х 65 = 6 х 7 = 42 приписываем 25 и получаем 4225.
3. Можно воспользоваться формулой (a + b)2 = a2 + 2ab + b2 . Как мы уже выяснили, возводить в квадрат числа, оканчивающиеся на 0, очень просто. Следовательно, а — это число, которое делится на 10, а b — остаток от деления на 10. Приведем пример. Возведем в квадрат 32. 32 можно представить как 30 (число делится на 10) и 2 (остаток от деления на 10): (30+2)2 = 302 + 2 х 30 х 2 + 22 = 900 + 120 + 4 =1024.
Для начала нужно выучить таблицу квадратов первого десятка, так как она используется чаще всего: 121, 144, 169, 196, 225, 256, 289, 324, 361.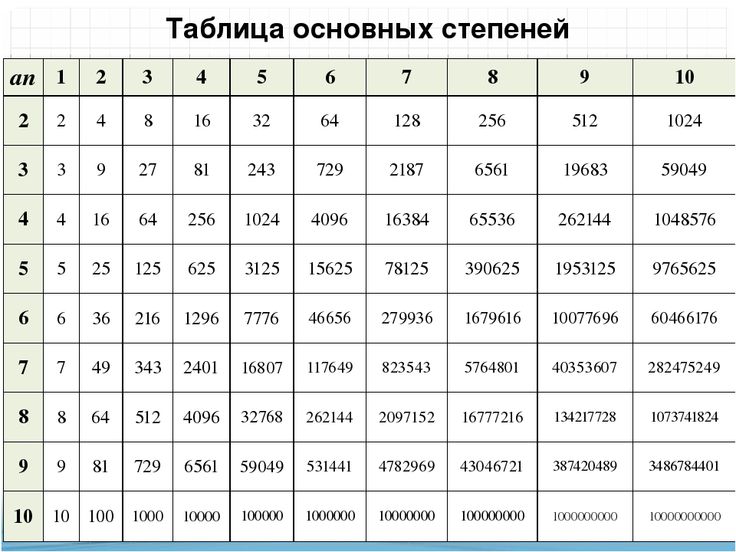 И важно запомнить, что не бывает квадратов, последняя цифра в которых 2, 3, 7, 8. Также часто используются квадраты таких чисел как 21, 24, 25, 26: они встречаются чаще других.
И важно запомнить, что не бывает квадратов, последняя цифра в которых 2, 3, 7, 8. Также часто используются квадраты таких чисел как 21, 24, 25, 26: они встречаются чаще других.
Выучить данные значения квадратов можно довольно быстро: попробуйте просто ежедневно выписывать значения в тетрадь.
Как извлечь корень числа без таблицы квадратов?
Число необходимо разложить на простые множители, например 1225 = 5 х 5 х 7 х 7 = 5272. Значит, √1225 = √(5272) = 5 х 7 = 35. Благодаря разложению на множители можно извлечь корень из многозначного числа, выходящего за рамки таблицы квадратов.
Сколько будет 10 в сотой степени?
Итак, вы хотите знать, сколько будет 10 в сотой степени? В этой статье мы объясним, как именно выполнить математическую операцию под названием «возведение в степень 10 в степени 100». Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
Что такое возведение в степень?
Давайте сначала зафиксируем наши термины, а затем посмотрим, как вычислить число 10 в сотой степени.
Когда мы говорим об возведении в степень, все, что мы на самом деле имеем в виду, это то, что мы умножаем число, которое мы называем 9) для обозначения показателя степени. Знак вставки полезен в ситуациях, когда вы не хотите или не нуждаетесь в использовании надстрочного индекса.
Итак, мы упомянули, что возведение в степень означает умножение базового числа само на себя для получения показателя степени число раз. Давайте посмотрим на это более наглядно:
10 в сотой степени = 10 x … x 10 (100 раз)
Итак, каков ответ?
Теперь, когда мы объяснили теорию, лежащую в основе этого, давайте поработаем над числами и выясним, чему равно 10 в сотой степени:
10 Власть на 100 = 10 100 = 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
Почему мы используем позиционирование, такие как 10 100 в любом случае? Что ж, нам намного проще писать умножения и выполнять математические операции как с большими, так и с маленькими числами, когда вы работаете с числами с большим количеством конечных нулей или большим количеством десятичных знаков.
Надеюсь, эта статья помогла вам понять, как и почему мы используем возведение в степень, и дала вам ответ, который вы изначально искали. Теперь, когда вы знаете, что такое 10 в сотой степени, вы можете продолжить свой веселый путь.
Не стесняйтесь поделиться этой статьей с другом, если вы считаете, что она поможет ему, или перейдите вниз, чтобы найти еще несколько примеров.
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Сколько будет 10 в сотой степени?». VisualFractions.com . По состоянию на 10 апреля 2023 г. http://visualfractions.
 com/calculator/exponent/what-is-10-to-the-100th-power/.
com/calculator/exponent/what-is-10-to-the-100th-power/.«Сколько будет 10 в сотой степени?». VisualFractions.com , http://visualfractions.com/calculator/exponent/what-is-10-to-the-100th-power/. По состоянию на 10 апреля 2023 г.
Сколько будет 10 в сотой степени?. VisualFractions.com. Получено с http://visualfractions.com/calculator/exponent/what-is-10-to-the-100th-power/.
Калькулятор возведения в степень
Хотите найти решение еще одной задачи? Введите число и мощность ниже и нажмите «Рассчитать».
Вычисление возведения в степень
Случайный список примеров возведения в степень
Если вы добрались до этого места, то вам ДЕЙСТВИТЕЛЬНО нравится возведение в степень! Вот несколько случайных вычислений для вас:
Сколько будет 95 в 98-й степени?
Сколько будет 69 в 27-й степени?
Сколько будет 12 в 9-й степени?
Сколько будет 6 в 11-й степени?
Сколько будет 72 в 26-й степени?
Сколько будет 53 в 86-й степени?
Сколько будет 83 в 61-й степени?
Сколько будет 29 в 63-й степени?
Сколько будет 57 в 64-й степени?
Сколько будет 26 в 62-й степени?
Сколько будет 20 в 80-й степени?
Сколько будет 21 в 13-й степени?
Сколько будет 32 в 13-й степени?
Сколько будет 85 в 37-й степени?
Сколько будет 70 в 78-й степени?
Сколько будет 93 в 8-й степени?
Сколько будет 71 в сотой степени?
Сколько будет 99 в 92-й степени?
Сколько будет 29 в 60-й степени?
Сколько будет 19 в 71-й степени?
Сколько будет 57 в 82-й степени?
Сколько будет 37 в 15-й степени?
Сколько будет 69 в 90-й степени?
Сколько будет 18 в 43-й степени?
Сколько будет 20 в 31-й степени?
Сколько будет 19 в 35-й степени?
Сколько будет 67 в 28-й степени?
Сколько будет 100 в 42-й степени?
Сколько будет 4 в 90-й степени?
Сколько будет 28 в 54-й степени?
Что такое 754 в 3-й степени?
Сколько будет 32 в 36-й степени?
Сколько будет 14 в 97-й степени?
Сколько будет 48 в 99-й степени?
Сколько будет 38 в 93-й степени?
Сколько будет 81 в 31-й степени?
Сколько будет 32 в 62-й степени?
Сколько будет 68 в 69-й степени?
Сколько будет 72 в 39-й степени?
Сколько будет 37 в 20-й степени?
Сколько будет 99 в 44-й степени?
Сколько будет 45 в 67-й степени?
Сколько будет 100 в 80-й степени?
Сколько будет 3 в 28-й степени?
Сколько будет 6 в 58-й степени?
Сколько будет 72 в 51-й степени?
Сколько будет 14 в 82-й степени?
Сколько будет 29 в 8-й степени?
Сколько будет 26 в 22-й степени?
Сколько будет 70 в 86-й степени?
Сколько будет 48 в 57-й степени?
Сколько будет 77 в 37-й степени?
Сколько будет 99 в 26-й степени?
Сколько будет 84 в 97-й степени?
Сколько будет 32 в 15-й степени?
Сколько будет 100 в 29-й степени?
Сколько будет 51 в 50-й степени?
Сколько будет 95 в 9-й степени?
Сколько будет 2 в 14-й степени?
Сколько будет 13 в 45-й степени?
Сколько будет 73 в 99-й степени?
Сколько будет 73 в 3-й степени?
Сколько будет 80 в 75-й степени?
Сколько будет 79 в 62-й степени?
Сколько будет 50 в 8-й степени?
Сколько будет 87 в 70-й степени?
Сколько будет 57 в 69-й степени?
Сколько будет 2 в 27-й степени?
Сколько будет 90 в 4-й степени?
Сколько будет 38 в 12-й степени?
Сколько будет 69 в 12-й степени?
Сколько будет 82 в 88-й степени?
Сколько будет 25 в 37-й степени?
Сколько будет 96 в 19-й степени?
Сколько будет 31 в 65-й степени?
Сколько будет 67 в 46-й степени?
Сколько будет 13 в 48-й степени?
Сколько будет 45 в 78-й степени?
Сколько будет 63 в 23-й степени?
Сколько будет 36 в 24-й степени?
Сколько будет 80 в сотой степени?
Сколько будет 89 в 24-й степени?
Сколько будет 33 в 38-й степени?
Сколько будет 17 в 73-й степени?
Сколько будет 75 в 69-й степени?
Сколько будет 39 в 24-й степени?
Сколько будет 94 в 66-й степени?
Сколько будет 86 в 34-й степени?
Сколько будет 23 в 68-й степени?
Сколько будет 66 в 59-й степени?
Сколько будет 55 в 50-й степени?
Сколько будет 90 в 94-й степени?
Сколько будет 25 в 84-й степени?
Сколько будет 86 в 74-й степени?
Сколько будет 16 в 52-й степени?
Сколько будет 85 в 10-й степени?
Сколько будет 94 в 53-й степени?
Сколько будет 99 в 34-й степени?
Сколько будет 53 в 10-й степени?
Сколько будет 96 в 91-й степени?
Сколько будет 32 в 29-й степени?
Как определить основание экспоненты? Определение, примеры, факты
Основание экспоненты – Введение
Ух ты, сколько нулей после единицы.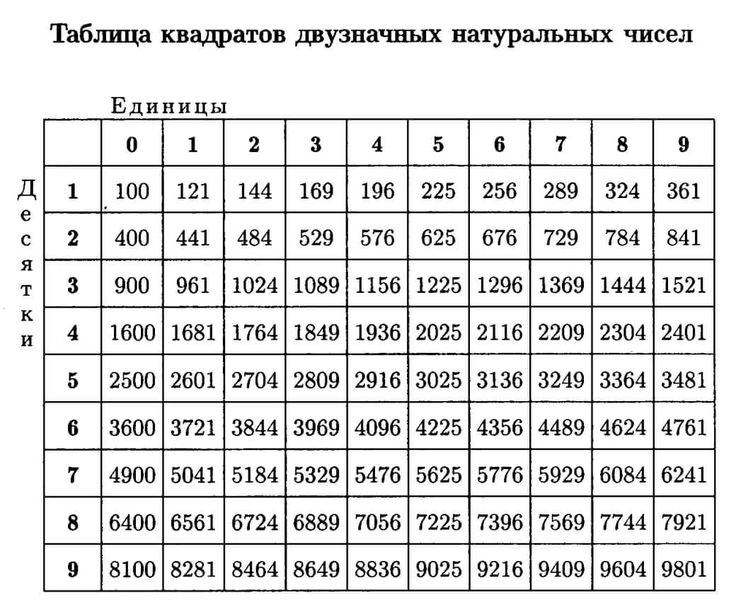 6$ число 10 называется 9.0291 по основанию , а 6 — это показатель степени выражения. Итак, показатель степени — это число или буква, написанная выше и справа от математического выражения, которое является основанием .
6$ число 10 называется 9.0291 по основанию , а 6 — это показатель степени выражения. Итак, показатель степени — это число или буква, написанная выше и справа от математического выражения, которое является основанием .
Напомним, показатель степени числа говорит, сколько раз использовать число с основанием при умножении. Он записывается в виде небольшого числа в верхнем правом углу основного номера . Мы хотим изучить и узнать все об этом числе с основанием 9.0292 номер. Давай начнем!
Связанные листы
Основание показателя степени Определение
Основание показателя степени — это число, возведенное в определенную степень. Итак, основание экспоненты представляет собой число, которое умножается само на себя.
Показатель степени показывает, сколько раз умножается базовое число.
Степень можно определить как число, полученное путем возведения основного числа в степень. Таким образом, это относится к полному выражению. 93 =10 х 10 х 10 = 1000$
Таким образом, это относится к полному выражению. 93 =10 х 10 х 10 = 1000$
Взгляните еще на несколько примеров и пересмотрите основание, мощность и показатели степени.
Интересные факты об экспонентах и их основаниях
- Слово экспонента было придумано в 1544 году Майклом Стифелем .
- В конце шестнадцатого века Йост Бюрги использовал римские цифры для показателя степени .
- Основание с 0 в степени всегда равно 1.
Пример: $92} = \frac{1}{36}$
Часто задаваемые вопросы
Почему показатели степени важны?
Экспоненты очень полезны при записи значений чисел. Повторное умножение записывается простым способом с помощью показателей степени.
Показатель степени важен, потому что очень сложно записать произведение, когда число повторяется само по себе много раз. Гораздо проще написать 4⁸, чем написать $4 \times 4 \times 4 \times 4 \times 4 \times 4 \times 4 \times 4$.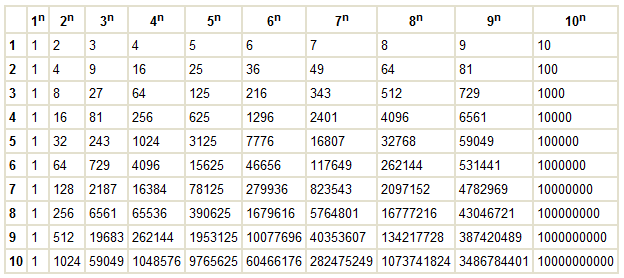

 com/calculator/exponent/what-is-10-to-the-100th-power/.
com/calculator/exponent/what-is-10-to-the-100th-power/.