Римская буква м. Римские цифры или как правильно написать дату римскими цифрами для тату
Здоровье
Мы все пользуемся римскими цифрами – отмечаем ими номера веков или месяцев года. Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.
Как устроены римские цифры
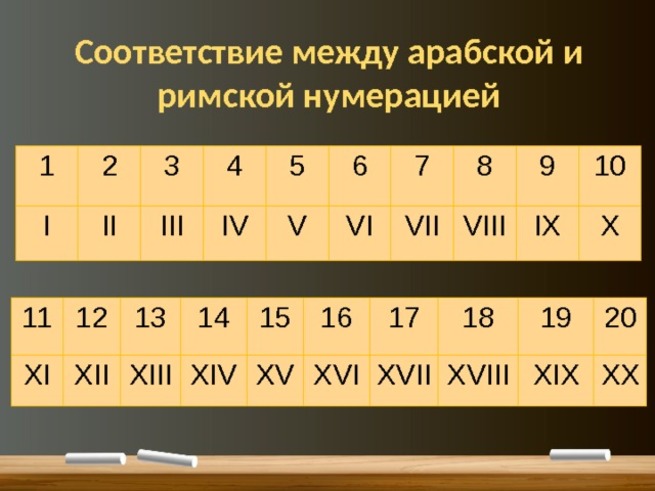
Римская система счета в ее современном варианте состоит из следующих базовых знаков:
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
Чтобы запомнить цифры, непривычные для нас, пользующихся арабской системой, существует несколько специальных мнемонических фраз на русском и английском языках:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
I Value Xylophones Like Cows Dig Milk
Система расположения этих цифр друг относительно друга такова: числа до трех включительно образуются при помощи сложения единиц (II, III), — четырехкратное повторение любой цифры запрещено. Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888 = DCCCLXXXVIII (500+100+100+100+50+10+10+10+5+1+1+1).
Альтернативные варианты
Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты IIII и VIIII вместо IV и IX, и даже IIIII или XXXXXX вместо V и LX. Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII.
Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль).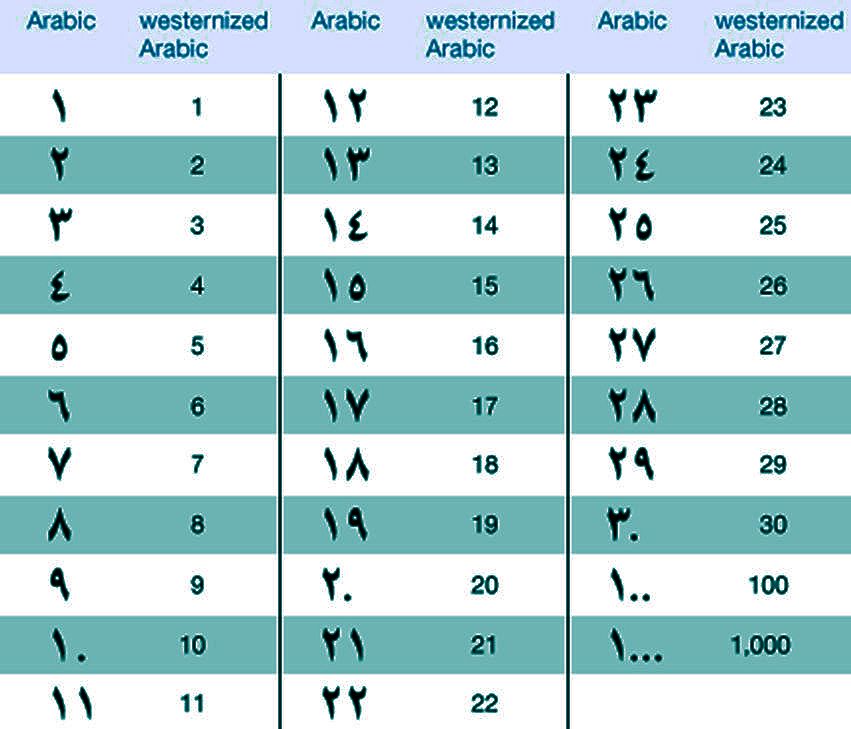 Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Происхождение
На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки.
Таким образом, цифра «I» — это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х. Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX.
Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику. Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру.
Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита.
Современное применение
Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий.
В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании).
Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).
Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).
Для запоминания буквенных обозначений цифр в порядке убывания придумано мнемоническое правило:
М ы D арим С очные L имоны, Х ватит V сем I х (соответственно M, D, C, L, X, V, I ).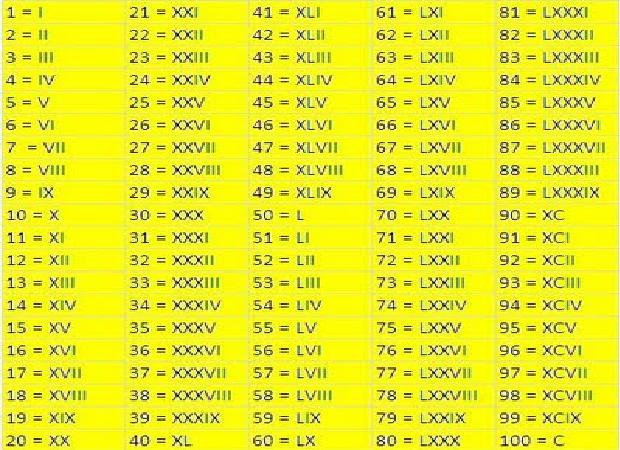
Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если слева, то вычитать, а именно:
VI — 6, т.е. 5 + 1
IV — 4, т.е. 5 — 1
XI — 11, т.е. 10 + 1
IX — 9, т.е. 10 — 1
LX — 60, т.е. 50 + 10
XL — 40, т.е. 50 — 10
ХС — 90, т.е. 100-10
MDCCCXII — 1812, т.е. 1000 + 500 + 100 + 100 + 100 + 10 + 1 + 1.
Возможно различное обозначение одного и того же числа. Например, число 80 можно обозначить как LXXX (50 + 10 + 10 + 10) и как ХХС (100 — 20).
Для записи чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
I (1) — unus (унус)
II (2) — duo (дуо)
III (3) — tres (трэс)
IV (4) — quattuor (кваттуор)
V (5) — quinque (квинквэ)
VI (6) — sex (сэкс)
VII (7) — septera (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decem (дэцем)
XI (11) — undecim (ундецим)
XII (12) — duodecim (дуодэцим)
ХШ (13) — tredecim (трэдэцим)
XIV (14) — quattuordecim (кваттуордэцим)
XV (15) — quindecim (квиндэцим)
XVI (16) — sedecim (сэдэцим)
XVII (17) — septendecim (сэптэндэцим)
XVIII (18) — duodeviginti (дуодэвигинти)
XIX (19) — undeviginti (ундэвигинти)
XXI (21) — unus et viginti или viginti unus
XXII (22) — duo et viginti или viginti duo и т.
 д.
д.XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) : triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (5O) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сзлтуагинта)
LXXX180) — octoginta (октогинта)
КС (90) — nonaginta (нонагинта)
C (100) centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sescenti(сэсценти) или sexonti (сэксцонти)
DCC (700) — septigenti (сэптигэнти)
DCCC (800) — octingenti (октингэнти)
CV (DCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
ММ (2000) — duo milia (дуо милиа)
V (5000) — quinque milla (квинквэ милиа)
X (10 000) — decem milia (дэцем милиа)
XX (20000) — viginti milia (вигинти милиа)
C (100000) — centum milia (центум милиа)
XI (1000000) — decies centena milia (дэциэс центэна милиа).
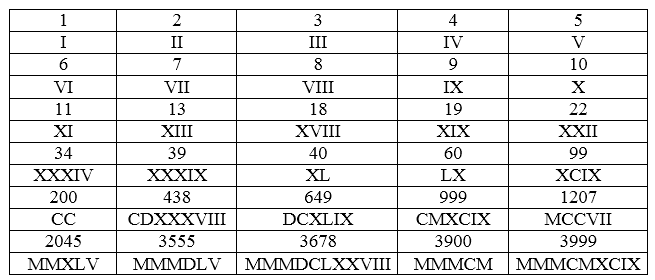
Если вдруг любознательный человек спросит, почему для обозначения цифр 50, 100, 500 и 1000 были выбраны латинские буквы V, L, С, D, М, то сразу скажем, что это вовсе не латинские буквы, а совсем иные знаки.
Дело в том, что основой для латинского алфавита послужил алфавит западногреческий. Именно к нему восходят три знака L, С и М. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. Их и приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уж стал похож на латинскую букву. Знак V (5) являлся всего навсего верхней половиной знака X (10).
Вот и вся история с этими римскими цифрами.
Задание для закрепления пройденного материала
Обратите внимание на обозначение трех дат.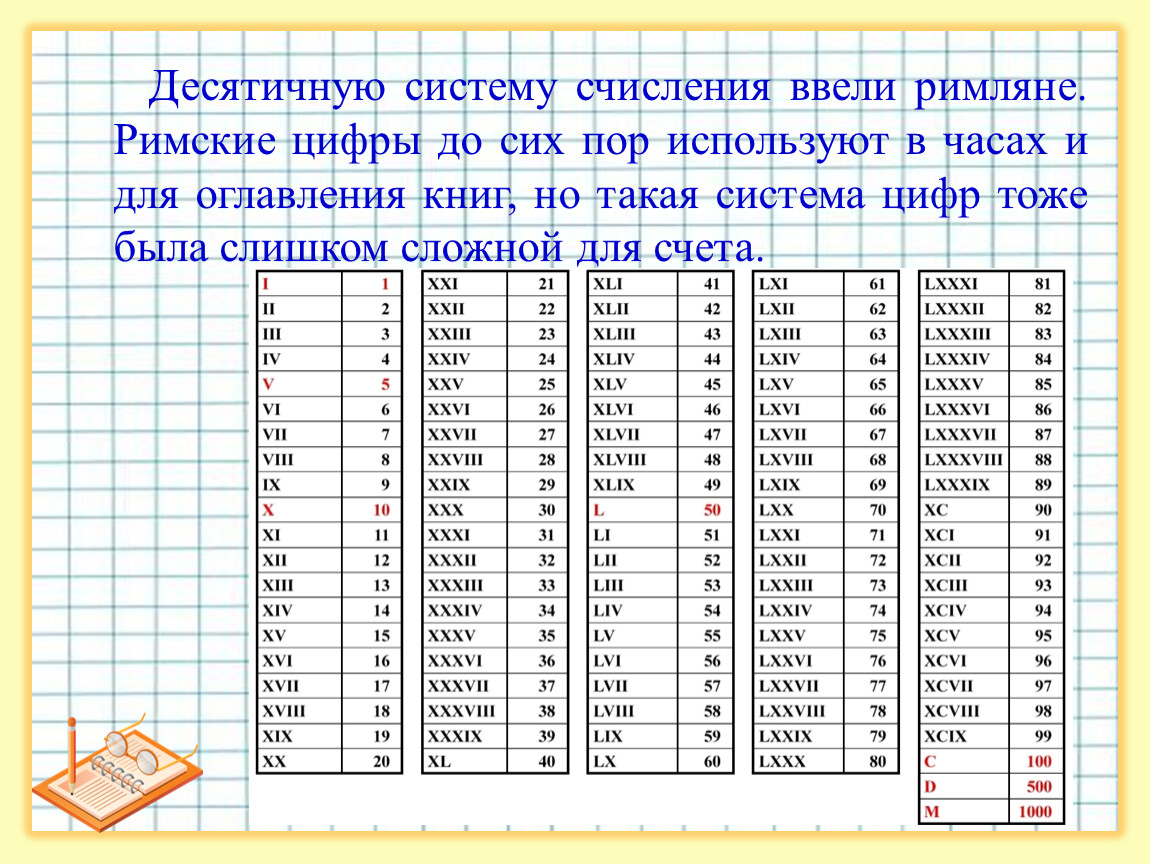 Здесь зашифрованы римскими цифрами годы рождения Александра Пушкина, Александра Герцена и Александра Блока, Решите сами, какому Александру принадлежит какая дата.
Здесь зашифрованы римскими цифрами годы рождения Александра Пушкина, Александра Герцена и Александра Блока, Решите сами, какому Александру принадлежит какая дата.
MDCCCXH
MDCCXCIX
MDCCCLXXX
Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.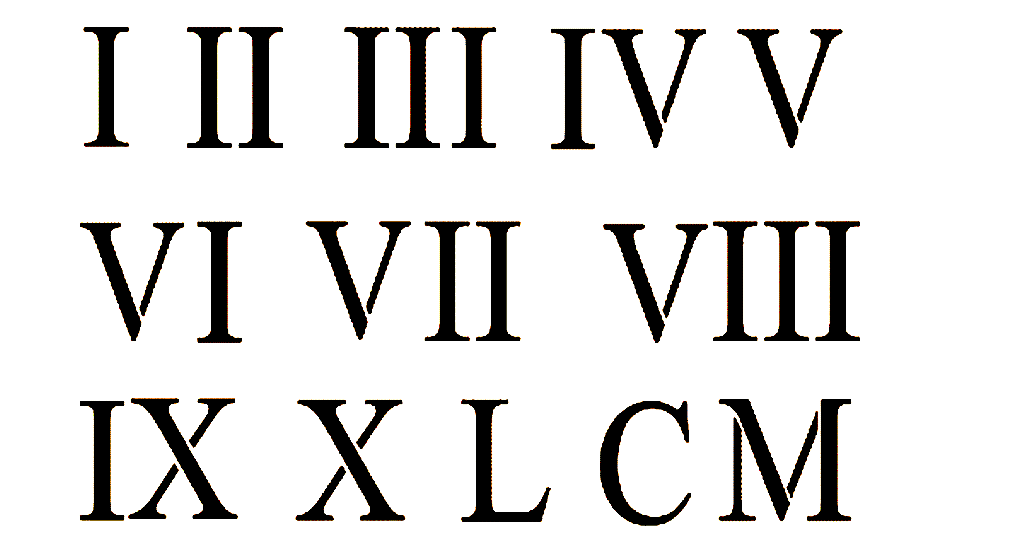 XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий.
XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий.
В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании).
Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).
В современном мире арабские цифры считаются общепризнанным стандартом исчисления.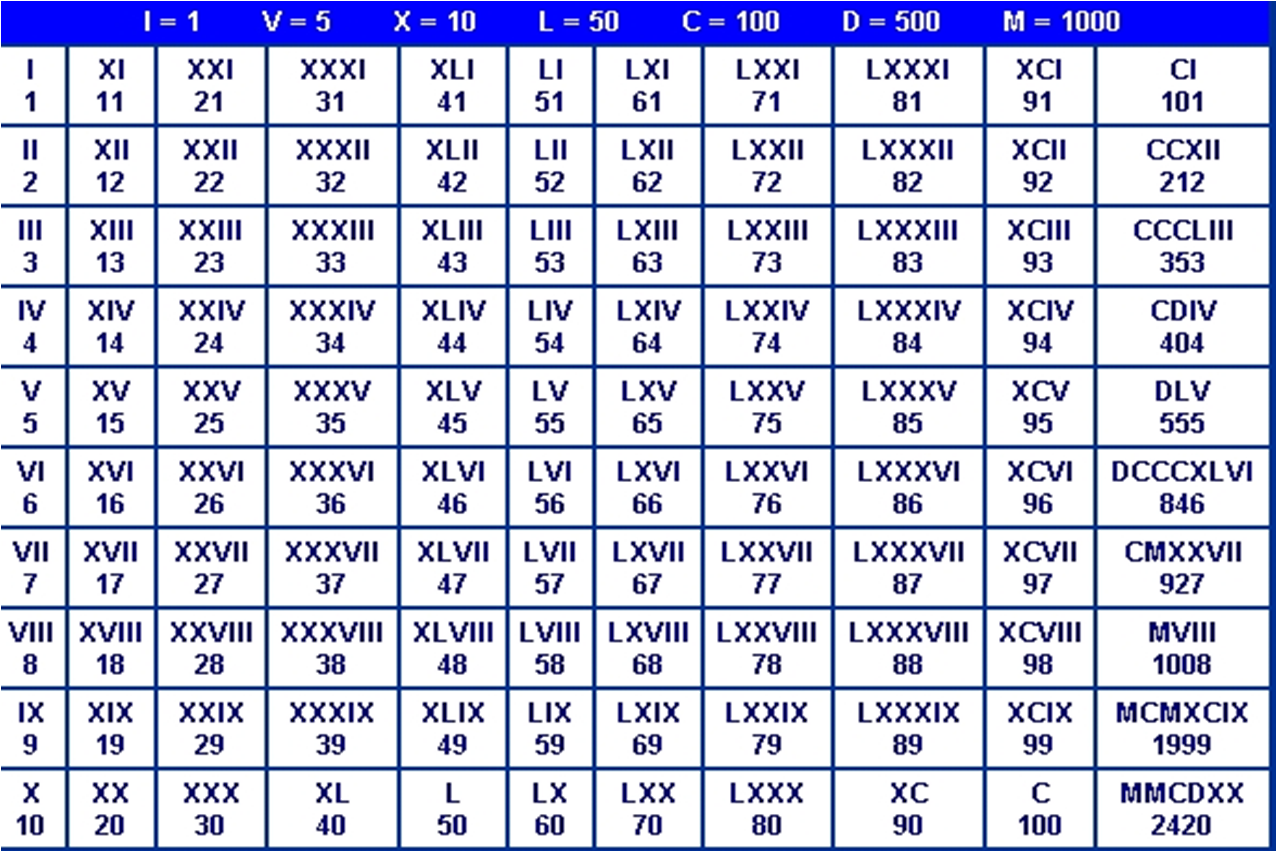 Десятичная система знаков используется для подсчетов и нумерации во всех развитых странах мира. При этом от римских цифр, которые использовались в непозиционной системе счисления древних римлян, полностью не отказались. Часто можно видеть, что с их помощью нумеруются разделы в книгах, отмечаются века в исторической литературе, указывается группа крови и многие другие параметры, для которых обозначение римскими цифрами стало стандартным.
Десятичная система знаков используется для подсчетов и нумерации во всех развитых странах мира. При этом от римских цифр, которые использовались в непозиционной системе счисления древних римлян, полностью не отказались. Часто можно видеть, что с их помощью нумеруются разделы в книгах, отмечаются века в исторической литературе, указывается группа крови и многие другие параметры, для которых обозначение римскими цифрами стало стандартным.
При работе за компьютером с браузером, текстовыми редакторами и другими приложениями может понадобиться ввести некоторые значения римскими цифрами. Отдельный цифровой блок с ними отсутствует на стандартном устройстве ввода, но есть сразу несколько способов, как написать римские цифры на клавиатуре быстро.
Римские цифры на клавиатуре в любом приложении
Лишь малая часть разработчиков приложений предусматривают удобные способы ввода в своих продуктах римских цифр при помощи клавиатуры. Большая часть программ не имеет специальной функциональности для работы с непозиционной системой счисления, что требует проявления смекалки от пользователя для ввода римских цифр в них. Можно выделить два удобных способа, как ввести римские цифры с клавиатуры в любой программе.
Можно выделить два удобных способа, как ввести римские цифры с клавиатуры в любой программе.
Замена римских цифр английскими буквами
На любом компьютере по умолчанию одним из доступных языков является английский. На него можно быстро переключиться за счет комбинации клавиш Alt+Shift или Windows+Пробел (в Windows 10). Английский алфавит полностью закрывает потребность в отдельной цифровой клавиатуре для ввода римских цифр, поскольку все их аналоги могут быть набраны с его помощью заглавными буквами.
Следующие буквы английского алфавита заменяют римские цифры:
- 1 – I;
- 5 – V;
- 10 – X;
- 50 – L;
- 100 – C;
- 500 – D;
- 1000 – M.
Еще в школе обучают, каким образом необходимо использовать римские цифры, чтобы вводить различные цифры. Принцип простой: до нужного числа добираются римские цифры максимально большие подходящие в данной ситуации.
Например:
Чтобы ввести число 33, потребуется использовать 10+10+10+1+1+1.
Соответственно, в римской вариации число 33 будет записано следующим образом: XXXIII.
Также имеются некоторые особые правила ввода римских цифр, позволяющие укоротить написание больших чисел.
Использование ASCII-кодов для ввода римских цифр
В операционной системе Windows поддерживаются ASCII-коды, предназначенные для ввода различных символов. Они могут использоваться, в том числе, для ввода римских цифр.
ASCII – это американская таблица кодирования, в которой приведены самые популярные печатные и непечатные символы в виде цифровых комбинаций. Чтобы использовать символы из данной таблицы на стандартной клавиатуре для ввода римских цифр, необходимо применить цифровой блок NUM – расположенный в правой части клавиатуры.
Активируйте работу дополнительного цифрового блока при помощи кнопки Num Lock. После этого зажмите левый ALT на клавиатуре и вводит комбинации римских цифр на правом цифровом блоке. После ввода каждого символа, нужно отпустить ALT, чтобы символ отобразился в поле для ввода. Далее вновь ALT требуется зажать и можно вводить следующий символ.
Далее вновь ALT требуется зажать и можно вводить следующий символ.
Следующие комбинации дополнительного цифрового блока идентичны римским цифрам:
- ALT+73 – I;
- ALT+86 – V;
- ALT+88 – X;
- ALT+76 – L;
- ALT+67 – C;
- ALT+68 – D;
- ALT+77 – M.
Способ ввода римских цифр с использованием ASCII-кодов нельзя назвать удобным, но он может применяться, например, когда по тем или иным причинам отключена английская раскладка на клавиатуре.
Как напечатать римские цифры в Word
Компания Microsoft при разработке офисного пакета и приложения Word учла, что пользователям, которые работают с текстами, может потребоваться ввести римские цифры. Поскольку делать это с помощью английской раскладки или ASCII-кодов не особо удобно, корпорация Microsoft ввела в Word поддержку специальной команды, автоматически переводящей арабские цифры в римские.
Римская система нумерации с помощью букв была распространена в Европе на протяжении двух тысяч лет. Только в позднем средневековье ее сменила более удобная для вычислений десятичная система цифр, заимствованная у арабов. Но, до сих пор римскими цифрами обозначаются даты на монументах, время на часах и (в англо-американской типографической традиции) страницы книжных предисловий. Кроме того, в русском языке римскими цифрами принято обозначать порядковые числительные.
Только в позднем средневековье ее сменила более удобная для вычислений десятичная система цифр, заимствованная у арабов. Но, до сих пор римскими цифрами обозначаются даты на монументах, время на часах и (в англо-американской типографической традиции) страницы книжных предисловий. Кроме того, в русском языке римскими цифрами принято обозначать порядковые числительные.
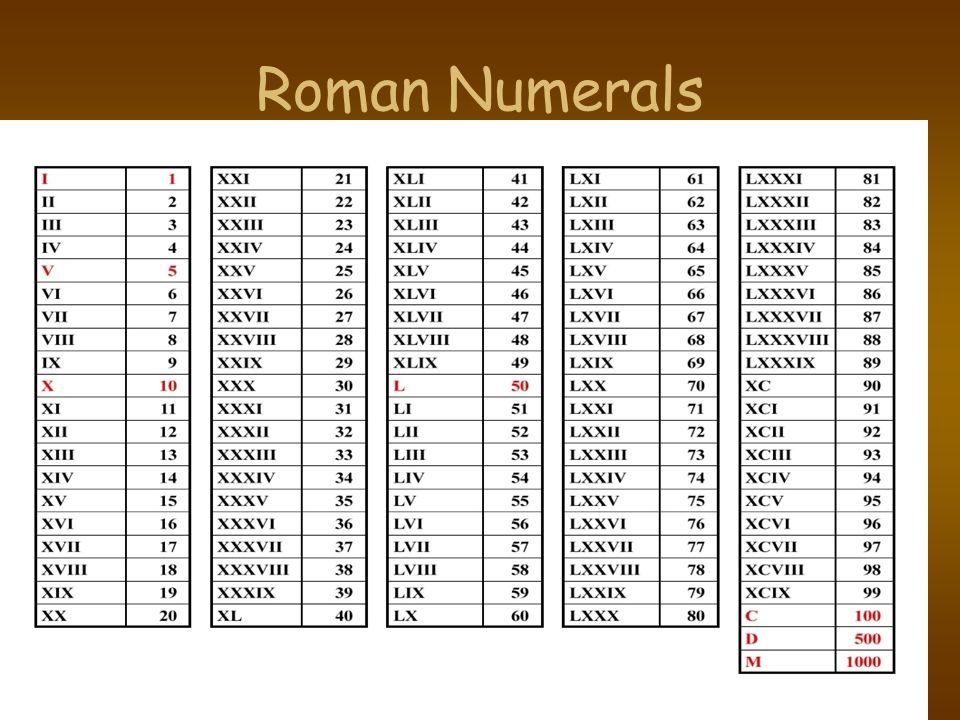
Для обозначения чисел применялось 7 букв латинского алфавита: I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000. Промежуточные числа образовывались путем прибавления нескольких букв справа или слева. Сначала писались тысячи и сотни, затем десятки и единицы. Таким образом, число 24 изображалось как XXIV. Горизонтальная линия над символом означала умножение на тысячу.
Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Например, I, Х, С ставятся соответственно перед Х, С, М для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400. Например, VI = 5+1 = 6, IV = 5 — 1 = 4 (вместо IIII). XIX = 10 + 10 — 1 = 19 (вместо XVIIII), XL = 50 — 10 =40 (вместо XXXX), XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д.
Например, I, Х, С ставятся соответственно перед Х, С, М для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400. Например, VI = 5+1 = 6, IV = 5 — 1 = 4 (вместо IIII). XIX = 10 + 10 — 1 = 19 (вместо XVIIII), XL = 50 — 10 =40 (вместо XXXX), XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д.
Выполнение арифметических действий над многозначными числами в этой записи весьма неудобно. Система Римских цифр настоящее время не применяется, за исключением, в отдельных случаях, обозначения веков (XV век и т.д.), годов н. э. (MCMLXXVII т. д.) и месяцев при указании дат (например, 1. V.1975), порядковых числительных, а также иногда производных небольших порядков, больших трёх: yIV, yV и т.д.
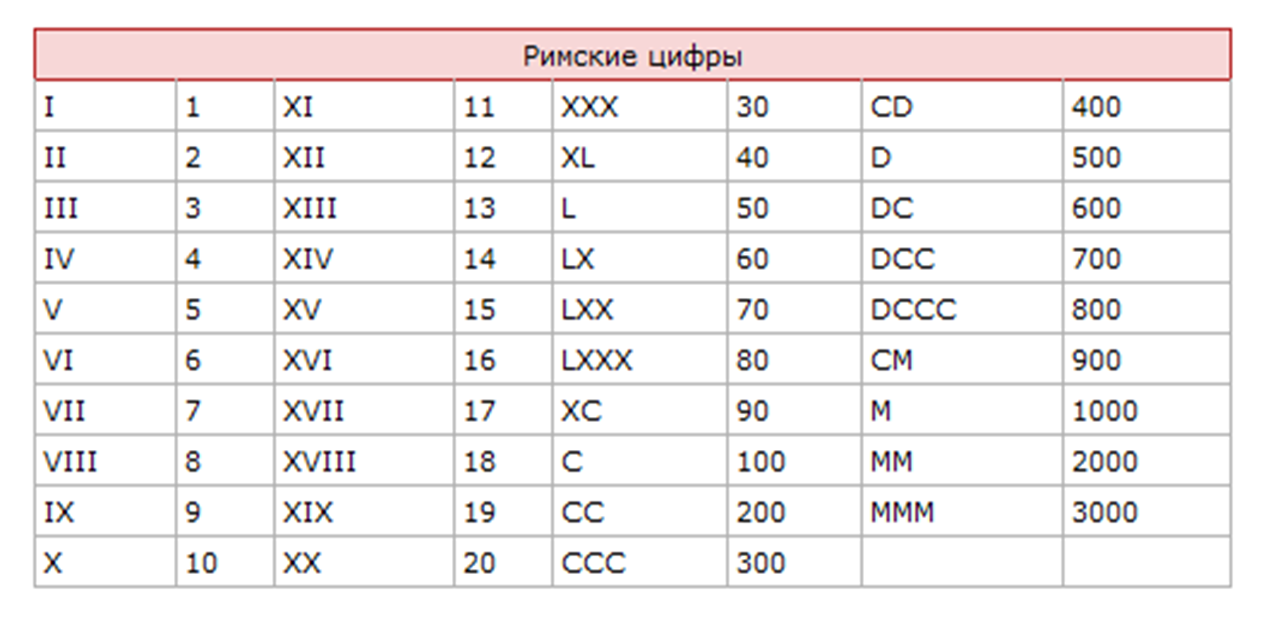
| Римские цифры | |||||||
| I | 1 | XI | 11 | XXX | 30 | CD | 400 |
| II | 2 | XII | 12 | XL | 40 | D | 500 |
| III | 3 | XIII | 13 | L | 50 | DC | 600 |
| IV | 4 | XIV | 14 | LX | 60 | DCC | 700 |
| V | 5 | XV | 15 | LXX | 70 | DCCC | 800 |
| VI | 6 | XVI | 16 | LXXX | 80 | CM | 900 |
| VII | 7 | XVII | 17 | XC | 90 | M | 1000 |
| VIII | 8 | XVIII | 18 | C | 100 | MM | 2000 |
| IX | 9 | XIX | 19 | CC | 200 | MMM | 3000 |
| X | 10 | XX | 20 | CCC | 300 | ||
Какими цифрами обозначаются века.
 Римские цифры (Roman numerals)
Римские цифры (Roman numerals)Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).
Для запоминания буквенных обозначений цифр в порядке убывания придумано мнемоническое правило:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх (соответственно M, D, C, L, X, V, I).
Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если слева, то вычитать, а именно:
VI — 6, т.е. 5 + 1
IV — 4, т.е. 5 — 1
XI — 11, т.е. 10 + 1
IX — 9, т.е. 10 — 1
LX — 60, т.е. 50 + 10
XL — 40, т.е. 50 — 10
СХ — 110, т.е. 100 + 10
ХС — 90, т.е. 100-10
MDCCCXII — 1812, т.е. 1000 + 500 + 100 + 100 + 100 + 10 + 1 + 1.
Возможно различное обозначение одного и того же числа. Например, число 80 можно обозначить как LXXX (50 + 10 + 10 + 10) и как ХХС (100 — 20).
Для записи чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
I (1) — unus (унус)
II (2) — duo (дуо)
III (3) — tres (трэс)
IV (4) — quattuor (кваттуор)
V (5) — quinque (квинквэ)
VI (6) — sex (сэкс)
VII (7) — septera (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decern (дэцем)
XI (11) — undecim (ундецим)
XII (12) — duodecim (дуодэцим)
ХШ (13) — tredecim (трэдэцим)
XIV (14) — quattuordecim (кваттуордэцим)
XV (15) — quindecim (квиндэцим)
XVI (16) — sedecim (сэдэцим)
XVII (17) — septendecim (сэптэндэцим)
XVIII (18) — duodeviginti (дуодэвигинти)
XIX (19) — undeviginti (ундэвигинти)
XX (20) — viginti (вигинти)
XXI (21) — unus et viginti или viginti unus
XXII (22) — duo et viginti или viginti duo и т.д.
XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) : triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (5O) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сзлтуагинта)
LXXX180) — octoginta (октогинта)
КС (90) — nonaginta (нонагинта)
C (100) centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sescenti(сэсценти) или sexonti (сэксцонти)
DCC (700) — septigenti (сэптигэнти)
DCCC (800) — octingenti (октингэнти)
CV (DCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
ММ (2000) — duo milia (дуо милиа)
V (5000) — quinque milla (квинквэ милиа)
X (10 000) — decem milia (дэцем милиа)
XX (20000) — viginti milia (вигинти милиа)
C (100000) — centum milia (центум милиа)
XI (1000000) — decies centena milia (дэциэс центэна милиа).
Если вдруг любознательный человек спросит, почему для обозначения цифр 50, 100, 500 и 1000 были выбраны латинские буквы V, L, С, D, М, то сразу скажем, что это вовсе не латинские буквы, а совсем иные знаки.
Дело в том, что основой для латинского алфавита послужил алфавит западногреческий. Именно к нему восходят три знака L, С и М. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. Их и приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уж стал похож на латинскую букву. Знак V (5) являлся всего навсего верхней половиной знака X (10).
Мы все пользуемся римскими цифрами – отмечаем ими номера веков или месяцев года. Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.
Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.
Как устроены римские цифры
Римская система счета в ее современном варианте состоит из следующих базовых знаков:
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
Чтобы запомнить цифры, непривычные для нас, пользующихся арабской системой, существует несколько специальных мнемонических фраз на русском и английском языках:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
I Value Xylophones Like Cows Dig Milk
Система расположения этих цифр друг относительно друга такова: числа до трех включительно образуются при помощи сложения единиц (II, III), — четырехкратное повторение любой цифры запрещено. Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888 = DCCCLXXXVIII (500+100+100+100+50+10+10+10+5+1+1+1).
Альтернативные варианты
Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты IIII и VIIII вместо IV и IX, и даже IIIII или XXXXXX вместо V и LX. Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII.
Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль). Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Происхождение
На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки.
Таким образом, цифра «I» — это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х. Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX.
Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику. Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру.
Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита.
Современное применение
Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий.
В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании).
Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).
Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий.
В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании).
Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).
Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).
Для запоминания буквенных обозначений цифр в порядке убывания придумано мнемоническое правило:
М ы D арим С очные L имоны, Х ватит V сем I х (соответственно M, D, C, L, X, V, I ).
Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если слева, то вычитать, а именно:
VI — 6, т.е. 5 + 1
IV — 4, т.е. 5 — 1
XI — 11, т.е. 10 + 1
IX — 9, т.е. 10 — 1
LX — 60, т.е. 50 + 10
XL — 40, т.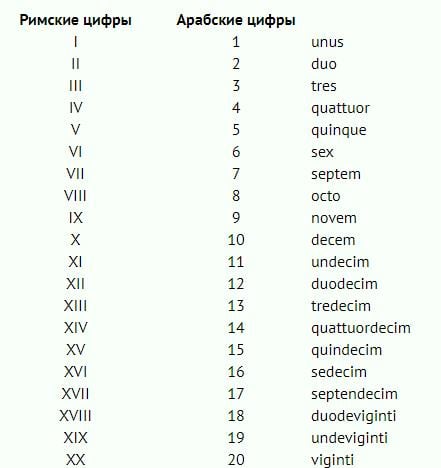 е. 50 — 10
е. 50 — 10
СХ — 110, т.е. 100 + 10
ХС — 90, т.е. 100-10
MDCCCXII — 1812, т.е. 1000 + 500 + 100 + 100 + 100 + 10 +
1 + 1.
Возможно различное обозначение одного и того же числа. Например, число 80 можно обозначить как LXXX (50 + 10 + 10 + 10) и как ХХС (100 — 20).
Для записи чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
I (1) — unus (унус)
II (2) — duo (дуо)
III (3) — tres (трэс)
IV (4) — quattuor (кваттуор)
V (5) — quinque (квинквэ)
VI (6) — sex (сэкс)
VII (7) — septera (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decem (дэцем)
XI (11) — undecim (ундецим)
XII (12) — duodecim (дуодэцим)
ХШ (13) — tredecim (трэдэцим)
XIV (14) — quattuordecim (кваттуордэцим)
XV (15) — quindecim (квиндэцим)
XVI (16) — sedecim (сэдэцим)
XVII (17) — septendecim (сэптэндэцим)
XVIII (18) — duodeviginti (дуодэвигинти)
XIX (19) — undeviginti (ундэвигинти)
XX (20) — viginti (вигинти)
XXI (21) — unus et viginti или viginti unus
XXII (22) — duo et viginti или viginti duo и т. д.
д.
XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) : triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (5O) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сзлтуагинта)
LXXX180) — octoginta (октогинта)
КС (90) — nonaginta (нонагинта)
C (100) centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sescenti(сэсценти) или sexonti (сэксцонти)
DCC (700) — septigenti (сэптигэнти)
DCCC (800) — octingenti (октингэнти)
CV (DCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
ММ (2000) — duo milia (дуо милиа)
V
(5000) — quinque milla (квинквэ милиа)
X
(10 000) — decem milia (дэцем милиа)
XX
(20000) — viginti milia (вигинти милиа)
C
(100000) — centum milia (центум милиа)
XI
(1000000) — decies centena milia (дэциэс центэна милиа).
Если вдруг любознательный человек спросит, почему для обозначения цифр 50, 100, 500 и 1000 были выбраны латинские буквы V, L, С, D, М, то сразу скажем, что это вовсе не латинские буквы, а совсем иные знаки.
Дело в том, что основой для латинского алфавита послужил алфавит западногреческий. Именно к нему восходят три знака L, С и М. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. Их и приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уж стал похож на латинскую букву. Знак V (5) являлся всего навсего верхней половиной знака X (10).
Вот и вся история с этими римскими цифрами.
Задание для закрепления пройденного материала
Обратите внимание на обозначение трех дат. Здесь зашифрованы римскими цифрами годы рождения Александра Пушкина, Александра Герцена и Александра Блока, Решите сами, какому Александру принадлежит какая дата.
Здесь зашифрованы римскими цифрами годы рождения Александра Пушкина, Александра Герцена и Александра Блока, Решите сами, какому Александру принадлежит какая дата.
MDCCCXH
MDCCXCIX
MDCCCLXXX
Мы все пользуемся римскими цифрами – отмечаем ими номера веков или месяцев года. Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.
Как устроены римские цифры
Римская система счета в ее современном варианте состоит из следующих базовых знаков:
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
Чтобы запомнить цифры, непривычные для нас, пользующихся арабской системой, существует несколько специальных мнемонических фраз на русском и английском языках:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
I Value Xylophones Like Cows Dig Milk
Система расположения этих цифр друг относительно друга такова: числа до трех включительно образуются при помощи сложения единиц (II, III), — четырехкратное повторение любой цифры запрещено. Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888 = DCCCLXXXVIII (500+100+100+100+50+10+10+10+5+1+1+1).
Альтернативные варианты
Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты IIII и VIIII вместо IV и IX, и даже IIIII или XXXXXX вместо V и LX. Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII.
Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль). Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Происхождение
На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки.
Таким образом, цифра «I» — это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х. Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX.
Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику.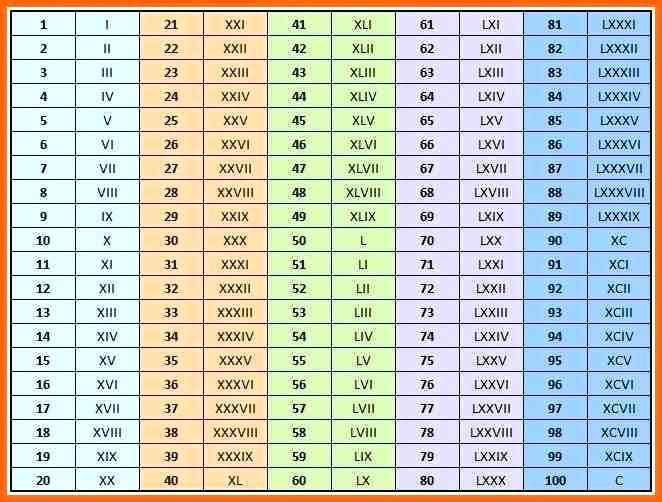 Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру.
Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита.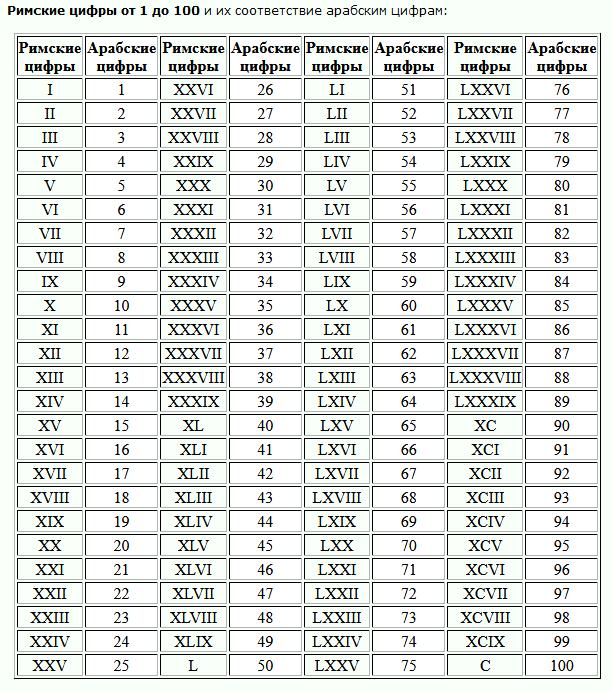
Современное применение
Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий.
В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее).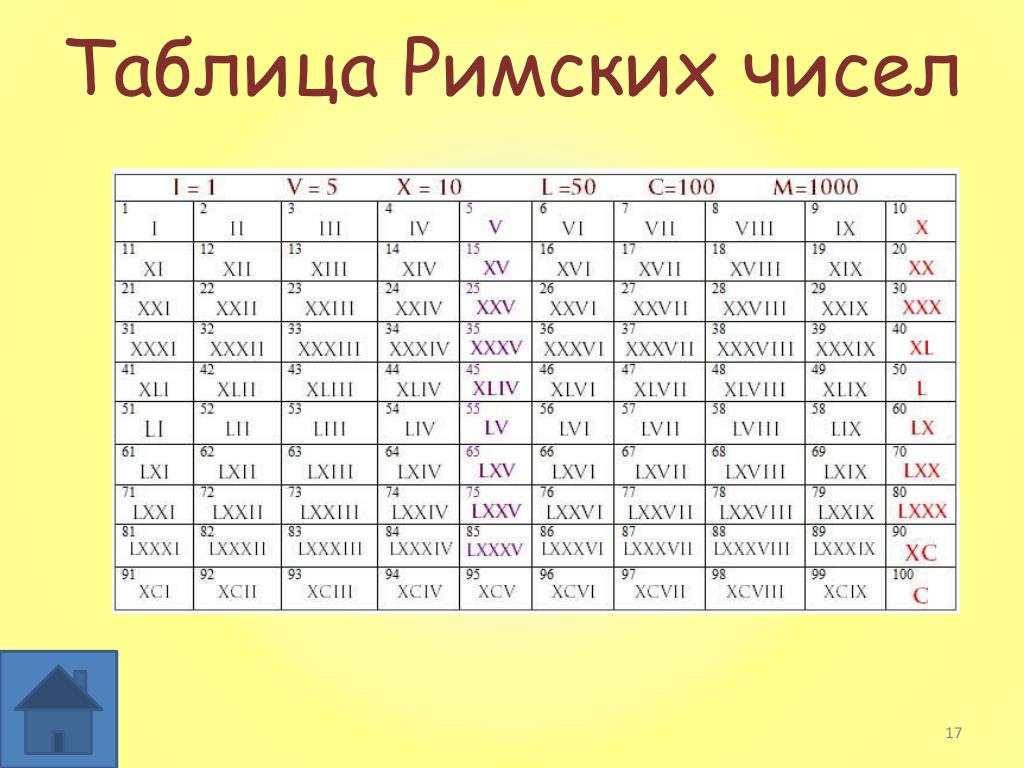 В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании).
Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).
Нет, это вирусное изображение не объясняет историю арабских цифр.
Друзья вашего двоюродного брата на Facebook, вероятно, сходят с ума по этому изображению, которое утверждает, что показывает, как ранняя история арабского геометрического дизайна влияет на то, как мы пишем цифры сегодня. «Каждая фигура содержит свое количество углов и углов», — говорится в тексте. Это наполовину верно для рисунков на изображении. Остальное заведомо ложно.
«Каждая фигура содержит свое количество углов и углов», — говорится в тексте. Это наполовину верно для рисунков на изображении. Остальное заведомо ложно.
Дизайн, который мы обычно называем арабскими цифрами сегодня, на самом деле происходит от индийской математики между 2-м веком до нашей эры и 3-м веком нашей эры. Именно тогда, по мнению ученых, была написана рукопись Бахшали, старейший из сохранившихся документов по индийской математике. Помимо своего возраста, рукопись примечательна выражением ранних примеров алгоритмов, а также основополагающей концепции математического нуля. Также довольно легко увидеть сходство между древней системой счисления (также известной как цифры Брахми) и современной арабской системой счисления (также известной как индуистско-арабская система счисления).
Цифры из рукописи Бахшали, обнаруженной Августом Хёрнле в 1887 году и предположительно написанной между 2 веком до н.э. и 3 веком н.э.
Очевидно, что дизайн развивался на протяжении многих веков. Система распространилась в Древней Персии в Средние века, и в конце концов европейцы переняли ее у арабов. Первое известное использование арабских цифр на Западе было в Codex Vigilanus , составленном тремя монахами в северной Испании между 881 г. н.э., когда он был впервые составлен, и 9 г.76 г. н.э., когда он последний раз обновлялся. Обратите внимание, как ряд цифр в нижней части фрагмента ниже написан справа налево:
Система распространилась в Древней Персии в Средние века, и в конце концов европейцы переняли ее у арабов. Первое известное использование арабских цифр на Западе было в Codex Vigilanus , составленном тремя монахами в северной Испании между 881 г. н.э., когда он был впервые составлен, и 9 г.76 г. н.э., когда он последний раз обновлялся. Обратите внимание, как ряд цифр в нижней части фрагмента ниже написан справа налево:
Codex Vigilanus содержит множество исторических документов, от раннего канонического и гражданского права до календаря.
Выглядит знакомо? За исключением цифр «4» и «5», почти все цифры прекрасно узнаваемы современным жителем Запада. Но эволюция на этом не останавливается. Индусско-арабская система была закреплена пару столетий спустя не кем иным, как Леонардо Фибоначчи. В 1202 году его Liber Abaci (или Book of Calculation на английском языке) популяризировал систему среди математиков по всей Европе. Это та же самая книга, в которой содержится знаменитая последовательность Фибоначчи.
Это та же самая книга, в которой содержится знаменитая последовательность Фибоначчи.
В течение следующих нескольких столетий индийско-арабская система получила широкое распространение в основном европейском обществе, распространившись на север от своих арабских корней в Испании. К 15-му и 16-му векам цифры появились на часах и надписях в Британии и были подробно описаны в немецких учебных рукописях, таких как руководство по фехтованию ниже:
Приведенный выше документ, известный как Ms.Thott.290.2º , был руководством, написанным Гансом Тальхоффером в 1459 году. Это 90 019 полно красивых иллюстраций тоже !
В преддверии эпохи Возрождения начинают появляться научные обзоры истории числительных. Эти исследования должны были показать, что индо-арабская система, ставшая популярной в Европе, была производной от древнего числа браминов и находилась под влиянием типографских систем, которые развились в Европе. Французский историк Жан-Этьен Монткула опубликовал свой Histoire de la Mathematique в 1757 году, а также несколько полезных диаграмм, изображающих корни арабских цифр. Вы заметите, что нигде на диаграмме не видите эту Х-образную восьмерку или перевернутую фигурную девятку.
Французский историк Жан-Этьен Монткула опубликовал свой Histoire de la Mathematique в 1757 году, а также несколько полезных диаграмм, изображающих корни арабских цифр. Вы заметите, что нигде на диаграмме не видите эту Х-образную восьмерку или перевернутую фигурную девятку.
Седьмая строка содержит десять очень знакомых символов. Обозначенная Chiffre Modernes («современные цифры»), система счисления, широко используемая в Европе к середине 18 века, более или менее идентична той, что мы используем сегодня. Нет, вы не можете сосчитать количество углов и выяснить, какое число представляет каждый символ. Но вы можете положиться на то, что история предоставит сложные, но разумные объяснения фактам. Ваша новостная лента Facebook не настолько надежна в предоставлении всей истории.
Свяжитесь с автором по телефону [email protected] .
Открытый ключ PGP
Отпечаток PGP: 91CF B387 7B38 148C DDD6 38D2 6CBC 1E46 1DBF 22
Индо-арабские цифры: история и как они произвели революцию в математике
Попробуйте добавить LIX до VII, и вы быстро поймете, почему математика не развилась далеко с римской системой счисления
До той эпохи, когда европейцам нужно было решить математическую задачу, они обычно использовали римские цифры, которые были сложными и громоздкими. Представьте, что вы пытаетесь прибавить LIX (59) к VII (7), и вы быстро поймете, почему математика как дисциплина не развилась так далеко с этой древней системой счисления. Гениальность индийско-арабской системы заключается в использовании в ней позиционной записи, также известной как позиционная запись. Каждая цифра может быть помещена в столбцы единиц, в то время как десятичную точку (введенную в 16 веке) можно перемещать влево или вправо по столбцам, чтобы увеличить или уменьшить значение числа в степени 10 — система, которая сделала возможным для выражения дробей с гораздо большей точностью.
Представьте, что вы пытаетесь прибавить LIX (59) к VII (7), и вы быстро поймете, почему математика как дисциплина не развилась так далеко с этой древней системой счисления. Гениальность индийско-арабской системы заключается в использовании в ней позиционной записи, также известной как позиционная запись. Каждая цифра может быть помещена в столбцы единиц, в то время как десятичную точку (введенную в 16 веке) можно перемещать влево или вправо по столбцам, чтобы увеличить или уменьшить значение числа в степени 10 — система, которая сделала возможным для выражения дробей с гораздо большей точностью.
Эта простая, но гениальная идея означает, что любое число может быть записано с использованием тех же девяти символов и нуля, что позволяет выполнять безграничные вычисления и перестановки. Тем не менее, несмотря на эту очевидную силу, только спустя столетия после того, как эти цифры и система позиционного обозначения были разработаны, они стали широко использоваться.
Радость шести
Ранние цивилизации разработали сложные математические теории, используя свои собственные системы. Вавилоняне, вышедшие из 19 в.до н.э. в долине Евфрата была разработана шестидесятеричная система счисления (основанная на числе 60), наследие которой сохранилось и сегодня в делении часов на 60 минут и секунд. Древние греки использовали аспекты этой шестидесятеричной системы, но записывали числа с помощью букв, а не специальных символов, а также, в отличие от вавилонян, использовали символ для обозначения нуля. Древнегреческие математики в основном занимались геометрией — длинами, формами и углами, которые обозначались буквами, а не числами, — и их идеи оказали огромное влияние на развитие этой дисциплины.
Вавилоняне, вышедшие из 19 в.до н.э. в долине Евфрата была разработана шестидесятеричная система счисления (основанная на числе 60), наследие которой сохранилось и сегодня в делении часов на 60 минут и секунд. Древние греки использовали аспекты этой шестидесятеричной системы, но записывали числа с помощью букв, а не специальных символов, а также, в отличие от вавилонян, использовали символ для обозначения нуля. Древнегреческие математики в основном занимались геометрией — длинами, формами и углами, которые обозначались буквами, а не числами, — и их идеи оказали огромное влияние на развитие этой дисциплины.
Больше похоже на это
Однако в первые века нашей эры в Индии начала процветать другая традиция математики, вероятно, основанная на идеях, заимствованных из китайской цивилизации. Ученые начали использовать девять специальных цифр для обозначения первых девяти чисел, а примерно в 600 году нашей эры они начали писать эти символы по порядку в соответствии с их значением.
Последним кусочком головоломки был ноль, который жизненно важен для системы позиционной записи, основанной на числе 10. Первоначально он был записан как точка для обозначения пустого значения в последовательности чисел. Важно отметить, что эта система была описана примерно в 625 году нашей эры индийским математиком по имени Брахмагупта в сложном астрономическом трактате, написанном на санскрите и названном Сиддханта .
Ученые, стекавшиеся в Багдад, правильно рассчитали окружность Земли с точностью до пары сотен миль Халиф аль-Мансур на излучине реки Тигр в качестве столицы своей растущей мусульманской империи. Один из них предполагает, что он был привезен непосредственно из Индии в 773 году приезжим ученым, но возможно, что к тому моменту индийско-арабские цифры уже были известны в Багдаде. Конечно, они достигли этой части света несколько раньше: в 662 году сирийский священник по имени Северус Себохт с восхищением писал о «девяти знаках» индейцев.
К началу девятого века нашей эры Багдад был крупным центром научных знаний, которым руководил неудержимо любопытный и умный халиф аль-Мамун. Это был также самый большой и самый важный город на Земле, столица огромной мусульманской империи, которая простиралась от атлантического побережья Африки до реки Инд, занимая поразительные пять миллионов квадратных миль. Люди приезжали со всей империи в поисках счастья, и город стал ярким центром обучения и культуры.
Следуя примеру нескольких просвещенных халифов, элита вложила свои значительные средства в создание библиотек и финансирование обучения. Ученые стекались, чтобы принять участие в интеллектуальных усилиях, и рукописи были привезены со всего Ближнего Востока и из-за его пределов для перевода и использования знаний, которые они хранили.
Ученые используют астрономические инструменты в Константинополе, следуя традиции, заложенной в первые века в Багдаде, месте первой обсерватории в мусульманском мире. (Изображение Universal Images Group/Getty Images)
Астрономия и математика были двумя наиболее важными предметами, и достижения ученых, изучавших их, были поистине поразительны.
Они правильно рассчитали окружность Земли с точностью до нескольких сотен миль. Они построили первую обсерваторию в мусульманском мире, где получали данные, изменившие человеческое представление о Вселенной. Они переводили, исправляли и улучшали древнегреческие научные теории, сочетая их с индийскими и своими собственными идеями, продвигая знания вперед.
Сила чисел
Во времена интеллектуального расцвета при аль-Мамуне в Багдаде было несколько выдающихся математиков, но самым талантливым был Мухаммад ибн Муса аль-Хорезми. Его имя говорит о том, что его происхождение лежало в провинции Хорезм, далеко на северо-востоке на берегу Аральского моря. Если это так, то он, как и многие звезды багдадской интеллектуальной сцены, был не арабом, а персом, хотя всегда писал по-арабски.
Аль-Хорезми читал Брахмагупту Siddhanta и понял, что индийско-арабские цифры и система позиционных значений имеют гораздо больший потенциал, чем системы, используемые в настоящее время в мусульманской империи, которые использовали счет пальцев и аспекты шестидесятеричной системы и выражали дроби словами вместо чисел.
. Книга Аль-Хорезми о сложении и вычитании по методу индусов была первой книгой на арабском языке, объясняющей индийско-арабскую систему, с главой о каждой из девяти цифр и демонстрацией того, как писать числа с использованием разряда. система.
Аль-Хорезми был дальновидным математиком. В самом деле, мы бы сейчас описали его как исключение. За исключением нескольких коллег-ученых, никто, похоже, не интересовался новой системой чисел, которую он восхвалял, а глубокие изменения парадигмы, необходимые для ее принятия, не происходили в течение нескольких столетий. Тем не менее, когда этот сдвиг, наконец, наступил, его книге суждено было сыграть ключевую роль: она была переведена на латынь в XII веке и стала важной частью европейской интеллектуальной традиции.
Статуя математика девятого века аль-Хорезми в Хиве, Узбекистан, возможно, регион его рождения (Konstik/Getty Images)
Имя Аль-Хорезми сегодня мало известно в Европе, но оно сохранилось в мире алгоритм, полученный из латинизированной версии его имени «Algorismus».
Он также дал нам слово алгебра, производное от al-jabr , часть арабского названия его Сводной книги по вычислениям путем завершения и уравновешивания , практического руководства по вычислениям, написанного по просьбе халифа аль-Ма’. мун. В нем аль-Хорезми впервые дал определение этой дисциплине, описав различные виды квадратных уравнений. Интересно, что он сделал это словами, а не системой обозначений, используемой сегодня в алгебре, которая была разработана в эпоху Возрождения.
Копии обеих книг аль-Хорезми были вывезены из Багдада в другие места, где их изучали и переводили. К десятому веку они достигли Испании, большая часть которой в то время находилась под властью мусульман. В XI и XII веках христианские силы на севере Пиренейского полуострова начали завоевывать великие города Аль-Андалуса. Толедо пал в 1085 году, и в последующие десятилетия европейские ученые приезжали в город в поисках арабских книг, в том числе текстов аль-Хорезми, которые они перевели на латынь.
Это был медленный процесс, отчасти из-за сопротивления со стороны христиан, которые считали числительные злыми и опасными — просто потому, что они пришли из мусульманского мира
Эти ученые, возможно, уже были знакомы с формами самих цифр, которые присутствовали на определенном типе счетов (счетной доске), которые, как считается, были введены монахом десятого века по имени Герберт (впоследствии Папа Сильвестр II), чей талант и страсть к математике привели его в Испанию в поисках знание. Таким образом, индо-арабские цифры и система позиционных значений были постепенно введены в Европу. Это был медленный процесс, отчасти из-за сопротивления со стороны христиан, которые считали числительные злыми и опасными просто потому, что они пришли из мусульманского мира.
- Гений средневековой науки: от медицины до механических часов
Фибоначчи и вычислительная революция цифры не в Испании, а в Африке: Леонардо Пизанский, известный сегодня как Фибоначчи (хотя это имя применялось к нему только с 19 века).
Родившийся около 1170 года, он был сыном успешного пизанского купца, назначенного в торговую палату в Бужи (теперь называемом Беджайя в Алжире) в эпоху, когда Пиза была одной из четырех основных итальянских торговых держав — другие Амальфи, Венеция. и Генуя — с торговыми связями и поселениями по всему Средиземноморью.
В Бужи арабские математики научили юного пизанца индо-арабским цифрам, вероятно, используя труды аль-Хорезми, и показали ему великолепие разрядной системы наряду с другими чудесами своей математической традиции.
Будучи подростком, Фибоначчи путешествовал со своим отцом по восточному Средиземноморью, тем самым получив возможность сравнить несколько систем исчисления, использовавшихся в то время. Он быстро осознал огромный потенциал индийско-арабской системы для преобразования обучения на Западе. В 1202 году он написал книгу под названием Liber abbaci (Книга расчетов). В этой книге, первой оригинальной работе на латыни по этому вопросу, он объяснил работу каждого из числительных и метод записи чисел в порядке их значения.
К 1220-м годам Фибоначчи вернулся в Пизу и провел некоторое время при дворе Фридриха II, императора Священной Римской империи, человека, по-видимому, настолько умного и великолепного, что его прозвали Stupor Mundi — «Чудо света». Фибоначчи процветал под покровительством Фридриха, и в 1228 году он выпустил исправленное издание 9-го числа.0018 Liber abbaci с упором на практическое применение в торговле. В нем подробно описывалось, как проводить транзакции в разных валютах и как использовать различные системы мер и весов — методы, которые приобретали все большее значение по мере того, как процветала Европа, а торговый мир расширялся и развивался. Торговцы должны были иметь возможность выполнять сложные вычисления и эффективно регистрировать свои счета — это стало возможным благодаря индийско-арабской системе чисел, изложенной Фибоначчи.
Первоначальным влиянием Фибоначчи было введение индо-арабских цифр и системы позиционных значений людям, которым математика была нужна для практических целей: торговцам, геодезистам и архитекторам, которые использовали их для выполнения вычислений, необходимых в их трудовой жизни.
Более сложные аспекты его работ были рассмотрены позже и помогли добиться прогресса в теоретической математике. В 15-м и 16-м веках ученые начали использовать цифры в своих исследованиях алгебры, особенно после 1585 года, когда фламандский математик Саймон Стевин опубликовал новаторскую брошюру о десятичных дробях.
Введение десятичной точки заставило людей задуматься о математике по-новому, проложив путь к альтернативным понятиям, таким как логарифмы, отрицательные и комплексные числа. Как обычно, было и много практических применений: измерения в инженерии и геодезии, расчеты в астрономии и коммерции. На этом этапе алгебраические задачи и уравнения записывались с использованием цифр, символов и букв, а не слов, что позволяло ученым выражать и вычислять чрезвычайно сложные задачи.
Введение десятичной точки заставило людей задуматься о математике по-новому, проложив путь к альтернативным концепциям
немецкий мастер Иоганн Гутенберг около 1440 г.
– изменил мир знаний. Поскольку количество доступных книг росло в геометрической прогрессии, их цена упала, что сделало их доступными для гораздо большего числа людей. Подсчитано, что к 1500 году, всего через полвека после начала книгопечатания в Европе, было выпущено около 20 миллионов книг. Печать также сделала тексты более стандартизированными, помогла зафиксировать форму индийско-арабских цифр и сделала их широко узнаваемыми и известными. В то же время ученые начали переводить математические тексты на местные языки (итальянский, немецкий, английский), вводя содержащиеся в них математические понятия в повседневную жизнь европейцев.
Подробнее: История Библии: кто и когда ее написал?
К 1550 году очень немногие люди в Европе все еще использовали старую римскую систему счисления для ведения счетов. Простота и элегантное великолепие индийско-арабской системы, наконец, победили, открыв удивительные новые пути в областях математики и естественных наук, создав мир, в котором мы живем сегодня, — мир, основанный на бесконечных последовательностях чисел.


 Они правильно рассчитали окружность Земли с точностью до нескольких сотен миль. Они построили первую обсерваторию в мусульманском мире, где получали данные, изменившие человеческое представление о Вселенной. Они переводили, исправляли и улучшали древнегреческие научные теории, сочетая их с индийскими и своими собственными идеями, продвигая знания вперед.
Они правильно рассчитали окружность Земли с точностью до нескольких сотен миль. Они построили первую обсерваторию в мусульманском мире, где получали данные, изменившие человеческое представление о Вселенной. Они переводили, исправляли и улучшали древнегреческие научные теории, сочетая их с индийскими и своими собственными идеями, продвигая знания вперед.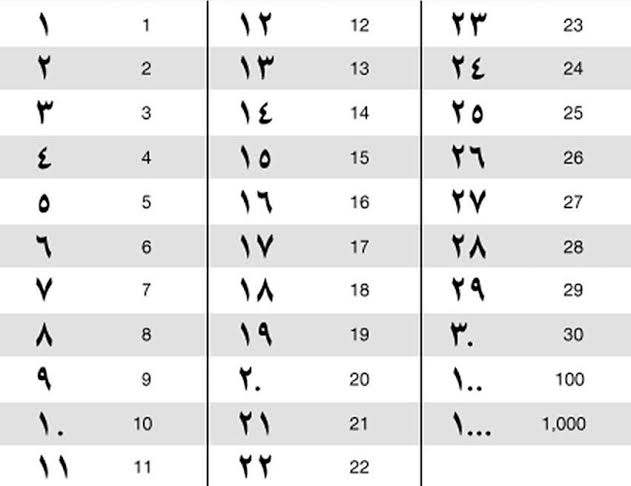 . Книга Аль-Хорезми о сложении и вычитании по методу индусов была первой книгой на арабском языке, объясняющей индийско-арабскую систему, с главой о каждой из девяти цифр и демонстрацией того, как писать числа с использованием разряда. система.
. Книга Аль-Хорезми о сложении и вычитании по методу индусов была первой книгой на арабском языке, объясняющей индийско-арабскую систему, с главой о каждой из девяти цифр и демонстрацией того, как писать числа с использованием разряда. система. Он также дал нам слово алгебра, производное от al-jabr , часть арабского названия его Сводной книги по вычислениям путем завершения и уравновешивания , практического руководства по вычислениям, написанного по просьбе халифа аль-Ма’. мун. В нем аль-Хорезми впервые дал определение этой дисциплине, описав различные виды квадратных уравнений. Интересно, что он сделал это словами, а не системой обозначений, используемой сегодня в алгебре, которая была разработана в эпоху Возрождения.
Он также дал нам слово алгебра, производное от al-jabr , часть арабского названия его Сводной книги по вычислениям путем завершения и уравновешивания , практического руководства по вычислениям, написанного по просьбе халифа аль-Ма’. мун. В нем аль-Хорезми впервые дал определение этой дисциплине, описав различные виды квадратных уравнений. Интересно, что он сделал это словами, а не системой обозначений, используемой сегодня в алгебре, которая была разработана в эпоху Возрождения.
 Родившийся около 1170 года, он был сыном успешного пизанского купца, назначенного в торговую палату в Бужи (теперь называемом Беджайя в Алжире) в эпоху, когда Пиза была одной из четырех основных итальянских торговых держав — другие Амальфи, Венеция. и Генуя — с торговыми связями и поселениями по всему Средиземноморью.
Родившийся около 1170 года, он был сыном успешного пизанского купца, назначенного в торговую палату в Бужи (теперь называемом Беджайя в Алжире) в эпоху, когда Пиза была одной из четырех основных итальянских торговых держав — другие Амальфи, Венеция. и Генуя — с торговыми связями и поселениями по всему Средиземноморью.
 Более сложные аспекты его работ были рассмотрены позже и помогли добиться прогресса в теоретической математике. В 15-м и 16-м веках ученые начали использовать цифры в своих исследованиях алгебры, особенно после 1585 года, когда фламандский математик Саймон Стевин опубликовал новаторскую брошюру о десятичных дробях.
Более сложные аспекты его работ были рассмотрены позже и помогли добиться прогресса в теоретической математике. В 15-м и 16-м веках ученые начали использовать цифры в своих исследованиях алгебры, особенно после 1585 года, когда фламандский математик Саймон Стевин опубликовал новаторскую брошюру о десятичных дробях. – изменил мир знаний. Поскольку количество доступных книг росло в геометрической прогрессии, их цена упала, что сделало их доступными для гораздо большего числа людей. Подсчитано, что к 1500 году, всего через полвека после начала книгопечатания в Европе, было выпущено около 20 миллионов книг. Печать также сделала тексты более стандартизированными, помогла зафиксировать форму индийско-арабских цифр и сделала их широко узнаваемыми и известными. В то же время ученые начали переводить математические тексты на местные языки (итальянский, немецкий, английский), вводя содержащиеся в них математические понятия в повседневную жизнь европейцев.
– изменил мир знаний. Поскольку количество доступных книг росло в геометрической прогрессии, их цена упала, что сделало их доступными для гораздо большего числа людей. Подсчитано, что к 1500 году, всего через полвека после начала книгопечатания в Европе, было выпущено около 20 миллионов книг. Печать также сделала тексты более стандартизированными, помогла зафиксировать форму индийско-арабских цифр и сделала их широко узнаваемыми и известными. В то же время ученые начали переводить математические тексты на местные языки (итальянский, немецкий, английский), вводя содержащиеся в них математические понятия в повседневную жизнь европейцев.