Тест с ответами: “Квадратный корень”
1. Является ли число x=-1,2 квадратным корнем из числа 1,44:
а) да +
б) нет
в) отчасти
2. Выберите число, которое может принимать а в выражении √8-а:
а) 16
б) 8
в) 24
3. Является ли число x=-6 арифметическим квадратным корнем из числа 36:
а) да
б) мало данных
в) нет
4. Вычислите √74:
а) 49 +
б) 280
в) 28
5. Какое слово из указанных ниже пропущено в определении квадратного корня: квадратным корнем из числа называется такое число b, … которого равен а:
а) куб
б) корень
в) квадрат +
6. Упростите выражение √50-√18-√8+1:
а) 1 +
б) 2
в) 0
7. Какое слово пропущено в определении арифметического квадратного корня: арифметическим квадратным корнем из числа а называется … число b, квадрат которого равен а:
а) отрицательное
б) любое
в) положительное +
8. Вычислите 0,3*√10*√6*√15+0,1
а) 9,1 +
б) 2,9
в) 8,9
9.
Вычислите √0,36*25:
а) 4
б) 2
в) 3 +
10. Выберите число, которое может принимать а в выражении √3-а:
а) 4
б) -5 +
в) 3,1
11. Вычислите √2*98:
а) 14 +
б) 24
в) 4
12. У каждого положительного вещественного числа существуют … противоположных по знаку квадратных корня:
а) три
б) два +
в) четыре
13. Вычислите √(-2)8:
а) 16
б) 6
в) 3
14. Квадратными корнями из числа 9 являются:
а) +4,5 и -4,5
б) +1 и -1
в) +3 и -3 +
15. Сравните числа: 4 и √16,5:
а) < +
б) >
в) =
16. Если требуется учесть двузначность корня, перед радикалом ставится знак:
а) только плюс
б) плюс-минус +
в) только минус
17. Сравните числа 3√1,2 и 2√2,1:
а) <
б) =
в) > +
18. Для любого положительного числа a существует ровно два вещественных корня, которые равны по … и противоположны по знаку:
а) дробям
б) модулю +
в) неизвестным членам
19.
Выясните, при каких значениях х имеет смысл выражение √16-4х:
а) х=4
б) х≥4
в) х≤4 +
20. Неотрицательный квадратный корень из неотрицательного числа a называется:
а) физическим квадратным корнем
б) арифметическим квадратным корнем +
в) математическим квадратным корнем
21. Упростите выражение (√7-√5)*(√7+√5):
а) 2 +
б) 4
в) 35
22. Квадратных корней из любого ненулевого комплексного числа всегда ровно:
а) три
б) два +
в) четыре
23. Упростите выражение (2√15+√5):√5-2√3:
а) 25
б) 3
в) 1 +
24. Квадратный корень является:
а) диагностической функцией
б) элементарной функцией +
в) сложной функцией
25. Вычислите √36:
а) 81
б) 9
в) 27 +
26. Квадратные корни тесно связаны с элементарной:
а) физикой
б) геометрией +
в) планиметрией
27. Упростите выражение 2√50-√18+√8+1:
а) 9√2+1
б) 9√2
в) 10√2+1
28. Как функция комплексного переменного корень – двузначная функция, листы которой соединяются:
а) в единице
б) в бесконечности
в) в нуле +
29.
Вычислите 0,5*√12*√6*√2+0,2:
а) 6,2 +
б) 12,4
в) 60,2
30. Нахождение или вычисление квадратного корня заданного числа называется:
а) уравнением квадратного корня
б) извлечением (квадратного) корня +
в) внесением квадратного корня
Квадратный корень из 25 — Как найти квадратный корень из 25?
LearnPracticeDownload
Квадратный корень из 25 выражается как √25 в радикальной форме и как (25) ½ или (25) 0,5 в экспоненциальной форме. Квадратный корень из 25 равен 5. Это положительное решение уравнения x 2 = 25. Число 25 — полный квадрат.
- Квадратный корень из 25: 5
- Квадратный корень из 25 в экспоненциальной форме: (25) ½ или (25) 0,5
- Квадратный корень из 25 в подкоренной форме: √25
| 1. | Чему равен квадратный корень из 25? |
2. | Является ли квадратный корень из 25 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 25? |
| 4. | Часто задаваемые вопросы о квадратном корне из 25 |
Что такое квадратный корень из 25?
Давайте сначала поймем значение квадратного корня. Квадратный корень числа – это число, которое при умножении на себя дает произведение исходного числа. Рассмотрим пример: 5 2 = ( 5 × 5) = 25,
Здесь 5 называется квадратным корнем из 25. 25 — полный квадрат. Таким образом, квадратный корень из 25 равен 5.
Квадратный корень из 25 рационален или иррационален?
Рациональное число может быть выражено в виде p/q. Потому что √25 = 5 и 5 можно записать в виде дроби 5/1. Это доказывает, что √25 рационально.
Как найти квадратный корень из 25?
Мы можем найти квадратный корень из 25, используя различные методы.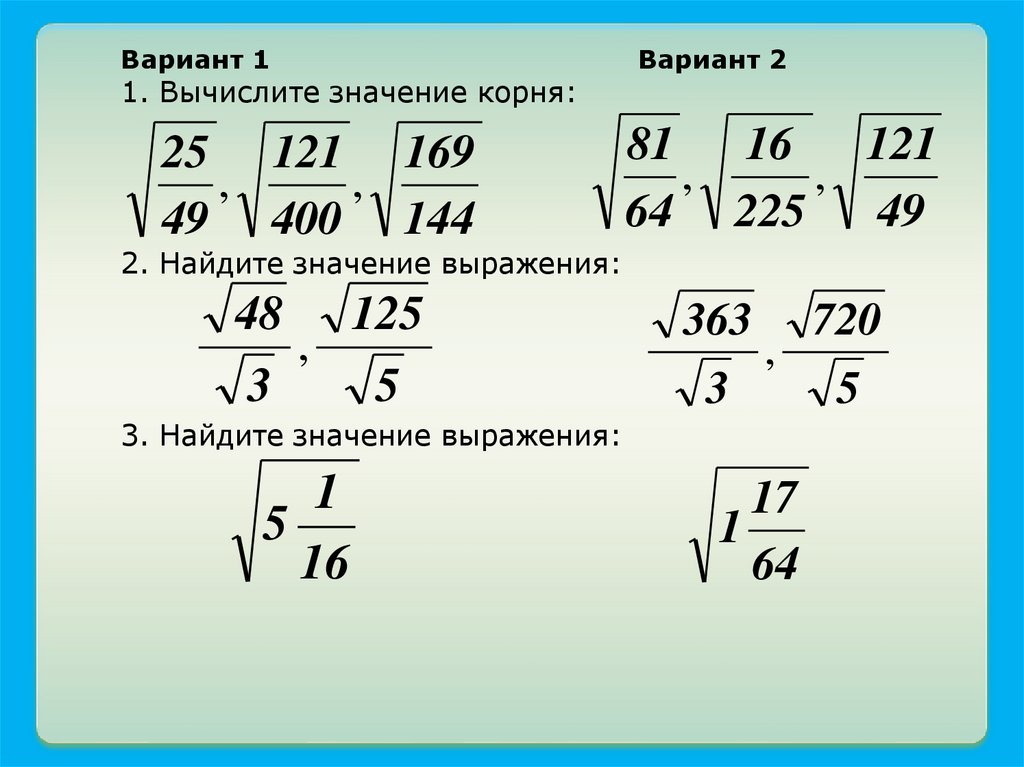
Если вы хотите узнать больше о каждом из этих методов, нажмите здесь. Поскольку мы обнаружили, что 25 — это полный квадрат, мы можем найти его квадратный корень, используя деление в большую сторону.
Квадратный корень из 25 можно найти с помощью деления в большую сторону следующим образом:
Поскольку остаток равен 0, нам не нужно продолжать деление в большую сторону, и мы рассматриваем частное (которое равно 5) как результат.
Важные примечания
- 25 — число в совершенном квадрате.
- Квадратный корень из 25 является рациональным числом.
Решенные примеры из 25 решенных примеров
Пример 1 Кейт хотела проверить, можно ли найти квадратный корень из 25 с помощью метода повторного вычитания. Давайте поможем ей!
Решение:
В методе повторного вычитания мы вычитаем нечетные числа, начиная с 1, пока не получим 0,
25 — 1 = 24
24 — 3 = 21
21 — 5 = 16
16 — 7 = 9
9 − 9 = 0Отсюда √25 = 5,
Пример 2: Помогите Кайли найти квадратный корень из 25, используя разложение на простые множители.
Решение:
Разложение числа 25 на простые множители = 5 × 5
√25 = √(5)(5) = 5
Пример: если площадь поверхности куба равна 150 в 2 . Найдите длину стороны куба.
Решение:
Пусть а будет длиной стороны куба.
⇒ Площадь куба = 6а 2 = 150 2
⇒ а = ±√25 в
Поскольку длина не может быть отрицательной,
⇒ а = √25
Мы знаем, что квадратный корень из 25 равен 5.
⇒ а = 5 в
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о квадратном корне из 25
Каково значение квадратного корня из 25?
Квадратный корень из 25 равен 5.