Каким является число 0 четным или нечетным. Нечетные числа. История и культура
- Нечётное число — целое число , которое не делится на без остатка : …, −3, −1, 1, 3, 5, 7, 9, …
Если m чётно, то оно представимо в виде m = 2 k, а если нечётно, то в виде m = 2 k + 1, где k \in \mathbb Z.
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь », а нечётные — «ян » .
В разных странах существуют связанные с количеством даримых цветов традиции. Например в США , Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье . В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т.
Практика
В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)
В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.
С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.
Напишите отзыв о статье «Чётные и нечётные числа»
Примечания
Ссылки
- Последовательность A005408 в OEIS : нечётные числа
- Последовательность A005843 в OEIS : чётные числа
- Последовательность A179082 в OEIS : чётные числа с чётной суммой цифр в десятичной записи
Отрывок, характеризующий Чётные и нечётные числа
– Так, так, – сказал князь Андрей, обращаясь к Алпатычу, – все передай, как я тебе говорил. – И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.
– И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.
От Смоленска войска продолжали отступать. Неприятель шел вслед за ними. 10 го августа полк, которым командовал князь Андрей, проходил по большой дороге, мимо проспекта, ведущего в Лысые Горы. Жара и засуха стояли более трех недель. Каждый день по небу ходили курчавые облака, изредка заслоняя солнце; но к вечеру опять расчищало, и солнце садилось в буровато красную мглу. Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли.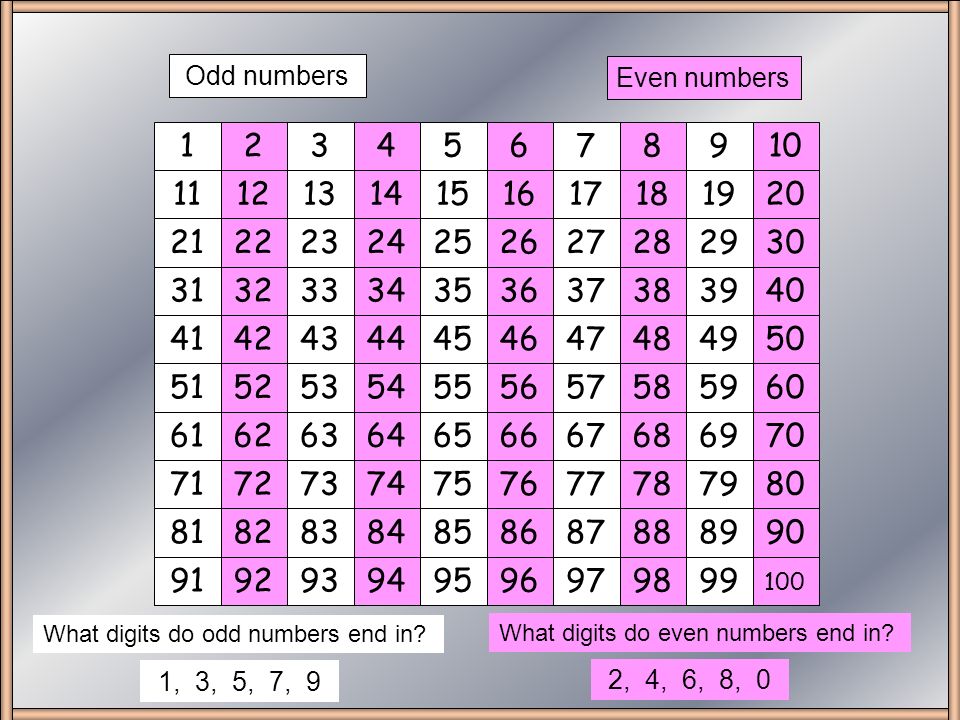
Князь Андрей командовал полком, и устройство полка, благосостояние его людей, необходимость получения и отдачи приказаний занимали его. Пожар Смоленска и оставление его были эпохой для князя Андрея. Новое чувство озлобления против врага заставляло его забывать свое горе. Он весь был предан делам своего полка, он был заботлив о своих людях и офицерах и ласков с ними. В полку его называли наш князь, им гордились и его любили.
 Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг. Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.Он велел оседлать себе лошадь и с перехода поехал верхом в отцовскую деревню, в которой он родился и провел свое детство. Проезжая мимо пруда, на котором всегда десятки баб, переговариваясь, били вальками и полоскали свое белье, князь Андрей заметил, что на пруде никого не было, и оторванный плотик, до половины залитый водой, боком плавал посредине пруда. Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками.

Он был глух и не слыхал подъезда князя Андрея. Он сидел на лавке, на которой любил сиживать старый князь, и около него было развешено лычко на сучках обломанной и засохшей магнолии.
Князь Андрей подъехал к дому. Несколько лип в старом саду были срублены, одна пегая с жеребенком лошадь ходила перед самым домом между розанами. Дом был заколочен ставнями. Одно окно внизу было открыто. Дворовый мальчик, увидав князя Андрея, вбежал в дом.
Алпатыч, услав семью, один оставался в Лысых Горах; он сидел дома и читал Жития. Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.
Признак чётности
Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42 , 104 , 11110 , 9115817342 — чётные числа.
31 , 703 , 78527 , 2356895125 — нечётные числа.
Арифметика
- Сложение и вычитание:
- Ч ётное ± Ч ётное = Ч ётное
- Ч ётное ± Н ечётное = Н ечётное
- Н ечётное ± Ч ётное = Н ечётное
- Н ечётное ± Н ечётное = Ч ётное
- Умножение:
- Ч ётное × Ч ётное = Ч ётное
- Ч ётное × Н ечётное = Ч ётное
- Н ечётное × Н ечётное = Н ечётное
- Деление:
- Ч ётное / Ч ётное — однозначно судить о чётности результата невозможно (если результат целое число , то оно может быть как чётным, так и нечётным)
- Ч ётное / Н ечётное = если результат целое число , то оно Ч ётное
- Н ечётное / Ч ётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н ечётное / Н ечётное = если результат целое число , то оно Н ечётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные — Ян .
Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные — Ян .
В разных странах существуют связанные с количеством даримых цветов традиции, например в США , Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье . В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
Wikimedia Foundation . 2010 .
- Нечетность
- Нечетные и четные функции
Смотреть что такое «Нечетные числа» в других словарях:
Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Числа — Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
ЧИСЛА — ♠ Значение сна зависит от того, где именно и в каком виде вы видели приснившееся вам число, а также от его значения. Если число было в календаре это предупреждение о том, что в этот день вас ждет важное событие, которое перевернет всю вашу… … Большой семейный сонник
КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь
Пифагор и пифагорейцы — Пифагор родился на Самосе. Расцвет его жизни приходится на 530 е годы до н.э., а смерть на начало V в. до н.э. Диоген Лаэртский, один из известных биографов античных философов, сообщает нам: Молодой и жадный до знаний, он покинул отечество,… … Западная философия от истоков до наших дней
сорит — (от греч. soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики
soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики
«Сакральный» смысл чисел в верованиях и учениях — К материалу «07.07.07. Влюбленные всего мира поверили в магию чисел» С глубокой древности числа играют важную и многогранную роль в жизни человека. Древние люди приписывали им особые, сверхъестественные свойства; одни числа сулили… … Энциклопедия ньюсмейкеров
НУМЕРОЛОГИЯ — и; ж. [лат. numero считаю и греч. logos учение] Учение, основанное на вере в сверхъестественное влияние на судьбу человека, страны и т.п. сочетаний определённых чисел, цифр. ◁ Нумерологический, ая, ое. Н ие предсказания. * * * НУМЕРОЛОГИЯ… … Энциклопедический словарь
Случайное простое число — В криптографии под случайным простым числом понимается простое число, содержащее в двоичной записи заданное количество битов, на алгоритм генерации которого накладываются определенные ограничения. Получение случайных простых чисел является… … Википедия
Получение случайных простых чисел является… … Википедия
Счастливое число — В теории чисел счастливое число является натуральным числом множества генерируемое «решетом», аналогичным решету Эратосфена, которое генерирует простые числа. Начнем со списка целых чисел, начиная с 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,… … Википедия
Книги
- Занимаюсь математикой. Для детей 6-7 лет , Сорокина Татьяна Владимировна. Основные задачи пособия — ознакомление ребенка с математическими понятиями «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность», «однозначные/двузначные числа», «четные/нечетные…
Определения
- Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
- Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …
В соответствии с этим определением нуль является чётным числом.
Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .
В разных странах существуют связанные с количеством даримых цветов традиции.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.
Примечания
Wikimedia Foundation . 2010 .
- Маарду
- Сверхпроводимость
Смотреть что такое «Чётные и нечётные числа» в других словарях:
Нечётные числа
Чётные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Нечётное — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Нечётное число — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Четные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Слегка избыточные числа — Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия
Совершенные числа — целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
Квантовые числа — целые (0, 1, 2,. ..) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия
..) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия
Книги
- Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
Определения
- Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
- Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …
В соответствии с этим определением нуль является чётным числом.
Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .
В разных странах существуют связанные с количеством даримых цветов традиции.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.
Примечания
Wikimedia Foundation . 2010 .
Смотреть что такое «Чётные и нечётные числа» в других словарях:
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия
Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия
Книги
- Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна.
 В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
Четные и нечетные числа. Понятие о десятичной записи числа. Нечетные числа
Во вселенной существуют пары противоположностей, которые являются важным фактором ее устройства. Основные свойства, которые нумерологи приписывают четным (1, 3, 5, 7, 9) и нечетным (2, 4, 6, 8) числам, как парам противоположностей, следующие:
1 — активный, целеустремленный, властный, черствый, руководящий, инициативный;
2 — пассивный, восприимчивый, слабый, сочувствующий, подчиненный;
3 — яркий, веселый, артистичный, удачливый, легко добивающийся успеха;
4 — трудолюбивый, скучный, безынициативный, несчастный, тяжелый труд и частое поражение;
5 — подвижный, предприимчивый, нервный, неуверенный, сексуальный;
6 — простой, спокойный, домашний, устроенный; материнская любовь;
7 — уход от мира, мистика, тайны;
8 — мирская жизнь; материальная удача или поражение;
9 — интеллектуальное и духовное совершенство.
Нечетные числа обладают гораздо более яркими свойствами. Рядом с энергией «1», блеском и удачливостью «3», авантюрной подвижностью и многогранностью «5», мудростью «7» и совершенством «9» четные числа выглядят не столь ярко. Насчитывается 10 основных пар противоположностей, существующих во Вселенной. Среди этих пар: четное — нечетное, один — много, правое — левое, мужское — женское, добро — зло. Один, правое, мужское и доброе ассоциировалось с нечетными числами; много, левое, женское и злое — с четными.
Нечетные числа обладают некой производящей серединой, в то время как в любом четном числе есть воспринимающее отверстие как бы лакуна внутри себя. Мужские свойства фаллических нечетных чисел вытекают из того факта, что они сильнее четных. Если четное число расщепить пополам, то, кроме пустоты, посередине ничего не останется. Нечетное число разбить непросто, потому что посередине остается точка. Если же соединить вместе четное и нечетное числа, то победит нечетное, так как результат всегда будет нечетным. Именно поэтому нечетные числа обладают мужскими свойствами, властными и резкими, а четные — женскими, пассивными и воспринимающими.
Именно поэтому нечетные числа обладают мужскими свойствами, властными и резкими, а четные — женскими, пассивными и воспринимающими.
Нечетных чисел нечетное число: их пять. Четных чисел четное число — четыре.
Нечетные числа — солнечные, электрические, кислотные и динамичные. Они являются слагаемыми; их с чем либо складывают. Четные числа — лунные, магнетические, щелочные и статичные. Они являются вычитаемыми, их уменьшают. Они остаются без движения, потому что имеют четные группы пар (2 и 4; 6 и 8).
Если мы сгруппируем нечетные числа, одно число всегда останется без своей пары (1 и 3; 5 и 7; 9). Это делает их динамичными. Два подобных числа (два нечетных числа или два четных) не являются благоприятными.
четное + четное = четное (статичное) 2+2=4
четное + нечетное = нечетное (динамичное) 3+2=5
нечетное + нечетное = четное (статичное) 3+3=6
Некоторые числа дружественны, другие — противостоят друг другу. Взаимоотношения чисел определяются отношениями между планетами, которые ими управляют (подробности в разделе «Совместимость чисел»). Когда два дружественных числа соприкасаются, их сотрудничество не очень продуктивно. Подобно друзьям, они расслабляются — и ничего не происходит. Но когда в одной комбинации находятся враждебные числа, они заставляют друг друга быть настороже и побуждают к активным действиям; таким образом, эти два человека работают намного больше. В таком случае, враждебные числа оказываются на самом деле друзьями, а друзья — настоящими врагами, тормозящими прогресс. Нейтральные числа остаются неактивными. Они не дают поддержки, не вызывают и не подавляют активность.
Когда два дружественных числа соприкасаются, их сотрудничество не очень продуктивно. Подобно друзьям, они расслабляются — и ничего не происходит. Но когда в одной комбинации находятся враждебные числа, они заставляют друг друга быть настороже и побуждают к активным действиям; таким образом, эти два человека работают намного больше. В таком случае, враждебные числа оказываются на самом деле друзьями, а друзья — настоящими врагами, тормозящими прогресс. Нейтральные числа остаются неактивными. Они не дают поддержки, не вызывают и не подавляют активность.
Признак чётности
Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42 , 104 , 11110 , 9115817342 — чётные числа.
31 , 703 , 78527 , 2356895125 — нечётные числа.
Арифметика
- Сложение и вычитание:
- Ч ётное ± Ч ётное = Ч ётное
- Ч ётное ± Н ечётное = Н ечётное
- Н ечётное ± Ч ётное = Н ечётное
- Н ечётное ± Н ечётное = Ч ётное
- Умножение:
- Ч ётное × Ч ётное = Ч ётное
- Ч ётное × Н ечётное = Ч ётное
- Н ечётное × Н ечётное = Н ечётное
- Деление:
- Ч ётное / Ч ётное — однозначно судить о чётности результата невозможно (если результат целое число , то оно может быть как чётным, так и нечётным)
- Ч ётное / Н ечётное = если результат целое число , то оно Ч ётное
- Н ечётное / Ч ётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н ечётное / Н ечётное = если результат целое число , то оно Н ечётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные — Ян .
Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные — Ян .
В разных странах существуют связанные с количеством даримых цветов традиции, например в США , Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье . В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
Wikimedia Foundation . 2010 .
- Нечетность
- Нечетные и четные функции
Смотреть что такое «Нечетные числа» в других словарях:
Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Числа — Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
ЧИСЛА — ♠ Значение сна зависит от того, где именно и в каком виде вы видели приснившееся вам число, а также от его значения. Если число было в календаре это предупреждение о том, что в этот день вас ждет важное событие, которое перевернет всю вашу… … Большой семейный сонник
КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь
Пифагор и пифагорейцы — Пифагор родился на Самосе. Расцвет его жизни приходится на 530 е годы до н.э., а смерть на начало V в. до н.э. Диоген Лаэртский, один из известных биографов античных философов, сообщает нам: Молодой и жадный до знаний, он покинул отечество,… … Западная философия от истоков до наших дней
сорит — (от греч. soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики
soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики
«Сакральный» смысл чисел в верованиях и учениях — К материалу «07.07.07. Влюбленные всего мира поверили в магию чисел» С глубокой древности числа играют важную и многогранную роль в жизни человека. Древние люди приписывали им особые, сверхъестественные свойства; одни числа сулили… … Энциклопедия ньюсмейкеров
НУМЕРОЛОГИЯ — и; ж. [лат. numero считаю и греч. logos учение] Учение, основанное на вере в сверхъестественное влияние на судьбу человека, страны и т.п. сочетаний определённых чисел, цифр. ◁ Нумерологический, ая, ое. Н ие предсказания. * * * НУМЕРОЛОГИЯ… … Энциклопедический словарь
Случайное простое число — В криптографии под случайным простым числом понимается простое число, содержащее в двоичной записи заданное количество битов, на алгоритм генерации которого накладываются определенные ограничения. Получение случайных простых чисел является… … Википедия
Получение случайных простых чисел является… … Википедия
Счастливое число — В теории чисел счастливое число является натуральным числом множества генерируемое «решетом», аналогичным решету Эратосфена, которое генерирует простые числа. Начнем со списка целых чисел, начиная с 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,… … Википедия
Книги
- Занимаюсь математикой. Для детей 6-7 лет , Сорокина Татьяна Владимировна. Основные задачи пособия — ознакомление ребенка с математическими понятиями «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность», «однозначные/двузначные числа», «четные/нечетные…
Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Например: -24, 0, 6, 38 — все это четные числа.
m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.
Пример нечетных чисел: 3, 1, 7 и 35.
n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.
Сложение и вычитание четных и нечетных чисел
В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.
Операция | Результат | Пример |
Четное + Четное | ||
Четное + Нечетное | Нечетное | |
Нечетное + Нечетное |
Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.
Умножение четных и нечетных чисел
При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Операция | Результат | Пример |
Четное * Четное | ||
Четное * Нечетное | ||
Нечетное * Нечетное | Нечетное |
А теперь рассмотрим дробные числа.
Десятичная запись числа
Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.
Например: 3,14; 5,1; 6,789 — это все
С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.
Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.
Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.
А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.
Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Прежде чем говорить про четные и нечетные числа, стоит уяснить несколько моментов о том, какие вообще группы чисел бывают. Это необходимо для того, чтобы не пытаться выяснять четность дроби.
С каких чисел начинается изучение в основной школе?
Первыми идут натуральные. Они также сначала появились исторически. Человечеству было необходимо подсчитывать предметы. Причем при счете ноль не используется, поэтому он не входит в группу натуральных чисел. Здесь все целые, которые больше единицы.
Именно для них впервые дается определение четности. Чтобы понять, какое число нечетное, нужно запомнить признак четного. Оно заканчивается на одну из цифр: 0, 2, 4, 6, 8. Все остальные будут нечетными. Минимальное из них равно единице. Максимального не существует.
Оно заканчивается на одну из цифр: 0, 2, 4, 6, 8. Все остальные будут нечетными. Минимальное из них равно единице. Максимального не существует.
Какие числа идут дальше?
Целые. В их множество входит уже ноль и все отрицательные числа. Цепочка натуральных чисел была ограничена слева, а вправо продолжалась бесконечно. С целыми оказывается бесконечное количество чисел и слева от нуля.
В этот момент немного меняется определение четности. Оно теперь должно делиться на два без остатка. Значит, нечетные числа при делении на два дают ответ с остатком.
Причем даже вводится общая запись: для четных — 2n, нечетные — (2n+1). Если для натуральных не существует только максимального четного или нечетного, то у целых нет и минимального.
А что потом?
Рациональные (другое название — вещественные) числа. Кроме уже упомянутых, в это множество входят еще и дроби. То есть числа, которые можно представить в виде двух. Первое из них является числителем и представляется в виде целого числа. Второе — знаменатель, который никогда не равен нулю.
Второе — знаменатель, который никогда не равен нулю.
Кстати, для них не вводится понятие четности. Поэтому нечетные числа, записанные в виде дроби, не существуют вовсе.
Какие результаты дают действия с четными и нечетными числами?
Их можно рассмотреть в порядке усложнения арифметического действия. Тогда первым и вторым пойдут сложение и вычитание. Неважно, какое из них выполняется, ответ будет зависеть только от начальной пары чисел. К примеру, если исходные числа четные, то результат действия будет делиться на два. Такой же итог будет, если стоит разность или сумма нечетных чисел. Чтобы получить нечетное число, придется складывать или вычитать четное с нечетным.
Это легко можно проверить, используя их общую запись. Например, сложение двух четных чисел: 2n+2n = 4n = 2*2n. Здесь 2n — четное число, которое еще умножается на два. Значит, оно точно будет делиться нацело на двойку. То есть ответ — четный.
При сложении четного с нечетным имеем такую запись: 2n + (2n + 1) = 4n + 1. Первое слагаемое — четное число, к которому прибавляется единица. Последнее слагаемое не даст разделить этот результат на два нацело.
Первое слагаемое — четное число, к которому прибавляется единица. Последнее слагаемое не даст разделить этот результат на два нацело.
Третье действие — умножение. При его выполнении всегда будет четный ответ, если есть хотя бы один множитель четный. В ситуации, когда перемножаются два нечетных числа, результатом окажется нечетное.
Для иллюстрации последнего потребуется сделать такую запись: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Опять первое слагаемое представляет собой четное число, а единица сделает его нечетным.
С четвертым действием — делением — все не так однозначно. Начать можно с двух четных. Во-первых, может получиться дробь, тогда о четности речи не идет. Во-вторых, результатом бывает целое число. Но и тогда однозначного ответа на вопрос о будущей четности получить невозможно. Оценить ее можно только после выполнения деления. Ответ может быть как четным, так и нечетным.
Если делится нечетное число на четное, то ответ оказывается всегда дробным. Значит, его четность не определяется.
Значит, его четность не определяется.
Когда в делении участвуют нечетные числа, то результатом также может оказаться дробь. Но если ответ целый, то он обязательно будет нечетным.
При делении четного на нечетное, как в предыдущей ситуации, возможно два варианта: дробь или целое число. Во втором случае оно всегда будет четным.
Урок математики во 2 классе по теме: Чётные и нечётные числа. план-конспект урока по математике (2 класс) на тему
2 класс математика четные и нечетные числа
Изучение нового материала с элементами исследовательской деятельности по теме «Четные и нечетные числа» , повторение табличных случаев умножения и деления на 2.
Скачать:
| matemat. doc | 103 КБ |
Предварительный просмотр:
,Урок математики учителя начальных классов МОУ СОШ № 5
ОЦ «Лидер» г. о. Кинель
Шеиной Людмилы Михайловны
Тип урока : изучение нового материала с элементами исследовательской деятельности.
Формы обучения: работа под руководством учителя, групповая, самостоятельная работа, фронтальная.
Тема: Чётные и нечётные числа. (СЛАЙД)
Цель : знакомство с чётными и нечётными числами.
познакомить с чётными и нечётными числами; закрепить знания таблицы умножения; закрепить знания таблицы умножения и деления с числом 2; расширять кругозор учащихся; прививать интерес к предмету.
Оборудование: учебник «Математика» ( автор В. Н.Рудницкая) , детская энциклопедия «Я познаю мир», рисунки, изречения Пифагора, компьютер, интерактивная доска.
I. Организация урока ( Мотивация, ведущая к выдвижению гипотез решения проблем ):
-Добрый день, дорогие ребята. Поприветствуем друг друга хорошим настроением, добрыми улыбками. Возьмитесь за руки и скажите своему соседу по парте «У нас всё будет хорошо». Спасибо, молодцы. А сейчас урок математики.
Вступительный рассказ учителя.
Прочитайте тему сегодняшнего урока на слайде. О чём будем говорить на уроке? Коллективное обсуждение цели урока, вопросов, на которые необходимо дать ответы.
Мы с вами отправимся к самой таинственной, ещё не разгаданной планете – математика (арифметика). Изучать науку математику люди начали очень давно, в VI веке до нашей эры (в Египте, Вавилоне). Греки обогнали в математике все другие народы.
— Вы спросите почему?
— Да потому, что они хорошо умели спорить.
В древние времена Греция состояла из многих маленьких государств. Чуть ли не каждый город с окрестными деревнями был отдельным государством. Каждый раз, когда приходилось решать какой-нибудь важный государственный вопрос, горожане собирались на площадь, обсуждали его, спорили, голосовали.
На собраниях приходилось опровергать противников, рассуждать, доказывать свою правоту.
Древние греки считали, что спор помогает найти самое лучшее, самое правильное решение. Они даже придумали следующее изречение:
(СЛАЙД 2) «В споре рождается истина»
И в науке греки стали поступать так же, как на народном собрании. Они не просто заучивали правила, а доискивались причины: почему правильно делать так, а не иначе. Они спорили друг с другом, старались найти в рассуждениях ошибки.
Они спорили друг с другом, старались найти в рассуждениях ошибки.
-Докажут одно правило рассуждения ведут к другому, более сложному, потом к третьему, четвёртому. Из правил складывались законы, а из законов – наука математика. (СЛАЙД 3)
Едва родившись, греческая математика сразу семимильными шагами пошла вперёд. Ей помогали чудесные сапоги — скороходы, которых раньше у других народов не было. Они назывались «Рассуждение», «Доказательство».
Изучение нового материала с элементами исследовательской деятельности по теме «Четные и нечетные числа» , повторение табличных случаев умножения и деления на 2.
| matemat. doc | 103 КБ |
Рудницкая, детская энциклопедия Я познаю мир, рисунки, изречения Пифагора, компьютер, интерактивная доска.
Nsportal. ru
17.06.2018 18:57:18
2018-06-17 18:57:18
Источники:
Https://nsportal. ru/nachalnaya-shkola/matematika/2012/08/23/urok-matematiki-vo-2-klasse-po-teme-chyotnye-i-nechyotnye
Четное нечетное – Чётные и нечётные числа — урок. Математика, 2 класс. — Таловская средняя школа » /> » /> .keyword { color: red; }
Математика, 2 класс. — Таловская средняя школа » /> » /> .keyword { color: red; }
2 класс математика четные и нечетные числа
Четные и нечетные числа — это… Что такое Четные и нечетные числа?
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]
Чётное число — целое число, которое Делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…
Нечётное число — целое число, которое Не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…
Иными словами, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Признак чётности
Если в десятичной форме записи числа Последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.
Арифметика
- Сложение и вычитание:
- ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± ЧЁтное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
- ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.
В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
↑ «Чётные числа» в БСЭ.
Wikimedia Foundation. 2010.
Четное число — это… Что такое Четное число?
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]
Чётное число — целое число, которое Делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…
Нечётное число — целое число, которое Не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…
Иными словами, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Признак чётности
Если в десятичной форме записи числа Последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.
Арифметика
- Сложение и вычитание:
- ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное =
- ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
- ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным) ЧЁтное / НЕчётное = если результат целое число, то оно ЧЁтное НЕчётное / ЧЁтное — результат не может быть целым числом, а соответственно обладать атрибутами чётности НЕчётное / НЕчётное = если результат целое число, то оно НЕчётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.
В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
↑ «Чётные числа» в БСЭ.
Wikimedia Foundation. 2010.
Четные и нечетные числа. Понятие о десятичной записи числа
Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Например: -24, 0, 6, 38 — все это четные числа.
M = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.
Пример нечетных чисел: 3, 1, 7 и 35.
N = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.
Сложение и вычитание четных и нечетных чисел
В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.
Операция
Результат
Пример
Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.
Умножение четных и нечетных чисел
При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Операция
Результат
Пример
А теперь рассмотрим дробные числа.
Десятичная запись числа
Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.
Например: 3,14; 5,1; 6,789 — это все десятичные дроби.
С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.
Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.
Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.
А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.
Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Четные и нечетные числа Википедия
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.
Определения[ | ]
Если M чётно, то оно представимо в виде m=2k, а если нечётно, то в виде m=2k+1, где k∈Z >.
С точки зрения теории сравнений, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Арифметика[ | ]
- Сложение и вычитание:
- ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
- Умножение:
- ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
Признак чётности[ | ]
В десятичной системе счисления[ | ]
Если в десятичной форме записи числа Последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.
В других системах счисления
Чётное число Википедия
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.
Определения[ | ]
Если M чётно, то оно представимо в виде m=2k, а если нечётно, то в виде m=2k+1, где k∈Z >.
С точки зрения теории сравнений, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Арифметика[ | ]
- Сложение и вычитание:
- ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
- Умножение:
- ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
- Деление:
- ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным) ЧЁтное / НЕчётное = если результат — целое число, то оно ЧЁтное НЕчётное / ЧЁтное — результат не может быть целым числом, и соответственно обладать атрибутами чётности не может НЕчётное / НЕчётное = если результат — целое число, то оно НЕчётное
Признак чётности[ | ]
В десятичной системе счисления[ | ]
Если в десятичной форме записи числа Последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.
В других системах счисления[
Чётные и нечётные числа — Википедия
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.
Если M чётно, то оно представимо в виде, а если нечётно, то в виде, где.
С точки зрения теории сравнений, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
- Деление:
- ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным)
- Сложение и вычитание:
- ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
- Умножение:
- ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
Признак чётности[править]
В десятичной системе счисления[править]
Если в десятичной форме записи числа Последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.
В других системах счисления[править]
Для всех систем счисления С чётным основанием (например, для шестнадцатеричной), действует тот же признак чётности: число делится на 2, если его Последняя цифра делится на 2. Для систем счисления С нечётным основанием существует другой признак чётности: число чётно тогда и только тогда, когда чётна Сумма его цифр [1] [2] . Например, число, обозначаемое записью «136», чётно в любой системе счисления, начиная с семеричной [1] .
История и культура[править]
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян» [3] .
В разных странах существуют связанные с количеством даримых цветов традиции. Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.
Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.
В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)
В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.
Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.
С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.
Согласно Правилам дорожного движения, в зависимости от чётности или нечётности числа месяца может быть разрешена стоянка под знаками 3.29, 3.30.
- Последовательность A005408 в OEIS: нечётные числа Последовательность A005843 в OEIS: чётные числа Последовательность A179082 в OEIS: чётные числа с чётной суммой цифр в десятичной записи
Чётные и нечётные числа — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.
Определения
Если M чётно, то оно представимо в виде m = 2 k, а если нечётно, то в виде m = 2 k + 1, где k \in \mathbb Z.
С точки зрения теории сравнений, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Арифметика
- Сложение и вычитание:
- ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
- Умножение:
- ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
- Деление:
- ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным) ЧЁтное / НЕчётное = если результат — целое число, то оно ЧЁтное НЕчётное / ЧЁтное — результат не может быть целым числом, и соответственно обладать атрибутами чётности не может НЕчётное / НЕчётное = если результат — целое число, то оно НЕчётное
Признак чётности
В десятичной системе счисления
Если в десятичной форме записи числа Последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.
В других системах счисления
Для всех систем счисления С чётным основанием (например, для шестнадцатеричной), действует тот же признак чётности: число делится на 2, если его Последняя цифра делится на 2. Для систем счисления С нечётным основанием существует другой признак чётности: число чётно тогда и только тогда, когда чётна Сумма его цифр [1] [2] . Например, число, обозначаемое записью «136», чётно в любой системе счисления, начиная с семеричной [1] .
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян» [3] .
В разных странах существуют связанные с количеством даримых цветов традиции. Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.
Практика
В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)
В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.
Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.
С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.
Согласно Правилам дорожного движения, в зависимости от чётности или нечётности числа месяца может быть разрешена стоянка под знаками 3.29, 3.30.
Напишите отзыв о статье «Чётные и нечётные числа»
Примечания
↑ 12Яков Перельман. Чёт или нечет? // Занимательная арифметика: загадки и диковинки в мире чисел. — Издание восьмое, сокращённое. — М.: Детгиз, 1954. — С. 66-68. ↑Ruth L. Owen [www. pentagon. kappamuepsilon. org/pentagon/Vol_51_Num_2_Spring_1992.pdf Divisibility in bases] (англ.) // The Pentagon: A Mathematics Magazine for Students : журнал. — 1992. — Vol. 51, fasc. 2. — P. 17–20. [web. archive. org/web/20150909051653/www. pentagon. kappamuepsilon. org/pentagon/Vol_51_Num_2_Spring_1992. pdf Архивировано] из первоисточника 9 сентября 2015. ↑Рифтин Б. Л. [ec-dejavu. ru/i/In_Yan. html#pigalev Инь и Ян. Мифы народов мира.] Том 1, М.: Сов. энциклопедия, 1991, с. 547.
pdf Архивировано] из первоисточника 9 сентября 2015. ↑Рифтин Б. Л. [ec-dejavu. ru/i/In_Yan. html#pigalev Инь и Ян. Мифы народов мира.] Том 1, М.: Сов. энциклопедия, 1991, с. 547.
Ссылки
- Последовательность A005408 в OEIS: нечётные числа Последовательность A005843 в OEIS: чётные числа Последовательность A179082 в OEIS: чётные числа с чётной суммой цифр в десятичной записи
Отрывок, характеризующий Чётные и нечётные числа
– Так, так, – сказал князь Андрей, обращаясь к Алпатычу, – все передай, как я тебе говорил. – И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.
От Смоленска войска продолжали отступать. Неприятель шел вслед за ними. 10 го августа полк, которым командовал князь Андрей, проходил по большой дороге, мимо проспекта, ведущего в Лысые Горы. Жара и засуха стояли более трех недель. Каждый день по небу ходили курчавые облака, изредка заслоняя солнце; но к вечеру опять расчищало, и солнце садилось в буровато красную мглу. Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром.
Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром. Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Князь Андрей командовал полком, и устройство полка, благосостояние его людей, необходимость получения и отдачи приказаний занимали его. Пожар Смоленска и оставление его были эпохой для князя Андрея. Новое чувство озлобления против врага заставляло его забывать свое горе. Он весь был предан делам своего полка, он был заботлив о своих людях и офицерах и ласков с ними. В полку его называли наш князь, им гордились и его любили. Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Правда, все в темном, мрачном свете представлялось князю Андрею – особенно после того, как оставили Смоленск (который, по его понятиям, можно и должно было защищать) 6 го августа, и после того, как отец, больной, должен был бежать в Москву и бросить на расхищение столь любимые, обстроенные и им населенные Лысые Горы; но, несмотря на то, благодаря полку князь Андрей мог думать о другом, совершенно независимом от общих вопросов предмете – о своем полку. 10 го августа колонна, в которой был его полк, поравнялась с Лысыми Горами. Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Он велел оседлать себе лошадь и с перехода поехал верхом в отцовскую деревню, в которой он родился и провел свое детство. Проезжая мимо пруда, на котором всегда десятки баб, переговариваясь, били вальками и полоскали свое белье, князь Андрей заметил, что на пруде никого не было, и оторванный плотик, до половины залитый водой, боком плавал посредине пруда. Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Он был глух и не слыхал подъезда князя Андрея. Он сидел на лавке, на которой любил сиживать старый князь, и около него было развешено лычко на сучках обломанной и засохшей магнолии.
Князь Андрей подъехал к дому. Несколько лип в старом саду были срублены, одна пегая с жеребенком лошадь ходила перед самым домом между розанами. Дом был заколочен ставнями. Одно окно внизу было открыто. Дворовый мальчик, увидав князя Андрея, вбежал в дом.
Алпатыч, услав семью, один оставался в Лысых Горах; он сидел дома и читал Жития. Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.
Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.
- Деление:
- ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным)
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]
Чётное число — целое число, которое Делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…
Нечётное число — целое число, которое Не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…
Иными словами, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Признак чётности
Если в десятичной форме записи числа Последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.
Арифметика
- Сложение и вычитание:
- ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± ЧЁтное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
- ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.
В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
↑ «Чётные числа» в БСЭ.
Wikimedia Foundation. 2010.
В китайской космологии и натурософии чётные числа соответствуют понятию инь, а нечётные ян 3.
Xn—-8sbanwvcjzh9e. xn--p1ai
31.01.2020 15:49:11
2017-07-21 01:20:39
Источники:
Https://xn—-8sbanwvcjzh9e. xn--p1ai/raznoe/chetnoe-nechetnoe-chyotnye-i-nechyotnye-chisla-urok-matematika-2-klass. html
Четные и нечетные числа в математике » /> » /> .keyword { color: red; }
2 класс математика четные и нечетные числаДелить или не делить — вот в чем вопрос. В этой статье разберем, что такое четные числа, чем они отличаются от нечетных и зачем вообще нам это знать.
О чем эта статья:
Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.
Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.
Четное число — это число, которое делится нацело на 2.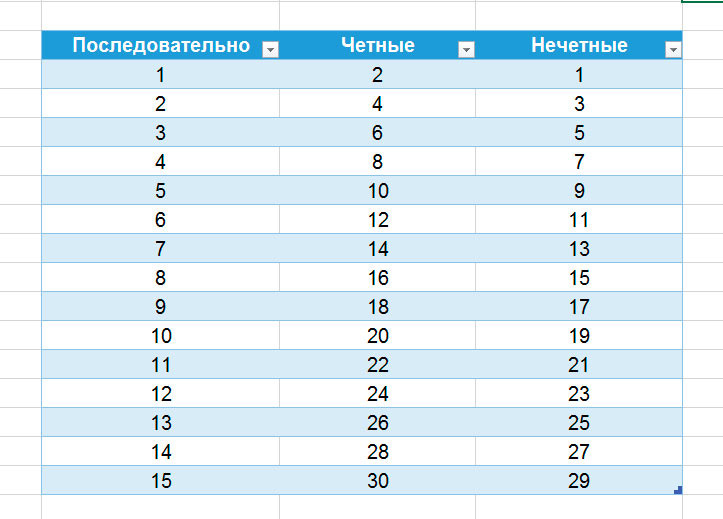
4 : 2 = 2
Это значит, что 4 — четное число.
Нечетное число — это число, которое не делится на 2 без остатка.
5 не делится на 2 без остатка — значит, 5 это нечетное число.
Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.
Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.
Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.
Свойства четных и нечетных чисел
- Если сложить два четных числа, получится четное число:
8 + 8 = 16
16 : 2 = 8 Если сложить два нечетных числа, получится четное число:
3 + 3 = 6
6 : 2 = 3 Если сложить четное число с нечетным, получится нечетное число:
4 + 5 = 9
9 : 2 = 4 (остаток 1) Если четное число умножить на четное число, получится четное число:
2 × 2 = 4
4 : 2 = 2 Если четное число умножить на нечетное число, получится четное число:
4 × 3 = 12
12 : 2 = 6 Если нечетное число умножить на нечетное, получится нечетное:
3 × 3 = 9
Четные и нечетные числа чередуются друг с другом
1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.
Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.
| 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 |
| 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 |
| 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| 4 | 14 | 24 | 34 | 44 | 54 | 64 | 74 | 84 | 94 |
| 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
| 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 | 86 | 96 |
| 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 |
| 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 | 88 | 98 |
| 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.
Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.
- Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Однозначные числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. Четные числа: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26. Нечетные числа: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25. Круглые числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120.
Онлайн-курсы по математике для детей помогут быстрее освоить новую тему при поддержке опытного преподавателя.
Задачи для практики
Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.
Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?
| 1 | ♥ | 17 |
| 2 | 10 | ♥ |
| ♥ | 11 | 19 |
| 4 | ♥ | 20 |
| 5 | 13 | ♥ |
| ♥ | 14 | 22 |
| 7 | 15 | 23 |
| 8 | ♥ | ♥ |
Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.
Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | |||||
| X : 2 |
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | 4 | 8 | 12 | 16 | 20 |
| X : 2 | 1 | 2 | 3 | 4 | 5 |
2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
10 : 2 = 5 — нечетное
Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
15 + 12 = 27 (к)
Отнимем от общего количества конфет получившееся число:
44 — 27 = 17 (к)
Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.
17 — нечетное число.
Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?
51 — 5 = 46 (ф)
46 — четное число.
Ответ: изначально у Маши в инстаграме было 46 фотографий.
Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.
| 1 | ☆ | 3 | ☆ | 5 |
| 6 | ☆ | ☆ | 9 | 10 |
| ☆ | 12 | 13 | ☆ | 15 |
| 16 | ☆ | ☆ | 19 | 20 |
| ☆ | 22 | 23 | ☆ | 25 |
Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.
Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70
Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
Число 126 оканчивается на четную цифру 6. Значит, число 126 — четное.
Значит, число 126 — четное.
Если нечетное число умножить на нечетное, получится нечетное 3 3 9.
Skysmart. ru
15.12.2018 16:35:38
2018-12-15 16:35:38
Источники:
Https://skysmart. ru/articles/mathematic/chetnye-i-nechetnye-chisla
Отсортировать четные и нечетные числа i 42 ii 89 iii 144 iv 321…
Перейти к
- Игра с числами. Упражнение 2.1.
- Игра с числами. Упражнение 2.8.
- Игра с числами. Упражнение 2.2.
- Игра с числами.
 Упражнение 2.3.
Упражнение 2.3. - Игра с числами. Упражнение 2.4.
- Игра с числами. Упражнение 2.5.
- Игра с числами. Упражнение 2.6.
- Игра с числами. Упражнение 2.7.
- Игра с числами. Упражнение 2.9.
- Игра с числами. Упражнение 2.
 10.
10. - Игра с числами. Упражнение 2.11.
- Зная свои числа
- Игра с числами
- Целые числа
- Действия над целыми числами
- Отрицательное число и целые числа
- Фракции
- Десятичные
- Введение в алгебру
- Соотношение, пропорция и унитарный метод
- Основные геометрические понятия
- Углы
- Треугольники
- Круги
- Пара прямых и поперечная
- Понимание трехмерных форм
- Симметрия
- Основные геометрические инструменты
- Геометрические построения
- Измерение
- Обработка данных Представление данных
- Обработка данных – II
- Гистограммы обработки данных
Главная >
РД Шарма Решения
Класс 6
Математика
>
Глава 2. Игра с числами
>
Игра с числами. Упражнение 2.1.
>
Вопрос 11
Игра с числами
>
Игра с числами. Упражнение 2.1.
>
Вопрос 11
Вопрос 11. Игра с числами. Упражнение 2.1. что
Числа, которые делятся на 2, являются четными, а те, которые не делятся на 2, являются нечетными числами.
Итак, мы получаем
42 144 — четные числа, а 89 321 — нечетные числа.
Связанные вопросы
Определите: (i) фактор (ii) множественный Приведите по четыре примера для каждого.
Определите: (i) фактор (ii) множественный Приведите по четыре примера для каждого.
Запишите все множители каждого из следующих чисел: (i) 60 (ii) 76 (iii) 125 (iv) 729.
Запишите первые пять кратных каждого из следующих чисел: (i) 25 (ii) 35 (iii) 45 (iv) 40.
Делитель какого из следующих чисел равен 15? (i) 15625 (ii) 123015
Какие из следующих чисел делятся на 21? (i) 21063 (ii) 20163
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Игра с числами Упражнение 2.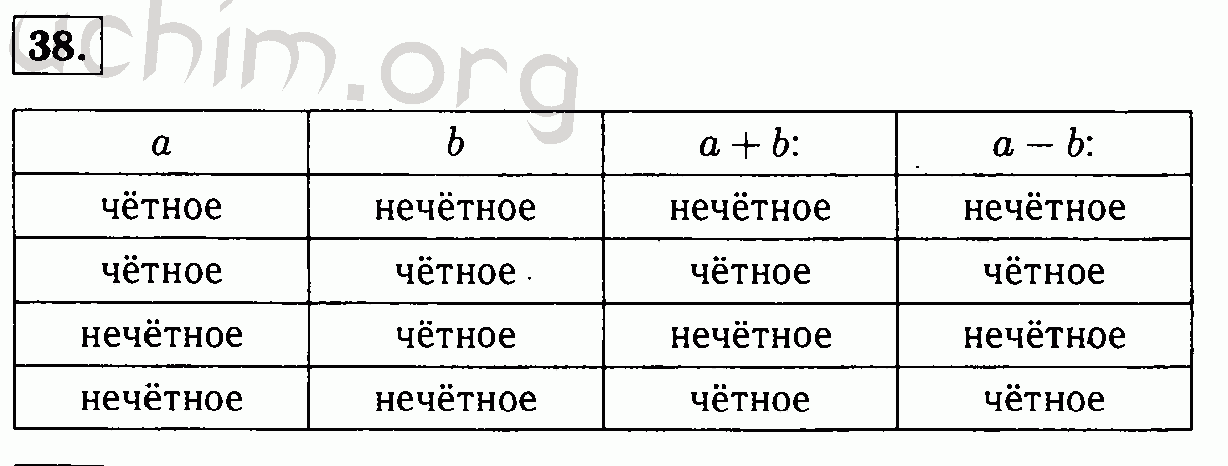 1
1
игра с номерами Упражнение 2.8
Игра с номерами Упражнение 2.2
Игра с номерами Упражнение 2.3
Игра с номерами Упражнение 2.4
Игра с номерами Упражнение 2.5
Игра с номерами Упражнение 2.6
Игра с номерами. 2,7
.
Игра с числами Упражнение 2.9
Игра с числами Упражнение 2.10
Игра с числами Упражнение 2.11
Главы
Знание ваших номеров
Игра с номерами
целые числа
Операции на целых числах
Отрицательные числа и целые числа
Фракции
Десятиц
Введение в Algebra
Коэффициент, доля и единая метода
Base Geometrical Concectts
.Углы
Треугольники
Окружности
Пара прямых и поперечная
Понимание трехмерных форм
Симметрия
Основные геометрические инструменты
Геометрические построения
Измерение
Обработка данных Представление данных
Обработка данных – II
Обработка данных Гистограммы
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Сортировка четных и нечетных чисел … | Помощь с домашним заданием
CBSE, JEE, NEET, NDA
Банк вопросов, пробные тесты, экзаменационные работы
Решения NCERT, образцы документов, заметки, видео
Установить сейчас
Сортировка четных и нечетных чисел 13 28 41 99 50 255 132 664 59 29 71 165 14
Автор: Рачита Рачита 1 год, 10 месяцев назад
CBSE > Класс 06 > Математика
- 1 ответ
Укажите, эквивалентны ли следующие пары 7/28,1/4
Автор: Суровый Сони 6 дней, 17 часов назад
CBSE > Класс 06 > Математика
- 5 ответов
__-1/5=1/2
Автор: Аруш Бхардвадж 2 недели назад
CBSE > Класс 06 > Математика
- 1 ответ
Длина ребра куба определяется по формуле нахождения общей длины ребер куба
Автор: Бхуван Виранагудра 1 день, 2 часа назад
CBSE > Класс 06 > Математика
- 1 ответ
У Аслама было 40 шариков он отдал по одному из этих двух своему брату и по одному своему другу сколько шариков осталось у Аслама
Автор: Шашват Шашват 1 неделя, 2 дня назад
CBSE > Класс 06 > Математика
- 3 ответа
Рита экономит 65 пайсов в день. Найдите наименьшее количество дней, за которые она сможет накопить точное количество рупий
Найдите наименьшее количество дней, за которые она сможет накопить точное количество рупий
Автор: Арти Верма 1 неделя назад
CBSE > Класс 06 > Математика
- 3 ответа
-1(-8)+4
Автор: Шрибардхан Махапатра Махапатра 1 неделя, 4 дня назад
CBSE > Класс 06 > Математика
- 3 ответа
Мобильный телефон
Автор: Амарджит Кумар 2 часа назад
CBSE > Класс 06 > Математика
- 0 ответов
Целое число от 0 до -10
Автор: Яшрадж Шаха 1 неделя, 2 дня назад
CBSE > Класс 06 > Математика
- 0 ответов
1+124+545+=
Автор: Амарджит Кумар 3 часа назад
CBSE > Класс 06 > Математика
- 0 ответов
Джавед получил 5/7 корзины апельсинов. Какая доля апельсинов осталась в корзине
Какая доля апельсинов осталась в корзине
Автор: Аарав Агравал 1 неделя, 4 дня назад
CBSE > Класс 06 > Математика
- 3 ответа
myCBSEguide
Доверяют 1 крор+ студентов
Установить сейчас
- Создавайте документы за считанные минуты
- Печать с вашим именем и логотипом
- Скачать в формате PDF
- 5 лакхов+ вопросов
- Включенные решения
- На основе учебного плана CBSE
- Подходит для школ и репетиторов
Создание документов
Тестовый генератор
Создание статей по цене 10 ₹/- за бумагу
Попроб.
Видео с вопросами: Использование таблиц сложения для исследования сумм нечетных и четных чисел
Стенограмма видео
В этой таблице сложения София покрасила все четные суммы в синий цвет, а все нечетные — в зеленый. Найдите шаблоны в таблице, чтобы решить, являются ли следующие суммы четными или нечетными. Четыре плюс три. Пять плюс шесть. Девять плюс семь. 17 плюс восемь. И 22 плюс 28.
Найдите шаблоны в таблице, чтобы решить, являются ли следующие суммы четными или нечетными. Четыре плюс три. Пять плюс шесть. Девять плюс семь. 17 плюс восемь. И 22 плюс 28.
Белый столбец и белая строка в этой таблице сложения дают нам два числа, которые мы складываем. Принцип работы таблицы заключается в том, что мы можем выбрать одно число из левого столбца. Например, мы можем выбрать число три. И одно число из верхнего ряда. Давайте выберем цифру два. И мы можем двигаться вдоль и поперек сетки, пока столбец и строка не встретятся. И мы видим, что они встречаются на вот этой площади. Квадрат дает нам ответ на сложение. Три плюс два равно пяти. Теперь, когда [София] заполнила таблицу, нам сказали, что она раскрасила все четные суммы синим цветом, а все нечетные — зеленым. Пять — нечетное число. Итак, это окрашено в зеленый цвет.
Теперь нам дано пять разных дополнений. И нам говорят искать закономерности в таблице, чтобы решить, будут ли суммы четными или нечетными. В таблице можно увидеть много шаблонов. Некоторые из них числовые. Например, если мы посчитаем числа в каждой строке, мы увидим, что они каждый раз увеличиваются на единицу. И то же самое с колонками. Другая закономерность, которую мы можем заметить, заключается в том, что если мы посмотрим на сетку по диагонали, то увидим квадраты с одинаковыми номерами в них. Но эти шаблоны на самом деле не помогут нам ответить на вопрос. Нам нужно искать закономерности в четных и нечетных числах.
Некоторые из них числовые. Например, если мы посчитаем числа в каждой строке, мы увидим, что они каждый раз увеличиваются на единицу. И то же самое с колонками. Другая закономерность, которую мы можем заметить, заключается в том, что если мы посмотрим на сетку по диагонали, то увидим квадраты с одинаковыми номерами в них. Но эти шаблоны на самом деле не помогут нам ответить на вопрос. Нам нужно искать закономерности в четных и нечетных числах.
Теперь, если мы посмотрим на пять различных расчетов, о которых нам нужно подумать, только один из них появится в сетке. Мы можем найти ответ на четыре плюс три, используя числа в сетке. Но наша сетка недостаточно велика, чтобы показать шесть из пяти плюс шесть. Или любое из чисел девять плюс 7, 17 плюс восемь или даже 22 плюс 28. Так как же мы можем использовать эти простые сложения? Все, что мы используем, — это цифры от одного до пяти, чтобы решить, являются ли эти большие суммы четными или нечетными.
Итак, для начала давайте воспользуемся сеткой, чтобы показать один расчет, который там есть. Четыре плюс три. Прежде всего, мы находим строку, которая представляет четыре, и столбец, который представляет три. Теперь, если мы будем двигаться вниз по столбцу и по строке, мы можем использовать для этого пальцы. В конце концов мы доберемся до квадрата, представляющего сумму. Вот. Четыре плюс три равно семь. Но нам не нужно беспокоиться о числе семь на самом деле. Нас просят решить, является ли сумма четной или нечетной. Итак, давайте просто посмотрим на цвет квадрата. Это зеленый квадрат. Итак, мы знаем, что сумма должна быть нечетной.
Четыре плюс три. Прежде всего, мы находим строку, которая представляет четыре, и столбец, который представляет три. Теперь, если мы будем двигаться вниз по столбцу и по строке, мы можем использовать для этого пальцы. В конце концов мы доберемся до квадрата, представляющего сумму. Вот. Четыре плюс три равно семь. Но нам не нужно беспокоиться о числе семь на самом деле. Нас просят решить, является ли сумма четной или нечетной. Итак, давайте просто посмотрим на цвет квадрата. Это зеленый квадрат. Итак, мы знаем, что сумма должна быть нечетной.
Теперь давайте сосредоточимся на нашем втором сложении, пять плюс шесть. Теперь ответ на этот вопрос не будет в сетке. Но мы можем использовать сетку, чтобы помочь нам. Что мы знаем о числах пять и шесть? Во-первых, мы знаем, что пять — нечетное число. Итак, давайте воспользуемся той же системой цветового кодирования, которую использует София. И напишем пять зеленым цветом. Шесть — четное число. Итак, давайте напишем шесть синим цветом. Теперь мы можем использовать эту информацию, чтобы найти ответ. Что произойдет, если мы сложим вместе нечетное число с четным числом. Давайте напишем все нечетные числа зеленым цветом, чтобы лучше видеть их. Раз, три, пять. И запишем все четные числа синим цветом, два, четыре.
Что произойдет, если мы сложим вместе нечетное число с четным числом. Давайте напишем все нечетные числа зеленым цветом, чтобы лучше видеть их. Раз, три, пять. И запишем все четные числа синим цветом, два, четыре.
Теперь мы можем использовать таблицу, чтобы определить, что произойдет, если мы сложим вместе нечетное и четное число. Давайте выберем любое нечетное число для начала. Почему у нас нет пяти? Потому что это число в нашем вопросе. А теперь давайте выберем четное число, чтобы добавить к нему. У нас в таблице нет шестерки. Но мы можем выбрать другое четное число. Выберем два. Что мы получим, если сложим нечетное и четное число вместе? Квадрат, к которому мы приходим, зеленый. Нечетное и четное число дают нечетный ответ или нечетную сумму.
Наш следующий расчет: девять плюс семь. Давайте воспользуемся тем же методом, чтобы помочь. И девять, и семь — нечетные числа. Итак, давайте выберем два нечетных числа, чтобы сложить их в нашей сетке. Мы могли бы облегчить себе задачу и выбрать один и один. Мы видим, что сумма этих чисел представляет собой синий квадрат. И это то же самое для любых двух нечетных чисел, которые мы решим сложить вместе. Нечетное число плюс еще одно нечетное число равняется четной сумме. Это всегда так. Неважно, девять плюс семь или один плюс один.
Мы видим, что сумма этих чисел представляет собой синий квадрат. И это то же самое для любых двух нечетных чисел, которые мы решим сложить вместе. Нечетное число плюс еще одно нечетное число равняется четной сумме. Это всегда так. Неважно, девять плюс семь или один плюс один.
Наш четвертый расчет равен 17 плюс восемь. 17 заканчивается цифрой семь. Итак, мы знаем, что это нечетное число. А мы знаем, что восемь — четное число. Теперь, если вы помните, мы уже пробовали складывать нечетное и четное числа вместе. Мы нашли ответ на пять плюс два, когда хотели выяснить, будет ли пять плюс шесть нечетным или четным. И мы сказали, что пять плюс шесть — это нечетно. Итак, мы знаем, что 17 плюс восемь, что является еще одним нечетным числом плюс четное число, также будет нечетным.
Наш окончательный расчет: 22 плюс 28. 22 имеет двойку на месте единиц. Итак, мы знаем, что это четное число. А в 28 восьмерка стоит на месте единиц. Это тоже четное число. Что произойдет, если мы сложим два четных числа вместе? Давайте выберем два четных числа в нашей сетке и посмотрим, какого цвета будет сумма.

 В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20… Упражнение 2.3.
Упражнение 2.3.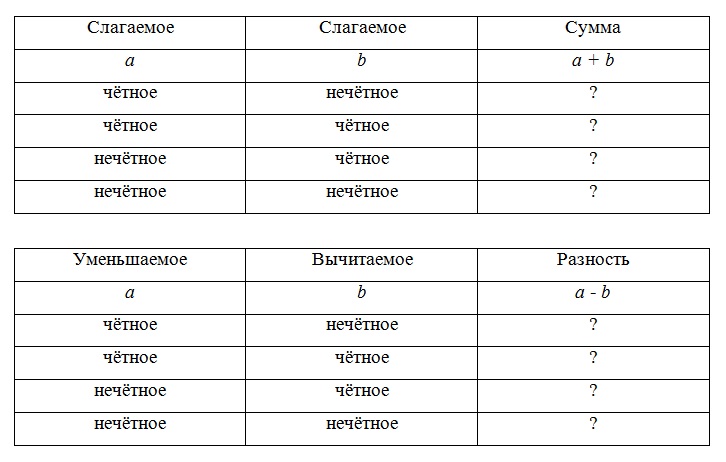 10.
10.