Интерактивный учебник языка Python
Занятие 8. Функции и рекурсия
1. Функции
Напомним, что в математике факториал числа n определяется как n! = 1 ⋅ 2 ⋅ … ⋅ n. Например, 5! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 = 120. Ясно, что факториал можно легко посчитать, воспользовавшись циклом for. Представим, что нам нужно в нашей программе вычислять факториал разных чисел несколько раз (или в разных местах кода). Конечно, можно написать вычисление факториала один раз, а затем используя Copy-Paste вставить его везде, где это будет нужно.
# вычислим 3!
res = 1
for i in range(1, 4):
res *= i
print(res)
# вычислим 5!
res = 1
for i in range(1, 6):
res *= i
print(res)Однако, если мы ошибёмся один раз в начальном коде, то потом эта ошибка попадёт в код во все места, куда мы скопировали вычисление факториала. Да и вообще, код занимает больше места, чем мог бы. Чтобы избежать повторного написания одной и той же логики, в языках программирования существуют функции.
Функции — это такие участки кода, которые изолированы от остальный программы и выполняются только тогда, когда вызываются.
Покажем, как написать функцию factorial(), которая принимает один параметр — число, и возвращает значение — факториал этого числа.
def factorial(n):
res = 1
for i in range(1, n + 1):
res *= i
return res
print(factorial(3))
print(factorial(5))Дадим несколько объяснений. Во-первых, код функции должен размещаться в начале программы, вернее, до того места, где мы захотим воспользоваться функцией factorial(). Первая строчка этого примера является описанием нашей функции. factorial — идентификатор, то есть имя нашей функции. После идентификатора в круглых скобках идет список параметров, которые получает наша функция.
Далее идет тело функции, оформленное в виде блока, то есть с отступом. Внутри функции вычисляется значение факториала числа n и оно сохраняется в переменной res. Функция завершается инструкцией return res, которая завершает работу функции и возвращает значение переменной res.
Инструкция return может встречаться в произвольном месте функции, ее исполнение завершает работу функции и возвращает указанное значение в место вызова. Если функция не возвращает значения, то инструкция return используется без возвращаемого значения. В функциях, которым не нужно возвращать значения, инструкция return может отсутствовать.
Приведём ещё один пример. Напишем функцию max(), которая принимает два числа и возвращает максимальное из них (на самом деле, такая функция уже встроена в Питон).
def max(a, b):
if a > b:
return a
else:
return b
print(max(3, 5))
print(max(5, 3))
print(max(int(input()), int(input())))Теперь можно написать функцию max3(), которая принимает три числа и возвращает максимальное их них.
def max(a, b):
if a > b:
return a
else:
return b
def max3(a, b, c):
return max(max(a, b), c)
print(max3(3, 5, 4))Встроенная функция max() в Питоне может принимать переменное число аргументов и возвращать максимум из них. Приведём пример того, как такая функция может быть написана.
def max(*a):
res = a[0]
for val in a[1:]:
if val > res:
res = val
return res
print(max(3, 5, 4)) Все переданные в эту функцию параметры соберутся в один кортеж с именем a, на что указывает звёздочка в строке объявления функции.
2. Локальные и глобальные переменные
Внутри функции можно использовать переменные, объявленные вне этой функции
def f():
print(a)
a = 1
f()Здесь переменной a присваивается значение 1, и функция f() печатает это значение, несмотря на то, что до объявления функции f эта переменная
не инициализируется. В момент вызова функции
В момент вызова функции f() переменной a уже присвоено значение, поэтому функция f() может вывести его на экран.
Такие переменные (объявленные вне функции, но доступные внутри функции) называются глобальными.
Но если инициализировать какую-то переменную внутри функции, использовать эту переменную вне функции не удастся. Например:
def f():
a = 1
f()
print(a)Получим ошибку NameError: name 'a' is not defined. Такие переменные, объявленные внутри функции,
называются локальными. Эти переменные становятся недоступными после выхода из функции.
Интересным получится результат, если попробовать изменить значение глобальной переменной внутри функции:
def f():
a = 1
print(a)
a = 0
f()
print(a)Будут выведены числа 1 и 0. Несмотря на то, что значение переменной a изменилось внутри функции, вне функции оно осталось прежним! Это сделано в целях
“защиты” глобальных переменных от случайного изменения из функции. Например, если функция будет вызвана из цикла по переменной
Например, если функция будет вызвана из цикла по переменной i, а в этой функции
будет использована переменная i также для организации цикла, то эти переменные должны
быть различными. Если вы не поняли последнее предложение, то посмотрите на следующий код и подумайте, как бы он работал,
если бы внутри функции изменялась переменная i.
def factorial(n):
res = 1
for i in range(1, n + 1):
res *= i
return res
for i in range(1, 6):
print(i, '! = ', factorial(i), sep='')Если бы глобальная переменная i изменялась внутри функции, то мы бы получили вот что:
5! = 1 5! = 2 5! = 6 5! = 24 5! = 120
Итак, если внутри функции модифицируется значение некоторой переменной, то переменная с таким именем становится локальной переменной, и ее модификация не приведет к изменению глобальной переменной с таким же именем.
Более формально: интерпретатор Питон считает переменную локальной для данной функции, если в её коде
есть хотя бы одна инструкция, модифицирующая значение переменной, то эта переменная считается локальной
и не может быть использована до инициализации.
=, +=, а также использование переменной в качестве параметра цикла for.
При этом даже если инструкция,
модицифицирующая переменную никогда не будет выполнена, интерпретатор это проверить
не может, и переменная все равно считается локальной. Пример:def f():
print(a)
if False:
a = 0
a = 1
f()Возникает ошибка: UnboundLocalError: local variable 'a' referenced before assignment.
А именно, в функции f() идентификатор a становится локальной переменной,
т.к. в функции есть команда, модифицирующая переменную a, пусть даже никогда и
не выполняющийся (но интерпретатор не может это отследить). Поэтому вывод переменной a приводит к обращению к неинициализированной локальной переменной.
Чтобы функция могла изменить значение глобальной переменной, необходимо объявить эту переменную
внутри функции, как глобальную, при помощи ключевого слова global:
def f():
global a
a = 1
print(a)
a = 0
f()
print(a)В этом примере на экран будет выведено 1 1, так как переменная a объявлена, как глобальная,
и ее изменение внутри функции приводит к тому, что и вне функции переменная
будет доступна.
Тем не менее, лучше не изменять значения глобальных переменных внутри функции. Если ваша функция должна поменять какую-то переменную, пусть лучше она вернёт это значением, и вы сами при вызове функции явно присвоите в переменную это значение. Если следовать этим правилам, то функции получаются независимыми от кода, и их можно легко копировать из одной программы в другую.
Например, пусть ваша программа должна посчитать факториал вводимого числа, который вы потом захотите сохранить в переменной f. Вот как это не стоит делать:
def factorial(n):
global f
res = 1
for i in range(2, n + 1):
res *= i
f = res
n = int(input())
factorial(n)
# дальше всякие действия с переменной fЭтот код написан плохо, потому что его трудно использовать ещё один раз. Если вам завтра понадобится в другой программе использовать функцию «факториал», то вы не сможете просто скопировать эту функцию отсюда и вставить в вашу новую программу. Вам придётся поменять то, как она возвращает посчитанное значение.
Гораздо лучше переписать этот пример так:
# начало куска кода, который можно копировать из программы в программу
def factorial(n):
res = 1
for i in range(2, n + 1):
res *= i
return res
# конец куска кода
n = int(input())
f = factorial(n)
# дальше всякие действия с переменной fЕсли нужно, чтобы функция вернула не одно значение, а два или более, то для этого функция может вернуть список из двух или нескольких значений:
return [a, b]
Тогда результат вызова функции можно будет использовать во множественном присваивании:
n, m = f(a, b)
3. Рекурсия
def short_story():
print("У попа была собака, он ее любил.")
print("Она съела кусок мяса, он ее убил,")
print("В землю закопал и надпись написал:")
short_story()Как мы видели выше, функция может вызывать другую функцию. Но функция также может вызывать и саму себя!
Рассмотрим это на примере функции вычисления факториала. Хорошо известно, что 0!=1, 1!=1.
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
print(factorial(5))Подобный прием (вызов функцией самой себя) называется рекурсией, а сама функция называется рекурсивной.
Рекурсивные функции являются мощным механизмом в программировании. К сожалению, они не всегда эффективны. Также часто использование рекурсии приводит к ошибкам. Наиболее распространенная
из таких ошибок – бесконечная рекурсия, когда цепочка вызовов функций никогда не завершается и продолжается,
пока не кончится свободная память в компьютере. Пример бесконечной рекурсии приведен в эпиграфе к этому разделу.
Две наиболее распространенные причины для бесконечной рекурсии:
Пример бесконечной рекурсии приведен в эпиграфе к этому разделу.
Две наиболее распространенные причины для бесконечной рекурсии:
- Неправильное оформление выхода из рекурсии. Например, если мы в программе вычисления факториала
забудем поставить проверку
if n == 0, тоfactorial(0)вызоветfactorial(-1), тот вызоветfactorial(-2)и т. д. - Рекурсивный вызов с неправильными параметрами. Например, если функция
factorial(n)будет вызыватьfactorial(n), то также получится бесконечная цепочка.
Поэтому при разработке рекурсивной функции необходимо прежде всего оформлять условия завершения рекурсии и думать, почему рекурсия когда-либо завершит работу.
Ссылки на задачи доступны в меню слева. Эталонные решения теперь доступны на странице самой задачи.
Факториал на языке паскаль — Altarena.ru — технологии и ответы на вопросы
Содержание
- Написать функцию вычисления факториала
- Решение
- Решение
- Как обозначается факториал в паскале
- Вычисление факториала в pascal с помощью цикла
- Задача
- Решение
- Математические сведения
- Первый способ
- Второй способ
- Третий способ
- Замечание
- Длинная арифметика.
 Факториал
Факториал - Решение
- Двойной факториал
- Видео
Написать функцию вычисления факториала
Написать рекурсивную функцию вычисления факториала
Нужно написать рекурсивную функцию вычисления n!. Обычную функции могу написать, а куда рекурсию.
Написать программу, которая вычисляет значение p = (для вычисления факториала использовать функцию)
Написать программу, которая вычисляет значение p =m!*(m-n)!/n! (для вычисления факториала.
Вычисление суммы, используя функцию вычисления факториала
Составить программу вычисления суммы (рис), используя функцию вычисления факториала натурального.
Вычислить величины. Использовать функцию вычисления факториала
Составить программу. В задаче предполагается, используя шестизначный учебный шифр (его.
простите меня на недогадливость, а в чём состоит существенная экономия?
Решение
очень хитро!
я бы лично вряд ли использовал подобный код в реале (не люблю в продакшн такие хитрозакрученные и слегка неочевидные вещи), но код вызывает восхищение! Просто супер!
Спасибо!
bormant, а эта строчка всё таки НЕ НУЖНА!
Закомментируйте и убедитесь в этом сами!
цикл for изменяет переменную m
Решение
Тут понимаете какая штука.
Для языка Паскаль недвусмысленно заявлено, что значение счетчика цикла for по окончании цикла не определено, если только цикл не завершился по Break. Это означает, что значение счетчика цикла может быть разным в зависимости как от реализации языка, так и от варианта оптимизации внутри конкретной реализации (например, равным последнему значению, следующему за последним значением, или вовсе начальному значению). Если какая-то реализация будет брать начальное значение счетчика из памяти в регистр, все обращения к счетчику транслировать в обращения к этому регистру, а возвращать значение из регистра в память только по Break, то, строго говоря, это не будет нарушением с точки зрения языка.
Наоборот, код не использует ни одной нестандартной или недокументированной возможности. Он просто помнит одно последнее значение и использует его, если возможно. В конкретно этом примере экономия невелика, но представьте вместо Longint длинную арифметику, и оценки времени сразу заиграют новыми красками 🙂
Пример по сути является наводящим для организации «ленивых вычислений». Если последнее значение заменить таблицей, вычисляемой по мере необходимости, то достигается экономия на повторных вычислениях одних и тех же значений (без проверок допустимых диапазонов, только идея):
Если последнее значение заменить таблицей, вычисляемой по мере необходимости, то достигается экономия на повторных вычислениях одних и тех же значений (без проверок допустимых диапазонов, только идея):
Или варианты с промежуточными значениями и довычисление от них необходимых.
Другое дело, что если бы в продакшн подобный участок был бы действительно критичным по времени, то вместо функции была бы таблица.
Источник
Как обозначается факториал в паскале
Факториал – произведение натуральных чисел от единицы до заданного числа. Имеет условное обозначение в виде восклицательного знака. n!=1*2*3*. *n (Например: 3!=1*2*3=6).
В Turbo Pascal факториал находится, как правило, двумя способами: с помощью цикла или с помощью рекурсии.
Вычисление факториала в pascal с помощью цикла
Данный способ нахождения факториала исключительно прост. В цикле от 1 до n умножается число само на себя. При этом необходимо учитывать условие, что 0!=1. Ниже представлена реализация программы с помощью цикла for. Аналогично используются repeat и while.
Аналогично используются repeat и while.
if (n=0) then writeln(‘0!=1’) else
Факториал числа – Вычисление с помощью цикла (1 способ)
Факториал – Нахождение факториала в паскале с помощью рекурсии (2 способ)
Задача
Факториал числа представляет собой произведение всех натуральных чисел от 1 до этого числа включительно. Например, факториал числа 7 выглядит так:
1 * 2 * 3 * 4 * 5 * 6 * 7
Факториал числа обозначается как само число после которого следует восклицательный знак. Например, 7!. Таким образом:
7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
С увеличением числа его факториал быстро возрастает. Так если 3! = 6, то уже 10! = 3628800. Поэтому для натуральных чисел больше 12-ти в языке программирования Паскаль просто так факториал вычислить нельзя.
Допустим, требуется определить факториал числа, которое ввел пользователь.
Решение
Переменной factorial сначала присваивается значение 1.
0! = 1 и 1! = 1.
Если пользователь ввел число больше единицы, то выполняется цикл, в теле которого на каждой итерации значение переменной factorial умножается на следующее натуральное число (переменную i ).
Обучение программированию идёт по пути от простого к сложному. Освоив типы данных и операторы языка, переходят к циклическим конструкциям. Задач на циклы существует бесчисленное количество: начиная от вывода цифр в столбик до подсчёта сумм по сложным формулам. Тем не менее у начинающих программистов остаётся вопрос: «Как вычислить факториал в «Паскале»?»
Реализовать задачу можно как минимум тремя способами. Отличаются они используемыми операторами.
Математические сведения
Перед тем как перейти к построению алгоритмов и написанию программ, следует изучить теорию. В математике факториалом называют произведение целого числа, для которого вычисляется выражение, на целые положительные числа меньше его.
Понять определение поможет пример. Пусть требуется выполнить нахождение факториала для числа 3. Решение: 3! = 3 * 2 * 1 = 6.
Обозначается действие восклицательным знаком, который ставится после числа. Важное замечание: факториал определён только для целых положительных чисел. Вместе с тем, введено понятия для нуля: 0! = 1.
Вместе с тем, введено понятия для нуля: 0! = 1.
Считать выражение для больших значений вручную – занятие долгое. Чтобы убыстрить процесс вычислений, используют компьютерные программы. Далее рассмотрены способы, как найти факториал в «Паскале».
Первый способ
Код ниже показывает вариант программы.
В примере используют составную конструкцию с условием, которое записывается перед телом цикла. Синтаксис записи:
Выполняется код следующим образом: программа проверяет истинность выражения , в случае положительной проверки переходит на .
Возвращаясь к программе, нужно обратить внимание на следующие строки:
Второй способ
Следующий предлагает вычислить факториал в «Паскале» с помощью оператора repeat.
Конструкция цикла: repeat until ;
Чтобы понять, как работает программа, рассмотрим её построчно:
Третий способ
Последняя программа также дает возможность вычислить факториал в «Паскале» и является самой компактной по размеру. Причина – используемый оператор for, для которого увеличение счётчика i задаётся в параметрах цикла.
Причина – используемый оператор for, для которого увеличение счётчика i задаётся в параметрах цикла.
Работает код следующим образом (цифрами указаны строки листинга):
Замечание
Даже для чисел из первой десятки факториал имеет значение больше, чем допускает тип данных integer. Поэтому программа в «Паскале» покажет сообщение об ошибке. Исправить её просто – нужно заменить тип данных для переменной-результата на longint или использовать типы для хранения вещественных значений.
Источник
Длинная арифметика. Факториал
Добрый вечер, господа программисты.
Сижу сейчас и разбираюсь с кодом для вычисления факториала из Окулова (задание 10, программа 5). Вот код без изменений из книги.
Всё вроде бы верно, но для факториала 27! возникает ошибка (большие числа не пробовал). Программа выдаёт 888869450418352160768000000, а двух цифр вначале не хватает: 10888869450418352160768000000.
Проблема, как мне кажется, в подчёркнутом условии. Ведь при выходе факториала за прежние границы массива первая цифра вне границ вполне может быть нулём, как в 27!, а исходник этого не учитывает.
Ведь при выходе факториала за прежние границы массива первая цифра вне границ вполне может быть нулём, как в 27!, а исходник этого не учитывает.
При замене указанного условия на i > a[0] (цифра с номером, большим, чем изначально указанный) всё становится на свои места.
Пожалуйста, подскажите, прав ли я.
длинная арифметика!
Вычислить точное значение эн в степени эн факториал!
длинная арифметика
помогите мне из этого умножения сделать сложение препод сказал тут нужно поменять умножить на плюс.
Длинная арифметика
Так вот я неаписал программу на сложение. Все с ней норм, а вот с произведением не идет почемуто.
Решение
Молодец! Возьми с полочки конфетку.
(Вообще не понятно почему размерность выбрана именно до 300 цифр? Всего лишь 170! имеет в своём составе уже 307 цифр.)
Только вот длину числа нужно вывести в отдельную переменную.
Короче! Я бы переписал всё примерно вот так:
Joy, только арифметика немного усложнится!
Не в данном конкретном случае, а при разработке своего модуля „длинной арифметики“.
Появятся проблемы с переполнением при выполнении простых арифметических операций, а значит появятся затруднения при отладке!
9 · 9 = 81 — влезет в байт. Нужно будет только сделать перенос десятичных регистров.
99 · 99 = 9801 — уже не лезет в байт. Следовательно нужно тратиться на приведение типов… Это — дополнительное время!
А ещё при больших основаниях преобразование в строку должно учитывать, что очередная порция цифр может быть меньше чем требуется, тогда ему слева дописывать нолики…
Ячейки:Значения = [00:00][01:11][02:01][03:10][04:01]
Что должно быть представлено публике как 110011100.
Если же не учитывать вышеприведённое условие добавление нолей, то кто-то может вывести так: 1101110.
Заказываю контрольные, курсовые, дипломные работы и диссертации здесь или здесь.
Длинная арифметика
Уважаемые, помогите решить задачку, горит ужасно помогите пожалуста, срочно надо: 1.Составить.
Длинная арифметика.Чтение и вывод.
Нашел процедуры чтения и выводы длинных чисел. Но есть несколько вопросов. procedure ReadLong(var.
Но есть несколько вопросов. procedure ReadLong(var.
Формирование матрицы, длинная арифметика.
1)натуральное число (длинное целое) можно представить в виде произведения нескольких натуральных.
Сортировка массивов и длинная арифметика
Ребят, помогите пожалуйста. Очень нужен ПОЛНЫЙ КОД. Вот задачи: 1. В городе имеется m банков.
Сортировка вставками.множества.длинная арифметика..
Завтра надо сдать практику иначе отчислят. помогите решить хоть что нибудь 1)Сортировка.
Источник
Двойной факториал
Задача: Дано натуральное число n. Получить n!! (!-факториал),равное произведению (1*3*. *n) для нечётного n и (2*4*. *n) для чётного n.
Требования:
Использовать оператор FOR.
Не использовать массивы и строки.
При вычислении факториалов обратить внимание на переполнение. Определить,при каких значениях параметров оно наступает. Постараться отодвинуть эту эту границу путём изменения типа параметров или сокращения дробей.
Двойной факториал
подскажите как написать функцию для вычисления х!!
Вычислить двойной факториал
привет всем. Суть задания такова найти для N значение (2N)!! нашел программу, но она работает для.
Суть задания такова найти для N значение (2N)!! нашел программу, но она работает для.
Вычислить двойной факториал
Написал программку под задание: Для числа n вывести произведение «n!!» с условием: если число.
Найти двойной факториал
Дано целое число N (> 0). Найти двойной факториал N: N!! = N•(N–2)•(N–4)•… (последний сомножитель.
у меня не нормально,на фор жалуется(
Добавлено через 3 минуты
вроде заработало,для чётных кажется правильно,но для неч ответ с минусом вылазит.
Задача: Дано натуральное число n. Получить n!! (!-факториал),равное произведению (1*3*. *n) для нечётного n и (2*4*. *n) для чётного n.
Требования:
Использовать оператор FOR.
Не использовать массивы и строки.
При вычислении факториалов обратить внимание на переполнение. Определить,при каких значениях параметров оно наступает. Постараться отодвинуть эту эту границу путём изменения типа параметров или сокращения дробей.
victor_g
прога работает,спасибо,но вроде нужно произведение факториалов,а вылазит просто факториал(
может нужно ввести в расчёты ещё n2 чётное? а потом перемножить чёт и нечет.
if (i mod 2)(n mod 2) then continue;
можно объяснение этой строки
if (i mod 2)(n mod 2) then continue;
можно объяснение этой строки
Заказываю контрольные, курсовые, дипломные работы и диссертации здесь или здесь.
Вычислить двойной факториал
Составьте, пожалуйста, программу для вычисления двойного факториала (2n+1)!! (например.
Двойной факториал
N!! = N*(N–2)*(N–4)*… (N > 0 — параметр целого типа; последний сомножитель в произведении равен 2.
Источник
Видео
Факториал в паскале ABC
Практикум Pascal. Урок 8: Задача № 13. Нахождения N факториала, n!
Уроки Pascal. Циклические алгоритмы. Вычисление факториала.
Факториал в паскале ABC
Pascal Полный курс с нуля за 4 часа
Уроки на языке Pascal. Урок 21. Рекурсия.
Урок 21. Рекурсия.
Информатика. Язык Pascal: Структура программы на языке Pascal. Центр онлайн-обучения «Фоксфорд»
Факториал
Урок 26. Рекурсия. Вычисление факториала
Пошаговое объяснение программы для вычисления факториала
Решение и ответы модуля 7.3 «Поколение python» stepik
Полное решение модуля (урока) 7.3 из курса «Пколение python: курс для начинающих» с сайта stepik.org на питоне.
Что покажет приведенный ниже фрагмент кода?
num1 = 4
num2 = 6
num1 += num2
num1 *= num1
print(num1)
100
Что покажет приведенный ниже фрагмент кода?
total = 0
for i in range(1, 6):
total += i
print(total)
15
Что покажет приведенный ниже фрагмент кода?
total = 0
for i in range(1, 6):
total += i
print(total, end=»)
1361015
Количество чисел
На вход программе подаются два целых числа a и b (a≤b).
Напишите программу, которая подсчитывает количество чисел в диапазоне от a до b включительно, куб которых оканчивается на 4 или 9.
Формат входных данных
На вход программе подаются два целых числа a и b (a≤b).Формат выходных данных
Программа должна вывести одно целое число в соответствии с условием программы.Примечание. Куб числа a – это его третья степень a3.
a = int(input())
b = int(input())
count = 0 # Установка значения счетчика
for i in range(a, b + 1): # Создания цикла с итерациями от a до b+1
if i % 10 == 4 or i % 10 == 9: # Проверка условия
count += 1 # Подсчет значений если условие True
print(count)Сумма чисел
На вход программе подается натуральное число n, а затем n целых чисел, каждое на отдельной строке. Напишите программу, которая подсчитывает сумму введенных чисел.

Формат входных данных
На вход программе подаются натуральное число n, а затем n целых чисел, каждое на отдельной строке.Формат выходных данных
Программа должна вывести сумму данных чисел.
a = int(input())
s = 0 # Установка переменной суммы 0
for i in range(a): # указываем программе сколько раз должен повторяться цикл
s += int(input()) # к сумме прибавляем введенное значение
print(s)Асимптотическое приближение
На вход программе подается натуральное число n. Напишите программу, которая вычисляет значение выражения
Примечание. Для вычисления натурального логарифма воспользуйтесь функцией
log(n), которая находится в модулеmath.
from math import log # Импортируем из math функцию log
diff = 0 # Задаем стартовое значение переменной для скобок
n = int(input()) # получаем число n
for i in range(1, n + 1): # Интервал начинаем с единицы, чтобы не делить на 0
diff += (1 / i) # Набиваем скобки суммами частных
print(diff - log(n)) # и дописываем формулу Сумма чисел
На вход программе подается натуральное число n.
Напишите программу, которая подсчитывает сумму тех чисел от 1 до n (включительно) квадрат которых оканчивается на 2, 5 или 8.
Формат входных данных
На вход программе подается натуральное число n.Формат выходных данных
Программа должна вывести единственное число в соответствии с условием задачи.Примечание. Если таких чисел нет в указанном диапазоне, то следует вывести 0.
n = int(input())
s = 0 # переменная для суммирования
for i in range(1, n + 1): # от 1 до n включительно
t = i**2 # поместим в t квадрат i - нашего счетчика в цикле
if t % 10 == 2 or t % 10 == 5 or t % 10 == 8: # если квадрат числа оканчивается на 2, 5, 8
s += i # прибавляем к переменной суммы подходящие числа
print(s)Факториал
На вход программе подается натуральное число n. Напишите программу, которая вычисляет n!.
Входные данные
На вход программе подается натуральное число n,(n≤12).Выходные данные
Программа должна вывести единственное число в соответствии с условием задачи.Примечание. Факториалом натурального числа nn, называется произведение всех натуральных чисел от 1 до n, то есть n!=1⋅2⋅3⋅…⋅n
n = int(input())
total = 1 # так как умножение на 0 даст 0
for i in range(1, n + 1):
total *= i # total умножаем на i
print(total)Без нулей
Напишите программу, которая считывает 10 чисел и выводит произведение отличных от нуля чисел.
Формат входных данных
На вход программе подаются 10 целых чисел, каждое на отдельной строке.Формат выходных данных
Программа должна вывести произведение отличных от нуля чисел.Примечание. Гарантируется, что хотя бы одно из 10 чисел является ненулевым.
total = 1 # переменная в которой будем собирать произведение
for i in range(10): # цикл на ввод 10 значений
num = int(input()) # принимаем 10 входящих
if num > 0: # условие что бы число было больше 0
total = num * total # произведение всех чисел больше 0
print(total)Сумма делителей
На вход программе подается натуральное число n. Напишите программу, которая вычисляет сумму всех его делителей.
Входные данные
На вход программе подается натуральное число n.Выходные данные
Программа должна вывести единственное число в соответствии с условием задачи.Примечание. Функция подсчета суммы всех делителей числа является очень важной в теории чисел.
n = int(input()) # получаем число
sum = 0 # присваиваем переменной суммы делителей 0
for i in range(1, n + 1): # цикл от 1 до нашего числа
if n % i == 0: # находим делитель, если остаток от деления равен нулю
sum += i # прибавлем к переменной текущий делитель
print(sum) Знакочередующаяся сумма
На вход программе подается натуральное число n.
Напишите программу вычисления знакочередующей суммы 1-2+3-4+5-6…+(−1)n+1n.
Входные данные
На вход программе подается натуральное число nn.Выходные данные
Программа должна вывести единственное число в соответствии с условием задачи.
n = int(input())
res = 0
for i in range(1, n + 1): # цикл от 1 до числа n
if i % 2 == 0:
res -= i # если i делиться без остатка то вычитает из предыдущего результата
if i % 2 != 0:
res += i # если i делиться с остатком то прибавляет к предыдущему результату
print(res)Наибольшие числа ?️?️
На вход программе подается натуральное число n, а затем n различных натуральных чисел, каждое на отдельной строке. Напишите программу, которая выводит наибольшее и второе наибольшее число последовательности.
Формат входных данных
На вход программе подаются натуральное число n≥2, а затем n различных натуральных чисел, каждое на отдельной строке.Формат выходных данных
Программа должна вывести два наибольших числа, каждое на отдельной строке.
n = int(input())
max1 = max2 = 1 # пусть самое большое число это минимально возможное
for i in range(1, n+1): # цикл от 1 до n
a = int(input()) # получаем следующее число
if a > max1: # если введенное число больше нашего максимума, то это новый максимум
max2 = max1 # запоминаем предыдущее наибольшее число в переменной max2
max1 = a # а само это число на входе становится наибольшим
elif a > max2: # если число не больше max1, то проверяем больше ли оно второго max2
max2 = a
print(max1)
print(max2)Only even numbers ?️
Напишите программу, которая считывает последовательность из 10 целых чисел и определяет является ли каждое из них четным или нет.
Формат входных данных
На вход программе подаются 10 целых чисел, каждое на отдельной строке.Формат выходных данных
Программа должна вывести строку «YES», если все числа четные и «NO» в ином случае.
flag = 'YES' # по умолчанию считаем что последовательность четная
for _ in range(10): # цикл до 10
a = int(input()) # получаем число
if a % 2 != 0: # проверяем делимость числа на остаток
flag = 'NO' # если число имеет остаток то NO
print(flag)Последовательность Фибоначчи ?️
Напишите программу, которая считывает натуральное число n и выводит первые n чисел последовательности Фибоначчи.
Формат входных данных
На вход программе подается одно число n (n≤100) – количество членов последовательности.Формат выходных данных
Программа должна вывести члены последовательности Фибоначчи, отделенные символом пробела.Примечание. Последовательность Фибоначчи – это последовательность натуральных чисел, где каждое последующее число является суммой двух предыдущих: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…
n = int(input()) # получаем кол-во циклов
num1 = 0 # число 1
num2 = 1 # число 2
for i in range(n): # цикл до N
num2 = num1 + num2 # присваиваем переменной num2 новое значение суммы этой переменной с предыдущей
num1 = num2 - num1 # переменной num1 присваиваем значение которое было в num2
print(num1,end=' ')Упростить выражение с факториалом – dj-sensor.
 ru
ruСодержание
- Наш искусственный интеллект решает сложные математические задания за секунды
- Факториалы
- Что такое факториалы и как их решать
- Бесплатный онлайн калькулятор факториалов
- Здравствуйте
Пользоваться нашим калькулятором факториалов предельно просто. Нужно нажать на клавиатуре !
Наш искусственный интеллект решает сложные математические задания за секунды
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Факториалы
Что такое факториалы и как их решать
Факториал числа n, который в математике обозначают буквой латиницы n, после которой следует восклицательный знак !. Произносится голосом это выражение как “н факториал”. Факториал – это результат последовательного умножения между собой последовательности натуральных чисел с 1 и до искомого числа n. Например, 5! = 1 х 2 х 3 х 4 х 5=720Факториал числа n обозначается латинской буквой n! и произносится как эн факториал. Представляет собой последовательное перемножение (произведение) всех натуральных чисел начиная с 1 до числа n. Например: 6! = 1 х 2 х 3 х 4 х 5=720
Представляет собой последовательное перемножение (произведение) всех натуральных чисел начиная с 1 до числа n. Например: 6! = 1 х 2 х 3 х 4 х 5=720
Факториал имеет математический смысл, только тогда, когда если это число целое и положительное (натуральное). Этот смысл следует из самого определения факториала, т.к. все натуральные числа неотрицательные и целые. Значения факториалов, а именно результат умножения последовательности от единицы до числа n можно посмотреть в таблице факториалов. Такая таблица возможна, по причине того, что значение факториала любого целого числа известно заранее и является, так сказать, табличным значением.
По определению 0! = 1. То есть если имеется ноль факториал, то мы ничего не перемножаем и результат будет первым натуральным существующим числом, то есть один.
Рост функции факториала можно отобразить на графике. Это будет дуга, похожая на функцию икса в квадрате, которая будет стремиться быстро вверх.
Читайте также: Темы на самсунг wave 525
Факториал – является быстрорастущей функцией. Она растет по графику быстрее, чем функция многочлена любой степени и даже экспоненциальная функция. Факториал растет быстрее многочлена любой степени и экспоненциальной функции (но при этом медленнее двойной экспоненциальной функции). Именно поэтому, чтобы посчитать факториал вручную могут быть сложности, так как результатом может получиться очень большое число. Чтобы не считать факториал вручную, можно воспользоваться калькулятором подсчёта факториалов, с помощью которого вы можете быстро получить ответ. Факториал применяется в функциональном анализе, теории чисел и комбинаторике, в которой имеет большой математический смысл, связанный с числом всевозможных неупорядоченных комбинаций объектов (чисел).
Она растет по графику быстрее, чем функция многочлена любой степени и даже экспоненциальная функция. Факториал растет быстрее многочлена любой степени и экспоненциальной функции (но при этом медленнее двойной экспоненциальной функции). Именно поэтому, чтобы посчитать факториал вручную могут быть сложности, так как результатом может получиться очень большое число. Чтобы не считать факториал вручную, можно воспользоваться калькулятором подсчёта факториалов, с помощью которого вы можете быстро получить ответ. Факториал применяется в функциональном анализе, теории чисел и комбинаторике, в которой имеет большой математический смысл, связанный с числом всевозможных неупорядоченных комбинаций объектов (чисел).
Чтобы быстро рассчитать число комбинаций n чисел, нужно всего лишь посчитать n!. После подсчёта значения факториала калькулятором, искомое значение можно использовать в решении более сложных задач. Вы можете посмотреть необходимый факториал в таблице: «Таблица факториалов»
Бесплатный онлайн калькулятор факториалов
Наш бесплатный решатель позволяет расчитать факториалы онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Все, что вам необходимо сделать – это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Факториал числа $n!$ равен произведению чисел от 1 до $n$. Например, $5! = 1cdot 2cdot 3cdot 4cdot 5$. Для решения примеров на пределы с факториалами понадобится знать и понимать формулу разложения на множители. $$ (n+1)! = n!(n+1) qquad (1) $$
Читайте также: Хотите проникнуться зимним спокойствием и умиротворением
Например, $5! = 4! cdot 5 $, или $5! = 3! cdot 4 cdot 5$, а можно еще так $5! = 2! cdot 3 cdot 4 cdot 5 $.
Основная суть идеи:
- Выносим наименьший факториал числа за скобки в числителе и знаменателе
- Сокращаем факториалы, избавляя тем самым предел от них
- Вычисляем предел подходящим способом
| Пример 1 |
| Вычислить предел с факториалами $lim_limits frac<(n+1)!>$ |
| Решение |
Подставляя $x=infty$ в предел получаем неопределенность бесконечность делить на бесконечность. Избавимся от факториалов. Для этого используем формулу (1) для их разложения на множители.
Избавимся от факториалов. Для этого используем формулу (1) для их разложения на множители.
Подставляем в предел полученное выражение и сокращаем на $n!$ числитель со знаменателем.
Теперь подставляя бесконечность в предел вычисляем ответ.
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
| Пример 2 |
| Решить предел с факториалом $ lim_limits frac<(2n+1)! + (2n+2)!> <(2n+3)!>$ |
| Решение |
| Ответ |
| $$ lim_limits frac<(2n+1)! + (2n+2)!> <(2n+3)!>= 0 $$ |
| Пример 3 |
| Найти предел $lim_limits frac<3(n+1)!> <2(n+1)!-n!>$ |
| Решение |
- Автор: Мария Сухоруких
- Распечатать
Читайте также: Я люблю пдф программа
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Нотация Big O и анализ алгоритмов с примерами Python
Автор оригинала: Usman Malik.
Существует несколько способов решения проблемы с помощью компьютерной программы. Например, существует несколько способов сортировки элементов в массиве. Вы можете использовать сортировку слиянием , сортировку пузырьками , сортировку вставкой и т. Д. Все эти алгоритмы имеют свои плюсы и минусы. Алгоритм можно рассматривать как процедуру или формулу для решения конкретной задачи. Вопрос в том, какой алгоритм использовать для решения конкретной задачи, когда существует несколько решений этой проблемы?
Анализ алгоритмов относится к анализу сложности различных алгоритмов и поиску наиболее эффективного алгоритма для решения поставленной задачи. Big-O Notation – это статистическая мера, используемая для описания сложности алгоритма.
В этой статье мы кратко рассмотрим анализ алгоритмов и нотацию Big-O. Мы увидим, как нотация Big-O может быть использована для определения сложности алгоритма с помощью различных функций Python.
Почему важен Анализ Алгоритмов?
Чтобы понять, почему важен анализ алгоритмов, воспользуемся простым примером.
Предположим, менеджер дает задание двум своим сотрудникам разработать алгоритм на языке Python, который вычисляет факториал числа, введенного пользователем.
Алгоритм, разработанный первым сотрудником, выглядит так:
def fact(n):
product = 1
for i in range(n):
product = product * (i+1)
return product
print (fact(5))
Обратите внимание, что алгоритм просто принимает целое число в качестве аргумента. Внутри функции fact переменная с именем product инициализируется значением 1. Цикл выполняется от 1 до N, и во время каждой итерации значение в product умножается на число, повторяемое циклом, и результат снова сохраняется в переменной product . После выполнения цикла переменная
После выполнения цикла переменная product будет содержать факториал.
Аналогично, второй сотрудник также разработал алгоритм, который вычисляет факториал числа. Второй сотрудник использовал рекурсивную функцию для вычисления факториала программы, как показано ниже:
def fact2(n):
if n == 0:
return 1
else:
return n * fact2(n-1)
print (fact2(5))
Менеджер должен решить, какой алгоритм использовать. Для этого он должен найти сложность алгоритма. Один из способов сделать это-найти время, необходимое для выполнения алгоритмов.
В записной книжке Jupyter вы можете использовать литерал %time it , за которым следует вызов функции, чтобы найти время, затраченное функцией на выполнение. Посмотрите на следующий сценарий:
Посмотрите на следующий сценарий:
%timeit fact(50)
Выход:
9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
Вывод говорит, что алгоритм занимает 9 микросекунд (плюс/минус 45 наносекунд) на цикл.
Аналогично выполните следующий сценарий:
%timeit fact2(50)
Выход:
15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
Второй алгоритм, включающий рекурсию, занимает 15 микросекунд (плюс/минус 427 наносекунд).
Время выполнения показывает, что первый алгоритм работает быстрее по сравнению со вторым алгоритмом, включающим рекурсию. Этот пример показывает важность алгоритмического анализа. В случае больших входных данных разница в производительности может стать более значительной.
Однако время выполнения не является хорошей метрикой для измерения сложности алгоритма, поскольку оно зависит от аппаратного обеспечения. Необходим более объективный анализ метрик сложности алгоритмов. Вот тут-то и вступает в игру нотация Big O.
Анализ алгоритмов с нотацией Big-O
Нотация Big-O-это метрика, используемая для определения сложности алгоритма. В принципе, обозначение Big-O означает связь между входными данными алгоритма и шагами, необходимыми для выполнения алгоритма. Он обозначается большой буквой “О”, за которой следуют открывающая и закрывающая скобки. n)
n)
Чтобы получить представление о том, как вычисляется нотация Big-O, давайте рассмотрим некоторые примеры постоянной, линейной и квадратичной сложности.
Постоянная сложность (O(C))
Сложность алгоритма называется постоянной, если шаги, необходимые для завершения выполнения алгоритма, остаются постоянными, независимо от количества входных данных. Постоянная сложность обозначается через O(c), где c может быть любым постоянным числом.
Давайте напишем простой алгоритм на Python, который находит квадрат первого элемента в списке и затем выводит его на экран.
def constant_algo(items):
result = items[0] * items[0]
print ()
constant_algo([4, 5, 6, 8])
В приведенном выше скрипте, независимо от размера ввода или количества элементов во входном списке элементов , алгоритм выполняет только 2 шага: находит квадрат первого элемента и выводит результат на экран. Следовательно, сложность остается постоянной.
Следовательно, сложность остается постоянной.
Если вы нарисуете линейный график с переменным размером входных данных items на оси x и количеством шагов на оси y, вы получите прямую линию. Чтобы визуализировать это, выполните следующий сценарий:
import matplotlib.pyplot as plt
import numpy as np
x = [2, 4, 6, 8, 10, 12]
y = [2, 2, 2, 2, 2, 2]
plt.plot(x, y, 'b')
plt.xlabel('Inputs')
plt.ylabel('Steps')
plt.title('Constant Complexity')
plt.show()
Выход:
Линейная сложность (O(n))
Сложность алгоритма называется линейной, если шаги, необходимые для завершения выполнения алгоритма, увеличиваются или уменьшаются линейно с числом входов. Линейная сложность обозначается через O(n).
Линейная сложность обозначается через O(n).
В этом примере давайте напишем простую программу, которая выводит все элементы списка на консоль:
def linear_algo(items):
for item in items:
print(item)
linear_algo([4, 5, 6, 8])
Сложность функции linear_algo в приведенном выше примере линейна, так как число итераций цикла for будет равно размеру входного элемента массива . Например, если в списке items есть 4 элемента, то цикл for будет выполнен 4 раза и так далее.
График линейной сложности с входами по оси x и количеством шагов по оси x выглядит следующим образом:
import matplotlib.pyplot as plt import numpy as np x = [2, 4, 6, 8, 10, 12] y = [2, 4, 6, 8, 10, 12] plt.plot(x, y, 'b') plt.xlabel('Inputs') plt.ylabel('Steps') plt.title('Linear Complexity') plt.show()
Выход:
Еще один момент, который следует отметить здесь, заключается в том, что в случае огромного количества входных данных константы становятся незначительными. Например, взгляните на следующий сценарий:
def linear_algo(items):
for item in items:
print(item)
for item in items:
print(item)
linear_algo([4, 5, 6, 8])
В приведенном выше скрипте есть два цикла for, которые повторяются по входному списку items . Поэтому сложность алгоритма становится O(2n), однако в случае бесконечных элементов во входном списке удвоение бесконечности все равно равно бесконечности, поэтому мы можем игнорировать константу 2 (так как она в конечном счете незначительна), и сложность алгоритма остается O(n).
Поэтому сложность алгоритма становится O(2n), однако в случае бесконечных элементов во входном списке удвоение бесконечности все равно равно бесконечности, поэтому мы можем игнорировать константу 2 (так как она в конечном счете незначительна), и сложность алгоритма остается O(n).
Мы можем дополнительно проверить и визуализировать это, построив входные данные по оси x и количество шагов по оси y, как показано ниже:
import matplotlib.pyplot as plt
import numpy as np
x = [2, 4, 6, 8, 10, 12]
y = [4, 8, 12, 16, 20, 24]
plt.plot(x, y, 'b')
plt.xlabel('Inputs')
plt.ylabel('Steps')
plt.title('Linear Complexity')
plt.show()
В приведенном выше сценарии вы можете ясно видеть, что, однако, вывод является линейным и выглядит следующим образом:
Квадратичная сложность (O(n^2))
Сложность алгоритма называется квадратичной, когда шаги, необходимые для выполнения алгоритма, являются квадратичной функцией количества элементов на входе. 2). Взгляните на следующий пример, чтобы увидеть функцию с квадратичной сложностью:
2). Взгляните на следующий пример, чтобы увидеть функцию с квадратичной сложностью:
def quadratic_algo(items):
for item in items:
for item2 in items:
print(item, ' ' ,item)
quadratic_algo([4, 5, 6, 8])
В приведенном выше сценарии вы можете видеть, что у нас есть внешний цикл, который повторяет все элементы во входном списке, а затем вложенный внутренний цикл, который снова повторяет все элементы во входном списке. Общее количество шагов, выполненных в * n, где n-количество элементов во входном массиве.
На следующем графике показано количество входов и шагов для алгоритма с квадратичной сложностью.
Нахождение сложности сложных функций
В предыдущих примерах мы видели, что на входе выполняется только одна функция. Что делать, если на входе выполняется несколько функций? Взгляните на следующий пример.
Что делать, если на входе выполняется несколько функций? Взгляните на следующий пример.
def complex_algo(items):
for i in range(5):
print ("Python is awesome")
for item in items:
print(item)
for item in items:
print(item)
print("Big O")
print("Big O")
print("Big O")
complex_algo([4, 5, 6, 8])
В приведенном выше скрипте выполняется несколько задач, во-первых, строка печатается 5 раз на консоли с помощью оператора print . Затем мы дважды печатаем входной список на экране, и, наконец, еще одна строка печатается три раза на консоли. Чтобы найти сложность такого алгоритма, нам нужно разбить код алгоритма на части и попытаться найти сложность отдельных частей.
Давайте разберем ваш сценарий на отдельные части. В первой части мы имеем:
for i in range(5):
print ("Python is awesome")
Сложность этой части равна O(5). Поскольку в этом фрагменте кода выполняются пять постоянных шагов независимо от входных данных.
Далее, у нас есть:
for item in items:
print(item)
Мы знаем, что сложность приведенного выше фрагмента кода равна O(n).
Аналогично, сложность следующего фрагмента кода также O(n)
for item in items:
print(item)
Наконец, в следующем фрагменте кода строка печатается три раза, следовательно, сложность равна O(3)
print("Big O")
print("Big O")
print("Big O")
Чтобы найти общую сложность, мы просто должны добавить эти индивидуальные сложности. Давайте так и сделаем:
Давайте так и сделаем:
O(5) + O(n) + O(n) + O(3)
Упрощая вышеизложенное, мы получаем:
O(8) + O(2n)
Ранее мы говорили, что когда вход (который в данном случае имеет длину n) становится чрезвычайно большим, константы становятся незначительными, то есть дважды или половина бесконечности все еще остается бесконечностью. Поэтому мы можем игнорировать константы. Конечная сложность алгоритма будет равна O(n).
Поэтому мы можем игнорировать константы. Конечная сложность алгоритма будет равна O(n).
Сложность худшего и Лучшего случая
Обычно, когда кто-то спрашивает вас о сложности алгоритма, он спрашивает вас о сложности наихудшего случая. Чтобы понять, каков наилучший и худший вариант сложности, посмотрите на следующий сценарий:
def search_algo(num, items):
for item in items:
if item == num:
return True
else:
return False
nums = [2, 4, 6, 8, 10]
print(search_algo(2, nums))
В приведенном выше сценарии у нас есть функция, которая принимает число и список чисел в качестве входных данных. Он возвращает true, если переданное число найдено в списке чисел, в противном случае он возвращает false. Если вы ищете 2 в списке, он будет найден в первом сравнении. Это наилучший случай сложности алгоритма, когда искомый элемент находится в первом искомом индексе. В лучшем случае сложность в этом случае равна O(1). С другой стороны, если вы ищете 10, он будет найден в последнем поисковом индексе. Алгоритм должен будет искать все элементы в списке, поэтому наихудшая сложность становится O(n).
Если вы ищете 2 в списке, он будет найден в первом сравнении. Это наилучший случай сложности алгоритма, когда искомый элемент находится в первом искомом индексе. В лучшем случае сложность в этом случае равна O(1). С другой стороны, если вы ищете 10, он будет найден в последнем поисковом индексе. Алгоритм должен будет искать все элементы в списке, поэтому наихудшая сложность становится O(n).
В дополнение к сложности наилучшего и наихудшего случая вы также можете вычислить среднюю сложность алгоритма, которая говорит вам: “Учитывая случайный вход, какова ожидаемая временная сложность алгоритма”?
Сложность пространства
В дополнение к временной сложности, где вы подсчитываете количество шагов, необходимых для завершения выполнения алгоритма, вы также можете найти пространственную сложность, которая относится к количеству пробелов, которые вам нужно выделить в пространстве памяти во время выполнения программы.
Взгляните на следующий пример:
def return_squares(n):
square_list = []
for num in n:
square_list. append(num * num)
return square_list
nums = [2, 4, 6, 8, 10]
print(return_squares(nums))
append(num * num)
return square_list
nums = [2, 4, 6, 8, 10]
print(return_squares(nums))
В приведенном выше скрипте функция принимает список целых чисел и возвращает список с соответствующими квадратами целых чисел. Алгоритм должен выделить память для того же количества элементов, что и во входном списке. Поэтому пространственная сложность алгоритма становится O(n).
Вывод
Обозначение Big-O-это стандартная метрика, используемая для измерения сложности алгоритма. В этой статье мы изучили, что такое нотация Big-O и как ее можно использовать для измерения сложности различных алгоритмов. Мы также изучали различные типы функций Big-O с помощью различных примеров Python. Наконец, мы кратко рассмотрели наихудшую и наилучшую сложность случая вместе с пространственной сложностью.
конвергенция дивергенция — Является ли $(2n)!$ таким же, как $2(n!)$?
спросил
Изменено 2 года, 10 месяцев назад
Просмотрено 3к раз
$\begingroup$
Я пытаюсь определить сходимость ряда $$\sum_{n=17}^{\infty} \frac{(n!)}{(2n)!}. $$ Используя тест отношения, я упростил $a_{n+1}/a_n$ до $$\frac{(2n!)}{2(n)!}.$$ Если $(2n)!$ совпадает с $2(n!)$, Я могу убрать факториал, чтобы разложить на множители отношение к $1$. Я признаю, что они, скорее всего, не совпадают, поскольку $2(n!)$ умножает результат $n!$, но я не уверен, как действовать дальше. 92)$ и аналогично $(2n)!\ne 2(n!)$
$$ Используя тест отношения, я упростил $a_{n+1}/a_n$ до $$\frac{(2n!)}{2(n)!}.$$ Если $(2n)!$ совпадает с $2(n!)$, Я могу убрать факториал, чтобы разложить на множители отношение к $1$. Я признаю, что они, скорее всего, не совпадают, поскольку $2(n!)$ умножает результат $n!$, но я не уверен, как действовать дальше. 92)$ и аналогично $(2n)!\ne 2(n!)$
И это может быть легко изменено.
$(2n)! = 1*2*3*…….*2n$
Тогда как $2(n!) = 2\times (1*2*3*…….*n)$
И очень простой случай:
$(2\cdot 3)! = 6! = 1*2*3*4*5*6 = 720$
И $2(3!) = 2\times (1*2*3) = 2*6 =12$.
Действительно, вы всегда получаете $(2n)! = (1*2*3*…..*n)*([n+1]*[n+2]*…… *2n)$, а
$2(n!) = ( 1*2*3*……*n)*2$
====
Ладно, хватит бить дохлую лошадь.
Вы можете сравнить $\frac {a_{n+1}}{a_n} = \frac {\frac {(n+1)!}{(2(n+1))!}}{\frac {n !}{(2n)!}}=$
$\frac {(n+1)!}{(2n+2)!}\cdot \frac {(2n)!}{n!}=$
$\frac {1*2*. …..*n*(n+1)}{1*2*……*2n*(2n+1)*(2n+2)} \cdot \frac {1*2*3*….*2n}{1*2*….*n}=$
…..*n*(n+1)}{1*2*……*2n*(2n+1)*(2n+2)} \cdot \frac {1*2*3*….*2n}{1*2*….*n}=$
$\frac {n+1}{(2n+1)(2n +2)}=$
$\frac {n+1}{(2n+1)\cdot2\cdot(n+1)}= \frac 1{2(2n+1)}$.
Не знаю, как вы сделали упрощение.
$\endgroup$
1 92} {12}$$
$\endgroup$
0
$\begingroup$
Проверка отношения в порядке. $$\frac {a_{n+1}}{a_n}=\frac {(n+1)!(2n)!}{(2n+2)(2n+1)(2n)!(n!)} =$$
$$ \frac {1}{2(2n+1)}\to 0 $$
Таким образом, ряды сходятся.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость 9n$ по индукции
спросил
Изменено 6 лет, 5 месяцев назад
Просмотрено 25 тысяч раз
$\begingroup$
У меня возникли трудности с решением упражнения в моем курсе. n$. 9n$ и иметь что-то вроде этого: $n+1 \ge 2$ или $n \ge 1$.
n$. 9n$ и иметь что-то вроде этого: $n+1 \ge 2$ или $n \ge 1$.
Но я думаю, что я где-то ошибся и надеялся, что кто-нибудь даст совет по этому поводу. Как я могу доказать вышеизложенное предположение?
Будем признательны за любую помощь, с уважением.
- неравенство
- индукция
- корректура
- факториал
$\endgroup$
2
$\begingroup$ 9л)\\[0,5эм] &< 2(k!)\tag{by $S(k)$}\\[0.5em] &< (k+1)(k!)\tag{начиная с $k\geq 4$}\\[0.5em] &= (к+1)!, \end{выравнивание} правая часть $S(k+1)$. На этом индуктивный шаг $S(k)\to S(k+1)$ завершается.
Таким образом, по математической индукции для всех $n\geq 4$ верно неравенство $S(n)$.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Факториал
Факториал— сокращение из $\frac{n!}{2n!}$?
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 237 раз
$\begingroup$
Возможно, довольно странный вопрос. Я делаю упражнение, и последняя часть заканчивается: $I = \frac{n!}{(2n)!}$
Теперь я знаю, что: $$I = \frac{n(n-1)(n-2)(n-3)\cdots}{2n(2n-1)(2n-2)(2n-3)\cdots}$$
Можно ли отменить некоторые условия? Или сделать его немного более «дружественным»?
- факториал
$\endgroup$
2
$\begingroup$
Я думаю, ваши возможные варианты можно резюмировать так:
Оставить это как $\frac{n!}{(2n)!}$, что само по себе является совершенно простым выражением.
 {-2n} \over \pars{n — 1/2}!}\,\root{\pi}} \\ &
\end{выравнивание} 9{\, \ подчеркнуть {\, — \, п \,}}
$$
{-2n} \over \pars{n — 1/2}!}\,\root{\pi}} \\ &
\end{выравнивание} 9{\, \ подчеркнуть {\, — \, п \,}}
$$$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Чему равен факториал 2n? – Отзывы Wiki
2n! = 2n × (2n-1) × (2n-2) u2026 3×2×1=2n×2n-1! Я думаю, что это факториал 2n = 2nu2217n(nu22121)(nu22122)….
 1u2217(2nu22121)(2nu22123)u2026..
1u2217(2nu22121)(2nu22123)u2026..Что такое 2n 2 )! Расширен? Сэнди. мост сказал: (2н)! =(2n*(2n-1)*(2n-2)*…
Как найти факториал 2n 1? 0
Во-вторых Чему равен n факториал? Говоря более математически, факториал числа (n!) равно n(n-1) . Например, если вы хотите вычислить факториал для четырех, вы должны написать: 4! = 4 x 3 x 2 x 1 = 24.
Что такое 2N?
2N или 2-N может означать: 2N или 2°N, 2-я параллель северной широты . MI 2N , тип электропоезда, работающего на французской железнодорожной сети регионального экспресс-метро. 2N, префикс, обозначающий некоторые транзисторы JEDEC, особенно 2N2222. 2N, индикатор уровня резервирования в (например) конфигурации источника бесперебойного питания.
com/embed/bFOkt9zQZGg» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Что такое факториал n 3?
Как упростить факториал 2x?
Как написать факториал? Символически факториал может быть представлен как как «!» . Итак, n факториал является произведением первых n натуральных чисел и представляется как n! Например, 4 факториал, то есть 4! можно записать как: 4! = 4×3×2×1 4 × 3 × 2 × 1 = 24.
Как найти n из n?
Найти! мы умножьте число от 1 до n , чтобы найти n из n!
Чему равен факториал n 1?
Таблица факториалов чисел от 1 до 10
n Факториал числа n! Значение 1 1! 1 2 2! 2 3 3! 6 4 4! 24 Что такое n в арифметической последовательности? Что такое n в формуле арифметической последовательности? В формуле арифметической последовательности для нахождения общего члена an=a1+(n−1)d an n = a 1 + ( n − 1 ) d , n относится к количеству членов в данной арифметической последовательности .

Можно ли умножать факториалы? Факториалы, обозначаемые a. … Вы также можете умножать факториалы вручную . Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе. Вы также можете использовать определенные правила факториалов для извлечения общих множителей, что может упростить процесс умножения.
Как вы делаете факториалы в математике?
факториал, в математике произведение всех положительных целых чисел, меньших или равных данному положительному целому числу и обозначаемое этим целым числом и восклицательным знаком. Таким образом, факториал семь записывается как 7!, что означает 1 × 2 × 3 × 4 × 5 × 6 × 7,9.0005
Вы умеете вычитать факториалы?
com/embed/pxh__ugRKz8″ frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Что такое формула 2n2?
Правило 1: Максимальное число электронов, присутствующих в конкретной оболочке, рассчитывается по формуле 2n 2 , где «n» представляет номер оболочки. … Точно так же оболочка L является второй оболочкой и может содержать до 2 (2) 2 = 8 электронов. Эта формула помогает рассчитать максимальное количество электронов, которое может разместиться на орбите.
Что такое правило 2n2? 2n 2 правило: первая оболочка K может содержать до 2 электронов , оболочка L может содержать до 8, третья оболочка M может содержать до 18 и четвертая оболочка N может содержать до 32 электронов. Это правило расположения электронов по оболочкам известно как правило 2n2, где n означает номер оболочки. … Атом гелия содержит 2 протона и 2 нейтрона.
Что означает выражение 2 N 2 , где n — номер электронной оболочки?
AS ОБЩЕЕ КОЛИЧЕСТВО ОРБИТАЛЕЙ В ОБОЛОЧКА ОЗНАЧАЕТ ‘ N²’ И КАЖДАЯ ОРБИТАЛЬ СОДЕРЖИТ ПО 2 ЭЛЕКТРОНА.
 ИТАК, ОБЩЕЕ ЧИСЛО ЭЛЕКТРОНОВ В ОБОЛОЧКЕ СОСТАВЛЯЕТ «2 N²».
ИТАК, ОБЩЕЕ ЧИСЛО ЭЛЕКТРОНОВ В ОБОЛОЧКЕ СОСТАВЛЯЕТ «2 N²».Можете ли вы распространять факториалы? Факторное распределение имеет место, когда набор переменных является независимыми событиями . Другими словами, переменные вообще не взаимодействуют; Учитывая два события x и y, вероятность x не изменится, если вы умножите y. Следовательно, вероятность x при условии, что произошло y — P(x|y) — будет такой же, как P(x).
Умеете ли вы умножать факториалы?
Факториалы, обозначаемые a. … Вы также можете умножать факториалы вручную . Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе. Вы также можете использовать определенные правила факториалов для извлечения общих множителей, что может упростить процесс умножения.
Как найти N в комбинациях?
14.
 2: Планирование экспериментов с помощью факторных планов
2: Планирование экспериментов с помощью факторных планов- Последнее обновление
- Сохранить как PDF
- Page ID
- 22537
- Jocelyn Anleitner, Stephanie Combs, Diane Feldkamp, Heeral Sheth, Jason Bourgeois, Michael Kravchenko, Nicholas Parsons, & Andrew Wang
- University of Michigan
- В первом столбце перечислите все отдельные экспериментальные комбинации
- Во втором столбце перечислите все суммы для каждой комбинации
- 1 st Четыре записи в третьем столбце (Этап 1) получаются путем сложения пар из «итогового списка» (предыдущий столбец). Следующие четыре числа получаются путем вычитания верхнего числа из нижнего числа каждой пары.
- Четвертый столбец (Этап 2) получается таким же образом, но на этот раз добавлением и вычитанием пар из Этапа 1.

- Пятый столбец (Этап 3) получается таким же образом, но на этот раз добавлением и вычитанием пар из Этапа 2.
- Продолжайте этапы до достижения n или количества факторов. Этот последний столбец представляет собой общий эффект. Положительное значение означает положительную корреляцию, а отрицательное значение означает отрицательную корреляцию. Однако все эти значения являются относительными, поэтому нет возможности сравнить разные суммарные эффекты из разных экспериментов.
- Тип 1 — очень здоровый
- Тип 2 — требуется тон
- Тип 3 — требуется прочность
- Тип 4 — Нужен тон и сила
- Больше времени
- Указывает, как каждый фактор влияет на ответ
- Не требует явного тестирования
- Не требует регрессии
- Ответить
уточняется
- существует относительная положительная корреляция между двумя факторами
- нет корреляции между двумя факторами
- существует относительная отрицательная корреляция между двумя факторами
- существует либо положительная, либо отрицательная относительная корреляция между двумя факторами
- Ответить
уточняется
- Box, George E.P., et. др. «Статистика для инженеров: введение в проектирование, анализ данных и построение моделей». Нью-Йорк: Джон Уайли и сыновья.
- Трохим, Уильям М.К. 2006. «Факториальные конструкции». База знаний по методам исследования.
- Перес, Хосе А., и др. др. «Влияние переменных процесса на предварительную обработку жидкой горячей водой пшеничной соломы для биоконверсии в топливо-этанол в реакторе периодического действия».
 Журнал химической технологии и биотехнологии. Том 82, Выпуск 10, Страницы 929-938. Опубликовано в Интернете 3 сентября 2007 г.
Журнал химической технологии и биотехнологии. Том 82, Выпуск 10, Страницы 929-938. Опубликовано в Интернете 3 сентября 2007 г. - Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Питер Вульф и др.

- Печать CSS
- Плотный
- Лицензия
- СС BY
- Версия лицензии
- 3,0
- Метки
- автор@Эндрю Ван
- автор @ Дайан Фельдкамп
- автор@Heeral Sheth
- автор @ Джейсон Буржуа
- автор @ Джоселин Анлейтнер
- автор@Михаил Кравченко
- автор@Николас Парсонс
- автор@Стефани Комбс
- факторный дизайн
- источник@https://open.
 umn.edu/opentextbooks/textbooks/chemical-process-dynamics-and-controls
umn.edu/opentextbooks/textbooks/chemical-process-dynamics-and-controls - Алгоритм Йейтса
- DOI:10.1007/s40003-013-0059-5
- Идентификатор корпуса: 17284823
- С.
 Даш, Р. Парсад, В. К. Гупта
Даш, Р. Парсад, В. К. Гупта - Опубликовано 10 мая 2013 г.
- Математика
- Сельскохозяйственные исследования
- П.
 К. Ван
К. Ван Математика
- 2017
- S. Dash, R. Parsad, V. K. Gupta
Математика
- 2014
- Ююн Джесси Янг, Н. Дрейпер
Математика
- 1997
- Ананта Саркар, Р. Прасад, В. Гупта, Чанделкар Кашинат, А. Ратор
Математика
- 2010
- P. C. Wang
Информатика
- 2004
- Г. Глонек, П. Соломон
Биология
Биостатистика
- 2004
- NAM-KY NGUYEN, E. Williams
Математика
- 2006
- Sudhir Gupta
Математика, биология
- 2006
Факторный план — важный метод определения влияния нескольких переменных на отклик. Традиционно эксперименты предназначены для определения влияния ОДНОЙ переменной на ОДНУ реакцию. Р.А. Фишер показал, что есть преимущества при объединении изучения нескольких переменных в одном и том же факторном эксперименте. Факторный дизайн может уменьшить количество экспериментов, которые необходимо выполнить, изучая несколько факторов одновременно. Кроме того, его можно использовать для поиска как основных эффектов (от каждого независимого фактора), так и эффектов взаимодействия (когда для объяснения результата необходимо использовать оба фактора). Однако факторный план может давать только относительные значения, и для получения фактических числовых значений математика становится сложной, поскольку необходимо выполнять регрессии (которые требуют минимизации суммы значений). Несмотря на это, факторный план является полезным методом планирования экспериментов как в лабораторных, так и в промышленных условиях.
Кроме того, его можно использовать для поиска как основных эффектов (от каждого независимого фактора), так и эффектов взаимодействия (когда для объяснения результата необходимо использовать оба фактора). Однако факторный план может давать только относительные значения, и для получения фактических числовых значений математика становится сложной, поскольку необходимо выполнять регрессии (которые требуют минимизации суммы значений). Несмотря на это, факторный план является полезным методом планирования экспериментов как в лабораторных, так и в промышленных условиях.
Факторный дизайн тестирует все возможные условия. Поскольку факторный план может привести к большому количеству испытаний, которые могут стать дорогостоящими и трудоемкими, факторный план лучше всего использовать для небольшого числа переменных с несколькими состояниями (от 1 до 3). Факторный дизайн хорошо работает, когда взаимодействия между переменными сильны и важны, и когда каждая переменная вносит значительный вклад.
Что такое факторный дизайн?
Пример факторного дизайна
Самый простой способ понять, как работает факторный план, — прочитать пример. Предположим, что вы, ученый, работающий в FDA, хотите изучить и измерить вероятность возникновения у пациентов приступов после приема нового фармацевтического препарата под названием CureAll. CureAll — это новый препарат на рынке, который может вылечить практически любое заболевание организма. Вы вместе со своими коллегами из FDA решили протестировать два уровня дозировки: 5 мг и 10 мг. Вы также заинтересованы в том, чтобы определить, различаются ли побочные эффекты лекарств у молодых людей (20 лет) и пожилых людей (40 лет). Исходя из приведенной информации, вы видите, что есть два фактора: дозировка и возраст. Факторы являются основными категориями, которые следует исследовать при определении причины приступов у пациентов. Под каждый из этих факторов существуют разные уровни: 5 и 10 мг на дозировку; 20 и 40 лет для возраста. Уровень — это, по сути, одно из подразделений, составляющих фактор. Из этой информации мы видим, что у нас есть факторный план 2 x 2, что означает, что у нас будет 2 * 2 = 4 группы. Группа — это набор условий, которые составляют этот конкретный эксперимент.
Уровень — это, по сути, одно из подразделений, составляющих фактор. Из этой информации мы видим, что у нас есть факторный план 2 x 2, что означает, что у нас будет 2 * 2 = 4 группы. Группа — это набор условий, которые составляют этот конкретный эксперимент.
Нулевой результат
Ситуация с нулевым результатом возникает, когда результат вашего эксперимента один и тот же независимо от того, как были объединены уровни в вашем эксперименте. В приведенном выше примере нулевой результат будет иметь место, если вы получите одинаковый процент приступов, возникающих у пациентов с различной дозой и возрастом. Приведенные ниже графики иллюстрируют отсутствие изменения процента припадков по всем факторам, поэтому можно сделать вывод, что на вероятность развития приступа не влияет ни дозировка препарата, ни возраст пациента.
Основные эффекты
Ситуация основных эффектов возникает, когда существует устойчивая тенденция среди различных уровней фактора. Из приведенного выше примера предположим, что вы обнаружите, что по мере увеличения дозы увеличивается и процент людей, страдающих от судорог. Вы также замечаете, что возраст не играет роли; и 20-, и 40-летние страдают одинаковым процентом приступов при данном количестве CureAll. Из этой информации можно сделать вывод, что вероятность возникновения у пациента приступа сводится к минимуму при более низких дозировках препарата (5 мг). Второй график показывает, что с увеличением дозы препарата увеличивается процент приступов, а первый график показывает, что с возрастом процент приступов не меняется. Оба этих графика содержат только один основной эффект, так как только доза влияет на процент приступов. Принимая во внимание, что графики 3 и 4 имеют два основных эффекта, поскольку и доза, и возраст влияют на процент припадков.
Вы также замечаете, что возраст не играет роли; и 20-, и 40-летние страдают одинаковым процентом приступов при данном количестве CureAll. Из этой информации можно сделать вывод, что вероятность возникновения у пациента приступа сводится к минимуму при более низких дозировках препарата (5 мг). Второй график показывает, что с увеличением дозы препарата увеличивается процент приступов, а первый график показывает, что с возрастом процент приступов не меняется. Оба этих графика содержат только один основной эффект, так как только доза влияет на процент приступов. Принимая во внимание, что графики 3 и 4 имеют два основных эффекта, поскольку и доза, и возраст влияют на процент припадков.
Эффекты взаимодействия
Ситуация эффектов взаимодействия — это последний результат, который можно обнаружить с помощью факторного плана. Из приведенного выше примера предположим, что вы обнаружите, что 20-летние люди будут страдать от судорог в 10% случаев, когда им будут давать таблетки CureAll 5 мг, а 20-летние будут страдать в 25% случаев, когда им будут давать таблетки CureAll 10 мг. Однако, когда 40-летним дают таблетки по 5 мг или 10 мг, 15% страдают от судорог при обеих этих дозировках. Эту корреляцию можно увидеть на графиках ниже. У 20-летних увеличивается вероятность возникновения судорог при приеме более высоких доз, но нет никакой разницы в степени судорожных припадков у 40-летних. Таким образом, должен существовать эффект взаимодействия между дозировкой CureAll и возрастом пациента, принимающего препарат. Когда у вас есть эффект взаимодействия, невозможно точно описать ваши результаты, не упомянув оба фактора. Вы всегда можете заметить взаимодействие на графиках, потому что когда есть линии, которые не параллельны, взаимодействие присутствует. Если вы посмотрите на приведенные выше графики основных эффектов, вы заметите, что все линии на графике параллельны. Напротив, для графиков эффекта взаимодействия вы увидите, что линии не параллельны.
Однако, когда 40-летним дают таблетки по 5 мг или 10 мг, 15% страдают от судорог при обеих этих дозировках. Эту корреляцию можно увидеть на графиках ниже. У 20-летних увеличивается вероятность возникновения судорог при приеме более высоких доз, но нет никакой разницы в степени судорожных припадков у 40-летних. Таким образом, должен существовать эффект взаимодействия между дозировкой CureAll и возрастом пациента, принимающего препарат. Когда у вас есть эффект взаимодействия, невозможно точно описать ваши результаты, не упомянув оба фактора. Вы всегда можете заметить взаимодействие на графиках, потому что когда есть линии, которые не параллельны, взаимодействие присутствует. Если вы посмотрите на приведенные выше графики основных эффектов, вы заметите, что все линии на графике параллельны. Напротив, для графиков эффекта взаимодействия вы увидите, что линии не параллельны.
Подход математического анализа
В предыдущем разделе мы рассмотрели качественный подход к определению влияния различных факторов с помощью факторного плана. Теперь мы собираемся переключиться и рассмотреть факторный план в количественном подходе, чтобы определить, насколько сильно факторы в эксперименте влияют на результат.
Теперь мы собираемся переключиться и рассмотреть факторный план в количественном подходе, чтобы определить, насколько сильно факторы в эксперименте влияют на результат.
Как работать с 2
n Факторный дизайнПредположим, у вас есть две переменные \(A\) и \(B\), каждая из которых имеет два уровня a 1 , а 2 и б 1 , б 2 . Вы должны измерить комбинированные эффекты \(A\) и \(B\) (a 1 b 1 , a 1 b 2 , a 2 b 1 , a 4 b 2 ). Поскольку у нас есть два фактора, каждый из которых имеет два уровня, мы говорим, что имеем факторный план 2 х 2 или 2 2 . Как правило, при выполнении факторного плана будет два уровня и n различных факторов. Таким образом, общая форма факторного плана 2 н .
Чтобы найти главный эффект \(A\), мы используем следующее уравнение:
\[A = (a_2b_1 — a_1b_1) + (a_2b_2 — a_1b_2) \nonumber \]
Аналогично, главный эффект B определяется как:
\[B = (b_2a_1 — b_1a_1) + (b_2a_2 — b_1a_2) \nonnumber \]
При традиционном экспериментировании каждый эксперимент должен быть изолирован отдельно, чтобы полностью обнаружить влияние на B. В результате было проведено 8 различных экспериментов. Обратите внимание, что в факторных планах потребовалось всего четыре эксперимента для решения восьми значений в A и B. Это показывает, насколько факторный план экономит время.
В результате было проведено 8 различных экспериментов. Обратите внимание, что в факторных планах потребовалось всего четыре эксперимента для решения восьми значений в A и B. Это показывает, насколько факторный план экономит время.
Взяв коэффициенты в A и B, была создана таблица ниже.
AB находится путем умножения коэффициентов a x b x , чтобы получить новый эффект коэффициента.
Дополнительная сложность заключается в том, что для точности требуется более одного испытания/повторения, поэтому для этого необходимо сложить каждый дополнительный эффект (например, сложить три испытания 1 b 1 ). Суммируя эффекты коэффициентов с дополнительными эффектами (коэффициент умножения на дополнительный эффект), получаем общий факторный эффект можно найти. Это значение будет определять, оказывает ли фактор значительное влияние на результат. Для больших чисел фактор можно считать чрезвычайно важным, а для меньших чисел фактор можно считать менее важным. Знак числа также имеет прямую зависимость от положительного или отрицательного эффекта.
Знак числа также имеет прямую зависимость от положительного или отрицательного эффекта.
Чтобы получить средний факторный эффект, общие суммы необходимо разделить на 2, умноженное на количество повторений , где повторение — это повторный эксперимент.
\[\text {средний факторный эффект} = \dfrac{\text{общий факторный эффект}}{2r} \nonumber \]
Путем добавления третьей переменной (\(C\)), процесс получения коэффициенты значительно усложняется. Главный факторный эффект для \(A\):
\[A=\left(a_{2} b_{1} c_{1}-a_{1} b_{1} c_{1}\right)+\ влево(a_{2} b_{2} c_{1}-a_{1} b_{2} c_{1}\right)+\left(a_{2} b_{1} c_{2}-a_{1 } b_{1} c_{2}\right)+\left(a_{2} b_{2} c_{2}-a_{1} b_{2} c_{2}\right) \nonumber \]
Таблица коэффициентов указана ниже
Понятно, что для того, чтобы найти общие факторные эффекты, вам нужно найти главные эффекты переменной, а затем коэффициенты. Алгоритм Йейтса может быть использован для упрощения процесса.
Алгоритм Йейтса
Фрэнк Йейтс создал алгоритм, позволяющий легко находить суммарные эффекты факториала в факториале 2 n , который легко программируется в Excel. Хотя этот алгоритм довольно прост, он также довольно утомителен и ограничен 2 n факторные конструкции. Таким образом, современные технологии позволяют проводить этот анализ с помощью статистических программ с помощью регрессии.
Хотя этот алгоритм довольно прост, он также довольно утомителен и ограничен 2 n факторные конструкции. Таким образом, современные технологии позволяют проводить этот анализ с помощью статистических программ с помощью регрессии.
Шаги:
В соответствии с приказом Йейтса, например, для факторного плана 2 3
— — —
+ — —
— + —
+ + —
— — 5 +
5 9
— + +
+ + +
Не обращая внимания на первую строку, посмотрите на последнюю стадию и найдите переменную с наибольшим относительным числом, тогда эта строка указывает на ГЛАВНЫЙ ОБЩИЙ ЭФФЕКТ . Основной суммарный эффект можно связать с входными переменными, перемещаясь по строке и просматривая первый столбец. Если строка в первом столбце представляет собой a 2 b 1 c 1 , то основной суммарный эффект равен A. Строка для a 1 b 2 c 1 будет для B. Строка за 2 b 1 c 2 будет для переменного тока.
Строка для a 1 b 2 c 1 будет для B. Строка за 2 b 1 c 2 будет для переменного тока.
Это значение основного общего эффекта для каждой переменной или комбинации переменных будет некоторым значением, которое указывает на связь между выходом и переменной. Например, если ваше значение положительное, то существует положительная связь между переменной и выходом (т. е. по мере увеличения переменной увеличивается и выход). Отрицательное значение будет означать отрицательное отношение. Обратите внимание, однако, что все значения относятся друг к другу. Таким образом, в то время как наибольшее значение основного общего эффекта в одном наборе экспериментов может иметь значение 128, в другом эксперименте наибольшее значение общего общего эффекта может быть равно 43. Невозможно определить, имеет ли значение 128 в одном эксперименте больший контроль. над его выходом, чем значение 43, но для целей сравнения переменных в рамках эксперимента основной общий эффект позволяет вам увидеть относительный контроль переменных над выходом.
Повторный пример факторного проектирования
Вспомните пример, приведенный в предыдущем разделе Что такое факторный дизайн? В примере было два фактора и два уровня, что дало факторный план 2 2 . Алгоритм Йейтса можно использовать для количественного определения того, какой фактор больше всего влияет на процент припадков. Для использования алгоритма Йейтса мы назовем фактор возраста А с 1 = 20 лет и 2 = 40 лет. Точно так же мы будем называть дозировочный фактор B, где b 1 = 5 мг и b 2 = 10 мг. Данные для трех исходов взяты из рисунков, приведенных в примере, при условии, что приведенные данные получены в результате нескольких испытаний.
Нулевой результат
Была построена следующая таблица алгоритма Йейтса с использованием данных для нулевого результата. Как видно из таблицы, значения основного суммарного факторного эффекта равны 0 для A, B и AB. Это доказывает, что ни дозировка, ни возраст не влияют на процент припадков.
Основной эффект
Следующая таблица алгоритма Йейтса была построена с использованием данных первых двух графиков раздела основных эффектов. Помимо первой строки в таблице, строка с наибольшим основным суммарным факторным эффектом — это строка B, тогда как основной суммарный эффект для A равен 0. Это означает, что дозировка (фактор B) влияет на процент припадков, а возраст (фактор А) не влияет, что и видно на графике.
По данным двух вторых графиков раздела основных эффектов была построена следующая таблица алгоритма Йейтса. Помимо первой строки в таблице, основное суммарное значение эффекта составило 10 для фактора А и 20 для фактора В. Это означает, что и возраст, и дозировка влияют на процент припадков. Однако, поскольку значение B больше, дозировка оказывает большее влияние на процент припадков, чем возраст. Это то, что было видно графически, так как график с дозировкой по горизонтальной оси имеет наклон с большей величиной, чем график с возрастом по горизонтальной оси.
Эффект взаимодействия
Следующая таблица алгоритма Йейтса была построена с использованием данных из раздела эффектов взаимодействия. Поскольку основной суммарный факторный эффект для AB отличен от нуля, существуют эффекты взаимодействия. Это означает, что невозможно соотнести результаты ни с тем, ни с другим фактором; оба фактора должны быть приняты во внимание.
Химическая инженерия
Должно быть совершенно ясно, что факторный дизайн может быть легко интегрирован в химическую инженерию. Многие инженеры-химики сталкиваются с проблемами на работе, пытаясь определить влияние различных факторов на их результаты. Например, предположим, что у вас есть реактор и вы хотите изучить влияние температуры, концентрации и давления на несколько выходов. Чтобы свести к минимуму количество экспериментов, которые вам пришлось бы проводить, вы можете использовать факторный план. Это позволит вам определить влияние температуры и давления, сэкономив при этом деньги на проведении ненужных экспериментов. 4 эксперимента.
4 эксперимента.
Источник: Perez, et. др.
Пример Minitab DOE
Minitab 15 Statistical Software — мощная статистическая программа, способная выполнять регрессии, ANOVA, контрольные диаграммы, DOE и многое другое. Minitab особенно удобен для создания и анализа результатов исследований DOE. В Minitab можно создавать ДОЭ факториала, поверхности отклика, смеси и метода Тагучи. Общий метод создания факториальных ДОЭ обсуждается ниже.
Создание факториала DOE
Minitab предлагает простой и удобный способ разработки таблицы экспериментов. Кроме того, с помощью Minitab легко выполнить анализ множественных ответов (результатов, полученных в результате экспериментов) для определения того, какие параметры существенно влияют на ответы. Статистическое программное обеспечение Minitab 15 можно использовать через Virtual CAEN Labs, выбрав «Пуск» > «Все программы» > «Математические и числовые методы» > «Решения Minitab» > «Статистическое программное обеспечение Minitab 15».
Первым шагом является создание DOE путем указания количества уровней (обычно 2) и количества ответов. Для этого перейдите в Stat>DOE>Factorial>Create Factorial Design, как показано на рисунке ниже.
Следующее изображение представляет собой меню опций «Создать факторный проект».
Для 2-уровневого дизайна щелкните переключатель «2-уровневый факториал (генераторы по умолчанию)». Затем укажите количество факторов от 2 до 15. Могут быть выбраны другие планы, такие как план Плакетта-Бермана или общий полный факторный план. Для получения информации об этих дизайнах, пожалуйста, обратитесь к меню «Помощь».
После того, как количество факторов выбрано, нажмите на опцию «Проекты…», чтобы увидеть следующее меню.
В этом меню можно выбрать дробный или полный факторный план. Хотя полный факториал обеспечивает лучшее разрешение и является более полным анализом, дробь 1/2 требует вдвое меньшего количества прогонов, чем полный факторный план. При нехватке времени или для того, чтобы получить общее представление о взаимосвязях, хорошим выбором будет схема дроби 1/2. Кроме того, в этом меню можно выбрать количество центральных точек на блок, количество повторений угловых точек и количество блоков. Обратитесь к меню «Справка» для получения подробной информации об этих параметрах. Нажмите «ОК», когда тип дизайна выбран.
При нехватке времени или для того, чтобы получить общее представление о взаимосвязях, хорошим выбором будет схема дроби 1/2. Кроме того, в этом меню можно выбрать количество центральных точек на блок, количество повторений угловых точек и количество блоков. Обратитесь к меню «Справка» для получения подробной информации об этих параметрах. Нажмите «ОК», когда тип дизайна выбран.
После выбора плана становятся активными кнопки «Факторы…», «Опции…» и «Результаты…» в меню параметров «Создать факторные планы». Нажмите кнопку «Факторы…», чтобы увидеть следующее меню.
Изображение выше относится к 4-факторному дизайну. Факторы A-D можно переименовать, чтобы представить фактические факторы системы. Коэффициенты могут быть числовыми или текстовыми. Кроме того, низкое и высокое значение изначально указаны как -1 и 1, где -1 — это низкое значение, а 1 — это высокое значение. Низкий и высокий уровни для каждого фактора могут быть изменены на их фактические значения в этом меню. Нажмите «ОК», как только это будет завершено.
Нажмите «ОК», как только это будет завершено.
Необходимые шаги для создания ДОЭ выполнены, но можно указать другие параметры «Результаты…» и «Параметры…». Меню «Результаты…» и «Параметры…» показаны ниже.
В главном меню «Создать факторный проект» нажмите «ОК», как только все спецификации будут заполнены. Следующая таблица получена для 2-уровневого, 4-факторного, полного факторного плана. Ни один из уровней не был указан, поскольку они отображаются как -1 и 1 для низкого и высокого уровней соответственно.
Приведенная выше таблица содержит все условия, необходимые для полного факторного ДОЭ. Minitab отображает стандартный порядок и рандомизированный порядок выполнения в столбцах C1 и C2 соответственно. Столбцы A-D — это факторы. Первый прогон (в соответствии с порядком случайного прогона) должен быть выполнен на низких уровнях A и C и высоких уровнях B и D. Всего для завершения DOE требуется 16 прогонов.
Изменение таблицы DOE
После создания таблицы испытаний для DOE при необходимости можно внести дополнительные изменения. Некоторые типичные модификации включают в себя изменение имени каждого фактора, указание высокого и низкого уровня каждого фактора и добавление повторений в план. Чтобы изменить текущий дизайн, перейдите в Stat>DOE>Modify Design…, как показано на рисунке ниже.
Некоторые типичные модификации включают в себя изменение имени каждого фактора, указание высокого и низкого уровня каждого фактора и добавление повторений в план. Чтобы изменить текущий дизайн, перейдите в Stat>DOE>Modify Design…, как показано на рисунке ниже.
Для изменения дизайна отображается следующее меню.
В меню «Изменить дизайн» пользователи могут изменять коэффициенты, копировать дизайн, рандомизировать дизайн, перенумеровывать дизайн, складывать дизайн и добавлять осевые точки. Кроме того, любые внесенные изменения могут быть помещены в новый рабочий лист. Чтобы изменить факторы, щелкните переключатель «Изменить факторы», а затем «Указать», чтобы увидеть следующее меню параметров.
Коэффициенты по умолчанию называются «A», «B», «C» и «D» и имеют соответствующие высокие и низкие уровни 1 и -1. Имя факторов можно изменить, просто щелкнув поле и введя новое имя. Кроме того, в этом меню можно изменить низкий и высокий уровни для каждого фактора. Поскольку верхний и нижний уровни для каждого фактора могут быть неизвестны при первом создании проекта, удобно определить их позже. Нажмите «ОК» после завершения изменений.
Поскольку верхний и нижний уровни для каждого фактора могут быть неизвестны при первом создании проекта, удобно определить их позже. Нажмите «ОК» после завершения изменений.
Другим типичным изменением является добавление реплик к проекту. Репликаты — это повторы каждого испытания, которые помогают определить воспроизводимость дизайна, тем самым увеличивая количество испытаний и точность DOE. Чтобы добавить реплики, щелкните переключатель «Репликация дизайна» в меню «Изменить дизайн». Появится следующее меню.
Единственным параметром в этом меню является количество добавляемых повторов. Число находится в диапазоне от 1 до 10. Чтобы иметь в общей сложности 3 испытания каждого, пользователь должен добавить 2 повторения в это меню. Если добавить 4 повтора, будет всего 5 испытаний каждого. Как правило, если одно и то же экспериментирование будет проводиться в течение 3 лабораторных периодов, будет добавлено 2 повторения.
Дополнительные модификации дизайна включают рандомизацию и изменение нумерации дизайна. Это очень простые модификации, которые влияют на порядок испытаний. Для получения информации о «Конструкции фальцовки» и «Добавить осевые точки» обратитесь к меню «Справка».
Это очень простые модификации, которые влияют на порядок испытаний. Для получения информации о «Конструкции фальцовки» и «Добавить осевые точки» обратитесь к меню «Справка».
Анализ результатов DOE
После завершения полного исследования DOE можно использовать Minitab для анализа влияния экспериментальных результатов (называемых реакциями) на факторы, указанные в плане. Первым шагом в анализе результатов является внесение ответов в таблицу DOE. Это делается так же, как добавление данных в лист данных Excel. В столбцах справа от последнего фактора введите каждый ответ, как показано на рисунке ниже.
Приведенный выше рисунок содержит три столбца ответа. Имена каждого ответа можно изменить, щелкнув имя столбца и введя нужное имя. На рисунке область, выделенная черным цветом, — это место, где будут вводиться ответы. Например, если в исследовании DOE измерялись чистота, выход и остаточное количество катализатора, их значения для каждого испытания должны быть введены в столбцы.
После ввода ответов можно выполнить статистический анализ данных. Перейдите в Stat>DOE>Factorial>Analyze Factorial Design…, как показано на следующем рисунке.
Меню, которое появляется для анализа факторного плана, показано ниже.
В меню «Анализ факторного плана» ответы отображаются в левой части экрана. Первым шагом является выбор ответов для анализа. Все ответы можно выбрать сразу или по отдельности. Чтобы выбрать их, щелкните (или щелкните и перетащите, чтобы выбрать несколько), а затем нажмите «Выбрать», чтобы добавить их в раздел «Ответы:», как показано ниже.
Следующим шагом является выбор терминов, которые будут анализироваться для ответов. Для этого нажмите «Условия…» и появится следующее меню.
В этом меню выбираются типы взаимодействия между факторами. Для модели первого порядка, которая исключает все межфакторные взаимодействия, следует выбрать «1» в раскрывающемся меню для «Включить термины в модель по порядку:». Чтобы включить термины более высокого порядка и учесть взаимодействие факторов, выберите 2, 3 или 4 в раскрывающемся меню. Если не ожидается значительных межфакторных взаимодействий, рекомендуется использовать модель первого порядка, которая представляет собой линейное приближение.
Чтобы включить термины более высокого порядка и учесть взаимодействие факторов, выберите 2, 3 или 4 в раскрывающемся меню. Если не ожидается значительных межфакторных взаимодействий, рекомендуется использовать модель первого порядка, которая представляет собой линейное приближение.
После того, как термины выбраны, следующим шагом является определение того, какие графики следует создать. Типы графиков можно выбрать, щелкнув «Графики…» в главном меню «Анализ факторного плана».
В показанном выше меню «График» были выбраны три графика эффектов «Нормальный», «Полунормальный» и «Парето». Эти графики представляют собой различные способы представления статистических результатов анализа. Примеры этих графиков можно найти в примере Minitab для анализа центробежных контакторов. В этом меню также можно выбрать альфа-значение, определяющее предел статистической значимости. Обычно значение альфа равно 0,05. Последний тип графиков, которые можно выбрать, это остаточные графики. Обычно выбирают «Остатки по сравнению с совпадениями», которые показывают, как расхождение между прогнозируемыми значениями модели и фактическими значениями.
Обычно выбирают «Остатки по сравнению с совпадениями», которые показывают, как расхождение между прогнозируемыми значениями модели и фактическими значениями.
Последний параметр, который необходимо указать, — результаты. Нажмите «Результаты…» в меню «Анализ факторного плана», чтобы увидеть следующий экран.
В этом меню выберите все «Доступные термины» и нажмите кнопку «>>», чтобы переместить их в «Выбранные термины». Это гарантирует, что все термины будут включены в анализ. Еще одна функция, которую можно выбрать в этом меню, — отобразить «Коэффициенты и таблицу дисперсионного анализа» для исследования DOE.
В меню «Анализ факториального плана» можно выбрать другие параметры, такие как «Ковариаты…», «Прогноз…», «Хранилище…» и «Веса…». Обратитесь к меню «Помощь» для описания других опций. После внесения всех необходимых изменений нажмите «ОК», чтобы выполнить анализ. Все графики появятся на экране, а текстовый файл результатов будет сгенерирован в файле сеанса.
Minitab Пример анализа центробежного контактора
Центробежные контакторы, также известные как центробежные контакторы Podbielniak (POD), используются для очистки загрязненного потока путем противоточной жидкостной экстракции. Две несмешивающиеся жидкости с разным удельным весом контактируют противотоком, и растворенное вещество из грязного потока извлекается чистым потоком. Обычное использование удаления метанола POD из биодизеля путем контакта потока с водой. Количество метанола, остающегося в биодизеле (мас.% MeOH) после очистки, и количество полученных теоретических стадий (No. Theor. Stages) зависят от условий работы POD. Четыре основных рабочих параметра POD: скорость вращения (об/мин), отношение биодизеля к воде (Ratio), общий расход биодизеля и воды (Flow Rate) и давление (Pressure). Было проведено исследование DOE, чтобы определить влияние четырех рабочих условий на реакцию % MeOH в биодизеле и количество достигнутых теоретических стадий. (ПРИМЕЧАНИЕ: фактические данные для этого примера были выдуманы)
С помощью Minitab было создано 4-факторное 2-уровневое исследование DOE. Поскольку эксперименты с POD требуют много времени, был использован дизайн половинной фракции из 8 испытаний. На рисунке ниже представлена таблица испытаний для DOE.
Поскольку эксперименты с POD требуют много времени, был использован дизайн половинной фракции из 8 испытаний. На рисунке ниже представлена таблица испытаний для DOE.
После того, как все испытания были проведены, были рассчитаны весовой процент метанола, оставшийся в биодизеле, и количество достигнутых теоретических стадий. На рисунке ниже представлена таблица испытаний DOE, включая два ответа.
Был проведен анализ исследования DOE для определения влияния каждого фактора на ответы. В анализ были включены только члены первого порядка для создания линейной модели. Диаграммы Парето для весового процента MeOH в биодизеле и количества теоретических стадий показаны ниже.
Диаграммы Парето показывают, какие факторы оказывают статистически значимое влияние на ответы. Как видно из приведенных выше графиков, число оборотов в минуту оказывает значительное влияние на оба отклика, а давление оказывает статистически значимое влияние на весовой процент метанола в биодизельном топливе. Ни скорость потока, ни соотношение не оказывают статистически значимого влияния ни на один из ответов. Диаграммы Парето представляют собой гистограммы, которые позволяют пользователям легко увидеть, какие факторы оказывают существенное влияние.
Ни скорость потока, ни соотношение не оказывают статистически значимого влияния ни на один из ответов. Диаграммы Парето представляют собой гистограммы, которые позволяют пользователям легко увидеть, какие факторы оказывают существенное влияние.
Полунормальные графики для весового процента метанола в биодизельном топливе и количества теоретических стадий показаны ниже.
Как и графики Парето, графики половинной нормы показывают, какие факторы оказывают существенное влияние на ответы. Факторы, оказывающие существенное влияние, показаны красным цветом, а факторы, не оказывающие существенного влияния, — черным. Чем дальше фактор от синей линии, тем большее влияние он оказывает на соответствующую реакцию. Для % метанола в биодизеле число оборотов в минуту находится дальше от синей линии, чем давление, что указывает на то, что число оборотов в минуту оказывает более значительное влияние на % метанола в биодизеле, чем давление.
Последним созданным графиком является график нормального эффекта. Нормальный график похож на полунормальный график по дизайну. Однако нормальный график показывает, является ли влияние фактора положительным или отрицательным на реакцию. Нормальные графики для ответов показаны ниже.
Нормальный график похож на полунормальный график по дизайну. Однако нормальный график показывает, является ли влияние фактора положительным или отрицательным на реакцию. Нормальные графики для ответов показаны ниже.
Как видно выше, число оборотов в минуту положительно влияет на количество теоретических ступеней, но оказывает отрицательное влияние на процентное содержание метанола в биодизеле. Положительный эффект означает, что с увеличением числа оборотов число теоретических ступеней увеличивается. В то время как отрицательный эффект указывает на то, что по мере увеличения числа оборотов массовый процент метанола в биодизеле уменьшается. К счастью для работы с POD, это желаемые результаты. При выборе рабочих условий для POD следует максимизировать число оборотов в минуту, чтобы свести к минимуму остаточный метанол в биодизеле и максимально увеличить количество достигнутых теоретических стадий.
Помимо приведенных выше графиков эффектов, Minitab рассчитывает коэффициенты и константы для уравнений отклика. Уравнения отклика можно использовать в качестве моделей для прогнозирования откликов при различных условиях эксплуатации (факторах). Коэффициенты и константы для % метанола в биодизеле и число теоретических ступеней показаны ниже.
Уравнения отклика можно использовать в качестве моделей для прогнозирования откликов при различных условиях эксплуатации (факторах). Коэффициенты и константы для % метанола в биодизеле и число теоретических ступеней показаны ниже.
Поскольку это линейная модель первого порядка, коэффициенты можно комбинировать с рабочими параметрами для определения уравнений. Уравнения этой модели показаны ниже.
Эти уравнения можно использовать в качестве прогностической модели для определения процентного содержания метанола в биодизеле и количества теоретических стадий, достигаемых при различных условиях эксплуатации, без фактического проведения экспериментов. Тем не менее, пределы модели должны быть проверены до того, как модель будет использоваться для прогнозирования откликов в различных условиях эксплуатации.
Пример \(\PageIndex{1}\)
Вы работали в SuperGym, местном спортивном зале для персональных тренировок, и вам нужен взгляд инженера на то, как предложить своим клиентам наилучшие планы. SuperGym в настоящее время классифицирует своих клиентов по 4 типам телосложения, чтобы помочь спланировать наилучшую возможную программу.
SuperGym в настоящее время классифицирует своих клиентов по 4 типам телосложения, чтобы помочь спланировать наилучшую возможную программу.
Кроме того, SuperGym предлагает 4 различных плана тренировок, от A до D, ни один из которых не предназначен непосредственно для какого-либо типа. Создайте экспериментальный факторный план, который можно использовать для проверки влияния разных планов тренировок на разных людей в спортзале.
Решение
Чтобы решить эту проблему, нам нужно определить, сколько различных экспериментов необходимо провести. Чтобы решить эту проблему, мы видим, что у нас есть два разных фактора: тип телосложения и план тренировок. Для каждого фактора существует четыре различных уровня. Таким образом, у нас есть факторный план 4 2 , что дает нам 16 различных экспериментальных групп. Создав таблицу всех различных групп, мы придем к следующему факторному плану:
Создав таблицу всех различных групп, мы придем к следующему факторному плану:
| А1 | В1 | С1 | Д1 |
| А2 | В2 | С2 | Д2 |
| А3 | В3 | С3 | Д3 |
| А4 | В4 | С4 | Д4 |
Где A-D — план тренировки, а 1-4 — типы
Пример \(\PageIndex{2}\)
Предположим, вы хотите изучить влияние часов сна (A), часов, проведенных с вторая половинка (B) и часы, потраченные на учебу (C) по результатам экзаменов студентов. Вам дана следующая таблица, которая связывает комбинацию этих факторов и баллов студентов в течение семестра. Используйте метод Йейтса, чтобы определить влияние каждой переменной на успеваемость учащихся в курсе.
| 1 | 17 | 24 | 19 | 21 | 22 | 28 | 25 | 24 |
|---|---|---|---|---|---|---|---|---|
| 2 | 18,5 | 21 | 20 | 19 | 26 | 22 | 27 | 19 |
| 3 | 16,5 | 22,5 | 22 | 25 | 24 | 26 | 21 | 20 |
| Всего | 52 | 67,5 | 61 | 65 | 72 | 76 | 73 | 63 |
Решение
Используя подход, представленный ранее в этой статье, мы приходим к следующему решению Йейтса.
| Стадия | Основная сумма | ||||
| Комбинация | Всего | 1 | 2 | 3 | Факторный эффект |
| а 1 б 1 в 1 | 52 | 119,5 | 245,5 | 529,9 | Неважно |
| а 2 б 1 с 1 | 67,5 | 126 | 284 | 13,5 | А |
| а 1 б 2 в 1 | 61 | 148 | 19,5 | -5,5 | Б |
| а 2 б 2 в 1 | 65 | 136 | -6 | -25,5 | АБ |
| а 1 б 1 в 2 | 72 | 15,5 | 6,5 | 38,5 | С |
| а 2 б 1 в 2 | 76 | 4 | -12 | -25,5 | АС |
| а 1 б 2 в 2 | 73 | 4 | -11,5 | -18,5 | г. до н.э. до н.э. | г.
| а 2 б 2 в 2 | 63 | -10 | -14 | -2,5 | Азбука |
Из этой таблицы видно, что существует положительная корреляция между факторами А и С, а это означает, что больше сна и больше учебы приводит к лучшей успеваемости в классе. Фактор B, однако, оказывает негативное влияние, а это означает, что время, проведенное с близким человеком, приводит к худшему результату теста. Таким образом, урок здесь заключается в том, чтобы проводить больше времени во сне и учебе и меньше времени со своим парнем или девушкой.
Пример \(\PageIndex{3}\)
Ваша мама выращивает огород для государственной ярмарки и провела несколько экспериментов, чтобы найти идеальные условия для выращивания своих овощей. Она попросит вас помочь в интерпретации результатов и покажет вам следующие данные:
Постройте графики, чтобы определить основные или взаимодействующие эффекты каждого фактора.
Решение
Вот график, который вы должны были получить для заданных данных.
Из этого видно, что существует эффект взаимодействия, так как линии пересекаются. Нельзя обсуждать результаты, не говоря ни о типе удобрения, ни о количестве использованной воды. Использование удобрения А и 500 мл воды привело к получению самого большого растения, а использование удобрения А и 350 мл дало самое маленькое растение. Удобрение B и 350 мл дали второе по величине растение, а удобрение B и 500 мл дали второе по величине растение. Очевидно, существует взаимодействие из-за количества используемой воды и присутствующих удобрений. Пожалуй, каждое удобрение наиболее эффективно при определенном количестве воды. В любом случае, ваша мама должна учитывать как тип удобрения, так и количество воды, подаваемой растениям, при определении правильных условий выращивания.
Упражнение \(\PageIndex{1}\)
Что из следующего не является преимуществом использования факторного плана перед однофакторным?
Упражнение \(\PageIndex{2}\)
В эксперименте с факторным планом 2 2 общее значение основного эффекта равно -5. Это означает, что
Это означает, что
Ссылки
Эта страница под названием 14.2: Дизайн экспериментов с помощью факторных планов распространяется под лицензией CC BY 3.0, авторами, ремиксами и/или кураторами являются Джоселин Анлейтнер, Стефани Комбс, Дайан Фельдкамп, Хирал Шет, Джейсон Буржуа, Майкл Кравченко, Николас Парсонс, Эндрю Ван и Эндрю Ван через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
[PDF] Планы строк-столбцов для 2n факторных экспериментов с двухцветными микрочипами для оценки основных эффектов и двухфакторных взаимодействий с ортогональной параметризацией
@article{Dash3013RowColumnDF,
title={Схемы строк-столбцов для 2n факториальных экспериментов с двухцветными микрочипами для оценки основных эффектов и двухфакторных взаимодействий с ортогональной параметризацией},
автор = {Суканта Кумар Дэш, Раджендер Парсад и В. К. Гупта},
журнал={Сельскохозяйственные исследования},
год = {2013},
объем = {2},
страницы = {172-182}
} Разработан в минимальном количестве метод построения планов «строка-столбец» для оценки основных эффектов и эффектов взаимодействия двух факторов в экспериментах с 2n факторными микроматрицами на основе ортогональной параметризации. репликаций. Подготовлен каталог дизайнов для 2 ≤ n ≤ 9. В каталоге также приведены основные эффекты и двухфакторные взаимодействия, смешанные в разных повторениях, и факторные эффекты, которые не смешаны в повторении. КПД…
View on Springer
link.springer.com
Построение факторных планов «строка-столбец»
Исследуется расположение 2n-факториалов в планах «строка-столбец» для оценки основных эффектов и двухфакторных взаимодействий. Даны однократные конструкции, которые позволяют оценить все…
Ортогональные планы главных эффектов в планах строк-столбцов для двухуровневых факторных экспериментов
АННОТАЦИЯ Планы двухуровневых факторных экспериментов по строкам и столбцам построены для оценки всех основных эффектов. Мы даем взаимодействия для блокировки строк и столбцов. На основе этих блокировок…
Факторные планы строк-столбцов с несколькими уровнями
Факторные планы строк-столбцов размера m × n представляют собой расположение элементов факторного плана в прямоугольный массив. Такой массив используется в экспериментальном дизайне, где строки и столбцы могут выступать…
Конструкции с рядовыми колоннами для факторных экспериментов в двух строках
ОТКРЫТИЯ 1-10 СПИСОК
.
Эффективные 2k-факториальные планы для блоков размера 2 с применением микроматриц взаимодействий с наименьшим количеством повторений и дает конструкцию для общего k, которая дает более экономичные конструкции, чем опубликованные ранее.

Двухуровневые факториальные и дробные факториальные планы в блоках размера два
7
7
размер два. Мы изучаем, какие комбинации планов в различных конфигурациях пар позволяют оценить все основные…
Эффективные схемы рядов и столбцов для экспериментов с микрочипами
В этой статье рассматривается проблема получения эффективных планов для экспериментов с двухцветными микрочипами, где одинаковый набор генов отмечен на каждом массиве В литературе аспекты оптимальности…
Дизайн двух
Предлагается несколько правил назначения для планирования хороших экспериментов, чтобы иметь дело с компромиссом между сокращением размера серии и возможно незначительные эффекты в двухуровневых факторных экспериментах.
Факторные и временные схемы для экспериментов с микрочипами кДНК.
как к популярным эталонным планам, которые крайне неэффективны, так и к планам, включающим все возможные прямые попарные сравнения.
Экспериментальные дизайны для 2-цветовых экспериментов с микрочипом кДНК
Kerr и Churchill (Biostatistics 2001; 2: 183–2016
Kerr и Churchill (Biostatistics 2001; 2: 183–2016
и Churchill. например, тип тканей, медикаментозное лечение и т. д.) объединяются в массивы с помощью каталога A-оптимальных дизайнов неполных блоков…
Сбалансированные факторные планы для экспериментов с микрочипами кДНК
В статье представлен систематический метод построения планов для экспериментов с микрочипами в отличие от алгоритмических и специальных методов, а также обобщается несколько дизайнов микрочипов, приведенных недавно в литературе.

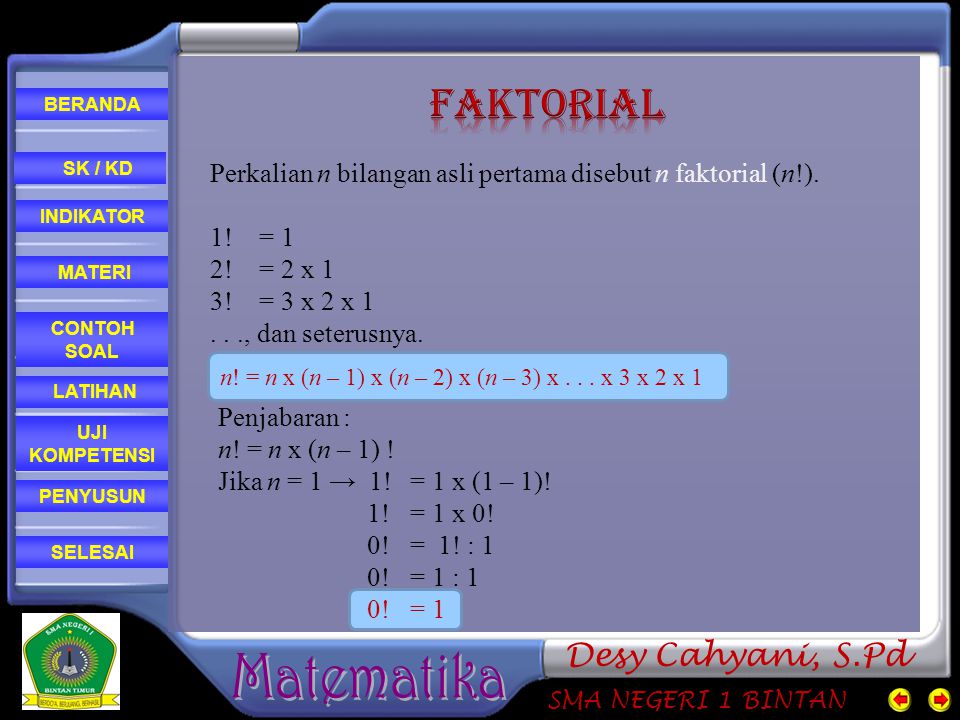 Факториал
Факториал