Преобразование чисел в различные системы счисления
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для iPad Excel для iPhone Excel для планшетов с Android Excel 2010 Excel 2007 Excel для Mac 2011 Excel для телефонов с Android Еще…Меньше
Система чисел является систематическим способом представления чисел символьными символами и использует базовое значение для удобной группировки чисел в сжатой форме. Самая распространенная система числов — десятичная, которая имеет базовое значение 10, и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Однако существуют и другие числовые системы, которые могут быть более эффективными для определенной цели. Например, так как на компьютерах используется логическое значение для вычислений и операций, для выполнения вычислений и операций используется двоичная числовая система, которая имеет базовое значение 2.
Microsoft Office Excel есть несколько функций, которые можно использовать для преобразования чисел в числовые системы и из них:
|
Система номеров |
Базовое значение |
Набор символьных знаков |
|
Двоичный |
2 |
0,1 |
|
Восьмеричном |
8 |
0, 1, 2, 3, 4, 5, 6, 7 |
|
Действительное. |
10 |
0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 |
|
Шестнадцатеричный |
16 |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Для этого используйте функцию ДВ.В.Е.
|
Для этого используйте функцию ДВ.В.EX.
|
|
Для этого используйте функцию ДВ.В.ВЕХ.
|
|
Для этого используйте функцию DEC2BIN.
|
Для этого используйте функцию DEC2HEX.
|
Для этого используйте функцию DEC2OCT.
|
Для этого используйте функцию HEX2BIN.
|
|
Для этого используйте функцию HEX2DEC.
|
|
Для этого используйте функцию HEX2OCT.
|
|
Для этого используйте функцию ВОСЬМ.В.ДВ.
|
Для этого используйте функцию ВОСЬМ.В.Е.
|
Для этого используйте функцию ВОСЬМ.В.EX.
|
Двоичная система счисления | Информатика
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, десятичная двойка является основанием двоичной системы счисления, аналогично тому, как в десятичной системе основанием является число десять.
Чтобы научиться считать в двоичной системе счисления, рассмотрим, как формируются числа в привычной для нас десятичной.
В десятичной системе счисления мы располагаем десятью знаками-цифрами: от 0 до 9. Когда счет достигает числа 9, вводится новый более старший разряд – десятки. При этом разряд единиц обнуляется и счет в этом разряде опять начинается с нуля. После числа 19 разряд десятков увеличивается на 1, а разряд единиц снова обнуляется. Получается число 20. Когда десятки дойдут до 9, впереди них появится третий разряд – сотни.
Формирование каждого последующего числа в двоичной системе счисления аналогично тому, как это происходит в десятичной за исключением того, что используются всего-лишь две цифры: 0 и 1. Как только разряд достигает своего предела, то есть единицы, появляется новый разряд, а старый обнуляется.
0 1 10 11 100 101 110 111
Итак, число три в двоичной системе записывается как 11, в десятичной – как 3. Количественно это одинаковые числа. Это одно и то же число, выраженное в различных системах счисления. Если есть вероятность неоднозначной трактовки числа, к нему приписывается нижний индекс в десятичной системе счисления, обозначающий, в какой системе счисления выражено данное число:
112 = 310
Индекс для числа, выраженного в десятичной системе, обычно опускается.
Перевод чисел из двоичной системы счисления в десятичную
В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:
5476 = 5000 + 400 + 70 + 6
Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:
5476 = 5 * 103 + 4 * 102 + 7 * 101 + 6 * 100
После равенства числа 5, 4, 7 и 6 – это набор цифр из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы. Так, например, 6 находится в первом разряде, поэтому она умножается на 10(1-1). Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.
Так, например, 6 находится в первом разряде, поэтому она умножается на 10(1-1). Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.
Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка. Здесь до знака равенства число представлено в двоичной системе счисления, после «равно» запись идет в десятичной:
10001001 = 1 * 27 + 0 * 26 + 0 * 25 + 0 * 24 + 1 * 23 + 0 * 22 + 0 * 21 + 1 * 20
Результат вычислений дает десятичное число, количественно равное двоичному 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 =
= 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык современной вычислительной техники.
Когда любые данные сохраняются на компьютере, они кодируются числами. С числами же компьютер выполняет операции, изменяя эти данные.
Допустим, у нас есть десятичное число 14, которое требуется сохранить в компьютерной памяти. Мы задействуем участок памяти, в данном случае состоящий как минимум из двух элементов, отводимых под разряды. В одном из разрядов мы сохраняем десятичное число 1, в другом – число 4.
Элемент памяти – это физическое устройство. Если проектировать его для хранения десятичной цифры, потребуется создать такое устройство, которое может находиться в десяти разных физических состояниях и способно переключаться между ними. Каждое из этих состояний будет соответствовать числу от 0 до 9.
Создать такой элемент памяти возможно, однако сложнее и дороже, чем создать элемент, способный находиться только в двух состояниях. Одно состояние сопоставить нулю, второе – единице. Кроме того, подобное хранение данных является более надежным.
Поэтому оказалось проще перевести число 14 в двоичную систему счисления, получив число 1110, и именно его сохранить в памяти. И пусть даже при этом будут задействованы не два, а четыре разряда, то есть четыре элементарных единиц памяти.
И пусть даже при этом будут задействованы не два, а четыре разряда, то есть четыре элементарных единиц памяти.
Перевод десятичного числа в двоичное
Одним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим «сбором» двоичного числа из остатков. Переведем таким образом число 14 в двоичное представление.
14 / 2 = 7, остаток 0 7 / 2 = 3, остаток 1 3 / 2 = 1, остаток 1 1 / 2 = 0, остаток 1
Собирать остатки надо с конца, то есть с последнего деления. Получаем 1110.
Выполним то же самое для числа 77:
77 / 2 = 38, остаток 1 38 / 2 = 19, остаток 0 19 / 2 = 9, остаток 1 9 / 2 = 4, остаток 1 4 / 2 = 2, остаток 0 2 / 2 = 1, остаток 0 1 / 2 = 0, остаток 1
Собираем остатки вместе, начиная с конца: 1001101.
Проверим, выполнив обратный перевод:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Сколько будет 10 в 3-й степени?
Математика касается не только чисел, но и различных вычислений с использованием чисел и переменных. Это то, что в основном известно как алгебра. Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Числа могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
Это то, что в основном известно как алгебра. Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Числа могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
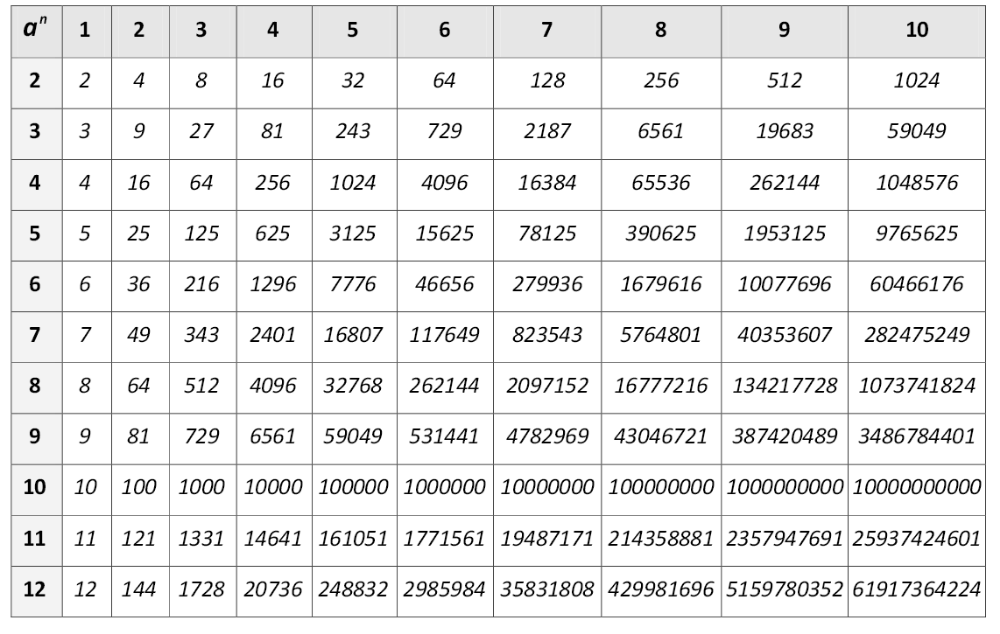
Показатели и степени
Экспоненты и степени — это основные операторы, используемые в математических вычислениях, экспоненты используются для упрощения сложных вычислений, включающих многократное самоумножение, самоумножение — это в основном числа, умноженные сами на себя. Например, 7 × 7 × 7 × 7 × 7 можно просто записать как 7 5 . Здесь 7 — базовое значение, 5 — показатель степени, а значение равно 16807. 11 × 11 × 11 можно записать как 11 3 , здесь 11 — базовое значение, а 3 — показатель степени или степень числа 11. Значение 11 3 равно 1331.
Показатель степени определяется как степень, заданная числу, сколько раз оно умножается само на себя. Если выражение записано как cx y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p. Это будет записано как
Если выражение записано как cx y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p. Это будет записано как
p × p × p × p … n раз = p n
Основные правила экспоненты наряду с другими математическими операциями, например, если есть произведение двух показателей, его можно упростить, чтобы упростить вычисления, и оно известно как правило произведения, давайте рассмотрим некоторые из основных правил показателей,
- Правило произведения ⇢ a n + a m = a n + m
- Частное правило ⇢ a n / a m 9000 8 = a n – m
- Силовое правило ⇢ (a a -м = 1/а м
- Нулевое правило ⇢ a 0 = 1
- Одно правило ⇢ a 1 = a
Сколько будет 10 в степени 3
rd ?Решение:
Любое число, имеющее степень 3, можно представить в виде куба этого числа. Куб числа — это число, умноженное само на себя трижды, куб числа представлен как показатель степени 3 этого числа. Если нужно записать куб x, это будет x 3 . Например, куб числа 5 представлен как 5 3 и равен 5 × 5 × 5 = 125. Другим примером может быть куб числа 12, представленный как 12 3 , что равно 12 × 12 × 12 = 1728.
Куб числа — это число, умноженное само на себя трижды, куб числа представлен как показатель степени 3 этого числа. Если нужно записать куб x, это будет x 3 . Например, куб числа 5 представлен как 5 3 и равен 5 × 5 × 5 = 125. Другим примером может быть куб числа 12, представленный как 12 3 , что равно 12 × 12 × 12 = 1728.
Давайте вернемся к постановке задачи и поймем, как она будет решаться, постановка задачи просила упростить 10 до степени 3 rd . Это означает, что вопрос требует решить куб 10, который представлен как 10 3 ,
10 3 = 10 × 10 × 10
= 100 × 10
= 10 00
Следовательно, 1000 третья степень числа 10.
Пример задачи
Вопрос 1: Решите выражение 4 3 – 2 3 .
Решение :
Чтобы решить выражение, сначала решите 3 -й степени числа, а затем вычтите второй член из первого члена.
Однако ту же проблему можно решить проще, просто применив формулу, формула: ху)
4 3 – 2 3 = (4 – 2)(4 2 + 2 2 + 4 × 2)
= 2 × (16 + 4 + 8)
= 2 × 28
9 0002 = 56
Вопрос 2: Решите выражение 11 2 – 5 2 .
Решение:
Чтобы решить выражение, сначала решите две степени -й степени чисел, а затем вычтите второй член из первого члена. Однако ту же проблему можно решить проще, просто применив формулу, формула
x 2 – y 2 = (x + y)(x – y)
11 2 – 5 2 = (11 + 5)(11 – 5) 9000 3
= 16 × 6
= 96
Вопрос 3: Решите выражение 3 3 + 9 3 .
Решение:
Чтобы решить выражение, сначала решите 3 -й степени чисел, а затем вычтите второй член из первого члена.
Однако ту же проблему можно решить проще, просто применив формулу, формула
x 3 + y 3 = (x + y)(x2 + y2 – xy)
3 3 + 9 3 = (9 + 3)(3 2 + 9 2 – 3 × 9)
= 16 × (9 + 81 – 27)
= 16 × 63
= 1008
Калькулятор дробей s базовые и расширенные операции с дробями, выражения с объединенными дробями с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически конвертируются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс | сложение | 1/2 + 1/3 |
| — | минус | вычитание | 90 238 1 1/2 — 2/3 |
| * | звездочка | умножение | 2/3 * 3/4 |
| × | знак умножения | умножение | 2/3 × 5/6 |
| : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|



 В.ШЕСТН(11111011; 4)
В.ШЕСТН(11111011; 4) В.ВОСЬМ(1001; 3)
В.ВОСЬМ(1001; 3) В.ДВ(9;4)
В.ДВ(9;4) В.ШЕСТН(100;4)
В.ШЕСТН(100;4) В.ВОСЬМ(58;3)
В.ВОСЬМ(58;3) В.ДВ(«F»; 8)
В.ДВ(«F»; 8) В.ДЕС(«A5»)
В.ДЕС(«A5») В.ВОСЬМ(«F»; 3)
В.ВОСЬМ(«F»; 3) В.ДВ(3; 3)
В.ДВ(3; 3) В.ДЕС(54)
В.ДЕС(54) В.ШЕСТН(100; 4)
В.ШЕСТН(100; 4)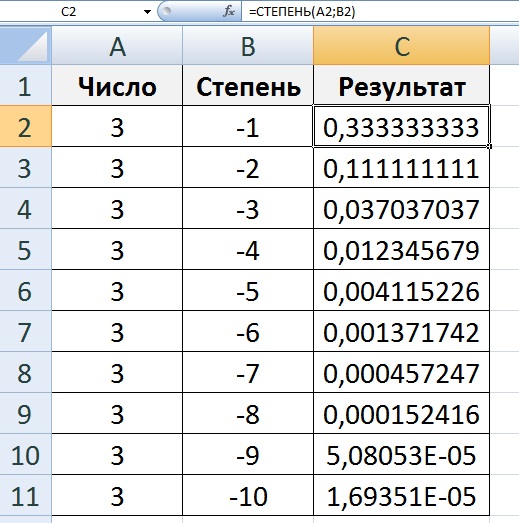 Однако ту же проблему можно решить проще, просто применив формулу, формула: ху)
Однако ту же проблему можно решить проще, просто применив формулу, формула: ху) Однако ту же проблему можно решить проще, просто применив формулу, формула
Однако ту же проблему можно решить проще, просто применив формулу, формула Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какая часть носков Макса коричневого или черного цвета?
Какая часть носков Макса коричневого или черного цвета?