Лучший ответ по мнению автора
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .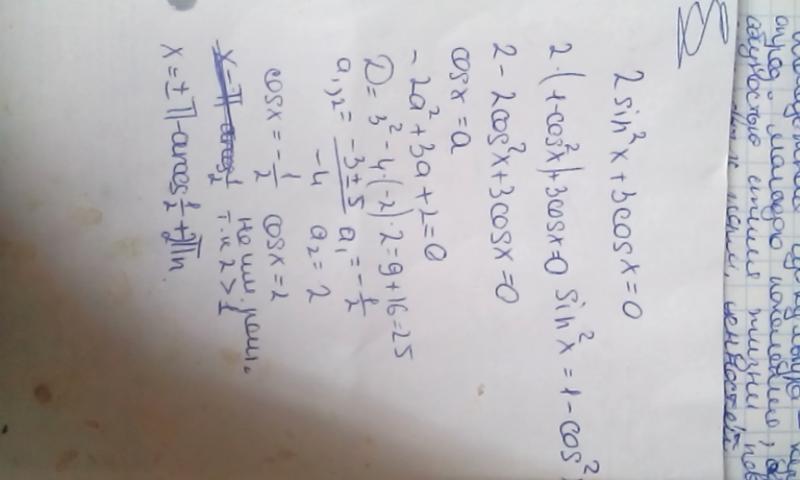 2 = 0
2 = 0
Решено
Даны два шара с радиусами 2 и 1. Во сколько раз объём первого шара больше объёма второго? Ответ:
Пользуйтесь нашим приложением
решить для x: 2sin²(x) + 3cos(x) — 3 = 0
Тригонометрия предварительного исчисления
Кайл К.
спросил 08.10.20Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старый Автор: Лучшие новыеСамые старыеУильям В. ответил 08.10.20
Репетитор
5,0 (838)
Опытный репетитор и инженер на пенсии
См. таких репетиторов
таких репетиторов
Смотрите таких репетиторов
2sin²(x) + 3cos(x) — 3 = 0
Используя тождество Пифагора sin 2 (x) + cos 2 (x) = 1, найдите sin 2 (x), чтобы получить sin 2 (x) = 1 — cos 2 (x), затем замените «1 — cos 2 (x)» на «sin 9″0035 2 (x)» следующим образом:
2(1 — cos 2 (x)) + 3cos(x) — 3 = 0
2 — 2cos 2 (x) + 3cos(x) — 3 = 0
-2cos 2
2cos 2 (x) — 3cos(x) + 1 = 0
Пусть w = cos(x), поэтому приведенное выше уравнение принимает вид:
2w 2 — 3w + 1 = 0 [теперь коэффициент для получения:
(2w — 1)(w — 1) = 0 [приравняйте каждый бином к нулю, чтобы получить:
w = 1/2 и w = 1 [теперь обратно подставьте, чтобы получить:
cos(x) = 1/2 и cos(x) = 1
Используя единичную окружность x = π/3, x = 5π/3 и x = 0
Это значения для области [ 0, 2π). Если ограничений домена нет, вам нужно будет включить все обходы по кругу следующим образом:
Если ограничений домена нет, вам нужно будет включить все обходы по кругу следующим образом:
x = π/3 + 2πk, x = 5π/3 + 2πk и x = 0 + 2πk, где k — любое целое число
.Голосовать за 1 голос против
Подробнее
92 — 3cosx + 1 = 0
(2cosx — 1)(cosx — 1) = 0
2cosx — 1 = 0 или cosx — 1 = 0
cosx = 1/2 или cosx = 1
x = 0 , 60, 180 и 300 градусов
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно 9{2}}x+3\\cos x=0 $ на интервале [0,2pi]?
Последняя обновленная дата: 01 -й февраля 2023 г.
•
Общее представление: 231,6K
•
Просмотр сегодня: 4.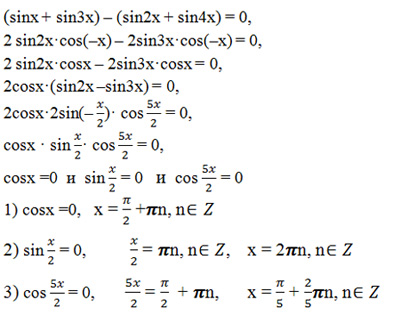 {2}}x $ и тогда уравнение преобразуется в квадратное уравнение и мы находим корни это даст нам возможное значение cos x. 9{2}}x+\cos x-4\cos x-2=0 $
{2}}x $ и тогда уравнение преобразуется в квадратное уравнение и мы находим корни это даст нам возможное значение cos x. 9{2}}x+\cos x-4\cos x-2=0 $
Мы можем взять cos x общие в первой половине уравнения и -2 общие во второй половине уравнения
Теперь мы можем взять $ 2\cos x+1 $ common
$ \Rightarrow \left( \cos x-2 \right)\left( 2\cos x+1 \right)=0 $
Таким образом, значение cos x может быть равно 2 или $ -\dfrac{1}{2} $, мы знаем, что диапазон cosx равен от -1 до 1
Таким образом, cosx не может быть равен 2. $ -\dfrac{1}{2} $ — единственное возможное значение cos x
В диапазоне от 0 до $ 2\pi $ решениями cos x= $ -\dfrac{1}{2} $ являются $ \dfrac{2\pi }{3} $ и $ \dfrac{4\pi } {3} $
Мы можем проверить, что в графе сначала мы нарисуем график $ y=\cos x $, а затем $ y=-\dfrac{1}{2} $
Затем проверим точку пересечения
Мы видим, что есть 2 решения между x=0 и $ x=2\pi $, одно решение A $ \left( \dfrac{2\pi }{3},-\dfrac{1}{2} \right) $ и B $ \left( \dfrac{4\pi }{3},-\dfrac{1}{2} \right) $.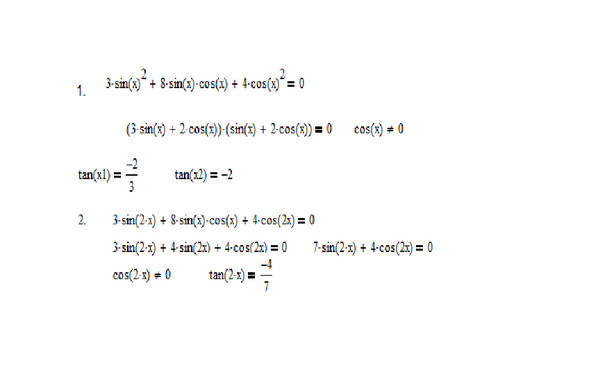

 06.15
06.15