3 в корне х 3 в корне: Mathway | Популярные задачи

Содержание

Помоги с вот этим уравнением! 3 в корне x в квадрате+4x-5… -reshimne.ru

Новые вопросы

Ответы

Здесь нужно решить уравнение относительно. решаем на фото

10.

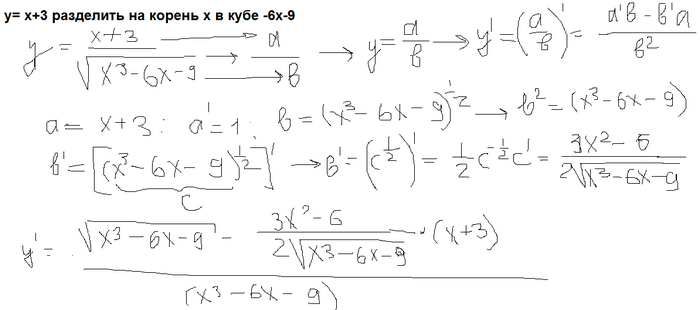5. Нахождение рациональных корней многочлена с целыми коэффициентами.

10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ

Теорема 4. Если многочлен с целыми коэффициентами f (x) = a_nxⁿ + a_n_-1xⁿ^-1 + … + a₁x+a₀ имеет рациональный корень x=p/q (q ≠ 0, дробь p/q несократимая), то р является делителем свободного члена (a₀), а q — делителем коэффициента при старшем члене а_n.

Если p/q является корнем многочлена f (х), то f(

p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем

a_n* pⁿ/qⁿ+ a_n-1 * p^n-1/q^n-1 + … + a₁ * p/q + a₀= 0.

(1)

Умножим обе части равенства (1) на (q ≠ 0). Получаем

а_nрⁿ + a_n-1p^n-1q + … + a₁pq^n-1 + a₀qⁿ= 0.

(2)

В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому

a₀qⁿ= -(а_nрⁿ

+ a_n-1p^n-1q + … + a₁pqⁿ^-1) делится на р.

Но когда мы записываем рациональное число в виде p/q, то эта дробь считается несократимой, то есть р и q не имеют общих делителей. Произведение a₀qⁿ может делиться на р (если р и q — взаимно простые числа) только тогда, когда a₀ делится на р. Таким образом, р — делитель свободного члена a₀.

Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда

a_npⁿ = -(a_n_-1pⁿ^-1q + … +

a₁pq^-1 + a₀qⁿ) делится на q. Поскольку р и q — взаимно простые числа, то a_n делится на q, следовательно, q — делитель коэффициента при старшем члене.

Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a₀. Таким образом, имеет место:

Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.

Если в заданном многочлене f (х) коэффициент а_n = 1, то делителями а_n могут быть только числа ±1, то есть q =±1, и имеет место:

Следствие 2.

Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.

Задача 1 Найдите рациональные корни многочлена 2х³ – х² + 12х – 6.

Пусть несократимая дробь p/q является корнем многочлена. Тогда р необходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.

Таким образом, рациональные корни многочлена необходимо искать среди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.

Кроме того, по схеме Горнера можно записать, что

2х³ – х² + 12х – 6 = (x – 1/2) (2x² + 12).

Многочлен 2х² + 12 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень x =1/2.

Задача 2 Разложите многочлен Р (х) = 2х⁴ + 3х³ – 2х² – х – 2 на множители.

Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.

Тогда Р (х) = (х – 1)(2х3 + 5х² + 3х + 2). Ищем целые корни кубического многочлена 2х³ + 5х² + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на

х + 2

Имеем Р (х) = (х – 1)(х + 2)(2х² + х +1).

Квадратный трехчлен 2х² + х +1 не имеет действительных корней и на линейные множители не раскладывается.

Ответ: Р (х) = (х – 1)(х + 2)(2х² + х +1).

Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х² + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры доказывается, что многочлен нечетной степени всегда можно разложить на линейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.

Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.

Задача 3 Разложите на множители многочлен х⁴ + х³ + 3х² + х + 6.

Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.

Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:

х⁴ + х³ + 3х² + х + 6 = (х² + ах + b)(х² + сх + d),

(3)

где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:

х⁴+ х³+ 3х² + х + 6 = x⁴+ cx³+ dx²+

+ ax³+ acx²+ adx +

+ bx²+ bcx + bd.

Получаем систему

(4)

Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.

Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рассматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.

Для каждой пары значений b и d из третьего равенства системы (4) найдем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.

Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид

x⁴ + х³ + 3х² + х + 6 = (х² – х + 2)(х² + 2х + 3).

(5)

Поскольку квадратные трехчлены х² – х + 2 и х² + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.

Упражнения

Найдите целые корни многочлена:

1) х³ – 5х + 4;

2) 2x³ + x² – 13x + 6;

3) 5х³ + 18х² – 10х – 8;

4) 4х⁴ – 11х² + 9х – 2.

Найдите рациональные корни уравнения:

1) х³ – 3х² + 2 = 0;

2) 2х³ – 5х² – х + 1 = 0;

3) 3х⁴ + 5х³ – х² – 5х – 2 = 0;

4) 3х⁴– 8х³ – 2х² + 7х – 2 = 0.

Разложите многочлен на множители:

1) 2х³ – х² – 5х – 2;

2) х³ + 9х²+ 23х +15;

3) х⁴ – 2х³ + 2х – 1;

4) х⁴ – 2х³ – 24х² + 50х – 25.

Найдите действительные корни уравнения:

1) х³ + х² – 4х + 2 = 0;

2) х³ – 7х – 6 = 0;

3) 2х⁴ – 5х³ + 5х² – 2 = 0;

4) 2х³ – 5х² + 1 = 0.

5*. Разложите многочлен на множители методом неопределенных коэффициентов:

1) х⁴ + х³ – 5х² + 13х – 6;

2) х⁴ – 4х³ – 20х² + 13х – 2.

6*. Разложите многочлен на множители, заранее записав его с помощью метода неопределенных коэффициентов в виде (х² + bх + с)² – (mх + n)²: :

1) х⁴+ 4х – 1;

2) х⁴ – 4х³ – 1;

3) х⁴ + 4а³х – а⁴.

Погода в Доброй Корне на 3 дня, прогноз погоды Добрая Корна на ближайшие 3 дня, Клетнянский район, Брянская область, Россия.

GISMETEO: Погода в Доброй Корне на 3 дня, прогноз погоды Добрая Корна на ближайшие 3 дня, Клетнянский район, Брянская область, Россия.

Перейти на мобильную версию

Пн, 3 октября Вт, 4 октября Ср, 5 октября Чт, 6 октября Пт, 7 октября Сб, 8 октября Вс, 9 октября Пн, 10 октября Вт, 11 октября Ср, 12 октября

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

+1254

+745

+439

+541

+643

+745

+1050

+948

+745

+1559

+1254

+1152

+745

+1457

+948

+745

+643

+1559

+1050

+948

+1050

+1661

+1152

+948

+846

+1763

+1254

+1050

+948

+1763

+1254

+1050

+948

+1864

+1355

Скорость ветра, м/cкм/ч

5-9 18-32

7-12 25-43

7-13 25-47

6-11 22-40

5-9 18-32

4-8 14-29

4-7 14-25

4-8 14-29

4-9 14-32

5-8 18-29

4-9 14-32

3-9 11-32

3-8 11-29

4-8 14-29

4-12 14-43

5-11 18-40

4-10 14-36

5-6 18-22

2-3 7-11

2-4 7-14

3-8 11-29

4-8 14-29

3-11 11-40

3-7 11-25

2-4 7-14

2-1 7-4

1-2 4-7

2-3 7-11

3-7 11-25

3-10 11-36

4-11 14-40

4-9 14-32

3-11 11-40

4-12 14-43

5-8 18-29

3-8 11-29

Осадки, мм

Распечатать. ..

Ветер, м/скм/ч

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Порывы

Пыльца, баллы

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Злаковые травы

Амброзия

Погода на дорогах

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Влажная дорога

Сухая дорога

Давление, мм рт. ст.гПа

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

726968

724965

727969

731974

732976

735980

738984

741988

742989

745993

748997

749998

748997

749998

7501000

7521002

7531004

7541005

7531004

7511001

7501000

749998

7501000

7511001

7501000

749998

747996

746994

Влажность, %

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Геомагнитная активность, Кп-индекс

Пн, 3 октября Вт, 4 октября Ср, 5 октября

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Ночь

Утро

День

Вечер

Осадки

Температура

Ветер

Облачность

Козловчик

Мирный

Свара

Коростовец

Каменец

Соловьяновка

Елисеевка

Камнев

Рабочая Кадра

Харитоновка

Болотня

Еловка

Узровье

Быстрянка

Семиричи

Ширковка

Красный Ятвиж

Тельча

Меловое

Титовка

Александровка

Красный Дворец

Борятино

Миголино

Пигосси — Корне: прогнозы 3 октября 2022

Пигосси

Монастир (WTA)

3 октября 20:00

3 окт. 20:00

Корне

Смотреть трансляцию

После неудачи на Открытом чемпионате США Ализе Корне попробовала свои силы в Портороже, но и там она уступила в первом же круге Кайе Йуван. С тех пор француженка взяла двухнедельный перерыв, чтобы отдохнуть и восстановить силы. Как она проявит себя в первом ивенте после паузы? ее первой соперницей в Тунисе станет бразильянка Лаура Пигосси.

Покрытие: хард

Скорость покрытия: 6/10

Текущий рейтинг Пигосси: 108

Баланс побед Пигосси (2022): 23-25

Баланс побед Пигосси (хард): 2-6

Текущий рейтинг Корне: 37

Баланс побед Корне (2022): 22-22

Баланс побед Корне (хард): 12-12

Статистические факты на матч Пигосси – Корне:

Пигосси проиграла в четырех последних матчах подряд.

Семь из десяти последних матчей Корне завершились в двух партиях.

Личные встречи Пигосси – Корне:

Теннисистки впервые сыграют друг с другом.

Прогноз на поединок Лаура Пигосси – Ализе Корне:

Очевидно, Пигосси – не самая яркая представительница теннисисток, которые предпочитают играть на харде. В этом сезоне бразильянка провела всего восемь игр на быстрых кортах, выиграть ей удалось лишь дважды, причем у соперниц уровня ITF. Ализе Корне для Лауры – это непреодолимая планка, до которой бразильянке точно не допрыгнуть.

Корне конечно не находится в оптимальной форме, за 24 матча на харде она выиграла 12 раз, но француженка превосходит соперницу в классе. К тому же, Пигосси последние пять матчей провела на грунте и впервые за полтора месяца ступит на хардовое покрытие. Здесь не должно быть затяжного противостояния, поэтому ставим на ТМ (19) или же, учитывая преимущество Ализе, можно поставить на Ф2 (-5. 5).

Автор прогноза: Мифтахов Артур

Прогнозы на матч Лаура Пигосси — Ализе Корне 3 октября 2022

📝Здесь вновь заиграем против бразильянки, которая на данный момент находится в посредственных для себя кондициях, даже на своём любимом грунте Пигосси за крайние 3 матча — взяла не более двух геймов в сете, На твёрдых покрытиях она и вовсе не умеет играть, результаты есть только на итф, где уровень оппозиций был слаб.

Корне не молодая, но очень цепкая и вредная теннисистка в плане спорта, Ализа просто так не даст выиграть поинт и постарается все мячи вернуть обратно в корт, заставляя ошибиться соперницу. Форма не пиковая, но приемлемая, думаю, что в сегодняшнем поединке проблем не должно возникнуть. Также француженка често обыгрывать более именитых соперниц достаточно уверено и с явным преимуществом, поэтому склоняюсь к очередному разносному матчу с участием Пигосси.

Даже можно взять за сравнения поединки Пигосси на харде этого года: против Мельниковой, Стоянович и Сандерс удалось взять не более 3 геймов в сете, в свою очередь Корне через ТМ обыгрывала Радукану, Ястремскую, Захарову, Мугурусу и Томову, причём именно через ТМ 18. 5, а не -6.5 фору, которую предлагает БК.

Прогноз: ТМ (18.5) с кэфом 1.82

Лаура Пигосси крайне слабая теннисистка по игре на жестких кортах. В прошлом году она можно сказать нафармила статистику на фьючерсах, выиграв парочку титулов на турнирах очень низкиз по классу это 15к и 25к, где теннисистки с рейтингом за 300. Реальный же расклад сил таков, что Пигосси не умеет играть в быстром темпе и у нее слишком мало вариативности на корте

Ализе Корне можно сказать немного не везет, сейчас она находится в хорошей физической форме, судя по ее последним матчам. Однако соперницы играющие в силовой теннис ей не удобны, сегодня же у нее не должно возникнуть проблем

Пигосси это совершенно другой уровень тенниса, тем более хардовые корты не ее профиль. Ализе не оставит шансов, ставим на инд тотал Лауры 6.5 меньше

Прогноз: ИТ1М (6.5) с кэфом 1.8

Завтра начнутся матчи первого раунда у женщин по теннису в тунисе , это будет очень интересно и увлекательно, редко там бывают турниры ведь. Сыграют Лаура Пигосси и Ализе Корне.

Пигосси в этом году немного поднялась в рейтинге и у неё весьма защитный стиль игры, грунт ей подходит намного больше. Но может упереться, сил в первом круге ведь много и умеет она играть против не сильно бьющих.

Корне отличный сезон провела, но уже ветеран, вряд ли с первого круга прям втянется и будет брать гейм за геймом, кажется будет не самый лёгкий матч здесь.

Форма непонятно какая у Ализе, поставлю фору 6.5 на Пигосси.

Прогноз: Ф1 (6.5) с кэфом 1.82

В последних своих матчах больше двух геймов за сет бразильская теннисистка не брала

Прогноз: ТМ (16.5) с кэфом 2.62

Да стоит попробовать рискнуть . Пигосси значительно слабее оппонентки и если Корне не будет валять дурака, то дважды по 6:2 сделать может. Если вообще баранку не повесит.

Прогноз: ТМ (16.5) с кэфом 2.61

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

исчисление — Длина дуги $y = 1/3 \sqrt{x} (x-3)$

Вопрос задан 10 лет, 4 месяца назад

Изменено 10 лет, 4 месяца назад

Просмотрено 14 тысяч раз

$\begingroup$

$y = 1/3 \sqrt{x} (x-3)$ от 1 до 9

В моей книге на самом деле $x = 1/3 \sqrt{y} (y-3)$, но я предпочитаю работать с y, поэтому я просто меняю местами две переменные и думаю, что все должно быть одинаково. 9{1/2} \right) = (9+3) — (1/3 + 1) = \dfrac{32}{3}$$

$\endgroup$

$\begingroup$

Ваша исходная функция равна

$$y(x) =\frac{1}{3}\sqrt x (x-3)$$

Ее производная равна

$$y'(x) =\frac {1}{3}\frac{1}{2\sqrt x} (x-3)+\frac{1}{3}\sqrt x$$

$$\eqalign{ & y'(x) = \frac{1}{3}\frac{{x — 3}}{{2\sqrt x }} + \frac{1}{3}\sqrt x \cr & y'(x) = \frac{1}{3}\frac{{x — 3 + 2x}}{{2\sqrt x }} \cr & y'(x) = \frac{1}{3}\frac{{3x — 3}}{{2\sqrt x }} \cr & y'(x) = \frac{{x — 1}}{{2\sqrt x }} \cr & y'(x) = \frac 1 2\left( \sqrt x -\frac{{ 1}}{{\sqrt x }} \right)\cr} $$ Затем 92} = \ frac {x} {4} + \ frac {1} {2} + \ frac {1} {{4x}} = \ frac {x} {4} + 2 \ frac {{\ sqrt x} }{2}\frac{1}{{2\sqrt x }} + \frac{1}{{4x}} \cr} $$

Попробуйте подражать ответам на другие вопросы по этой теме.

$\endgroup$

$\begingroup$

Я стараюсь использовать логарифмическое дифференцирование везде, где это уместно, когда имеешь дело с функциями, включающими рациональные функции и/или радикалы в качестве факторов. Преимущество состоит в том, что приходится иметь дело с аддитивными условиями вместо факторов, которыми часто легко манипулировать и уменьшать: 92-2x+1}dx=\frac{1}{2\sqrt{x}}\left(x+1\right)dx=\frac{1}{2}\left(\frac{1}{\ sqrt{x}}+\sqrt{x}\right)dx$$

Один метод, который я сам нахожу очень удобным, когда вы привыкнете к нему, — это «проталкивание» выражений под $d$ с использованием правила: $$d\влево(f(x)\вправо)=f'(x)dx$$ Все, что для этого нужно, — это вспомнить некоторые стандартные производные из таблицы. Все, что он дает, — это разбивать сложные выражения на управляемые блоки без необходимости вводить новые переменные. Затем изменение переменных понимается так же, как присвоение имен частям программного кода, которые вы должны последовательно использовать повторно и без какой-либо «магии». Если вы посмотрите на похожие вопросы, на которые я ответил здесь, вы увидите, что я везде использую один и тот же «метод». Ниже, просто заметив, что $$\left(\sqrt{x}\right)’=\frac{1}{2\sqrt{x}}$$ можно не иметь дело с дробными показателями, уменьшить пределы и добиться большей прозрачности вычислений: 93=3+9-1-\frac{1}{3}=\frac{32}{3}$$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Напишите квадратное уравнение, зная его решения

Все ресурсы Precalculus

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

Precalculus Help » Графические функции » Решение квадратных уравнений » Напишите квадратное уравнение, зная его решения

Какое из следующих уравнений может быть уравнением для функции, корни которой находятся в точках и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Если корни уравнения находятся в точках x= -4 и x=3, то мы можем работать в обратном направлении, чтобы увидеть, из какого уравнения были получены эти корни. Если бы мы разложили квадратное уравнение на множители и получили данные решения, это означало бы, что факторизованная форма выглядела бы примерно так:

Потому что это форма, которая дает решения x = -4 и x = 3. Если мы действуем в обратном порядке и снова перемножаем множители, мы получаем следующее квадратное уравнение:

Сообщить об ошибке

С учетом корней . Напишите квадратный полином, у которого есть корни.

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем составить квадратный многочлен с , перемножив линейные многочлены, корнями которых они являются, и перемножив их.

Начало

Распределите отрицательный знак

ФОЛЬГИРОВАНИЕ двух многочленов. Это означает умножение первых членов, затем внешних, затем внутренних и, наконец, последних членов.

Упростить

Сообщить об ошибке

Если мы знаем решения квадратного уравнения, то мы можем построить это квадратное уравнение.

Найдите квадратное уравнение, зная, что:

и являются решениями.

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку мы знаем решения уравнения, мы знаем, что:

Мы просто выполняем умножение в левой части уравнения, чтобы получить квадратное уравнение.

Сообщить об ошибке

Какая из следующих функций является квадратичной, проходящей через точки и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Эти две точки говорят нам о том, что квадратичная функция имеет нули в точках и в .

Им соответствуют линейные выражения , и .

Разверните их продукт, и вы получите правильный ответ.

Если квадратное выражение открывается вверх, коэффициент перед квадратом члена будет положительным. Таким образом получаем:

Если квадратное число раскрывается вниз, оно проходит через те же две точки, но имеет уравнение:

Поскольку в вариантах ответа отображается только , это правильный ответ.

Сообщить об ошибке

Какой из следующих корней даст уравнение .

Возможные ответы:

Правильный ответ:

3 1

918 Объяснение:
Когда мы решаем квадратные уравнения, мы получаем решения, называемые корнями или местами, где эта функция пересекает ось x. Не все будут пересекать ось x, поскольку мы видели, что функции можно смещать, но многие будут. Когда они это делают, это является особым и красноречивым обстоятельством в математике. Поскольку мы знаем, что корни этих типов уравнений имеют форму x-k, получив список корней, мы можем работать в обратном направлении, чтобы найти уравнение, к которому они относятся, и мы делаем это, умножая множители (метод фольги).
Если вам дали ответ в форме , просто сложите или перемножьте два множителя. Если вам даны только два значения x корней, поместите их в форму , которая даст вам эти два значения x (если установить их равными нулю), и умножьте, чтобы увидеть, получите ли вы исходную функцию.
Для нашей задачи правильный ответ .
Используйте метод фольги для получения исходного квадратичного уравнения.
Сначала умножьте 2x на все члены в  :
, затем умножьте 2 на все члены в : .
Затем мы объединяем    для окончательного ответа.
Сообщить об ошибке
Выберите квадратное уравнение, имеющее следующие корни:
и
Возможные ответы:
Правильный ответ:
3
30
3 Пояснение:
Корнями или решениями квадратного уравнения являются его множители, приравненные к нулю и затем найденные для x. Когда даны корни и ищется квадратное уравнение, запишите корни с правильным знаком, чтобы получить этот корень, когда он установлен равным нулю и решен. Например, квадратное уравнение имеет корень -5 и +3. Как можно получить тот же самый корень, если его приравнять к нулю? С и  потому что они решают давать -5 и +3. Таким образом, эти факторы, перемноженные вместе, дадут вам правильное квадратное уравнение.
Наши корни были .
Таким образом, наши факторы  и .
Теперь фольгает эти два фактора:
Сначала:
Внешний:
Внутренний:
Последний:
Упрощение:
Упрощение:
13
.

Возможные ответы:
Ни один из этих ответов не является правильным.
Правильный ответ:
Объяснение:
Следовательно…
Эти два условия дают вам решение. Итак, работайте в обратном направлении.
No related posts.

3 в корне х 3 в корне: Mathway | Популярные задачи

Помоги с вот этим уравнением! 3 в корне x в квадрате+4x-5… -reshimne.ru

Ответы

Похожие вопросы

10.

Погода в Доброй Корне на 3 дня, прогноз погоды Добрая Корна на ближайшие 3 дня, Клетнянский район, Брянская область, Россия.

Пигосси — Корне: прогнозы 3 октября 2022

Прогнозы на матч Лаура Пигосси — Ализе Корне 3 октября 2022

исчисление — Длина дуги $y = 1/3 \sqrt{x} (x-3)$

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

Напишите квадратное уравнение, зная его решения

Все ресурсы Precalculus

Добавить комментарий Отменить ответ