В ответ запишите меньший корень уравнения….
9-3(3-х)=7+5х
сделайте…
Помогите пожалуйста ))…
Разложите н множители:
(Х+1)2(квадрат)-(х-1)2(квадрат)…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
ОбществознаниеОкружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Буква греческого алфавита, 3 буквы
Ответ на вопрос в сканворде (кроссворде) «Буква греческого алфавита», 3 буквы (первая — и, последняя — с):
икс
(ИКС)
Другие определения (вопросы) к слову «икс» (65)
- Перед игреком
- «Мистер …»
- Латинская «X»
- Неизвестное число
- Латинская буква в лексиконе математика
- Инкогнито в уравнении
- Буква латинского алфавита
- Математическая буква
- «Х» в математике
- Искомое в уравнении
- Американский борец за права темнокожих, идеолог движения «Нация ислама», оказавший огромное влияние на «чёрных пантер» и движение за сецессию «чёрных штатов»
- Буква оси абсцисс
- Буква, которую ищут
- Коллега игрек и зет
- Математическое инкогнито
- Фильм «Люди-…»
- Мистер из оперетты
- Буква, часто обозначающая неизв.
 величину в математике
величину в математике - Условное обозначение неизвестного или не называемого лица
- Математический инкогнито
- Мистер Неизвестный
- плюс игрек
- Партнёр игрека по координатам
- Латинская «Х»
- Триллер Кертиса «Доктор …»
- Латинская буква, часто обозначающая неизвестную величину в математике
- Инкогнито из математики
- Х (мат.)
- Коллега игрека
- Мистер … (фильм)
- Мистер с «Выходной арией»
- Греческая, латинская буква
- «Темная лошадка» уравнения
- Напарник игрека
- Неизвестное в математике
- Латинская буква
- Собрат игрека
- Абсцисса — ось …
- «Секретная» буква
- Буква, заменяющая искомую величину
- Математический неизвестный
- Неизвестная буква
- Кроме неё ещё есть зет и игрек
- Буква абсциссы
- Буква, часто обозначающая неизвестную величину в математике
- Буква латинского алфавита, часто обозначающая неизвестную величину в математике
- За ним игрек
- Математическое неизвестное
- Математическое обозначение неизвестной или переменной величины
- Некий мистер Имре Кальмана
- Буква внедорожника БМВ
- Таинственная буква
- Мистер в исполнении Отса
- Мистер Незвестный
- Анаграмма к слову «кси»
- Мистер-неизвестность
- Трактат мексиканского писателя Альфонсо Рейеса «… на челе»
- Какой буквой Вильгельм Рентген обозначил открытые им удивительные лучи?
- Математический «аноним» в уравнении
- Латино-математическая буква
- Неизвестный мистер Георга Отса
- Группа «… миссия»
- Раскруч.
 Кальманом лат. буква
Кальманом лат. буква - «Мистер …» (Георг Отс)
- Буква вместо цифры
- название латинской буквы X ◆ Французский язык преподавал Густав Самойлович Бюрнанд — швейцарец, .. с таинственным большим шрамом в виде буквы икс на лбу. 〈…〉 Утверждали, что в молодости Густав дрался на дуэли и противник успел рапирой начертать у него косой крест на лбу. Л. Д. Троцкий, «Моя жизнь», 1929–1933 гг. ◆ Рентген решил назвать неизвестное, вновь открытое им явление «лучами икс». Икс — это латинская буква. В алгебре этой буквой принято обозначать неизвестные величины. И в самом деле, обнаруженная Рентгеном «сила» была совершенно неизвестной величиной. М. П. Бронштейн, «Солнечное вещество», 1936 г. ◆ Хромосомы первой пары (I) называются также половыми; их обозначают буквами «икс» и «игрек». 〈…〉 Поскольку самец всегда получает свою X‑хромосому от матери, ему передаются все гены, расположенные в материнской X‑хромосоме. Так некоторые наследственные признаки всегда передаются только от матерей к сыновьям и от отцов к дочерям.
 М. Голубовский, «Та самая дрозофила…» // «Химия и жизнь», № 4, 1966 г. ◆ По той же причине раввин из МТИ Плаут пользуется распространённым среди религиозных англоязычных евреев кодовым обозначением Xmas. По-английски рождество — Christmas, но, избегая называть Христа по имени, раввин подставляет букву Икс. Михаэль Дорфман, «Еврейское Рождество» (2004) // «Интернет-альманах “Лебедь”», 04.01.2004 г.
М. Голубовский, «Та самая дрозофила…» // «Химия и жизнь», № 4, 1966 г. ◆ По той же причине раввин из МТИ Плаут пользуется распространённым среди религиозных англоязычных евреев кодовым обозначением Xmas. По-английски рождество — Christmas, но, избегая называть Христа по имени, раввин подставляет букву Икс. Михаэль Дорфман, «Еврейское Рождество» (2004) // «Интернет-альманах “Лебедь”», 04.01.2004 г. - матем. (математический термин) неизвестная или переменная величина, обозначаемая латинской буквой «x» ◆ — Видите ли, я употребил особый метод… Как бы вам это объяснить… Ну, одним словом, из высшей математики… Я взглянул в густые столбцы цифр и разглядел в них и иксы, и игреки, и зеты, и квадратные корни, и бесконечные дроби, и чуть ли даже не логарифмы. 〈…〉 Мы рекомендовали ему первые четыре правила арифметики, которых было совершенно достаточно для осуществления нашей грандиозной задачи. И. Н. Потапенко, «Секретарь Его Превосходительства», 1891 г. ◆ От Гончарова меня оторвал Юра: снова понадобилось моё математическое вмешательство.
 Стали разбираться. Выяснилось, что, наседая на тригонометрию, Пиголица имел весьма неясное представление об основах алгебры и геометрии, тангенсы цеплялись за логарифмы, логарифмы за степени, и вообще было непонятно, почему доброе русское «х» именуется иксом. И. Л. Солоневич, «Россия в концлагере», 1935 г. ◆ Стеша не кончила восьмой класс — на вечорках поплясывать стала, парни провожали, сидеть за партой, решать, чему равно «а» плюс «б» в квадрате, казалось стыдновато, да и ни к чему, в её жизни «иксы» да «игреки» не пригодятся. В. Ф. Тендряков, «Не ко двору», 1954 г. ◆ .. я предложил двум моим коллегам-аспирантам решить знаменитую задачу, которую чеховский гимназист-репетитор задал купеческому сынку Пете. В ней условие начиналось традиционной фразой: «Купец купил…» — и её следовало решать без икса — ведь папаша-купец посрамил гимназистика, решив её на счётах. Аспиранты это никак не могли сделать. И. С. Шкловский, «Из истории развития радиоастрономии в СССР», 1982 г.
Стали разбираться. Выяснилось, что, наседая на тригонометрию, Пиголица имел весьма неясное представление об основах алгебры и геометрии, тангенсы цеплялись за логарифмы, логарифмы за степени, и вообще было непонятно, почему доброе русское «х» именуется иксом. И. Л. Солоневич, «Россия в концлагере», 1935 г. ◆ Стеша не кончила восьмой класс — на вечорках поплясывать стала, парни провожали, сидеть за партой, решать, чему равно «а» плюс «б» в квадрате, казалось стыдновато, да и ни к чему, в её жизни «иксы» да «игреки» не пригодятся. В. Ф. Тендряков, «Не ко двору», 1954 г. ◆ .. я предложил двум моим коллегам-аспирантам решить знаменитую задачу, которую чеховский гимназист-репетитор задал купеческому сынку Пете. В ней условие начиналось традиционной фразой: «Купец купил…» — и её следовало решать без икса — ведь папаша-купец посрамил гимназистика, решив её на счётах. Аспиранты это никак не могли сделать. И. С. Шкловский, «Из истории развития радиоастрономии в СССР», 1982 г. ◆ В сущности, расследование любого преступления — это не что иное как логическое решение определённой задачи. Математика в чистом виде. Только вместо иксов и игреков — живые люди, и ведут они себя куда более непредсказуемо. Елизавета Козырева, «Дамская охота», 2001 г.
◆ В сущности, расследование любого преступления — это не что иное как логическое решение определённой задачи. Математика в чистом виде. Только вместо иксов и игреков — живые люди, и ведут они себя куда более непредсказуемо. Елизавета Козырева, «Дамская охота», 2001 г. - некое неизвестное или неназываемое лицо, место, время, явление ◆ Они говорят: дело в преуспеянии, а не в том, что к нам пристанет нечисть; мы иксы и игреки, которые обязываются внести свою лепту и исчезнуть, — кому же какая надобность справляться, замараны они или не замараны? Оттого, мол, и запустение у нас идёт, что люди, которые что-нибудь могут, предпочитают в светозарных одеждах ходить. М. Е. Салтыков-Щедрин, «Письма к тётеньке», 1881–1882 гг. ◆ .. пребывание моё у вас, сближение с Антониной Алексеевной, которую я в первый раз хорошо узнал, с милыми молодыми людьми, преимущественно с Борей, потом Алёшей, остальные двое остались для меня иксами, — было для меня одним из самых радостных дней моей жизни.
 Л. Н. Толстой, «Письма», 1894 г. ◆ Опять разговоры о физическом труде, о прогрессе, о таинственном иксе, ожидающем человечество в отдалённом будущем. Доктор не любил нашего хозяйства, потому что оно мешало нам спорить, и говорил, что пахать, косить, пасти телят недостойно свободного человека и что все эти грубые виды борьбы за существование люди со временем возложат на животных и на машины, а сами будут заниматься исключительно научными исследованиями. А. П. Чехов, «Моя жизнь», 1896 г. ◆ Человек — потенциальный икс; он сам не знает, сколько чертей в нём сидит, и только история выводит этих метафизиков, как микробы, на свежую воду. В. О. Ключевский, «Записи 1900‑х годов», 1900–1909 гг. ◆ Субъекту здесь приписывается лишь призрачное существование .. (и только на самом заднем плане помещается некоторый таинственный икс, иррациональный внешний толчок). С. Н. Булгаков, «Философия хозяйства (мир как хозяйство)», 1912 г. ◆ Тем более что в тридцать седьмом предстояло уничтожить людей, Горькому близко знакомых: Бабеля, например, или Пильняка.
Л. Н. Толстой, «Письма», 1894 г. ◆ Опять разговоры о физическом труде, о прогрессе, о таинственном иксе, ожидающем человечество в отдалённом будущем. Доктор не любил нашего хозяйства, потому что оно мешало нам спорить, и говорил, что пахать, косить, пасти телят недостойно свободного человека и что все эти грубые виды борьбы за существование люди со временем возложат на животных и на машины, а сами будут заниматься исключительно научными исследованиями. А. П. Чехов, «Моя жизнь», 1896 г. ◆ Человек — потенциальный икс; он сам не знает, сколько чертей в нём сидит, и только история выводит этих метафизиков, как микробы, на свежую воду. В. О. Ключевский, «Записи 1900‑х годов», 1900–1909 гг. ◆ Субъекту здесь приписывается лишь призрачное существование .. (и только на самом заднем плане помещается некоторый таинственный икс, иррациональный внешний толчок). С. Н. Булгаков, «Философия хозяйства (мир как хозяйство)», 1912 г. ◆ Тем более что в тридцать седьмом предстояло уничтожить людей, Горькому близко знакомых: Бабеля, например, или Пильняка. 〈…〉 Одно дело какие-то там иксы и игреки, мелькающие на газетных страницах (продавшиеся иностранным разведкам), другое — Пильняк или Бабель, которых он знает насквозь. Л. К. Чуковская, «Прочерк», 1980–1994 гг. ◆ Несмотря ни на какие трудности, завод сохранял и продолжает сохранять мобилизационные мощности для выполнения (в случае, если в стране наступит тревожный «час икс») мобилизационного задания государства. Невыполнение мобзадания, с одной стороны, подсудное дело. А с другой стороны, экономической, содержание нужных для его выполнения мощностей крайне невыгодно для завода. Людмила Пирогова, «В курсе дела» (2003) // «Встреча», (Дубна), 05.03.2003 г.
〈…〉 Одно дело какие-то там иксы и игреки, мелькающие на газетных страницах (продавшиеся иностранным разведкам), другое — Пильняк или Бабель, которых он знает насквозь. Л. К. Чуковская, «Прочерк», 1980–1994 гг. ◆ Несмотря ни на какие трудности, завод сохранял и продолжает сохранять мобилизационные мощности для выполнения (в случае, если в стране наступит тревожный «час икс») мобилизационного задания государства. Невыполнение мобзадания, с одной стороны, подсудное дело. А с другой стороны, экономической, содержание нужных для его выполнения мощностей крайне невыгодно для завода. Людмила Пирогова, «В курсе дела» (2003) // «Встреча», (Дубна), 05.03.2003 г.
Значение слова
ИКС,
-а, мужской род
1. Название третьей от конца буквы (x) латинского алфавита.
2. Неизвестная величина, обозначаемая этой буквой (наряду с буквами y, z) (мат.).
||
Условное обозначение неизвестного или умышленно не называемого лица.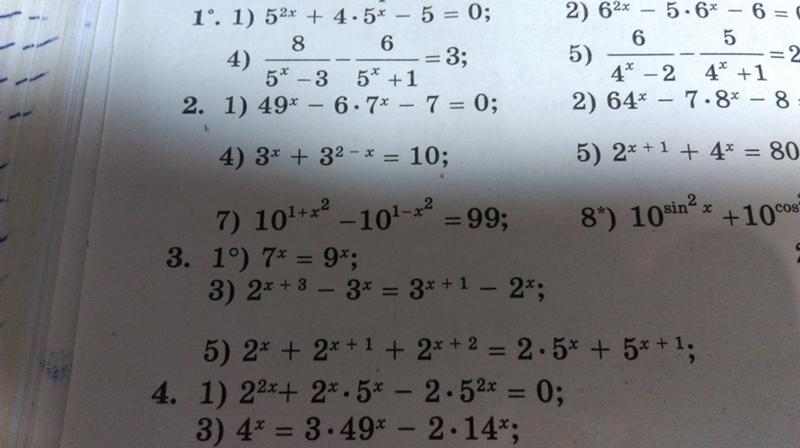 Господин Икс.
Господин Икс.
X (латиница)
X, x (латинское «икс») — 24-я буква базового латинского алфавита. В английском алфавите называется экс [ɛks]. В других алфавитах у этой буквы встречаются и другие названия.
В римской системе счисления обозначает число 10.
Буквой X часто обозначают неизвестное значение или неизвестный объект (в математике, литературе, разговорной речи).
В польском, финском, румынском и ряде других языков эта буква используется только в заимствованных словах.
Является 32-й буквой албанского алфавита, обозначает звук [d͡z] и называется дза (алб. xë [d͡zə]).
Латинская буква X произошла от греческой кси (Ξ, ξ).
Показать дальше
1. Значение слова икс. 2. Синонимы «икс». 3. Антонимы «икс». 4. Разбор по составу «икс». 5. Ассоциации «икс». 6 фонетический разбор «икс».
- Поиск занял 0.071 сек. Вспомните, как часто вы ищете, чем заменить слово? Добавьте sinonim.org в закладки, чтобы быстро искать синонимы, антонимы, ассоциации и предложения.

Пишите, мы рады комментариям
Вверх ↑
Как умножать степени — SAT Math
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 Следующая →
SAT Math Help » Алгебра » Экспоненты » Экспоненциальные операции » Как умножить показатели степени
Если (300)(400) = 12 * 10 n , n =
Возможные ответы:
7
2
3
12
4
Правильный ответ:
4
Объяснение:
(300)(400) = 120 000 или 12 * 10 4 .
Сообщить об ошибке
(2×10 3 ) x (2×10 6 ) x (2×10 12 ) = ?
Возможные ответы:
6×10 23
6×10 21
8×10 21
8×10 23
8×10 21
Объяснение:
Три два умножаются на 8, а степени десяти можно сложить, чтобы получить 10 21 .
Сообщить об ошибке
Если 3 x = 27, то 2 2x = ?
Возможные ответы:
3
8
9
32
64
Правильный ответ:
64
Объяснение:
- Найдите x в 3 x = 27. x = 3, потому что 3 * 3 * 3 = 27.
- Поскольку x = 3, можно заменить x на 3 в 2 2x
- Теперь выражение равно 2 2*3
- Это выражение можно интерпретировать как 2 2 * 2 2 * 2 2 . Поскольку 2 2 = 4, выражение можно упростить до 4 * 4 * 4 = 64,9.0124
- Вы также можете умножить степени , чтобы упростить выражение. Когда вы умножаете степени , вы получаете 2 6 или 2 * 2 * 2 * 2 * 2 * 2
- 2 6 = 64.
Отчет о ошибке
Найдите значение x такова, что:
8 X-3 = 16 4-X
Возможные ответы:
19/4
7/2
4 40005
19/4
7/2
4
11/3
25/7
Правильный ответ:
25/7
Объяснение:
Чтобы решить это уравнение, нам сначала нужно найти общее основание для показателей. Мы знаем, что 2
Мы знаем, что 2
8 x-3 = (2 3 ) x-3
Нам нужно помнить наше свойство показателей, которое говорит, что (a б ) с = а бк .
Таким образом (2 3 ) x-3 = 2 3(x-3) = 2 3x — 9 .
То же самое можно сделать с 16 4-x .
16 4-x = (2 4 ) 4-x = 2 4 (4-x) = 2 16-4x .
Итак, теперь наше уравнение принимает вид
2 3x — 9 = 2 16-4x
Чтобы решить это уравнение, степени должны быть равны.
3x — 9 = 16 — 4x
Добавьте 4x с обеих сторон.
7x — 9 = 16
Добавьте 9 с обеих сторон.
7x = 25
Разделить на 7.
x = 25/7.
Сообщить об ошибке
Что из следующего равно 4 10 + 4 10 + 4 10 + 4 10 + 4 11 ?
Возможные ответы:
2 60
2 15
2 40
2 50
2 23
Правильный ответ:
2 23
5
5 Объяснение:
Мы можем начать с перезаписи 4 1 1 как 4 * 4 10 . Это позволит собрать однотипные термы 4 10 в один терм.
4 10 + 4 10 + 4 10 + 4 10 + 4 11
= 4 10
= 8 * 4 10
, потому что выбор ответов написан с базовой базовой 2 2
, потому что выбор ответов на базовый , нам нужно переписать 8 и 4 с основанием двойки. Помните, что 8 = 2 3 и 4 = 2 2 .
Помните, что 8 = 2 3 и 4 = 2 2 .
8 * 4 10
= (2 3 )(2 2 ) 10
Нам также нужно использовать свойство показателей, что (4 b
015) с = а до н.э. . Мы можем переписать (2 2 ) 10 как 2 2×10 = 2 20 .
(2 3 ) (2 2 ) 10
= (2 3 ) (2 20 )
Наконец, мы должны использовать собственность, что B * A с = а б+с .
(2 3 )(2 20 ) = 2 23
Ответ: 2 23 .
Сообщить об ошибке
Если 3 + 3 n +3 = 81, чему равно 3 n +2 ?
Возможные ответы:
81
26
3
18
Правильный ответ:
26
Объяснение:
3 + 3 n +3 = 81
В этом уравнении есть общий делитель 3, который можно вынести за скобки.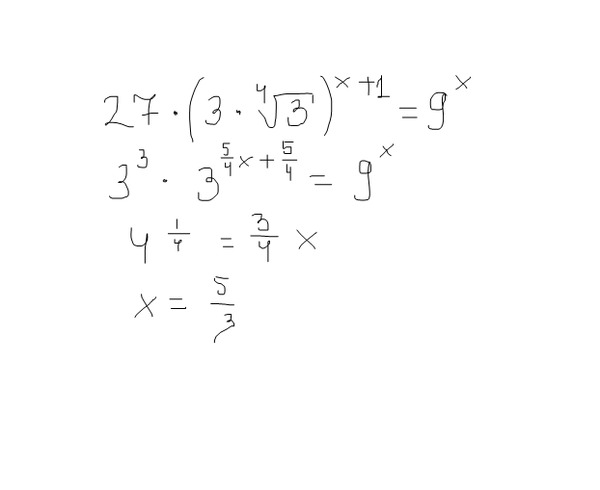
Таким образом, 3(1 + 3 N +2 ) = 81
ПРИМЕЧАНИЕ. Когда 3 учитывается из 3 N +3 , результат — 3 N +2 Потому что (3 N +3 . = 3 1 * 3 n +2 ). Помните, что показатели степени добавляются при умножении общих оснований. Также помните, что 3 = 3 1 .
3(1 + 3 n +2 ) = 81
(1 + 3 n +2 ) = 27
3 n +2 = 26
Примечание: не решайте для n отдельно. Но лучше постарайтесь решить то, о чем просит проблема, а именно 3 n+2 .
Сообщить об ошибке
Если f(x) = (2 – x) (x/3) и 4 n = f(10), то каково значение n?
Возможные ответы:
–2
5
0
2
–5
Правильный ответ:
5
Объяснение:
Сначала воспользуемся определением f(x), чтобы найти f(10).
f(x) = (2 – x) (x/3)
f(10) = (2 – 10) (10/3)
= (–8) (10/3) )
Чтобы вычислить приведенное выше выражение, мы можем использовать свойство показателей степени, которое утверждает, что a bc = (a b ) c = (a c ) b .
(–8) (10/3) = (–8) 10(1/3) = ((–8) (1/3) ) 10 .
(–8) (1/3) требует от нас извлечь кубический корень из –8. Кубический корень из –8 равен –2, потому что (–2) 3 = –8.
Вернемся к упрощению ((–8) (1/3) ) 10 .
((–8) (1/3) ) 10 = (–2) 10 = f(10)
Нас просят найти n такое, что 4 n = (–2) 10 . Давайте перепишем 4 n с основанием –2, потому что (–2) 2 = 4.
4 n = ((–2) 2 ) n = (–2) 2n = (–2) 10
Чтобы (–2) 10 2n 2n ) 10 , 2n должно равняться 10.
2n = 10
Разделите обе части на 2.
n = 5.
Ответ: 5.
Сообщите об ошибке
удовлетворяет следующему уравнению?2 n ·4 n ·8 n · 16 = 2 -N · 4 — N · 8 — N
. 0
–1/3
–2/3
Правильный ответ:
–1/3
Объяснение:
Чтобы решить это уравнение, нам понадобится общее основание. Поскольку 2, 4, 8 и 16 являются степенями числа 2, мы можем переписать обе части уравнения, взяв за основу 2. С 2 2 = 4, 2 3 = 8 и 2 4 = 16, мы можем переписать исходное уравнение следующим образом:
2 N * 4 N * 8 N * 16 = 2 – n * 4 – n * 8 – n
2 n (2 2 ) № (2 3 ) № (2 4 ) = 2 – n (2 2 ) – n (2 3 ) – n
Теперь воспользуемся свойством показателей, которое гласит, что ( a b ) c = a bc .
2 n (2 2 n )(2 3 n ) (2 4 ) = 2 — N (2 — 2 N ) (2 — 3 ) (2 — 3 ). теперь записывается как степень числа 2. Затем мы можем применить свойство экспонент, которое гласит, что a b a c = a b + c .
2 ( n +2 n +3 n +4) = 2 (– n + –2 n + –3 n )
Теперь мы можем приравнять показатели степени и найти n .
N + 2 N + 3 N + 4 = — N + –2 N + –3 N
Давайте комбинируем N ‘S с обеих сторон.
6 n + 4 = –6 n
Добавьте 6 n с обеих сторон.
12 п + 4 = 0
Вычесть 4 с обеих сторон.
12 n = –4
Разделите обе части на 12.
n = –4/12 = –1/3
Ответ: –1/3.
Сообщить об ошибке
Если 125 2 x –4 = 625 7– x , то каков наибольший простой делитель x ?
Возможные ответы:
7
5
3
11
2
Правильный ответ:
2
Объяснение:
Сначала нам нужно решить 125 2 x –4 = 625 7–x . При решении уравнений с показателями мы обычно хотим получить общее основание. Обратите внимание, что числа 125 и 625 заканчиваются на пять. Это означает, что они делятся на 5, и они оба могут быть степенями 5. Давайте проверим, написав первые несколько степеней 5. = 125
= 125
5 4 = 625
Теперь мы можем видеть, что 125 и 625 являются степенью числа 5, поэтому давайте заменим 125 на 5 3 и 625 на 5 4 .
(5 3 ) 2 x –4 = (5 4 ) 7– x
4 Далее, мы должны применить правило степени ) с = а до н.э. .
5 3(2 x –4) = 5 4(7– x )
Теперь у нас есть общее основание, выраженное одним показателем с каждой стороны. Мы должны установить показатели степени равными друг другу, чтобы найти x .
3(2 x – 4) = 4(7 – x )
Распределите 3 слева и 4 справа.
6 x – 12 = 28 – 4 x
Добавьте 4 x с обеих сторон.
10 x – 12 = 28
Добавьте 12 с обеих сторон.
10 x = 40
Разделить на 10 с обеих сторон.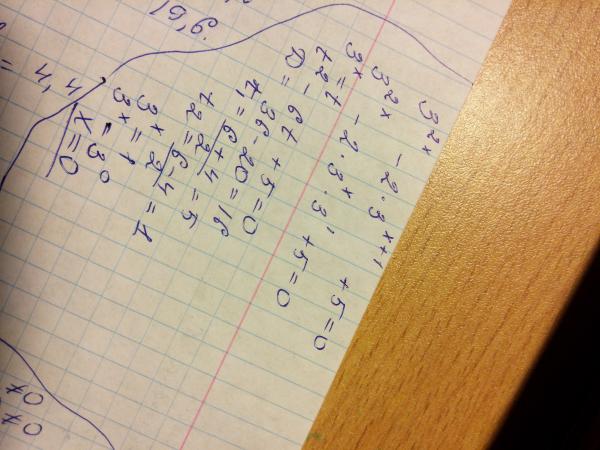
x = 4
Однако вопрос требует от нас указать наибольший простой множитель x . Единственными делителями 4 являются 1, 2 и 4. И из них единственный простой делитель равен 2.
Ответ равен 2.
Сообщить об ошибке
( x 3 ) 2 * x – 2 =
Возможные ответы:
x 6
x 2
x – 4
x 4
x
Correct answer:
х 4
Объяснение:
Когда показатель степени возводится в степень, мы умножаем. Но когда перемножаются два показателя степени с одинаковым основанием, мы их складываем. Итак ( х 3 ) 2 = х 3*2 = х 6 .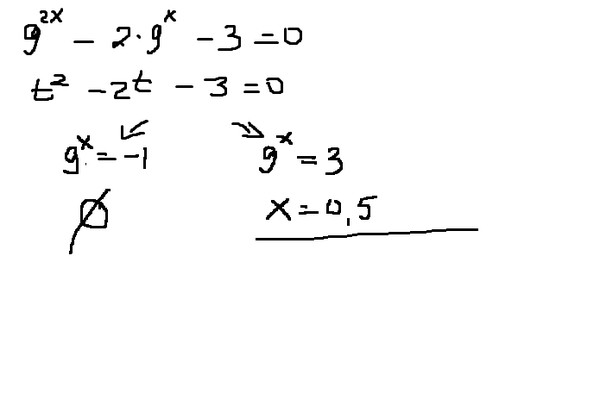

 величину в математике
величину в математике Кальманом лат. буква
Кальманом лат. буква М. Голубовский, «Та самая дрозофила…» // «Химия и жизнь», № 4, 1966 г. ◆ По той же причине раввин из МТИ Плаут пользуется распространённым среди религиозных англоязычных евреев кодовым обозначением Xmas. По-английски рождество — Christmas, но, избегая называть Христа по имени, раввин подставляет букву Икс. Михаэль Дорфман, «Еврейское Рождество» (2004) // «Интернет-альманах “Лебедь”», 04.01.2004 г.
М. Голубовский, «Та самая дрозофила…» // «Химия и жизнь», № 4, 1966 г. ◆ По той же причине раввин из МТИ Плаут пользуется распространённым среди религиозных англоязычных евреев кодовым обозначением Xmas. По-английски рождество — Christmas, но, избегая называть Христа по имени, раввин подставляет букву Икс. Михаэль Дорфман, «Еврейское Рождество» (2004) // «Интернет-альманах “Лебедь”», 04.01.2004 г.  Стали разбираться. Выяснилось, что, наседая на тригонометрию, Пиголица имел весьма неясное представление об основах алгебры и геометрии, тангенсы цеплялись за логарифмы, логарифмы за степени, и вообще было непонятно, почему доброе русское «х» именуется иксом. И. Л. Солоневич, «Россия в концлагере», 1935 г. ◆ Стеша не кончила восьмой класс — на вечорках поплясывать стала, парни провожали, сидеть за партой, решать, чему равно «а» плюс «б» в квадрате, казалось стыдновато, да и ни к чему, в её жизни «иксы» да «игреки» не пригодятся. В. Ф. Тендряков, «Не ко двору», 1954 г. ◆ .. я предложил двум моим коллегам-аспирантам решить знаменитую задачу, которую чеховский гимназист-репетитор задал купеческому сынку Пете. В ней условие начиналось традиционной фразой: «Купец купил…» — и её следовало решать без икса — ведь папаша-купец посрамил гимназистика, решив её на счётах. Аспиранты это никак не могли сделать. И. С. Шкловский, «Из истории развития радиоастрономии в СССР», 1982 г.
Стали разбираться. Выяснилось, что, наседая на тригонометрию, Пиголица имел весьма неясное представление об основах алгебры и геометрии, тангенсы цеплялись за логарифмы, логарифмы за степени, и вообще было непонятно, почему доброе русское «х» именуется иксом. И. Л. Солоневич, «Россия в концлагере», 1935 г. ◆ Стеша не кончила восьмой класс — на вечорках поплясывать стала, парни провожали, сидеть за партой, решать, чему равно «а» плюс «б» в квадрате, казалось стыдновато, да и ни к чему, в её жизни «иксы» да «игреки» не пригодятся. В. Ф. Тендряков, «Не ко двору», 1954 г. ◆ .. я предложил двум моим коллегам-аспирантам решить знаменитую задачу, которую чеховский гимназист-репетитор задал купеческому сынку Пете. В ней условие начиналось традиционной фразой: «Купец купил…» — и её следовало решать без икса — ведь папаша-купец посрамил гимназистика, решив её на счётах. Аспиранты это никак не могли сделать. И. С. Шкловский, «Из истории развития радиоастрономии в СССР», 1982 г. ◆ В сущности, расследование любого преступления — это не что иное как логическое решение определённой задачи. Математика в чистом виде. Только вместо иксов и игреков — живые люди, и ведут они себя куда более непредсказуемо. Елизавета Козырева, «Дамская охота», 2001 г.
◆ В сущности, расследование любого преступления — это не что иное как логическое решение определённой задачи. Математика в чистом виде. Только вместо иксов и игреков — живые люди, и ведут они себя куда более непредсказуемо. Елизавета Козырева, «Дамская охота», 2001 г.  Л. Н. Толстой, «Письма», 1894 г. ◆ Опять разговоры о физическом труде, о прогрессе, о таинственном иксе, ожидающем человечество в отдалённом будущем. Доктор не любил нашего хозяйства, потому что оно мешало нам спорить, и говорил, что пахать, косить, пасти телят недостойно свободного человека и что все эти грубые виды борьбы за существование люди со временем возложат на животных и на машины, а сами будут заниматься исключительно научными исследованиями. А. П. Чехов, «Моя жизнь», 1896 г. ◆ Человек — потенциальный икс; он сам не знает, сколько чертей в нём сидит, и только история выводит этих метафизиков, как микробы, на свежую воду. В. О. Ключевский, «Записи 1900‑х годов», 1900–1909 гг. ◆ Субъекту здесь приписывается лишь призрачное существование .. (и только на самом заднем плане помещается некоторый таинственный икс, иррациональный внешний толчок). С. Н. Булгаков, «Философия хозяйства (мир как хозяйство)», 1912 г. ◆ Тем более что в тридцать седьмом предстояло уничтожить людей, Горькому близко знакомых: Бабеля, например, или Пильняка.
Л. Н. Толстой, «Письма», 1894 г. ◆ Опять разговоры о физическом труде, о прогрессе, о таинственном иксе, ожидающем человечество в отдалённом будущем. Доктор не любил нашего хозяйства, потому что оно мешало нам спорить, и говорил, что пахать, косить, пасти телят недостойно свободного человека и что все эти грубые виды борьбы за существование люди со временем возложат на животных и на машины, а сами будут заниматься исключительно научными исследованиями. А. П. Чехов, «Моя жизнь», 1896 г. ◆ Человек — потенциальный икс; он сам не знает, сколько чертей в нём сидит, и только история выводит этих метафизиков, как микробы, на свежую воду. В. О. Ключевский, «Записи 1900‑х годов», 1900–1909 гг. ◆ Субъекту здесь приписывается лишь призрачное существование .. (и только на самом заднем плане помещается некоторый таинственный икс, иррациональный внешний толчок). С. Н. Булгаков, «Философия хозяйства (мир как хозяйство)», 1912 г. ◆ Тем более что в тридцать седьмом предстояло уничтожить людей, Горькому близко знакомых: Бабеля, например, или Пильняка. 〈…〉 Одно дело какие-то там иксы и игреки, мелькающие на газетных страницах (продавшиеся иностранным разведкам), другое — Пильняк или Бабель, которых он знает насквозь. Л. К. Чуковская, «Прочерк», 1980–1994 гг. ◆ Несмотря ни на какие трудности, завод сохранял и продолжает сохранять мобилизационные мощности для выполнения (в случае, если в стране наступит тревожный «час икс») мобилизационного задания государства. Невыполнение мобзадания, с одной стороны, подсудное дело. А с другой стороны, экономической, содержание нужных для его выполнения мощностей крайне невыгодно для завода. Людмила Пирогова, «В курсе дела» (2003) // «Встреча», (Дубна), 05.03.2003 г.
〈…〉 Одно дело какие-то там иксы и игреки, мелькающие на газетных страницах (продавшиеся иностранным разведкам), другое — Пильняк или Бабель, которых он знает насквозь. Л. К. Чуковская, «Прочерк», 1980–1994 гг. ◆ Несмотря ни на какие трудности, завод сохранял и продолжает сохранять мобилизационные мощности для выполнения (в случае, если в стране наступит тревожный «час икс») мобилизационного задания государства. Невыполнение мобзадания, с одной стороны, подсудное дело. А с другой стороны, экономической, содержание нужных для его выполнения мощностей крайне невыгодно для завода. Людмила Пирогова, «В курсе дела» (2003) // «Встреча», (Дубна), 05.03.2003 г. 