Решение уравнений
РКР №1 6-7 класс
Вариант 1
1.Упростить выражение: -2x+3-4x+11
1) 14-6x 2)2x+14 3)8-6x 4) другой ответ
2. Упростить выражение: 6-(8+3x)
1)14+3x 2)-2-3x 3) 3x-2 4)5x+4
3. Упростить выражение: -10-2(2x-7)
1) 4-4x 2)-24-4x 3)28x 4)2x-24
4. Решить уравнение: 3(x+3)- x=8
1) 1 2)-1 3)- 4)другой ответ
5. Решить уравнение: 3(x-1)-2(2-x)=6
1)7 2)4 3) 2 4)
6. Решить уравнение: 2(3x-0,5)=6-(x+8)
1) — 2)0,5 3)4,2 4) другой ответ
Вариант 2
1.Упростить выражение:0,2x-4- x+7
1)11-0,4x 2) 3 3)2x-3 4)другой ответ
2. Упростить выражение: 4x-(2-6x)
1)10x-2 2)-2x-2 3)-2x+2 4) 2x-2
3. Упростить выражение: -2(4+3x)+8x
1) 22x 2) -14x-8 3) 2x-8 4) -6x-2
4. Решить уравнение: x+6(3- x)=17
1)-8 2) 3)-2 4)2
5. Решить уравнение 2(x-3)-3(4-x)=5
1) -23 2)4 3) -11 4)-
6.
Решить уравнение: 5-2(x-1)=0,5(8x-4)
1) 3,6 2)2,1 3) 1,5 4) другой ответ
Вариант 3
1.Упростить выражение: -0,4y+3y-4,2+y
1)-3,4y 2)-0,6y 3)3,6y-4,2 4)другой ответ
2. Упростить выражение: 9x-(12x-2)
1) 2-3x 2)-12x+7 3)21x-2 4)другой ответ
3. Упростить выражение: 28x-5(6x-0,2)
1) 11x-1 2)1-2x 3)-58x 4)другой ответ
4. Решить уравнение: x+8(3- x)=1
1) 2)-5 3)5 4)-
5. Решить уравнение 5(x+2)-4(3-x)=7
1)19 2) 3 3) 3 4)1
6. Решить уравнение: 0,6(x+7)=0,5(x-3)+6,8
1)11 2)0,18 3)1,8 4)3,21
Вариант 4
1.Упростить выражение: 3y- y+0,6-1,2y
1) 1,4y+0,6 2)4,6y+0,6 3)5,2y 4)другой ответ
2. Упростить выражение: -12x-(2-8x)
1)-20x+2 2)30x 3)-4x-2 4) другой ответ
3. Упростить выражение: -5(2x-1)+15
1)20-10x 2)10x 3)20x 4)7-10x
4. Решить уравнение: x+3(2- x)=5
1)1 2)-1 3)-4 4)4
5. Решить уравнение 7(3+x)-2(x-5)=8
1) 18 2)4,6 3)-18 4)-4,6
6.
Решить уравнение: 0,4(x-9)-0,3(x+2)=0,7
1) 49 2)4,9 3) 0,3 4)0,8
Ответы:
РКР№1 | №1 | №2 | №3 | №4 | №5 | №6 |
В1 | 1 | 2 | 1 | 2 | 3 | 1 |
В2 | 2 | 1 | 3 | 2 | 2 | 3 |
В3 | 3 | 1 | 2 | 3 | 4 | 1 |
В4 | 1 | 3 | 1 | 1 | 4 | 1 |
РКР №2 6-7класс
Вариант 1
1.Вычислить: (2-5+7-1) :(-3) -21
1)22 2)-22 3)-20 4)20
2. Разложить на множители: ab+3ab
1)ab(1+3b) 2)a(b+3b) 3)3ab(a+b) 4) другой ответ
3. Разложить на множители: 2y+6y-4y
1)2y(1+3y-4y) 2)2(y+3y-2y) 3)2y(y+3y-2) 4) другой ответ
4.
Разложить на множители: 25x-9y
1) 5xy(5 x-9y) 2)(25x-9y)(25x+9y) 3)(5x-3y)(5x+3y) 4) другой ответ
5. Сократить дробь:
1) 2)3(x-y) 3)(x-y) 4) другой ответ
6.Решить уравнение: -3x+4x=0
1) 0; 2) 0;-1 3)0,75 4) другой ответ
Вариант 2
1.Вычислить(5-3+1-6):3+7
1) 8 2)-6 3)6 4)7
2. Разложить на множители: 7x y-xy
1) 7xy(x-y) 2) xy(7x-y) 3) x y(7y-x) 4) другой ответ
3. Разложить на множители: 12c+4c
1)12c(1-4c) 2)c(12c+4c) 3)4c(3c+1) 4) другой ответ
4. Разложить на множители: 144a-25b
1) ab(144a-25b) 2)(12a-5b)(12a+5b) 3)12ab(12a-25b) 4) другойответ
5. Сократить дробь:
1) 2) 3) 4) другой ответ
6.Решить уравнение: -3 x +7x=0
1) 0;2 2)0;7 3)3,5;7 4) другой ответ
Вариант 3
1.Вычислить: (3-5+1) (-1) -12
1)12 2)-11 3)13 4)-12
2. Разложить на множители: 2cx-4cx
1)2cx(1-2x) 2)4cx(2-x) 3)2x(c-2) 4) другой ответ
3.
Разложить на множители: 4b-3b
1)4b(b-3b) 2)4b(1-3b) 3)b(4-3b) 4) другой ответ
4. Разложить на множители: 1-49y
1)(1-7y)(1+7y) 2)49y(1-y) 3)(1-49y)(1+49y) 4) другой ответ
5. Сократить дробь:
1) 2)8x-1 3) 4) другой ответ
6.Решить уравнение: 1 x-5x=0
1) 0;4 2)3;5 3)0;5 4) другой ответ
Вариант 4
1.Вычислить: (7-5+3-18):13-4
1) 9 2)-4 3)4 4)-6
2. Разложить на множители:ab+5a b
1)a b (a+5) 2)b (a+5b) 3)ab(b+5a) 4) другойответ
3. Разложить на множители: 2c-4c+2c
1) 2c(1-4c+2c) 2) 2c(c-2c+1) 3)2(c-2c+1) 4) другой ответ
4. Разложить на множители: 9a-16b
1)(9a-16b)(9a+16b) 2)(3a-4b)(3a+4b) 3)9a (1-16b ) 4) другойответ
5. Сократить дробь:
1) 2) 3)1+10x 4) другой ответ
6.Решить уравнение: 121-100x=0
1) 10;-10 2)0;11 3)1,1;-1,1 4) другой ответ
Ответы:
РКР№2 | №1 | №2 | №3 | №4 | №5 | №6 |
В1 | 3 | 1 | 2 | 3 | 1 | 2 |
В2 | 1 | 2 | 3 | 2 | 3 | 1 |
В3 | 2 | 1 | 3 | 1 | 3 | 1 |
В4 | 1 | 3 | 2 | 2 | 1 | 3 |
Адрес публикации: https://www.
3}=3b $$
1) Упростите выражение а)10х(2 степень)у * (-3ху(2 степень))(3 степень),б)(х+4у)(2 степень)-(4у-х)(х+4у)
2) Разложите на множители а) ав(3 степень)-9а(3 степень)в,б)-25а+10а(2 степень)-а(2 степень)
3) Решите уравнение 5х-4 разделить на 4 — х+2 разделить на 3 равняется 2
4) Задача: Над выполнением заказа ученик работал 8 часов, а мастер выполнил такой же заказ за 6 часов. Сколько деталей составляет заказ, если мастер и ученик за 1 час вместе изготовляют 7 деталей.
Решение: 1) а) 10х2у * (-3ху2)3 = 10х2у *(-27х3у6) = -270х5у7
б) (х+4у)2 — (4у-х)(х+4у) = х2+8ху+16у2 — 16у2 +х2 = 2х2 +8ху
2) а) ав3 — 9а3в = ав (в2 — 9а2) = ав (в-3а)(в+3а)
б) -25а +10а2 — а2 = -25а +9а2 = а (9а — 25)
3)
(5х-4)/4 — (x+2)/3 = 2 I *12
3(5x-4) — 4(x+2) = 24
15x — 12 — 4x — 8 = 24
11x = 44
x=4
$$ 1) \\ a) \\ 10x^2y(-3xy^2)^3 = 10x^2y(-27x^3y^6) =\\= -270x^5y^7\ b) (x+4y)^2 — (4y-x)(x+4y) = \\= (x+4y)((x+4y) — (4y-x)) =\\= (x+4y)*2x = 2x^2 + 8xy $$
2) $$ a) \\ ab^3 — 9a^3b = ab(b^2 — 9a^2) \\ b) -25a+10a^2-a^2 = -25a+9a^2 = \\ a(9a — 25) $$
3) $$ (5x-4)/4 — (x +2)/3 = 2 \\ (5x-4)/4 — (x +2)/3 = 2 | * 12 \\ (5x-4)*3 — (x +2)*4 = 24 \\ 15x — 12 — 4x — 8 = 24 \\ 11x = 44 \\ x = 4 $$
4) 2*x = 6*m + 8*u
x — количество деталей в заказе.
2=3.14*4=12.56
2. Выполните действие:
4 в минус второй степени / (-4) в минус третьей степени + 0,4 в минус первой — (-3) в нулевой степени=(1/16)/(-1/64)+(4/10) в минус первой — (-3) в нулевой степени=(1/16)/(-1/64)+(10/4) — 1=(1/16)*(-64/1)+(10/4) — 1=-4+(10/4) — 1=-5+2,5=-2,5
3. Упростите выражение:
(А в минус третьей) в минус второй*(А в минус седьмой) в минус первой/А в минус третьей и найдите его значение, при А=0,2.
Воспользуемся свойствами степени:
(А в минус третьей) в минус второй*(А в минус седьмой) в минус первой/А в минус третьей =(А в (минус три* минус два)*(А в (минус семь* минус один)/А в минус третьей =(А в шестой)*(А в седьмой)/А в минус третьей =А в (шесть+семь-минус три) =А в шестнадцатой
(0,2) в шестнадцатой=(1/5) в шестнадцатой=1/152587890625
4. Найдите значение n, удовлетворяющее условию: 7 в минус тринадцатой *7 в восемнадцатой/7 в степени n=1/7(одна седьмая)
7 в (минус тринадцать+ восемнадцать- n)=7 в минус первой
7 в (пять- n)=7 в минус первой
5- n=-1
n=5+1=6
n=6
Упростите выражение: 14 в степени n+3 умножить на 28 в степени n-1 и разделить на 8 в степени n умножить на 7 в степени2n+1
Решение:
приведем степени к одинаковым основаниям (7 и 2)
числитель: 14^(n+3) * 28^(n-1) = (7*2)^(n+3) * (7*4)^(n-1) = 7^(n+3) * 2^(n+3) * 7^(n-1) * (2^2)^(n-1) =
7^(n+3+n-1) * 2^(n+3+2n-2) = 7^(2n+2) * 2^(3n+1)
знаменатель: 8^n * 7^(2n+1) = (2^3)^n * 7^(2n+1) = 2^(3n) * 7^(2n+1)
при делении степеней с одинаковым основанием показатели степеней вычитаются
получим: 7^(2n+2-2n-1) * 2^(3n+1-3n) = 7^(1) * 2^(1) = 14
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
..
| |||||||||||||||||
02.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
В какой системе увеличение давления и понижение температуры смещает хим.
равновесие в сторону продуктов реакции? 1)2SO2 (г)+O2(г)→2SO3 (г)+Q; 2) N2(г)+O2 (г)→2NO (г)-Q; 3) CO2 ( г)+2C (тв.)→2CO
Зная что самолет в течении 4 ч20 мин летел со средней скоростью 540 км\ч, ответь на следующий вопросы.1) Какой должна быть средняя скорость самолета,…
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение
Как решить задачу? Из 2 кг муки выходит 3 кг печёного хлеба. Сколько хлеба выйдет из 1 ц муки? Из 1 т муки?
Решение задачи: В воду объемом 1 л, температура которой 20 градусов, бросают кусок железа массой 100 г, нагретый до 500 градусов С. При этом температура воды повышается до 24 градусов и некоторое коли
Пользуйтесь нашим приложением
Решить уравнение
Короткое обучающее видео
Посмотрите Обучающее Видео, объясняющее как вводить условие задачи.
Как ввести условие задачи
Нажмите на кнопку «Ввести свою задачу». После этого вводите условие либо с вашей клавиатуры, либо с клавиатуры на экране. Для добавления специальных математических конструкций, таких как интеграл или дробь, пользуйтесь клавиатурой на странице. По условию можно перемещаться с помошью кнопок на вашей клавиатуре: влево, вправо, вверх, вниз или с помощью мыши кликая в нужную область. Если вы хотите скопировать условие или чсть условия, выделите ее(зажимаете кнопку shift и стрелочками влево или вправо выделяете нужную область) и нажмите ctrl+c. Для вставки в необходимое место нажите ctrl+v. При копировании происходит автоматическая трансформация в математический формат латех, поэтому ваше условие вы можете скопировать как в свой текстовый редактор, так и в другое окно ввода на сайте.
За один раз можно решить только одну задачу.Как ввести систему уравнений
Если вы ввели несколько условий, они буду рассматриваться как система, например система уравнений или неравенств.
Как упростить выражение
Просто введите ваше выражение как условие и нажмите на кнопку «Решить». Не нужно ставить знак «=» в конце вашего выражения или выполнять какие-либо еще другие действия
Переменные и параметры
По умолчанию при решении переменными являются x,y,z, a параметрами:a,b,c. Если у вас в задаче указаны другие переменные или параметры, нажмите на кнопку «Настройки», введите ваши переменные и параметры через запятую в соответствующие поля и нажмите на кнопку «ОК».
Как вводить геометрию
Старайтесь вводить геометрию точь в точь как в учебнике. Орфография очень важна. Используйте перенос строки на клавиатуре.
Как заполнять серые квадратики
Чтобы заполнить серый квадратик переведите в него курсор. Сделать это можно либо нажимая стрелки <-,-> на клавиатуре, либо просто кликните мышкой в него. Далее введите туда ваши данные и нажмите на пробел либо на стрелку ->.
Как вводить начальные условия для дифференциальных уравнений
Начальные условия вводите как обычные условия. Порядок не важен.
Например:
Условие 1: y’=y+x
Условие 2: y(0)=1Сдвиг курсора на один символ влево: ←
Чтобы сдвинуть курсор влево от текущей позиции, нажмите на кнопку ←.
Сдвиг курсора на один символ вправо: →
Чтобы сдвинуть курсор вправо от текущей позиции, нажмите на кнопку →.
Удаление одного символа назад: ←
Чтобы удалить символ, поставьте курсор после символа и нажмите на кнопку ←. Передвинуть курсор можно либо с помошью стрелок влево и вправо на клавиатуре либо кликнуть мышью в область после символа.
Удаление одного символа вперед: del
Чтобы удалить символ, поставьте курсор перед символом и нажмите на кнопку del.
Передвинуть курсор можно либо с помошью стрелок влево
и вправо на клавиатуре либо кликнуть мышью в область перед символом.Цифра: 0
Чтобы ввести цифру 0, нажмите на кнопку 0.
Цифра: 1
Чтобы ввести цифру 1, нажмите на кнопку 1.
Цифра: 2
Чтобы ввести цифру 2, нажмите на кнопку 2.
Цифра: 3
Чтобы ввести цифру 3, нажмите на кнопку 3.
Цифра: 4
Чтобы ввести цифру 4, нажмите на кнопку 4.
Цифра: 5
Чтобы ввести цифру 5, нажмите на кнопку 5.
Цифра: 6
Чтобы ввести цифру 6, нажмите на кнопку 6.
Цифра: 7
Чтобы ввести цифру 7, нажмите на кнопку 7.
Цифра: 8
Чтобы ввести цифру 8, нажмите на кнопку 8.
Цифра: 9
Чтобы ввести цифру 9, нажмите на кнопку 9.
Точка для ввода нецелых чисел
Чтобы ввести точку для ввода нецелого числа(например 10.2), нажмите на кнопку .
Ввести переменную: x
Чтобы ввести переменную x, нажмите на кнопку x. Стандартными переменными являются: x,y,z. Для ввода нестандартной переменной, нажмите на соответствующий символ на вашей клавиатуре и добавьте данную переменную в настройках. См. подсказку «Переменные и параметры»
Ввести переменную: y
Чтобы ввести переменную y, нажмите на кнопку y.
Стандартными переменными являются: x,y,z.
Для ввода нестандартной переменной, нажмите на соответствующий символ на вашей
клавиатуре и добавьте данную переменную в настройках. См. подсказку «Переменные и параметры»Ввести переменную: z
Чтобы ввести переменную z, нажмите на кнопку z. Стандартными переменными являются: x,y,z. Для ввода нестандартной переменной, нажмите на соответствующий символ на вашей клавиатуре и добавьте данную переменную в настройках. См. подсказку «Переменные и параметры»
Ввести корень
Чтобы ввести корень, установите курсор в место, куда необходимо ввести корень (сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на клавиатуре).
Далее нажмите на кнопку на клавиатуре. Появится корень. Курсор
автоматически окажется под корнем. Далее введите подкоренное выражение и после этого
нажмите на стрелку вправо.Ввести переменную в степени
Чтобы ввести переменную в степени, установите курсор в место, куда необходимо ввести (сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на клавиатуре). Далее нажмите на кнопку на клавиатуре. Появится x в степени. Курсор автоматически окажется в степени. Далее введите степень и после этого нажмите на стрелку вправо. Если нужно изменить перемменную, кликнете на x мышью либо передвиньтесь на него используя стрелки влево, вправо на клавиатуре. Далее удалите x с помошью красных клавиш на клавиатуре(красная стрелка влево или del) и введите нужную вам переменную.
Чтобы продолжить ввод формулы справа, кликнете в самую правую часть мышью либо используя
стрелку вправо переведите курсор максимально в правую часть.Ввести выражение в степень
Чтобы ввести выражение в степень, установите курсор в место, куда необходимо ввести (сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на клавиатуре). Далее нажмите на кнопку на клавиатуре. Появится () в степени. Курсор автоматически окажется в степени. Далее введите степень и после этого перейдите внутрь скобок(сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на клавиатуре). Далее введите нужное выражение в скобках. Чтобы продолжить ввод формулы справа, кликнете в самую правую часть мышью либо используя стрелку вправо переведите курсор максимально в правую часть.
Корень n-ой степени
Чтобы ввести корень n-ой степени, установите курсор в место, куда необходимо ввести корень (сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на клавиатуре). Далее нажмите на кнопку на клавиатуре. Появится корень. Курсор автоматически окажется под корнем. Далее введите подкоренное выражение и после этого нажмите на квадратик степени мышью, либо перейдите туда использую стрелки влево, вправо на клавиатуре. Введите степень.
Дробь
Чтобы ввести дробь, установите курсор в место, куда необходимо ввести дробь (сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на клавиатуре).
Далее нажмите на кнопку на клавиатуре. Появится дробь. Курсор автоматически
окажется в числителе. Далее введите числитель и после этого нажмите на квадратик
знаменателя мышью, либо перейдите туда использую стрелки влево, вправо на клавиатуре.
Введите знаменатель.+
Чтобы ввести +, нажмите на кнопку +
—
Чтобы ввести -, нажмите на кнопку —
Знак умножения
Чтобы ввести знак умножения, нажмите на кнопку $\cdot$·
Знак деления
Чтобы ввести знак деления, нажмите на кнопку :
Модуль
Чтобы ввести модуль, нажмите на кнопку, курсор автоматически окажется внутри моддуля, введите выражение, далее нажмите на стрелку вправо.
Круглые скобки
Чтобы ввести круглые скобки, нажмите на кнопку, курсор автоматически окажется внутри скобок, введите выражение, далее нажмите на стрелку вправо.
cos
Чтобы ввести cos, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
sin
Чтобы ввести sin, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
tan
Чтобы ввести tan, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
cot
Чтобы ввести cot, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
ln
Чтобы ввести ln, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
lg
Чтобы ввести lg, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
log
Чтобы ввести log, нажмите на кнопку, введите выражение под логарифмом, далее нажмите на квадратик для ввода основания(сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на клавиатуре), введите основание и перейдите стрелками в нужную область для продолжения ввода.
a
Параметр a. Стандартными параметрами являются: a,b,c.
Для ввода нестандартного параметра,
добавьте данный параметр в настройках. См. подсказку «Переменные и параметры»b
Параметр b. Стандартными параметрами являются: a,b,c. Для ввода нестандартного параметра, добавьте данный параметр в настройках. См. подсказку «Переменные и параметры»
c
Параметр c. Стандартными параметрами являются: a,b,c. Для ввода нестандартного параметра, добавьте данный параметр в настройках. См. подсказку «Переменные и параметры»
arccos
Чтобы ввести arccos, нажмите на кнопку, введите выражение, нажмите на стрелку вправо.
arcsin
Чтобы ввести arcsin, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
arctan
Чтобы ввести arctan, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
arccot
Чтобы ввести arccot, нажмите на кнопку, введите выражение, далее нажмите на стрелку вправо.
‘
Чтобы ввести значок производной, нажмите на кнопку.
∫
Чтобы ввести неопределенный интеграл, нажмите на кнопку. Далее введите подинтегральное выражение, после этого нажмите на кнопку d и введите переменную, по которой нужно провести интегрирование.
Серые квадратики оставьте незаполненными. Чтобы ввести
определенный интеграл, нажмите на кнопку. Далее введите подинтегральное выражение, после
этого нажмите на кнопку d(на своей клавиатуре или клавиатуре сайта) и введите
переменную, по которой нужно провести интегрирование. После этого кликните на нижний
серый квадратик и введите нижний пределе, кликните на верхний серый квадратик и введите
верхний предел.(перейти на серые квадраты можно либо кликнув на них, либо используя
кнопки влево, вправо)d
Знак дифференциала. Обозначение переменной, по которой нужно произвести интегрирование.
lim
Чтобы ввести предел нажмите на кнопку lim на клавиатуре.
Курсор автоматически установится
в место, где нужно ввести функцию. Далее нажмите на серый квадратик ниже значка lim
мышью либо перейдите туда используя клавишы влево, вправо. Введите условие предела.
Далее нажмите на кнопку решить(писать знак равенства после предела не нужно).->(стремится)
Чтобы ввести значок ->(стремится), нажмите на кнопку.
Знак бесконечности
Чтобы ввести значок бесконечности, нажмите на соответствующую кнопку.
Знак суммы(ряда)
Чтобы ввести ряд, нажмите на кнопку суммы на клавиатуре. Курсор автоматически установится в место, где нужно ввести ряд. Далее нажмите на серый квадратик ниже значка суммы мышью либо перейдите туда используя клавишы влево, вправо.
Введите нижнее условие. Далее
нажмите на серый квадратик выше значка суммы мышью либо перейдите туда используя клавишы
влево, вправо. Введите верхнее условие. Далее нажмите на кнопку Проверить
сходимость.Матрица
Чтобы ввести матрицу, нажмите на кнопку. Появится матрица 2 на 2. Каждая ячейка матрицы должна быть в фигурных скобках {}. Чтобы ввести данные в ячейку, кликните мышью внутрь фигурных скобок либо перейдите туда используя кнопки влево, вправо. Для того чтобы добавить ячейку, установите курсор вне фигурных скобок с помошью мыши либо кнопок влево, вправо и нажмите кнопку добавления элемента. Появятся фигурные скобки, введите туда значение элемента. Для добавления строки нажмите кнопку добавления строки.
Добавить элемент в матрицу
Для того чтобы добавить новый элемент(ячейку) в матрицу, установите курсор вне фигурных скобок с помошью мыши либо кнопок влево, вправо и нажмите кнопку добавления элемента.
Добавить строку в матрицу
Для того чтобы добавить новую строку в матрицу, нажмите кнопку добавления строки.
Факториал(!)
Чтобы ввести факториал, нажмите на кнопку !
n
Чтобы ввести переменную n, нажмите на кнопку n
Разложить в ряд Фурье
Чтобы разложить в ряд Фурье, необходимо ввести задачу в виде двух условий, например:
1. y(x) = 5x
2. (-3,3)
Разложить в ряд Тэйлора
Чтобы разложить в ряд Тэйлора, необходимо ввести задачу в виде двух условий, например:
1.
y(x) = sinx2. x = 0
Провести анализ функции
Полное исследование функций:
— Промежутки возрастания, убывания
— Экстремумы
— Промежутки выпуклости, вогнутости
Задайте функцию в виде одного условия, например:
1. y(x) = x+5
Например: 
Передвинуть курсор можно либо с помошью стрелок влево
и вправо на клавиатуре либо кликнуть мышью в область перед символом.
Стандартными переменными являются: x,y,z.
Для ввода нестандартной переменной, нажмите на соответствующий символ на вашей
клавиатуре и добавьте данную переменную в настройках. См. подсказку «Переменные и параметры»
Далее нажмите на кнопку на клавиатуре. Появится корень. Курсор
автоматически окажется под корнем. Далее введите подкоренное выражение и после этого
нажмите на стрелку вправо.
Чтобы продолжить ввод формулы справа, кликнете в самую правую часть мышью либо используя
стрелку вправо переведите курсор максимально в правую часть.
Далее нажмите на кнопку на клавиатуре. Появится дробь. Курсор автоматически
окажется в числителе. Далее введите числитель и после этого нажмите на квадратик
знаменателя мышью, либо перейдите туда использую стрелки влево, вправо на клавиатуре.
Введите знаменатель.
Для ввода нестандартного параметра,
добавьте данный параметр в настройках. См. подсказку «Переменные и параметры»
Серые квадратики оставьте незаполненными. Чтобы ввести
определенный интеграл, нажмите на кнопку. Далее введите подинтегральное выражение, после
этого нажмите на кнопку d(на своей клавиатуре или клавиатуре сайта) и введите
переменную, по которой нужно провести интегрирование. После этого кликните на нижний
серый квадратик и введите нижний пределе, кликните на верхний серый квадратик и введите
верхний предел.(перейти на серые квадраты можно либо кликнув на них, либо используя
кнопки влево, вправо)
Курсор автоматически установится
в место, где нужно ввести функцию. Далее нажмите на серый квадратик ниже значка lim
мышью либо перейдите туда используя клавишы влево, вправо. Введите условие предела.
Далее нажмите на кнопку решить(писать знак равенства после предела не нужно).
Введите нижнее условие. Далее
нажмите на серый квадратик выше значка суммы мышью либо перейдите туда используя клавишы
влево, вправо. Введите верхнее условие. Далее нажмите на кнопку Проверить
сходимость.
y(x) = sinx| 1 | Найти том | сфера (5) | | ||||||
| 2 | Найти площадь | круг (5) | | ||||||
| 3 | Найдите площадь поверхности | сфера (5) | | ||||||
| 4 | Найти площадь | круг (7) | | ||||||
| 5 | Найти площадь | круг (2) | | ||||||
| 6 | Найти площадь | круг (4) | | ||||||
| 7 | Найти площадь | круг (6) | | ||||||
| 8 | Найти том | сфера (4) | | ||||||
| 9 | Найти площадь | круг (3) | | ||||||
| 10 9(1/2) | |||||||||
| 11 | Найти простую факторизацию | 741 | |||||||
| 12 | Найти том | сфера (3) | | ||||||
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | |||||||
| 14 | Найти площадь | круг (10) | | ||||||
| 15 | Найти площадь | круг (8) | | ||||||
| 16 | Найдите площадь поверхности | сфера (6) | | ||||||
| 17 | Найти простую факторизацию | 1162 | |||||||
| 18 | Найти площадь | круг (1) | | ||||||
| 19 | Найдите окружность | круг (5) | | ||||||
| 20 | Найти том | сфера (2) | | ||||||
| 21 | Найти том | сфера (6) | | ||||||
| 22 | Найдите площадь поверхности | сфера (4) | | ||||||
| 23 | Найти том | сфера (7) | | ||||||
| 24 | Оценить | квадратный корень из -121 | |||||||
| 25 | Найти простую факторизацию | 513 | |||||||
| 26 | Оценка | квадратный корень из 3/16* квадратный корень из 3/9 | |||||||
| 27 | Найти том | коробка (2)(2)(2) | | ||||||
| 28 | Найдите окружность | круг (6) | | ||||||
| 29 | Найдите окружность | круг (3) | | ||||||
| 30 | Найдите площадь поверхности | сфера (2) | | ||||||
| 31 | Оценить | 2 1/2÷22000000 | |||||||
| 32 | Найдите Том | коробка (5)(5)(5) | | ||||||
| 33 | Найти том | коробка (10)(10)(10) | | ||||||
| 34 | Найдите окружность | круг (4) | | ||||||
| 35 | Преобразование в проценты | 1,7 | |||||||
| 36 | Оценить | (5/6)÷(4/1) | |||||||
| 37 | Оценить | 3/5+3/5 | |||||||
| 38 | Оценить | ф(-2) | 92 | ||||||
| 40 | Найти площадь | круг (12) | | ||||||
| 41 | Найти том | коробка (3)(3)(3) | | ||||||
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2|||||||
| 45 | Найти простую факторизацию | 228 | |||||||
| 46 | Оценить | 0+0 | |||||||
| 47 | Найти площадь | круг (9) | | ||||||
| 48 | Найдите окружность | круг (8) | | ||||||
| 49 | Найдите окружность | круг (7) | | ||||||
| 50 | Найти том | сфера (10) | | ||||||
| 51 | Найдите площадь поверхности | сфера (10) | | ||||||
| 52 | Найдите площадь поверхности | сфера (7) | | ||||||
| 53 | Определить, является простым или составным | 5 | |||||||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | |||||||
| 61 | Найдите площадь поверхности | сфера (12) | | ||||||
| 62 | Найти том | сфера (1) | | ||||||
| 63 | Найдите окружность | круг (2) | | ||||||
| 64 | Найти том | коробка (12)(12)(12) | | ||||||
| 65 | Добавить | 2+2= | |||||||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | ||||||
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | |||||||
| 68 | Оценить | 7/40+17/50 | |||||||
| 69 | Найти простую факторизацию | 1617 | |||||||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | |||||||
| 71 | Оценить | 9÷4 | |||||||
| 72 | Оценка 92 | ||||||||
| 74 | Оценить | 1-(1-15/16) | |||||||
| 75 | Преобразование в упрощенную дробь | 8 | |||||||
| 76 | Оценка | 656-521 | 9-2 | ||||||
| 79 | Оценить | 4-(6)/-5 | |||||||
| 80 | Оценить | 3-3*6+2 | |||||||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | ||||||
| 82 | Найдите площадь поверхности | сфера (8) | | ||||||
| 83 | Найти площадь | круг (14) | | ||||||
| 84 | Преобразование в десятичное число | 5 ноября | |||||||
| 85 9-2 | |||||||||
| 88 | Оценить | 1/2*3*9 | |||||||
| 89 | Оценить | 4/4-17/-4 | |||||||
| 90 | Оценить | 11. 02+17.19 | |||||||
| 91 | Оценить | 3/5+3/10 | |||||||
| 92 | Оценить | 4/5*3/8 | |||||||
| 93 | Оценить | 6/(2(2+1)) | |||||||
| 94 | Упростить | квадратный корень из 144 | |||||||
| 95 | Преобразование в упрощенную дробь | 725% | |||||||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | |||||||
| 97 | Оценить | 7/10-2/5 | |||||||
| 98 | Оценить | 6÷3 | |||||||
| 99 | Оценить | 5+4 | |||||||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 | |||||||
ответил 21.08.12
3
08.12
93. Видите ли вы шаблон с x и y. Числа в треугольнике паскалей показывают, сколько различных комбинаций можно получить из ограниченного количества чего-либо. (Пример. Сколькими способами можно взять 3 сотрудников из 5 сотрудников). Ответ будет 10 способов, если вы используете уравнение. Вот более подробное объяснение Факториала. Представьте, что у вас есть пять конфет. Если вы выберете один, вы можете выбрать только четыре других. Если вы выберете еще одну конфету, вы сможете выбрать еще только три и так далее, пока не получите 1. (5*4*3*2*1). Этот метод сэкономит вам много времени, если вам придется иметь дело с большими показателями. Если вы не понимаете, я буду рад объяснить более ясно.
Так, в произведении 4 ab коэффициент a равен 4 b ; коэффициент 4 a равен b ; и так далее. В этом продукте x ( x − 1), коэффициент при ( x — 1) равен x .| а) | x 2 | 1 2 | Сравните Урок 6, Задача 7b. |
| б) | 3 x 4 | 3 4 | 3 x 4 | = | 3 4 | · х | Урок 4. |
Проблема 5. Как добавить похожие термины?
Сложите их коэффициенты.
909:50 Задача 6. Добавить похожие термины.| а) 6 x + 2 x | = 8 х | б) 6 х − 2 х | = 4 х | |
| в) 5 х + х | = 6 х | г) 5 х − х | = 4 х | |
| e) −4 x + 5 x | = х | е) 4 x − 5 x | = − х | |
Опять же мы не записываем коэффициенты 1 или −1. | ||||
| ж) −5 x − 3 x | = −8 х | ч) − x − x | = -2 x | |
i) -3 x — 4 + 2 x + 6 = — x + 2
j) x — 2 — 4 x — 5 = -3 x — 7
k) 4 x + y − 2 x + y = 2 x + 2 y
l) 3 x − y − 8 x + 2 y = −5 x + y
м) 4 x ² − 5 x ² + x ² = 0
Задача 7. Добавить похожие термины.
а) 2 а + 3 б это не как термины.
b) 2 a + 3 b + 4 a − 5 ab = 6 a + 3 b − 5 ab .
Термины, которые нельзя комбинировать, просто перепишите.
Проблема 8.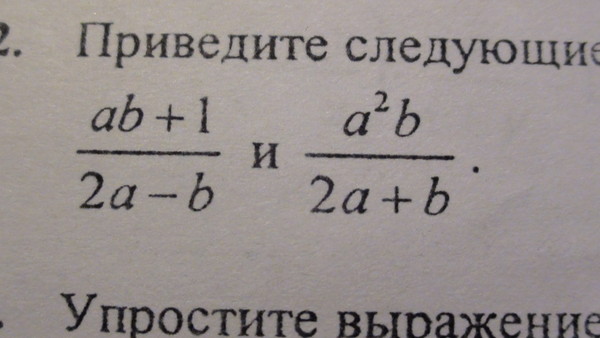
Удалите скобки и добавьте похожие термины.
| а)   (2 a − 3 b + c ) + (5 a − 6 b + с ) | = | 2 a − 3 b + c + 5 a − 6 b + c |
| = | 7 а − 9 б + 2 в | |
| б) ( а + 2 б + 4 в — 3г) — (3 а − 8 б − 2 в + г) | |
| = a + 2 b + 4 c − 3 d −3 a + 8 b + 2 c 1 − 0 5 d 1 − 0 5 | |
| = −2 a + 10 b + 6 c − 4 d | |
| в) (4 x − 3 y ) + (3 y − 5 x ) + (5 z 5 9 1 0 1 1 − 0 4 9) | |
| = 4 x − 3 y + 3 y − 5 x + 5z − 4 x | |
| = −5 x + 5z | |
| D) (5 x y — 3 x + 2 y — 1) — (2 x y — 7 x — 8 y + 6) | |
| = 5 xy − 3 x + 2 y − 1 −2 x y + 7 x + 8 y 0 − 5 | |
| = 3 xy + 4 x + 10 y − 7 | |
E) ( x — Y ) — ( Y + xy — x ) — (2 x — 4 x 1111111111111011111111111111111) — 4 x Y — 2 1111111111111111111111). | |
| = x − y − y − x у + х — 2 х + 4 ху + 2 у | |
| = 3 xy | |
| f) (4 x ² − 7 x − 3) − ( x ² − 4 x + 1) | |
| = 4 x ² − 7 x − 3 − х ² + 4 х − 1 | |
| = 3 x ² − 3 x − 4 | |
| g) (6 x 3 + 4 x ² − 2 x − 6) − (2 x 3 − 8 x ² + x − 2 ) | |
| = 6 x 3 + 4 x ² — 2 x — 6 — 2 x 3 + 8 x ² — x 2 0 + 5 | |
| = 4 x 3 + 12 x ² − 3 x − 4 | |
| h) ( x ² + x + 1) + (2 x ² + 2 x + 2) − ( x 10 − x 99 ²1011 − 1) | |
| = x ² + x + 1 + 2 x ² + 2 x + 2 − x ² + x + 1 | |
| = 2 x ² + 4 x + 4 | |
Задача 9.
5 abc + 2 cba . Это как термины?
Да. Порядок факторов не имеет значения.
Объединив их, мы получим 7 abc .
При записи итоговой суммы принято сохранять алфавитный порядок.
Задача 10. Добавить похожие термины.
| а) | 4 xy − 9 yx = −5 xy | б) | у
в) 9 xyz + 3 yzx + 5 zxy = 17 xyz
d) 3 xy − 4 xyz + 3 x − 8 yx + 5 yzx − 9 x = −5 xy + xyz − 6 х
Задача 11. Добавить похожие термины.
а) 2 n + 2 − n = п + 2
б) n − 2 − 3 n + 1 = −2 n − 1
в) 2 n + 4 − 2 n − 2 = 2
Задача 12.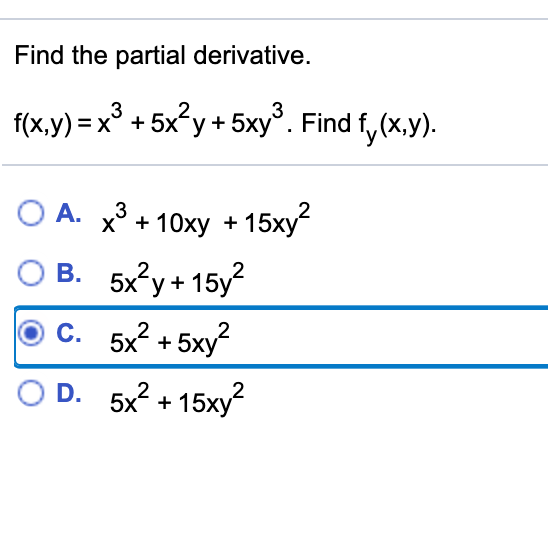
Добавить похожие термины, которые находятся в ( x + 2). Не удаляйте скобки.
а) 3( x + 2) + 7( x + 2) = 10 ( х + 2).
б) 2( x + 2) − 5( x + 2) = −3 ( х + 2).
c) x ( x + 2) + 4( x + 2) = ( х + 4)( х + 2).
Мы добавили коэффициенты.
г) х ( x + 2) − ( x + 2) = ( х — 1)( х + 2).
Задача 13. Добавьте похожие термины, которые находятся в x или y . Добавьте коэффициенты.
а) пикселей + qx = ( p + q ) x .
б) ах + по − сх + dy = ( а − в ) х + ( б + г ) у .
c) x + x = (1 + a ) x . г) x — x = ( a — 1) x .
e) ( a + b ) x + cx = ( а + б + в ) х .
f) ( a − b ) x − cx = ( a − b − c ) x .
f) ( a + b ) x − ( b + a ) x = 0.
Задача 14. Добавить похожие термины.
а) 3 а 2 b 3 − 2 a b 2 + a 3 b 2 − 5 b 2 a + b 3 а 2 = 4 A 2 B 3 — 7 A B 2 + A 3 B 2 .
б) х y 2 − xy + x 2 y − y 2 x + 2 y x 2 + yx = 3 x 2 у .
*
В исчислении учащийся не увидит ни одной задачи с формулировкой «Вычесть a из b ». Однако на некоторых стандартных экзаменах эта формулировка имеет тенденцию появляться. Отсюда следующее правило.
Правило вычитания
«Вычесть a из b .» Это a − b или b − a ?
Это b − a . a это номер вычитано. Его называют вычитаемым. Вычитаемое появляется справа от знака «минус» — перед словом «от».
Пример 2. Вычтите 2 x − 3 от 5 x − 4
Решение . 2 x − 3 — это вычитаемое.
| (5 х — 4) — (2 х — 3) | = | 5 х — 4 — 2 х + 3 |
| = | 3 x − 1. | |
Уведомление : Знаки вычитаемого меняются.
2 x − 3 меняет на −2 x + 3.
Таким образом, мы можем сформулировать следующее правило вычитания.
Измените знаки всех членов в вычитаемом.
Затем добавьте подобные термины.
Задача 15. Вычтите 4 a − 2 b из a + 3 b .
Измените знаки вычитаемого и добавьте:
а + 3 б — 4 а + 2 б = -3 а + 5 б .
Задача 16. Вычтите x ² − 5 x + 7 из 3 x ² − 8 x − 2.
| 3 x ² − 8 x − 2 − x ² + 5 x − 7 | |
| = | 2 x ² − 3 x − 9. |
Следующий урок: Линейные уравнения
Содержание | Главная
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Упростите следующие выражения и оцените их, как указано i x23 2x x2 for x 1 x 1 x 23 и x …
Перейти к
- Алгебраические выражения и тождества. Упражнение 10.1.
- Алгебраические выражения и тождества. Упражнение 10.2.
- Алгебраические выражения и тождества. Упражнение 10.3.
- Алгебраические выражения и тождества. Упражнение 10.4.
- Алгебраические выражения и тождества. Упражнение 10.5.
Упражнение 10.5.- Рациональное число
- Показатели и силы
- Квадраты и квадратные корни
- Кубы и кубические корни
- Игра с числами
- Операции над множествами Диаграммы Венна
- Процент
- Простой и сложный процент
- Прямая и обратная вариация
- Алгебраические выражения и тождества
- Факторизация
- Линейные уравнения и неравенства с одной переменной
- Понимание четырехугольников
- Построения четырехугольников
- Круг
- Отражение и вращение симметрии
- Визуализация твердых фигур
- Измерение
- Обработка данных
Главная >
ML Aggarwal Solutions
Класс 8
Математика
>
Глава 10.
Алгебраические выражения и тождества
>
Алгебраические выражения и тождества. Упражнение 10.2.
>
Вопрос 10
Вопрос 10 Алгебраические выражения и тождества Упражнение 10.2
Упростите следующие выражения и вычислите их, как указано: 92-35(2)(-1)-27(-1)-8
= 18 х 4 х (-1) + 17 х 2 х 1 – 35 х 2 х (-1) – 27 х (-1) ) – 8
= -74 + 34 + 70 + 27 – 8
= 131 – 80
= 51
Родственные вопросы
Найдите произведение: (i) 4×3 и -3xy (ii) 2xyz и 0 (iii) – (2/3) p 2q, (3/4) pq2 и 5pqr (iv) -7ab, -3a…
** Найдите произведение: ****(i) 4×3 и -3xy****(ii) 2xyz и 0****(iii) –(2/3)p2q, (3/4)pq2 и 5пкр*…
**Умножьте:****(i) (3x – 5y + 7z) на – 3xyz****(ii) (2p2 – 3pq + 5q2 + 5) на – 2pq****(iii) (2/ 3а2б .
..
Умножьте: (i) (3x – 5y + 7z) на – 3xyz(ii) (2p2– 3pq + 5q2 + 5) на – 2pq(iii) (2/3a2b – 4/5ab2 + 2/7…
Найдите площади прямоугольников со следующими парами одночленов как их длины и ширины…
**Найдите площади прямоугольников со следующими парами одночленов в качестве длины и ширины**…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Exercises
Algebraic Expressions and Identities Exercise 10.1
Algebraic Expressions and Identities Exercise 10.
2
Algebraic Expressions and Identities Exercise 10.3
Algebraic Expressions and Identities Exercise 10.4
Algebraic Expressions and Identities Exercise 10.5
Chapters
Rational Numbers
Показатели и степени
Квадраты и квадратные корни
Кубы и кубические корни
Playing with Numbers
Operation on sets Venn Diagrams
Percentage
Simple and Compound Interest
Direct and Inverse Variation
Algebraic Expressions and Identities
Factorisation
Linear Equations and Inequalities In one Variable
Understanding Quadrilaterals
Построение четырехугольников
Окружность
Симметрия, отражение и вращение
Визуализация объемных фигур
Измерение
Обработка данных
Курсы
Быстрые ссылки
Термины и политики
Термины и политики
2022 © Качественные учебные пособия Pvt Ltd.
в степени трех над отрицательным 𝑥 в квадрате 𝑦 в степени
три, где 𝑥𝑦 не равно нулю, и оценить это выражение, когда 𝑥 равно
минус один, а 𝑦 равно минус два.
Теперь первый этап этой задачи состоит в том, чтобы на самом деле упростить три 𝑥𝑦 в кубе. отрицательное 𝑥 в квадрате 𝑦 все в кубе. Ну, во-первых, что мы собираемся сделать, так это умножить скобки. Итак, начнем с числителя. И на самом деле мы можем подумать, что если у нас есть три 𝑥𝑦, все в кубе, и это на самом деле означает, что каждый из этих терминов возведен в куб, так что это как три в кубе, умноженные на 𝑥 в кубе умножить на 𝑦 в кубе, что даст нам 27𝑥 в кубе 𝑦 в кубе. Это потому, что три в кубе, три умножить на три, будет девять, умножить на другое. три равно 27,
И тогда у нас есть 𝑥 в кубе 𝑦 в кубе. Что ж, тогда у нас будет то же самое для знаменателя. Итак, у нас есть минус 𝑥 в квадрате, умноженный на 𝑦 в кубе.
Что ж, поэтому мы собираемся использовать один из наших индексных законов, чтобы переписать его.
это потому, что у нас есть индексный закон, который говорит нам, что если у нас есть 𝑥 в степени
𝑎, то в степени 𝑏 это равно 𝑥 степени 𝑎, умноженной на 𝑏.
Таким образом, наш знаменатель будет отрицательным 𝑥 в шестой степени, потому что мы имел 𝑥 степени двойки в степени трое, умножаем три и два, получаем шесть, тогда 𝑦 в кубе. Итак, теперь, чтобы упростить это, мы применим еще один индексный закон, что говорит нам, что если у нас есть 𝑥 в степени 𝑎, деленное на 𝑥 в степени 𝑏, то это будет равно 𝑥 в степени 𝑎 минус 𝑏.
Таким образом, наш полностью упрощенный ответ будет отрицательным в 27𝑥 степени отрицательного числа.
три. Это потому, что если у нас есть 𝑥 в степени три, деленное на 𝑥 в степени шесть,
мы на самом деле вычтем их друг из друга. Итак, у нас есть три минус шесть, что дает нам минус три.
И тогда, если у вас есть 𝑦 в степени три, деленное на 𝑦 в степени три, мы
вычесть три из трех, что дает нам ноль. Итак, у нас осталось минус 27𝑥 в степени минус три.
Так здорово! Это первая часть ответа на вопрос. Но теперь нам нужно на самом деле вычислить выражение, когда 𝑥 равно отрицательная единица, а 𝑦 равно отрицательной двойке. Таким образом, чтобы фактически оценить это выражение и узнать, сколько оно равно, когда 𝑥 равно отрицательной единице, а 𝑦 равно отрицательной двойке, все, что нам нужно сделать, это на самом деле замена в 𝑥 равна отрицательной единице. И это потому, что когда мы упростили это, у нас на самом деле нет никаких терминов 𝑦 оставил.
Таким образом, мы можем переписать это как отрицательное 27 вместо отрицательного 1 все
в кубе. И это потому, что мы заменили 𝑥 на отрицательную. И причина, по которой мы можем написать это так, заключается в том, что у нас есть другие отношения, которые мы
знаю, что 𝑥 в отрицательной степени 𝑎 равно единице над 𝑥 в
сила 𝑎.
Итак, это даст нам отрицательное число 27, деленное на отрицательное. И это потому, что отрицательная единица в кубе равна отрицательной единице. Поэтому, поскольку отрицательное, деленное на отрицательное, является положительным, это просто дает нам
ответ от 27.
Итак, теперь, несмотря на то, что мы полностью упростили и нашли ответ, что мы что мы можем сделать, это проверить, потому что мы можем проверить, подставив 𝑥 равно минус единице, а 𝑦 равно минус двум в исходном выражении. И мы действительно можем видеть там, действительно ли нам удалось полностью правильно упростить и найти правильное значение, потому что это должно дать нам такое же значение.
Таким образом, если мы подставим в наши значения 𝑥 и 𝑦, мы получим три
умножить на отрицательную единицу умножить на отрицательную два все в кубе на отрицательное затем
минус один в квадрате умножается на минус два, а потом все это возводится в куб.
Следовательно, это даст нам шесть в кубе. Это потому, что мы умножили три на отрицательную единицу, что равно отрицательной тройке,
умножить на минус два, что даст нам шесть, вызвать отрицательное умножение
отрицательным является положительным, поэтому шесть в кубе, больше, тогда у нас есть два в кубе. Это потому, что у нас был отрицательный отрицательный один в квадрате. Ну, минус в квадрате — это плюс. Но мы делаем отрицательную причину знаком минус впереди, так что у нас есть отрицательная единица.
умножить на минус два, что равно плюсу два. А потом все это в кубе, что даст нам 216 на восемь, что даст нам 27,
такой ответ мы получили, когда разрабатывали первый метод.
Так здорово! Что мы можем сказать, так это то, что, полностью упрощая, три 𝑥𝑦 в степени три над
отрицательное 𝑥 в квадрате 𝑦 в степени три отрицательно 27𝑥 в отрицательной степени
три. И значение этого выражения, когда 𝑥 равно отрицательной единице, а 𝑦 равно
минус два равно 27.
Алгебраические выражения
Алгебраические выражения — это выражения, составленные из целочисленных констант, переменных и алгебраических операций.
Например, следующее выражение является алгебраическим выражением:
a + b + 4
Алгебраические выражения можно использовать для записи законов, формул и уравнений. Умение манипулировать алгебраическими выражениями – залог хорошего знания алгебры и высшей математики.
Любая серьезная задача по математике сводится к решению уравнений. А чтобы уметь решать уравнения, нужно уметь работать с алгебраическими выражениями.
Для работы с алгебраическими выражениями необходимо знать основы арифметики: сложение, вычитание, умножение, деление, основные законы математики, дроби, действия с дробями, пропорции. И не просто выучить, а понять досконально.
Переменные
Буквы, содержащиеся в алгебраических выражениях, называются переменными .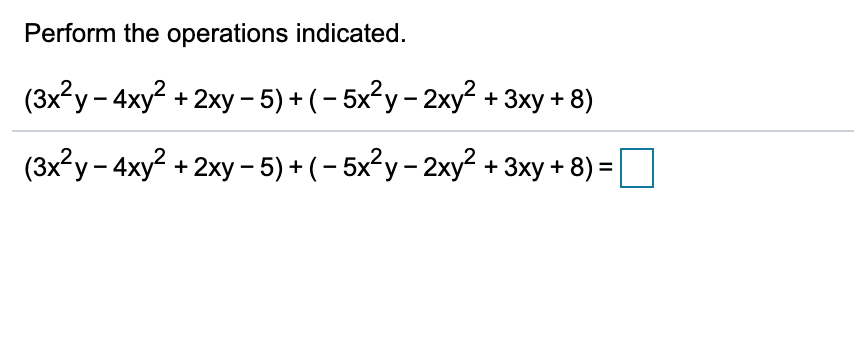
Например, в выражении a + b + 4 буквы a и b являются переменными. Если вместо этих переменных подставить какие-либо числа, то алгебраическое выражение a + b + 4 превратится в числовое выражение, значение которого можно найти.
Числа, подставляемые вместо переменных, называются значениями переменных .
Значение переменной – константа, представляющая собой число, которое выражается как.
Например, измените значения переменных a и b. Знак равенства используется для замены переменных их значениями.
a = 2 , b = 3
Переменной a присвоено значение 2, а переменной b присвоено значение 3. В результате алгебраическое выражение a +b+4 превращается в обычное числовое выражение 2+3+4, значение которого можно найти:
2 + 3 + 4 = 9
При умножении переменных они записываются вместе.
Например, запись ab означает то же самое, что запись a × b. Если мы подставим числа 2 и 3 вместо переменных a и b, то получим 6
2 × 3 = 6
. Вы также можете написать умножение числа на выражение в скобках.
Например, вместо a × (b + c) вы можете написать a(b + c). Применяя распределительный закон умножения, получаем a(b + c) = ab + ac.
Коэффициенты
В алгебраических выражениях вы часто встречаете обозначения, в которых число и переменная записываются вместе, например ‘ 3a’ . На самом деле это короткая запись умножения числа 3 на переменную a, и эта запись выглядит как 3 × a.
Другими словами, выражение 3a является произведением числа 3 и переменной a. Число 3 в этом произведении называется коэффициентом . Этот коэффициент показывает, во сколько раз будет увеличена переменная а. Это выражение можно прочитать как «трижды а» или «увеличить значение а в три раза».
Например, если переменная a равна 5, то значение выражения 3a равно 15.
3 × 5 = 15
Проще говоря, частное — это число, стоящее перед переменной (перед буквой ).
Переменных может быть несколько, например 5abc. Здесь коэффициентом является число 5. Этот коэффициент показывает, что произведение переменных abc увеличивается на пять. Это выражение можно прочитать как «пять раз абв».
Если мы подставим числа 2, 3 и 4 вместо переменных abc, то значение выражения 5abc будет 120
5 × 2 × 3 × 4 = 120
Вы можете мысленно представить себе сначала умножение чисел 2, 3 и 4, а полученное значение умножить на пять:
Знак коэффициента относится только к коэффициенту, а не к переменным!
Рассмотрим выражение -6b. Минус перед коэффициентом 6 относится только к коэффициенту 6 и не относится к переменной b. Понимание этого факта поможет вам не ошибиться с приметами в будущем.
Пример 1. Найдите значение выражения -6b, когда b = 3.
-6b — это краткая форма -6 × b. Для наглядности запишем выражение -6b в развернутом виде и подставим значение переменной b
−6 b = −6 × b = −6 × 3 = −18
Пример 2. Найдите значение выражения -6b при b = -5
Запишем выражение -6b в развернутом виде
−6 b 929Пример 3. Найдите значение выражения -5a + b, если a = 3 и b = 2
-5a + b является краткой формой -5 × a + b, поэтому для ясности запишем выражение -5 × a + b в развернутом виде и подставить значения переменных a и b
−5 a + b = −5 × a + b = −5 × 3 + 2 = −15 + 2 = −13
Иногда переменные записывают без коэффициента , например a или ab. В этом случае коэффициент равен 1:
1 a , 1 ab
но единицу обычно не записывают, поэтому пишут просто a или ab.
Если перед переменной стоит минус, коэффициент равен -1.
Например, выражение -a на самом деле выглядит как -1a.
Это произведение минус единицы и переменной а. Получается следующим образом:
−1 × a = −1 a
Здесь есть небольшая загвоздка. В выражении -a минус перед переменной a на самом деле относится к невидимой единице, а не к переменной a. Поэтому следует быть осторожным при решении проблем.
Например, если дано выражение -а и нас просят найти его значение при а = 2, то в школе мы подставляли два вместо переменной а и получали ответ -2, не особо задумываясь о том, как это произошло . На самом деле мы умножили минус один на положительное число 2.
−a = −1 × a
−1 × a = −1 × 2 = −2
Если задано выражение -a и мы хотим найти его значение для a = -2 , подставим -2 вместо переменной a
−a = −1 × a
−1 × a = −1 × (−2) = 2
единицы могут быть записаны явно.
Пример 4. Вычислите выражение abc для a=2, b=3 и c=4
Выражение abc представляет собой краткую форму 1×a×b×c.
Для наглядности запишем abc в развернутом виде и подставим значения переменных a, b, c
1 × a × b × c = 1 × 2 × 3 × 4 = 24
Пример 5. Вычислите выражение abc для a=-2, b=-3 и c=-4
Запишите выражение abc в развернутом виде и подставьте значения переменных a, b и c
1 × a × b × c = 1 × (−2) × (−3) × (−4) = −24
Пример 6. Вычислить выражение -abc для a=3, b=5 и c=7
Выражение -abc представляет собой краткую форму -1×a×b×c. Для наглядности напишем выражение -abc в развернутом виде и подставим значения переменных a, b и c
−abc = −1 × a × b × c = −1 × 3 × 5 × 7 = −105
Пример 7. Вычислить выражение -abc для a=-2, b=-4 и c=-3
Запишите выражение -abc в расширенной форме:
−abc = −1 × a × b × c
Подставим значения переменных a, b и c
−abc = −1 × a × b × c = −1 × (−2) × (−4) × (−3) = 24
Как вычислить коэффициент
Иногда вам нужно решить задачу, в которой вы хотите вычислить коэффициент выражения.
В принципе, эта проблема очень проста. Достаточно уметь правильно умножать числа.
Чтобы вычислить частное выражения, умножьте числа в выражении отдельно и перемножьте переменные отдельно. Полученный числовой множитель и будет коэффициентом.
Пример 1. Вычислите коэффициент в выражении: 7m×5a×(-3)×n
Выражение состоит из нескольких множителей. Это хорошо видно, если записать выражение в развернутом виде. То есть произведения 7m и 5a запишем в виде 7×m и 5×a
7×m×5×a×(−3)×n
Применим ассоциативный закон умножения, который позволяет нам умножайте множители в любом порядке. А именно, умножать отдельно числа и отдельно умножать буквы (переменные):
−3 × 7 × 5 × m × a × n = −105man
Коэффициент равен -105. После завершения желательно расположить переменную часть в алфавитном порядке:
−105amn
Пример 2. Вычислим коэффициент в выражении: -a×(-3)×2
Умножим числа и переменные отдельно:
−a × (−3) × 2 = −3 × 2 × (−a) = −6 × (−a) = 6a
Коэффициент равен 6,
Пример 3.
Рассчитаем коэффициент в выражении:
Перемножим числа и переменные отдельно:
Коэффициент равен -1. Обратите внимание, единицу не пишут, потому что коэффициент 1 принято не писать.
Эти, казалось бы, простые задачи могут сыграть с нами очень злую шутку. Часто оказывается, что знак у частного неправильный: либо отсутствует знак минус, либо, наоборот, он поставлен зря. Чтобы избежать этих досадных ошибок, тему умножения целых чисел нужно изучить на хорошем уровне.
Слагаемые в алгебраических выражениях
При сложении нескольких чисел получается сумма чисел. Добавляемые числа называются слагаемыми. Может быть более одного слагаемого, например:
1 + 2 + 3 + 4 + 5
Когда выражение состоит из слагаемых, его гораздо легче вычислить, потому что сложение проще, чем вычитание. Но выражение может содержать не только сложение, но и вычитание, например:
1 + 2 − 3 + 4 − 5
В этом выражении числа 3 и 5 являются вычитателями, а не слагаемыми.
Но ничто не мешает нам заменить вычитание сложением. Тогда снова получаем выражение, состоящее из слагаемых:
1 + 2 + (−3) + 4 + (−5)
Неважно, что числа -3 и -5 теперь со знаком минус. Главное, чтобы все числа в этом выражении были соединены знаком сложения, то есть выражение представляло собой сумму.
Оба выражения 1 + 2 — 3 + 4 — 5 и 1 + 2 + (-3) + 4 + (-5) равны одному и тому же значению — минус один:
1 + 2 — 3 + 4 — 5 = -1
1 + 2 + (-3) + 4 + (-5) = -1
Таким образом, значение выражения не изменится, если мы подставим сложение для вычитания где-то.
Вы также можете заменить вычитание сложением в алгебраических выражениях. Например, рассмотрим следующее выражение:
7a + 6b — 3c + 2d — 4s
Замените вычитание сложением, где это возможно:
7a + 6b + (-3c) + 2d + (-4s)
При любых значениях переменных a, b, c, d и s выражения 7a + 6b — 3c + 2d — 4s и 7a + 6b + (-3c) + 2d + (-4s) будут равны ценность.
Будьте готовы к тому, что учитель в школе или преподаватель в институте может назвать даже те числа (или переменные), которые не являются слагаемыми.
Например, если на доске написана разница a — b, учитель не скажет, что a — это уменьшаемое, а b — это вычитаемое. Он будет называть обе переменные одним общим словом — слагаемые. Это потому, что математик видит выражение формы a — b как сумму a + (-b). В этом случае выражение становится суммой, а переменные a и (-b) становятся слагаемыми.
Похожие термины
Подобные термины (аналогичные термины) — это термины, которые имеют одинаковые переменные .
Например, рассмотрим выражение 7a + 6b + 2a. Слагаемые 7а и 2а имеют одни и те же переменные — переменную а. Таким образом, слагаемые 7а и 2а подобны.
Обычно подобные члены добавляются для упрощения выражения или решения уравнения. Это действие называется , объединяющим подобные термины .
Чтобы объединить одинаковые члены, просуммируйте все коэффициенты этих членов и умножьте результат на одну и ту же переменную часть.
Например, объедините одинаковые термины в выражении 3a + 4a + 5a. В этом случае все слагаемые одинаковы. Сложите их коэффициенты и умножьте результат на общую переменную часть — на переменную а
3а + 4а + 5а = (3 + 4 + 5)×а = 12а
результат записывается сразу:
3а + 4а + 5а = 12а
Также можно рассуждать так:
Было 3 переменных a , добавлены еще 4 переменные a и еще 5 переменных a . В результате получилось 12 переменных a
Давайте рассмотрим несколько примеров комбинирования подобных терминов. Учитывая, что эта тема очень важная, сначала подробно распишем каждую деталь. Несмотря на то, что здесь все очень просто, большинство людей допускают массу ошибок. В основном по невнимательности, а не по незнанию.
Пример 1.
Объединение одинаковых членов в выражение 3a + 2a + 6a + 8a
Сложите коэффициенты в этом выражении и умножьте результат на ту же переменную часть:
3 а + 2 а + 6 а + 8 а = (3 + 2 + 6 + 8) × a = 19 a
Построение (3 + 2 + 6 + 8) × a можно не записывать, поэтому сразу запишем ответ
3 a + 2 a + 6 а + 8 а = 19 а
Пример 2. Объедините одинаковые члены в выражении 2a + a
Второе слагаемое a написано без коэффициента, но на самом деле ему предшествует коэффициент 1, которого мы не видим, потому что он не записан. Таким образом, выражение выглядит следующим образом:
2а + 1а
Теперь соединим подобные члены. То есть складываем коэффициенты и результат умножаем на общую переменную часть:
2а + 1а = (2 + 1) × а = 3а
Запишем решение вкратце:
2a + a = 3a
Соединяя одинаковые члены в выражении 2a+a, можно рассуждать иначе:
Было 2 переменные a , мы добавили еще одну переменную и , так что мы получили 3 переменные и .
Пример 3. Объединить одинаковые члены в выражении 2a − a
Заменить вычитание сложением:
2a + (−a)
Второе слагаемое (-a) записывается без коэффициента, но на самом деле выглядит как (-1a). Коэффициент -1 снова невидим, потому что не записывается. Следовательно, выражение выглядит так:
2a + (−1a)
Теперь объединим одинаковые члены. Сложите коэффициенты и умножьте результат на равную переменную часть:
2а + (−1а) = (2 + (−1)) × а = 1а = а
Обычно записывают короче:
2a − a = a
Соединяя одинаковые слагаемые в выражении 2a−a , можно рассуждать иначе: оставив одну единственную переменную a
Пример 4. Объединить одинаковые члены в выражении 8а = 6а + (-3а) + 4а + (-8а)
Теперь давайте объединим подобные термины. Складываем коэффициенты и умножаем результат на равную переменную часть
(6 + (−3) + 4 + (−8)) × a = −1a = −a
Запишем решение кратко:
6a − 3a + 4a − 8a = −a
Существуют выражения, содержащие несколько различных одинаковых терминов.
Например, 3а + 3б + 7а + 2б. Для таких выражений действуют те же правила, что и для остальных, а именно сложение коэффициентов и умножение результата на общую переменную часть. Но во избежание ошибок удобно подчеркивать разные группы слагаемых разными чертами.
Например, в выражении 3a + 3b + 7a + 2b те термины, которые содержат переменную a , можно подчеркнуть одной чертой, а те термины, которые содержат переменную b , можно подчеркнуть двумя черточками:
Теперь давайте объединим одинаковые термины. То есть сложить коэффициенты и умножить результат на общую переменную часть. Сделайте это для обеих групп слагаемых: для слагаемых, содержащих переменную и , и для слагаемых, содержащих переменную 9.2942 б .
3a + 3b + 7a + 2b = (3+7)×a + (3 + 2)×b = 10a + 5b
Опять же, выражение несложное, и подобные термины можно комбинировать в уме:
3A + 3B + 7A + 2B = 10A + 5B
Пример 5.
Комбавление, как термины в выражении 5A — 6A -7B + B
заменить подтрон с входом в добавление. 5a − 6a −7b + b = 5a + (−6a) + (−7b) + b
Подчеркнем одинаковые термины разными черточками. Одной чертой подчеркните термы, содержащие переменные a , а двумя черточками подчеркните термы, содержащие переменные b :
Теперь объединим одинаковые термы. Сложите коэффициенты и умножьте результат на общую переменную часть:
5a + (−6a) + (−7b) + b = (5 + (−6))×a + ((−7) + 1) ×b = −a + (−6b)
Если выражение содержит обычные числа без каких-либо переменных множителей, они складываются отдельно.
Пример 6. Объединить в выражении одинаковые члены (−5) + 2b + 7
Теперь давайте объединим одинаковые члены. Числа -5 и 7 не имеют буквенных множителей, но они подобны слагаемым — вам просто нужно их сложить. А терм 2b останется неизменным, потому что это единственный член в выражении, имеющий буквальный множитель 9.
2942 b , и добавить не к чему:
4a + 3a + (−5) + 2b + 7 = (4 + 3)×a + 2b + (−5) + 7 = 7a + 2b + 2
Запишем решение вкратце:
4a + 3a − 5 + 2b + 7 = 7a + 2b + 2
Термы можно расположить так, чтобы в одна и та же часть выражения.
Пример 7. Объединение одинаковых членов в выражение 5t+2x+3x+5t+x
Поскольку выражение представляет собой сумму нескольких слагаемых, это позволяет нам вычислять его в любом порядке. Следовательно, мы можем записать термы, содержащие переменную t , в начало выражения, а термы, содержащие переменную x , в конец выражения:
5t + 5t + 2x + 3x + x
Теперь можно комбинировать подобные члены:
5t + 5t + 2x + 3x + x = (5+5)×t + (2+3+1)×x = 10t + 6x
Запишем решение коротко:
5t + 2x + 3x + 5t + x = 10t + 6x
Сумма противоположных чисел равна нулю. Это правило работает и для алгебраических выражений.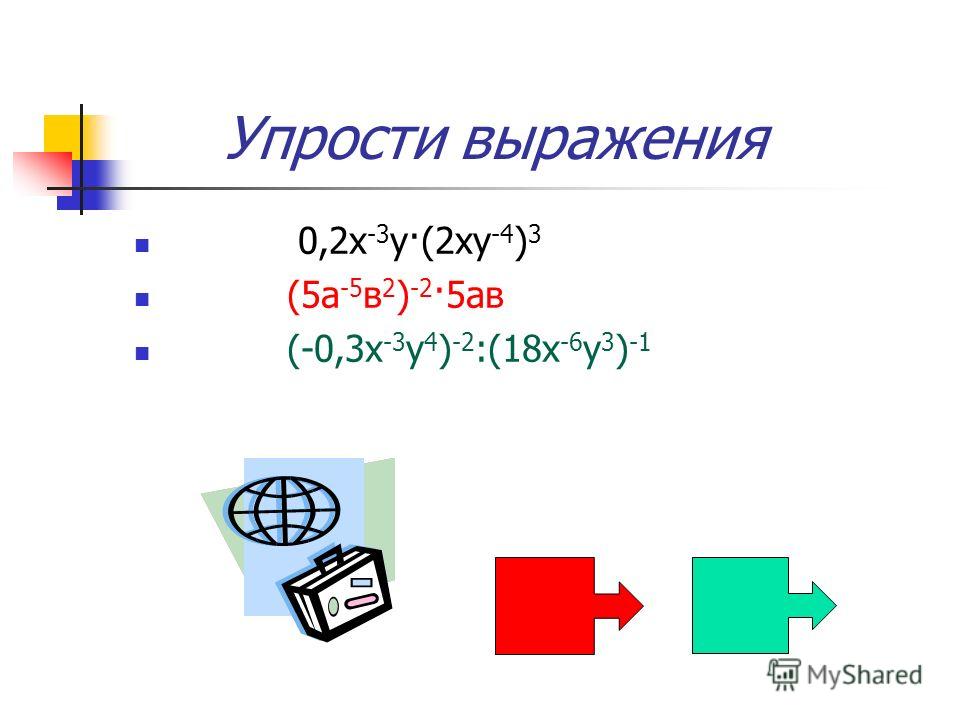
Если в выражении есть одинаковые слагаемые, но с противоположными знаками, от них можно избавиться на этапе объединения однородных членов . Другими словами, просто вычеркните их из выражения, так как их сумма равна нулю.
Пример 8. Объединить одинаковые члены в выражение 3t − 4t − 3t + 2t
По возможности заменить вычитание сложением:
3t − 4t − 3t + 2t = 3t + (−4t) + (−3t) + 2t противоположный. Сумма противоположных членов равна нулю. Если мы удалим этот ноль из выражения, значение выражения не изменится, поэтому мы его удалим. И убираем его, просто зачеркнув слагаемые 3t и (-3t)
В итоге у нас осталось выражение (-4t)+2t. В этом выражении мы можем объединить одинаковые члены и получить окончательный ответ:
(−4t) + 2t = ((−4) + 2)×t = −2t
Кратко запишем решение:
Упрощение выражений
» упростить выражение » , а затем дает выражение, которое вы хотите упростить.
Упростить выражение означает сделать его проще и короче.
На самом деле, мы уже упрощали выражения, когда сокращали дроби. После сокращения дробь становится короче и понятнее.
Рассмотрим следующий пример. Упростите выражение
.
Это назначение можно буквально понимать как: « Примените любые возможные действия к этому выражению, но упростите его «.
В этом случае можно уменьшить дробь, а именно разделить числитель и знаменатель дроби на 2:
Что еще можно сделать? Мы можем вычислить полученную дробь
. Тогда мы получим десятичную дробь 0,5.
В результате дробь
была упрощена до 0,5.
Первый вопрос, который вы должны задать себе при решении подобных задач, должен быть: «Что можно сделать?» Потому что есть действия, которые можно совершить, и есть действия, которые нельзя совершить.
Еще одна важная вещь, о которой следует помнить, это то, что значение выражения не должно меняться после упрощения выражения.
Вернемся к выражению
. Это выражение представляет собой деление, которое можно выполнить. Выполнив это деление, мы получим значение этого выражения, равное 0,5
Но мы упростили выражение
и получили новое упрощенное выражение. Значение нового упрощенного выражения по-прежнему равно 0,5.
Таким образом, как бы мы ни упростили выражение, значение полученных выражений все равно равно 0,5. Таким образом, упрощение было выполнено правильно на каждом шаге. Это то, к чему мы должны стремиться при упрощении выражений — на значение выражения не должны влиять наши действия.
Часто бывает необходимо упростить переменные выражения. К ним применяются те же правила упрощения, что и к числовым выражениям. Любые допустимые действия могут быть выполнены до тех пор, пока значение выражения не изменится.
Давайте рассмотрим несколько примеров.
Пример 1.
Упростите выражение 5,21s × t × 2,5
Чтобы упростить это выражение, вы можете умножать числа отдельно и умножать переменные отдельно. Эта задача очень похожа на ту, которую мы рассматривали, когда учились определять коэффициент:
5,21s × t × 2,5 = 5,21 × 2,5 × s × t = 13,025 × st = 13,025st
Таким образом, выражение 5,21s × t × 2,5 упрощается до 13,025st.
Пример 2. Упростим выражение -0,4 × (-6,3b) × 2
Второе произведение (-6,3b) можно перевести в понятный нам вид, а именно записать в виде ( -6,3)×b, затем перемножить числа отдельно и перемножить переменные отдельно:
− 0,4 × (−6,3b) × 2 = − 0,4 × (−6,3) × b × 2 = 5,04b
Таким образом, выражение -0,4 × (-6,3b) × 2 упрощается до 5,04b
Пример 1. Упростить выражение
Давайте разберем это выражение более подробно, чтобы ясно видеть, где числа и где переменные:
Теперь умножьте числа отдельно и умножьте переменные отдельно:
Таким образом, выражение
упрощается до -abc.
Это решение можно записать в более короткой форме:
При упрощении выражений дроби можно сокращать в процессе их решения, а не в самом конце, как мы это делали с правильными дробями.
Например, если при решении мы встретим выражение типа
, то не обязательно вычислять числитель и знаменатель, а сделать примерно так:
Дроби можно сократить, выбрав множитель в числителе и множитель в знаменателе и уменьшив эти множители на их наибольший общий делитель. Другими словами, используйте краткий вариант сокращения дроби, в котором мы не описываем подробно, на что были разделены числитель и знаменатель.
Например, в числителе множитель 12, а в знаменателе множитель 4 можно уменьшить на 4. Четверку держим в уме, и после деления 12 и 4 на эту четверку записываем ответы рядом с этими чисел, предварительно зачеркнув их
Тогда в числителе множитель 9, а в знаменателе множитель 3 можно уменьшить на 3
Тогда в числителе множитель 6, а в знаменателе множитель 2 уменьшить к 2
Теперь можно умножить полученные маленькие множители.
В данном случае их немного и их можно перемножать в уме:
Со временем вы можете обнаружить, что при решении той или иной задачи выражения начинают «укорачиваться», поэтому желательно привыкнуть к быстрым вычислениям. То, что вы можете просчитать в своей голове, вы должны просчитать в своей голове. То, что можно быстро сократить, должно быть сокращено быстро.
Пример 4. Упростим выражение
Перемножим числа отдельно и переменные отдельно:
Таким образом, выражение
упрощается до
Таким образом, выражение
упрощается до mn .
Пример 6. Упростим выражение
Распишем это выражение подробнее, чтобы было понятно, где числа, а где переменные:
Теперь умножьте числа отдельно и переменные отдельно. Для удобства десятичное -6,4 и смешанное число
можно преобразовать в дроби:
Таким образом, выражение
упрощается до -6.
4stx
Решение для этого примера может быть записано в гораздо более короткой форме. Это будет выглядеть следующим образом:
Пример 7. Упростим выражение
Умножать числа и переменные отдельно. Для удобства смешанное число
и десятичные дроби 0,1 и 0,6 можно преобразовать в дроби:
Таким образом, выражение
упрощается до abcd. Если опустить детали, это решение можно записать гораздо короче:
Обратите внимание, как сокращается дробь. Новые множители, полученные в результате уменьшения предыдущих множителей, также могут быть уменьшены.
Теперь поговорим о том, чего делать не следует. При упрощении выражений совершенно нельзя умножать числа и переменные, если выражение представляет собой сумму, а не произведение.
Например, если вы хотите упростить выражение 5a + 4b, вы не можете написать так:
Это эквивалентно тому, как если бы нас попросили сложить два числа, а мы их умножили бы вместо сложения.
При подстановке любых значений переменных a и b выражение 5a +4b превращается в обычное числовое выражение. Предположим, что переменные a и b имеют следующие значения:
a = 2, b = 3
Тогда значение выражения будет 22
5a + 4b = 5 × 2 + 4 × 3 = 10 + 12 = 22
Сначала выполняется умножение, а затем результаты суммируются. А если бы мы попытались упростить это выражение, перемножив числа и переменные, то получили бы следующее:
5a + 4b = 5 × 4 × a × b = 20ab
20ab = 20 × 2 × 3 = 120
Получается совсем другое значение выражения. В первом случае это 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было сделано неправильно .
После упрощения выражения его значение не должно меняться при тех же значениях переменных. Если подстановка любых значений переменных в исходное выражение дает одно значение, то после упрощения выражения значение должно быть таким же, как и до упрощения.
Вы ничего не можете сделать с выражением 5a + 4b. Это не упрощенно.
Если выражение содержит одинаковые члены, их можно добавить, если наша цель — упростить выражение.
Пример 8. Упростите выражение 0,3a-0,4a+a
Чтобы упростить это выражение, вы можете объединить подобные члены:
0,3a − 0,4a + a = 0,3a + (−0,4a) + a = (0,3 + (−0,4) + 1)×a = 0,9a
или короче: 0,3a − 0,4a + a = 0,9a
Таким образом, выражение 0,3a-0,4a +a упрощается до 0,9a
Пример 9. Упростите выражение −7,5a − 2,5b + 4a
Чтобы упростить это выражение, вы можете объединить подобные термины:
−7,5a − 2,5b + 4a = −7,5a + (−2,5b) + 4a = ((−7,5) + 4)×a + (−2,5b) = −3,5a + (−2,5b)
или короче: −7,5a − 2,5b + 4a = −3,5a + (−2,5b)
Слагаемое (-2,5b) осталось неизменным, поскольку к нему нечего было добавить.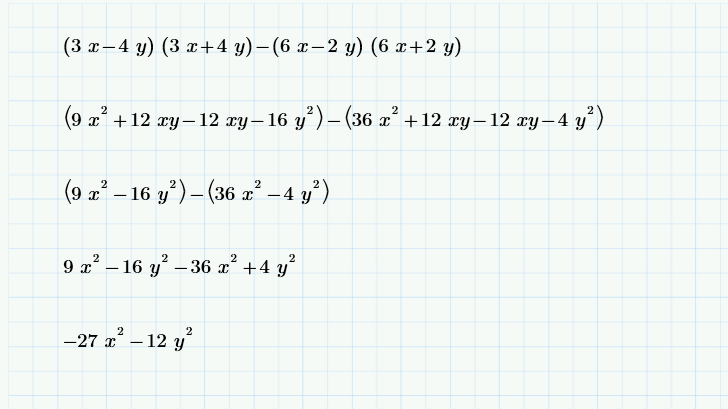
Пример 10. Упростите выражение
Чтобы упростить это выражение, вы можете объединить подобные члены:
Коэффициент
был преобразован в неправильную дробь для простоты вычисления.
Таким образом, выражение
упростится до
Пример 11. Упростите выражение
Чтобы упростить это выражение, вы можете объединить подобные члены:
Таким образом, выражение
В этом примере было бы разумнее сначала добавить первый и последний коэффициенты. В этом случае мы получим короткое решение. Это будет выглядеть так:
Пример 12. Упростите выражение
Чтобы упростить это выражение, вы можете объединить подобные члены:
Таким образом, выражение
упрощается до .
Слагаемое
осталось без изменений, потому что к нему нечего было добавить.
Это решение можно записать гораздо короче. Это будет выглядеть следующим образом:
В кратком решении отсутствуют этапы замены вычитания сложением и подробный отчет о том, как дроби приводились к общему знаменателю.
Другое отличие состоит в том, что в подробном решении ответ выглядит как
, а в кратком — как . По сути, это одно и то же выражение. Отличие состоит в том, что в первом случае вычитание заменено сложением, потому что в начале, когда мы записывали решение в развернутой форме, мы везде, где это возможно, заменяли вычитание сложением, и эта замена сохраняется для ответ.
Личность. Эквивалентные выражения
После упрощения выражения оно становится проще и короче. Чтобы проверить правильность упрощения выражения, просто подставьте любые значения переменных сначала в предыдущее выражение, которое нужно упростить, а затем в новое упрощенное выражение. Если значение в обоих выражениях одинаковое, это означает, что выражение упрощено правильно.
Рассмотрим простой пример. Пусть выражение 2a × 7b упростится. Чтобы упростить это выражение, мы можем перемножить числа и переменные отдельно:
2 a × 7 b = 2 × 7 × a × b = 14 ab
Проверим, правильно ли мы упростили выражение. Для этого подставляем любые значения переменных a и b сначала в первое выражение, которое мы хотели упростить, а затем во второе выражение, которое мы упростили.
Пусть значения переменных a, b будут следующими:
a = 4
b = 5
Подставляем их в первое выражение которое получается в результате упрощения выражения 2a × 7b, а именно в выражении 14ab
14 ab = 14 × 4 × 5 = 280
Мы видим, что при a = 4 и b = 5 значение первого выражения 2a × 7b, а значение второго выражения 14ab равно
2 a × 7 b = 2 × 4 × 7 × 5 = 280
14 ab = 14 × 4 × 5 = 280
То же самое произойдет для любых других значений. Например, пусть a = 1 и b = 2
2 a × 7 b = 2 × 1 × 7 × 2 = 28
14 × 1 × 849 3 1 929
Таким образом, выражения 2a × 7b и 14ab равны одному и тому же значению для всех значений переменных. Такие выражения называются эквивалентных выражений .
Делаем вывод, что между выражениями 2a × 7b и 14ab можно поставить знак равенства, так как они равны одному и тому же значению: любое выражение, соединенное знаком равенства (=).
Равенство вида 2a × 7b = 14ab называется тождественным уравнением .
Тождество — это равенство, истинное для всех значений переменных. 9
a(b + c) = ab + ac законы математики, которые мы изучали, тождественны.
Истинные числовые уравнения тоже тождества. Например:
2 + 2 = 4
3 + 3 = 5 + 1
10 = 7 + 2 + 1
При решении сложной задачи для упрощения расчета сложное выражение заменяется на более простое выражение, тождественно равное предыдущему.
Например, мы упростили выражение 2a × 7b и получили более простое выражение 14ab. Это упрощение можно назвать преобразованием идентичности .
Вы часто будете видеть задание, в котором говорится « доказать равенство уравнения», за которым следует равенство, которое вы хотите доказать. Обычно это равенство состоит из двух частей: левой и правой частей равенства. Наша задача — произвести тождественные преобразования с одной частью равенства и получить другую часть. Или выполните преобразования идентичности для обеих частей равенства и сделайте так, чтобы обе части равенства имели одинаковые выражения.
Например, докажите, что равенство 0,5a × 5b = 2,5ab является тождеством.
Упростим левую часть этого равенства. Для этого перемножьте числа и переменные по отдельности:
0,5 × 5 × a × b = 2,5ab
2,5ab = 2,5ab
В результате небольшого тождественного преобразования левая часть равенство стало равным правой части равенства. Итак, мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.
Из тождественных преобразований мы научились складывать, вычитать, умножать и делить числа, сокращать дроби, добавлять одинаковые термины и упрощать некоторые выражения.
Но это не все тождественные преобразования, существующие в математике. Есть еще много одинаковых преобразований. Мы еще не раз увидимся в будущем.
Упражнения:
Вычислите выражение 2xy для и
Показать решение
Оцените выражение -xy для
Показать решение
Вычислите выражение -xyz для и и
Показать решение
Вычислите выражение -0.02ab для и
Показать решение
Задание 5. Запишите следующую последовательность действий в виде алгебраического выражения:
- умножьте на на три и из этого произведения вычтите пятнадцать
- умножьте т на девять, и прибавьте к произведению тридцать пять.
Показать решение
Задание 6. Объединить одинаковые члены в следующее выражение:
Показать решение
Задание 7. Объединить одинаковые члены в следующее выражение:
Показать решение 6.0 похожие члены в следующем выражении:
Показать решение
Задача 9. Объединить одинаковые члены в следующем выражении:
Показать решение
Задача 10. Combine like terms in the following expression:
Show Solution
Task 11. Simplify the expression:
Show Solution
Task 12. Simplify the expression:
Show Solution
Task 13. Упростите выражение:
Показать решение
Задача 14. Упростите выражение:
Показать решение
Задача 15. Упростите выражение:
Показать решение
Задача 16.