Приведение дроби к наименьшему общему знаменателю: правила
Основное определение понятия общего знаменателя
Определение
Общий знаменатель значения — это любое из положительных данных числа, которое является кратным для всех значений дробей.
Иными словами, можно сказать, что общим знаменателем дроби, будет характеризоваться натуральное простое числовое значение. Оно должно делиться без остатка на все значения знаменателей данных дробей.
Натуральные числа имеют свойство бесконечности и поэтому ряд обыкновенных дробных значений имеет характерное множество общих значений знаменателя. Чтобы определить общий знаменатель для дроби, нужно применить его основное определение.
Рассмотрим два значения дробных выражений: 1/6 и 3/5
Общим дробным знаменателем будет являться любое число с положительным значением. Оно должно быть кратным значениям 6 и 5.
Перечислим подходящие значения: 30,35,65,95,125,155,185,215 и так далее.
Пример решения задачи данного типа: Зададим для решения три дробных значения: 1/321/65/12.
Их необходимо проанализировать и привести к общему знаменателю, который равняется 150.
Для этого нужно выяснить, делится ли 150 на все числовые знаменатели дроби и является для них кратным числом.
Это значит, что 150 должно без остаточного значения делиться на 3,6,12.
Составляем выражения и проводим вычисления: 150/3=50; 150/6=25; 150/12=12,5.
При делении на 12 получается остаточное значение.
Из этого следует, что число 150 не будет являтся общим кратным знаменателем, для заданных дробей.
Наименьший общий знаменатель дробей
Данное определение звучит следующим образом: минимальное значение числа, на которое можно разделить знаменатель дроби, обязательно без остаточного значения.
Аббревиатура данного значения, выглядит как НОК.
В определенном перечне числовых значений, которые являются общими знаменателями данных дробей, будет иметь место наименьшее простое значение.
Оно будет характеризоваться, как наименьший общий знаменатель. Сформулируем определение наименьшего общего знаменателя данных дробей.
Как правильно определить наименьший общий знаменатель числа дроби?
Так как НОК, будет иметь значение наименьшего положительного общего делителя данного набора чисел. Тогда НОК знаменателей любых дробей, представлен, как минимальный общий знаменатель дроби.
Из этого следует, что определение наименьшего знаменателя дроби, будет сводиться к определению НОК знаменателя дроби.
Рассмотрим данное правило на примере решения.
Пример:
Задано два значения дроби: 3/10 и 277/28
Знаменатели дробей равняются 10 и 28 соответственно.
Наименьший знаменатель будет определяться как НОК чисел 10 и 28.
Разложим числа на простые множители: 10=2*5, 28=2*2*7, следовательно, НОК (15 и 28)=2*2*5*7=140.
Ответ задачи: 140.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Приведение дробей к наименьшему общему знаменателю
Когда простые обыкновенные дроби, имеют одинаковые по значению знаменатели, то это характеризуется как дроби приведены к общему знаменателю.
Например: значения 45/76 и 143/76 приведены к общему знаменателю, числу 76. Рассмотрим еще несколько дробей. Рассмотрим еще несколько дробей 1/3, 3/3, 17/3 и 1000/3.
Все эти значения приведены к общему знаменателю 3.
В случае, если знаменатели дробных чисел, являются разными по значениям и не равны друг другу. Можно их привести к общему числовому знаменателю. Для этого значение числителя и знаменателя данных значений перемножим с дополнительным множителем.
Например: 2/5 и 7/4 — эти дроби имеют разные знаменатели, поэтому воспользуемся приведение к общему знаменателю, при помощи дополнительных множителей, а именно 4 и 5.
Применяя данные значения приведем и вычисления и получим общий множитель: значение равное 20. При перемножении числителя и знаменателя дроби 2/5 на значение равное 4, получим дробь вида 8/20.
Проводим аналогичные действия, но только с дробью При перемножении числителя и знаменателя дроби 7/4 на 5 и приведем ее к дроби вида 35/20 .
Теперь можно сформулировать определение, приведение дробей к общему знаменателю.
Приведение дробей к знаменателю одинаковых значений – это вычислительный процесс, который включает в себя: умножение числителей и знаменателей любых значений дробей на определенные значения дополнительных множителей, чтобы результаты проведенных вычислений получились дроби с одинаковыми знаменателями.
В математике существует правило, которое помогает привести дроби к общему наименьшему знаменателю.
Данное правило включает в себя три основных пункта.
Принцип приведения дробного значения к наименьшему общему знаменателю:
- Для начала определяется значение наименьшего общего знаменателя дробей.
- Затем для каждой дроби определяется дополнительный множитель.
Он должен соответствовать правилу: деление наименьшего общего знаменателя на знаменатель, каждой рассматриваемой при решении, дроби. - Перемножаем числитель и знаменатель на принятый дополнительный множитель.
Он должен соответствовать правилу: деление наименьшего общего знаменателя на знаменатель, каждой рассматриваемой при решении, дроби.Примеры решения задач, используя приведение к наименьшему знаменателю.
Пример №1:
Нужно привести к наименьшему знаменателю следующие дроби:
Для решения применим алгоритм решения, рассмотренный в вышеприведенном пункте.
Для начала определим наименьшее значение общего знаменателя, который равен минимальному и кратному числу 14 и 18.
Разложим значения знаменателей на множители: 14=2*7, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=126. Следующим шагом, будет вычисление дополнительных множителей. С их помощью приведем дробные значения 5/14 и 7/18 будут приведены к числу 126. Дробному значению 5/14 дополнительный множитель будет равняться 126/14=9.
Для значения второй дроби равной 7/18 аналогичный множитель будет равняться 129/18=7.
Числители и знаменатели дробей перемножаем на дополнительный множитель 9 и 7 соответственно.
Записываем следующие выражения:
\[ \frac{5}{14}=\frac{5 \cdot 9}{14 \cdot 9}=\frac{45}{126} \]
\[ \frac{7}{18}=\frac{7 \cdot 7}{18 \cdot 7}=\frac{49}{126} \]
Итоги проведенных вычислений: заданные дроби 5/14 и 7/18 приведены к общему знаменателю. Итоговое значение выражения: 45/26 и 49/126.
Пример №2:
Нужно привести к наименьшему знаменателю следующие дроби: 3/12 и 5/18. В этом примере, также применим алгоритм решения, состоящий из трех главным действий.
Используя алгоритм решения, определим наименьшее значение общего знаменателя, который равен самому минимальному значению и кратному числам 12 и 18.
Следующим шагом, разлом данные значения на множители: 12=2*6, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=216. Произведем вычисление дополнительных множителей. С их помощью приведем дробные значения
Данные значений дробей, нужно перемножить на дополнительный числовой множитель равный числам 9 и 7 соответственно. Подставим эти данные и вычислим составленные выражения.
Записываем следующие выражения:
\[ \frac{3}{12}=\frac{3 \cdot 9}{12 \cdot 9}=\frac{27}{108} \]
\[ \frac{5}{18}=\frac{5 \cdot 7}{18 \cdot 7}=\frac{35}{126} \]
Итоги проведенных вычислений: заданные дроби 5/14 и 7/18 не приведены к общему знаменателю.
Ответ: значение 216 не будет являться наименьшим общим знаменателем.
Аналогичным способом, используя алгоритм решения можно определить значение наименьшего знаменателя трех и более дробных значений.
Наибольший общий делитель чисел 14 и 35 (НОД 14, 35)
Вы ищете НОД чисел 14 и 35? Так как вы находитесь на этой странице, я так думаю! В этом кратком руководстве мы расскажем, как вычислить наибольший общий делитель для любых чисел, которые вам нужно проверить. Давайте прыгать!
Хотите быстро узнать или показать учащимся, как найти НГК двух или более чисел? Включи это очень быстрое и веселое видео прямо сейчас!
Во-первых, если вы торопитесь, вот ответ на вопрос «каков GCF 14 и 35?» :
GCF 14 и 35 = 7
Что такое наибольший общий делитель?
Проще говоря, GCF набора целых чисел — это наибольшее положительное целое число (т.
е. целое число, а не десятичное), которое без остатка делится на все числа набора. Он также широко известен как:
- Наибольший общий знаменатель (GCD)
- Наивысший общий множитель (HCF)
- Наибольший общий делитель (НОД)
Существует несколько различных способов расчета GCF набора чисел в зависимости от того, сколько чисел у вас есть и насколько они велики.
Для меньших чисел вы можете просто посмотреть на множители или кратные для каждого числа и найти их наибольшее общее кратное.
Для 14 и 35 эти коэффициенты выглядят следующим образом:
- Факторы для 14: 1, 2, 7 и 14
- Факторы для 35: 1, 5, 7 и 8 Когда вы перечислите делители каждого числа, вы увидите, что 7 — это наибольшее число, на которое делятся 14 и 35.
Простые множители
По мере того, как числа становятся больше, или если вы хотите сравнить несколько чисел одновременно, чтобы найти GCF, вы можете увидеть, что перечисление всех множителей стало бы слишком большим.
Чтобы исправить это, вы можете использовать простые множители.Перечислите все простые множители для каждого числа:
- Простые множители для 14: 2 и 7
- Простые множители для 35: 5 и 7
Теперь, когда у нас есть список простых множителей, нам нужно найти любые, которые являются общими для каждого числа.
В этом случае имеется только один общий простой делитель, 7. Поскольку других нет, наибольшим общим делителем является этот простой делитель:
GCF = 7
Найдите GCF с помощью алгоритма Евклида расчет GCF 14 и 35 заключается в использовании алгоритма Евклида. Это более сложный способ вычисления наибольшего общего множителя, который на самом деле используется только калькуляторами НОД.
Если вы хотите узнать больше об алгоритме и, возможно, попробовать его самостоятельно, загляните на страницу Википедии.
Надеюсь, сегодня вы немного изучили математику и поняли, как вычислять НОД чисел. Возьмите карандаш и бумагу и попробуйте сами.
(или просто используйте наш калькулятор GCD — мы никому не скажем!)Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте инструмент ниже, чтобы убедитесь, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Наибольший общий делитель чисел 14 и 35». VisualFractions.com . По состоянию на 25 апреля 2023 г. http://visualfractions.com/calculator/greatest-common-factor/gcf-of-14-and-35/.
«Наибольший общий делитель чисел 14 и 35». VisualFractions.com , http://visualfractions.com/calculator/greatest-common-factor/gcf-of-14-and-35/. По состоянию на 25 апреля 2023 г.
Наибольший общий делитель чисел 14 и 35.
VisualFractions.com. Получено с http://visualfractions.com/calculator/greatest-common-factor/gcf-of-14-and-35/.
GCF 35 и 14
На этой странице мы определим GCF 35 и 14, научим вас различным способам расчета GCF 35 и 14, и показать вам, для чего вы можете использовать GCF 35 и 14.
Что такое GCF 35 и 14?
GCF — это аббревиатура от Greatest Common Factor. Следовательно, GCF 35 и 14 совпадает с наибольшим общим делителем. 35 и 14. GCF 35 и 14 — это наибольшее натуральное число, на которое можно разделить как 35, так и 14. Кроме того, как 35, так и 14 имеют набор факторов, и GCF является наибольшим фактором, общим для 35 и 14.Сравните коэффициенты, чтобы получить GCF 35 и 14
Согласно приведенному выше определению, чтобы найти GCF 35 и 14, вы можете сравнить коэффициенты 35 с множители 14, чтобы увидеть, какой множитель больше. Когда мы это сделали, мы обнаружили что наибольший общий делитель (НОК) чисел 35 и 14 равен 7.Используйте НОК, чтобы получить НОД чисел 35 и 14
Наименьшее общее кратное (НОК) чисел 35 и 14 равно 70. Вы можете найти НОД чисел 35 и 14 путем деления произведения чисел 35 и 14 на НОК чисел 35 и 14. Вот формула и математика:Продукт 35 и 14 LCM 35 и 14 = GCF 35 × 14 70 = 7 Используйте компьютерную таблицу, чтобы получить GCF 35 и 14
Если у вас есть компьютер, вы также можете использовать электронную таблицу в Excel или Numbers для расчета GCF 35 и 14. Вы хотите ввести
=gcf(35, 14) в ячейку, чтобы получить ответ.gcf(35, 14) = 7
Используйте GCF 35 и 14, чтобы упростить дробь
GCF 35 и 14 можно использовать для многих целей. Вы можете, например, упростить дробь, разделив числитель и знаменатель на GCF выглядит следующим образом:35 ÷ 7 14 ÷ 7 = Используйте GCF, равный 35 и 14, для упрощения отношения
Аналогично, вы можете использовать GCF, равный 35 и 14, для упрощения отношения, разделив каждую часть отношения на= 35 : 14
= (35 ÷ 7) : (14 ÷ 7)
= 5 : 2Используйте НОК 35 и 14, чтобы найти НОК 35 и 14
Поскольку использование наименьшего общего кратного (НОК) является одним из способов найти НОК 35 и 14, вы можете использовать НОК 35 и 14, чтобы найти НОК 35 и 14. МОК 35 и 14 можно, например, использовать для сложения и вычитания дробей со знаменателем 35 и 14.
НОК 35 и 14 – это произведение 35 и 14, деленное на НГК 35 и 14. Вот математика:Продукт 35 и 14 GCF 35 и 14 = LCM 35 × 14 7 = 70 Вот и все! Мы надеемся, что эта страница выполнила свою задачу по определению GCF 35 и 14, показав вам, как рассчитать GCF, примеры его использования и его отношение к LCM.
Чтобы исправить это, вы можете использовать простые множители.
(или просто используйте наш калькулятор GCD — мы никому не скажем!)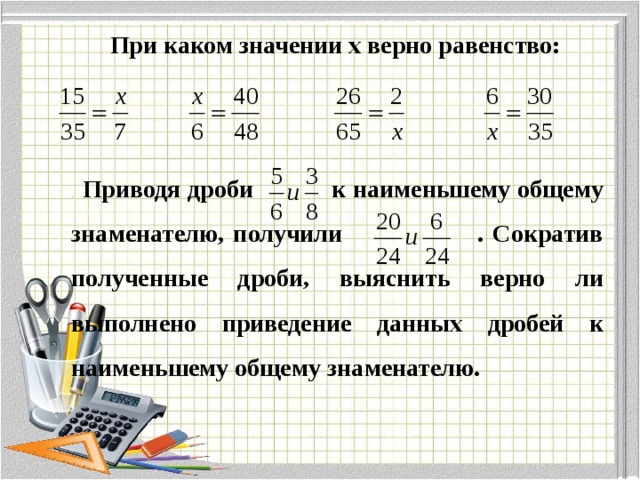
VisualFractions.com. Получено с http://visualfractions.com/calculator/greatest-common-factor/gcf-of-14-and-35/.
Вы хотите ввести
=gcf(35, 14) в ячейку, чтобы получить ответ.
МОК 35 и 14 можно, например, использовать для сложения и вычитания дробей со знаменателем 35 и 14.
НОК 35 и 14 – это произведение 35 и 14, деленное на НГК 35 и 14. Вот математика: